Abstract
Advances in network technology have enhanced the concern for network security issues. In order to address the problem that hopping graph are vulnerable to external attacks (e.g., the changing rules of fixed graphs are more easily grasped by attackers) and the challenge of achieving both interactivity and randomness in a network environment, this paper proposed a scheme for a dynamic graph based on chaos and cryptographic random mapping. The scheme allows hopping nodes to compute and obtain dynamically random and uncorrelated graph of other nodes independently of each other without additional interaction after the computational process of synchronous mirroring. We first iterate through the chaos algorithm to generate random seed parameters, which are used as input parameters for the encryption algorithm; secondly, we execute the encryption algorithm to generate a ciphertext of a specified length, which is converted into a fixed point number; and finally, the fixed point number is mapped to the network parameters corresponding to each node. The hopping nodes are independently updated with the same hopping map at each hopping period, and the configuration of their own network parameters is updated, so that the updated graph can effectively prevent external attacks. Finally, we have carried out simulation experiments and related tests on the proposed scheme and demonstrated that the performance requirements of the random graphs can be satisfied in both general and extreme cases.
1. Background
Cyber security has recently become a more severe concern, with cyber security breaches contributing to an increase in cyber assaults. According to a Bloomberg story and two people familiar with the situation, Colonial Pipeline, the largest operator of refined oil pipelines in the United States, paid a ransom of roughly USD 5 million in untraceable cryptocurrency to Eastern European hackers on 7 May 2021. On 14 May 2021, Ireland’s health sector declared that the healthcare delivery system had been shut down as a matter of urgency, and that various hospital operations had been impacted owing to repeated severe ransomware assaults on the network. This is the second cyber security crisis triggered by a hacking attempt since May 7, when Colonial Pipeline, the largest gasoline pipeline operator in the United States, was hacked and its major transmission trunk line was shut down.
Traditional network defense methods such as signatures, access control, security vulnerability screening, firewalls, and intrusion detection have all been created in response to common network attacks by hackers such as Trojan horses, worms, viruses, and DoS. These defense technologies have significantly enhanced network defense and have become the industry standard for network security defense. However, as network assaults progress, they become increasingly ineffective in the face of attacks such as Trojan port hopping, proxy hopping, protocol translation attacks, DDoS attacks, and other unknown attacks. The US Department of Defense-led APOD project study has introduced the notion of Moving Target Defense (MTD) [1,2,3,4,5], which gives a new technological approach to defend these new forms of assaults. Unlike earlier theories in cyber security, MTD is committed to creating a dynamic, diverse, and uncertain network, known as a hopping network, that may avoid, delay, or stop cyber assaults by increasing the system’s unpredictability or decreasing its predictability. This technique is called dynamic or active defense because it breaks from the standard defense idea of “static defense” against specific assaults, while remaining effective against some unknown threats. According to popular opinions, a genuinely powerful network defense must rely on a combination of active and passive defenses.
As previously stated, network active defense systems are based on hopping networks and are capable of preventing, delaying, or blocking network assaults; therefore, hopping networks have been the most popular area of cybersecurity study. Early research efforts concentrated on how to implement network hopping and improve its security, and people have achieved notable results. To mitigate DoS attacks, Zhang et al. [6] presented a port hopping strategy based on an SDN network. Port hopping strategies for SDN-based networks are somewhat overwhelming in the face of multiple network attacks. Chang et al. [7] advocated an IP address randomization for SDN. In addition, in order to further improve port and IP address defense techniques, Luo et al. [8] proposed a port and address hopping mechanism, known as Random Port and Address Hopping (RPAH). In order to apply active defense technology to physical addresses, [9] proposed a scheme deploying MAC address randomization to protect user privacy and prevent adversaries from tracking persistent hardware identifiers. To increase the security of data transmission, [10,11,12,13] introduced the network hopping technique to increase packet transmission security. Chang et al. [14] presented a resource-based channel access strategy that keeps the attacker responsible for channel reservations. Because of the restricted mutation space and speed, Al-shaer et al. [15] proposed a revolutionary transparent IP mutation approach that enables high-speed and unexpected IP mutation while preserving active session integrity and minimal overhead. Since sophisticated worms that utilize precomputed hitlists of vulnerable targets are particularly difficult to handle, Antonatos et al. [16] developed a novel proactive defensive technique called Network Address Space Randomization (NASR) with the goal of hardening networks specifically against hitlist worms. Because of the way IPv6 addresses are created, privacy-related crimes are easier to commit in Ipv6. Dunlop et al. [17] presented a Moving Target Ipv6 Defense (MT6D) that takes use of Ipv6′s massive address space. A broad class of security exploits take use of software implementation flaws such as uncontrolled buffers.
As defense technologies improve, the research emphasis is shifting to the security and other performance impacts of hopping networks on traditional networks, as well as how to mitigate them. According to research, the major impact on the hopping network’s performance is that an attacker can step on, scan, or follow the network parameters (IP, port, and so on) to grasp the pattern of operation and wait for a chance to launch an assault. Second, hopping networks crowd out resources to some extent. In order to accomplish network hopping, additional system resources must always be consumed that is resulting in a decrease in network transmission performance.
The key to resisting network attacks is that the network parameters change faster than the attacker’s reaction time. In a hopping network, the change of network parameters needs to meet two basic requirements: firstly, the nodes need to constantly change their network parameters to hide themselves, which also makes the change rules less likely to be tracked by attackers, or the cost of tracking the change rules is very high; secondly, the change of network parameters of each node must be consistent with the change of network parameters of other nodes to ensure the normal communication between nodes.
There are various approaches to satisfy the above basic requirements for network parameter changes, the most representative of which is fixed graph. The basic idea is to combine a pre-programmed sequence of all node network parameter changes into a two-dimensional parameter table, which is sent to all nodes one by one before the network hopping, and to configure the nodes according to this parameter table. Fixed graph are simple to apply and do not require interaction, but by intercepting packets and analysing the pattern of network parameter changes, an attacker may master some or all of the network parameters, thus invalidating fixed graphs in network defence. Although network assaults can be monitored by network-aware techniques in order to switch to a new fixed graph before an attack, in essence, the attacker may still discover the rules of change in the fixed graph by tracking and analysing it over time.
Compared to fixed graph, random graph has uncertain change rules, so people have focused on studying random graph. The idea of random mapping is to randomly combine sequences of network parameter changes into a two-dimensional parameter table, the length of which is theoretically approximately infinite, with obvious advantages: the change pattern is uncertain and therefore not easy to be tracked and analysed; and it is also appropriate for general network environments. However, random graph can be challenging to implement in a general network environment, and the challenges are in four main aspects.
- (1)
- Non-interactivity: since network parameters are spontaneously and randomly changed, it is difficult to connect and communicate data with other nodes without exchanging one’s own network parameters with those of other nodes.
- (2)
- Randomness: Because chaotic algorithms and linear shift registers have randomness over small sets and may have mapping degeneracy problems over infinitely large sets, it may be hard to satisfy the requirement that random graph whose length is approximately infinite in theory also have randomness.
- (3)
- Uncorrelatedness: As the attacker is likely to have the ability to infer the previous or next network parameters by the change pattern of the current network parameters, and may also have the ability to infer the change rule of the network parameters of other nodes, the random graph has to satisfy the requirement that each column element and each row element are uncorrelated with each other when it is dynamically generated.
- (4)
- Distributivity: Since the network hopping is generally carried out in a multi-node network environment, the requirement of dynamically generating the same random map on multiple hosts in different locations needs to be satisfied.
To address the above challenges, this paper presents a dynamic random graph based on chaos and cryptographic mapping. Firstly, the calculation is carried out using the mirroring principle to achieve the non-interactivity requirement of the random graph. Secondly, the same system and algorithm parameters are initialized simultaneously to satisfy the distributivity in a trusted network environment, then the chaos and cryptographic algorithms are used to achieve the randomness and irrelevance requirement of the random graph through random mapping. Finally, the collision algorithm is used to ensure that the randomly generated graph elements are not identical under the time synchronisation mechanism. The contributions of this paper are mainly the following three points.
- (1)
- We propose the idea of mapping chaos to cryptography and mathematically show that cryptographic ciphertexts have very good randomness and security.
- (2)
- We present a random graph scheme (CandCRM) based on chaos and cryptographic mapping. the random graph generated by CandCRM is effective against network attacks due to its excellent randomness and non-correlation.
- (3)
- The CandCRM scheme has good application. In a hopping network, it is suitable for deployment on multiple hopping hosts operating independently with little interaction between hosts.
The first section is an introduction that briefly discusses the thesis’ history, as well as the important work done by relevant researchers, and outlines the motivation and main contributions of the article. The second section provides the basic model of random graphs as well as the problem description. The design of the dynamic spectral map is presented in Section 3. The findings of the simulated experiments are presented in Section 4. An analytical overview is provided in Section 5.
2. Solution Design
In order to address the shortcomings of fixed graph (R = (xij)z×n), we propose a random graph protection solution based on chaotic and cryptographic random mapping. The overall solution framework is shown in Figure 1 and consists of three parts: (1) system initialization; (2) random graph calculation; (3) update of network parameters. Firstly, the system initialization comprises the initialization of the total controller and nodes, including the assignment time period (T), the initial value (μ, X0) of logistic mapping, the initial value of the encryption algorithm (key sequence K = {k0, k1, ki,…, kθ}), and the set of candidate network parameters (V = {vi |0 ≤ I ≤ + Z}), as shown in steps ① and ③ of Figure 1. Next, the listener program is always listening and once the start synchronization signal is received, the hopping period (T − 0.1~T + 0.1) is started and timed while the random graph is being calculated, as shown in step ⑤.
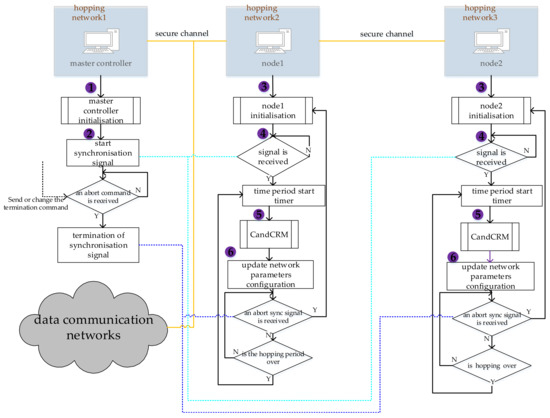
Figure 1.
Framework of dynamic graph solution based on chaos and encrypted mapping.
2.1. Chaos and Cryptographic Random Mapping (CandCRM) Algorithm
In a hopping network, we need to change the network parameters periodically, and the way to do this is usually to call a random number function directly. The random number function is actually a pseudo-random number function, so it is not ideal for randomising the set of network parameters. Chaos algorithms have very good randomisation properties and are more effective in randomising the set of network parameters. Therefore, the chaos algorithm is currently a better choice. However, its possible that in a few cases, chaotic algorithms may lead to uneven output results due to initial value length limitations or chaotic degeneracy properties. This can affect the effectiveness of the chaotic algorithm for mapping the set of network parameters. Existing mature encryption algorithms [18] have decent randomness, irrelevance, confidentiality, and irreversibility when the encryption key is large enough (Figure 2), so we have considered using existing mature encryption algorithms to implement random mapping, but it requires request and interaction without good non-interactivity during the task. Therefore, in this paper, we propose the improved encryption algorithms, i.e., the chaotic and cryptographic random mapping (CandCRM) algorithm (Figure 3) where the CandCRM is based on Enck(m) (m = Xi, k = ki) for encryption mapping, the plaintext Xi is a chaotic sequence, and the encryption secret key ki is also a chaotic sequence, so that it satisfies the requirements of randomness, irrelevance, non-interactivity, and distribution at the same time.
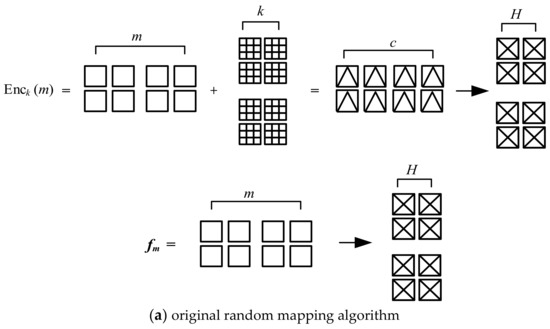
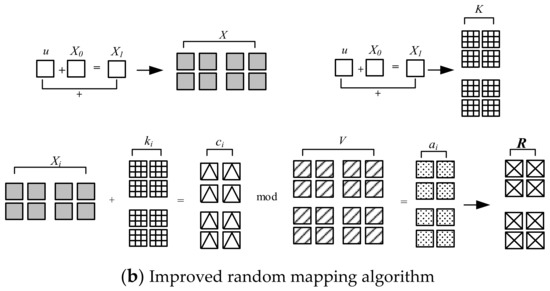
Figure 2.
(a,b) Comparison of two random mapping algorithms.
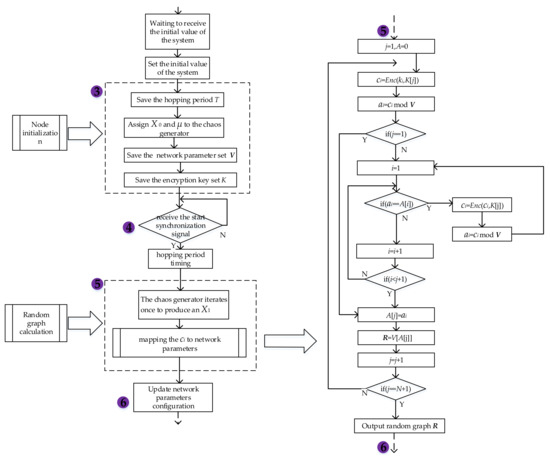
Figure 3.
CandCRM algorithm framework.
To illustrate the improved encryption algorithm with randomness and irrelevance, the following two assumptions need to be satisfied: (1) assume that the input parameters of the encryption algorithm are chaotic sequences, denoted as X = {Xi|1 ≤ i ≤ θ} and K = {ki|1 ≤ i ≤ θ}, and that the chaotic sequences satisfy the randomness and irrelevance requirements; and (2) assume that the encryption algorithm satisfies cryptographic security.
Firstly, for randomness, mainly synchronous mirroring technique is used, i.e., the same initial parameters and chaotic algorithms are used to generate random sequences, after which cryptographic algorithms are introduced to improve the randomness and non-correlation of the cipher text generated by chaotic sequence encryption while maintaining uniformity. The encryption algorithm Enck(m) encrypts the chaotic sequence item Xi and the secret key (ki) to generate the cipher text (ci), then modulo V using ci (first collate ci as a fixed number of points) to obtain the modulus (ai), then match ai with the subscript of V elements to obtain the element corresponding to the subscript of V, and write it as ri = V[ai], and check whether the current matched element collides with the already matched element, if so, regenerate X, and encrypt, modulo and map again until no more collision occurs (see Algorithm 1).
Second, because chaotic sequences are random and uncorrelated, the cipher text ci generated by the encryption algorithm Enck(m) is random and uncorrelated. In terms of the law of probability distribution, when because the probability distribution of the input chaotic sequences is uniform, random and uncorrelated, after encrypting them, then the probability distribution of the output cipher text is similarly uniform when random, as stated in Theorems 1 and 2.
Theorem 1
([19]). Suppose that g(x) is an invertible function. Let X be an element on the domain of definition of g. X is randomly selected according to uniform distribution (that is, X is a random variable), then the corresponding output g(x) is random and uniformly distributed in the elements of the upper domain.
Proof of Theorem 1.
Assume that b is any element in the above domain, and according to the definition of the inverse function g−1 of g, the element g(x) of the random above domain is equal to b as long as the element X of the random definition domain is equal to g−1(b). The probability of X = g−1(b) is 1 divided by the number of elements of the definition domain, so the probability of g(X) = b is also 1 divided by the number of elements of the definition domain. □
Theorem 2
([19]). Define the function fclear = m(k) as fclear = m(k) = f(m,k) for each plaintext m, if the function fm is invertible for each plaintext m, then the cryptosystem using the encryption function f is perfectly confidential.
Proof of Theorem 2.
The encryption key k is chosen randomly according to a uniform distribution, such that m denotes a plaintext. The cipher text is a random variable fm(k). By Theorem 1, the probability distribution of this random variable is uniform. □
Finally, time synchronization mechanism and mirroring technique are used to achieve non-interactivity and distribution. The basic idea of mirroring technique is to setup consistent system initial values, control parameters, and encryption algorithms in the trusted environment where the distributed nodes are located.
The CandCRM algorithm can resolve the shortcomings of the original random mapping algorithm, and also has the following capabilities.
- (1)
- Improved non-interactivity capability in a network environment. The traditional random mapping algorithm is more commonly used in the case of interaction, while the improved algorithm requires almost no interaction, and it satisfies the randomness of random mapping in both space and time.
- (2)
- It has improved the resistance to network attacks, such as resistance to known plaintext and cipher text attacks, key attacks, etc. Since the chaotic sequence generated by the chaotic algorithm itself has randomness, when the terms of the chaotic sequence are used as plaintext and cipher text, the probability distribution of the cipher text generated by encrypting the plaintext and the key multiple times is uniform and random, so it can effectively defend against network assault.
2.1.1. CandCRM Algorithm Implementation
The CandCRM algorithm (Algorithm 1) is implemented by generating chaotic sequences in both space and time and encrypting the chaotic sequences with a random mapping of the resulting cipher text. First, logistic mapping generates chaotic sequence X = {X1,…,Xi,…,Xθ}, Enck(Xi) encrypts Xi, generates cipher text ci, and collates ci into fixed points, modulo cipher text ci with V, i.e., ai = Mod(ci,V), chooses the corresponding element V[ai] from the set of network parameters V = {V1,V2,…, VN}, ai =1,…,N, R + = V[ai], and eliminates V[ai] from V. Finally, R is output.
| Algorithm 1 CandCRM algorithm |
| Input: array A = {a1, a2,…, an}, i, j, X, V, ki; else then let i = i + 1.; |
| Output: R; |
| Initialization, j = 1, A = 0, ci = 0; |
| 1: Compute the cipher text ci = Enck(X[j]), ai = Mod(ci,V); |
| 2: If j = = 1, then execute step 6. |
| else then execute step 3. |
| 3: i = 1; |
| 4: If (ai = A[i]) = = 1, then compute ci = Enck(X[j]), ai = Mod(ci,V) and return to perform step 3. |
| 5: if (i < j + 1) = = 1, execute step 6. |
| else then execute step 4: |
| 6: j = ai, R = V[A[j]], j = j + 1; |
| 7: if (j = N + 1) = = 1, then output R |
| else return to execution step 1. |
2.1.2. Security Analysis
The random graph security problem primarily refers to the fact that dynamically constructed random graphs are not vulnerable even when attackers are aware of them. The following are the major components of dynamic random graph security analysis for typical network threats.
- (1)
- Irreversibility
Theorem 3.
Assuming the attacker has a random graph R, inferring the latest periodic element hi,j−1 from the current element hij is difficult because the computational complexity of inferring hi,j−1 is 2O(2l) (where, l is the word length of secret key).
Proof of Theorem 3.
If the attacker only obtains R, hi,j−1 can only be deduced using exhaustive method, and the computational complexity of cryptographic random mapping for hi,j are 2O(2l). It is difficult to obtain hi,j−1 in polynomial time, so it is difficult to introduce hi,j−1 based on hi,j, and thus has irreversibility. □
- (2)
- Unpredictability
Theorem 4.
Assuming that the attacker obtains the random graph R, it is difficult to predict the elements hi,j+1 in the next period based on the current elements hi,j, because the computational complexity of hi,j+1 is estimated to be 2O(2l).
Proof of Theorem 4.
If the attacker obtains hi,j, hi,j+1 can only be inferred by exhaustive method, and the computational complexity of cryptographic random mapping of hi,j is also 2O(2l). It is difficult to obtain hi,j+1 in polynomial time, so it is difficult to predict hi,j+1 and thus possesses unpredictability. □
- (3)
- Resistance to external and internal attacks. The hopping network has its own characteristics to actively resist various external attacks such as DoS, DDoS, and traffic analysis, and random graph R can resist both external and internal attacks. In addition, assuming that the algorithm operates in a TrustZone environment with secure hardware and the initial values of the algorithm are passed in a secure channel, the internal attack is mainly on the random graph itself, and according to Theorems 3 and 4 above, the attacker cannot infer the value of the previous period from the current value of the random graph, nor can he predict the value of the next period, so the random graph can defend against the internal attack in this case. The random graph is thus resistant to internal attacks in this case.
3. Experimental Analysis
3.1. Data set and Environment Description
The method in this paper is experimented on two types of data. One is to simulate network parameters’ IP data packets and ports. The data of the port can be expressed as V = {vi}, i = 1, …, 256 and vi is enumeration type values, the other is a set of pseudo random sequences, expressed as Y(t) = {Y1(t), Y2(t), …, Y10(t), t∈T}, Y1(t), Y2(t), …, Y10(t).
Our experiments are performed on a PC with Intel Core i5-8500 CPU @ 3.00 GHz and 8 GB RAM and operating system Windows 10. In our experiments, firstly, the chaos sequence is based on the Logistic Algorithm Generator implementation. Secondly the encryption of the pseudo-random sequence is based on the RC4 encryption algorithm generator. Finally, the random mapping of the ciphertext is performed by MATLAB’s own modulo operation function, mod. The experimental processes and results are programmed in MATLAB language at MATLAB R2017b.
3.2. Parameter Setting and Evaluation Index
The random graph can be obtained by cryptographic mapping of chaotic sequences, and the relevant indicators of the random graph are as follows.
- (1)
- Balance check: the balance reflects the uniform distribution of the random sequence, so it is necessary to check whether the balance of the random sequence is reasonable, that is, to check the difference between the “maximum” and “minimum” values in the sequence, the formula is:
Among them, the number of “maximum” and “minimum” in the random sequence is denoted as n0 and n1, respectively, n = n0 + n1. The calculated value is compared with the χ2 value with 1 degree of freedom, and the significant effect is taken as a = 0.05 in the test. From the χ2 distribution table, it can be found that the χ2 value with a significant effect of 0.05 is 3.841. If the calculated value is less than 3.841, the random graph passes the balance check.
- (2)
- The variance checks, as an indicator of the equilibrium check of the random series, is given by:
- (3)
- The autocorrelation checks, which can be expressed as an autocorrelation function, is given by:
- (4)
- The cross-correlation check, which can be expressed as an autocorrelation function, is given by:
In a general hopping network, the period of network hopping is T (1 × 105 ms). In the simulated experimental environment, one iteration of the algorithm corresponds to one hopping period. In the experiments, CandCRM was performed for 1 × 104 iterations with different initial values and different control parameters, and the vi frequency as well as the frequency was counted. In Figure 4, the results show that the frequencies and frequencies maintain a uniform distribution. On the basis of the above statistical results, we made the following additional check:
Figure 4.
Frequency and frequency comparison under different parameters: (a,c) frequency comparison of network parameters, (b,d) comparison of frequency statistics.
3.2.1. Balance Check
The equilibrium check is the most basic randomness check, and thus we use different control parameters to check the equilibrium of the results generated by CandCRM. The results of the balance check for Y (Figure 5) where the values of Y1(t), Y2(t), …, Y10(t) are much lower than the reference value of 3.841 for the initial values X0 = 0.35 and X0 = 0.36 and the control parameters μ = 3.7 and μ = 3.8, which indicates the balance effect of CandCRM well. In addition, we compare CandCRM with three other network parameter mapping methods, which are m-linear shift register (m-LSR) based on m-sequence [20,21,22], pseudo-random number generator (PRNG) [23], and function f(Ni,k) of the network parameter randomization method [24]. The experimental comparison results are shown in Figure 6. Compared with the remaining three methods, the method in this paper has obvious advantages in terms of balance.
Figure 5.
(a,b) Comparison of balance check results.
Figure 6.
(a,b) Comparison of balance check results between different methods. (a,b) Comparison of variance levels between different methods.
3.2.2. Variance Check
After 1 × 104 iterations of CandCRM were completed, we counted the frequency of each network parameter (vi) and the variance of the frequency, as shown in Figure 7 and Figure 8. The results show that the mean values of the frequencies of the network parameters are equal for different initial values and different control parameters. Also, variance tests were performed on the frequencies at different initial values and different control parameters, and the frequencies of the network parameters deviate from their means to a lesser extent and are generally smooth.
Figure 7.
(a,b) Comparison of variance check results.
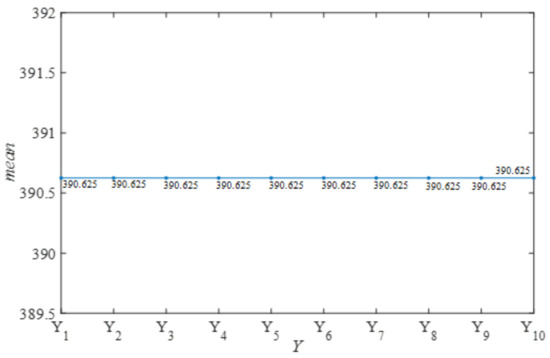
Figure 8.
X0 = 0.35 and X0 = 0.36, mean values at μ = 3.7 and μ = 3.8.
3.2.3. Autocorrelation Check
CandCRM complete 1 × 104 iterations to generate 256 network parameters (ri) for Y1(t), Y2(t), …, Y10(t), respectively, and to check the level of autocorrelation between these elements, we carry out an autocorrelation correlation check. As shown in Figure 9, the autocorrelation levels of these random variables are always below 0.15 for different initial values and different control parameters, indicating that they pass the autocorrelation test.
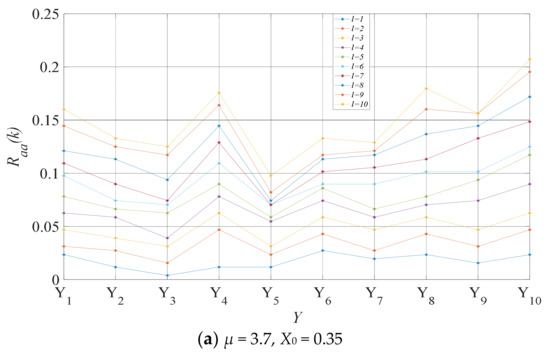
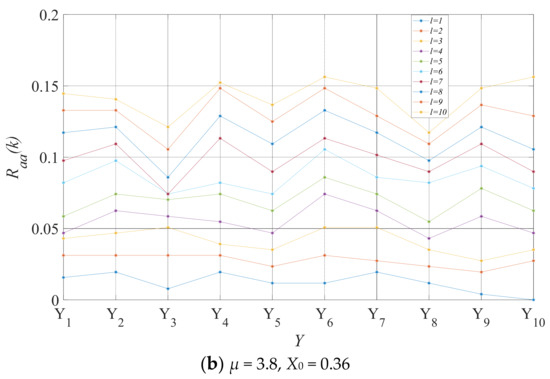
Figure 9.
(a,b) Comparison of autocorrelation check results.
3.2.4. Cross-Correlation Check
Similarly, after passing the above autocorrelation check, we examine the mutual correlation of the 256 networks, as shown in Figure 10. The results show that when the displacement length is 0, the level of cross-correlation of these random variables is very low. In addition, as shown in Figure 10c,d, when the displacement length is 1 ≤ l ≤ 10, the mean value of the uncorrelation is below 0.15, and all of them pass the cross-correlation check.
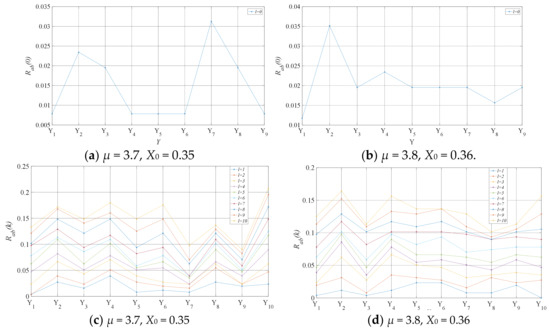
Figure 10.
(a,b) Comparison of check results Rab(0); (c,d) Comparison of intercorrelation check results Rab(l).
Since the pseudo-random sequence Y(t) has passed the balance, autocorrelation, and cross-correlation checks, it illustrates that CandCRM may generate random sequences satisfying the requirements of randomness, autocorrelation, and cross-correlation. Although the nodes are located in different geographic regions and at different times, CandCRM can generate random graph that satisfy randomness, non-interactivity, distribution, and uncorrelatedness dynamically by setting the same initial system values and different control parameters.
4. Discussion
Equilibrium Check in Extreme Cases
The chaotic nature of logistic mapping and the properties of finite precision implementations can produce degeneracy. Based on the characteristics of degeneracy of logistic mapping, the random properties of logistic mapping algorithms (LMAs) [25] and CandCRM schemes are compared. First, the initial values X0 = 0.38 and µ = 4.0 are set as the initial values of the LMAs and the initial values of the logistic mapping generator in the CandCRM scheme. Next, iterate through the LMAs and the logistic mapping generator 1 × 107 times, respectively. It should be noted that starting from the uneven results generated by the LMAs and the logistic mapping generator, the output values of the LMAs are modelled directly to V, from which the corresponding values are obtained through the modelling results. The values generated by the iterations of the logistic mapping generator are used as parameters of the encryption algorithm in the CandCRM, and the cipher text is encrypted with the parameters and processed into fixed-point numbers, and the fixed-point numbers are used to modulo V. The values are obtained from V through the modulo results. The statistical values are shown in Figure 11 and the results show that CandCRM is better balanced than LMAs.
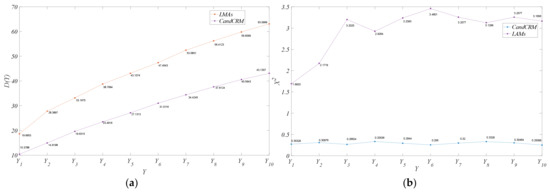
Figure 11.
(a,b) Comparison of balance levels and variance between CandCRM and LMAs. (a) Comparison of balance level between CandCRM and LMAs, (b) comparison of variance between CandCRM and LMAs.
5. Conclusions and Future Research
In this paper, we construct a CandCRM scheme based on chaotic sequences and cryptographic mapping. A series of experiments were conducted to test the validity and reliability of CandCRM. In the experiments, the equilibrium level is well below 3.81 and lower than that of other methods, followed by autocorrelation and intercorrelation levels below 0.15. Furthermore, CandCRM has good stochasticity despite the kinetic degradation of the logistic algorithm. Thus, CandCRM has excellent balance, autocorrelation, and intercorrelation. This is because the pseudo-random sequence itself has a long and controllable period, is well balanced, and has no correlation. The pseudo-random sequence obtained by combining the chaotic sequence with the initial value of the system in an encrypted manner combines the advantages of balance, non-correlation, and confidentiality of the chaotic sequence and the encryption algorithm, and overcomes the drawbacks of both in practical applications where extreme situations such as dynamics degradation and leakage of encrypted information may occur. In summary, CandCRM is well suited for generating dynamic random graphs. When the network nodes change with the random graph, no interactivity is required for communication between the network nodes and the random graph is suitable for hopping networks in general.
The first suggestion for future research is related to the latter discussion regarding the rationality of the set of network parameters. In CandCRM, we propose the idea of randomly mapping a larger set of network parameters and using the result of the mapping as the network parameters for the network hopping nodes. This has the advantage of being simple to use and easy to manage (only a little anti-collision detection is needed at the time of mapping), and the control node only needs to distribute the set of network parameters to each node once during system initialisation. However, there is a downside: if one of the nodes is attacked, it is possible to leak the network parameters of the other nodes. Therefore, a second suggestion for future research is that we would set up many small sets of network parameters. In CandCRM, the control node sends the system parameters and the small set of network parameters to each node, and CandCRM only maps the small network parameters and uses the result as its own network parameters, so that even if the node is attacked, it is not possible to leak the network parameters of the other nodes. In addition, we will continue to evaluate the balance and relevance of CandCRM.
Author Contributions
All authors reviewed the literature, drafted the manuscript, and critically revised and approved the final version before submission. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China. Funding number: 41971407.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jajodia, S.; Ghosh, A.K.; Swarup, V.; Wang, C.; Wang, X.S. (Eds.) Moving Target Defense: Creating Asymmetric Uncertainty for Cyber Threats; Springer Publishing Company: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Carvalho, M.; Ford, R. Moving-target defenses for computer networks. IEEE Secur. Priv. 2014, 12, 73–76. [Google Scholar] [CrossRef]
- Gao, C.; Wang, Y.; Xiong, X.; Fysarakis, K. A Cyber Deception Defense Method Based on Signal Game to Deal with Network Intrusion. Secur. Commun. Netw. 2022, 2020, 3949292. [Google Scholar] [CrossRef]
- Cai, G.L.; Wang, B.S.; Wang, T.Z.; Luo, Y.; Wang, X.; Cui, X. Research and development of moving target defense technology. J. Comput. Res. Dev. 2016, 53, 968. [Google Scholar]
- Maleki, H.; Valizadeh, S.; Koch, W.; Bestavros, A.; van Dijk, M. Markov modeling of moving target defense games. In Proceedings of the 2016 ACM Workshop on Moving Target Defense, Vienna, Austria, 24 October 2016; pp. 81–92. [Google Scholar]
- Zhang, L.; Guo, Y.; Yuwen, H.; Wang, Y. A port hopping based dos mitigation scheme in sdn network. In Proceedings of the 2016 12th International Conference on Computational Intelligence and Security (CIS), Wuxi, China, 16–19 December 2016; pp. 314–317. [Google Scholar]
- Chang, S.-Y.; Park, Y.; Babu, B.B.A. Fast IP hopping randomization to secure hop-by-hop access in SDN. IEEE Trans. Netw. Serv. Manag. 2018, 16, 308–320. [Google Scholar] [CrossRef]
- Luo, Y.-B.; Wang, B.-S.; Wang, X.-F.; Hu, X.-F.; Cai, G.-L.; Sun, H. Rpah: Random port and address hopping for thwarting internal and external adversaries. In Proceedings of the 2015 IEEE Trustcom/BigDataSE/ISPA, Helsinki, Finland, 20–22 August 2015; Volume 1, pp. 263–270. [Google Scholar]
- Fenske, E.; Brown, D.; Martin, J.; Mayberry, T.; Ryan, P.; Rye, E. Three years later: A study of mac address randomization in mobile devices and when it succeeds. Proc. Priv. Enhancing Technol. 2021, 2021, 164–181. [Google Scholar] [CrossRef]
- Hong, S.; Xu, L.; Wang, H.; Gu, G. Poisoning network visibility in software-defined networks: New attacks and countermeasures. In Proceedings of the NDSS, San Diego, CA, USA, 8–11 February 2015; Volume 15, pp. 8–11. [Google Scholar]
- Albanese, M.; Benedictis, A.D.; Jajodia, S.; Sun, K. A moving target defense mechanism for manets based on identity virtualization. In Proceedings of the Communications & Network Security, Berlin, Germany, 4–8 November 2013. [Google Scholar]
- Xu, J.; Kalbarczyk, Z.; Iyer, R.K. Transparent runtime randomization for security. In Proceedings of the 22nd International Symposium on Reliable Distributed Systems, Florence, Italy, 6–8 October 2003. [Google Scholar]
- Park, Y.; Chang, S.-Y.; Krishnamurthy, L.M. Watermarking for detecting freeloader misbehavior in software-defined network. In Proceedings of the International Conference on Computing, Greater Noida, India, 29–30 April 2016. [Google Scholar]
- Chang, S.-Y.; Hu, Y.-C.; Liu, Z. Securing wireless medium access control against insider denial-of-service attackers. In Proceedings of the 2015 IEEE Conference on Communications and Network Security (CNS), Florence, Italy, 28–30 September 2015; pp. 370–378. [Google Scholar]
- Al-Shaer, E.; Duan, Q.; Jafarian, J.H. Random host mutation for moving target defense. In Proceedings of the International Conference on Security and Privacy in Communication Systems, Padua, Italy, 3–5 September 2012; pp. 310–327. [Google Scholar]
- Antonatos, S.; Akritidis, P.; Markatos, E.P.; Anagnostakis, K.G. Defending against hitlist worms using network address space randomization. Comput. Netw. 2007, 51, 3471–3490. [Google Scholar] [CrossRef]
- Dunlop, M.; Groat, S.; Urbanski, W.; Marchany, R.; Tront, J. Mt6d: A moving target ipv6 defense. In Proceedings of the 2011-MILCOM 2011 Military Communications Conference, Baltimore, MD, USA, 7–10 November 2011; pp. 1321–1326. [Google Scholar]
- Qiao, L.; Nahrstedt, K. Comparison of MPEG encryption algorithms. Comput. Graph. 1998, 22, 437–448. [Google Scholar] [CrossRef]
- Ellis, S.R. A Cryptography Primer. In Computer and Information Security Handbook; Morgan Kaufmann: Burlington, MA, USA, 2013; pp. 25–46. [Google Scholar]
- Tyagi, A.; Pandey, N.; Gupta, K. PFSCL based Linear Feedback Shift Register. In Proceedings of the International Conference on Computational Techniques in Information & Communication Technologies, New Delhi, India, 11–13 March 2016. [Google Scholar]
- Wang, L.T.; McCluskey, E.J. Linear feedback shift register design using cyclic codes. IEEE Trans. Comput. 1988, 37, 1302–1306. [Google Scholar] [CrossRef]
- Jetzek, U. Galois Fields, Linear Feedback Shift Registers and Their Applications; Carl Hanser Verlag: Munich, Germany, 2018; pp. 59–80. [Google Scholar]
- Marinet, F. Pseudo-Random Number Generator. U.S. Patent US20010023423A1, 13 March 2001. Publication number: EP1143616A1. [Google Scholar]
- Lee, H.C.J.; Thinh, V.L.L. Port hopping for resilient networks. In Proceedings of the IEEE 60th Vehicular Technology Conference, 2004, VTC2004-Fall, Los Angeles, CA, USA, 26–29 September 2004. [Google Scholar]
- Chen, D.; Qing, D.; Wang, D. AES Key Expansion Algorithm Based on 2D Logistic Mapping. In Proceedings of the 2012 Fifth International Workshop on Chaos-Fractals Theories and Applications (IWCFTA), Dalian, China, 18–21 October 2012. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).