Extensions of the Maximum Bichromatic Separating Rectangle Problem ^†

Abstract

An important topic in the field of geometric optimization is finding the largest rectangle separating two different points sets, which has significant applications in circuit design and data science. We consider some extensions of the maximum bichromatic separating rectangle (MBSR) problem. In one of the extensions, the optimal rectangle may include up to k outliers, where k is given as part of the input. This extension and is called MBSR with outliers or MBSR-O. In this paper, we improve the current known time bounds for MBSR-O from $O(k^{7}m \log m+n)$ to $O(k^{3}m+km \log m+n)$ using a clever staircase sweep approach. We also propose another extension, which is named MBSR among circles or MBSR-C and asks for the largest rectangle separating red points from blue unit circles. Our solution to MBSR-C is an $O(m^2+n)$-time algorithm that involves an optimized scanning of all candidate circle arcs for locations of potential optimal solutions.

1. Introduction

Geometric optimization deals with optimization problems involving large sets of geometric objects. Bichromatic separability of point sets is a well-known topic in the field of geometric optimization. Typically, we are given a set of “red” points and a set of “blue” points in two or three dimensions, and the goal is to separate them using various geometric loci, such as lines, planes, circles, spheres, rectangles, or boxes.

The Maximum Bichromatic Separating Rectangle (MBSR) problem was introduced by Armaselu et al. in [1] (see also [2]) and is stated as follows. Given a red point set R and a blue point set B in the plane, with $\left|R\right|=n,\left|B\right|=m$, compute the axis-aligned rectangle S satisfying the following:

(1)

S contains all points in R;

(2)

S contains the fewest points in B among all rectangles satisfying (1);

(3)

S has the largest area of all rectangles satisfying (1) and (2).

Such a rectangle is called maximum bichromatic separating rectangle (MBSR) or simply largest separating rectangle.

Denote the smallest axis-aligned rectangle enclosing R by $S_{min}$.

In this paper, we consider two extensions of the MBSR problem.

The first extension, introduced in [3], is called MBSR with outliers (MBSR-O) or simply outliers version. It seeks to find the largest axis-aligned rectangle containing all red points and up to k blue points outside $S_{min}$, where k is given as part of the input. That is, MBSR-O is a relaxation of condition (2) from the original MBSR problem. The running time of the algorithm in [3] is $O(k^{7}m\log m+n)$. However, when the k is large (e.g., $k=\mathsf{\Theta }\left(m\right)$), this running time bound can be unreasonably high. We will show how to improve this time bound to $O(k^{3}m+kmlogm+n)$ using a more clever sweep line-based approach.

We also introduce another extension of MBSR, called MBSR among circles (MBSR-C) or simply circles version, in which there are red points and blue unit circles, and the goal is to find the largest rectangle containing no point of any blue circle outside $S_{min}$ while containing all red points.

For both extensions, we assume no unbounded solution and also that all points are in general positions.

The outliers version can have applications in various domains. For instance, in VLSI or circuit design, one might seek to place a hardware component (e.g., cooler) on a board with minor fabrication defects (blue points), where up to k defects are tolerated for component placement. The red points may indicate “hot spots” that must be covered by the component on the board.

The circles version is motivated by problems involving “imprecise” data, such as probabilistic applications, machine learning applications, and tumor extraction with large or imprecise cells as red or blue points. For instance, the goal is to surgically remove a tumor using a rectangular tool, with tumor cells marked by red points while blue points denote healthy cells and osteoclasts that should not be removed or cut out.

Various other applications of bichromatic separation with imprecise points can be found in spatial databases and data science.

1.1. Related Work

Geometric separability of point sets, which deals with finding a geometric locus that separates two or more point sets whilst achieving a specific optimum criterion, is an important topic in computational geometry. Various approaches deal with finding a specific type of separator (e.g., hyperplane) when the points are guaranteed to be separable. However, this is not always the case, hence the need for results on weak separability, i.e., either minimizing the misclassifications or allowing up to a fixed number of them.

The problem of finding the smallest separating circle among red and blue points (i.e., containing all red points and the fewest blue points), was introduced by Bitner and Daescu et al. [4]. They provide two algorithms that find all optimal solutions: the first one runs in $O(m^{1.5}{log}^{O\left(1\right)}n+nlogn)$ time and the second one runs in $O(mnlogm+nlogn)$-time. The dynamic version of the problem, in which blue points may be dynamically inserted and deleted at run time, was later addressed by Armaselu and Daescu [5], who provided three data structures foir this version. The first one is a unified data sdtructure supporting both insertion and deletion queries in $O(nlogm)$ time, as well as $O\left(\right(m+n)logm)$ time updates. The other two are deletion-specific (resp., insertion-specific) and allow $O{(log}^2\left(mn\right))$ (resp., $O(log(mn\left)\right)$) query time, at the expense of $O(mnlog(mn\left)\right)$ update time.

Armaselu and Daescu were the first to address the MBSR problem. Their algorithm runs in $O(mlogm+n)$ time [1,2]. When the axis-alignment restriction on the MBSR is dropped, they have an $O(m^3+nlogn)$ time algorithm. They also come up with an $O\left(m^2(m+n)\right)$-time algorithm to compute the maximum-volume separating box in three dimensions [2]. Later, this wasr improved to $O(m^2+n)$ time [6].

Separability of imprecise points has also been considered. In such setting, points are asscoiated with an region of imprecision. For instance, blue unit circles (i.e., MBSR-C) can be thought of as imprecision regions, where the imprecise points are their centers. When the imprecisions are axis-aligned rectangles, de Berg et al. [7] come up with a linear-time algorithm to compute certain separators, i.e., that are 100% likely to separate the point sets. They also show how to compute possible separators (>0% likely to separate) in $O(nlogn)$ time.

It is worth mentioning that all these results on separators deal with blue points. However, there are also results for blue obstacles. In a more recent paper [3], Armaselu, Daescu, Fan, and Raichel give an algorithm to find a largest rectangle separating red points from blue axis-aligned rectangles in $O(mlogm+n)$ time.

Computing the largest empty (axis-aligned) rectangle problem is a very popular and studied topic. Given a set of planar points P, the goal is to compute the largest axis-aligned rectangle that has a point $p\in P$ on each of its sides but none inside it. For the axis-aligned version, Agarwal et al. [8] provided the best currently known time bound, $O\left(n{log}^{2}n\right)$, for computing one optimal solution, while Hsu et al. [9] got the best-known result for computing all optimal solutions, namely, in $O(nlogn+M)$ time, where M is the number of maximal empty rectangles. Mukhopadhyay et al. [10] solved the arbitrary orientation version and gave an $O\left(n^3\right)$ time algorithm that outputs all optimal solutions. In addition, Chaudhuri et al. [11] proved a lower bound of $\mathsf{\Omega }\left(n^3\right)$ optimal solutions in the worst case.

Nandy et al. considered the problem of finding the maximal empty axis-aligned rectangle among a given set of rectangles isothetic to a given bounding rectangle [12]. They show how to solve the problem in $O(nlogn+R)$ time, where R is the number of rectangles. Later, they solved the version where obstacles have arbitrary orientation using an algorithm that takes $O\left(n{log}^{2}n\right)$ time [13]. Finally, they consider the problems of locating the largest empty rectangle inside a simple polygon, as well as avoiding a bunch of simple polygons [13].

1.2. Our Results

First, we improve upon the MBSR-O result in [3]. Specifically, we provide a slight improvement of $O(k^{7}m+mlogm+n)$ time for k outliers, which we further improve to $O(k^{3}m+kmlogm+n)$ time. The latter is faster than the former whenever $k>{(logm)}^{\frac{1}{4}}$). After that, we come up with an $O(m^2+n)$ time algorithm for MBSR-C.

The rest of the paper is structured as follows. In Section 2, we describe our improvements to MBSR-O, in Section 3 we describe our solution to MBSR-C, and finally, in Section 4 we draw the conclusions and suggest some future directions.

2. Finding the Largest Separating Rectangle with k Outliers

The goal is to compute the largest axis-aligned rectangle enclosing R while containing no more than k blue points of B (“outliers”), for a given $k\ge 0$. We call this rectangle maximum bichromatic separating rectangle with outliers (MBSR-O).

We first discard the blue points inside $S_{min}$, as they cannot be avoided.

In [3], the given algorithm for MBSR-O operates as follows. We first compute the smallest rectangle $S_{min}$ enclosing R in linear time, and then partition the space outside $S_{min}$ into 8 regions, using the lines bounding $S_{min}$. Specifically, there are 4 “corner” regions $NE,NW,SW,SE$. (also known as “quadrants”), and 4 “side” regions $E,N,W,S$. In each such region Q, we consider the set $B_Q$ of blue points inside Q.

Definition 1.

[3] A point $p\in B_{NE}$ dominates another point $q\in B_{NE}$, if $x\left(p\right)>x\left(q\right)$ and $y\left(p\right)>y\left(q\right)$. Similarly, a point $p\in B_{NW}$ dominates another point $q\in B_{NW}$, if $x\left(p\right)<x\left(q\right)$ and $y\left(p\right)>y\left(q\right)$, a point $p\in B_{SE}$ dominates another point $q\in B_{SE}$, if $x\left(p\right)>x\left(q\right)$ and $y\left(p\right)<y\left(q\right)$, and a point $p\in B_{SW}$ dominates another point $q\in B_{SW}$, if $x\left(p\right)<x\left(q\right)$ and $y\left(p\right)<y\left(q\right)$.

Definition 2.

[3] For each $B_Q$ and for any t such that $0\le t\le k$, the t-th level staircase of $B_Q$ is the rectilinear polygon formed by the blue points in $B_Q$ that dominate exactly t blue points in $B_Q$.

Note that an optimal solution contains t points from $B_Q$ if and only if it is bounded by the t-th level staircase of $B_Q$, shown in Figure 1.

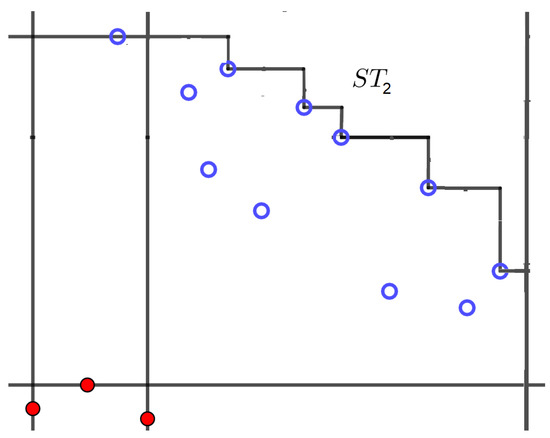
Figure 1. The 2nd level staircase of $B_{NE}$.

For each partition of k into 8 smaller natural numbers $k=k_E+k_{NE}+\cdots +k_{SE}$, that is, one natural number for each region, we do the following.

• Consider the $k_Q+1$-th closest to $S_{min}$ blue point from each side region Q. Note that, by extending $S_{min}$ in each direction until reaching these points, one obtains a rectangle $S_{max}$ which definitely contains the target rectangle.
• For each quadrant Q, compute the $k_Q$-level staircase $S{T}_{k_Q}\left(Q\right)$ of Q in $O(mlogm)$ time.
• Solve a “staircase” problem on $S_{min},S_{max}$, and $ST$ in $O\left(m\right)$ time. That is, compute the largest rectangle enclosing $S_{min}$, supported by points of the staircases, and contained in $S_{max}$.

Since there are $O\left(k^7\right)$ ways of partitioning the integer k into 8 smaller natural numbers, it follows that the running time of this approach is $O(k^{7}mlogm+n)$.

2.1. A Slight Improvement on the Running Time

We improve the running time bounds for MBSR-O. To do that, instead of computing the t-th level staircase $S{T}_t\left(Q\right)$ for each quadrant and each natural number $t\le k$, we pre-compute all staircases in a more clever fashion that involves sweeping the blue points in each quadrant Q with a line and computing all $S{T}_t\left(Q\right)$’s in a single sweep.

Lemma 1.

The t-level staircases $S{T}_t\left(Q\right)$ can be computed in $O(mlogm+mk)$ time for all quadrants Q and integers $t\le k$.

Proof. 

We show how to compute $S{T}_t\left(NE\right)$ for all $t\le k$ with a sweep line algorithm, as for other quadrants the approach is similar. For simplicity, denote $S{T}_t\left(NE\right)$ as $S{T}_t$, that is, without specifying the quadrant. Sort and label the points in $B_{NE}$ by increasing x-coordinate, and denote the resulting sequence as $p_1,\dots ,p_m$. Sweep a vertical line l from $x_0=max\left\{x\right|(x,y)\in S_{min}\}$ to $x_1=\infty$. For any given position of l, let $P_l=\{p_1,\dots ,p_i\}$ be the set of blue points to the left of l. We maintain a balanced binary search tree T over $P_l$, indexed by the y-coordinates of its elements. The intersection of $S{T}_t$ with l is a single point $q_i^t$, which is the highest point on l that lies above at most t points of $P_l$. That is, $q_i^t$ is the $(t+1)$-th smallest indexed entry in T, which we record. As we move l from left to right, $q_i^t$ can only change when l intersects a point $p_i\in B_{NE}$. When we cross the point $p_{i+1}$ (called event point), we insert it into T and, for each $t\le k$, we have two cases.

• If $p_{i+1}$ is higher than $q_i^t$, then the height of $S{T}_t$ does not change.
• If $p_{i+1}$ is lower than $q_i^t,q_i^{t-1},\dots ,q_i^s$, for some $0\le s\le t$, then $q_i^t$ is set to $q_i^{t-1}$ (which is done in $O\left(1\right)$ time), and $S{T}_t$ moves to the height of this entry. This update is repeated by setting $q_i^{t-1}$ to $q_i^{t-2}$ and so on down to $q_i^{s+1}$. Finally, $q_i^s$ is set to $p_{i+1}$.

If $S{T}_t$ changes when sweeping over $p_{i+1}$, we also record a point $r_i^t$ whose x-coordinate is that of $p_{i+1}$ and whose y-coordinate is that of the updated $q_i^t$. Let $B^t$ be the set of all such points $q_i^t,r_i^t$ recorded during this process for all $t\le k,i=1,\dots ,m$. It is not hard to argue that ${\cup }_{t\le k}S{T}_t\subseteq B^t$. Moreover, $|B^t|\le m$ holds, as a point is added to Q only when the sweep line crosses a point of $B_{NE}$. Finally, note that we encountered $O\left(m\right)$ event points $p_i$. Inserting each of them into T requires $O(logm)$ time, and $O\left(k\right)$ extra time is needed $q_i^t,r_i^t$ pointer updates. Hence, the running time bound follows. □

See Figure 2 for an illustration of the proof of Lemma 1.

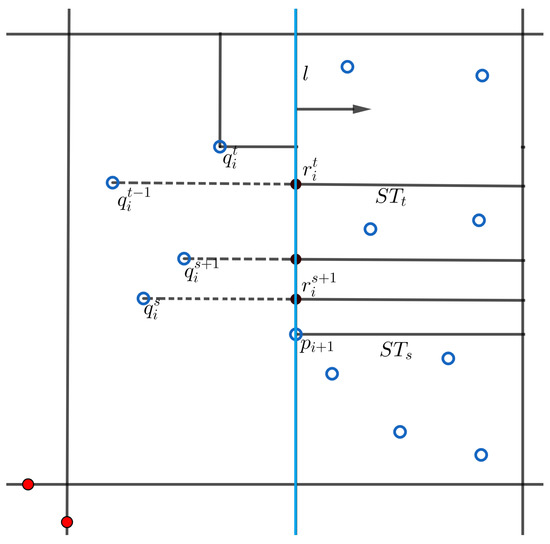
Figure 2. While sweeping vertical line l over point $p_{i+1}$, the staircase $S{T}_t$ is updated.

Instead of computing the $S{T}_t$’s for each partition of k, we compute all of them in $O(mlogm+mk)$ time before considering such partitions. Then we only need to solve a staircase problem in $O\left(m\right)$ time for each of the $O\left(k^7\right)$ partitions, giving us the following result.

Theorem 1.

Given two point sets, $R:\left|R\right|=n$ and $B:\left|B\right|=m$, as well as an integer $k\ge 0$, the largest rectangle enclosing R and containing up to k points in B can be computed in $O(k^{7}m+mlogm+n)$ time.

2.2. A Closer Look at the Number of Candidate Partitions of k

In the previous section, we reduced the running time by a factor of $logm$. However, it seems hard to further improve this bound given the high number of partitions of k. Thus, in this subsection, we show how to reduce the number of candidate partitions of k, to further improve the running time bound.

To do that, we first compute all the t-level staircases $S{T}_t,0\le t\le k$ as described in the previous section. We then consider the blue points in 4 pairs of adjacent regions, e.g., N and $NE$. That is, we suppose the total number of outliers coming from $B_N\cup B_{NE}$, denoted $k_{NNE}=k_N+k_{NE}$, is fixed. Similarly, we suppose $k_{ESE}=k_E+k_{SE},k_{SSW}=k_S+k_{SW},k_{WNW}=k_W+k_{NW}$ are fixed. Let $ST\left(Q\right)={\cup }_{t=1}^{k}S{T}_t\left(Q\right)$, for any quadrant Q. From now on, we focus on the N and $NE$ regions and, for simplicity, we denote $ST\left(NE\right)$ as simply $ST$ and $S{T}_t\left(NE\right)$ as simply $S{T}_t$.

We notice that even though any points of any t-th level staircase, $t\le k_{NE}$, may be a corner for a candidate rectangle, most of these rectangles can be discarded as they are guaranteed to be smaller than the optimal rectangle.

Definition 3.

For every pair $P=(P_1,P_2)$ of regions and every integer $t:0\le t\le k$, denote by $S_t^P$ the set of pairs $(p,q)\in {(B_{P_1}\cup B_{P_2})}^2$ such that p is the top support and q is the right support for an optimal solution, among all rectangles containing t blue points from $B_{P_1}\cup B_{P_2}$.

From now on, for simplicity, we are going to remove the superscript and simply write $S_t$, e.g., $S_{k_{NNE}}$ instead of $S_{k_{NNE}}^{NNE}$. For every t, we store $S_t$ as an array.

The goal is to compute $S_{k_{NNE}}$. Refer to Figure 3 for an illustration. Suppose we have already computed all $S_{t^{\prime }}:t^{\prime }<k_{NNE}$. Sweep $B_N\cup B_{NE}$ with a horizontal line $l_H$ going upwards, starting at the $k_{NNE}+1$-th lowest blue point in $B_N\cup B_{NE}$. For every blue point p encountered as top support, let $below\left(p\right)$ be the highest point in $B_N$ below p, and $above\left(p\right)$ be the lowest point in $B_N$ above p. For every $p\in B_{NE}$, let $rb\left(p\right)$ be the leftmost point in $B_{NE}$ to the right of p and below p. Let $t_N$ be the blue point count below p from $B_N$. Furthermore, let t be the number of points dominated by p from $B_N\cup B_{NE}$.

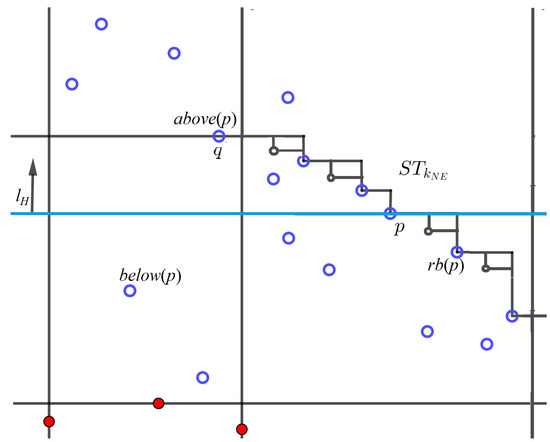
Figure 3. $B_N\cup B_{NNE}$ is swept with a horizontal line $l_H$ sliding upwards from the lowest blue point. The set $S_{k_{NNE}}$ is updated at every blue point p encountered. Staircase points that are not blue points are marked with black dots.

First, assume $p\in B_{NE}$ and let $t_{NE}=t-t_N$ be the number of points dominated by p from $B_{NE}$, i.e., $p\in S{T}_{t_{NE}}$. When sweeping the next blue point q, we consider the following cases.

Case 1. If q is to the right of p, then q is below $above\left(p\right)$ but dominates p, the points dominated by p, and the points in $T(p,q)=\{s\in B_{NE}\cap S{T}_{t_{NE}}|x\left(p\right)<x\left(s\right)<x\left(q\right)\}$ (Figure 4). If $t+t_{pq}=k_{NNE}$, then we add $(q,rb(q\left)\right)$ to $S_{t+t_{pq}}$, where $t_{pq}=1+\left|T(p,q)\right|$.

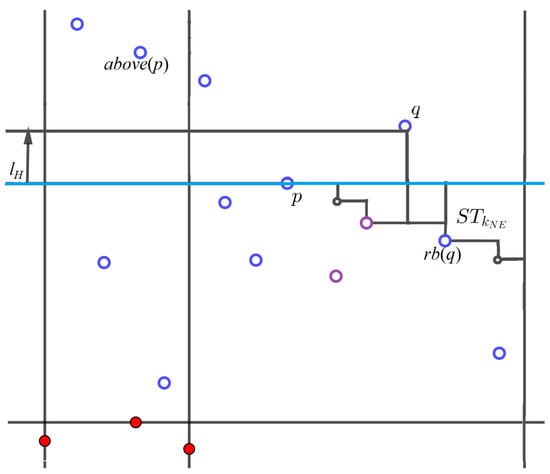
Figure 4. Case 1. $p\in B_{NE}$, q to the right of p. The purple empty dots denote $T(p,q)$.

Case 2. If $q\in B_{NE}$ and q is to the left of p, then q is below $above\left(p\right)$ (otherwise $(p,q)\notin S_{k_{NNE}}$), but dominates the points dominated by p, except the ones in $U(q,p)=\{s\in B_{NE}|x\left(q\right)<x\left(s\right)<x\left(p\right),y\left(s\right)<y\left(p\right)\}$ (Figure 5). For each $s\in U(q,p)$, if $t-i\left(s\right)=k_{NNE}$, then we add $(q,s)$ to $S_{t-i\left(s\right)}$, where $i\left(s\right)$ is the index of s in $U(q,p)$ in decreasing order of X coordinates. Finally, if $t=k_{NNE}$, then we add $(q,p)$ to $S_t$.

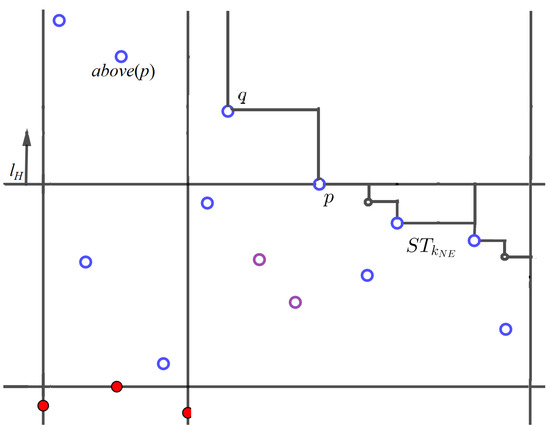
Figure 5. Case 2. $p\in B_{NE}$, $q\in B_{NE}$, and q is to the left of p. The purple empty dots denote $U(q,p)$.

Case 3. If $q\in B_N$ then, for each $s\in U\left(p\right)=\{s\in B_{NE}|x\left(s\right)<x\left(p\right),y\left(s\right)<y\left(p\right)\}$ such that $t-i\left(s\right)=k_{NNE}$, we add $(q,s)$ to $S_{t-i\left(s\right)}$, where $i\left(s\right)$ is the index of s in $U\left(p\right)$ in decreasing order of X coordinates. Finally, if $t=k_{NNE}$, then we add $(q,p)$ to $S_t$ (Figure 6).

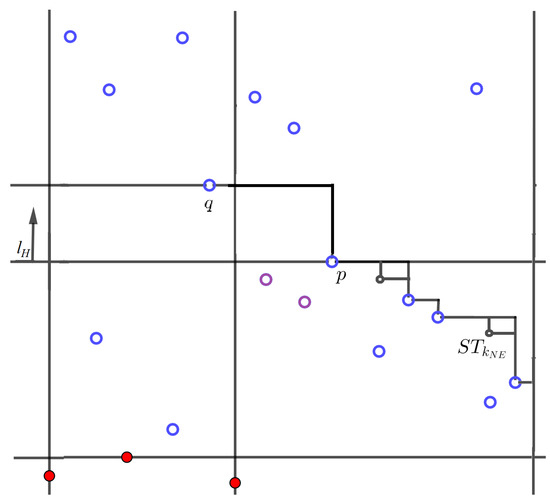
Figure 6. Case 3. $p\in B_{NE},q\in B_N$. The purple empty dots denote $U\left(p\right)$.

Now assume $p\in B_N$ and let $t_{NE}$ be the largest $t^{\prime }$ such that all points in any $S{T}_{t^{\prime }}$ are below p. Let $b\left(p\right)$ be the leftmost point of $S{T}_{t_{NE}}$ below p. When sweeping the next blue point q, we consider the following cases.

Case 4. If q is to the right of $b\left(p\right)$ then, if $t=k_{NNE}-1$, we add $(q,rb(q\left)\right)$ to $S_{t+1}$. For each $s\in U\left(q\right)$ such that $t-i\left(s\right)=k_{NNE}$, we also add $(q,s)$ to $S_{t-i\left(s\right)}$ (Figure 7).

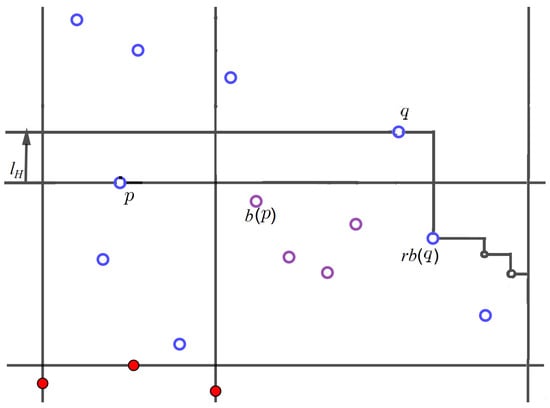
Figure 7. Case 4. $p\in B_N$, q is to the right of $b\left(p\right)$. The purple empty dots denote $U\left(q\right)$.

Case 5. If $q\in B_{NE}$ and q is to the left of $b\left(p\right)$, then, if $t=k_{NNE}-1$, we add $(q,s)$ to $S_{t+1}$ for every $(p,s)\in S_t$ (Figure 8).

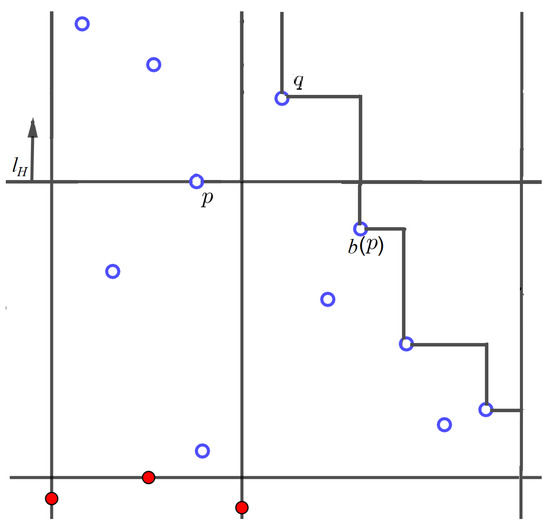
Figure 8. Case 5. $p\in B_N$, $q\in B_{NE}$ and q is to the left of $b\left(p\right)$.

Case 6. If $q\in B_N$, then, if $t=k_{NNE}-1$, we add $(q,s)$ to $S_{t+1}$ for every $(p,s)\in S_t$ (Figure 9).

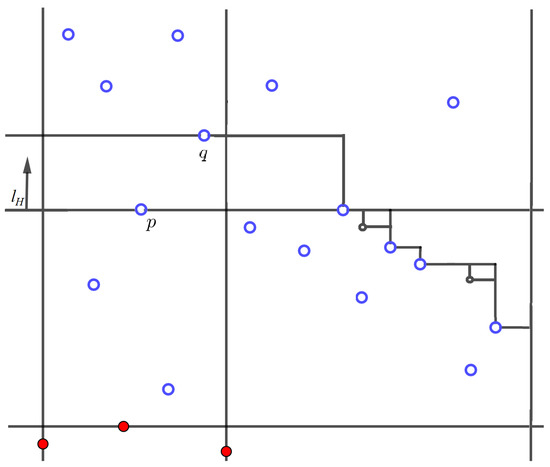
Figure 9. Case 6. $p\in B_N,q\in B_N$.

The following lemma puts an upper bound on the storage required by $S_{k_{NNE}}$.

Lemma 2.

$|S_{k_{NNE}}|=O\left(m\right)$.

Proof. 

In case 1, we only add one pair to $S_{k_{NNE}}$. In case 2, even though we consider $\left|U\right(q,p\left)\right|$ points, we only add the pair $(q,s)$ such that $t-i\left(s\right)=k_{NNE}$. Similarly, in cases 3 and 4 we only add the pair $(q,s):t-i\left(s\right)=k_{NNE}$, even though we consider $\left|U\right(p\left)\right|$ (resp., $\left|U\right(q\left)\right|$) points. In case 5, we add at most $|S{T}_{t_{NE}}|$ pairs if $t=k_{NNE}-1$. However, note that for the subsequent point $q^{\prime }$ swept, we would have a larger number $t^{\prime }$ of blue points in $B_N\cup B_{NE}$ dominated by $q^{\prime }$. Thus, we only add at most $|S{T}_{t_{NE}}|=O\left(m\right)$ pairs once. Similarly, in case 6 we only add $O\left(m\right)$ pairs once. □

The following lemma states the running time of the aforementioned sweeping algorithm.

Lemma 3.

For any $t:0\le t\le k$, the horizontal line sweeping described above takes $O(mlogm)$ time.

Proof. 

We store the blue points in $B_N\cup B_{NE}$ in two balanced binary search trees $X,Y$, indexed by X (resp., Y) coordinates. Thus, for each blue point p swept, we require $O(logm)$ time. We require an extra $O(logm)$ time to compute $above\left(p\right),below\left(p\right)$, and $rb\left(p\right)$. In case 1, note that we can compute $t_{pq}$ by finding the position of q in the X-sorted order of $S{T}_{k_{NE}}$, and thus the number of blue points $s:x\left(p\right)<x\left(s\right)<x\left(q\right)$, in $O(logm)$ time, since $S{T}_{k_{NE}}$ is maintained as a binary search tree. Thus, we only require an extra $O(logm)$ time to handle case 1. In cases 2 and 4, note that we only need to add $(q,s)$ to $S_{k_{NNE}}$ if $i\left(s\right)=t-k_{NNE}$, so we query for s in X using $O(logm)$ time. Similarly, in case 3 we only add $(q,p)$ to $S_{k_{NNE}}$ if $i\left(s\right)=t-k_{NNE}$, so we query X for s in $O(logm)$ time. Now in cases 5 and 6 we spend $O\left(m\right)$ time to traverse $S_t$, since we store $S_t$ as an array for any t, but they only occur once, so this gives us $O\left(m\right)$ total time. In every case, since $S_t$ is an array, adding a pair to $S_t$ takes $O\left(1\right)$ time. Since we sweep $O\left(m\right)$ blue points, the result follows. □

Corollary 1.

For any pair of quadrants, we compute $S_t$ in $O(kmlogm)$ time for all $t:0\le t\le k$.

We reduce the number of candidate partitions of k from $O\left(k^7\right)$ to $O\left(k^3\right)$ as follows. By writing $k=k_{NNE}+k_{ESE}+k_{SSW}+k_{WNW}$, we can deduce $k_{NNE}=k-k_{WNW}-k_{ESE}-k_{SSW}$ for every combination of $k_{WNW},k_{ESE},k_{SSW}$. Therefore, there are $O\left(k^3\right)$ such combinations.

Initially, we compute $S_t^Q$ for every quadrant Q and $0\le t\le k$. Then, for each combination $(k_1,k_2,k_3),k_1,k_2,k_3=0,\dots k,k_1+k_2+k_3\le k$, we set $k_4=k-k_1-k_2-k_3$ and solve the staircase problem in [2] with the pairs $S_{t_1}^{WNW}\cup S_{t_2}^{ESE}\cup S_{t_3}^{SSW}\cup S_{k_4}^{NNE}$ as pairs of supports. Each staircase problem takes $O\left(m\right)$ time to solve, so we require $O\left(k^{3}m\right)$ time for all candidate partitions of k. Putting this together with the result in Lemma 1, we get the following result.

Theorem 2.

Given two point sets, $R:\left|R\right|=n$ and $B:\left|B\right|=m$, as well as an integer $k\ge 0$, the MBSR-O for R and B with k outliers can be computed in $O(k^{3}m+kmlogm+n)$ time.

3. Finding the Largest Axis Aligned Rectangle Enclosing R and Avoiding Unit Circles

In this extension, B consists of $S_{min}$-disjoint unit circles, and the goal is to find the largest axis-aligned rectangle that avoids all circles while enclosing R. We call such rectangle an MBSR among circles or MBSR-C.

Again, we discard blue circles intersecting $S_{min}$ from consideration, as they cannot be avoided.

One may wonder whether the reduction in [3] for finding the largest separating rectangle among axis-aligned rectangles can be tailored to MBSR-C. However, it can be shown that it does not always work. If we let $C_{NW},C_{SW},C_{SE},C_{NE}$ be circles in the regions $B_{NW},B_{SW},B_{SE},B_{NE}$, pick any point p on the quadrant of $C_{NW}$ that is the closest to $S_{min}$, and add it to $B^{\prime }$, then any rectangle enclosing R, avoiding $B^{\prime }$, and top or right-bounded by p will intersect $C_{NW}$. See Figure 10 for a depiction of why this is the case.

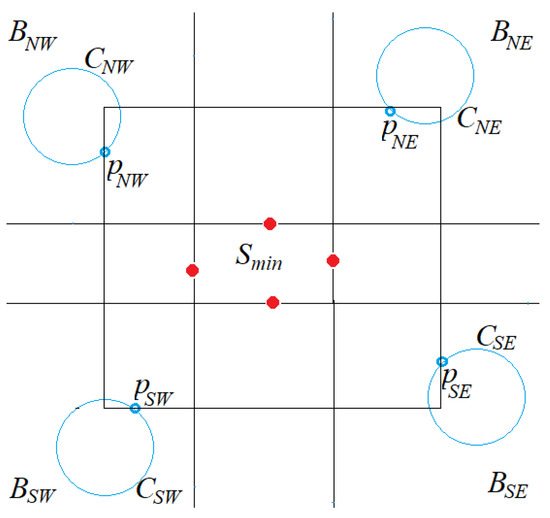
Figure 10. If the MBSR among R and $B^{\prime }$ were bounded by a point $p\in C$, it would intersect C.

We call a candidate separating rectangle (CSR) a rectangle that encloses R and cannot be extended in any direction without intersecting some circle. Note that a CSR may touch a circle either at a corner or at an edge. If it is bounded at an edge, then that edge is fixed in terms of X or Y coordinate and the arc it touches at each endpoint of the edge is uniquely determined (Figure 11). On the other hand, if it is bounded at a corner, then the corner can be slid along the appropriate arc of the circle (Figure 12). Each position of the corner determines the X or Y coordinates of its two adjacent edges, and thus the arcs pinning the two adjacent corners, if any.

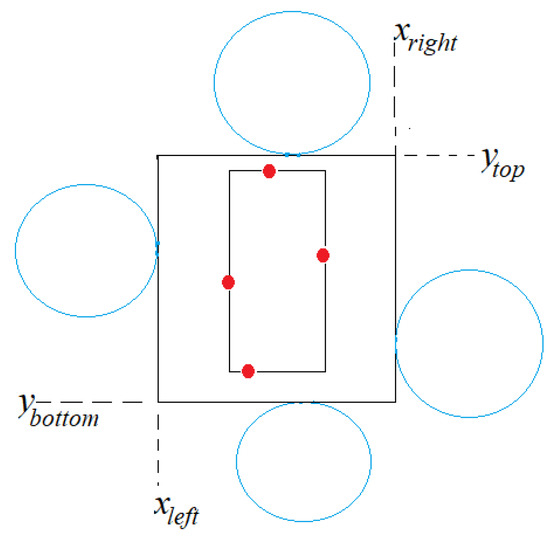
Figure 11. A circle bounding a rectangle at an edge makes that edge fixed in terms of either X or Y coordinate.

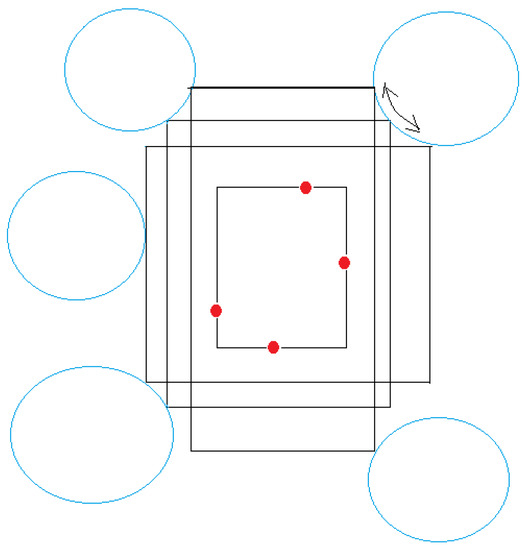
Figure 12. A circle bounding the rectangle at a corner allows the corner to slide along the arc. Each position of the corner uniquely determines its two adjacent edges.

We say that an edge e of a CSR is pinned by a circle C if C touches the interior of e.

A horizontal (resp., vertical) edge e is said to be fixed by two circles $C_1,C_2$ in terms of Y (resp., X) coordinate, if:

(1)

the ends of e are on $C_1$ and $C_2$, respectively, and

(2)

changing its Y (resp., X) coordinate would result in either e intersecting $C_1$ or $C_2$ or failing to touch both $C_1$ and $C_2$.

3.1. A Description of All Cases in Which a CSR Can Be Found

We consider all the cases in which a CSR can be found, based on the number of edges pinned by circles.

Case 1. Three edges pinned by circles (Figure 13). In this case, we extend the the fourth edge outward from $S_{min}$ until it touches a circle. Hence, the CSR is uniquely determined.

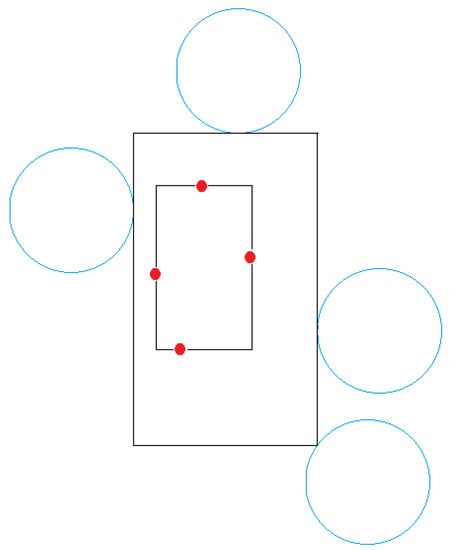
Figure 13. Case 1: Three circles pin the CSR on edges, which uniquely determines its fourth edge.

Case 2. Two edges are pinned by two circles $C_1,C_2$. In this case, we further distinguish the following subcases.

Case 2.1. Two adjacent edges are pinned by $C_1,C_2$. Note that their common corner q is fixed. We extend one of the edges by moving its other end p away from q until it touches a circle $C_3$, and then extend the third edge until it touches a circle $C_4$ at a point r (Figure 14). The resulting CSR is unique.

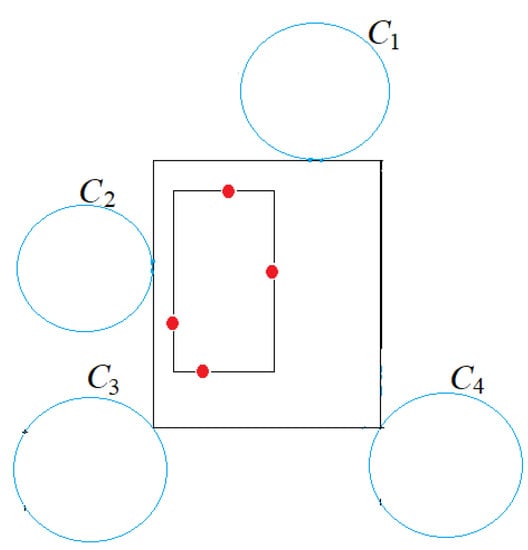
Figure 14. Case 2.1: Two circles $C_1,C_2$ pin two adjacent edges of the CSR. When extending one of the edges until it touches a circle $C_3$, the resulting CSR is unique.

Case 2.2. Two adjacent edges are pinned by $C_1,C_2$. We extend one of the edges by moving its other end p away from q, until the orthogonal line through p touches a circle $C_3$ at a point r (see Figure 15). While moving p, the point r can slide along one or more circles in the same quadrant, giving an infinite number of CSRs.

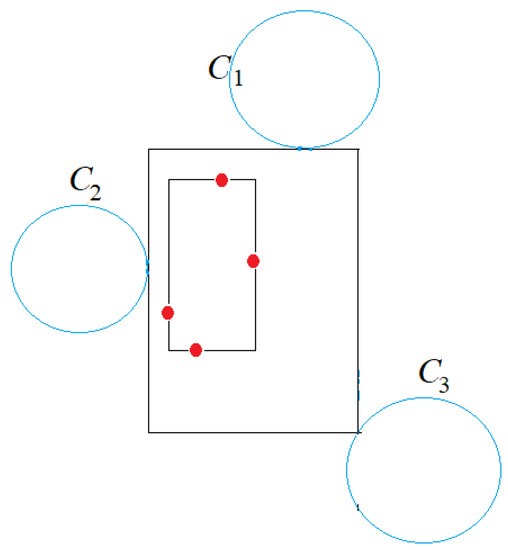
Figure 15. Case 2.2: Two circles $C_1,C_2$ pin the CSR on the north and west edges. The SE corner may slide along a circle $C_3$.

Case 2.3. Two opposite edges are pinned by $C_1,C_2$. We slide the other two edges outward from $S_{min}$ until each of them touches some circle (see Figure 16). This gives us a unique CSR.

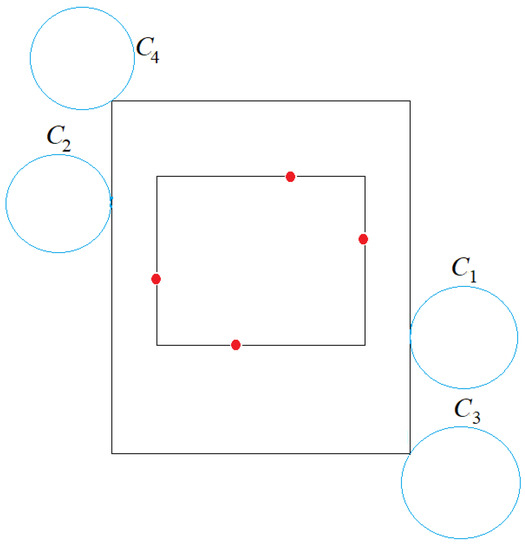
Figure 16. Case 2.3: Two circles $C_1,C_2$ pin the CSR on the east and west edges. The other two edges are uniquely determined.

Case 3. One edge e is pinned by a circle $C_1$. We have the following subcases.

Case 3.1. When e is extended in both directions, it touches two circles $C_2,C_3$ (Figure 17). We then slide the fourth edge outward from $S_{min}$ until it touches a circle $C_4$ and we have a unique CSR.

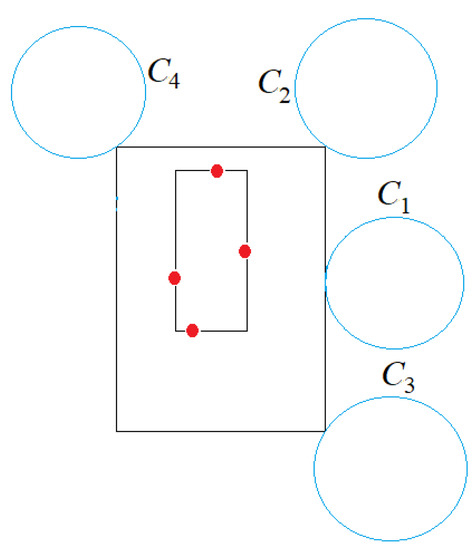
Figure 17. Case 3.1: Circle $C_1$ supports the CSR on the east edge, which, when extended in both directions, it eventually touches circles $C_2,C_3$.

Case 3.2. When e is extended in both directions, the orthogonal line through one of the ends p touches a circle $C_2$ at point q (Figure 18). While moving p, q can slide along one or more circles in the same quadrant, yielding an infinite number of CSRs. After establishing the position of q, we slide the fourth edge away from $S_{min}$ until it touches a circle $C_3$.

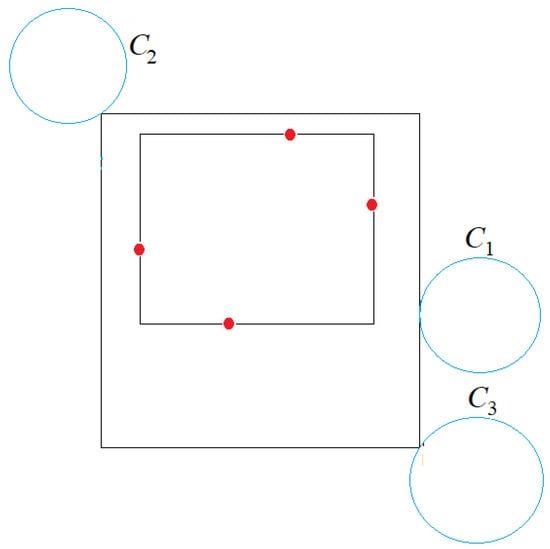
Figure 18. Case 3.2: The CSR is supported by $C_1$ on the east edge. One of the adjacent edges is uniquely determined, while the opposite corner may slide along a circle $C_2$.

Case 4. No edge is pinned by any circle. In this case, all corners can slide along circles until one of the edges becomes pinned by some circle, giving an infinite number of CSRs. Suppose the position of a corner p along a circle $C_1\in B_{NE}$ is known. We consider the following subcases.

Case 4.1, while extending the CSR in the two directions away from p, the CSR touches a circle in $B_{SE}$ or $B_{NW}$ at some point q before touching any circle in $B_{SW}$ (Figure 19). The other two corners are determined by sliding the edge opposite to $pq$ outwards until it touches a circle at some point r. In this case, the CSR is uniquely defined.

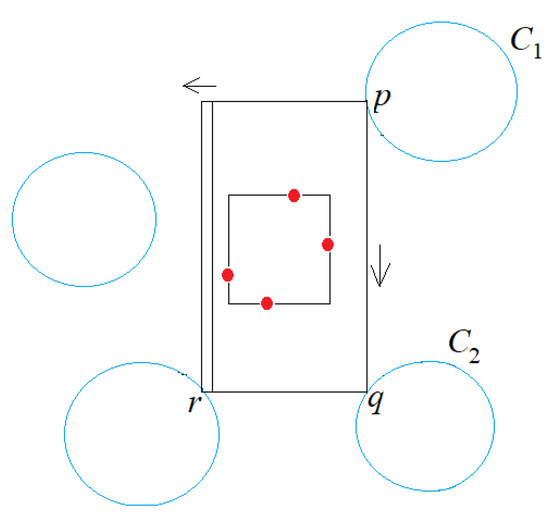
Figure 19. Case 4.1: No edge is pinned by any circle, and the position of p on $C_1\in NE$ is known. While sliding the CSR left-downward from $S_{min}$, we first touch circle $C_2$ at corner q adjacent to p. The other two corners are uniquely determined.

Case 4.2, while extending the CSR in the two directions away from p, the first circle that CSR touches, at a point q, is located in $B_{SW}$ (Figure 20). This gives us an infinite number of CSRs.

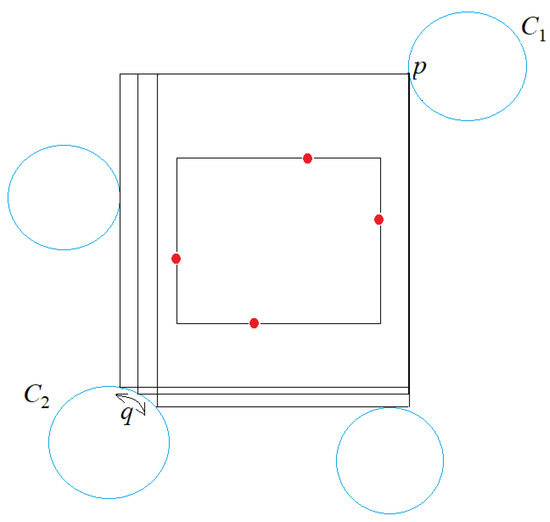
Figure 20. Case 4.2: No edge is pinned by any circle, and the position of p on $C_1\in NE$ quadrant is known. While sliding the CSR left-downward from $S_{min}$, we first touch circle $C_2$ at a corner q opposite to p. There are an infinite number of CSRs in this case.

3.2. Dominating Envelopes

Definition 4.

The dominating envelope of a corner region $B_i$ is a curve $\mathcal{C}$ satisfying the following:

• $B_i$ fully contains $\mathcal{C}$,
• $\forall p\in \mathcal{C}$, the rectangle cornered at p and the closest corner of $S_{min}$ from p is empty, and
• property (2) no longer holds if one extends $\mathcal{C}$ away from $S_{min}$.

Note that $\mathcal{C}$ is a sequence of horizontal and vertical segments, circle arcs, as well as a horizontal and a vertical infinite ray (see Figure 21). We shall reveal the use of dominating envelopes later.

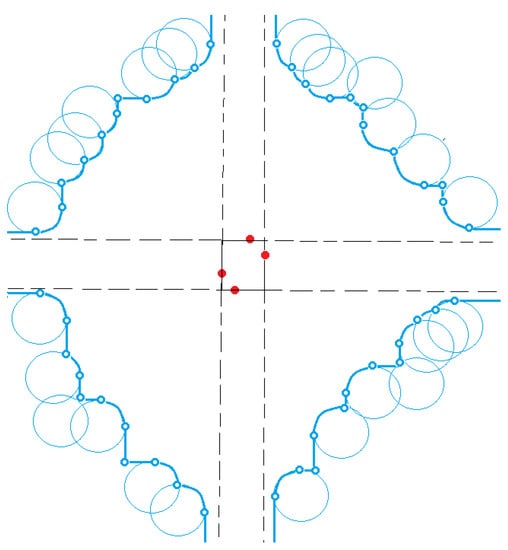
Figure 21. In each region, the circles define a dominating envelope $\mathcal{C}$, which is a sequence of arcs and horizontal or vertical segments. Two consecutive arcs or segments define a breakpoint on $\mathcal{C}$.

The dominating envelope changes direction at breakpoints, which can be between two consecutive arcs, segments, or an infinite ray. Every two consecutive breakpoints define a range of motion for a CSR corner.

A breakpoint p is said to be a corner breakpoint, if a CSR cornered at p cannot be extended away from $S_{min}$ in all directions without crossing some circle, even if its other corners are not located on any envelope.

To compute the dominating envelope $\mathcal{C}$ of $B_{NE}$, we do the following. First, sort the circles by X coordinate of their centers. Let p be the current breakpoint (initially, the first breakpoint is the left endpoint l of the left-most circle, with a vertical infinite ray upwards from l). For each two adjacent circles $C_1(c_1,1),C_2(c_2,1)$, depending on the relative positions of $c_1,c_2$, we do the following.

Case A. $c_2\in C_1$. In this case, we add the lower intersection between $C_1$ and $C_2$ as a new corner breakpoint q, along with the arc $pq$ of $C_1$.

Case B. $y\left(c_1\right)-1\le y\left(c_2\right)\le y\left(c_1\right)$ and $x\left(c_2\right)>x\left(c_1\right)+1$. We add a breakpoint q at the bottom of $C_1$, the arc $pq$ of $C_1$, a corner breakpoint r at the intersection between the horizontal through q and $C_2$, and the line segment $qr$.

Case C. $x\left(c_1\right)+1\le x\left(c_2\right)\le x\left(c_1\right)+1$ and $y\left(c_2\right)<y\left(c_1\right)-1$. We add a breakpoint r at the left endpoint of $C_2$, a corner breakpoint q at the intersection between the vertical through r and $C_1$, the line segment $qr$, and the arc $pq$ of $C_1$.

Case D. $x\left(c_2\right)>x\left(c_1\right)+1$ and $y\left(c_2\right)<y\left(c_1\right)-1$. We add the breakpoints q at the bottom of $C_1$, r at the left end of $C_2$, the corner breakpoints at the intersection between the horizontal through q and the vertical through r, the arc $pq$ of $C_1$, and the segments $qs$ and $sr$.

We then set p to the rightmost breakpoint added and repeat the process for the next pair of adjacent circles. Finally, for the last circle, we add an arc from p to its bottom b, the breakpoint b, and then a horizontal infinite ray emanating from b to the right. In each case, we say that a pair of circles $(C_1,C_2)$ defines breakpoints $p_1,\dots ,p_k$, if all of $p_1,\dots ,p_k$ are added as breakpoints in the process described above. Similarly, we say $(C_1,C_2)$ defines arcs $a_1,\dots ,a_k$, if all of $a_1,\dots ,a_k$ are added as arcs in the process. See Figure 22 for an illustration of this process.

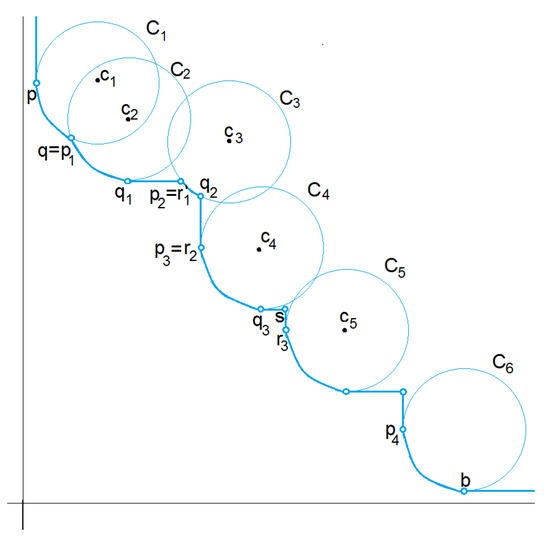
Figure 22. Each pair of adjacent circles gives a different case.

Note that deciding the case a circle belongs to can be done in constant time.

3.3. Finding an Optimal Solution in Each Case

We first slide the edges of $S_{min}$ outward until each of them touches a circle. Since we assumed no unbounded solutions, we are guaranteed that every edge will eventually hit a circle. Denote by $S_{max}$ the resulting rectangle and discard the region outside $S_{max}$ from the dominating envelopes of all quadrants. The endpoints of the resulting envelopes are also counted as breakpoints. We also sort the blue circles by the X coordinate and then (to break ties) by the Y coordinate of their centers.

Now we give a specific algorithm to compute the MBSR-C in each of the cases listed in Section 3.1.

Case 1. We consider all corner breakpoints that are defined by pairs of adjacent circles in Case D, and add them to a set $B^{\prime }$. We also consider all arcs $pq$ of circles that are part of pairs in Case D (p to the west of q), the vertical line $l_p$ through p and the horizontal line $l_q$ through q, and add $l_p\cap l_q$ to $B^{\prime }$. We then find the largest rectangle $S^{*}$ enclosing R and containing the fewest points in $B^{\prime }$ using the algorithm in [1] in $O(m+n)$ time. It is easy to check that $S^{*}$ is an optimal solution for Case 1, since any circle containing points in $B^{\prime }$ intersects a circle in B. Thus, Case 1 can be done in $O(m+n)$ time.

Case 2. Assume wlog that two circles pin the north and the west edges of a CSR. The cases where the two circles define a different pair of adjacent edges of a CSR can be handled in a similar fashion.

If we are in Case 2.1, we consider all corner breakpoints q defined by pairs of adjacent circles in Case D, as well as the intersection between the south horizontal tangent $t_H$ to the eastmost circle in $B_{NE}$ and the east vertical tangent $t_V$ to the northmost circle in $B_{NW}$ south of $t_H$. For every such point, the north and west edges are fixed, and we either find the south edge by extending the west edge southwards until it hits a blue circle, or the east edge by extending the north edge eastwards until it hits a blue circle. In both approaches, the fourth edge is uniquely determined. For each circle in $C\in B_{NE}$, we store pointers to the northmost circle in $B_{NW}$ south of C and to the eastmost circle in $B_{SE}$ west of C, as well as similar pointers for the other quadrants and directions, Thus, once the first two edges are fixed, we can find the third and fourth edges in $O\left(1\right)$ time. Since there are $O\left(m\right)$ circles in Case 2.1 and they all can be found in $O\left(m\right)$ time, Case 2.1 can be solved in $O\left(m\right)$ time.

For Case 2.2, we consider all points q as in Case 2.1. Having selected such point q defined by two circles $C_1\in B_{NE}\cup B_{NW}$ and $C_2\in B_{NW}\cup B_{SW}$, we consider the dominating envelope of $B_{SE}$ starting from the east tangent to $C_1$ or the east edge of $S_{min}$, whichever is eastmost, and ending at the south tangent to $C_2$ or the south edge of $S_{min}$, whichever is southmost. This gives us a range of motion for the $SE$ corner r of the CSR spanning $O\left(m\right)$ circle arcs. For each such arc, we find the optimal CSR in $O\left(1\right)$ time as we shall prove in the next section. Since there are $O\left(m\right)$ choices of q, we handle Case 2.2 in $O\left(m^2\right)$ time.

As for Case 2.3, note that the pairs of circles defining the $NW$ and the $SE$ corners, respectively, must belong to a dominating envelope. We scan the dominating envelope of $B_{NW}$ for pairs of circles $C_1,C_2$ in Cases B and C and, for each such pair, we scan the dominating envelope of $B_{SE}$ for pairs of circles in Cases B and C, starting from the east tangent to $C_1$ or the east edge of $S_{min}$, whichever is eastmost, and ending at the south tangent to $C_2$ or the south edge of $S_{min}$, whichever is southmost. Once these pairs are established, the CSR is determined. Since scanning each dominating envelope takes $O\left(m\right)$ time, we handle Case 2.3 in $O\left(m^2\right)$ time.

Case 3. Assume wlog that a circle C pins the east edge of the CSR. The cases where the circle define a different edge of the CSR can be handled in a similar fashion.

For Case 3.1, we scan the dominating envelope of $B_{NE}$ (similarly, $B_{SE}$) for pairs of circles $(C_1,C)$ in cases C and D, (C is the rightmost circle of the pair). For every such pair of circles in $B_{NE}$, we consider all circles $C_2\in B_{SE}$ that are intersected by the west vertical tangent to C. It is possible that some of these circles were already considered for a previous pair of circles in $B_{NE}$, so we may have to consider $O\left(m^2\right)$ triplets of circles $(C,C_1,C_2)$. We also traverse the circles in $B_E$ in increasing X order of their centers. Denote by C the current circle. We consider the sequences of circles $C_{NE}\in B_{NE}$ and $C_2\in B_{SE}$ that are intersected by the west tangent to C. Since these sequences may include circles already considered for a previous circle in $B_E$, we may need to spend $O\left(m^2\right)$ to find all such triplets $(C,C_1,C_2)$ for which there exists a vertical line intersecting both $C_1,C_2$. Once a triplet is established, the west, north, and south edges are established, and the west edge can be determined in $O\left(1\right)$ time by extending the north or the south edge until it hits a circle. Thus, Case 3.1 requires $O\left(m^2\right)$ time.

For Case 3.2, we scan the dominating envelope of $B_{SE}$ (similarly, $B_{NE}$) for pairs of circles $(C_1,C)$ in cases C and D (C is the rightmost circle of the pair). We also traverse the circles $C\in B_E$ in increasing X order and consider the sequences of circles $C_1\in B_{SE}$ that are intersected by the west tangent to C. For each pair $(C_1,C)$, the east and south edges of the CSR are defined. This provides a range of eligible circles from the dominating envelope of $B_{NW}$ such that the $SW$ and $NE$ corners of the CSR are not supported by any circle, and the $NW$ corner slides along some circle arc. There are $O\left(m\right)$ $(C_1,C)$ pairs and each of them gives $O\left(m\right)$ circles from $B_{NW}$. Hence, Case 3.2 takes $O\left(m^2\right)$ time.

Case 4. Consider all arcs defined by pairs of adjacent circles in one of the cases A, B, C, or D. Consider all arcs defined by pairs of adjacent circles. Each such arc a establishes the range of motion for the appropriate corner p of a CSR, say $[p_{start},p_{end}]$ in X order. Suppose a belongs to a circle in $B_{NE}$, which establishes the range of motion of the NE corner p of the CSR. This gives us a range of sliding motion for the north and the east edges of the CSR, which are supported by two rays $r_W,r_S$ shooting from p to the west and south, respectively. Since only the SW corner q may also slide along a circle, the west edge can be neither to the west of the first intersection $W\left(p\right)$ between $r_W$ and a circle, nor to the west of the easternmost point in $B_W$ of a circle. Similarly, the south edge can be neither be to the south of the first intersection $S\left(p\right)$ between $r_S$ and a circle, nor to the south of the northernmost point in $B_S$ of a circle. This gives a range of motion for q, which may span multiple circle arcs with X coordinates within the range $arcs(p_{start},p_{end})$ = $[min(X\left(W\left(S\left(p_{end}\right)\right)\right)$, $X\left(S\left(W\left(p_{end}\right)\right)\right))$, $max(X\left(W\left(S\left(p_{start}\right)\right)\right)$, $X\left(S\left(W\left(p_{start}\right)\right)\right)\left)\right]$. In fact, there are $O\left(m\right)$ arcs in the worst case, yielding $O\left(m^2\right)$ pairs of arcs for all possible pairs $(p,q)$. By computing the pointers $west\left(p\right),south\left(p\right),east\left(p\right)$, and $north\left(p\right)$ for every p, from the dominating envelope, we can find each pair of arcs in $O\left(1\right)$ time, as we take them in X order. That is, we consider all arcs $[p_{start},p_{end}]$ defined by pairs of adjacent circles in X order and, for each such arc, we compute the points $W\left(S\left(p_{start}\right)\right)$, $S\left(W\left(p_{start}\right)\right)$, $W\left(S\left(p_{end}\right)\right)$, and $S\left(W\left(p_{end}\right)\right)$, and then consider the arcs in $B_{SW}$ with X coordinates within $arcs(p_{start},p_{end})$.

Handling each pair of arcs in $O\left(1\right)$ time will be detailed in the next subsection. Thus, computing the optimal solution takes $O\left(m^2\right)$ time in Case 4.

3.4. Finding the CSR Once the Arcs Pinning Its Corners Are Selected

For each quadrant Q, let ${\theta }_Q\in [{\alpha }_Q,{\beta }_Q]$ be the angular position of the corner within the arc belonging to Q, say $C(c,1)$. Let $f({\theta }_{NE},{\theta }_{NW},{\theta }_{SW},{\theta }_{SE})$ denote the area of the CSR with the corners defined in terms of ${\theta }_Q$ as above. Our goal is to find the maximum of f over the feasible set of arguments, along with its arguments. First, assume ${\theta }_{SE},{\theta }_{NW},{\theta }_{SW}$ are fixed, with the left and bottom supports denoted as $l,b$ (Figure 23). We refer to $f({\theta }_{NE},{\theta }_{NW},{\theta }_{SW},{\theta }_{SE})$ as simply $f_{NE}\left(\theta \right)$ (that is, refer to ${\theta }_{NE}$ as simply $\theta$).

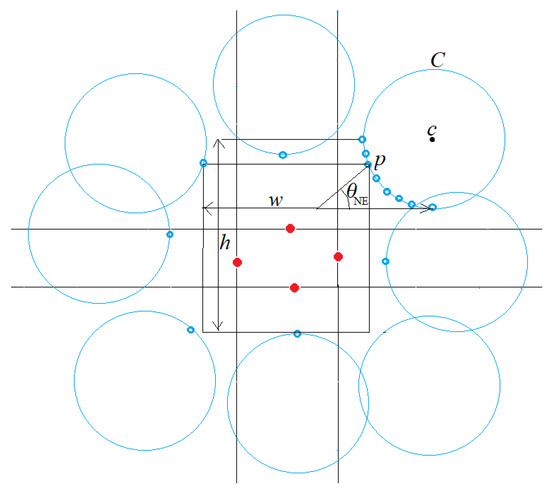
Figure 23. Area of the CSR cornered on circle $C(c,1)$ as a function $f_{NE}\left({\theta }_{NE}\right)$ of that corner’s location.

Lemma 4.

$f_{NE}$ has at most 3 maxima.

Proof. 

We have

$$f_{NE}\left(\theta \right)=(w-sin\theta )·(h-cos\theta ),$$

(1)

where $w=x\left(c\right)-x\left(l\right)$ and $h=y\left(c\right)-y\left(b\right)$. For simplicity, assume that all circles are fully contained in some quadrant, so $w,h>1$. Furthermore,

$$f_{NE}^{\prime }\left(\theta \right)=wsin\theta -hcos\theta +{sin}^2\theta -co{s}^2\theta .$$

(2)

Letting $x=tan\theta$, we get

$$f_{NE}^{\prime }\left(x\right)=\frac{wx-h}{\sqrt{1+x^2}}+\frac{x^2-1}{1+x^2},$$

(3)

so $f_{NE}^{\prime }\left(x\right)=0\iff$

$(wx-h)\sqrt{1+x^2}=1-x^2\iff$

${(wx-h)}^2(1+x^2)={(1-x^2)}^2\iff$

$(w^2-1)x^4-2wh{x}^3+(w^2+h^2+2)x^2-2whx+h^2-1=0\iff$

$(w^2-1)x^2(x^2-1)-2whx(x^2-1)+(h^2-1)(x^2-1)=0\iff$

$((w^2-1)x^2-2whx+h^2-1)(x^2-1)=0$,

which solves to

$$x_1=1,$$

(4)

$$x_{2,3}=\frac{wh+-\sqrt{2(w^2+h^2)-1}}{w^2-1}$$

(5)

(we ignore negative roots since $x\ge 0$). Since $x=tan\theta$, it follows that ${\theta }_1=\frac{\pi }{4},{\theta }_{2,3}=arctan{x}_{2,3}$ are extrema for $f_{NE}$. That is, $f_{NE}$ has no more than 3 maxima. □

Similarly, it follows that $f_{NW},f_{SW},f_{SE}$ each have no more than 3 maxima. Note that the position of two opposite corners of a CSR, say $NE$ and $SW$, determine the position of the other two corners. Since there are only two variables, f has at most 9 maxima we need to consider. We compute all these maxima in $O\left(1\right)$ time and then choose the one that gives the largest CSR.

Thus, we have proved the following result.

Theorem 3.

Given a set of n red points R and a set of m blue unit circles B with $\left|B\right|=m$, the MBSR-C among R and B can be computed in $O(m^2+n)$ time.

4. Conclusions and Future Work

We improve upon the existing result for the maximum bichromatic separating rectangle with outliers problem (MBSR-O) of $O(k^{7}mlogm+n)$ and provide an $O(k^{3}m+kmlogm+n)$ time algorithm. We also consider the problem of finding the maximum bichromatic separating rectangle among unit circles (MBSR-C), for which we give an algorithm that takes $O(m^2+n)$ time [14].

We leave for future consideration proving lower bounds and finding efficient approximation algorithms for MBSR-C and MBSR-O. Other interesting related problems would be finding the smallest and largest circle enclosing red points while avoiding blue circles. Finally, we leave for future work finding the largest rectangle separating red points from blue polygons, as well as solving the weighted version, in which red points have a positive weight, blue points have a negative weight, and the goal is to find the largest rectangle of maximum weight. This weighted version would have promising applications in circuit design, where the board defects may have various severity levels.