Adaptive Propagation Graph Convolutional Networks Based on Attention Mechanism
Abstract
:1. Introduction
2. Related Work
3. Models and Definitions
3.1. APAT-GCN Model
- Setting a different number of convolutional layers for each node, which can speed up training, while reducing memory consumption.
- Sampling of neighboring nodes and discarding some of them can alleviate the problem of over-smoothing during deep convolution.
- Introducing an attention mechanism, so that the central nodes can access more information useful to them when aggregating.
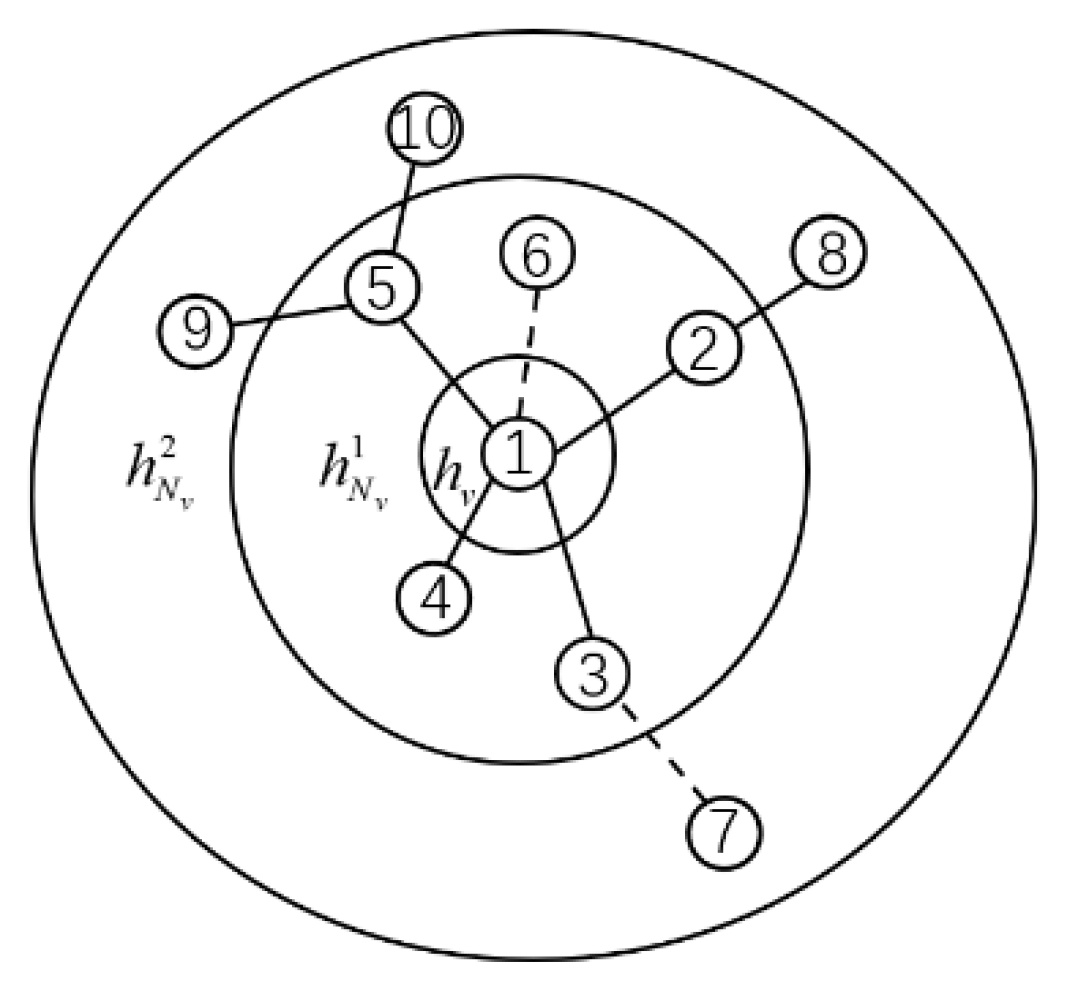
3.2. Definition of Graph
3.3. Designing and Training Deep Graph Convolutions
4. Adaptive Aggregated Graph Convolutional Network
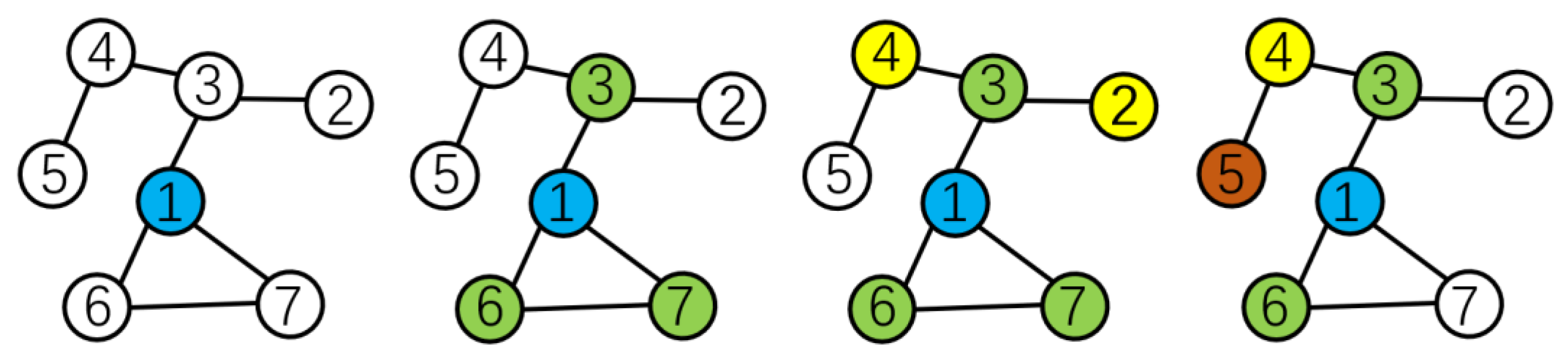
4.1. Graph Centrality Sampling
- Adjacency matrix of the input graph structure data.
- Calculate the centrality of each node in the adjacency matrix, and then obtain a portion of the nodes with higher scores from their neighbors.
- Remove the obtained nodes from the adjacency matrix to obtain a new adjacency matrix.
- Repeat steps 2 and 3, until the number of neighboring nodes obtained is sufficient.
- Feed all selected nodes into the model for training.
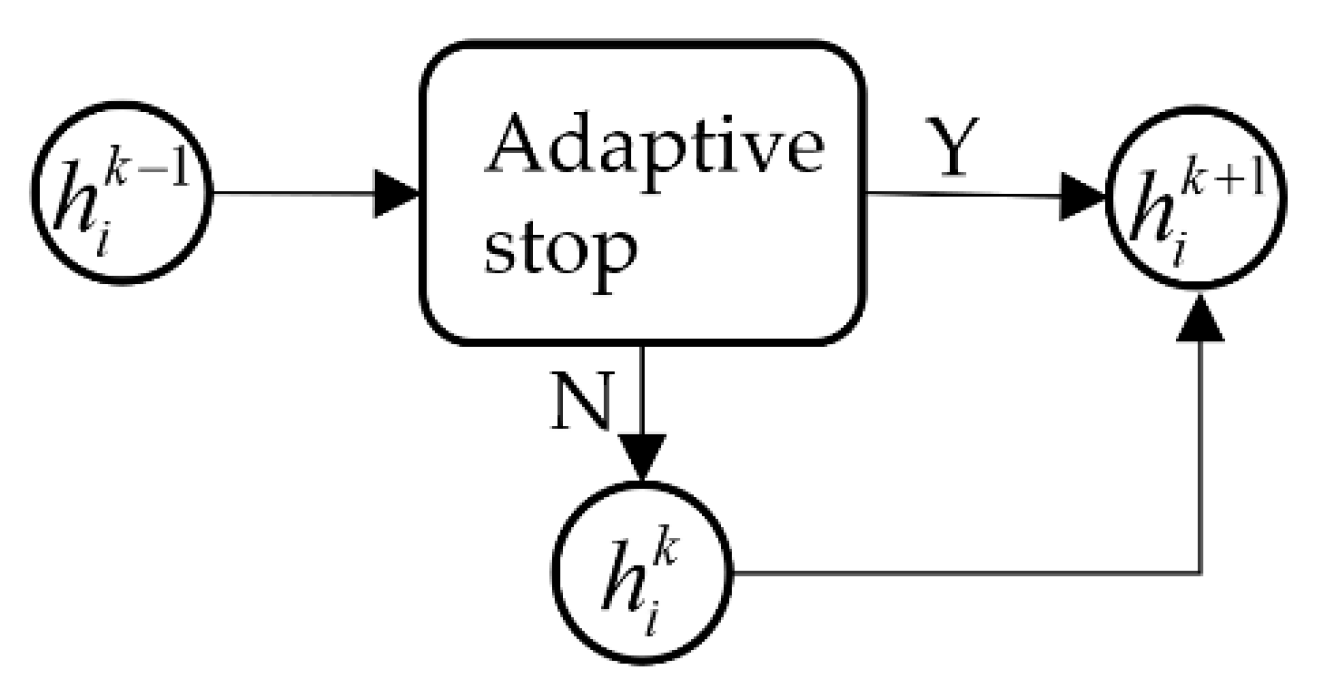
4.2. Adaptive Propagation Stop
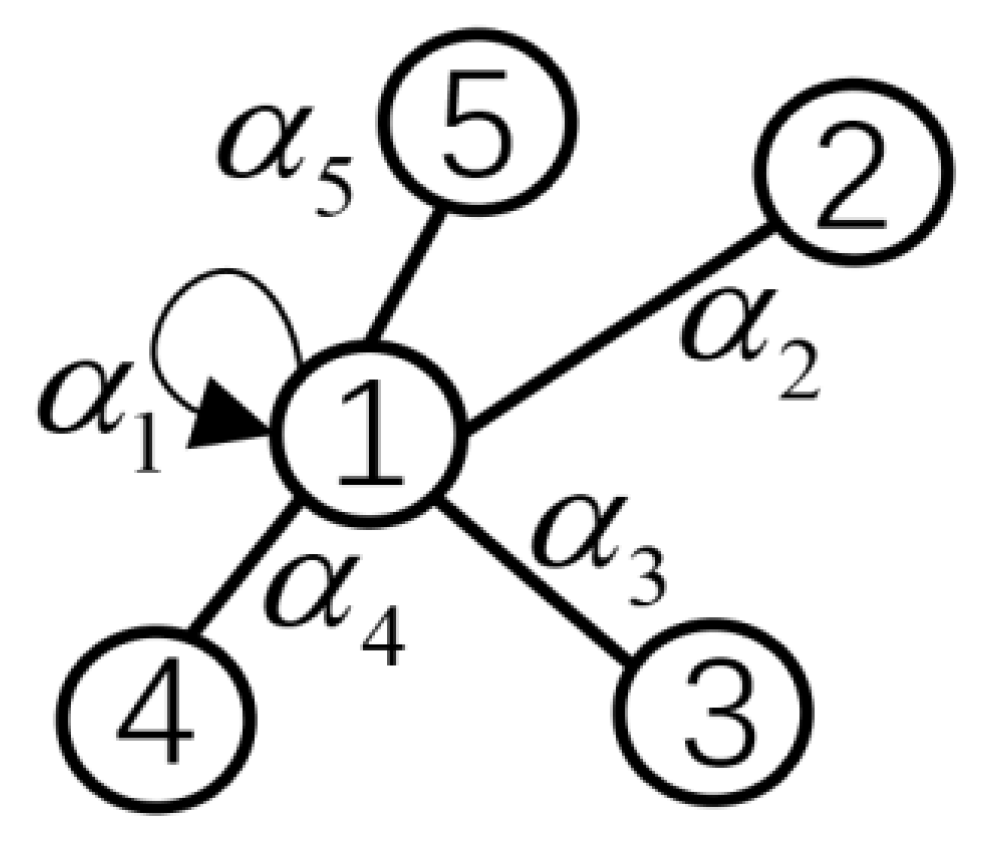
4.3. Attention Mechanism
5. Experimental Analysis
5.1. Data Set and Experimental Setup
5.2. Over-Smoothing Problems
5.3. Parameter Settings for the Baseline Model
5.4. Comparison of Experimental Effects
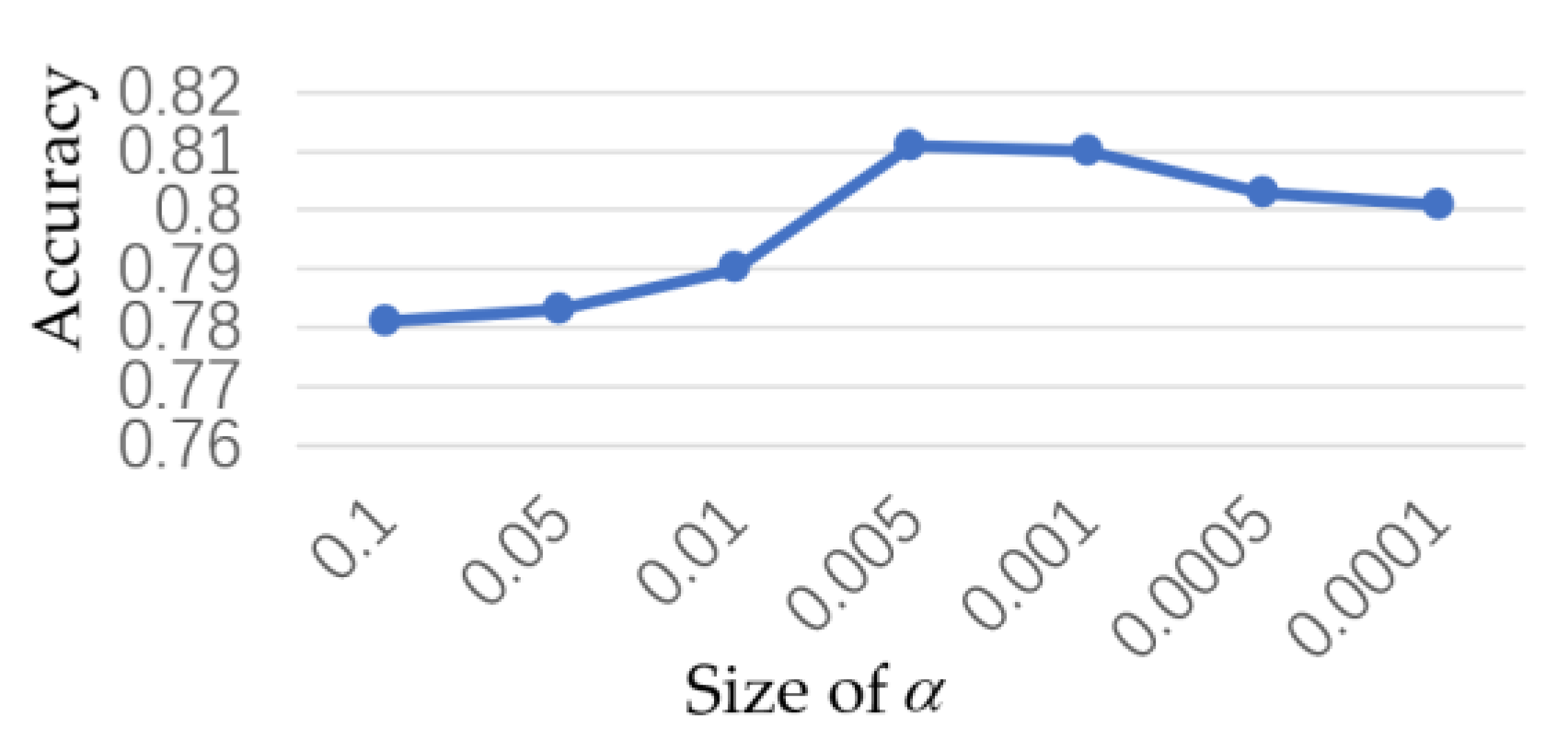
5.5. Adjustment of Hyperparameters
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef] [PubMed]
- Ciresan, D.C.; Meier, U.; Masci, J.; Gambardella, L.M.; Schmidhuber, J. Flexible, High Performance Convolutional Neural Networks for Image Classification. In Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence, Barcelona, Spain, 19 June 2011. [Google Scholar]
- Liao, R.; Brockschmidt, M.; Tarlow, D.; Gaunt, A.L.; Urtasun, R.; en Zemel, R. Graph Partition Neural Networks for Semi-Supervised Classification. In Proceedings of the Sixth International Conference on Learning Representations, Vancouver, BC, Canada, 30 May 2018. [Google Scholar]
- Zhang, M.; Chen, Y. Inductive Matrix Completion Based on Graph Neural Networks. arXiv 2020, arXiv:1904.12058. [Google Scholar]
- Capela, F.; Nouchi, V.; van Deursen, R.; Tetko, I.V.; Godin, G. Multitask Learning On Graph Neural Networks Applied To Molecular Property Predictions. arXiv 2019, arXiv:1910.13124. [Google Scholar]
- Jeon, Y.; Kim, J. Active Convolution: Learning the Shape of Convolution for Image Classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 26 July 2017. [Google Scholar]
- Chen, Z.; Chen, F.; Zhang, L.; Ji, T.; Fu, K.; Zhao, L.; Chen, F.; Wu, L.; Aggarwal, C.; Lu, C. Bridging the Gap between Spatial and Spectral Domains: A Survey on Graph Neural Networks. arXiv 2021, arXiv:2002.11867. [Google Scholar]
- Shuman, D.I.; Narang, S.K.; Frossard, P.; Ortega, A.; Vandergheynst, P. The Emerging Field of Signal Processing on Graphs: Extending High-Dimensional Data Analysis to Networks and Other Irregular Domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef]
- Fang, Z.; Xiongwei, Z.; Tieyong, C. Spatial-temporal slow fast graph convolutional network for skeleton-based action recognition. Neural Inf. Processing 2021, 16, 205–217. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral Networks and Locally Connected Networks on Graphs. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 21 May 2014. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering. In Proceedings of the Advances in Neural Information Processing Systems, San Francisco, CA, USA, 5 December 2016. [Google Scholar]
- Xu, B.; Shen, H.; Cao, Q.; Qiu, Y.; Cheng, X. Graph Wavelet Neural Network. In Proceedings of the Seventh International Conference on Learning Representations, New Orleans, LA, USA, 6 April 2019. [Google Scholar]
- Atwood, J.; Towsley, D. Diffusion-Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5 December 2016. [Google Scholar]
- Niepert, M.; Ahmed, M.; Kutzkov, K. Learning Convolutional Neural Networks for Graphs. In Proceedings of the 33rd International Conference on International Conference on Machine Learning, New York, NY, USA, 19 June 2016. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive Representation Learning on Large Graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4 December 2017. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural Message Passing for Quantum Chemistry. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6 July 2017. [Google Scholar]
- Sandeep, C.R.; Salim, A.; Sethunadh, R.; Sumitra, S. An efficient scheme based on graph centrality to select nodes for training for effective learning. arXiv 2021, arXiv:2104.14123. [Google Scholar]
- Graves, A. Adaptive Computation Time for Recurrent Neural Networks. arXiv 2016, arXiv:1603.08983. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the Sixth International Conference on Learning Representations, Vancouver, BC, Canada, 30 May 2018. [Google Scholar]
- Zhou, J. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Shuai, M.; Jianwei, L. Survey on Graph Neural Network. J. Comput. Res. Dev. 2022, 59, bll 47. [Google Scholar]
- Krzysztof, C.; Han, L.; Arijit, S. From block-Toeplitz matrices to differential equations on graphs: Towards a general theory for scalable masked Transformers. arXiv 2021, arXiv:2107.07999. [Google Scholar]



| Type of Task | Data Sets | Number of Nodes | Number of Sides |
|---|---|---|---|
| Node classification | Core | 2708 | 5429 |
| CiteSeer | 3312 | 4732 | |
| Figure classification | Protein | 43,471 | 162,088 |
| Reddit-5K | 122,737 | 265,506 |
| Models | Core | CiteSeer | Protein | Reddit-5K |
|---|---|---|---|---|
| Graph-SAGE | 0.778 | 0.791 | 0.921 | 0.908 |
| AP-GCN | 0.806 | 0.811 | 0.917 | 0.897 |
| GAT | 0.802 | 0.801 | 0.933 | 0.907 |
| APAT-GCN 1 | 0.811 | 0.816 | 0.941 | 0.912 |
| Sampling Method | Micro-Averaged F1 (Core) |
|---|---|
| Random | 0.304 |
| Deep walk | 0.742 |
| Chart center degree sampling | 0.799 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Gan, Y.; Yang, R. Adaptive Propagation Graph Convolutional Networks Based on Attention Mechanism. Information 2022, 13, 471. https://doi.org/10.3390/info13100471
Zhang C, Gan Y, Yang R. Adaptive Propagation Graph Convolutional Networks Based on Attention Mechanism. Information. 2022; 13(10):471. https://doi.org/10.3390/info13100471
Chicago/Turabian StyleZhang, Chenfang, Yong Gan, and Ruisen Yang. 2022. "Adaptive Propagation Graph Convolutional Networks Based on Attention Mechanism" Information 13, no. 10: 471. https://doi.org/10.3390/info13100471
APA StyleZhang, C., Gan, Y., & Yang, R. (2022). Adaptive Propagation Graph Convolutional Networks Based on Attention Mechanism. Information, 13(10), 471. https://doi.org/10.3390/info13100471






