Influence of Sea Surface Current on Wave Height Inversion in Shadow Statistical Method
Abstract
:1. Introduction
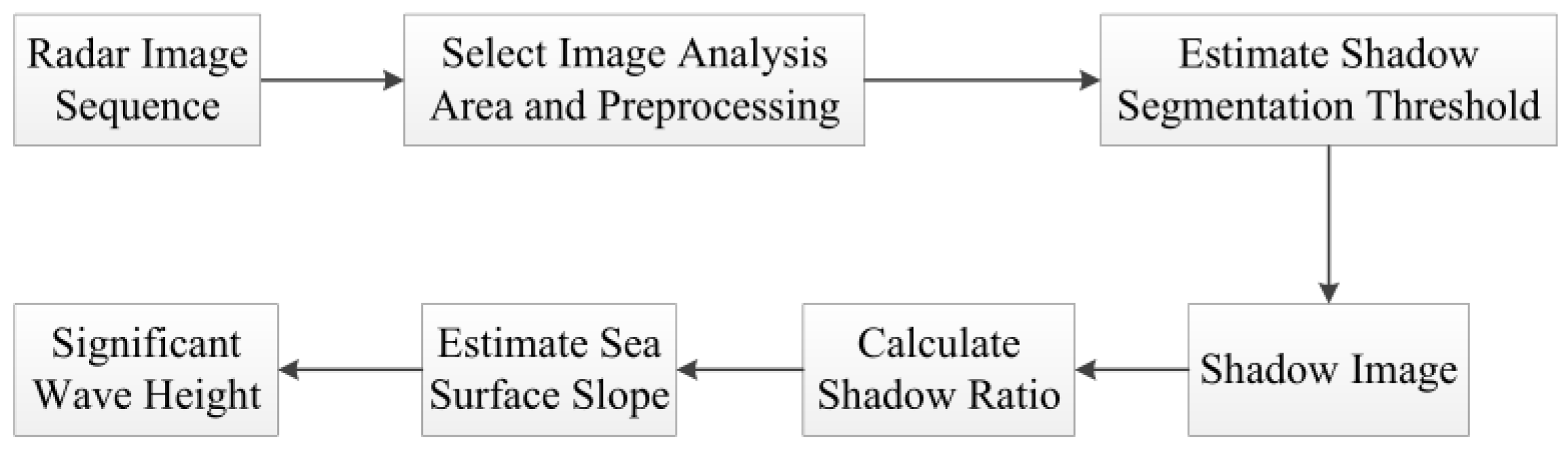
2. Basic Principle of Calculating Wave Height by Using the Shadow Statistical Method
2.1. The Estimation of the Shadow Segmentation Threshold
2.2. The Illumination Ratio of the Radar Image
2.3. The Estimation of the Sea Wave Surface Slope
2.4. The Estimation of the Significant Wave Height
3. Theory Analysis of the Effect of Sea Surface Current on Wave Height Inversion
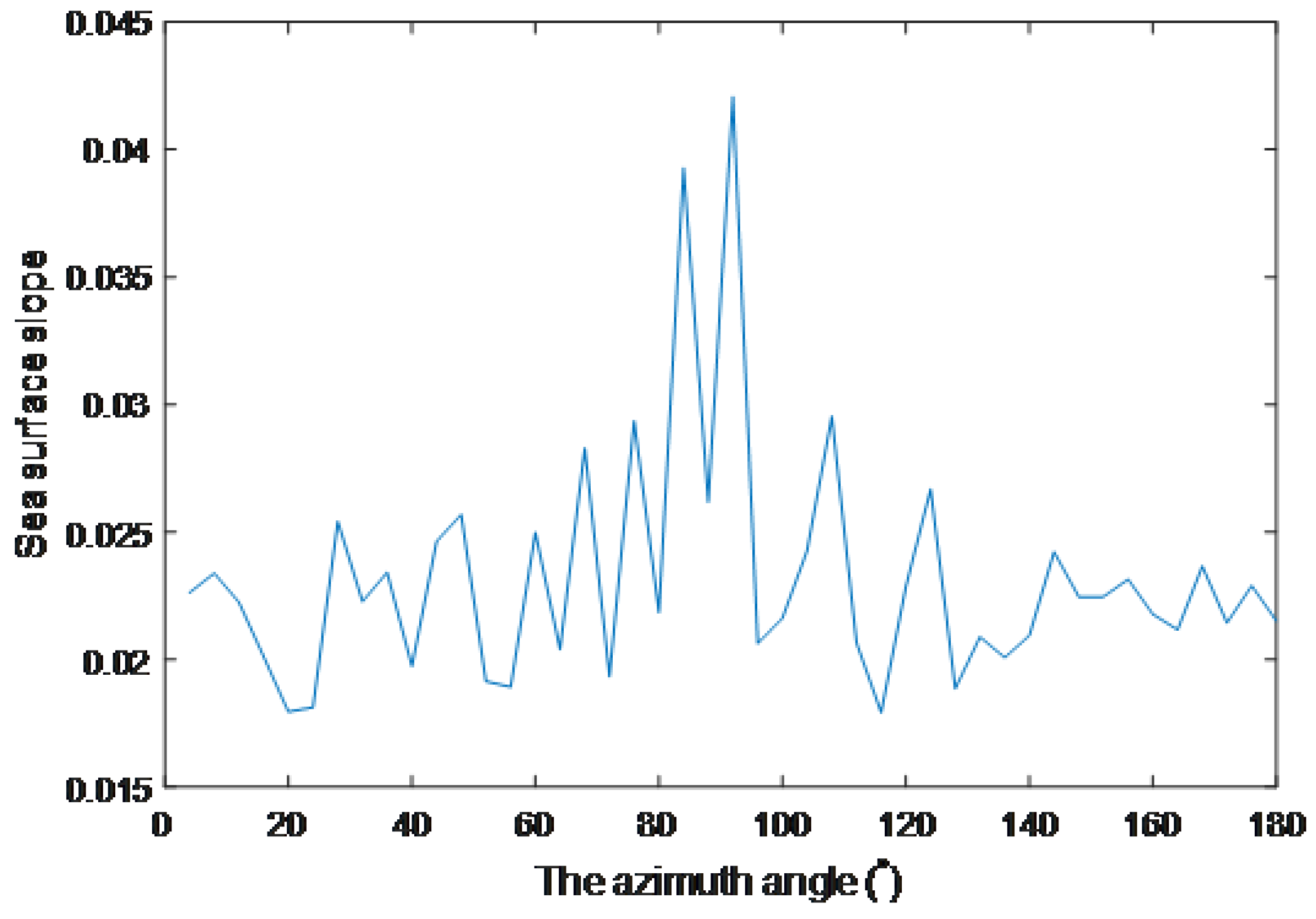
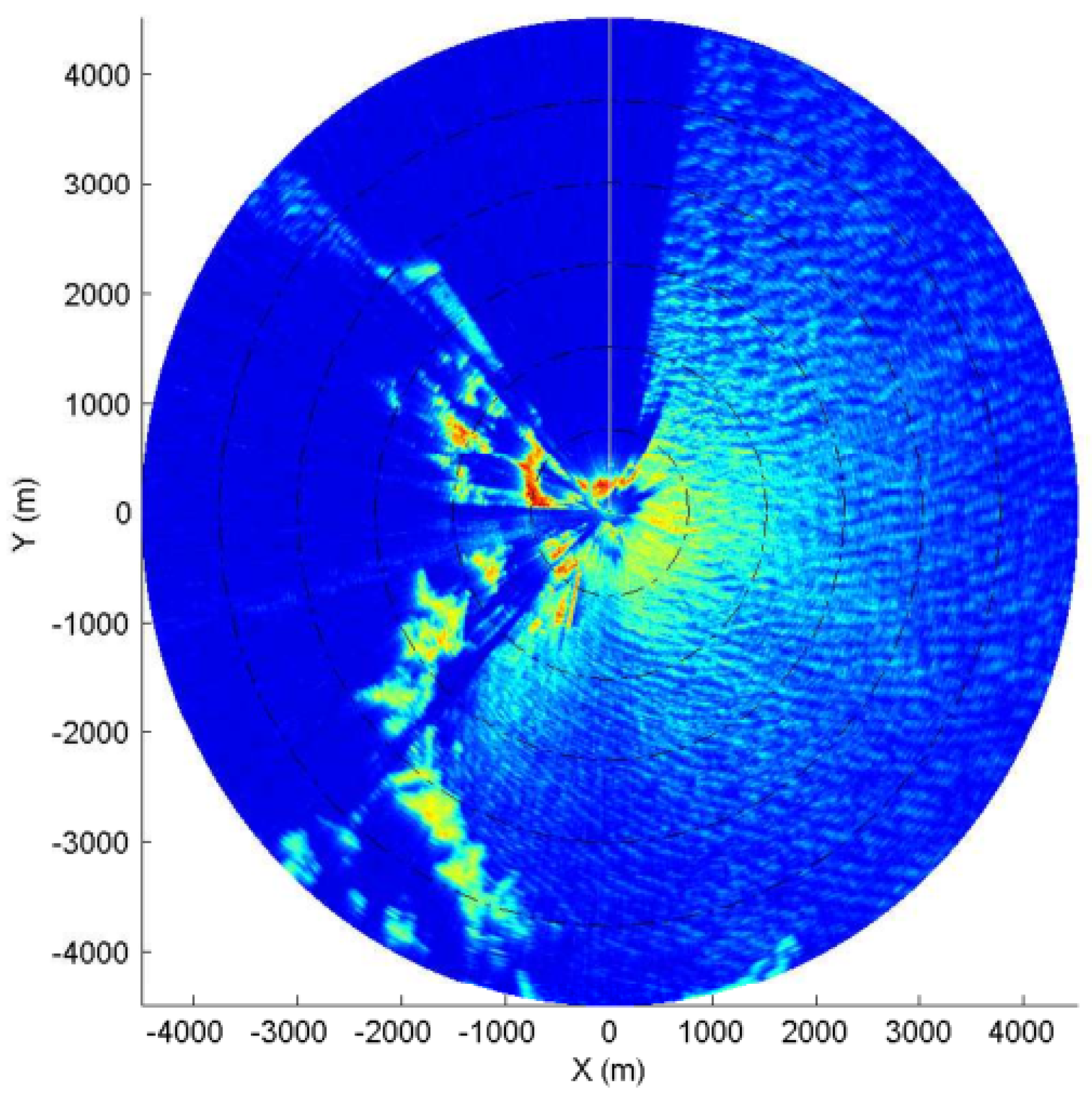
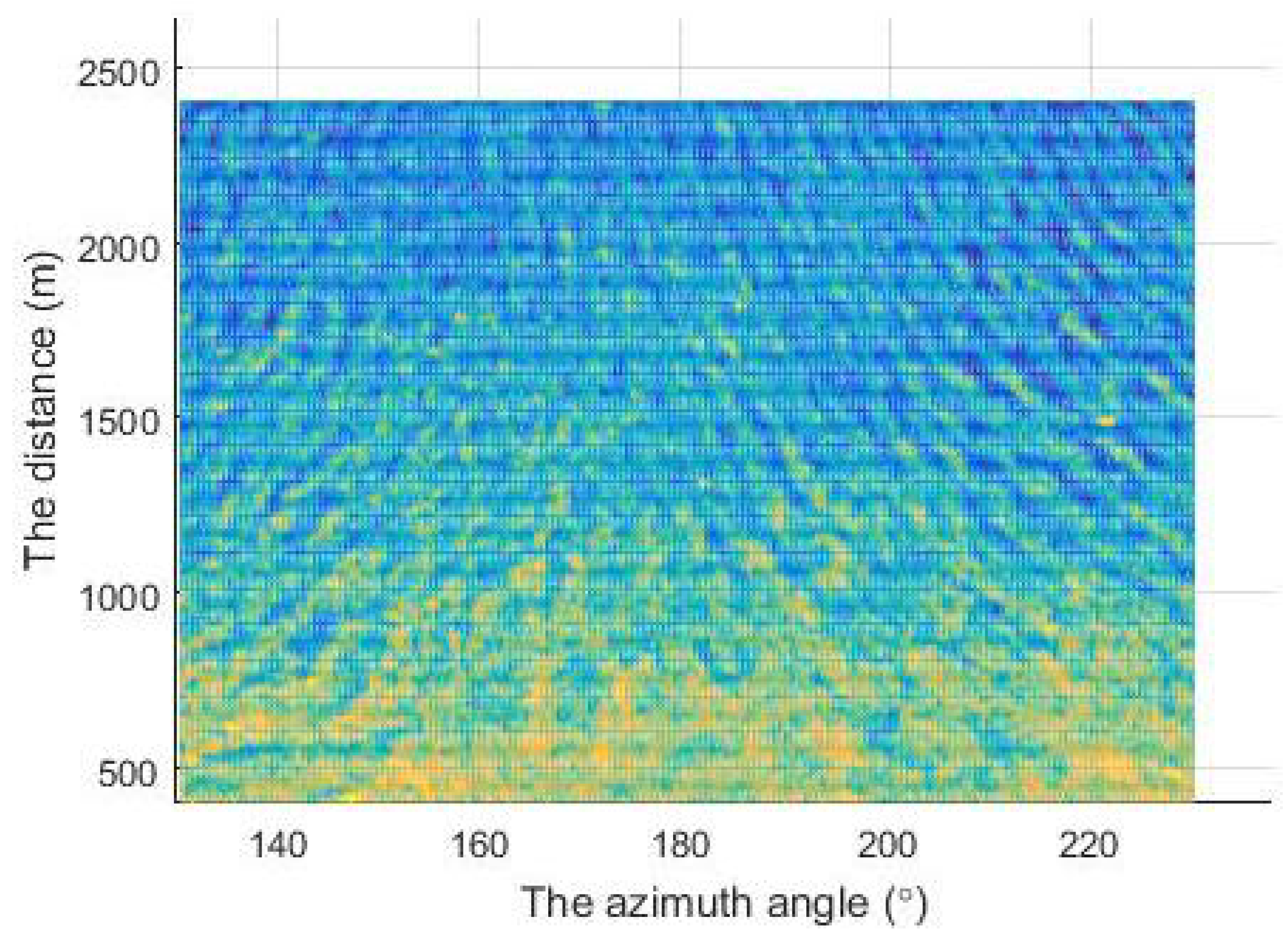
4. Experimental Results and Analysis
4.1. Synthetic Radar Images and Experiment
4.2. Shore-Based Radar Images and Experiment
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
References
- Huang, W.; Liu, X.; Gill, E.W. Ocean wind and wave measurements using X-band marine radar: A comprehensive review. Remote Sens. 2017, 9, 1261. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Huang, W. Identification of rain and low-backscatter regions in X-band marine radar images: An unsupervised approach. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4225–4236. [Google Scholar] [CrossRef]
- Lu, Z.; Yang, J.; Huang, Y. Sea wind direction extraction by X-band radar in moving platform. Syst. Eng. Electron. 2016, 38, 799–803. [Google Scholar]
- Chernyshov, P.; Vrecica, T.; Streßer, M.; Carrasco, R.; Toledo, Y. Rapid wavelet-based bathymetry inversion method for nearshore X-band radars. Remote Sens. Environ. 2020, 240, 111688. [Google Scholar] [CrossRef]
- Gangeskar, R. Verifying high-accuracy ocean surface current measurements by x-band radar for fixed and moving installations. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4845–4855. [Google Scholar] [CrossRef]
- Wei, Y.; Zheng, Y.; Lu, Z. A Method for retrieving wave parameters from synthetic X-band marine radar images. IEEE Access 2020, 8, 204880–204890. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, X.; Zhao, C.; Li, J.; Huang, W.; Gill, E.W. Observation and intercomparison of wave motion and wave measurement using shore-based coherent microwave radar. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7594–7605. [Google Scholar] [CrossRef]
- Young, I.; Rosenthal, W.; Ziemer, F. A three dimensional analysis of marine radar images for the determination of ocean wave directionality and surface currents. J. Geophys. Res. 1985, 90, 142–149. [Google Scholar] [CrossRef] [Green Version]
- Nieto-Borge, J.C.; Hessner, K.; Jarabo-Amores, P.; MataMoya, D. Signal-to-noise ratio analysis to estimate ocean wave heights from x-band marine radar image time series. IET Radar Sonar Navig. 2008, 2, 35–41. [Google Scholar] [CrossRef] [Green Version]
- Plant, W.J.; Gordon, F. Wave shadowing and modulation of microwave backscatter from the ocean. J. Geophys. Res. Ocean. 2012, 117, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Gangeskar, R. An algorithm for estimation of wave height from shadowing in X-band radar sea surface images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3373–3381. [Google Scholar] [CrossRef]
- Lund, B.; Collins, C.O.; Graber, H.C.; Terrill, E.; Herbers, T.H.C. Marine radar ocean wave retrieval’s dependency on range and azimuth. Ocean. Dyn. 2014, 64, 999–1018. [Google Scholar] [CrossRef]
- Dankert, H.; Horstmann, J.; Rosenthal, W. Wind- and wave-field measurements using marine X-band radar-image sequences. IEEE J. Ocean. Eng. 2013, 30, 534–542. [Google Scholar] [CrossRef]
- Vicen-Bueno, R.; Horstmann, J.; Terril, E.; Paolo, T.D.; Dannenberg, J. Real-time ocean wind vector retrieval from marine radar image sequences acquired at grazing angle. J. Atmos. Ocean. Technol. 2013, 30, 127–139. [Google Scholar] [CrossRef]
- Liu, X.; Huang, W.; Gill, E.W. Wave height estimation from shipborne X-band nautical radar images. J. Sens. 2016, 2016, 1078053. [Google Scholar] [CrossRef]
- Liu, X.; Huang, W.; Gill, E.W. Comparison of wave height measurement algorithms for ship-borne X-band nautical radar. Can. J. Remote Sens. 2016, 42, 343–353. [Google Scholar] [CrossRef]
- Wei, Y.; Lu, Z.; Pian, G.; Liu, H. Wave height estimation from shadowing based on the acquired X-band marine radar images in coastal area. Remote Sens. 2017, 9, 859. [Google Scholar] [CrossRef] [Green Version]
- Ardhuin, F.; Gille, S.T.; Menemenlis, D.; Rocha, C.B.; Rascle, N.; Chapron, B.; Gula, J.; Molemaker, J. Small-scale open ocean currents have large effects on wind wave heights. J. Geophys. Res. Ocean. 2017, 122, 4500–4517. [Google Scholar] [CrossRef] [Green Version]
- Breivik, Ø.; Mogensen, K.; Bidlot, J.-R.; Balmaseda, M.A.; Janssen, P.A.E.M. Surface wave effects in the NEMO ocean model: Forced and coupled experiments. J. Geophys. Res. Ocean. 2015, 120, 2793–2992. [Google Scholar] [CrossRef] [Green Version]
- Ludeno, G.; Reale, F.; Dentale, F.; Carratelli, E.P.; Natale, A.; Serafino, F. Estimating Nearshore Bathymetry from X-Band Radar Data. Coast. Ocean Obs. Syst. 2015, 265–280. [Google Scholar] [CrossRef]
- Atkinson, J.; Esteves, L.S.; Williams, J.J.; Bell, P.S.; McCann, D.L. Nearshore monitoring with X-band radar: Maximizing utility in dynamic and complex environments. J. Geophys. Res. Ocean. 2021, 126, e2020JC016841. [Google Scholar] [CrossRef]
- Ludeno, G.; Serafino, F. Estimation of the significant wave height from marine radar images without external reference. J. Mar. Sci. Eng. 2019, 7, 432. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Huang, W.; Gill, E.W. Estimation of significant wave height from X-band marine radar images based on ensemble empirical mode decomposition. IEEE Geosci. Remote Sens. Lett. 2017, 17, 1740–1744. [Google Scholar] [CrossRef]
- Wang, L.; Hong, L. Oean wave height inversion under low sea state from horizontal polarized X-band nautical radar images. J. Spat. Sci. 2021, 66, 75–87. [Google Scholar] [CrossRef]
- Chen, X.; Huang, W. Spatial-temporal convolutional gated recurrent unit network for significant wave height estimation from shipborne marine radar data. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Wu, L.-C.; Doong, D.-J.; Lai, J.-W. Influences of nononshore winds on significant wave height estimations using coastal X-band radar images. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Shen, C.; Huang, W.; Gill, E.W.; Carrasco, R.; Horstmann, J. An algorithm for surface current retrieval from X-band marine radar images. Remote Sens. 2015, 7, 7753–7767. [Google Scholar] [CrossRef] [Green Version]
- Hessner, K.G.; El Naggar, S.; von Appen, W.-J.; Strass, V.H. On the reliability of surface current measurements by X-band marine radar. Remote Sens. 2019, 11, 1030. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Zhang, B.; Kudryavtsev, V.; He, Y.; Chu, X. Estimation of sea surface current from X-band marine radar images by cross-spectrum analysis. Remote Sens. 2019, 11, 1031. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.; Carrasco, R.; Shen, C.; Gill, E.W.; Horstmann, J. Surface current measurements using X-band marine radar with vertical polarization. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2988–2997. [Google Scholar] [CrossRef]
- Yang, Z.; Huang, W.; Chen, X. Evaluation and mitigation of rain effect on wave direction and period estimation from X-band marine radar images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5207–5219. [Google Scholar] [CrossRef]
- Yuan, G.; Jia, R.; Dai, Y.; Li, Y. Research on the extraction algorithm of ocean surface current based on sea clutter image. Chin. J. Sci. Instrum. 2011, 32, 1845–1850. [Google Scholar]



| Surface Current (m/s) | Wave Peak Period (s) | Estimated Wave Slope | Retrieved Wave Height (m) | |
|---|---|---|---|---|
| Ignoring the Current | Considering the Current | |||
| 0 | 11.0 | 0.027 | 3.68 | 3.68 |
| 0.5 | 10.7 | 0.029 | 3.84 | 3.62 |
| 1 | 10.4 | 0.030 | 3.98 | 3.54 |
| 2 | 9.8 | 0.032 | 4.29 | 3.38 |
| 3 | 9.3 | 0.032 | 4.27 | 3.04 |
| 4 | 8.9 | 0.037 | 4.98 | 3.28 |
| 5 | 8.5 | 0.038 | 5.01 | 3.08 |
| Radar Parameters | The Performance |
|---|---|
| Electromagnetic Wave Frequency | 9.3 GHz |
| Polarization | HH |
| Antenna Length | 1.8 m |
| Horizontal Beam Width | 0.9° |
| Vertical Beam Width | 21° |
| Antenna Angular Speed | 22 r.p.m. |
| Pulse Width | 50 ns |
| Pulse Repetition Frequency | 1300 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Liu, Y.; Lu, Z.; Zhang, Y. Influence of Sea Surface Current on Wave Height Inversion in Shadow Statistical Method. Information 2021, 12, 303. https://doi.org/10.3390/info12080303
Wei Y, Liu Y, Lu Z, Zhang Y. Influence of Sea Surface Current on Wave Height Inversion in Shadow Statistical Method. Information. 2021; 12(8):303. https://doi.org/10.3390/info12080303
Chicago/Turabian StyleWei, Yanbo, Yike Liu, Zhizhong Lu, and Yuying Zhang. 2021. "Influence of Sea Surface Current on Wave Height Inversion in Shadow Statistical Method" Information 12, no. 8: 303. https://doi.org/10.3390/info12080303
APA StyleWei, Y., Liu, Y., Lu, Z., & Zhang, Y. (2021). Influence of Sea Surface Current on Wave Height Inversion in Shadow Statistical Method. Information, 12(8), 303. https://doi.org/10.3390/info12080303







