Adaptive Multi-Scale Wavelet Neural Network for Time Series Classification
Abstract
1. Introduction
- A multi-scale combined with a depthwise CNN is proposed to learn the candidate frequency decompositions of the time series.
- The optimal frequency decomposition is selected from the candidates by a selector.
- The experiments performed on the UCR archive [5] demonstrate that the AMSW-NN could achieve a better performance based on different classification networks compared with the classical wavelet transform.
2. Background
2.1. Lifting Scheme
2.2. Adaptive Lifting Scheme
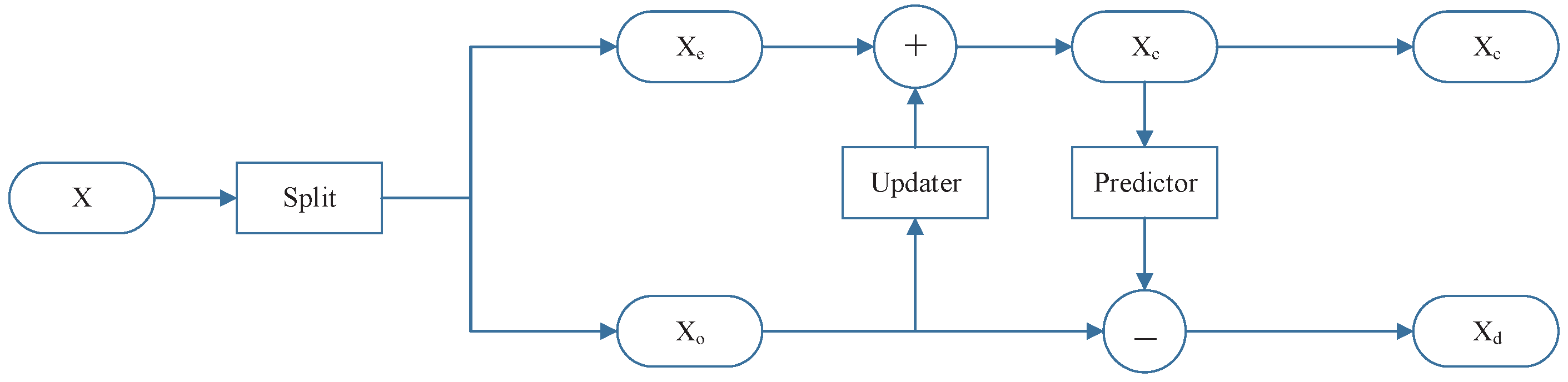
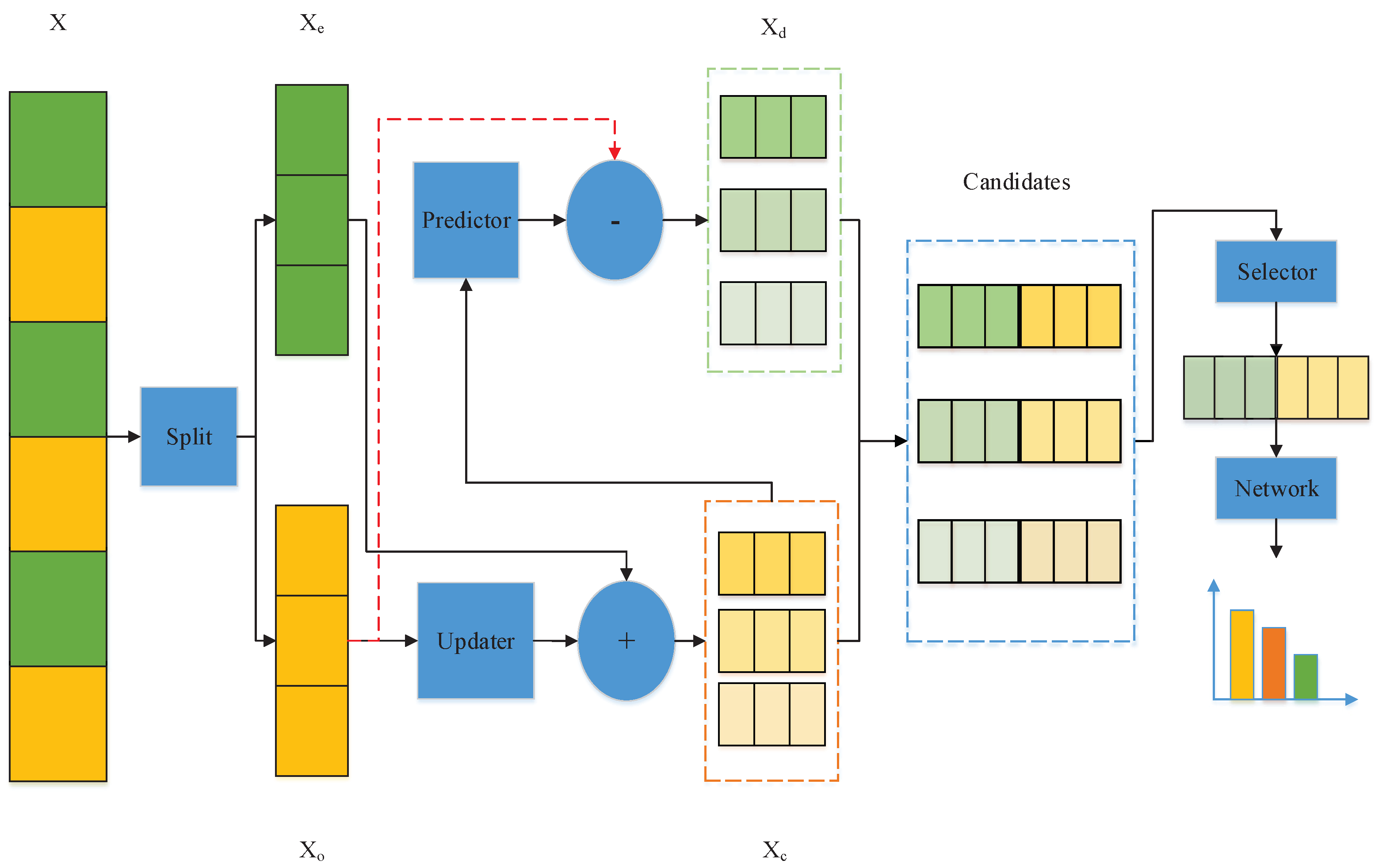
3. Adaptive Multi-Scale Wavelet Neural Network (AMSW-NN)
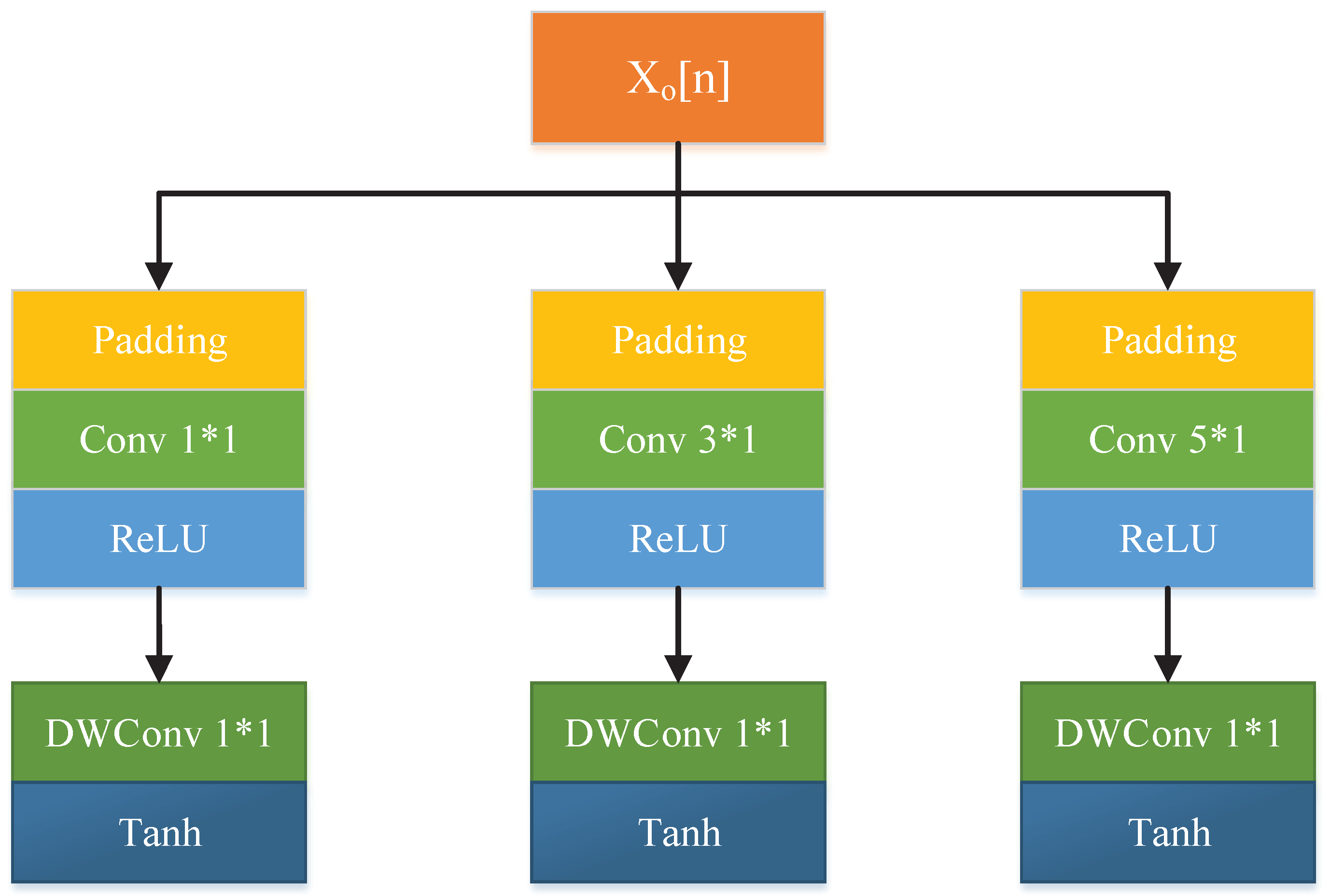
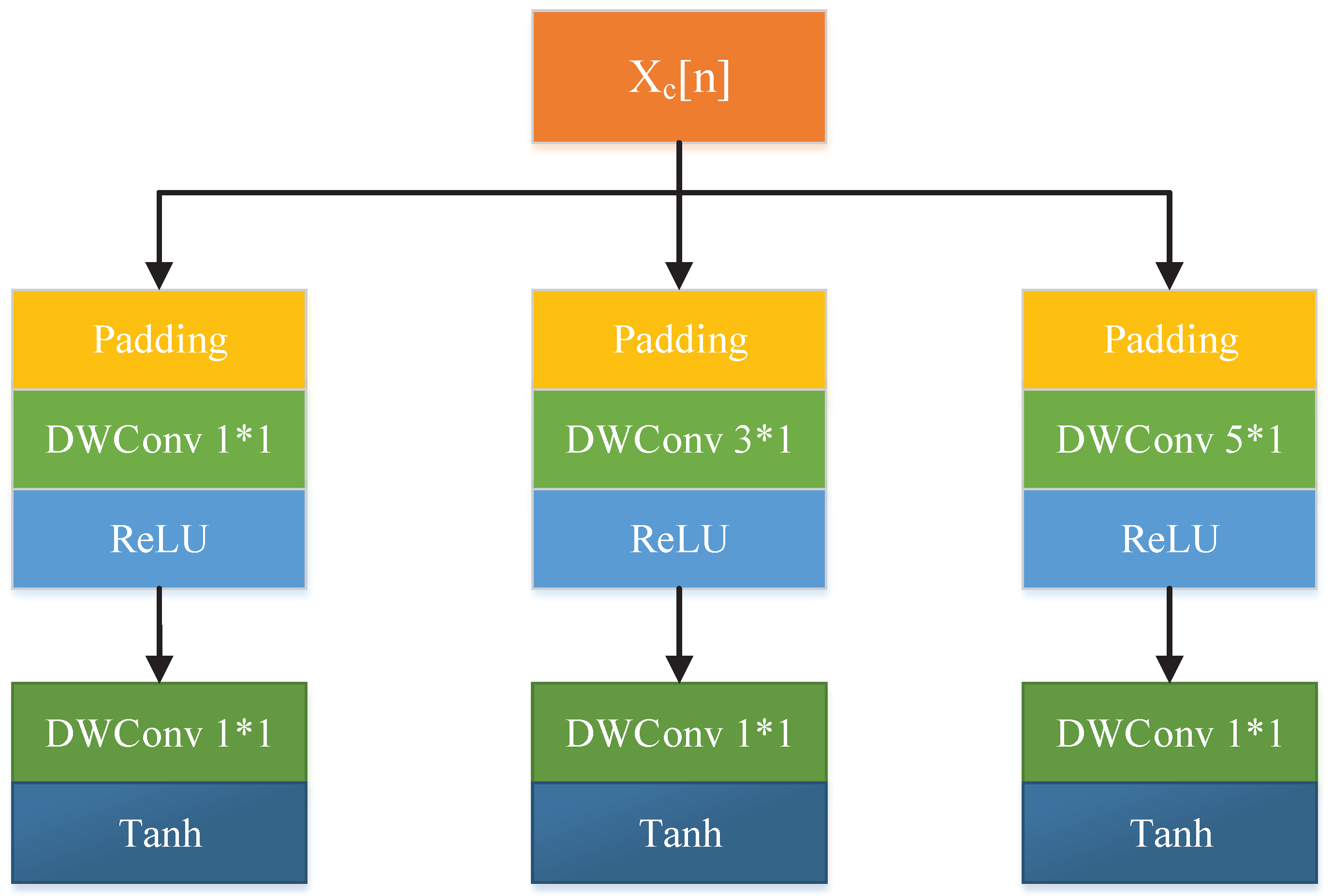
3.1. Updater
3.2. Predictor
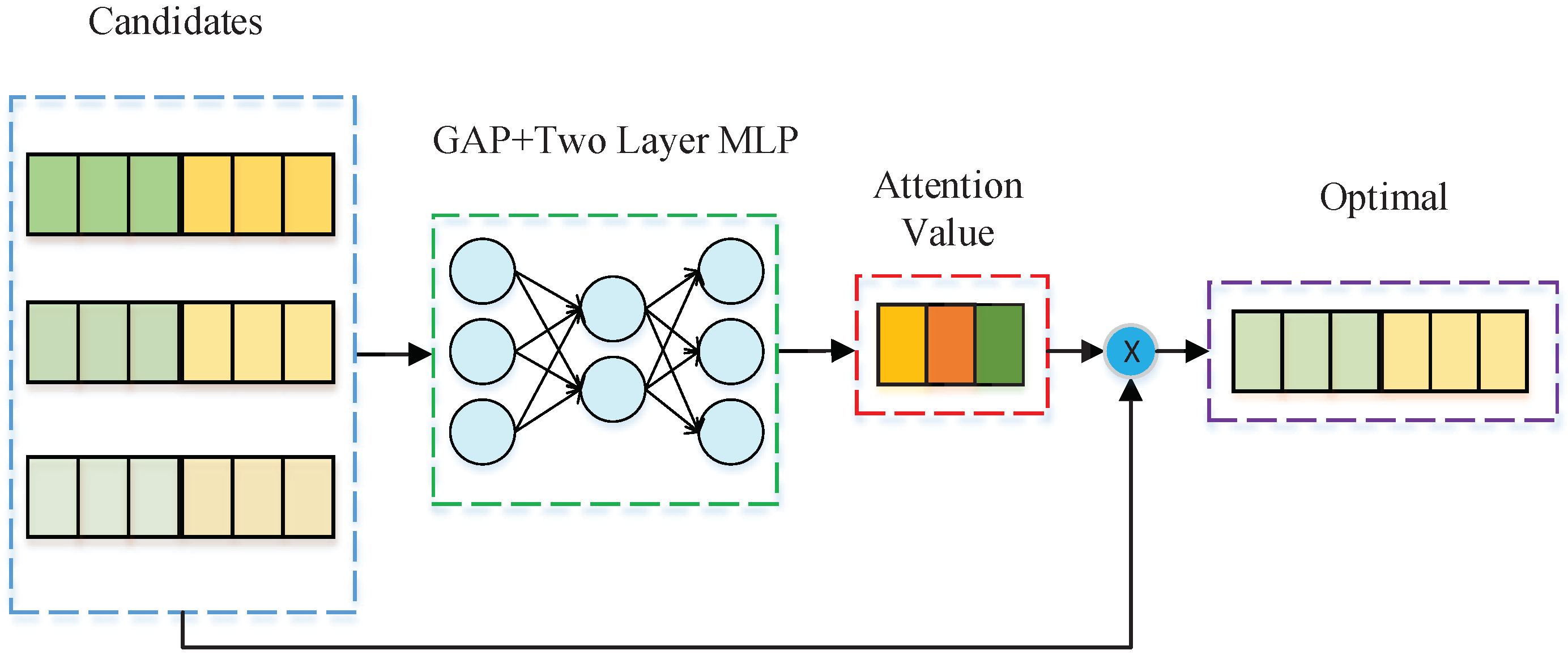
3.3. Selector
3.4. Loss Function
4. Experiment
4.1. Experimental Settings
4.1.1. Dataset
4.1.2. Compared Methods
4.1.3. Evaluation Metrics
4.1.4. Parameter Settings
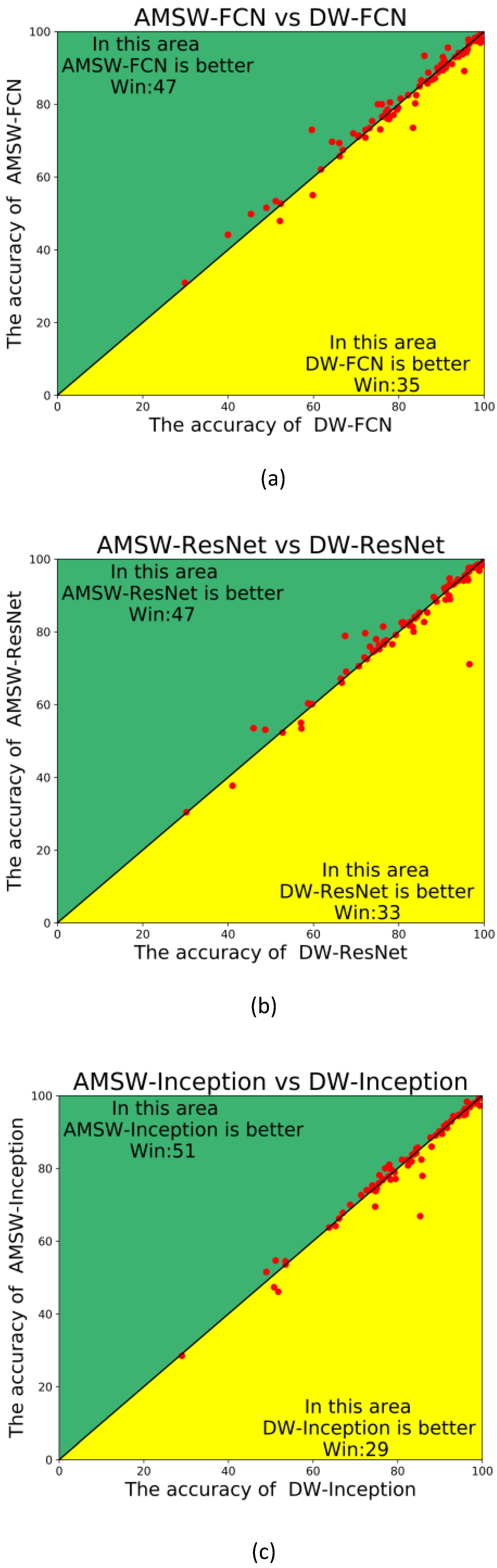
4.2. Experimental Results
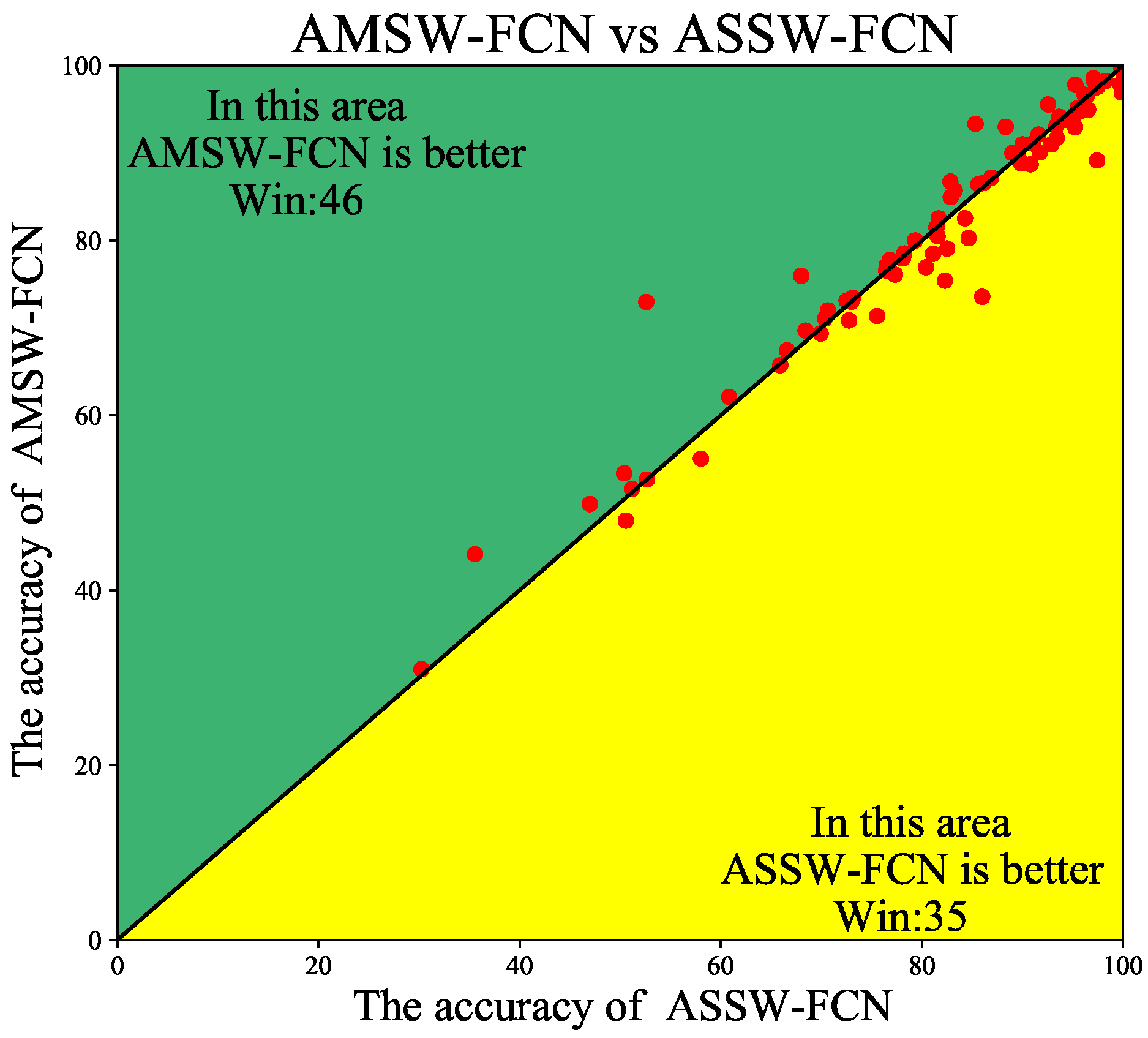
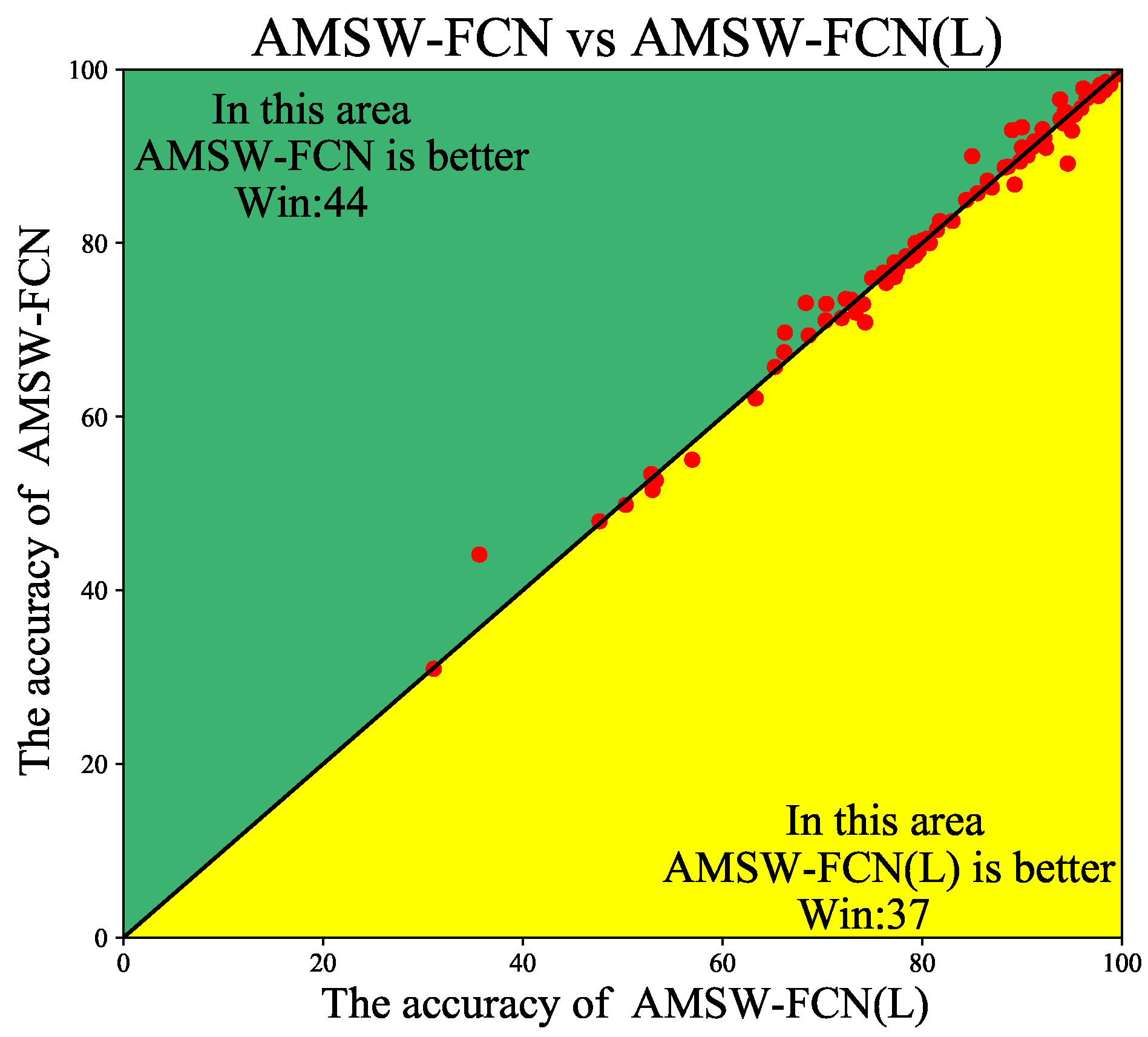
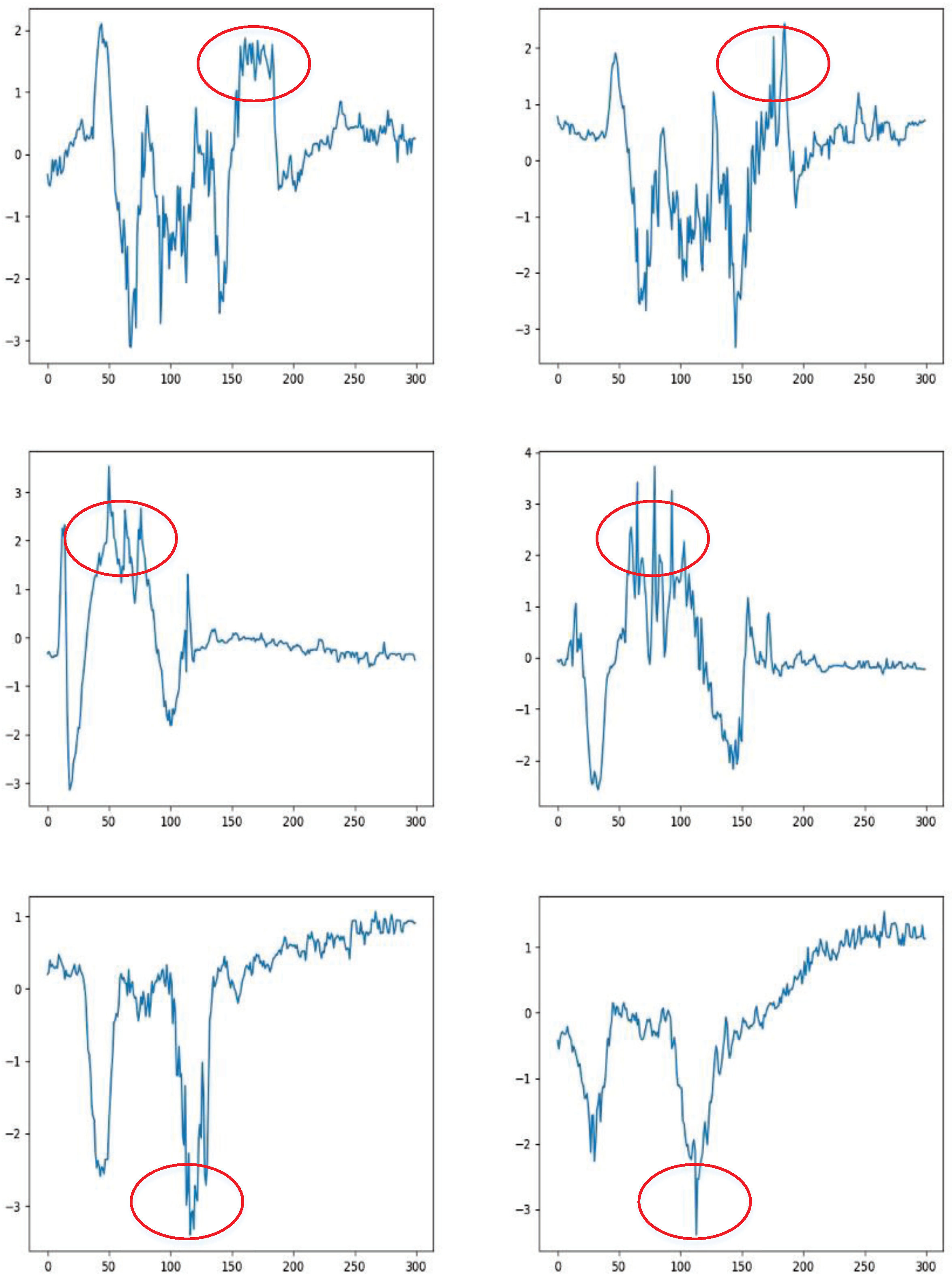
4.3. Ablation Studies
4.4. Complexity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, C.L.; Hsaio, W.H.; Tu, Y.C. Time series classification with multivariate convolutional neural network. IEEE Trans. Ind. Electron. 2018, 66, 4788–4797. [Google Scholar] [CrossRef]
- Ordóñez, F.J.; Roggen, D. Deep convolutional and lstm recurrent neural networks for multimodal wearable activity recognition. Sensors 2016, 16, 115. [Google Scholar] [CrossRef] [PubMed]
- Übeyli, E.D. Wavelet/mixture of experts network structure for EEG signals classification. Expert Syst. Appl. 2008, 34, 1954–1962. [Google Scholar] [CrossRef]
- Al-Jowder, O.; Kemsley, E.; Wilson, R.H. Detection of adulteration in cooked meat products by mid-infrared spectroscopy. J. Agric. Food Chem. 2002, 50, 1325–1329. [Google Scholar] [CrossRef] [PubMed]
- Dau, H.A.; Bagnall, A.; Kamgar, K.; Yeh, C.C.M.; Zhu, Y.; Gharghabi, S.; Ratanamahatana, C.A.; Keogh, E. The UCR time series archive. IEEE/CAA J. Autom. Sin. 2019, 6, 1293–1305. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Li, J.; Wu, J. Multilevel wavelet decomposition network for interpretable time series analysis. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2437–2446. [Google Scholar]
- Ye, L.; Keogh, E. Time series shapelets: A new primitive for data mining. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–12 July 2009; pp. 947–956. [Google Scholar]
- Lines, J.; Bagnall, A. Time series classification with ensembles of elastic distance measures. Data Min. Knowl. Discov. 2015, 29, 565–592. [Google Scholar] [CrossRef]
- Schäfer, P. The BOSS is concerned with time series classification in the presence of noise. Data Min. Knowl. Discov. 2015, 29, 1505–1530. [Google Scholar] [CrossRef]
- Schäfer, P.; Leser, U. Fast and accurate time series classification with weasel. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 637–646. [Google Scholar]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1578–1585. [Google Scholar]
- Fawaz, H.I.; Lucas, B.; Forestier, G.; Pelletier, C.; Schmidt, D.F.; Weber, J.; Webb, G.I.; Idoumghar, L.; Muller, P.A.; Petitjean, F. Inceptiontime: Finding alexnet for time series classification. Data Min. Knowl. Discov. 2020, 34, 1936–1962. [Google Scholar] [CrossRef]
- Li, D.; Bissyandé, T.F.; Klein, J.; Traon, Y.L. Time series classification with discrete wavelet transformed data. Int. J. Softw. Eng. Knowl. Eng. 2016, 26, 1361–1377. [Google Scholar] [CrossRef]
- Akansu, A.N.; Haddad, P.A.; Haddad, R.A.; Haddad, P.R. Multiresolution Signal Decomposition: Transforms, Subbands, and Wavelets; Academic Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Sweldens, W. The lifting scheme: A construction of second generation wavelets. SIAM J. Math. Anal. 1998, 29, 511–546. [Google Scholar] [CrossRef]
- Rodriguez, M.X.B.; Gruson, A.; Polania, L.; Fujieda, S.; Prieto, F.; Takayama, K.; Hachisuka, T. Deep adaptive wavelet network. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikola, HI, USA, 5–9 January 2021; pp. 3111–3119. [Google Scholar]
- Sweldens, W. Wavelets and the lifting scheme: A 5 minute tour. Zamm-Z. Angew. Math. Mech. 1996, 76, 41–44. [Google Scholar]
- Ma, H.; Liu, D.; Xiong, R.; Wu, F. iWave: CNN-Based Wavelet-Like Transform for Image Compression. IEEE Trans. Multimed. 2019, 22, 1667–1679. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, R.; Li, J. Nonlinear wavelets and BP neural networks adaptive lifting scheme. In Proceedings of the 2010 International Conference on Apperceiving Computing and Intelligence Analysis Proceeding, Chengdu, China, 17–19 December 2010; pp. 316–319. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]

| Parameter | Value |
|---|---|
| Kernel size | 5, 3, 1 |
| FD channel | 32 |
| Ratio | 8 |
| Training epoch | 1500/2000 |
| Learning rate | 0.001 |
| 0.01 | |
| 0 |
| Dataset | DWF | AMSWF | DWR | AMSWR | DWI | AMSWI |
|---|---|---|---|---|---|---|
| Adiac | 0.849 | 0.850 | 0.838 | 0.837 | 0.765 | 0.770 |
| ArrowHead | 0.867 | 0.864 | 0.848 | 0.853 | 0.834 | 0.838 |
| Beef | 0.760 | 0.800 | 0.747 | 0.780 | 0.713 | 0.727 |
| BeetleFly | 0.890 | 0.900 | 0.910 | 0.910 | 0.780 | 0.810 |
| BirdChicken | 0.900 | 0.910 | 0.920 | 0.890 | 0.880 | 0.860 |
| Car | 0.903 | 0.930 | 0.907 | 0.920 | 0.910 | 0.917 |
| CBF | 0.982 | 0.974 | 0.989 | 0.968 | 0.996 | 0.997 |
| ChlorineConcentration | 0.796 | 0.785 | 0.835 | 0.801 | 0.856 | 0.824 |
| CinCECGTorso | 0.852 | 0.866 | 0.837 | 0.841 | 0.844 | 0.855 |
| Coffee | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Computers | 0.774 | 0.785 | 0.764 | 0.768 | 0.748 | 0.738 |
| CricketX | 0.774 | 0.769 | 0.811 | 0.818 | 0.838 | 0.838 |
| CricketY | 0.773 | 0.779 | 0.810 | 0.827 | 0.841 | 0.843 |
| CricketZ | 0.798 | 0.791 | 0.843 | 0.843 | 0.845 | 0.855 |
| DiatomSizeReduction | 0.907 | 0.917 | 0.939 | 0.941 | 0.931 | 0.944 |
| DistalPhalanxOutlineAgeGroup | 0.706 | 0.714 | 0.725 | 0.725 | 0.747 | 0.695 |
| DistalPhalanxOutlineCorrect | 0.773 | 0.761 | 0.785 | 0.766 | 0.778 | 0.778 |
| DistalPhalanxTW | 0.660 | 0.694 | 0.676 | 0.691 | 0.653 | 0.642 |
| Earthquakes | 0.757 | 0.731 | 0.744 | 0.748 | 0.737 | 0.741 |
| ECG200 | 0.904 | 0.894 | 0.882 | 0.896 | 0.898 | 0.902 |
| ECG5000 | 0.940 | 0.941 | 0.934 | 0.937 | 0.944 | 0.944 |
| ECGFiveDays | 0.996 | 0.978 | 1.000 | 1.000 | 0.999 | 0.999 |
| ElectricDevices | 0.662 | 0.657 | 0.666 | 0.660 | 0.661 | 0.662 |
| FaceAll | 0.878 | 0.867 | 0.825 | 0.818 | 0.824 | 0.808 |
| FaceFour | 0.932 | 0.930 | 0.955 | 0.955 | 0.927 | 0.932 |
| FacesUCR | 0.954 | 0.948 | 0.962 | 0.964 | 0.956 | 0.956 |
| FiftyWords | 0.705 | 0.711 | 0.765 | 0.766 | 0.831 | 0.818 |
| Fish | 0.981 | 0.976 | 0.987 | 0.985 | 0.986 | 0.983 |
| FordA | 0.940 | 0.931 | 0.961 | 0.948 | 0.957 | 0.958 |
| FordB | 0.822 | 0.825 | 0.826 | 0.826 | 0.848 | 0.857 |
| GunPoint | 0.996 | 1.000 | 1.000 | 0.999 | 0.992 | 0.992 |
| Ham | 0.722 | 0.709 | 0.754 | 0.752 | 0.670 | 0.678 |
| HandOutlines | 0.869 | 0.887 | 0.929 | 0.931 | 0.959 | 0.964 |
| Haptics | 0.523 | 0.527 | 0.571 | 0.550 | 0.535 | 0.545 |
| Herring | 0.644 | 0.697 | 0.588 | 0.603 | 0.688 | 0.700 |
| InlineSkate | 0.400 | 0.441 | 0.411 | 0.377 | 0.518 | 0.461 |
| InsectWingbeatSound | 0.453 | 0.498 | 0.597 | 0.602 | 0.638 | 0.638 |
| ItalyPowerDemand | 0.959 | 0.949 | 0.960 | 0.944 | 0.960 | 0.948 |
| LargeKitchenAppliances | 0.910 | 0.901 | 0.909 | 0.889 | 0.890 | 0.891 |
| Lightning2 | 0.738 | 0.754 | 0.721 | 0.797 | 0.770 | 0.800 |
| Lightning7 | 0.838 | 0.803 | 0.833 | 0.814 | 0.833 | 0.819 |
| Mallat | 0.964 | 0.965 | 0.965 | 0.966 | 0.959 | 0.959 |
| Meat | 0.860 | 0.933 | 0.977 | 0.977 | 0.957 | 0.947 |
| MedicalImages | 0.761 | 0.766 | 0.765 | 0.773 | 0.783 | 0.769 |
| MiddlePhalanxOutlineAgeGroup | 0.490 | 0.516 | 0.460 | 0.535 | 0.490 | 0.516 |
| MiddlePhalanxOutlineCorrect | 0.751 | 0.800 | 0.764 | 0.814 | 0.792 | 0.790 |
| MiddlePhalanxTW | 0.512 | 0.534 | 0.487 | 0.531 | 0.512 | 0.547 |
| MoteStrain | 0.906 | 0.921 | 0.910 | 0.922 | 0.877 | 0.885 |
| NonInvasiveFetalECGThorax1 | 0.961 | 0.951 | 0.952 | 0.941 | 0.962 | 0.958 |
| NonInvasiveFetalECGThorax2 | 0.958 | 0.943 | 0.957 | 0.950 | 0.958 | 0.958 |
| OliveOil | 0.693 | 0.720 | 0.867 | 0.853 | 0.727 | 0.740 |
| OSULeaf | 0.979 | 0.983 | 0.964 | 0.976 | 0.926 | 0.929 |
| PhalangesOutlinesCorrect | 0.804 | 0.815 | 0.807 | 0.825 | 0.810 | 0.824 |
| Phoneme | 0.299 | 0.309 | 0.302 | 0.304 | 0.290 | 0.285 |
| Plane | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| ProximalPhalanxOutlineAgeGroup | 0.841 | 0.825 | 0.860 | 0.827 | 0.844 | 0.842 |
| ProximalPhalanxOutlineCorrect | 0.892 | 0.888 | 0.918 | 0.899 | 0.903 | 0.902 |
| ProximalPhalanxTW | 0.787 | 0.771 | 0.771 | 0.777 | 0.755 | 0.759 |
| RefrigerationDevices | 0.522 | 0.479 | 0.528 | 0.523 | 0.508 | 0.474 |
| ScreenType | 0.598 | 0.550 | 0.572 | 0.534 | 0.535 | 0.536 |
| ShapeletSim | 0.833 | 0.736 | 0.966 | 0.711 | 0.853 | 0.669 |
| ShapesAll | 0.912 | 0.910 | 0.920 | 0.931 | 0.916 | 0.923 |
| SmallKitchenAppliances | 0.777 | 0.759 | 0.732 | 0.759 | 0.757 | 0.782 |
| SonyAIBORobotSurface1 | 0.953 | 0.892 | 0.963 | 0.942 | 0.859 | 0.780 |
| SonyAIBORobotSurface2 | 0.950 | 0.938 | 0.919 | 0.947 | 0.905 | 0.895 |
| StarLightCurves | 0.975 | 0.975 | 0.973 | 0.977 | 0.978 | 0.978 |
| Strawberry | 0.982 | 0.982 | 0.984 | 0.984 | 0.982 | 0.979 |
| SwedishLeaf | 0.965 | 0.967 | 0.958 | 0.952 | 0.962 | 0.952 |
| Symbols | 0.983 | 0.985 | 0.979 | 0.979 | 0.971 | 0.969 |
| SyntheticControl | 0.991 | 0.969 | 0.993 | 0.982 | 0.994 | 0.973 |
| ToeSegmentation1 | 0.963 | 0.978 | 0.939 | 0.944 | 0.956 | 0.959 |
| ToeSegmentation2 | 0.925 | 0.911 | 0.922 | 0.928 | 0.945 | 0.948 |
| Trace | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| TwoLeadECG | 0.992 | 0.995 | 0.999 | 0.998 | 0.963 | 0.983 |
| TwoPatterns | 0.915 | 0.956 | 1.000 | 1.000 | 1.000 | 1.000 |
| UWaveGestureLibraryAll | 0.867 | 0.857 | 0.885 | 0.891 | 0.963 | 0.964 |
| UWaveGestureLibraryX | 0.769 | 0.778 | 0.793 | 0.791 | 0.822 | 0.824 |
| UWaveGestureLibraryY | 0.669 | 0.674 | 0.707 | 0.706 | 0.764 | 0.767 |
| UWaveGestureLibraryZ | 0.731 | 0.734 | 0.739 | 0.745 | 0.766 | 0.771 |
| Wafer | 0.998 | 0.998 | 0.999 | 0.998 | 0.997 | 0.997 |
| Wine | 0.596 | 0.730 | 0.674 | 0.789 | 0.785 | 0.796 |
| WordSynonyms | 0.618 | 0.621 | 0.664 | 0.671 | 0.740 | 0.753 |
| Worms | 0.779 | 0.805 | 0.753 | 0.764 | 0.795 | 0.771 |
| WormsTwoClass | 0.722 | 0.730 | 0.719 | 0.730 | 0.751 | 0.745 |
| Yoga | 0.885 | 0.872 | 0.889 | 0.883 | 0.917 | 0.912 |
| Number of win | 13 | 16 | 23 | 16 | 16 | 25 |
| AVG-AR | 3.824 | 3.729 | 3.153 | 3.082 | 3.271 | 3.141 |
| AVG-GR | 3.297 | 3.138 | 2.612 | 2.658 | 2.765 | 2.536 |
| MPCE | 0.047 | 0.046 | 0.044 | 0.044 | 0.045 | 0.046 |
| Component | Parameter Amount |
|---|---|
| FD-Network | 3564 |
| FCN | 271,154 |
| ResNet | 526,964 |
| Inception | 426,642 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, K.; Hou, Y.; Zhou, S.; Zhang, Y. Adaptive Multi-Scale Wavelet Neural Network for Time Series Classification. Information 2021, 12, 252. https://doi.org/10.3390/info12060252
Ouyang K, Hou Y, Zhou S, Zhang Y. Adaptive Multi-Scale Wavelet Neural Network for Time Series Classification. Information. 2021; 12(6):252. https://doi.org/10.3390/info12060252
Chicago/Turabian StyleOuyang, Kewei, Yi Hou, Shilin Zhou, and Ye Zhang. 2021. "Adaptive Multi-Scale Wavelet Neural Network for Time Series Classification" Information 12, no. 6: 252. https://doi.org/10.3390/info12060252
APA StyleOuyang, K., Hou, Y., Zhou, S., & Zhang, Y. (2021). Adaptive Multi-Scale Wavelet Neural Network for Time Series Classification. Information, 12(6), 252. https://doi.org/10.3390/info12060252






