A Secure Steganographic Channel Using DNA Sequence Data and a Bio-Inspired XOR Cipher

Abstract

Secure communication is becoming an urgent need in a digital world where tera bytes of sensitive information are sent back and forth over public networks. In this paper, we combine the power of both encryption and Steganography to build a secure channel of communication between two parties. The proposed method uses DNA sequence data as a cover to hide the secret message. The hiding process is performed in phases that start with a complementary substitution operation followed by a random insertion process. Furthermore, and before the hiding process takes place, the message is encrypted to secure its contents. Here, we propose an XOR cipher that is also based on how DNA data is digitally represented and stored. A fixed-size header is embedded right before the message itself to facilitate the blind extraction process. The experimental results showed an outstanding performance of the proposed technique, in comparison with other methods, in terms of capacity, security, as well as blind extraction.

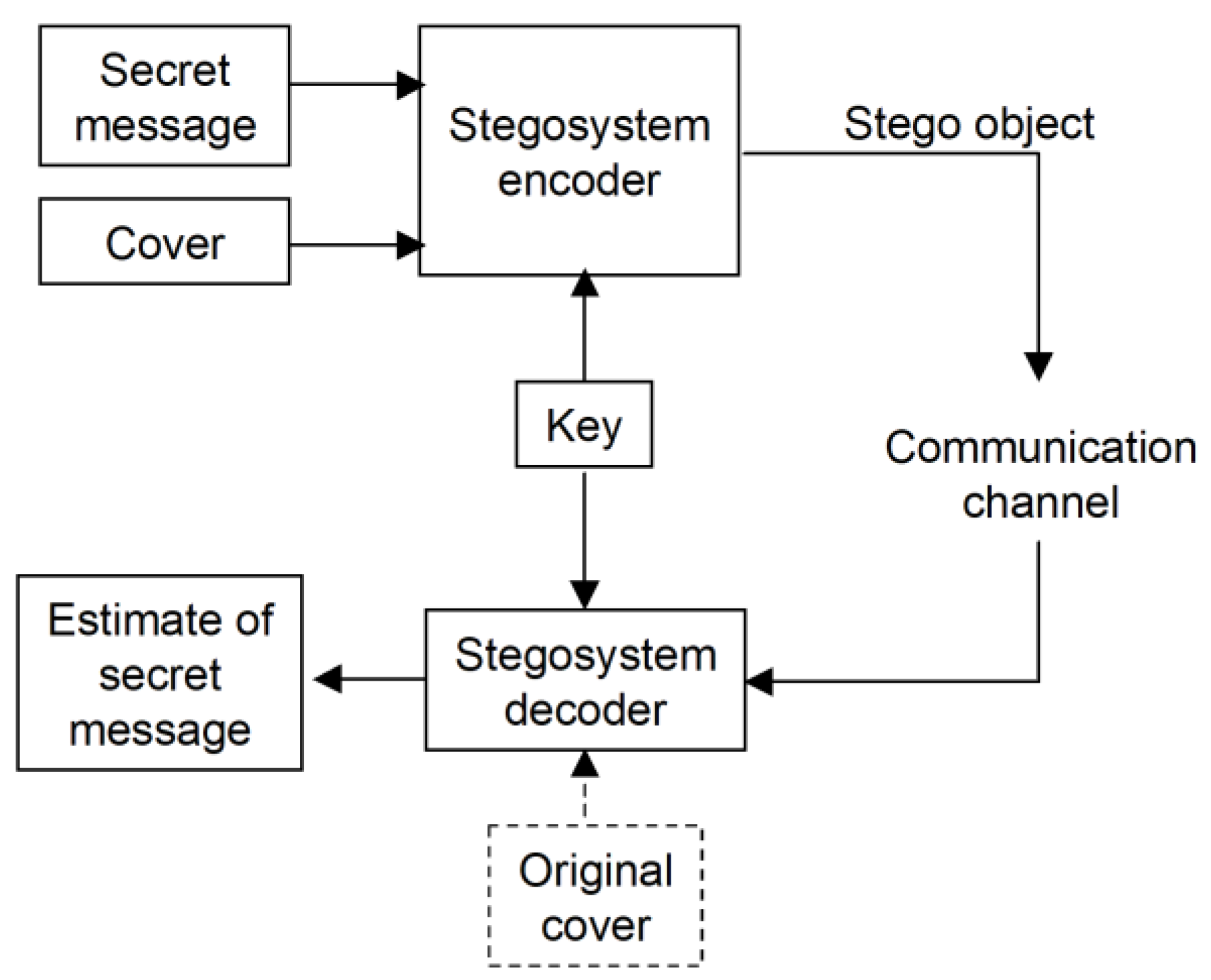
1. Introduction

Cryptography has been recognized as one of the oldest and most effective security tactics. It relies on transforming the content of the data being communicated to make it incomprehensible for everyone except the target recipient. Hence, all encryption algorithms require the sender and receiver to agree on a secret key to facilitating the decryption process. Therefore, if a good key management policy is not in place, the secrecy of the data can be compromised. Usually, the longer the key, the harder is the cipher to break. However, with the advances in computers and computation, cryptanalysis techniques made it impossible to claim that any encryption technique is 100% secure.

On the other hand, steganography provides a wide set of methods that hide the secret message into some cover media to achieve secure and undetectable communication. Unlike cryptography, the structure of the message is not changed, instead, it is embedded into the stego-media which cannot be easily distinguished from the original cover. This is considered one of the great advantages of using steganographic techniques, as it hides the very existence of the communication making it very difficult for an attacker to suspect its contents. An even better strategy is to encrypt the data before embedding them. In this case, even if the steganographic shield is exposed, the attacker still needs to crack the encryption code to reveal the contents of the secret message.

Simmon [1] proposed a model for a steganographic system that mainly consists of two modules: embedding and extraction. As shown in Figure 1, the embedding module is used by the sender to hide the message into some cover-object using a secret key. On the other side of the communication, the extraction module is used by the receiver to retrieve the secret message from the transmitted stego-object. This is usually done using the same key used for hiding. With respect to extraction, steganographic methods can be classified into: blind and cover-escrow. Cover-escrow methods require the original cover-object to successfully extract the hidden information while blind methods do not. That is why blind techniques are more favorable since only the secret key needs to be exchanged between the sender and the receiver before the actual communication takes place.

As far as the cover media is concerned, classical steganography used physical objects such as wooden tablets to conceal information [2]. However, modern techniques rely on the redundancy in digital covers such as: text [3], music tracks [4], images [5], videos [6], 3D object models [7], and TCP/IP packet headers [8]. With the availability and ease of access to public genomic databases, Deoxyribonucleic Acid (DNA) sequence data recently joined the list of prospective covers serving a wide spectrum of purposes.

After proven to be practically unbreakable [9], DNA-based steganography is gaining more attention providing unconventional security solutions with applications ranging from key encapsulation for cryptosystems [10] to long-term data storage [11]. On one extreme, some methods were designed to hide information in the genome of living organisms for the purpose of copyright protection [12,13]. Genetically engineered organisms such as transgenic crops can be protected by a watermark hidden inside their DNA sequence data without affecting the functionality of the host organism [14]. However, changing the genomic structure of an organism is not as easy as it looks. The embedded data can evolve through the natural selection process. Some techniques proposed encrypting the message before hiding and using block-sum checking to detect errors in mutations [15].

On the other hand, more methods relied on the way DNA data is stored in computer files for the purpose of secure communication. In [16], the authors proposed three different cover-escrow methods for embedding a secret message in a reference sequence. Despite the high robustness of the proposed techniques to brute-force attacks, the reference sequence is randomly modified without any consideration of its biological functionality. To address this issue, the authors of [17] introduced a hiding method that exploits the codon redundancy feature of DNA to hide a message into a sequence without affecting the structure of the protein it encodes for. Furthermore, an extension to the methods introduced in [16] was proposed in [18] to facilitate blind extraction. The method succeeded to substitute the bases of the cover sequence with an encrypted message using a generic complementary rule. Subsequently, the method employs a self-embedding algorithm that inserts the resultant sequence into the reference one in a random fashion. Another modification to the insertion method [16] was proposed in [19] where the binary encoded message is divided into 8-bit long segments that are successively XORed using a key to cipher the message before embedding. In [20] the authors described a reversible hiding technique that uses multilevel histogram shifting where the cover sequence is coded into symbols represented by integer values. More recent research investigated using DNA steganography and PCR technology for the purpose of quantum key distribution (QKD) [21].

In this paper, we present a blind scheme for DNA-based Steganography. As shown in Figure 2, the proposed method consists of two main processes: the hiding process and the extraction process. The first one is carried out by the sender while the latter is performed by the receiver where both should share a secret key in advance. This key is used in different steps of the hiding process to make sure that only the intended recipient will be able to retrieve the hidden message. The method we propose here is an extension of the work published by the author in [18]. The main modification is centered around the use of a different cipher to encrypt the secret message before hiding. The original research used a DNA-based Playfair ciphering that requires adding some extra bits to the message data which reduces the hiding capacity of the technique. Instead, we propose using a DNA-based XOR cipher with a key that is generated randomly based on the properties of the cover sequence. In addition, the original research used a palindromic motif from the cover sequence as a signal to find the end of the embedded message. While here, we propose embedding a fixed-size header to store the size of the hidden message.

The rest of the paper is organized as follows: Section 2 gives a brief overview of some preliminary concepts that are required to build a foundation for the proposed technique. Section 3 describes the details of the proposed method in terms of its embedding and the extraction modules. In Section 4, the method is tested using several DNA sequence data that were pulled from a public database. Section 5 analyzes the performance of the proposed approach in terms of hiding capacity and robustness and compares these with some existing techniques. Finally, conclusions are summarized in Section 6.

2. Preliminaries

2.1. DNA

Located in the nucleus, DNA stores the genetic information that is responsible for the development and functioning of all known living organisms and some viruses. With a unique double helix structure, the DNA molecule is made of two strands of nucleotides linked by hydrogen bonding between complementary base pairs. A nucleotide base can be either purine: adenine (A) and guanine (G), or pyrimidine: thymine (T), and cytosine (C). As shown in Figure 3 purine base can only bond with its complementary pyrimidine base. This unique complementary rule pairs (A) and (G) with (T) and (C), respectively [22].

Even though DNA bases in nature pair with their complements in a specific way, the authors in [16] proposed an interesting approach to define generic complementary rules for DNA data. According to their definition, a legal complementary rule should satisfy:

x ≠ C(x) ≠ C(C(x)) ≠ C(C(C(x))) ≠ C(C(C(C(x))))

(1)

where x refers to the DNA alphabet and C is the complement function. Taking this a step further, the authors in [23] defined a double-base complementary rule where, for example, the complement of AA is TC.

Looking at DNA sequence data from a computational perspective would define it as a string over the alphabet {A, C, G, T}. Hence, there should be a rule that can be used to convert those characters into binary. Since we have only four different nucleotide letters or symbols, we can easily represent them using two bits. In this case, as shown in Figure 4, the bases A; C; G and T are mapped into 00, 01, 10, and 11, respectively. Thus, the sequence AGTAGTCATCAT, for example, will be encoded into 001011001011010011100011. Notice that this is only one rule out of the 24 (4!) possible binary encoding rules. 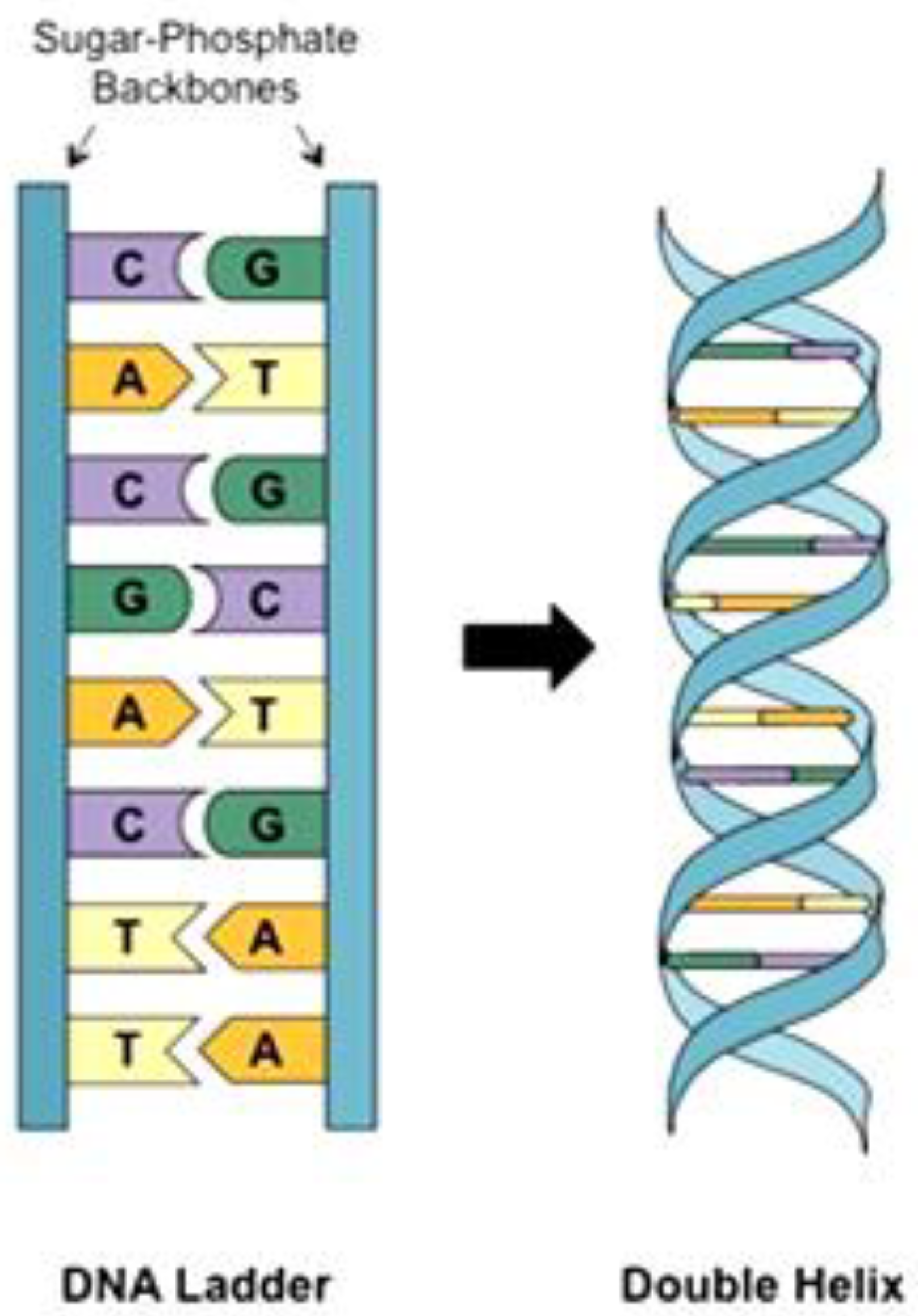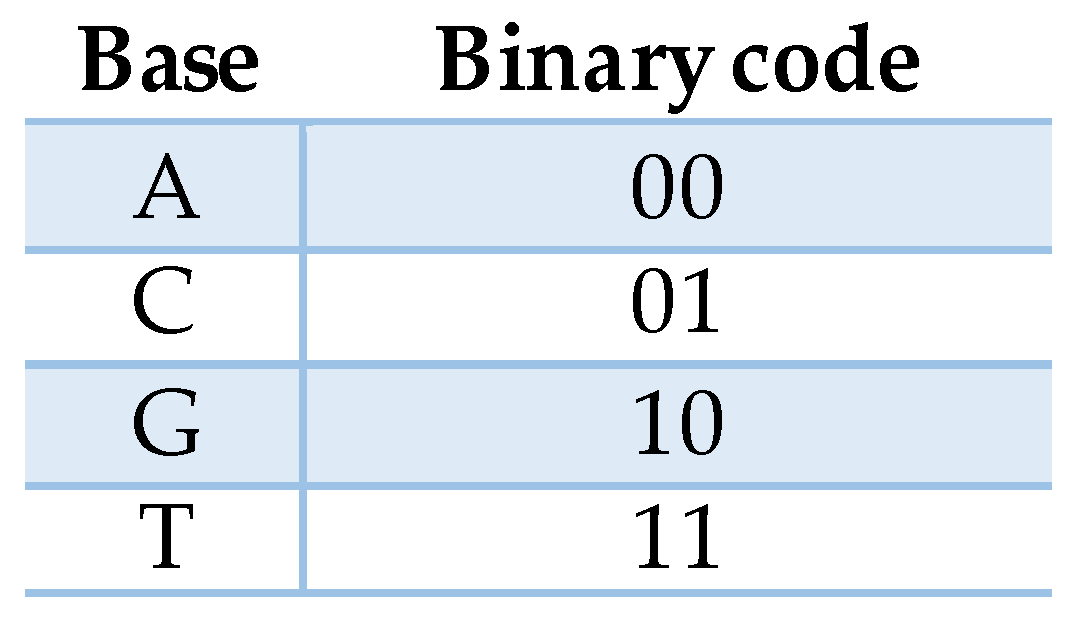With the help of such rules, it is possible to convert DNA sequence data into binary format and vice versa.

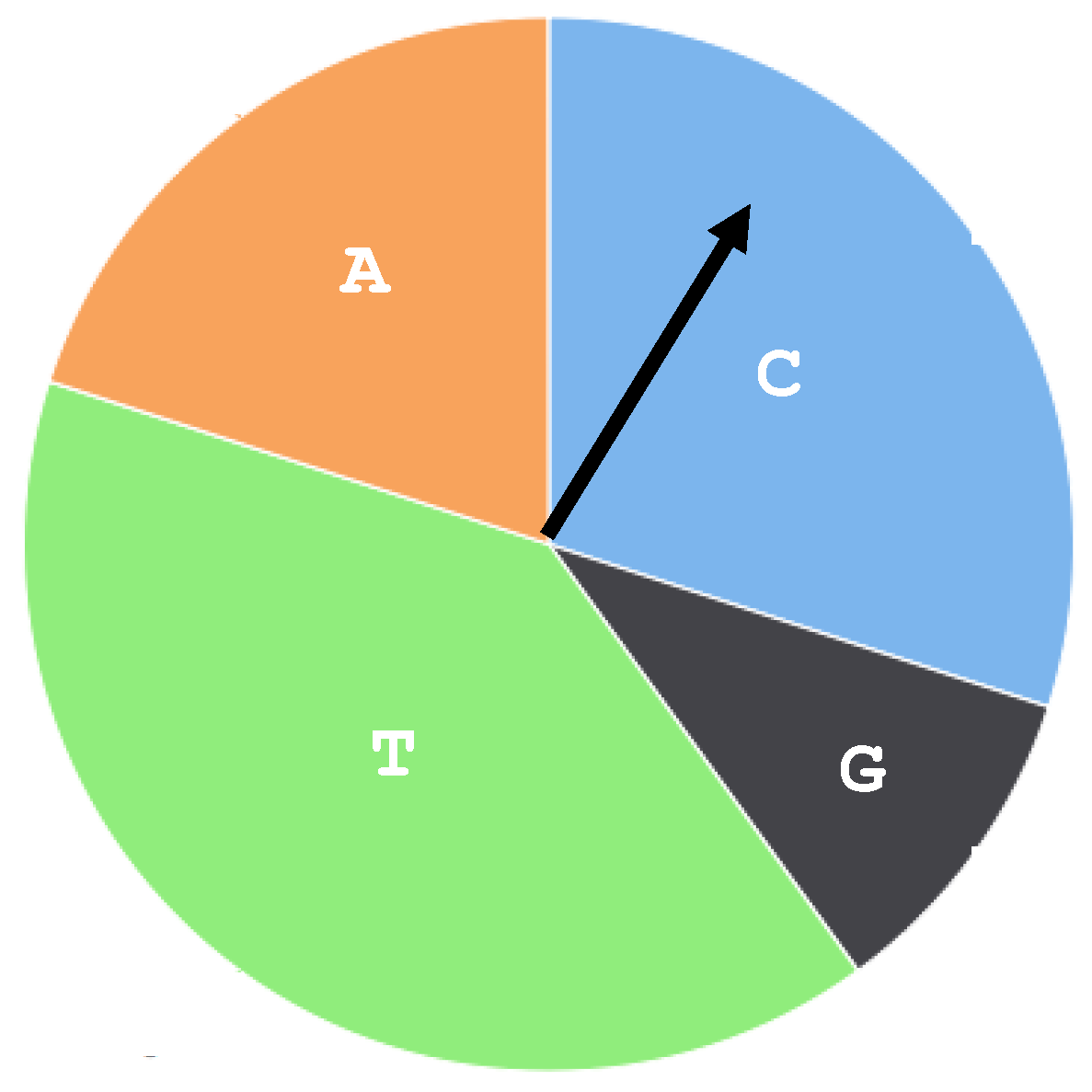
2.2. The Multinomial Model

DNA sequence analysis usually requires applying statistical and mathematical techniques using probabilistic models. The simplest model of DNA sequences is the multinomial distribution which assumes that the nucleotide bases in the sequence independently exist and are identically distributed [24]. In other words, the base composition of a DNA sequence follows a multinomial probability distribution with four parameters pA, pC, pG, pT where px refers to the frequency of the base x in the sequence such that pA+ pC+ pG+ pT = 1. Knowing these parameters, for any given sequence, makes it possible to randomly generate a sequence by choosing a base for each position in that sequence.

To help you visualize this process, imagine spinning the arrow in the center of the wheel in Figure 5. With each spin, the arrow will land on one specific base depending on the distribution of their probability. The larger the portion, the higher the probability and vice versa. Spinning this wheel so many times will eventually generate a random sequence that has a similar base composition as the input sequence. following the same approach, Algorithm 1 lists the steps needed to generate a random DNA sequence of a certain length using a multinomial model. Notice that we need to find a way to map the value returned from the standard random number generator, which follows a uniform distribution, to the proportion of values determined by the parameters of the multinominal distribution of the input sequence.

Algorithm 1. Generate Sequence

Input:Seq: A pattern DNA sequence    Seed: The seed value for the random number generator Output: randSeq: A random DNA sequence 1. Compute the multinomial parameters      1.1 let L be the length of Seq      1.2 Count the bases in Seq as countA, countC, countG, countT      1.3 Compute the probabilities as:       pA = countA/L       pC = countC/L       pG = countG/L       pT = countT/L 2. Generate the sequence      2.1 Compute the cumulative probabilities as:       cpA = pA       cpC = cpA + pC       cpG = cpC + pG       cpT = cpG + pT      2.2 Initialize the random number generator with Seed.      2.3 for i = 1 to L         Generate a random number (b) between 0 and 1         if b < cpA then randSeqi = A         else if b < cpC then randSeqi = C         else if b < cpG then randSeqi = G         else randSeqi = T        end 3. return randSeq

2.3. The XOR Cipher

The XOR cipher is an additive cipher that uses a randomly generated key and the XOR logic to encrypt a message. During the decryption process, the same key should be used and XOR operation is reapplied to remove the cipher [25]. The XOR cipher offers the highest level of security when the random key is as long as the message itself. In this case, it is almost impossible for the attacker to generate and try random keys until the correct one is found. This property makes this cipher unbreakable in theory.

The logical exclusive disjunction (XOR) operation accepts two binary digits as inputs and the output is true when the inputs differ.

Table 1. Bit-Wise XOR operation.

a	b	a XOR b
0	0	0
0	1	1
1	0	1
1	1	0

shows the truth table for the bitwise XOR operation. As an extension of this concept, we propose using the XOR operation on the DNA alphabet. The truth table is given in

Table 2. DNA base-wise XOR operation.

a	b	a XOR b
A	A	A
A	C	C
A	T	T
A	G	G
C	A	C
C	C	A
C	T	G
C	G	T
T	A	T
T	C	G
T	T	A
T	G	C
G	A	G
G	C	T
G	T	C
G	G	A

. Notice that since the truth table should list all the possible permutations of input values, the 4 DNA bases result in 16 different cases.

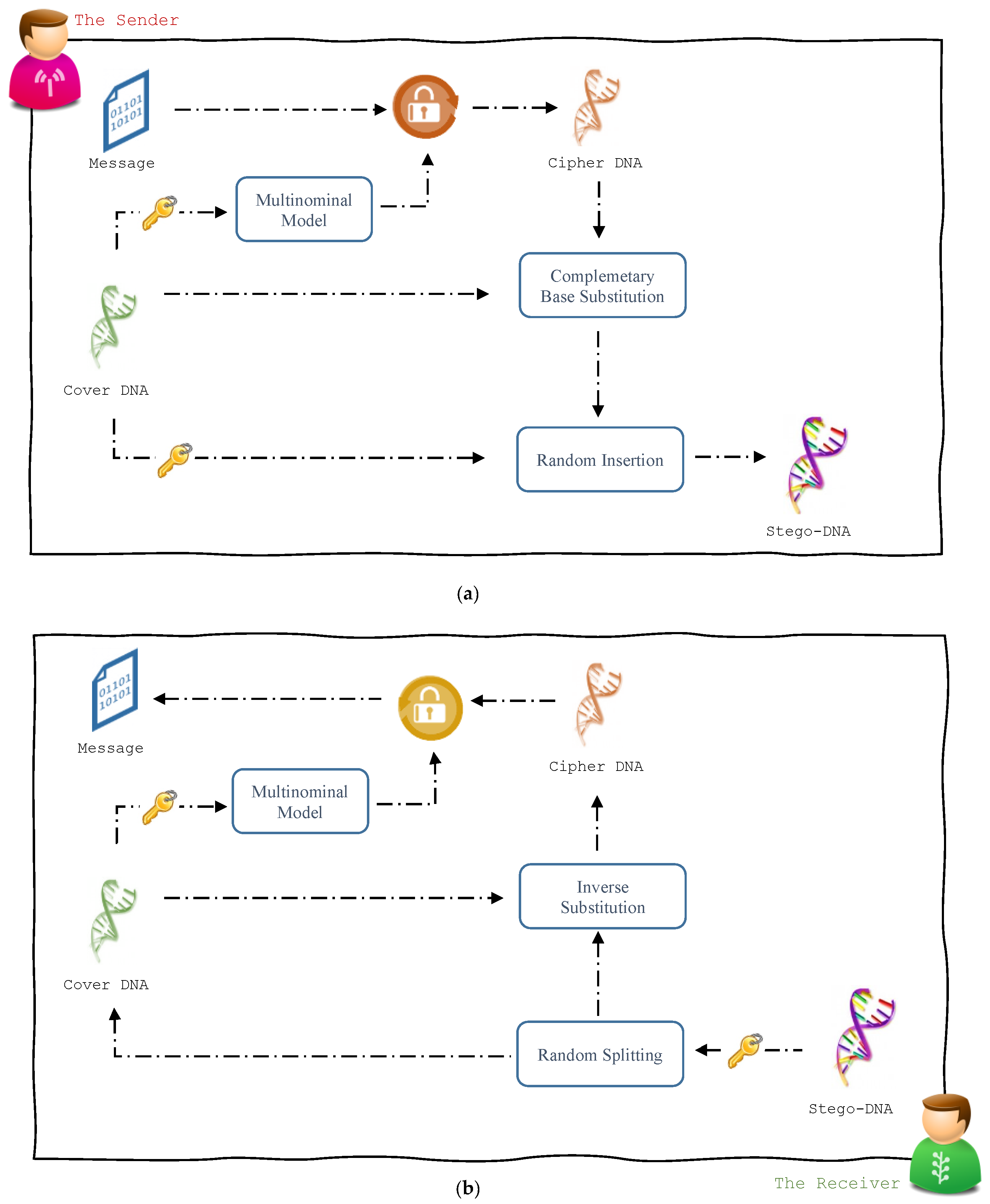
3. The Steganographic Approach

The following subsections discuss in detail the two processes of the proposed steganographic channel. The main steps of both the Hiding and Recovery processes are summarized in Figure 2.

3.1. Message Hiding Module

At the beginning of the hiding process, the message is encrypted using the XOR cipher. As mentioned in Section 2.3, the cipher expects two inputs: the plain text and a cipher key. Here, we propose generating the cipher key based on the multinominal model parameters of the cover sequence using Algorithm 1. Using that generated key, the secret message is encrypted into a DNA sequence that will then be substituted into the bases of the cover sequence using a generic complementary rule.

During the substitution phase, the bases of the cover sequence are modified based on the content of the encrypted message. As shown in Algorithm 2, the cover base is substituted with its first, second, or third complement if the encrypted message base is C, G, or T, respectively. In case the encrypted message base is A, the cover base is left unchanged. The implementation of this step requires a valid complement function (C). In addition, we also choose to randomize the order in which the cover bases are visited during this process. This is done by generating a pseudo random permutation of the bases of the cover sequence. This permutation is controlled by a seed value that is derived from the secret key. Notice that a header that stores the length of the encrypted message; in bases, is also hidden into the cover sequence following the same approach. Here, we suggest using a fixed length header in order to facilitate its detection and retrieval during the extraction process. For example, using a 10-base long header will be enough to represent an integer value as large as 2²⁰ − 1 since each base represents two bits.

Once header information as well as all the encrypted message bases are hidden into the cover sequence, a random splicing process is applied on both the original cover sequence and the substituted one. Once more, the randomization process is controlled by two values that are derived from the secret key. This is followed by an insertion process that merges both sequences together to form the stego-sequence [16].

Algorithm 2. Message Hiding

Input:Cover: reference DNA sequence, used as a cover media    Msg: secret message    Key: secret key-word Output: Stego: Stego-DNA sequence 1. Message Encryption      1.1 Encode Msg into a DNA sequence MsgDNA using a coding rule.      1.2 Let seed be a value derived from Key.      1.3 Generate Keyxor using multinominal model where Cover is the pattern sequence        and seed as the seed value.      1.4 Let m = |MsgDNA|      1.5 for i = 1 to m         Msgcph[i] = MsgDNA[i] XOR Keyxor[i]         end 2. Header Preparation      2.1 Let m = |Msgcph|      2.2 Let Head be the DNA representation of the binary value of m.      2.3 Concatenate Head with Msgcph. 3. The Substitution Phase:      3.1 Let n = |Cover| and Let m = |Msgcph|      3.2 Generate a set (p1, p2, p3, …., pn) as the random permutation of n using seed      3.3 Initialize Coversub to be a copy of Cover      3.4 Initialize i to 1      3.5 for j = 1 to m         if Msgcph [j] is equal to A then          Coversub [pi] = Cover [pi]         else if Msgcph [j] is equal to C then          Coversub [pi] = C(Cover[pi])         else if Msgcph [j] is equal to G then          Coversub [pi] = C(C(Cover[pi]))         else          Coversub [pi] = C(C(C(Cover[pi])))         end         Increment i         end 4. The Insertion Phase:      4.1 Let i and j be two different values derived from Key      4.2 Generate a sequence of random numbers (i1, i2, i3, ….) using i as the seed value      4.3 Generate a sequence of random numbers (j1, j2, j3, ….) using j as the seed value      4.4 Find the smallest integer tc such that ${{\displaystyle \sum }}_{k=1}^{tc}{i}_k>\left|Cover\right|$      Find the smallest integer tm such that ${{\displaystyle \sum }}_{k=1}^{tm}{i}_k>\left|Cove{r}_{sub}\right|$      4.5 if tc < tm then          return        else          Let t = tm        end      4.6 Divide Cover into t − 1 segments (C1, C2, C3, ….) with lengths (i1, i2, i3, ….)        respectively and keep the residual part in Ct      4.7 Divide Coversub into t − 1 segments (M1, M2, M3, ….) with lengths (j1, j2, j3, ….)        respectively and keep the residual part in Mt      4.8 Initialize Stego as an empty sequence.      4.9 for k = 1 to t         Append Ck to Stego         Append Mk to Stego         end 5. return Stego

3.2. Message Recovery Module

The steps to be followed during the extraction process need to reverse those that were used for hiding. As listed in Algorithm 3, we need to start by splitting the stego-sequence in order to separate the original cover sequences from the substituted ones. Once the segments of both sequences are extracted and concatenated, the bases of the two sequences are compared to extract the ciphered message. This is done by comparing the corresponding bases of the sequences to reverse the substitution operation and determine the embedded message base. For example, if the two corresponding bases from the cover and the substituted cover sequences are the same then the message base was A. However, if one of the bases is the complement of the other, then we can say that the embedded message bit was C and so on.

Notice that although the two sequences have the same length, this comparison process stops as soon as the message ends. This depends on the message length information extracted from the header that proceeds the message itself. Furthermore, the header is embedded using the same substitution operation, hence it needs to be retrieved the same way the message bases are extracted. The following step will then take care of decrypting the retrieved ciphered message by reapplying the XOR cipher. Once more, the key to be used in the decryption process will be generated using the multinominal model listed in Algorithm 1 where the cover is used as the pattern sequence.

Algorithm 3. Message Retrieval

Input:Stego: Stego-DNA sequence    Key: secret key-word Output: Msg: secret message 1. Sequence Splitting      1.1 Let i and j be two different values derived from Key      1.2 Generate a sequence of random numbers (i1, i2, i3, ….) using i as the seed value      1.3 Generate a sequence of random numbers (j1, j2, j3, …. using j as the seed value      1.4 Let n = |Stego|/2      1.5 Find the smallest integer t such that ${{\displaystyle \sum }}_{k=1}^t{i}_k>n$      1.6 Divide S into t − 1 segments (S1, S2, S3, …. St−1) with lengths        (i1 + j1, i2 + j2, i3 + j3…., it−1 + jt−1) respectively and keep the residual in St      1.7 Initialize Cover as an empty sequence      1.8 Initialize Coversub as an empty sequence      1.9 for k = 1 to t − 1         Append the ik bases of Sk to Cover         Append the jk bases of Sk to Coversub         end      1.10 Append the it bases of St to Cover      1.11 Append the jt bases of St to Coversub 2. Header Retrieval      2.1 Let seed be a value derived from Key.      2.2 Generate a set (p1, p2, p3, …., pn) as the random permutation of n using seed      2.3 Initialize Head as fixed length sequence      2.4 Initialize i to 1      2.5 for j = 1 to |Head|         if Coversub [j] == Cover [pi] then          Head[j] = A         else if Coversub [j] == C(Cover [pi]) then          Head[j] = C         else if Coversub [j] == C(C(Cover [pi])) then          Head[j] = G         else          Head[j] = T         end         Increment i        end      2.6 Convert Head into an integer m 3. Inverse Substitution:      3.1 Initialize Msgcpr as an empty sequence      3.2 for j = |Head|+1 to m + |Head|         if Coversub [j] == Cover [pi] then          Msgcpr [j] = A         else if Coversub [j] == C(Cover [pi]) then          Msgcpr [j] = C         else if Coversub [j] == C(C(Cover [pi])) then          Msgcpr [j] = G         else          Msgcpr [j] = T         end         Increment i        end 4. Message Decryption      4.1 Generate Keyxor using multinominal model where Cover is the pattern sequence       and seed as the seed value.      4.2 Initialize MsgDNA as an empty sequence      4.3 for i = 1 to m        MsgDNA [i] = Msgcpr[i] XOR Keyxor[i]         end      4.4 Decode MsgDNA into Msg using the coding rule 5. return Msg

4. Experimental Results

In this set of experiments, 12 sequences were drawn from the National Center for Biotechnology Information (NCBI) website. Each sequence is indexed in the GenBank database using a unique accession number. When downloaded, the sequence data files were saved as text following the standard FASTA file format. A FASTA file starts with a single-line header with a description that is followed by fined-length lines listing the sequence data using the {A, C, T, G} alphabet. Furthermore, the hiding and the extraction process were implemented and tested using randomly generated textual data of size approximately 30.55 KB. It is worthy to note that this approach can be used to hide any type of digital data as long as a proper encoding rule is used to handle the conversion operation to DNA data and vice versa.

The proposed algorithms were coded and implemented using Matlab. In our implementation, we decided to convert the secret key into a number by adding the code for each character in the string and use it to initialize the random number generator. Then, we generate three random numbers in the range from 1 to 99,999 to be used as seed, i and j as described in Algorithm 1. So, for example, in this case, the string “My12345Key “ was used as the secret key word with the character codes 77, 121, 49, 50, 51, 52, 53, 75, 101, and 121 which gives 750 when summed up. Furthermore, the numbers 9584, 5603, and 4910 were the values generated for seed, i and j, respectively.

Table 3. Experimental results for hiding 30.55KB of text.

Accession Number	Length (bp)	Base Composition (pA, pC, pG, pT)	Payload (bpn)	Longest Palindrome Word Length (bp)	Shortest Palindrome Word and Repeat
AL645637	207,629	(0.27, 0.21, 0.21, 0.32)	1.205	52	GAATTC	57
AAEX03000080	305,811	(0.33, 0.18, 0.17, 0.32)	0.818	44	TATATA	284
AAEX03000038	133,800	(0.29, 0.21, 0.20, 0.29)	1.870	39	AAGCTT	26
AAEX03000069	474,719	(0.31, 0.19, 0.19, 0.31)	0.527	48	TGATCA	147
AL772265	212,009	(0.31, 0.18, 0.17, 0.33)	1.18	40	GAATTC	75
AL645625	226,754	(0.24, 0.26, 0.26, 0.23)	1.103	42	GAATTC	47
AC153526	200,117	(0.28, 0.21, 0.20, 0.31)	1.250	66	TATATA	96
ADDN03000005	7,768,011	(0.26, 0.24, 0.24, 0.26)	0.032	106	AAATTT	6033
ADDN03000030	633,545	(0.26, 0.24, 0.25, 0.25)	0.395	32	CCGCGG	158
ADDN03000022	380,649	(0.25, 0.25, 0.24, 0.26)	0.657	27	ATGCAT	188
AAEX03000999	22,099	(0.23, 0.27, 0.26, 0.23)	--	25	AGGCCT	--
SOZC01000013	50,017	(0.30, 0.21, 0.19, 0.30)	--	20	ATATAT	--

lists the lengths of each used cover sequence as well as its base composition. The payload is also computed in each case as the ratio of message length; in bits, to cover length in bases. For example, the payload for the sequence AL645637 that is 207629 base long can be computed as 30.55 * 1024 * 8/207629 which results in 1.205 bit-per-nucleotide (bpn). Notice that that in some cases, when the sequence is too short to accommodate the secret message, the embedding process fails to execute due to a violation of the condition checked at step 4.6 in Algorithm 2. This was the case for the sequences AAEX03000999 and SOZC01000013 of lengths 22,099 and 50,017, respectively.

The experiments were extended to further discuss the advantage of using a message header over the palindrome motif to signal the end of the embedded message in [18]. A palindrome word in genetics is equal to its complementary sequence if read backwards [26]. For example, the sequence AAGCTT is palindromic because its complement is TTCGAA is equal to the original sequence in reverse order. So, if the longest palindrome word is used as the end-of-message signal, it may decrease the hiding capacity. On the other hand, using the shortest palindrome word may result in errors in the retrieved message because of the high probability that the same motif will be formed by chance, multiple times, in the substituted cover sequence. In other words, the extraction process may return a truncated message due to detecting the end of the message signal too soon than it should be. To illustrate this point, the last three columns in Table 1 were dedicated to showing some details of the detected palindrome words in the cover sequence, both the longest and the shortest ones. For example, the longest palindrome motif found in the sequence, ADDN03000005, reached 106 base long while the shortest was AAATTT. Notice that when we searched for that palindromic word in the substituted cover sequence, we found it 6033 times. Although the method in [18] suggested to pad this word with a specific base from both sides, there is still a probability that such a motif will be formed by chance due to several factors such as the randomness of the message contents.

5. Performance Evaluation

This section is dedicated to analyzing the performance of the proposed method with respect to two measures: capacity and robustness to brute-force attacks. The performance is then compared with a number of existing techniques.

5.1. Hiding Capacity

The capacity offered by a hiding method usually reflects the maximum number of bits to be embedded into a given cover. In the case of DNA sequence data, the hiding capacity is measured in bit-per-nucleotide (bpn). This represents the ratio between the message size (in bits) and the cover sequence length (in nucleotides). Applying this to the proposed method, you will find that each base in the cover sequence can be substituted with another one depending on the value of the message base. This means that we can hide up to 2 bits in each cover base which makes the hiding capacity of the proposed method reaches 2 bits per nucleotide as computed in Equation (2) where |C| refers to the length of the cover sequence in base pairs (bp).

$$\frac{2 \left|C\right|}{\left|C\right|}=2 \mathrm{bpn}$$

(2)

5.2. Security

In case an attacker tries to crack the implementation of the proposed method using a brute-force strategy, there are several parameters that need to be guessed correctly to successfully extract the hidden message. First of all, the binary rule is used for DNA encoding. Since there are only 4 nucleotides, there are 4! = 24 possible rules to choose from. Secondly, the attacker needs to guess the sequence of numbers generated to randomly slice the sequences in the insertion phase. The authors of [16] showed that the number of possible guesses on this parameter can be computed using Equation (3), where n represents the length of the cover sequence and $\left(\begin{array}{c}n\\ k\end{array}\right)$ is the set of all k-combinations of n.

$$\left(\begin{array}{c}n\\ n-1\end{array}\right)+\left(\begin{array}{c}n\\ n-2\end{array}\right)+\left(\begin{array}{c}n\\ n-3\end{array}\right)+\dots +{\left(\begin{array}{c}n\\ 0\end{array}\right)}^{}={\displaystyle \sum }_{k=0}^{n-1}\left(\begin{array}{c}n\\ n-1-k\end{array}\right)=2^n-1$$

(3)

Since this guess needs to be repeated for both the slices of the cover as well as the message, which can be as long as the cover itself, the probability of an attacker making a successful guess on the details of the insertion process is $\frac{1}{{(2^{\left|C\right|}-1)}^2}$. One more parameter that needs to be guessed is the complementary substitution rule. There are six different possible rules that satisfy the property: x ≠ C(x) ≠ C(C(x)) ≠ C(C(C(x))) ≠ C(C(C(C(x)))). Furthermore, during the substitution process, the cover bases are visited randomly based on a permutation function. Since the number of possible permutations of a set of n items is n!, there are |C|! different ways to arrange the bases of the cover sequence. Thus, the probability of making a successful guess to crack only the proposed hiding technique can be formulated as follows:

$$\frac{1}{\left|C\right|!}\times \frac{1}{{(2^{\left|C\right|}-1)}^2}\times \frac{1}{24}\times \frac{1}{6}$$

(4)

Considering that |C| can reach hundreds of thousands, it is obvious that this probability is practically zero which means it is almost impossible to crack this method.

5.3. Comparisons

Table 4. A comparison with some existing techniques.

Author	Method	Capacity (bpn)	Security	Extraction
Shiu [16], 2010	Insertion	0.58	$\frac{1}{1.63\times {10}^8}\times \frac{1}{n-1}\times \frac{1}{2^m-1}\times \frac{1}{2^{S-1}}\times \frac{1}{24}$	Non-blind
	Complementary	0.07	$\frac{1}{1.63\times {10}^8}\times \frac{1}{{24}^2}$	Non-blind
	Substitution	0.82	$\frac{1}{{\left(2^{\left|S\right|}-1\right)}^2}\times \frac{1}{6}$	Non-blind
Khalifa [18], 2016	Generic Complementary Base Substitution (GCBS)	1.5	$\frac{1}{{\left(2^{\left|S\right|}-1\right)}^2}\times \frac{1}{6}\times \frac{1}{24}$	Blind
Malathi [19], 2017	Improved Insertion	1.52	$\frac{1}{1.63\times {10}^8}\times \frac{1}{n-1}\times \frac{1}{2^m-1}\times \frac{1}{2^{S-1}}\times \frac{1}{24}\times \frac{1}{2^{8m}}$	Non-blind
Lee [20], 2018	Noncircular type (NHS)	1.243	NA	Blind
	Circular type (CHS)	1.865	NA	Blind
Proposed	Enhanced GCBS	2	$\frac{1}{\left|S\right|!}\times \frac{1}{{\left(2^{\left|S\right|}-1\right)}^2}\times \frac{1}{24}\times \frac{1}{6}$	Blind

lists a number of existing techniques as well as their performance measured in terms of hiding capacity and security. The last column in Table 2 indicates whether the method is blind or not. If the steganographic technique is blind, the extraction process can be performed without a reference to the original cover sequence. This is a favorable feature in any steganographic technique since it eliminates the need for the sender and the receiver to communicate anything in advance which can be suspicious and may affect the security of the communication itself. Notice that, and for the sake of consistency, the symbol S used in the security expressions listed in Table 4 refers to the cover sequence and m refers to the length of the message in bits.

As shown in Table 4, the proposed method can hide up to 2 bits per cover nucleotide, which outperforms all the other techniques in terms of the hiding capacity. notice that the enhancement introduced here increased the hiding capacity of the original implementation of the GCBS [18] due to the smart use of the XOR cipher which eliminated the need for embedding the ambiguous bases to perform deciphering. On the other hand, the method proposed here succeeded to improve its robustness against brute-forth attacks as well. Furthermore, with respect to security, the insertion method proposed by Shui [16] and its modification in [19] are more robust than the proposed method. However, both of them are cover-screw and the proposed method is not only blind but also provides more hiding capacity. Finally, methods in [20] are both blind providing a relatively high hiding capacity, but their robustness analysis is not available and thus the comparison cannot be done in this regard.

6. Conclusions

This paper describes a secure communication technique that enhances the GBCS method presented in [18]. The proposed hiding process consists of several phases that starts with encrypting the secret message using a bio-inspired XOR-cipher. The encrypted message which is encoded as DNA sequence is then substituted into the cover sequence using some generic complementary rule. Finally, the modified cover sequence is hidden into the original cover using a random insertion operation. On the other side of the communication, the receiver can extract the hidden message by reversing the hiding process and deciphering the hidden message. The sender and the receiver are expected to agree on a secret key in advance to protect the security of the communication channel.

The results clearly show that the modifications presented on [18] resulted in a higher hiding capacity as well as enhanced security. When compared with other techniques, experimental results highlighted the superior performance of the proposed method with a hiding capacity of two bits per cover nucleotide. Beside the high capacity, the method succeeded in showing strong robustness against brute-force attacks which proved the hiding technique to be almost unbreakable. This research can be extended in the future to consider introducing some randomness in the insertion phase of the hiding process. In other words, the segments of both the cover and the substituted sequence can be merged in a random order, based on the value of the secret key, to further enhance the security of the steganographic channel.