Pedestrian Arching Mechanism at Bottleneck in Subway Transit Hub

Abstract

Under the massive pedestrian flow, pedestrians arching phenomenon forms easily at bottleneck in subway hubs, which might stampede and crush. To explore pedestrian arching mechanism at bottleneck in subway transit hub, this paper conducts a series of simulation experiment. Firstly, movement preference characteristic in subway transit hubs was introduced into the social force model which considers multiple force. Then, after setting basic experiment scenario, unidirectional flow at different bottlenecks were simulated. Finally, the mechanism of pedestrian arching phenomenon at bottleneck was quantitative analyzed with the help of experimental data. Some main conclusions are summarized. Pedestrian arching phenomenon could be divided into four stages: Free, arching formation, arching stabilization and arching dissipation. In addition, the relationship between bottleneck scenario and passing time could be built to a function model. With the different of bottleneck width ratio, passing time presents positive correlation. The research results could give some helps for understanding the dynamic evolution process of unidirectional flow at bottleneck, improving the pedestrian efficiency at bottleneck and optimizing pedestrian facilities in subway transit hub.

1. Introduction

With the rapid development of urban public transport, due to the advantages of large capacity, convenience and efficiency, and green environmental protection, subway undertakes the most public transportation pedestrian flow [1]. The highest average daily pedestrian volume has been more than 13 million in Beijing subway in 2019, meaning the “massive pedestrian flow” has become the “new normalcy” in Beijing subway. Under the “massive pedestrian flow”, pedestrians keep gathering at the bottleneck in the transit hub. When the pedestrian flow far exceeds the capacity of the bottleneck, pedestrian arching will occur at the bottleneck [2], as shown in Figure 1. At this time, the force between pedestrians in the arch is transmitted to each other, and the huge pressure is concentrated at the bottleneck entrance, which is not conducive to the passage of pedestrians. The safety hazard exists, and a stampede accident may occur in serious cases. Therefore, it is necessary to study the inherent law of pedestrian arching. Accurately grasp pedestrian behavior characteristic of arching and study the evolution of the pedestrian arching, is a pressing issue to pedestrian management and subway facility design.

Figure 1. Pedestrian arching at bottleneck in subway transit hub.

In recent years, pedestrian behavior has been a research focus [3,4]. Aiming at the reduction of pedestrian efficiency and safety caused by bottleneck, scholars began to study the pedestrian behavior characteristics at bottleneck. Through image processing technology, Daamen and Hoogendoorn [5] extracted and analyzed the pedestrian motion characteristics at narrow bottleneck in the evacuation, such as free speed, density and walking direction. Hoogendoorn and Daamen [6] studied the oscillating effect, stratification effect and zipper effect by extracting the pedestrian trajectories at bottleneck in the pedestrian experiment. Moreover, Liu et al. [7], Seyfried et al. [8,9], Tian et al. [10] all carried out pedestrian experiments, and extracted pedestrian trajectories to analyze pedestrian motion characteristics, such as density, basic diagram of speed, sway frequency and sway amplitude. Through field experiments, Sun et al. [11] and Luo et al. [12] studied the influence of bottleneck on pedestrian movement in subway stations, and proved some optimization measures such as funnel shape, column obstacle.

With the development of computer technology and simulation model, scholars began to study pedestrians at the bottleneck based on simulation. Guo [13] proposed a revised social force model to simulate the pedestrian counter flow through a bottleneck. Based on the extended cellular automata, Li and Han [14] proposed a pedestrian evacuation simulation model to study pedestrian’s behavioral effect at bottleneck. Tang et al. [15] built a bypassing behavior model to analyze pedestrian arching at the bottleneck in the emergent evacuation situation. Li and Guo [16] simulated bi-directional pedestrian flow through a bottleneck by an extended cell transmission model with regular hexagonal cell representation. Through designing a safety evacuation model for pedestrians within limited spaces, Li and Xu [17] analyzed bottleneck area density, evacuation efficiency and similar factors.

The social force model proposed by Helbing and Molnar [18] has been extensively applied to the simulation of pedestrian. Xu and Duh [19] simulated the bonding effects inside pedestrian crowds by social force model and found delays in walking and the overtaking phenomenon. Base on social force model, Yuen and Lee [20] proposed an overtaking force, which can reflect overtaking behavior. Wang et al. [21] proposed a composite social force model with a multi-exit utility function. Kolivand et al. [22] proposed a model that improves the social force model by introducing four new characteristics, which are gender, walking speed, intention outlook and grouping, to make simulations more realistic. Yang et al. [23] adopted the social force model as a fundamental driven equation of passengers’ movements, then studied the effect of passenger attribute namely the homogeneity and heterogeneity in passengers on the alighting and boarding efficiency in the subway stations. Ru et al. [24] divided a crowd into three categories that have different kinds of movement based on different force models. Simulation results indicated that luggage-laden pedestrians bring great difficulty to evacuation.

To sum up, the scholars have done a large amount of in-depth researches on the pedestrian behavior at bottleneck, which obtained some significant findings. Some recognized that pedestrian arching is related to pedestrian safety [2,15]; however, pedestrian arching mechanism at bottleneck in subway transit hub need be studied deeply. Besides, social force model is one of the most widely used pedestrian simulation models. Thus, through the establishment of simulation model based on social force and consideration of movement preference characteristic in subway transit hub, this paper quantitative analyze pedestrian arching mechanism in scenario of subway transit hub. The results are helpful to understand the dynamic evolution process of one-way pedestrian flow, reveal the basic law of pedestrian movement, improve the pedestrian efficiency at bottleneck and optimize pedestrian facilities in subway transit hub.

This paper is organized as follows: Section 1 introduces background. Section 2 describes the building of simulation model. Section 3 designs pedestrian experiment. Section 4 presents the analysis of pedestrian arching mechanism. Finally, Section 5 concludes this study and suggests future research recommendations.

2. Building of Simulation Model

2.1. Comparison of Basic Model

More than 30 pedestrian simulation models have been applied around the world. According to the degree of pedestrian detail description, simulation model can be divided into macroscopic model, medium model and microscopic model. Due to pedestrian behavioral modeling at bottleneck belongs to micro-level, microscopic model is compared in this paper, including cellular automata model, benefit cost cellular model, magnetic model and social force model. Comparison and analysis of 9 aspects of microscopic simulation model are summarized, as shown in Table 1, including principle of walking, driving force, and so on.

Table 1. Comparison of microscopic simulation model.

	Cellular Automata Model	Benefit Cost Cellular Model	Magnetic Model	Social Force Model
Principle of walking	Grid	Grid	Coordinate system	Coordinate system
Driving force	Define direction	Benefit value of mobile	Anode and cathode magnetic force	Expected speed
Influence force	Update rule	Cost value of mobile	Anode and cathode magnetic force	Interaction force
Walking space	Discreet	Discreet	Continuous	Continuous
Describe the phenomenon	Queuing, self-organization	Queuing	Routing search	Self-organization and evacuation
Principia mathematica	Rule based	Optimization objective based	Optimization objective based	Variance based
Calibration of model parameters	Analysis of basic data	Observation	Observation	Observation
Calibration of model variables	0 or 1	Any assignment	Physical significance	Physical significance
Programmability	Easy	Easy	Ordinary	Difficulty

The above microscopic simulation models all can effectively describe the basic pedestrian characteristics during moving. However, there are large differences in basic principles. By contrast, social force model has four advantage for this study. (1) pedestrian behavior is generated under the influence of three elements, that are environment, psychology and behavior, which is consistent with the building principle of social force model. Thus, social force model can simulate pedestrian behavior more realistically. (2) in the subway transit hub, pedestrian usually has interaction behaviors with surrounding individuals, such as avoidance, waiting and competition. The social force model is based on complex mechanical model, which can simulate these pedestrians’ interactions more reasonable. (3) pedestrian is constantly affected by the surrounding people and environment, so direction of motion and speed may be adjusted at any time. In social force model, the coordinates of pedestrian and time is continuous. Thus, social force model can simulate the elements of time and space more properly. (4) under the massive pedestrian flow, spatial compression and break step caused by crowded pedestrians will occur in the subway transit hub. Because the grid model is limited by the width of the spatial grid, the grid will be scattered and deformed in the simulation process, which will affect the simulation results. The meshless model with no spatial constraints could avoid these situations and improve the accuracy of numerical simulation. In conclusion, social force model is chosen to analyze pedestrian arching mechanism in subway transit hub.

2.2. Principle of Social Force Model

Helbing and Molnar [18] firstly constructed the basic social force model of pedestrian movement under the normal state. The core idea of social force model is that the pedestrians’ movement is influenced by purpose, interaction between pedestrians and influence from surrounding obstacles, as shown in Figure 2. Moreover, these influences are expressed by equation, which is similar to mechanics. Pedestrian movement process can be described by the following partial differential equation.

$$\begin{array}{l}\stackrel{\rightharpoonup }{f_i}\left(t\right)=m_i\frac{d\stackrel{\rightharpoonup }{v_i}\left(t\right)}{dt}=m_i\stackrel{\rightharpoonup }{a_i}\left(t\right)\\ =\stackrel{\rightharpoonup }{f_i{}^0}\left(t\right)+{\displaystyle \sum _{j(\ne i)}\stackrel{\rightharpoonup }{f_{ij}}\left(t\right)+{\displaystyle \sum _w\stackrel{\rightharpoonup }{f_{iw}}\left(t\right)}+{\displaystyle \sum _a\stackrel{\rightharpoonup }{f_{ia}}\left(t\right)}+{\displaystyle \sum _g\stackrel{\rightharpoonup }{f_{ig}}\left(t\right)}}+\stackrel{\rightharpoonup }{{\xi }_i}\left(t\right)\end{array}$$

(1)

where $\stackrel{\rightharpoonup }{f_i}\left(t\right)$ is the resultant force of pedestrian i under all force at time t; $\stackrel{\rightharpoonup }{a_i}\left(t\right)$ is acceleration of pedestrian i at time t; $\stackrel{\rightharpoonup }{f_i{}^0}\left(t\right)$ is the personal desire force, which is pointing to pedestrian’s next objective; ${\displaystyle \sum _{j(\ne i)}\stackrel{\rightharpoonup }{f_{ij}}\left(t\right)}$ is the interaction force of pedestrian i from pedestrian j at time t; ${\displaystyle \sum _w\stackrel{\rightharpoonup }{f_{iw}}\left(t\right)}$ is the interaction force of pedestrian i from obstacle w at time t; ${\displaystyle \sum _a\stackrel{\rightharpoonup }{f_{ia}}\left(t\right)}$ is the attraction force of pedestrian i from surrounding at time t; ${\displaystyle \sum _g\stackrel{\rightharpoonup }{f_{ig}}\left(t\right)}$ is the attraction force of pedestrian i from surrounding pedestrians at time t and $\stackrel{\rightharpoonup }{{\xi }_i}\left(t\right)$ is a random variable.

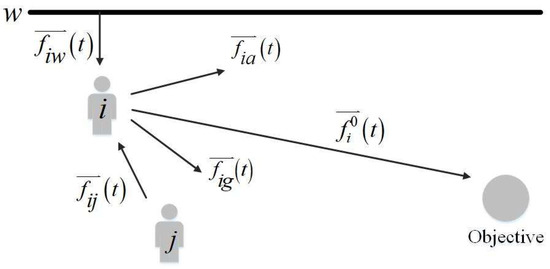
Figure 2. Schematic diagram of social force model.

However, pedestrians have strong travel purpose in subway transit hub, which is less attracted by surrounding pedestrians and things. Thus, in this paper, the social force model can be simplified to three force, including personal desire force, interaction force between pedestrians, interaction force between pedestrian and obstacle, as follows.

$$\stackrel{\rightharpoonup }{f_i}\left(t\right)=\stackrel{\rightharpoonup }{f_i{}^0}\left(t\right)+{\displaystyle \sum _{j(\ne i)}\stackrel{\rightharpoonup }{f_{ij}}\left(t\right)+{\displaystyle \sum _w\stackrel{\rightharpoonup }{f_{iw}}\left(t\right)}}+\stackrel{\rightharpoonup }{{\xi }_i}\left(t\right)$$

(2)

2.2.1. The Personal Desire Force

The personal desire force is the most striking force in model, which determine the pedestrian walk toward to the destination with desired speed. If a pedestrian walks without any disturbances, he will walk toward to desired direction $\stackrel{\rightharpoonup }{e_a}\left(t\right)$ with speed $v_a$. The Equation of personal desire force is given below.

$$\stackrel{\rightharpoonup }{f_i{}^0}\left(t\right)=m_i\frac{v_i^0\stackrel{\rightharpoonup }{e_{\mathrm{i}}}\left(t\right)-\stackrel{\rightharpoonup }{v_i}\left(t\right)}{{\tau }_i}$$

(3)

where $m_i$ is mass of pedestrian i; $v_i^0$ is desired speed of pedestrian i and $\stackrel{\rightharpoonup }{e_i}\left(t\right)$ is unit vector of pedestrian i from the current position to the next target position $r_{ij}$ at time t.

$$\stackrel{\rightharpoonup }{e_i}\left(t\right)=\frac{{\stackrel{\rightharpoonup }{r}}_i^k-\stackrel{\rightharpoonup }{r_i}\left(t\right)}{\Vert {\stackrel{\rightharpoonup }{r}}_i^k-\stackrel{\rightharpoonup }{r_i}\left(t\right)\Vert }$$

(4)

where $\stackrel{\rightharpoonup }{v_i}\left(t\right)$ is the current speed of pedestrian i at time t and ${\tau }_i$ is relaxation time, meaning the time of pedestrian i from current speed $\stackrel{\rightharpoonup }{v_i}\left(t\right)$ to desired speed $v_i^0$.

2.2.2. The Interaction Force

In the process of movement, pedestrian will initiatively keep a certain distance with others. The closer a pedestrian is to strangers, the more uncomfortable he feels, which lead to repulsive force. This repulsion force is exponential function relation with distance between pedestrians. The Equation is expressed as follow.

$$\stackrel{\rightharpoonup }{f_{ij}}\left(t\right)=m_i\frac{A_i}{B_i}\exp \left(-\frac{\Vert \stackrel{\rightharpoonup }{r_{ij}}\left(t\right)\Vert }{B_i}\right)\frac{\stackrel{\rightharpoonup }{r_{ij}}\left(t\right)}{\Vert \stackrel{\rightharpoonup }{r_{ij}}\left(t\right)\Vert }$$

(5)

where $\stackrel{\rightharpoonup }{r_{ij}}\left(t\right)$ is position vector difference between pedestrian i and j at time t, $\stackrel{\rightharpoonup }{r_{ij}}\left(t\right)=\stackrel{\rightharpoonup }{r_i}\left(t\right)-\stackrel{\rightharpoonup }{r_j}\left(t\right)$; $A_i$ is strength of pedestrian interaction force and $B_i$ is distance of pedestrian interaction force.

2.2.3. The Obstacles Forces

In the process of movement, pedestrians will keep a certain distance to the boundary of obstacles, walls, buildings, and so on. The influence of boundary and obstacles to pedestrians is similar to the interaction between the pedestrian. Pedestrian will initiatively avoid obstacles to prevent injuries. The Equation of obstacles forces is expressed as follow.

$$\stackrel{\rightharpoonup }{f_{iw}}\left(t\right)=m_i\frac{A_w}{B_w}\exp \left(-\frac{\Vert \stackrel{\rightharpoonup }{r_{iw}}\left(t\right)\Vert }{B_w}\right)\frac{\stackrel{\rightharpoonup }{r_{iw}}\left(t\right)}{\Vert \stackrel{\rightharpoonup }{r_{iw}}\left(t\right)\Vert }$$

(6)

where $\stackrel{\rightharpoonup }{r_{iw}}\left(t\right)$ is position vector difference between position $\stackrel{\rightharpoonup }{r_i}\left(t\right)$ of pedestrian i and position $\stackrel{\rightharpoonup }{r_w^i}\left(t\right)$ of obstacle w, $\stackrel{\rightharpoonup }{r_{iw}}\left(t\right)=\stackrel{\rightharpoonup }{r_i}\left(t\right)-\stackrel{\rightharpoonup }{r_w^i}\left(t\right)$; $A_w$ is interaction strength of obstacle force and $B_w$ is interaction distance of obstacle force.

2.3. Movement Preference Characteristic in Subway Transit Hub

The pedestrian speed and occupancy space in subway transit hub is different from other environments. Movement preference characteristic in subway transit hub need to be analyzed. The characterization parameters of speed and occupancy space in social force model are revised, including desired speed, initial speed and pedestrian diameter. Furthermore, $A_i$ and $B_i$ in Equations (5) and (6) are constant. Drawing on the results of previous subway pedestrian studies [25], $A_i$ and $B_i$ are discretized, where the discrete values are set respectively:

$$A_i=\{0.3,0.6,0.9,1.2,1.5,1.8,2.1\}$$

$$B_i=\{0.18,0.20,0.22,0.24,0.26,0.28,0.30\}$$

2.3.1. Desired Speed

Desired speed refers to the speed that pedestrian expects to achieve without any, interferences of other pedestrians and obstacles, which is according to the travel purposes, physical conditions, pedestrian facilities and so on. Desired speed is approximately to the free flow speed, which is the equilibrium value between the largest comfort and the least energy expenditure. Henderson and Lyons’ research findings of pedestrian are approved [26]: Under normal conditions, the pedestrian desired speed distribution is in concordance with the Guass distribution, averaged 1.34 m/s, standard deviation 0.26 m/s.

Due to pedestrians have specific walking purpose in subway transit hub, and pedestrians have the psychological tendency to walk out of the crowded space under the narrow and long corridor, pedestrian behavior is different in other environments. To determine the desired speed, pedestrian motion parameters in corridor in Beijing subway transit hub was captured in this study. The average of the free flow speed is 1.61 m/s, and the standard deviation is 0.27. Compared with the Henderson’s results, the average of desired speed in corridor in Beijing subway transit hub is higher, and the standard deviation is approximate.

2.3.2. Initial Speed

Initial speed refers to the initial speed in simulation experiment, which can be walking speed in corridor in subway transit hub. Through summarizing previous studies, it found that the pedestrian speed in corridor in Beijing subway transit hub studied by different scholars is different. In order to ensure the accuracy of the initial speed, through collecting the field video and video in transportation operations coordination center (TOCC), speed distribution in corridor in Beijing subway transit hub was obtained. The statistics show that speed distribution follows Poisson distribution, N (1.57, 0.32).

2.3.3. Pedestrian Diameter

Pedestrian diameter refers to the diameter of pedestrian space, namely, the diameter of the static space. Static space refers to the body space under stationary state. According to pedestrian static space demand and constraints on pedestrians in different static space, static space can be divided into four grades, contact areas, none contact areas, personal comfort zones and actionable areas, as shown in Table 2 [27]. Considering pedestrian density is high and pedestrian is close to pedestrian, combining spacing survey of the bottleneck in reality, the pedestrian diameter is set to random distribution of between 0.35~0.45.

Table 2. Classification of pedestrian static space.

Grades	Contact Areas	None Contact Areas	Personal Comfort Zones	Actionable Areas
Equivalent diameter (m)	0.235	0.457	0.533	0.609

To sum up, desired speed is obeyed to normal distribution, N (1.61, 0.27), initial speed is obeyed to normal distribution, N (1.57, 0.32) and pedestrian diameter is obeyed to uniform distribution, U (0.35, 0.45).

3. Design of Pedestrian Experiment

3.1. Experiment Scenario

Refer to typical transit hub bottleneck (changes in width), experiment scenario was set, as shown in Figure 3. The corridor length is 10 m, which is fixed. Besides, the corridor width is 5 m, 4 m and 3 m, which is variable. The bottleneck corridor length is 10 m, 5 m and 1 m, which is variable. Moreover, the bottleneck corridor width is 2 m, 1.5 m and 1 m, which is variable too. In total, 27 scenarios are set up for analysis. Pedestrian enters in experiment scenario at the entrance A, and leave at the exit B. The walking direction is indicated by the green arrow.

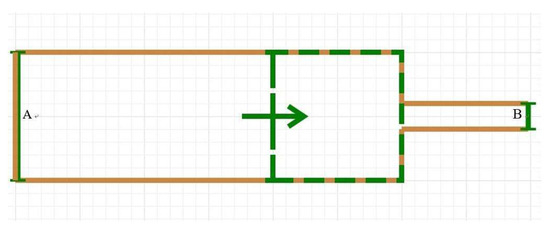
Figure 3. Basic scene in simulation experiment.

3.2. Pedestrian Volume

According to the Transit Capacity and Quality of Service Manual [28], the level of service of public transport corridor was divided into six level. Considering service level mostly is D in Beijing subway transit hub corridor in rush hour, 60 p/m/min is choosing as simulation flow, which is under level D. In addition, considering intermittent arrived and admit degree of experimental basic scene, the number of pedestrians in simulation experiment is set to 200.

4. Analysis of Pedestrian Arching Mechanism

4.1. Description of Arching Phenomenon

According to the simulation results, pedestrian arching presents a common regularity, as shown in Figure 4. When pedestrian density is low, pedestrians walk straight to the bottleneck entrance. As the number of pedestrians gradually increased, the density of the pedestrian increased too. Then pedestrians start queuing in line, appearing an arching phenomenon at the bottleneck entrance. Due to the periodicity of the pedestrian flow in subway transit hub, when pedestrian arching reaches a certain length, the dissipation is beginning.

Figure 4. Process of pedestrians into arch and dissipation.

4.2. Stage Division of the Arching Evolutionary

In order to analyze the evolution of the pedestrian arching further, speed detection lines were set at the position of 1, 2, 3 and 4 in the simulation scenario, as shown in Figure 5. Each detection line is 1 m wide.

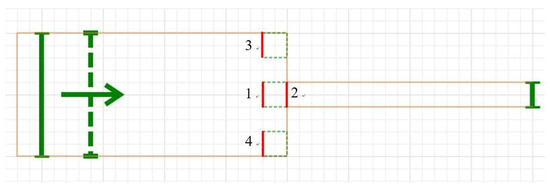
Figure 5. Setting of speed detection lines.

According to the simulation results, some interesting facts are summarized.

(1)

When the arching phenomenon is not occurred yet, pedestrian speed is higher at detection line 1 and 2. However, as the arching phenomenon occurred, pedestrian speed is decreased significantly at detection line 1 and 2. Then, speed is beginning to flatten.

(2)

At first, there are no pedestrians pass through detection line 3 and 4. Thus, pedestrian speed is 0 at detection line 3 and 4. With the emergence of the arching, a higher pedestrian speed occurred at detection line 3 and 4. As the arching stabilizes, pedestrian speed starts to stabilize at detection line 3 and 4.

(3)

The pedestrian speed at detection line 1 is slightly lower than pedestrian speed at detection line 2, indicating that the speed of the pedestrian crossing the bottleneck is higher than the speed at the entrance of the bottleneck.

(4)

The pedestrian speed at detection line 3 is higher than pedestrian speed at detection line 4, which is related to keep to the right in china traffic. This leads to pedestrian congestion at detection line 3 is more serious than at detection line 4.

According to the change of speed, pedestrian arching phenomenon can be divided into four stages: Free, arching formation, arching stabilization, and arching dissipation, as shown in Figure 6. the phases of the process can be characterized as follow:

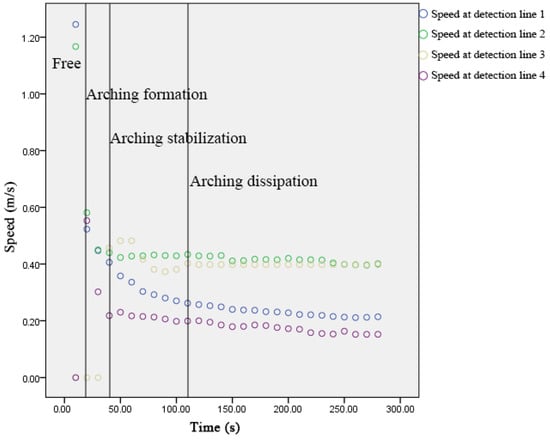
Figure 6. Speed scatterplot for different detection position.

Free: $\{\begin{array}{c}{V}_1\ge 1\\ V_2\ge 1\\ V_3=0\\ V_4=0\end{array}$

Arching formation: $\{\begin{array}{c}\Delta V_1<0\\ \Delta V_2<0\\ \Delta V_3>0\\ \Delta V_4>0\end{array}$

Arching stabilization: $\{\begin{array}{c}\Delta V_1<0\\ \Delta V_2\approx 0\\ \Delta V_3\ne 0\\ \Delta V_4<0\end{array}$

Arching dissipation: $\{\begin{array}{c}\Delta V_1\approx 0\\ \Delta V_2\approx 0\\ \Delta V_3\approx 0\\ \Delta V_4\approx 0\end{array}$

where $V_1$ and $\Delta V_1$ represents pedestrian speed and acceleration at detection line 1, $V_2$ and $\Delta V_2$ represents pedestrian speed and acceleration at detection line 2, $V_3$ and $\Delta V_3$ represents pedestrian speed and acceleration at detection line 3 and $V_4$ and $\Delta V_4$ represents pedestrian speed and acceleration at detection line 4.

4.3. Passing Time

The passing time, an overall indicator of pedestrian traffic, is defined as the total time starting from the first pedestrian entering the entrance A to the departure of the last pedestrian from exit B. The total passing time T was calculated according to Equation (7).

$$T=t_{Bn}-t_{A1}$$

(7)

where $t_{A1}$ represents the time when the first pedestrian entered the entrance A and $t_{Bn}$ represents the time when the last pedestrian n departed from the exit B.

The passing time is an important parameter to describe the level of service and efficiency in subway transit hub. Thus, passing time is analyzed under different bottleneck scenarios. The simulation results show that with increase of width ratio, passage time presents a certain degree of increased trend. Moreover, with increase of length ratio, passage time has no significant change, as shown in Figure 7. Pearson’s correlation is used in analyzing the relation of passing time, width ratio, length ratio, as shown in Table 3. A good relationship between passing time and width ratio is seen (Pearson’s r correlation coefficient is less than 0.05). There is no correlation between the passing time and length ratio (Pearson’s r correlation coefficient is more than 0.05). The correlation results show that as the width ratio is different, the passing time would show the correlation change.

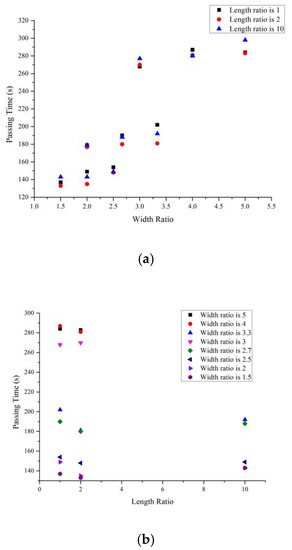
Figure 7. Relations between bottleneck scenario and passing time. (a) scatter diagram of width ratio and passing time and (b) scatter diagram of length ratio and passing time.

Table 3. Pearson’s correlation analysis

		Passing Time	Width Ratio	Length Ratio
Pearson’s Correlation	Passing Time	1.000	0.856	0.022
	Width Ratio	0.856	1.000	0.000
	Length Ratio	0.022	0.000	1.000
Sig. (one-tailed)	Passing Time		0.000	0.457
	Width Ratio	0.000		0.500
	Length Ratio	0.457	0.500
N	Passing Time	27	27	27
	Width Ratio	27	27	27
	Length Ratio	27	27	27

To clear the specific relevance of width ratio and passing time, function fitting is conducted to observe the trend. Function model is as following.

$$T=48.081w+64.322=48.081\frac{w_1}{w_2}+64.322$$

$$R^2=0.7223$$

where $T$ is total passing time, s; $w$ is width ratio of corridor and corridor bottleneck; $w_1$ is corridor width, m and $w_2$ is corridor bottleneck width, m.

5. Conclusions

This paper focuses on pedestrians arching phenomenon at bottleneck in subway transit hub. After discussing the characteristics and advantages of the current mainstream pedestrian simulation models, social force model is choosing to construct the bottleneck scenario. Moreover, movement preference characteristic in subway transit hub is considered to model. Then, simulations and experimental studies is carried out, which is used to conduct the quantitative analysis of pedestrians arching mechanism at bottleneck in subway transit hub. The results show that according to the change of speed, pedestrian arching phenomenon can be divided into four stages: Free, arching formation, arching stabilization and arching dissipation, which is a new insight. With the different of bottleneck width ratio, passing time presents positive correlation, which is rarely focused on in previous studies. Research results could provide theoretic support and practical reference to improve the pedestrian efficiency at bottleneck, and optimize pedestrian facilities in subway transit hub. However, this study has the limitation that more factors affecting the pedestrian behavior should be taken into building simulation model, such as gender and age. In future studies, different bottleneck scenario and different pedestrian volumes will also be considered. Besides, further mechanisms of pedestrian’s behavior can be introduced to the model, like following behavior, polite behavior and group behavior. Moreover, pedestrian behavior in some special situations can also be studied, like epidemic situation.