Deep Learning-Based Indoor Distance Estimation Scheme Using FMCW Radar
Abstract
1. Introduction
2. System Description
2.1. System Overview
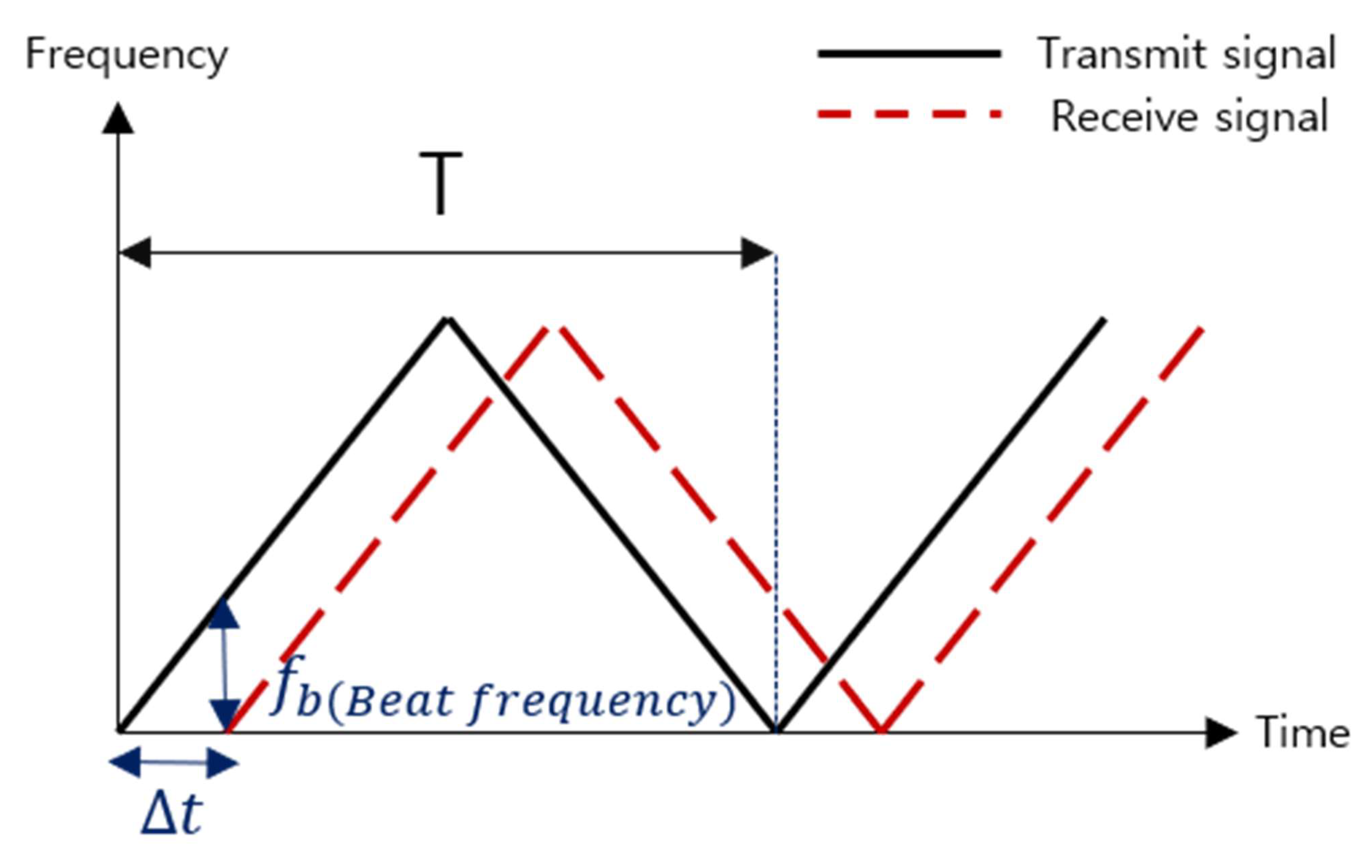
2.2. Conventional Scheme
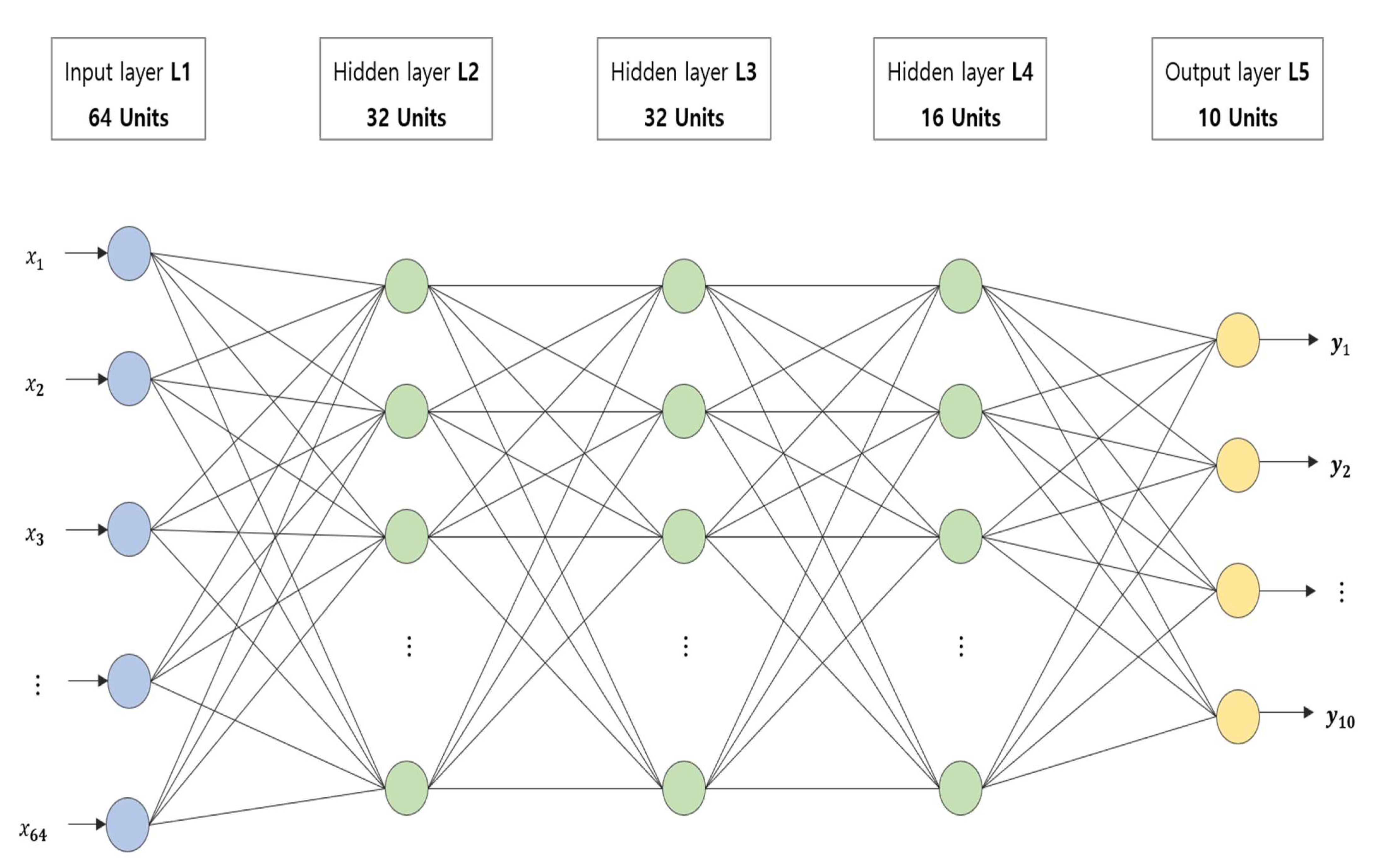
3. Proposed Scheme
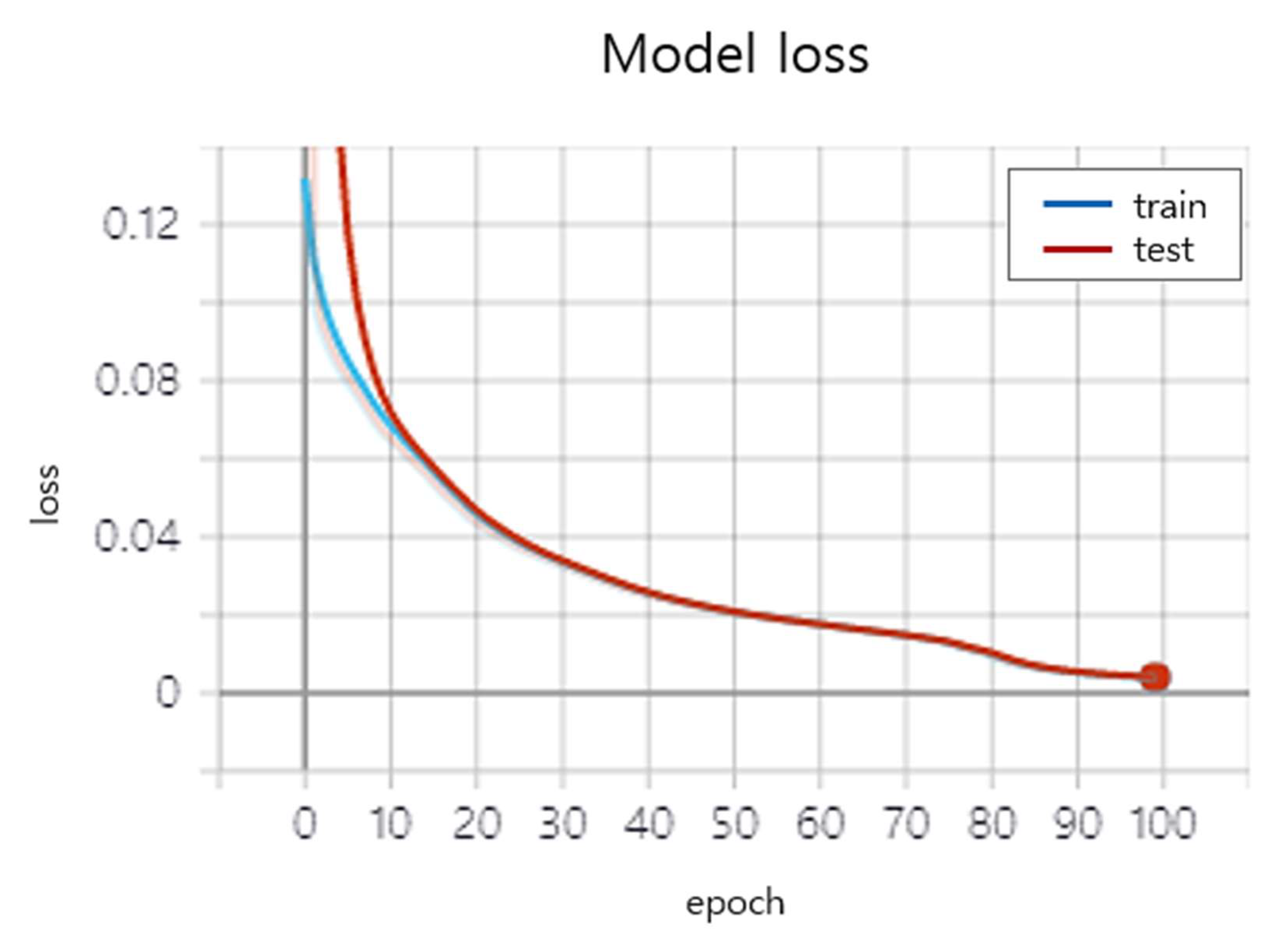
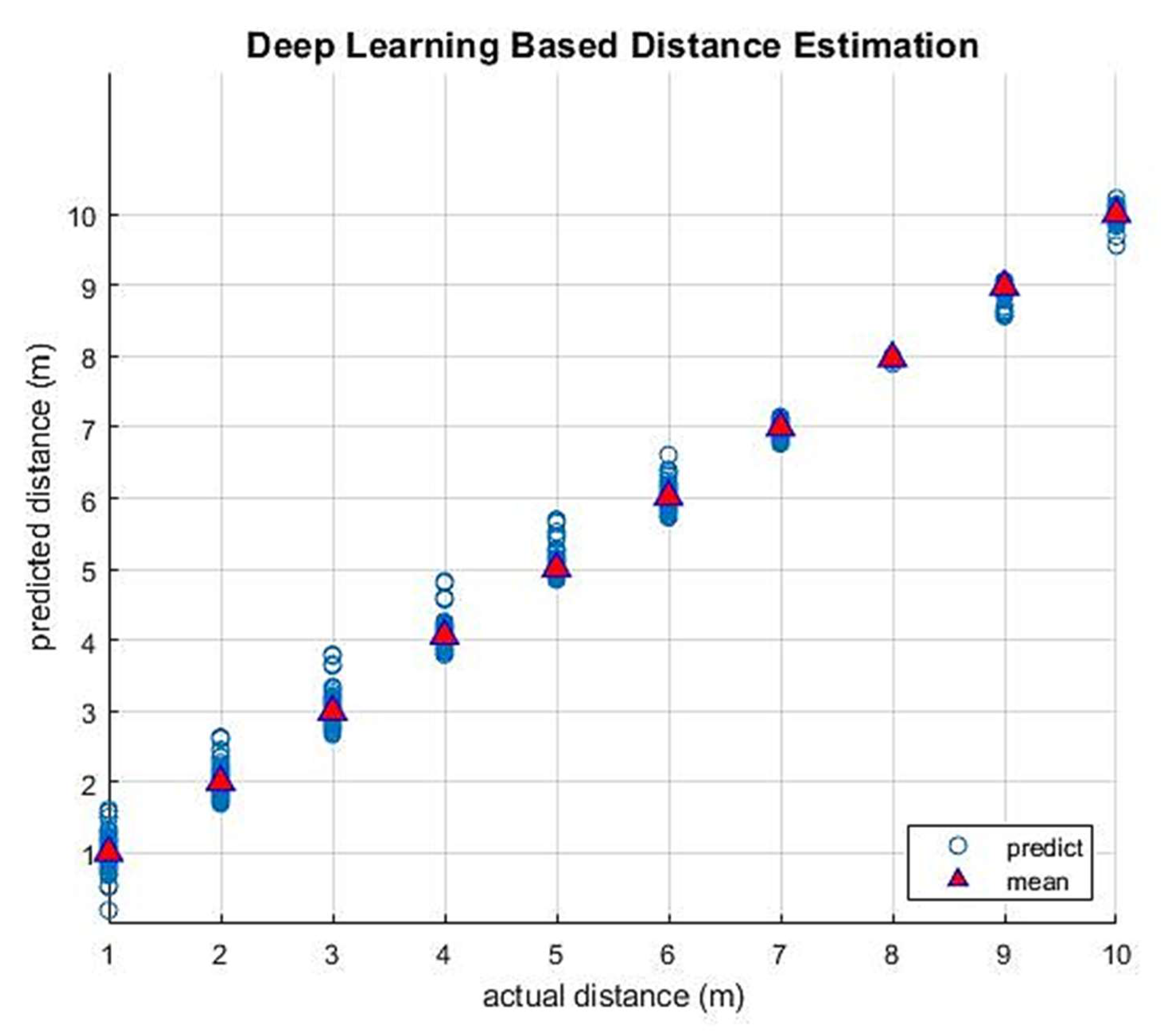
4. Experiment Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Kim, C.-M.; Jang, B. Indoor Localization Technology Survey. J. Korean Soc. Comput. Inf. 2016, 21, 17–24. [Google Scholar] [CrossRef]
- Park, S.-J. Trends in the Development of Interior Location Identification Technology and Services; Korea Institute of Communication Sciences: Seoul, Korea, 2017; Volume 34, pp. 3–9. [Google Scholar]
- Jeon, H.; Jo, U.; Jo, M.; Kim, N.; Kim, Y. An adaptive AP selection scheme based on RSS for enhancing positioning accuracy. Wirel. Pers. Commun. 2013, 69, 1535–1550. [Google Scholar] [CrossRef]
- Gustafsson, F.; Gunnarsson, F. Mobile positioning using wireless networks: Possibilities and fundamental limitations based on available wireless network measurements. IEEE Signal Process. Mag. 2003, 22, 41–53. [Google Scholar] [CrossRef]
- Jain, V.K.; Tapaswi, S.; Shukla, A. Location estimation based on semi-supervised locally linear embedding (SSLLE) approach for indoor wireless networks. Wireless Pers. Commun. 2012, 67, 879–893. [Google Scholar] [CrossRef]
- Remondino, F.; Stoppa, D. TOF Range-Imaging Cameras; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sun, Y.; Liu, M.; Meng, M.Q.H. Motion removal for reliable RGB-D SLAM in dynamic environments, Robotics and Autonomous Systems. Robot. Auton. Syst. 2018, 108, 115–128. [Google Scholar] [CrossRef]
- Yun, Y.; Park, Y.; Lee, B.M.; Hyun, B.; Kim, Y. Distance Estimation Scheme Exploiting IR-UWB Radar with Clutter Suppressing Algorithm in Indoor Environments. J. Electr. Eng. Technol. 2019, 14, 1759–1769. [Google Scholar] [CrossRef]
- Van Delden, M.; Guzy, C.; Musch, T. Investigation on a System for Positioning of Industrial Robots Based on Ultra-Broadband Millimeter Wave FMCW Radar. In Proceedings of the 2019 IEEE Asia-Pacific Microwave Conference (APMC), Singapore, 10–13 December 2019; pp. 744–746. [Google Scholar] [CrossRef]
- Moghaddam, M.H.; Aghdam, S.R.; Filippi, A.; Eriksson, T. Statistical Study of Hardware Impairments Effect on mmWave 77 GHz FMCW Automotive Radar. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Han, J.-H. Study on 24GHz Short Range Radar System Using Delayed FMCW Signal; Kwangwoon University: Seoul, Korea, 2014. [Google Scholar]
- Kim, N.; Yu, M.; Lee, S. A method for improving range estimation accuracy in narrowband indoor FMCW radar range sensors. In Proceedings of the Annual Conference of IEIE, Jeju, Korea, 26–28 June 2019; pp. 345–348. [Google Scholar]
- Mu, R.; Zeng, X. A Review of Deep Learning Research. KSII Trans. Internet Inf. Syst. (TIIS) 2019, 13, 1738–1764. [Google Scholar] [CrossRef]
- Song, W.-K. A Research on Range Estimation Method Using an FMCW Radar for Smart Cars; Hanyang University: Seoul, Korea, 2016. [Google Scholar]
- Hyun, E.; Jin, Y.S.; Kim, B.S.; Lee, J.H. Development of Human Detection Algorithm for Automotive Radar. Trans. Korean Soc. Automot. Eng. 2017, 25, 92–102. [Google Scholar] [CrossRef]
- Winkler, V. Range Doppler detection for automotive FMCW radars. In Proceedings of the 2007 European Radar Conference, Munich, Germany, 10–12 October 2007; pp. 166–169. [Google Scholar] [CrossRef]
- Sandström, S.-E.; Akeab, I.K. A study of some FMCW radar algorithms for target location at low frequencies. Radio Sci. 2016, 51, 1676–1685. [Google Scholar] [CrossRef]
- Hua, S.; Zhou, Z.; Wang, Y.; Zhou, S. Multi-target detection in FMCW radar. In Proceedings of the International Radar Conference, Beijing, China, 8–10 October 1996; pp. 367–370. [Google Scholar] [CrossRef]
- Kim, C.K.; Kim, N.R.; Lee, S.J. FMCW LiDAR System with Variable Point FFT and Analog Filter; Korea Institute of Communication Sciences: Seoul, Korea, 2020; pp. 594–595. Available online: http://www.dbpia.co.kr/journal/articleDetail?nodeId=NODE09346447 (accessed on 10 February 2021).
- Kim, M.J.; Cheon, I.H.; Kim, J.H. FMCW Radar Signal Process Using Real FFT; The Korea Institute of Information and Communication Engineering: Seoul, Korea, 2007; pp. 2227–2232. Available online: http://www.dbpia.co.kr/journal/articleDetail?nodeId=NODE02249456 (accessed on 10 February 2021).
- Kim, Y.-H.; Shin, G.-W.; Lee, Y.-H. The Predict of Future Technology Based on Deep Learning; Korean Institute of Information Technology: Seoul, Korea, 2015; pp. 219–220. [Google Scholar]
- Park, J.H.; Jeong, Y.-S. Learning Algorithms in AI System and Services. JIPS J. Inf. Process. Syst. 2019, 15, 1029–1035. [Google Scholar] [CrossRef]
- Wang, W.; Wu, L.; Huang, Y.; Wang, H.; Zhu, R. Link Prediction Based on Deep Convolutional Neural Network. Information 2019, 10, 172. [Google Scholar] [CrossRef]
- Wang, J.; Liu, L. A Neural Network Sparseness Algorithm Based on Relevance Dropout. In Proceedings of the 2019 IEEE 6th International Conference on Industrial Engineering and Applications (ICIEA), Tokyo, Japan, 12–15 April 2019; pp. 480–484. [Google Scholar] [CrossRef]
- Özgür, A.; Nar, F. Effect of Dropout layer on Classical Regression Problems. In Proceedings of the 2020 28th Signal Processing and Communications Applications Conference (SIU), Gaziantep, Turkey, 5–7 October 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Liaqat, S.; Dashtipour, K.; Zahid, A.; Assaleh, K.; Arshad, K.; Ramzan, N. Detection of Atrial Fibrillation Using a Machine Learning Approach. Information 2020, 11, 549. [Google Scholar] [CrossRef]
- Lee, K.; Lim, J.; Bok, K.; Yoo, J. Handling Method of Imbalance Data for Machine Learning: Focused on Sampling. J. Korea Contents Assoc. 2019, 19, 567–577. [Google Scholar] [CrossRef]
- Lotte, F.; Bougrain, L.; Cichocki, A.; Clerc, M.; Congedo, M.; Rakotomamonjy, A.; Yger, F. A review of classification algorithms for EEG-based brain–computer interfaces: A 10 year update. J. Neural Eng. 2018, 15, 031005. [Google Scholar] [CrossRef] [PubMed]
- Grosse-Wentrup, M.; Buss, M. Multiclass Common Spatial Patterns and Information Theoretic Feature Extraction. IEEE Trans. Biomed. Eng. 2008, 55, 1991–2000. [Google Scholar] [CrossRef] [PubMed]




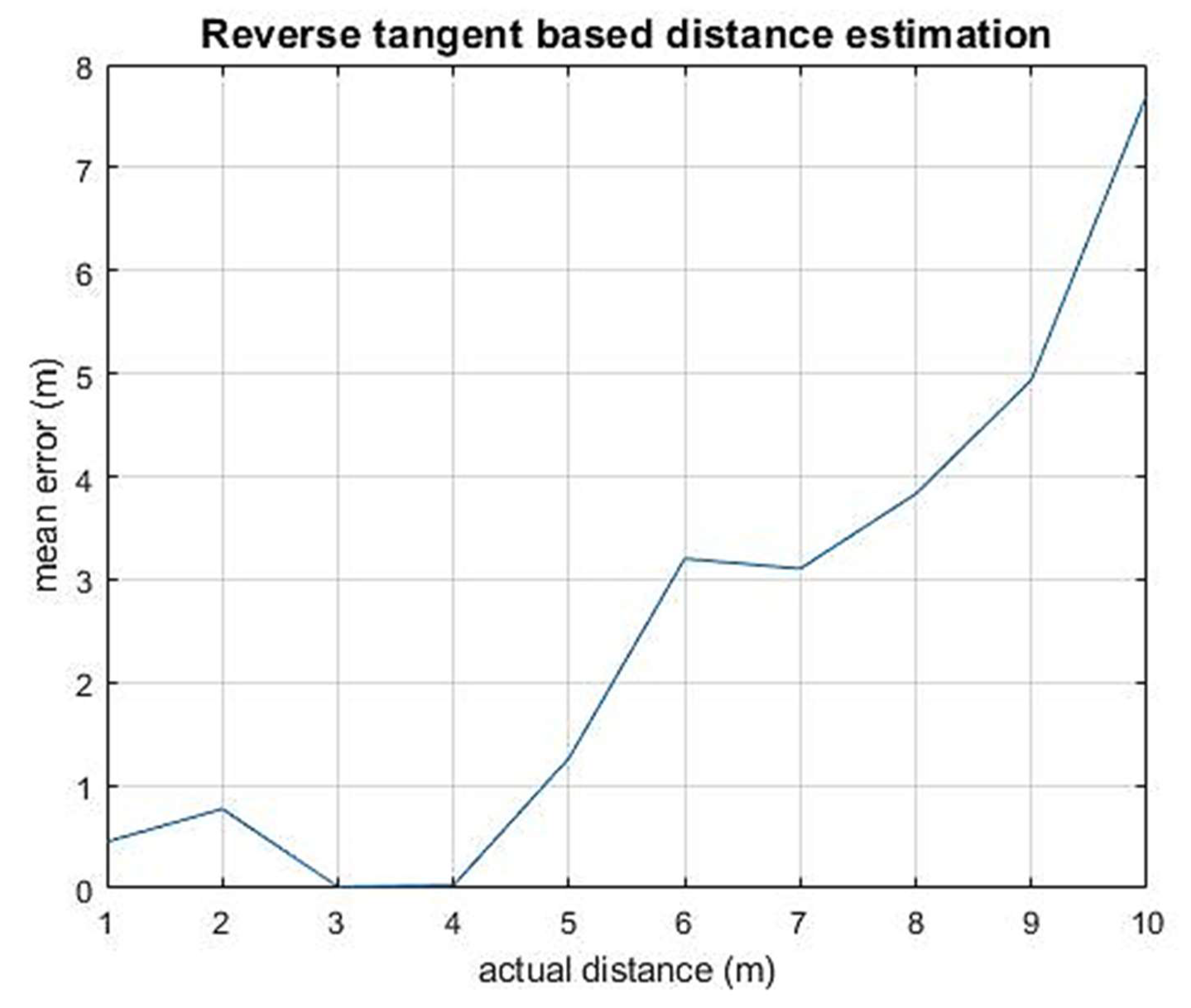

| True Distance | 1m | 2m | 3m | 4m | 5m | 6m | 7m | 8m | 9m | 10m |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean error(m) | 0.4515 | 0.7701 | 0.0144 | 0.0281 | 1.2653 | 3.2012 | 3.1036 | 3.8320 | 4.9379 | 7.7134 |
| Layers | Learning Rate | Training Epochs | Batch Size | |
|---|---|---|---|---|
| Value | 5 | 0.001 | 100 | 500 |
| Total Data | Train Data | Validation Data | Test Data | |
|---|---|---|---|---|
| Number | 20000 | 12800 | 4000 | 3200 |
| Ratio | 1 | 0.64 | 0.2 | 0.16 |
| Conventional Scheme | Reverse Tangent Scheme | CSP Scheme | Regression Model | Proposed Scheme | |
|---|---|---|---|---|---|
| Mean error | 1.9 m | 2.5317 m | 0.2923 m | 0.1647 m | 0.069 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, K.-E.; Lee, J.-P.; Kim, Y. Deep Learning-Based Indoor Distance Estimation Scheme Using FMCW Radar. Information 2021, 12, 80. https://doi.org/10.3390/info12020080
Park K-E, Lee J-P, Kim Y. Deep Learning-Based Indoor Distance Estimation Scheme Using FMCW Radar. Information. 2021; 12(2):80. https://doi.org/10.3390/info12020080
Chicago/Turabian StylePark, Kyung-Eun, Jeong-Pyo Lee, and Youngok Kim. 2021. "Deep Learning-Based Indoor Distance Estimation Scheme Using FMCW Radar" Information 12, no. 2: 80. https://doi.org/10.3390/info12020080
APA StylePark, K.-E., Lee, J.-P., & Kim, Y. (2021). Deep Learning-Based Indoor Distance Estimation Scheme Using FMCW Radar. Information, 12(2), 80. https://doi.org/10.3390/info12020080






