Ensemble and Quick Strategy for Searching Reduct: A Hybrid Mechanism

Abstract

Attribute reduction is commonly referred to as the key topic in researching rough set. Concerning the strategies for searching reduct, though various heuristics based forward greedy searchings have been developed, most of them were designed for pursuing one and only one characteristic which is closely related to the performance of reduct. Nevertheless, it is frequently expected that a justifiable searching should explicitly involves three main characteristics: (1) the process of obtaining reduct with low time consumption; (2) generate reduct with high stability; (3) acquire reduct with competent classification ability. To fill such gap, a hybrid based searching mechanism is designed, which takes the above characteristics into account. Such a mechanism not only adopts multiple fitness functions to evaluate the candidate attributes, but also queries the distance between attributes for determining whether two or more attributes can be added into the reduct simultaneously. The former may be useful in deriving reduct with higher stability and competent classification ability, and the latter may contribute to the lower time consumption of deriving reduct. By comparing with 5 state-of-the-art algorithms for searching reduct, the experimental results over 20 UCI data sets demonstrate the effectiveness of our new mechanism. This study suggests a new trend of attribute reduction for achieving a balance among various characteristics.

1. Introduction

Attribute reduction [1,2], as one filter feature selection technique emerges in rough set [3,4,5], plays a crucial role in the field of data dimension reduction. Generally speaking, given a constraint, the purpose of attribute reduction is to obtain an appropriate attribute subset through some specific searchings.

In general, if the form of the attribute reduction is fully defined, then how to derive such qualified reduct is the key. Up to now, exhaustion and heuristics based searchings are two frequently used strategies. Though the optimal reduct can be obtained through using exhaustion, the time consumption is frequently too high to be accepted because exhaustion is designed for finding all reducts. For such reason, the heuristics based searching [6,7] has been paid much attention to for its low complexity.

As a poster child of heuristic searching, forward greedy [8] is effective. However, some limitations can also be observed in forward greedy searching. On the one hand, the elapsed time of obtaining reduct may be higher with dramatically increasing volume of data [9]. For instance, if we are facing high-dimensional data [10,11], then for each iteration in the process of forward greedy searching, one and only one attribute is selected and immediately, the times of iterations may be greater. On the other hand, in the processes of most of the forward greedy searchings, each candidate attribute is evaluated based on one and only one fitness function, i.e., one measure with respect to the form of attribute reduction is calculated for each candidate attribute. Obviously, such device is only the single-view [12,13] based evaluation and then it may not be applicable to the stability requirement of selecting attribute.

By considering what has been discussed above and the learning task, it is not difficult to emphasize that a reasonable algorithm for deriving reduct should be equipped with the following important characteristics.

(1)

Low time consumption of deriving reduct. This is the first perspective which should be considered in designing algorithm, especially when large-scale and high-dimensional data appear.

(2)

High stability of derived reduct. A reduct with low stability indicates that such reduct is susceptible if data perubation happens, and then it may be unsuitable for further data processing.

(3)

Competent classification of derived reduct. Attribute reduction can be regarded as an important step of data pre-processing, and then it does expect that the obtained reduct will offer competent performance if the classification task is explored.

Presently, to the best of our knowledge, most of the previous approaches for searching reduct mainly focus on one and only one of the above characteristics. For example, Chen et al. [14] have proposed an attribute group approach for calculating reduct based on the consideration of the relationship among attributes. Such approach consists of two main phases: (1) raw attributes are divided into different groups; (2) in the process of searching reduct, only the attributes in the group contain at least one attribute in the potential reduct should be evaluated. From this point of view, such process can reduce the times of evaluating candidate attributes, it follows that the elapsed time of deriving reduct may be decreased. Though Chen et al.’s attribute group has achieved success for low time consumption of deriving reduct, it may not be suitable for generating reduct with high stability. This is mainly because: (1) in such approach, each candidate attribute is still evaluated based on one and only one fitness function [13,15], which will lead to ignore the distribution of the samples; (2) the groups of attributes strongly depend on the process of K-means, which will result in some degrees of randomness for adding appropriate attributes into the potential reduct.

To overcome the above limitations, a new hybrid mechanism will be developed in this paper, where multiple characteristics are considered simultaneously. Firstly, to obtain the reduct with high stability, the ensemble selector [13,16] will be introduced into our approach, in which each attribute can be fully evaluated with respect to multiple fitness functions. Secondly, it is worth noting that the usage of ensemble selector will imply higher time consumption. Therefore, the dissimilarity relationship among attributes obtained by using the distance between attributes will be further employed, by which multiple different attributes can be selected and added into the potential reduct for each iteration in the process of deriving reduct. This is the core for effectively reducing the time consumption. In additional, following the researches shown in Refs. [13,17], it can be observed that the reducts obtained by both ensemble selector and dissimilarity are frequently equipped with competent generalization performance. For such reason, our hybrid mechanism is also expected to be with justifiable classification ability. The specific details of our mechanism will be shown in the following Figure 1.

In Figure 1,

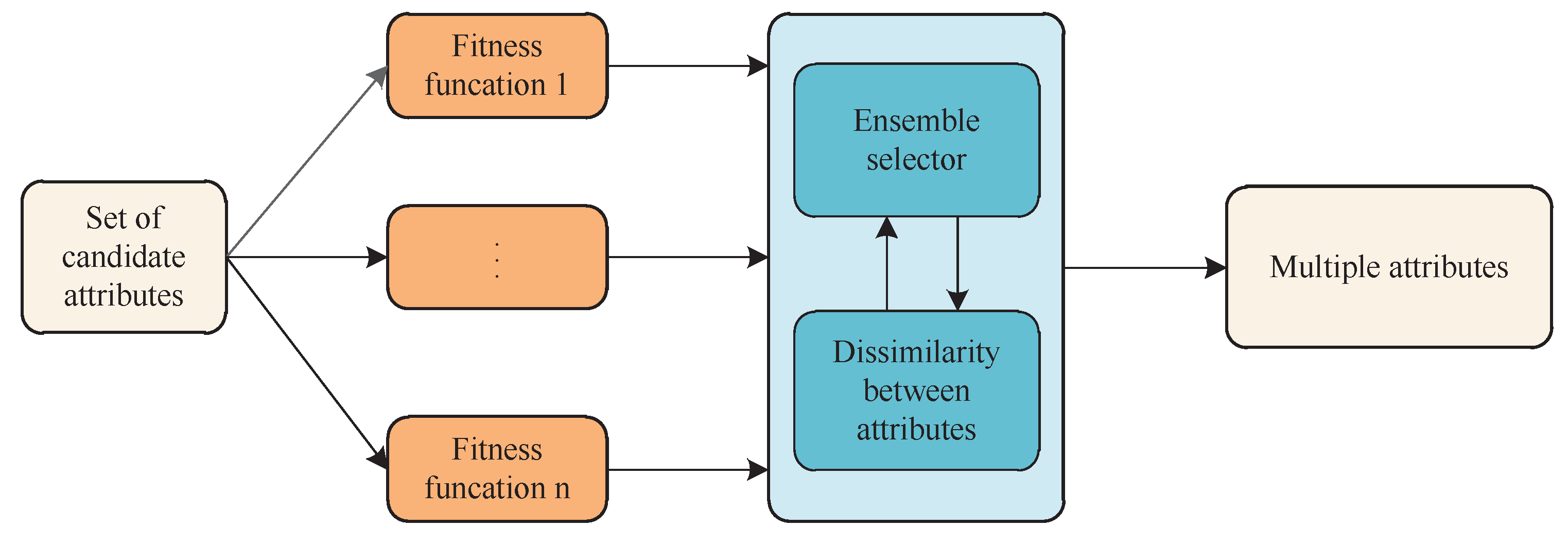
(1)

each candidate attribute will be evaluated from different perspectives by using multiple fitness functions;

(2)

an appropriate attribute can be obtained by adopting the mechanism of ensemble selector based on the results of the attribute evaluations;

(3)

one or more attributes, which bear a striking dissimilarity to the attribute obtained in (2), will also be selected;

(4)

more than one attributes can be added into the potential reduct simultaneously.

The main contribution of this research can be summarized as the following aspects: (1) observing that most of the state-of-the-art approaches are designed for pursuing one and only one characteristic which is closely related to the performance of reduct, a hybrid based searching mechanism is proposed to make a trade-off between the stability of derived reduct and the elapsed time of searching reduct; (2) though the neighborhood rough set based reduct is conducted by using the hybrid based searching mechanism in the context of this paper, it worth to point out that our hybrid based searching mechanism is independent of rough set model and then can be employed to any other attribute reduction.

The remainder of this paper is organized as follows. In Section 2, we will review the basic notions related to attribute reduction and some used measures. A new hybrid mechanism for searching reduct will be presented in Section 3. Comparative experimental results and the corresponding analyses will be shown in Section 4. This paper will come to an end with conclusions and future perspectives in Section 5.

2. Preliminaries

2.1. Attribute Reduction

Presently, a variety of definitions of attribute reduction [18,19] have been proposed with respect to different requirements [20,21]. Through extracting the commonness of those definitions, Yao et al. [22], have proposed a general form which is shown in the following Definition 1.

Definition 1.

Given a decision system $\mathcal{DS}=<U,AT,D>$, U is a nonempty finite set of samples, AT is a nonempty finite set of raw attributes and D is a decision attribute. Supposing that ρ-constraint is a constraint based on a considered measure ρ such that $\rho :P\left(AT\right)\to \mathcal{R}$ ($P\left(AT\right)$ is the power set of $AT$, $\mathcal{R}$ is the set of all real numbers), then $\forall A\subseteq AT$, A is referred to as a reduct if and only if

(1)

A satisfies the ρ-constraint;

(2)

$\forall B\subset A$, B does not satisfy the ρ-constraint.

Following Definition 1, the open problem is how to obtain a qualified reduct. As one of the widely used heuristic algorithms, the forward greedy searching [8,23] has been favored by many researchers. The details of such strategy are shown in the following Algorithm 1.

In Algorithm 1, fitness value can be obtained by a fitness function such that $\varphi$: $AT\to \mathcal{R}$, it follows that the importance of each attribute can be quantitatively characterized. It must be noticed that the form of fitness function is closely related to the measure $\rho$ used in given constraint. For example, if the constraint is required to preserve the measure of approximation quality, then $\varphi \left(a\right)$ can be regarded as the variation of the approximation quality [24] if a is added into the pool set.

It is not difficult to reveal that the process of Algorithm 1 contains two main phases. The first phase, adds the qualified attributes into the potential reduct. The second phase, removes redundant attributes from the potential reduct. Obviously, this process fits the two requirements shown in Definition 1. The time complexity of Algorithm 1 is $\mathcal{O}(|U{|}^2\times |AT{|}^2)$, where $|U|$ and $|AT|$ denote the numbers of samples and raw attributes, respectively.

Algorithm 1. Forward Greedy Searching (FGS) .

Input: Decision system $\mathcal{DS}$, $\rho$-constraint and fitness function $\varphi$.

Output: One reduct A.

Step 1. Calculate the measure-value $\rho \left(AT\right)$ over the raw attribute set $AT$;

Step 2.$A=\varnothing$;

Step 3. Do

(1) Evaluate each candidate attribute $a\in AT-A$ by calculating $\varphi \left(a\right)$;

(2) Select a qualified attribute $b\in AT-A$ with the justifiable evaluation;

(3) $A=A\cup \left\{b\right\}$;

(4) Calculate $\rho \left(A\right)$;

Until $\rho$-constraint is satisfied;

// Adding the qualified attributes into the potential~reduct

Step 4. Do

(1) $\forall a\in A$, calculate $\rho (A-\{a\left\}\right)$;

(2) If $\rho$-constraint is satisfied

$A=A-\left\{a\right\}$;

End

Until A does not change or $|A|$ =1;

// Removing redundant attributes from the potential~reduct

Step 5. Return A.

2.2. Stability Measure

Generally speaking, the stability of reduct can be regarded as the sensitivity of the attribute preferences if an algorithm produces differences in training sets drawn from the same generating distribution. Therefore, the stability of reduct can be quantified as the changing degree of reducts if sample disturbance happens.

To quantitatively characterize the concept of the stability, a series of measures [25,26,27,28] has been proposed. Furthermore, to make the comparisons among different measures more reasonable, Nogueira et al. [28] suggested five desirable properties that a stability measure should possess: (1) fully defined; (2) strict monotonicity; (3) bounds; (4) maximum stability; (5) correction for chance. Therefore, with a critical reviewing of the previous stability measures, it is not difficult to observe that only the measures designed by Akashata et al. [27] and Nogueira et al. [28] fully possess the above five properties. Such two measures will be shown in the following Definitions 2 and 3.

Definition 2.

Given a set of reducts $\mathcal{Z}=\{A_1,A_2,...,A_M\}$, supposing that $AT$ is a raw attribute set, the stability measure proposed by Akashata with respect to $\mathcal{Z}$ is defined as:

$$\widehat{\mathsf{\Phi }}\left(\mathcal{Z}\right)=\frac{1}{M(M+1)}\sum _{i=1}^M\sum _{j=1,j\ne i}^M\psi (A_i,A_j),$$

(1)

$$\psi (A_i,A_j)=\alpha \left(\frac{I_{ij}-\frac{|A_i{|}^2}{|AT|}}{|A_i|-\frac{|A_i{|}^2}{|AT|}}\right)+\beta \left(\frac{I_{ij}-E_{ij}}{M_{ij}-{\mu }_{ij}}\right),$$

(2)

where $I_{ij}$, $E_{ij}$, ${\mu }_{ij}$ and $M_{ij}$ represent the intersection, expected intersection, minimum intersection and maximum intersection of attributes with respect to $A_i$ and $A_j$, respectively. If $|A_i|=|A_j|$, then α = 1 and β = 0; otherwise, α = 0 and β = 1.

Definition 3.

Given a set of reducts $\mathcal{Z}=\{A_1,A_2,...,A_M\}$, supposing that $AT$ is a raw attribute set and $\overline{k}$ is the mean value of the numbers of attributes in reducts, the stability measure proposed by Nogueira with respect to $\mathcal{Z}$ is defined as:

$$\widehat{\mathsf{\Phi }}\left(\mathcal{Z}\right)=1-\left[\frac{\frac{1}{|AT|}{\sum }_{a\in AT}{s}_a^2}{\frac{\overline{k}}{|AT|}\left(1-\frac{\overline{k}}{|AT|}\right)}\right],$$

(3)

where $s_a^2$ is unbiased sample variance of the selected attribute a.

Following the above discussions, Akashata’s measure shown in Definition 2 is based on the similarity over reducts. Nogueira’s measure shown in Definition 3 is based on the frequency over attributes. It is not difficult to reveal that both of them take the advantage of the differences among reducts for obtaining the quantified value. The former pay much attention to the overall differences between two different reducts, while the latter focuses on the difference of each attribute among multiple reducts.

3. A New Hybrid Mechanism for Attribute Reduct

3.1. Dissimilarity for Attribute Reduction

Through FGS, we can observe that one and only one appropriate attribute will be selected and added into the potential reduct for each iteration of evaluating candidate attributes. Therefore, if the number of attributes is large, then the elapsed time of deriving reduct may still be unacceptable. For such reason, the strategy of searching reduct by considering the dissimilarity between attributes has been proposed by Rao et al. [17], which can simultaneously add more than one attribute into the potential reduct for each iteration of evaluating candidate attributes. The detail is shown in the following Algorithm 2.

Algorithm 2. Dissimilarity for Attribute Reduction (DAR)

Input: Decision system $\mathcal{DS}$, $\rho$-constraint, fitness function $\varphi$ and number of attributes in one combination t.

Output: One reduct A.

Step 1. Calculate the measure-value $\rho \left(AT\right)$ over the raw attribute set AT;

Step 2. Calculate the dissimilarities between attributes such that $\Psi =\{\Delta (a,b):\forall a,b\in AT\}$;

// $\Delta (a,b)$denotes the distance between attributesaandb

Step 3.$A=\varnothing$;

Step 4. Do

(1) Evaluate each candidate attribute $a\in AT-A$ by calculating $\varphi \left(a\right)$;

(2) Select a qualified attribute $b\in AT-A$ with the justifiable evaluation;

(3) Obtain ${\Psi }_b=\{\Delta (b,c):\forall c\in AT-(A\cup \left\{b\right\})\}$ from $\Psi$;

(4) By ${\Psi }_b$, derive attribute subset B with $t-1$ attributes, in which the attributes bear the striking dissimilarity to b;

(5) $A=A\cup \left\{b\right\}\cup B$;

// Selection of a combination of~attributes

(6) Calculate $\rho \left(A\right)$;

Until $\rho$-constraint is satisfied;

Step 5. Do

(1) $\forall a\in A$, calculate $\rho (A-\{a\left\}\right)$;

(2) If $\rho$-constraint is satisfied

$A=A-\left\{a\right\}$;

End

Until A does not change or $|A|$ = 1;

Step 6. Return A.

Compared with FGS, Algorithm 2 can significantly reduce the elapsed time of obtaining reduct. The time complexity of Algorithm 2 is $\mathcal{O}(|U{|}^2\times |AT|\times m)$, in which $m=\lfloor \frac{|AT|}{t}\rfloor$. Obviously, ${\mathcal{O}(|U|}^2\times |AT|\times {m)<\mathcal{O}(|U|}^2\times {|AT|}^2)$, i.e., the complexity of Algorithm 2 is lower. However, for the reason that more than one attribute can be selected during each iteration, then Algorithm 2 may derive reduct with lower stability.

3.2. Ensemble Selector for Attribute Reduction

As what has been shown in Section 2.1, the fitness function is actually used to evaluate the importance of the candidate attributes. However, it must be pointed out that only one fitness function cannot be used to characterize the importance of the candidate attributes with multiple views. Furthermore, the using of only one fitness function does not take the distribution of the samples into account and then it will lead to the instability of deriving reduct. To fill such gap, Yang and Yao [13] have proposed the ensemble selector for attribute reduction, which employs multiple fitness functions for evaluating the candidate attributes. Immediately, the voting mechanism can be used for selecting the appropriate attribute. The detailed process will be shown in the following Algorithm 3.

Algorithm 3. Ensemble Selector for Attribute Reduction (ESAR)

Input: Decision system $\mathcal{DS}$, $\rho$-constraint and fitness function ${\varphi }_1,{\varphi }_2,...,{\varphi }_s$.

Output: One reduct A.

Step 1. Calculate the measure-value $\rho \left(AT\right)$ over the raw attribute set AT;

Step 2.$A=\varnothing$;

Step 3. Do

(1) Let multiset $T=\varnothing$;

(2) For i = 1 to s

(i) Evaluate each candidate attribute $a\in AT-A$ by calculating ${\varphi }_i\left(a\right)$;

(ii) Select a qualified attribute $b_i\in AT-A$ with the justifiable evaluation;

(iii) $T=T\cup \left\{b_i\right\}$;

End

(3) Select an attribute $b\in T$ with the maximal frequency of occurrences;

// Ensemble selector mechanism

(4) $A=A\cup \left\{b\right\}$;

(5) Calculate $\rho \left(A\right)$;

Until $\rho$-constraint is satisfied;

Step 4. Do

(1) $\forall a\in A$, calculate $\rho (A-\{a\left\}\right)$;

(2) If $\rho$-constraint is satisfied

$A=A-\left\{a\right\}$;

End

Until A does not change or $|A|$ = 1;

Step 5. Return A.

By comparing with both Algorithms 1 and 2, the time complexity of Algorithm 3 is significantly increased. This is mainly because multiple fitness functions have been used. Without loss of generality, the time complexity of Algorithm 3 is $\mathcal{O}(|U{|}^2\times |AT{|}^2\times s)$, in which s is the number of used fitness functions.

3.3. A New Hybrid Mechanism for Attribute Reduction

Reviewing the researches of attribute reduction, most of the previous approaches pay much attention to improving the performance of one aspect. For example, compared with Algorithm 1, Algorithm 2 can significantly reduce the elapsed time of calculating reduct while Algorithm 3 can generate reduct with higher stability. However, as what have been pointed out in Section 3.1 and Section 3.2, the above two algorithms are highly possible to lead to performance degradation in some other aspects, e.g., Algorithm 2 may derive reduct with lower stability because more than one attribute have been selected for each iteration and Algorithm 3 may be with higher time consumption because multiple fitness functions should be used.

Without loss of generality, it is expected to design an algorithm for deriving reduct with the following three characteristics.

(1)

Low time consumption of deriving reduct. Though many accelerators have been proposed for quickly deriving reduct, the dissimilarity approach presented in Algorithm 2 will be used in our research, this is mainly because such algorithm will provide us reduct with low stability, and then it is possible for us to optimize it for quickly obtaining reduct with high stability.

(2)

High stability of derived reduct. To search reduct with high stability, the ensemble selector presented in Algorithm 3 will be introduced into our research. However, though such algorithm may contribute to the reduct with high stability, it frequently result in a high time consumption of obtaining reduct. Then it is possible for us to optimize such algorithm for quickly obtaining reduct with high stability.

(3)

Competent classification of derived reduct. In the studies of Yang et al. [13] and Rao et al. [17], it has been pointed out that the reducts obtained by using Algorithms 2 and 3 possess the justifiable classification ability. For such reason, it is possible that the combination of those two algorithms can also preserve competent classification ability.

Therefore, a new hybrid mechanism for attribute reduction will be proposed. The specific process is shown in the following Algorithm 4.

Algorithm 4. Hybrid Mechanism for Attribute Reduction (HMAR)

Input: Decision system $\mathcal{DS}$, $\rho$-constraint, fitness function ${\varphi }_1,{\varphi }_2,...,{\varphi }_s$ and number of attributes in one combination t.

Output: One reduct A.

Step 1. Calculate the measure-value $\rho \left(AT\right)$ over the raw attribute set AT;

Step 2. Calculate the dissimilarities between attributes such that $\Psi =\{\Delta (a,b):\forall a,b\in AT\}$;

// $\Delta (a,b)$denotes the distance between attributesaandb

Step 3.$A=\varnothing$;

Step 4. Do

(1) Let multiset $T=\varnothing$;

(2) For i = 1 to s

(i) Evaluate each candidate attribute $a\in AT-A$ by calculating ${\varphi }_i\left(a\right)$;

(ii) Select a qualified attribute $b_i\in AT-A$ with the justifiable evaluation;

(iii) $T=T\cup \left\{b_i\right\}$;

End

(3) Select an attribute $b\in T$ with the maximal frequency of occurrences;

// Ensemble selector~mechanism

(4) Obtain ${\Psi }_b=\{\Delta (b,c):\forall c\in AT-(A\cup \left\{b\right\})\}$ from $\Psi$;

(5) By ${\Psi }_b$, derive attribute subset B with $t-1$ attributes, in which the attributes bear the striking dissimilarity to b;

// Using the main thinking of the dissimilarity~approach

(6) $A=A\cup \left\{b\right\}\cup B$;

(7) Calculate $\rho \left(A\right)$;

Until $\rho$-constraint is satisfied;

Step 4. Do

(1) $\forall a\in A$, calculate $\rho (A-\{a\left\}\right)$;

(2) If $\rho$-constraint is satisfied

$A=A-\left\{a\right\}$;

End

Until A does not change or $|A|$ =1;

Step 5. Return A.

In Algorithm 4, on the one hand, ensemble selector is employed, which can provide higher stability. On the other hand, the dissimilarity between candidate attributes is also taken into account, and then multiple attributes can be added into the potential reduct simultaneously, which contributes to the lower time complexity. Therefore, the time complexity of Algorithm 4 is $\mathcal{O}({\sum }_{i=1}^s(|U{|}^2\times |AT|\times m\left)\right)={O(|U|}^2\times |AT|\times m\times s)$, in which $m=\lfloor \frac{|AT|}{t}\rfloor$ and s is the number of used fitness functions. Obviously, ${\mathcal{O}(|U|}^2\times |AT|\times {m)<\mathcal{O}(|U|}^2\times |AT|\times m\times {s)<\mathcal{O}(|U|}^2\times {|AT|}^2\times s)$, i.e., though the time complexity of Algorithm 4 is higher than that of Algorithm 2, compared with that of Algorithm 3, it is lower.

4. Experimental Analysis

4.1. Data Sets and Configuration

To demonstrate the effectiveness of the algorithm proposed in this paper, 20 UCI data sets have been selected to conduct the experiments. The detailed description of those data sets will be shown in the following

Table 1. Data sets description.

ID	Data Sets	Samples	Attributes	Decision Classes
1	Breast Cancer Wisconsin (Diagnostic)	569	30	2
2	Connectionist Bench (Sonar, Mines vs. Rocks)	208	60	2
3	Dermatology	366	34	6
4	Fertility	100	9	2
5	Forest Type Mapping	523	27	4
6	Glass Identification	214	9	6
7	Ionosphere	351	34	2
8	Libras Movement	360	90	15
9	LSVT Voice Rehabilitation	126	256	2
10	Lymphography	98	18	3
11	QSAR Biodegradation	1055	41	2
12	Quality Assessment of Digital Colposcopies	287	62	2
13	Statlog (Australian Credit Approval)	690	14	2
14	Statlog (Heart)	270	13	2
15	Statlog (Image Segmentation)	2310	18	7
16	Steel Plates Faults	1941	33	2
17	Synthetic Control Chart Time Series	600	60	6
18	Urban Land Cover	675	147	9
19	Waveform Database Generator (Version 1)	5000	21	3
20	Wine	178	13	3

. All the experiments have been carried out on a personal computer with Windows 10, AMD R7 3750H CPU (2.30 GHz) and 8.00 GB memory. The programming language is Matlab R2017a.

4.2. Experimental Setup

In the following experiments, the neighborhood rough set [8,10,29] will be employed to define forms of attribute reduction. Note that the 5-fold cross-validation is also used in our experiments to test the performances of reducts. In other words, for each data set, the set of raw samples is randomly partitioned into 5 groups with the same size, the 4 groups compose the training samples for computing reducts and the remaining 1 group is regarded as the testing samples. The threshold of approximation quality is set to be 0.95 (95%). Such value is beneficial to avoid a series of problems caused by too strict constraints, and reduce the time consumption of the experiments.

Furthermore, five state-of-the-art algorithms are selected for comparing with our proposed algorithm. The above five algorithms are shown as following.

(1)

Forward Greedy Searching (FGS) [8].

(2)

Attribute Group for Attribute Reduction (AGAR) [14].

(3)

Ensemble Selector for Attribute Reduction (ESAR) [13].

(4)

Dissimilarity for Attribute Reduction (DAR) [17].

(5)

Data-Guidance for Attribute Reduction (DGAR) [30].

4.3. Comparisons of Stability

In this section, the stability of reducts obtained by using different algorithms will be compared with each other. The detailed results will be shown in the following

Table 2. Stability of reducts based on different measures.

ID	Akashata’s Measure						Nogueira’s Measure
	FGS	AGAR	ESAR	DAR	DGAR	HMAR	FGS	AGAR	ESAR	DAR	DGAR	HMAR
1	0.4376	0.1822	0.8602	0.3218	0.3419	0.4379	0.4126	0.1617	0.8632	0.3596	0.3782	0.3935
2	0.1090	0.1077	0.9400	0.5233	0.0610	0.6964	0.1048	0.1035	0.8333	0.5142	0.0580	0.6305
3	0.5212	0.2893	0.9529	0.3992	0.5202	0.4933	0.4292	0.2442	0.7882	0.3311	0.3976	0.4234
4	0.4074	0.2442	0.7732	0.4601	0.2255	0.7157	0.4246	0.2516	0.9042	0.6065	0.3546	0.7274
5	0.2006	0.2457	0.8084	0.6306	0.3716	0.2745	0.3719	0.2588	0.9089	0.7023	0.5784	0.4402
6	0.2766	0.2041	1.0000	0.5754	0.5463	0.2908	0.4257	0.2417	1.0000	0.7776	0.7135	0.4389
7	0.2562	0.1213	0.6545	0.2986	0.2818	0.4416	0.2236	0.0991	0.7011	0.2799	0.2858	0.3750
8	0.3152	0.0923	0.7122	0.3102	0.2372	0.5412	0.2992	0.1091	0.8588	0.2949	0.3304	0.4629
9	0.2964	0.2914	0.9826	0.3807	0.8621	0.7349	0.3072	0.3025	0.9178	0.3876	0.7324	0.7257
10	0.4763	0.2500	0.9130	0.1723	0.3761	0.4964	0.3882	0.2097	0.8933	0.1275	0.2685	0.4013
11	0.8079	0.4508	0.5458	0.6669	0.3626	0.8083	0.7016	0.4217	0.7529	0.7824	0.6108	0.7129
12	0.3981	0.3877	1.0000	0.5867	0.4768	0.7933	0.3981	0.3877	1.0000	0.5867	0.4983	0.7933
13	0.5537	0.3129	0.6449	0.9493	0.4495	0.5537	0.7037	0.3278	0.8548	0.9793	0.6331	0.7037
14	0.7561	0.3097	0.9282	0.1332	0.5158	0.4592	0.7194	0.2896	0.9705	0.3318	0.5467	0.4139
15	0.5620	0.3396	1.0000	0.8977	0.4722	0.6383	0.7296	0.3506	1.0000	0.9576	0.6279	0.8050
16	0.9583	0.8941	0.8927	0.8628	0.8781	0.9716	0.9657	0.9049	0.9345	0.8371	0.8237	0.9788
17	0.3443	0.2441	0.9470	0.5399	0.6782	0.7534	0.3335	0.2346	0.8720	0.5330	0.6001	0.6988
18	0.2927	0.2494	0.9594	0.5600	0.3615	0.6861	0.2902	0.2471	0.9002	0.5467	0.3359	0.6338
19	0.2991	0.1192	0.8556	0.3828	0.4245	0.5248	0.3200	0.1135	0.9288	0.4304	0.4613	0.5132
20	0.3349	0.2423	0.8913	0.4258	0.5288	0.4619	0.2801	0.2020	0.8854	0.4095	0.4471	0.3938
Average	0.4302	0.2789	0.8631	0.5039	0.4486	0.5887	0.4414	0.2731	0.8884	0.5388	0.4841	0.5833

.

To further reveal the differences between the stability of reducts obtained by using HMAR and other five algorithms from the statistical perspective. The changing ratio related to the stability of reducts obtained by different measures will be shown in the following

Table 3. The changing ratio related to stability of reducts based on Akashata’s measure.

ID	HMAR & FGS	HMAR & AGAR	HMAR & ESAR	HMAR & DAR	HMAR & DGAR
1	0.0009	1.4036	−0.4909	0.3610	0.2807
2	5.3867	5.4643	−0.2592	0.3309	10.4126
3	−0.0535	0.7050	−0.4823	0.2359	−0.0517
4	0.7570	1.9303	−0.0743	0.5556	2.1740
5	0.3685	0.1175	−0.6604	−0.5647	−0.2613
6	0.0516	0.4252	−0.7092	−0.4946	−0.4676
7	0.7240	2.6415	−0.3252	0.4790	0.5669
8	0.7169	4.8644	−0.2401	0.7447	1.2817
9	1.4792	1.5223	−0.2521	0.9302	−0.1475
10	0.0422	0.9860	−0.4563	1.8810	0.3199
11	0.0006	0.7931	0.4809	0.2121	1.2290
12	0.9929	1.0460	−0.2067	0.3523	0.6638
13	0.0000	0.7695	−0.1414	−0.4167	0.2319
14	−0.3926	0.4829	−0.5053	2.4467	−0.1097
15	0.1357	0.8795	−0.3617	−0.2890	0.3518
16	0.0139	0.0868	0.0884	0.1261	0.1065
17	1.1881	2.0861	−0.2044	0.3954	0.1109
18	1.3438	1.7509	−0.2849	0.2252	0.8982
19	0.7546	3.4040	−0.3866	0.3710	0.2362
20	0.3791	0.9061	−0.4818	0.0848	−0.1265
Average	0.6945	1.6132	−0.2977	0.3984	0.8850

and

Table 4. The changing ratio related to stability of reducts based on Nogueira’s measure.

ID	HMAR & FGS	HMAR & AGAR	HMAR & ESAR	HMAR & DAR	HMAR & DGAR
1	−0.0463	1.4333	−0.5441	0.0943	0.0406
2	5.0186	5.0904	−0.2434	0.2261	9.8752
3	−0.0134	0.7341	−0.4628	0.2786	0.0651
4	0.7132	1.8906	−0.1956	0.1992	1.0515
5	0.1837	0.7006	−0.5157	−0.3733	−0.2390
6	0.0310	0.8158	−0.5611	−0.4356	−0.3848
7	0.6772	2.7850	−0.4651	0.3397	0.3121
8	0.5472	3.2431	−0.4610	0.5697	0.4009
9	1.3624	1.3986	−0.2093	0.8720	−0.0092
10	0.0339	0.9138	−0.5507	2.1466	0.4946
11	0.0161	0.6907	−0.0531	−0.0888	0.1672
12	0.9929	1.0460	−0.2067	0.3523	0.5920
13	0.0000	1.1466	−0.1768	−0.2814	0.1115
14	−0.4247	0.4291	−0.5735	0.2473	−0.2430
15	0.1034	1.2963	−0.1950	−0.1594	0.2820
16	0.0136	0.0816	0.0474	0.1693	0.1883
17	1.0954	1.9788	−0.1986	0.3112	0.1644
18	1.1841	1.5649	−0.2959	0.1593	0.8867
19	0.6039	3.5202	−0.4474	0.1923	0.1125
20	0.4060	0.9493	−0.5552	−0.0383	−0.1191
Average	0.6249	1.5854	−0.3432	0.2391	0.6875

.

Following Table 2, Table 3 and Table 4, it is not difficult to observe that the reduct obtained by using HMAR is relatively high in terms of Akashat’s and Nogueira’s measures in most cases. Take “Ionosphere” data set and Akashata’s measure as an example, the stability of reducts which obtained by using FGS, AGAR, ESAR, DAR, DGAR and HMAR are 0.2562, 0.1213, 0.6545, 0.2986, 0.2818 and 0.4416, respectively. Obviously, though the stability of the reduct obtained by using HMAR is lower than that by using ESAR which can generate reduct with high stability, compared with FGS, AGAR, DAR and DGAR, the obtained reduct by using HMAR is equipped with higher stability.

Furthermore, from the perspective of changing ratio related to the stability, the above conclusion can be further verified. For example, by using Akashata’s measure and Nogueira’s measure, the changing ratios of stability are 0.7240, 2.6415, −0.3252, 0.4790, 0.5669 and 0.6772, 2.7850, −0.4651, 0.3397, 0.3121, respectively. Through observing these values, it can be observed that compared with FGS, AGAR, DAR and DGAR, the changing ratios related to stability of the reduct obtained by using HMAR are greater than 0. It means that the stability of the reduct obtained by using HMAR is higher than that by using those four approaches.

4.4. Comparisons of Elapsed Time

In this section, the elapsed time of obtaining reducts and the changing ratio related to the elapsed time of deriving reducts will be shown in the following

Table 5. The elapsed time of obtaining the reducts (seconds).

ID	FGS	AGAR	ESAR	DAR	DGAR	HMAR
1	2.2809	2.0935	2.5233	0.5945	12.6258	1.9478
2	0.1373	0.1221	0.3528	0.0722	1.5168	0.2124
3	0.2474	0.2100	0.5156	0.1093	2.2288	0.2640
4	0.0161	0.0137	0.0217	0.0050	0.0724	0.0175
5	1.7524	1.3389	1.5266	0.3328	7.2682	1.3123
6	0.0252	0.0185	0.0318	0.0058	0.3710	0.0252
7	0.2694	0.2641	0.4229	0.0919	1.8400	0.2420
8	2.5036	1.6398	6.7867	0.4981	13.3538	1.7414
9	0.2086	0.2201	2.2628	0.2399	16.6473	2.0956
10	0.0150	0.0130	0.0420	0.0070	0.1270	0.0251
11	25.7033	23.6295	29.4748	5.7647	122.9442	21.1693
12	0.0505	0.0541	0.9240	0.0259	0.8575	0.0823
13	1.4953	1.0072	1.1725	0.2832	5.9333	1.0844
14	0.0740	0.0652	0.1114	0.0220	0.3521	0.0762
15	28.7973	22.0794	22.8940	5.7499	305.8399	20.2366
16	11.7424	16.2051	68.6182	8.1615	154.9014	16.4106
17	2.1993	1.9011	1.1649	1.0003	23.8315	0.7656
18	8.9002	8.0912	9.4483	5.9042	141.7593	6.5005
19	142.1194	112.4183	120.0497	32.7325	632.6569	103.9153
20	0.0286	0.0256	0.0480	0.0114	0.1828	0.0360
Average	11.4283	9.5705	13.4196	3.0806	72.2655	8.9080

and

Table 6. The changing ratio related to the elapsed time of deriving reducts.

ID	HMAR & FGS	HMAR & AGAR	HMAR & ESAR	HMAR & DAR	HMAR & DGAR
1	−0.1460	−0.0696	−0.2281	2.2765	−0.8457
2	0.5477	0.7397	−0.3978	1.9413	−0.8600
3	0.0673	0.2570	−0.4879	1.4144	−0.8816
4	0.0871	0.2828	−0.1936	2.4795	−0.7579
5	−0.2512	−0.0199	−0.1404	2.9433	−0.8194
6	0.0006	0.3646	−0.2060	3.3309	−0.9320
7	−0.1015	−0.0838	−0.4278	1.6345	−0.8685
8	−0.3044	0.0620	−0.7434	2.4965	−0.8696
9	9.0439	8.5205	−0.0739	7.7355	−0.8741
10	0.6782	0.9374	−0.4014	2.6051	−0.8020
11	−0.1764	−0.1041	−0.2818	2.6722	−0.8278
12	0.6299	0.5203	−0.9110	2.1718	−0.9041
13	−0.2748	0.0766	−0.0752	2.8284	−0.8172
14	0.0303	0.1697	−0.3155	2.4605	−0.7835
15	−0.2973	−0.0835	−0.1161	2.5195	−0.9338
16	0.3976	0.0127	−0.7608	1.0107	−0.8941
17	−0.6519	−0.5973	−0.3428	−0.2347	−0.9679
18	−0.2696	−0.1966	−0.3120	0.1010	−0.9541
19	−0.2688	−0.0756	−0.1344	2.1747	−0.8357
20	0.2592	0.4060	−0.2507	2.1671	−0.8031
Average	0.4500	0.5559	−0.3400	2.3364	−0.8616

.

With deep investigation of Table 5 and Table 6, it is not difficult to reveal that the time consumption of obtaining reduct by using HMAR is significantly lower than that by using ESAR. Take “Forest Type Mapping” data set as an example, the elapsed time of obtaining reducts by using FGS, AGAR, ESAR, DAR, DGAR and HMAR, 0.0161, 0.0137, 0.0217, 0.0050, 0.0724 and 0.0175 s are required, respectively. Obviously, though the elapsed time of obtaining reduct by using HMAR is higher than that by using FGS, AGAR and DAR, compare with that by using ESAR, the elapsed time of obtaining reduct by using HMAR is lower.

Furthermore, from the perspective of changing ratio related to the time consumption the above conclusion can be further verified. For example, the changing ratio of the elapsed time of obtaining reduct the by using HMAR relative to by using ESAR is −0.4879. It means that the elapsed time of obtaining reduct by using HMAR is significantly lower than that by using ESAR.

4.5. Comparisons of Classification Performances

In this section, the classification accuracies of reducts obtained by six different algorithms will be compared. KNN classifier is employed to test the classification performance. It is worth noting that the parameter k used in KNN classifier is 5. The corresponding results and the value of the changing ratio related to the classification accuracy of deriving reducts will be presented in the following

Table 7. Classification accuracies based on KNN classifier (k = 5).

ID	FGS	AGAR	ESAR	DAR	DGAR	HMAR
1	0.9609	0.9637	0.9647	0.9629	0.9614	0.9634
2	0.7669	0.7726	0.7703	0.7965	0.7879	0.7390
3	0.9273	0.8990	0.9344	0.9262	0.9488	0.8744
4	0.8635	0.8630	0.8600	0.8655	0.8710	0.8790
5	0.8762	0.8816	0.8792	0.8820	0.8801	0.8770
6	0.6426	0.6540	0.6399	0.6399	0.6408	0.6422
7	0.8567	0.8454	0.8633	0.8633	0.8666	0.8461
8	0.6982	0.6879	0.7250	0.6739	0.7125	0.5939
9	0.8199	0.8202	0.7544	0.8127	0.7437	0.6838
10	0.7050	0.7278	0.7292	0.7005	0.7886	0.7164
11	0.8570	0.8564	0.8543	0.8562	0.8553	0.8557
12	0.7514	0.7514	0.7842	0.7512	0.7295	0.7393
13	0.8436	0.8499	0.8435	0.8435	0.8435	0.8436
14	0.8181	0.8106	0.8056	0.8031	0.8183	0.8120
15	0.9526	0.9518	0.9528	0.9527	0.9527	0.9524
16	0.9991	0.9982	0.9785	0.9958	0.9984	0.9996
17	0.8189	0.8497	0.5089	0.7855	0.6984	0.6687
18	0.7314	0.7281	0.7631	0.7368	0.7354	0.7235
19	0.7937	0.7923	0.8113	0.8058	0.7984	0.7935
20	0.9563	0.9516	0.9103	0.9598	0.9646	0.9337
Average	0.8320	0.8328	0.8166	0.8307	0.8298	0.8069

and

Table 8. The changing ratio related to classification accuracies based on KNN classifier.

ID	HMAR & FGS	HMAR & AGAR	HMAR & ESAR	HMAR & DAR	HMAR & DGAR
1	0.0026	−0.0004	−0.0014	0.0005	0.0021
2	−0.0363	−0.0435	−0.0406	−0.0722	−0.0621
3	−0.0571	−0.0273	−0.0642	−0.0560	−0.0785
4	0.0180	0.0185	0.0221	0.0156	0.0092
5	0.0009	−0.0052	−0.0025	−0.0056	−0.0036
6	−0.0007	−0.0180	0.0036	0.0036	0.0022
7	−0.0124	0.0008	−0.0199	−0.0200	−0.0236
8	−0.1494	−0.1367	−0.1808	−0.1187	−0.1665
9	−0.1659	−0.1663	−0.0935	−0.1585	−0.0805
10	0.0161	−0.0157	−0.0175	0.0226	−0.0916
11	−0.0015	−0.0008	0.0017	−0.0005	0.0006
12	−0.0161	−0.0161	−0.0573	−0.0159	0.0135
13	0.0000	−0.0074	0.0002	0.0002	0.0002
14	−0.0075	0.0018	0.0080	0.0111	−0.0077
15	−0.0001	0.0007	−0.0004	−0.0003	−0.0002
16	0.0005	0.0014	0.0216	0.0038	0.0012
17	−0.1835	−0.2130	0.3139	−0.1487	−0.0426
18	−0.0108	−0.0063	−0.0519	−0.0181	−0.0162
19	−0.0003	0.0015	−0.0219	−0.0153	−0.0062
20	−0.0235	−0.0187	0.0258	−0.0271	−0.0320
Average	−0.0314	−0.0325	−0.0078	−0.0300	−0.0291

, respectively.

Through observing Table 7 and Table 8, it is not difficult to observe that our proposed approach will not lead to poorer classification accuracy compared with other approaches. Take “Dermatology” data set as an example, if k = 5, then the classification accuracies of reducts obtained by using FGS, AGAR, ESAR, DAR, DGAR and HMAR, are 0.9273, 0.8990, 0.9344, 0.9262, 0.9488 and 0.8744, respectively.

Furthermore, from the perspective of changing ratio related to the classification accuracies the above conclusion can be further verified. For example, the changing ratios of classification accuracies are −0.0571, −0.0273, −0.0642, −0.0560 and −0.0758. Through observing the these values, it can be observed that the changing ratios of classification accuracy of obtained reduct by using HMAR relative to that by using other five approaches are between −0.1 and 0.1. It means that our proposed approach performs similarly with other compared algorithms in classification ability.

4.6. Discussion of Experimental Results

In Section 4.3, the stability of reduct is discussed. In most cases, the reducts obtained by using ESAR and HAMR have relatively high stability. Take “Ionosphere” data set and Akashata’s measure as the example, the stability of reducts which obtained by using FGS, AGAR, ESAR, DAR, DGAR and HMAR are 0.2562, 0.1213, 0.6545, 0.2986, 0.2818 and 0.4416, respectively.

In Section 4.4, the time consumption of obtaining reduct is discussed. In most data sets, the elapsed time of obtaining reduct by using HMAR is less than that by using ESAR. Take “Forest Type Mapping” data set as an example, the elapsed time of obtaining reducts by using FGS, AGAR, ESAR, DAR, DGAR and HMAR, 0.0161, 0.0137, 0.0217, 0.0050, 0.0724 and 0.0175 s are required, respectively.

In Section 4.5, the classification ability of reduct is discussed. The reducts obtained by using FGS, AGAR, ESAR, DAR and HMAR have similar classification ability. Take “Dermatology” data set as an example, if KNN classifier with k = 5 is used, then the classification accuracies of reducts obtained by using FGS, AGAR, ESAR, DAR, DGAR and HMAR, are 0.9273, 0.8990, 0.9344, 0.9262, 0.9488 and 0.8744, respectively.

Obviously, the approach of HMAR which proposed by us can be used to generate reduct with high stability. Furthermore, compared with the previous approaches which can generate reducts with high stability, our approach can obtain reduct in lesser time. Concurrently, it must be pointed out that the reduct obtained by using HMAR is equipped with justifiable classification ability. Above situations are mainly caused by both the ensemble selector and the acceleration strategy have been used in our hybrid searching.

5. Conclusions and Future Perspectives

In this paper, through considering multiple characteristics related to the searching of reduct, a hybrid based searching mechanism has not only been explored but also been developed. Different from the previous approaches in which only single characteristic is fully considered, our approach takes the time consumption of deriving reduct, the stability of the derived reduct and the classification ability offered by the reduct into account, simultaneously. The experimental results demonstrate that our proposed approach can make a trade-off between the stability of derived reduct and the elapsed time of searching reduct. This is mainly because both the ensemble selector and the acceleration strategy have been used in our hybrid searching. Moreover, it must be pointed out that the reduct derived by using our approach can also provide competent classification performance by comparing with several state-of-the-art approaches. In general, a hybrid based searching mechanism is proposed by us for attribute reduction considering multiple characteristics, simultaneously. However, in terms of the time consumption of obtaining reduct and the classification ability of the obtained reduct, there are some limitations in such two performances of our approach. Therefore, we will confront the following challenges in the further research.

(1)

The elapsed time of obtaining reducts can be further reduced through combining some other acceleration strategies [31,32].

(2)

Supervised information granulation [33,34] strategy can be further introduced into our approach for improving the generalization performance offered by the reduct.