A Method of Personalized Driving Decision for Smart Car Based on Deep Reinforcement Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Personalized Driving Indicator Selection
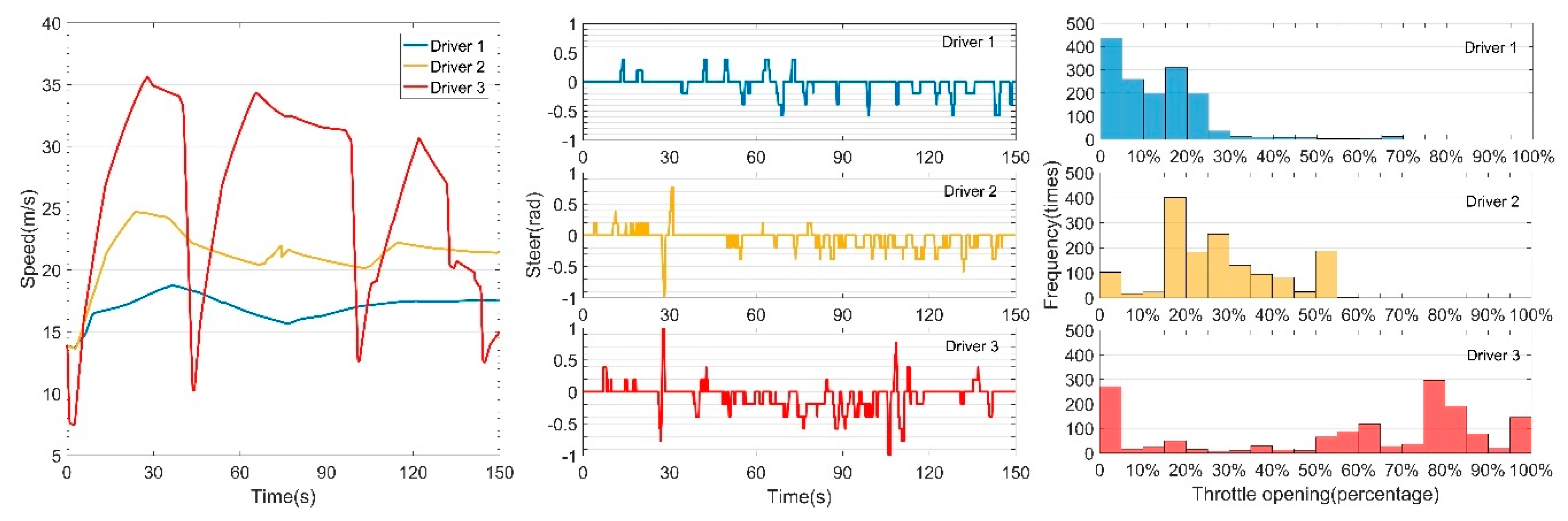
2.1.1. Manual Driving Scene Setting
2.1.2. Manual Driving Analysis
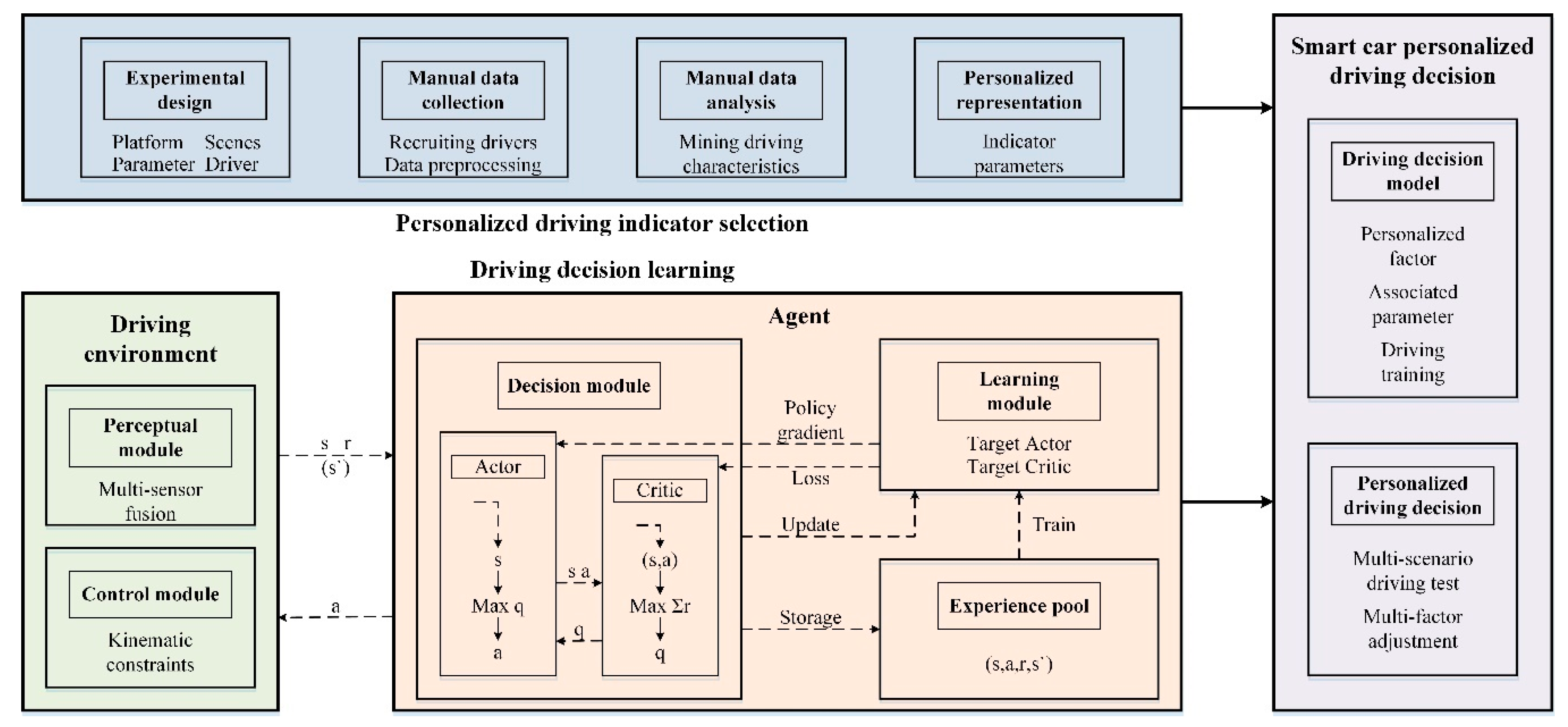
2.2. Driving Decision System Based on Deep Reinforcement Learning
2.2.1. Reinforcement Learning
2.2.2. Driving Decision System Design
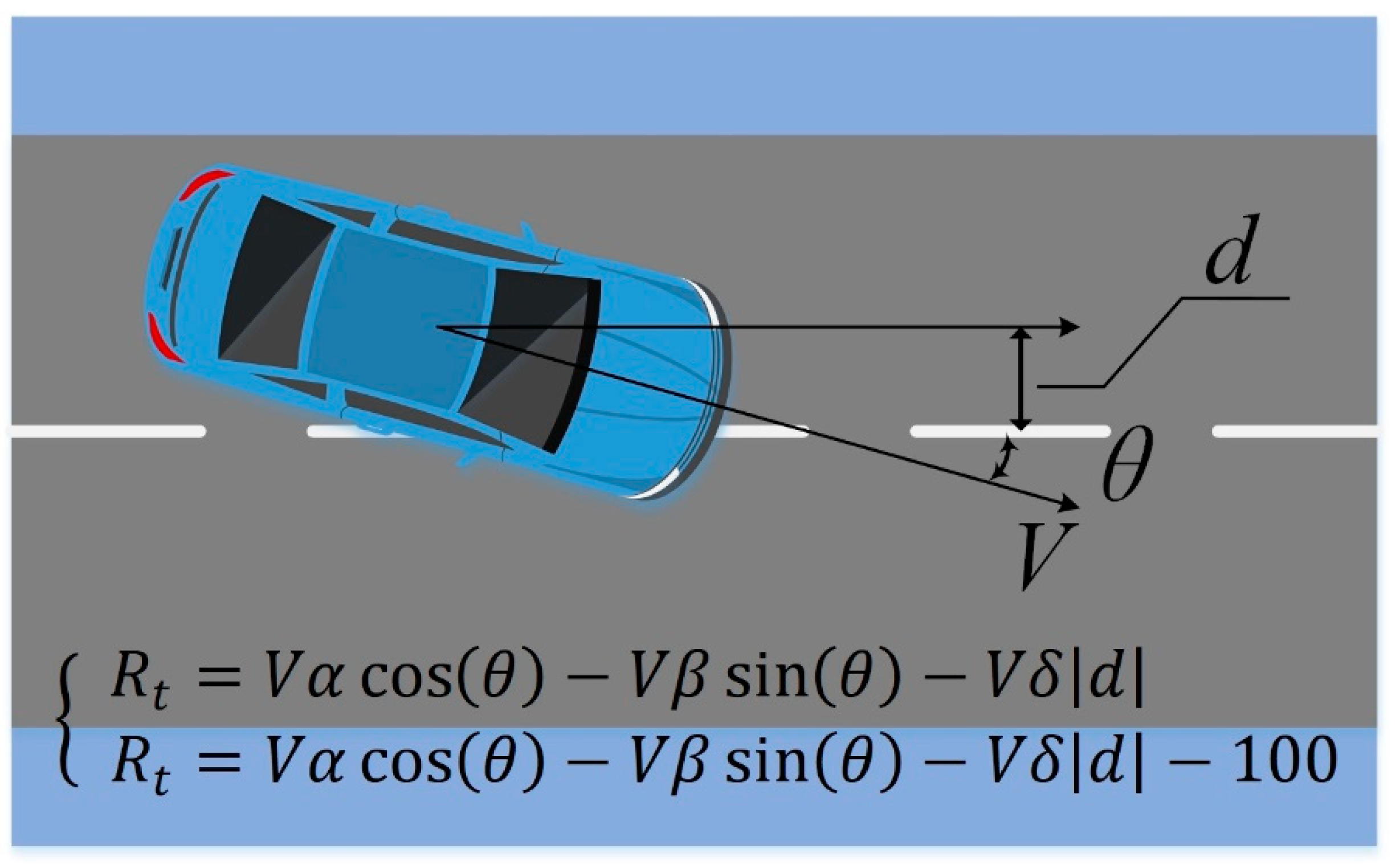
2.3. Personalized Driving Decision Model
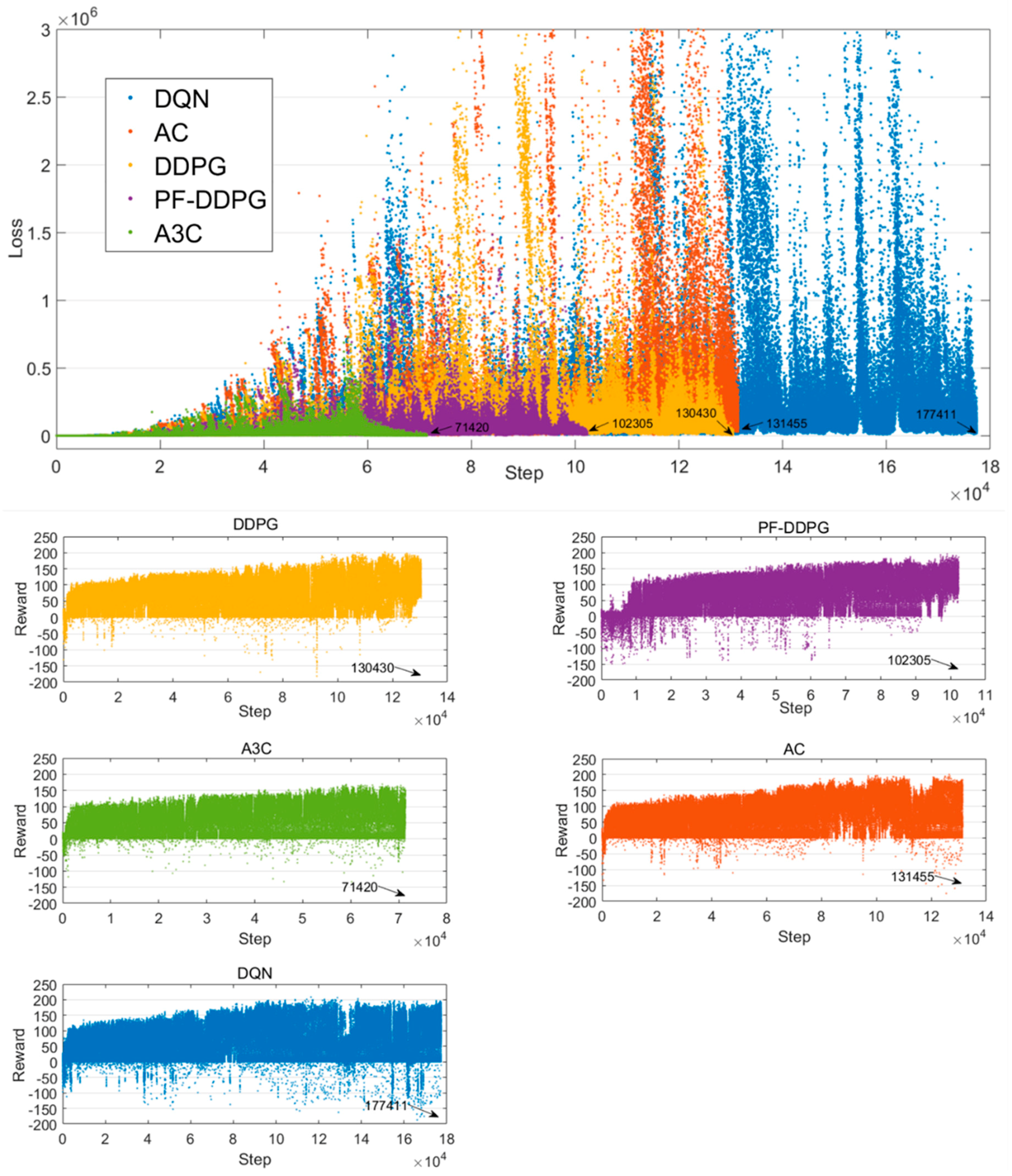
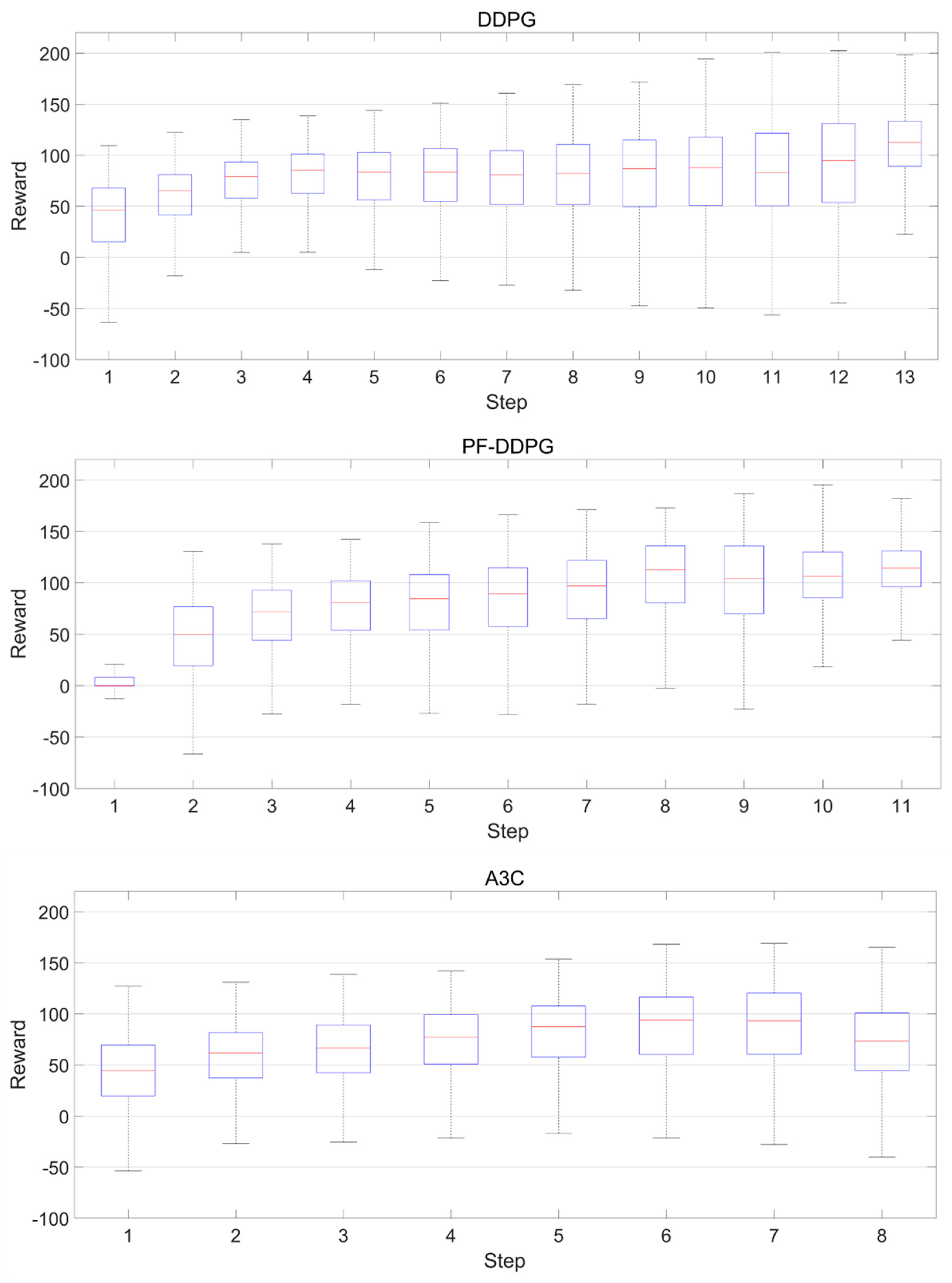
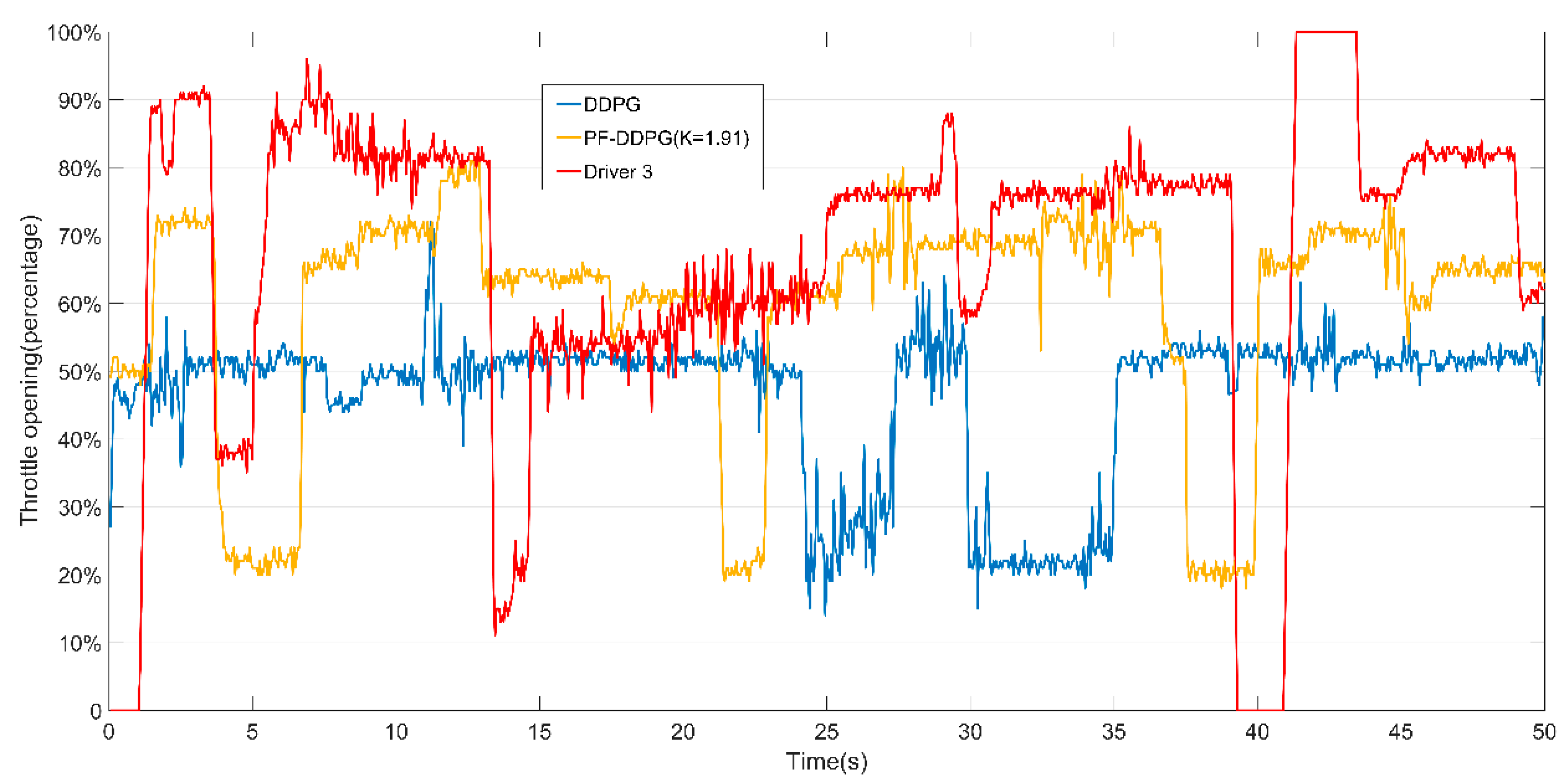
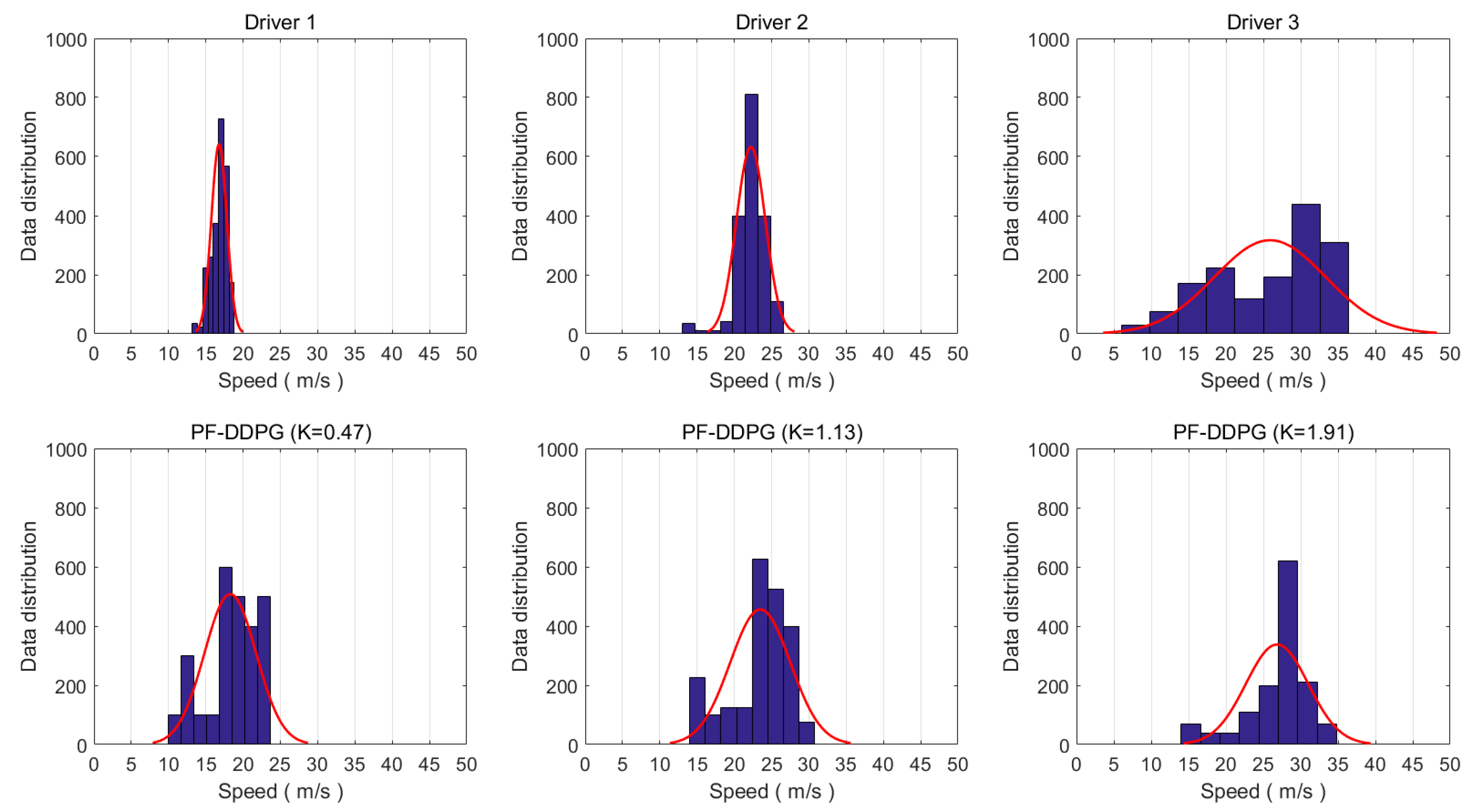
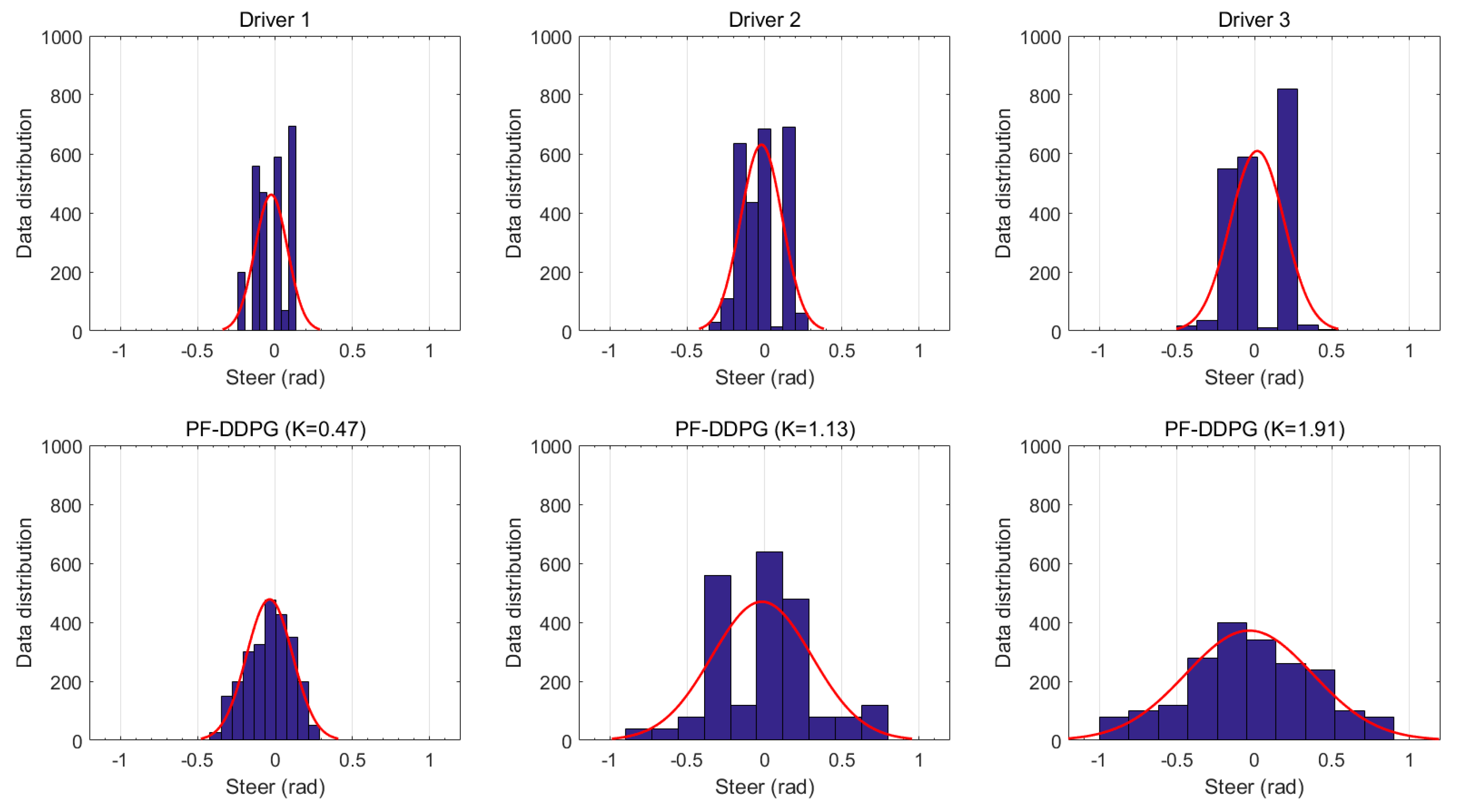
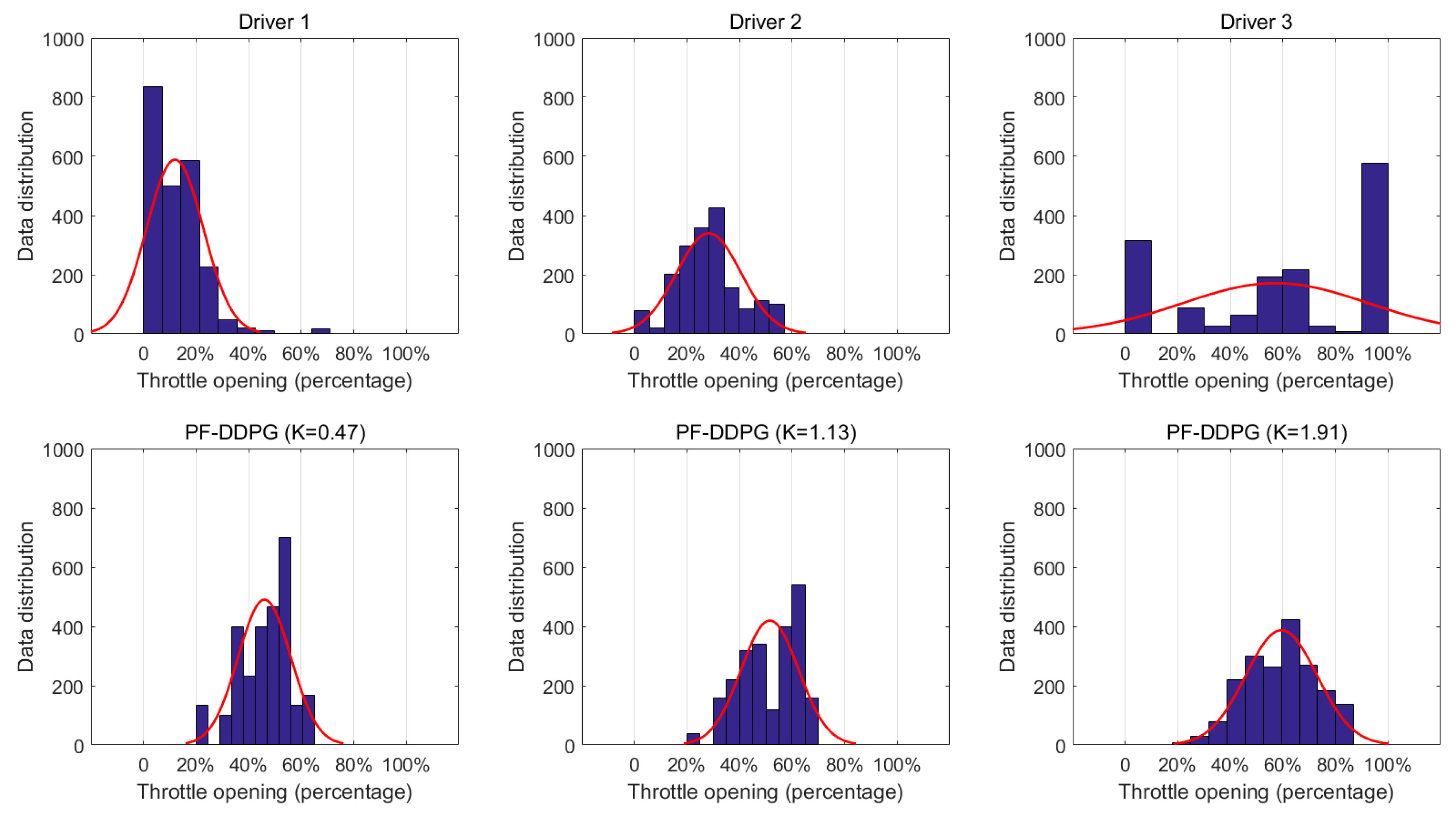
3. Results
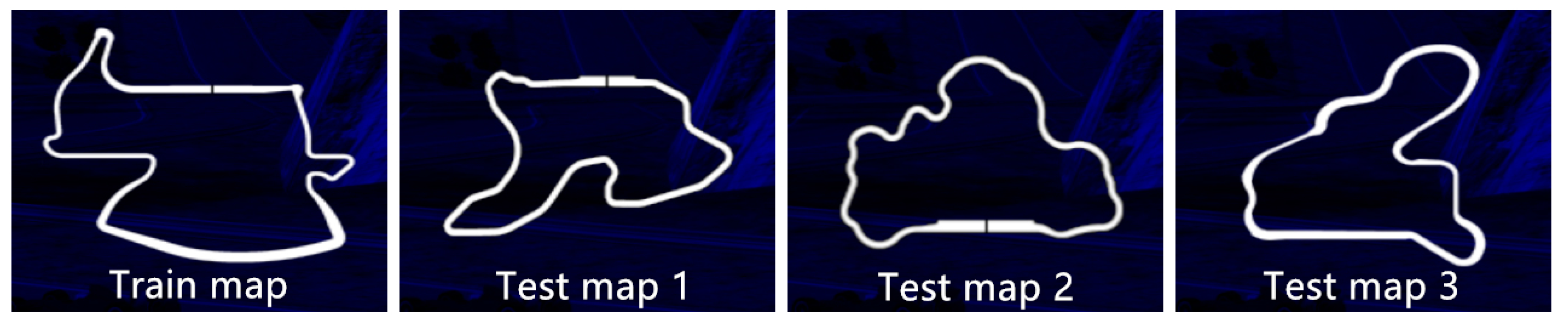
Training and Test Results
4. Discussion
- The proposed method does show differences in personalized indicators. Compared to manual driving data, the difference was not obvious enough. Personalization needs to be improved.
- The personalized driving decision model is somewhat unstable during the acceleration phase. This phenomenon disappears after the speed of the vehicle is stable.
- During training and testing, no other vehicles were added to the road. Since our work is exploratory, the introduction of other vehicles will greatly increase the complexity of the research. In the follow-up work, we will add other vehicles to the scene.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, Z.; Zhang, Y.; Wu, C.; Ran, B. Understanding Individualization Driving States via Latent Dirichlet Allocation Model. IEEE Intell. Trans. Syst. Mag. 2019, 11, 41–53. [Google Scholar] [CrossRef]
- Ziegler, J.; Bender, P.; Schreiber, M.; Lategahn, H.; Strauss, T.; Stiller, C.; Dang, T.; Franke, U.; Appenrodt, N.; Keller, C.G.; et al. Making Bertha Drive-An Autonomous Journey on a Historic Route. Intell. Trans. Syst. Mag. 2014, 6, 8–20. [Google Scholar] [CrossRef]
- Xue, J.; Van Gelderc, P.H.A.J.M.; Reniers, G.; Wu, C. Multi-attribute decision-making method for prioritizing maritime traffic safety influencing factors of autonomous ships’ maneuvering decisions using grey and fuzzy theories. Saf. Sci. 2019, 120, 323–340. [Google Scholar] [CrossRef]
- Chen, Z.; Cai, H.; Zhang, Y.; Wu, C.; Mu, M.; Li, Z.; Sotelo, M.A. A novel sparse representation model for pedestrian abnormal trajectory understanding. Expert Syst. Appl. 2019, 138, 112753. [Google Scholar] [CrossRef]
- Montemerlo, M.; Becker, J.; Bhat, S.; Dahlkamp, H.; Dolgov, D.; Ettinger, S.; Haehnel, D.; Hilden, T.; Hoffmann, G.; Huhnke, B.; et al. Junior: The Stanford entry in the Urban Challenge. J. Field Robot 2008, 25, 569–597. [Google Scholar] [CrossRef]
- Leonard, J.; How, J.; Teller, S.; Berger, M.; Campbell, S.; Fiore, G.; Fletcher, L.; Frazzoli, E.; Huang, A.; Karaman, S.; et al. A Perception-driven Autonomous Urban Vehicle. J. Field Robot. 2008, 25, 727–774. [Google Scholar] [CrossRef]
- Okumura, B.; James, M.R.; Kanzawa, Y.; Derry, M.; Sakai, K.; Nishi, T.; Prokhorov, D. Challenges in Perception and Decision Making for Intelligent Automotive Vehicles: A Case Study. Trans. Intell. Veh. 2016, 1, 20–32. [Google Scholar] [CrossRef]
- Bojarski, M.; Testa, D.D.; Dworakowski, D.; Firner, B.; Flepp, B.; Goyal, P.; Jackel, L.D.; Monfort, M.; Muller, U.; Zhang, J.; et al. End to End Learning for Self-Driving Cars. In Proceedings of the 29th IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June 2016. [Google Scholar]
- Chen, C.; Seff, A.; Kornhauser, A.L. DeepDriving: Learning Affordance for Direct Perception in Autonomous Driving. In Proceedings of the 15th Annual Meeting of the International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Hubmann, C.; Becker, M.; Althoff, D.; Lenz, D.; Stiller, C. Decision Making for Autonomous Driving Considering Interaction and Uncertain Prediction of Surrounding Vehicles. In Proceedings of the 28th Annual Meeting of the Intelligent Vehicles Symposium, Los Angeles, CA, USA, 11–14 June 2017. [Google Scholar]
- Tan, B.; Xu, N.; Kong, B. Autonomous Driving in Reality with Reinforcement Learning and Image Translation. In Proceedings of the 31th IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 19–21 June 2018. [Google Scholar]
- Loiacono, D.; Prete, A.; Lanzi, P.L.; Cardamone, L. Learning to overtake in TORCS using simple reinforcement learning. In Proceedings of the Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010. [Google Scholar]
- Xue, J.; Wu, C.; Chen, Z.; Van Gelderc, P.H.A.J.M.; Yan, X. Modeling human-like decision-making for inbound smart ships based on fuzzy decision trees. Expert Syst. Appl. 2019, 115, 172–188. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, L.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Vecerik, M.; Hester, T.; Scholz, J.; Wang, F.; Pietquin, O.; Piot, B.; Heess, N.; Rothörl, T.; Lampe, T.; Riedmiller, M. Leveraging Demonstrations for Deep Reinforcement Learning on Robotics Problems with Sparse Rewards. In Proceedings of the Artificial Intelligence Conference, San Francisco, CA, USA, 17–20 September 2017. [Google Scholar]
- Tai, L.; Paolo, G.; Liu, M. Virtual-to-real deep reinforcement learning: Continuous control of mobile robots for mapless navigation. In Proceedings of the 30th International Conference on Intelligent Robots and Systems, Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar]
- Filev, D.; Lu, J.; Tseng, F.; Kwaku, P.A. Real-time driver characterization during car following using stochastic evolving models. In Proceedings of the 2011 IEEE International Conference on Systems, Man, and Cybernetics, Anchorage, AK, USA, 9–12 October 2011. [Google Scholar]
- Deng, H.; Zheng, C.Q.; Shao, C.; Li, Y.H. Construction and Application of 3D Traffic Environment Build Platform Based on UC-Win/Road. Appl. Mech. Mater. 2014, 505, 1225–1229. [Google Scholar] [CrossRef]
- Gilman, E.; Keskinarkaus, A.; Tamminen, S. Personalised assistance for fuel-efficient driving. Trans. Res. Part C Emerg Technol. 2015, 58, 681–705. [Google Scholar] [CrossRef]
- Kim, J.; Sim, H.; Oh, J. The flexible EV/HEV and SOC band control corresponding to driving mode, driver’s driving style and environmental circum-stances. In Proceedings of the SAE 2012 World Congress and Exhibition, Detroit, MI, USA, 24–26 April 2012. [Google Scholar]
- Wang, W.; Xi, J.; Chen, H. Modeling and recognizing driver behavior based on driving data: A survey. Math. Probl. Eng. 2014, 1, 1–20. [Google Scholar] [CrossRef]
- Dorr, D.; Grabengiesser, D.; Gauterin, F. Online driving style recognition using fuzzy logic. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems, Qingdao, China, 8–11 October 2014. [Google Scholar]
- Sutton, R.S. Reinforcement Learning: An Introduction; MIT: Cambridge, UK, 1998. [Google Scholar]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, Perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. In Proceedings of the 3th Annual Meeting of the International Conference on Learning Representations, San Juan, PR, USA, 7–9 May 2015. [Google Scholar]
- Loiacono, D.; Lanzi, P.L.; Togelius, J.; Onieva, E.; Pelta, D.A.; Butz, M.V.; Lönneker, T.D.; Cardamone, L.; Perez, D.; Sáez, Y. The 2009 simulated car racing championship. IEEE Trans. Comput. Intell. AI Games 2010, 2, 131–147. [Google Scholar] [CrossRef]
- Kim, K.J.; Seo, J.H.; Park, J.G.; Na, J.C. Generalization of TORCS car racing controllers with artificial neural networks and linear regression analysis. Neurocomputing 2012, 88, 87–99. [Google Scholar] [CrossRef]
- Bhatnagar, S.; Ghavamzadeh, M.; Lee, M.; Sutton, R.S. Incremental Natural Actor-Critic Algorithms. In Proceedings of the 21th Neural Information Processing Systems, Vancouver, BC, Canada, 3–6 December 2007. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.P.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the 33th International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]
| Parameter Name | Interpretation |
|---|---|
| Vehicle Motion Parameters | |
| angle | Angle between the vehicle direction and the direction of the track |
| damage | Current damage of the vehicle |
| rpm | Number of rotation per minute of the car engine |
| speed X | Speed of the car along the longitudinal axis of the vehicle |
| speed Y | Speed of the car along the transverse axis of the vehicle |
| track Dis | Vehicle distance from track edge |
| track Pos | Distance between the car and the track axis |
| wheel Spin Vel | Vector of 4 sensors representing the rotation speed of the wheels |
| Driving ActionParameters | |
| accel | The throttle opening (0 means no gas, 100% full gas) |
| steering | Steering value: −1 and +1 means respectively full left and right |
| brake | Brake level (0 means no brake, 100% full brake) |
| Parameter Name | Interpretation |
|---|---|
| Input Parameters (State Space) | |
| angle | Angle between the vehicle direction and the direction of the track |
| damage | Current damage of the vehicle |
| rpm | Number of rotation per minute of the vehicle engine |
| speed X | Speed of the car along the longitudinal axis of the vehicle |
| speed Y | Speed of the car along the transverse axis of the vehicle |
| track | Vector of 19 range finder sensors: indicates the distance of the vehicle from the edge of the track |
| track Pos | Distance between the vehicle and the track axis |
| wheel Spin Vel | Vector of 4 sensors representing the rotation speed of the wheels |
| Output Parameters (Action Space) | |
| accel | The throttle opening (0 means no gas, 100% full gas) |
| steering | Steering value: −1 and +1 means respectively full left and right |
| brake | Brake level (0 means no brake, 100% full brake) |
| The Proposed Method | Time of Completion/s | Time Difference from Training Map/s | Top Speed/(m/s) | Min Speed/(m/s) | Damage |
|---|---|---|---|---|---|
| Train Map | |||||
| K = 0.47 | 38.4 | / | 30.1 | 18.7 | 0 |
| K = 1.13 | 34.4 | / | 35.1 | 21.4 | 0 |
| K = 1.91 | 32.2 | / | 36.9 | 24.3 | 0 |
| Test Map 1 | |||||
| K = 0.47 | 41.9 | +3.5 | 30.3 | 17.6 | 0 |
| K = 1.13 | 38.4 | +4.0 | 34.7 | 18.7 | 0 |
| K = 1.91 | 37.1 | +4.9 | 37.2 | 16.8 | 0 |
| Test Map 2 | |||||
| K = 0.47 | 41.2 | +2.8 | 30.4 | 19.6 | 0 |
| K = 1.13 | 37.9 | +3.5 | 35.4 | 23.5 | 0 |
| K = 1.91 | 36.3 | +4.1 | 36.8 | 25.2 | 0 |
| Test Map 3 | |||||
| K = 0.47 | 40.1 | +1.7 | 30.1 | 20.8 | 0 |
| K = 1.13 | 36.8 | +2.4 | 35.6 | 24.5 | 0 |
| K = 1.91 | 34.1 | +1.9 | 37.3 | 25.3 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wu, C.; Xue, J.; Chen, Z. A Method of Personalized Driving Decision for Smart Car Based on Deep Reinforcement Learning. Information 2020, 11, 295. https://doi.org/10.3390/info11060295
Wang X, Wu C, Xue J, Chen Z. A Method of Personalized Driving Decision for Smart Car Based on Deep Reinforcement Learning. Information. 2020; 11(6):295. https://doi.org/10.3390/info11060295
Chicago/Turabian StyleWang, Xinpeng, Chaozhong Wu, Jie Xue, and Zhijun Chen. 2020. "A Method of Personalized Driving Decision for Smart Car Based on Deep Reinforcement Learning" Information 11, no. 6: 295. https://doi.org/10.3390/info11060295
APA StyleWang, X., Wu, C., Xue, J., & Chen, Z. (2020). A Method of Personalized Driving Decision for Smart Car Based on Deep Reinforcement Learning. Information, 11(6), 295. https://doi.org/10.3390/info11060295






