Emotion-Semantic-Enhanced Bidirectional LSTM with Multi-Head Attention Mechanism for Microblog Sentiment Analysis
Abstract
1. Introduction
- We collect and sort out the correlation structures that have a turning or progressive effect on the global sentiment of microblog in the Chinese grammatical structure. The special correlation structures are maintained in the pre-processed corpus to avoid the model wrongly judging posts’ sentiment polarity.
- We collect and organize the new words appearing on Weibo in the past ten years, and then add them to the user-defined dictionary of jieba word segmentation toolkit to avoid the loss of important semantic information and word segmentation errors, meanwhile, indirectly expand the vocabulary of Word2Vec model.
- We sort out the common emoticons in Sina Weibo and regard them as an important basis for sentiment analysis. The multi-head attention mechanism is used to calculate the contribution of words to global sentiment analysis, and the emotional semantic enhancement of emoticons is exerted.
2. Related Works
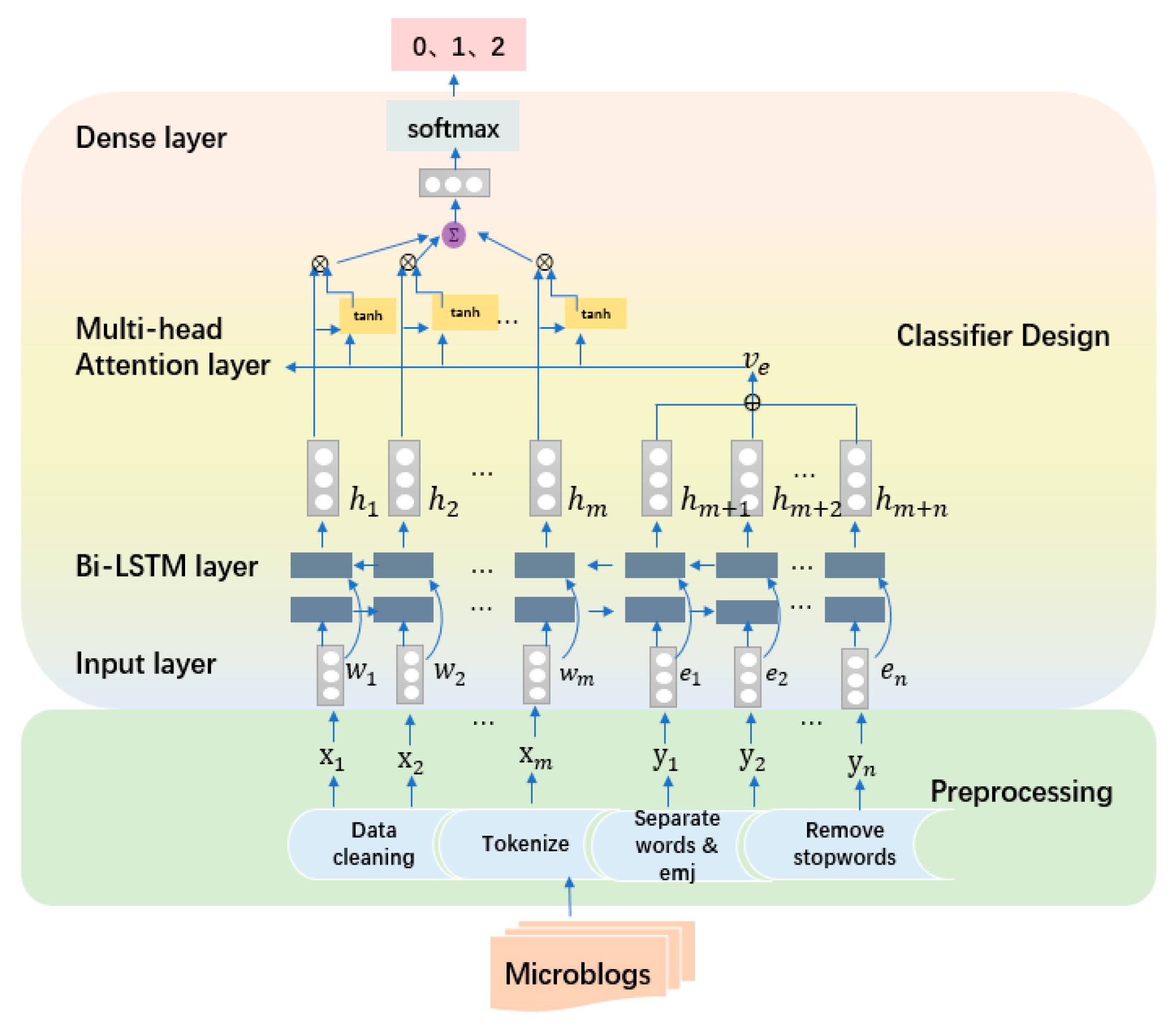
3. EBILSTM-MH Structure
3.1. Data Preprocessing
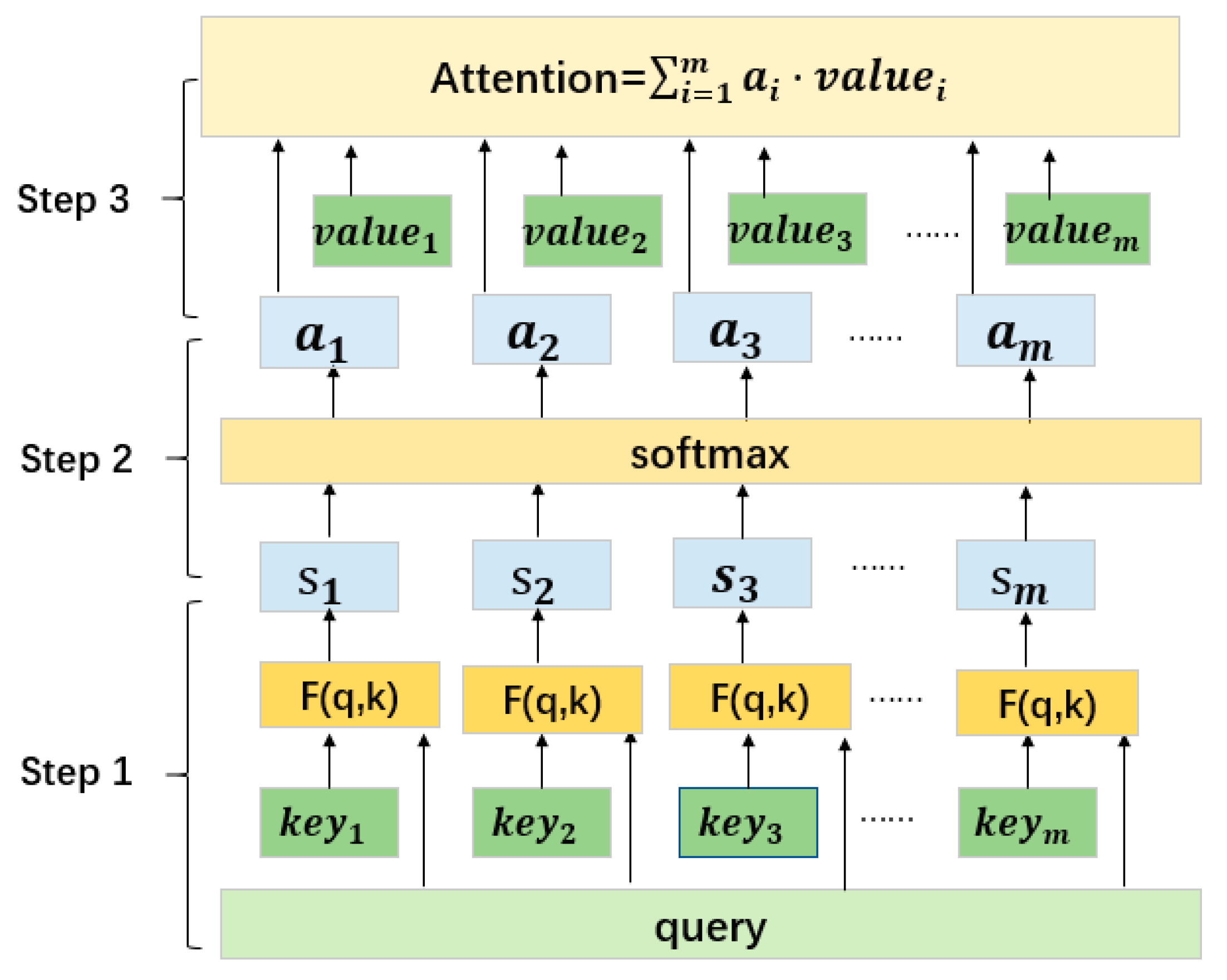
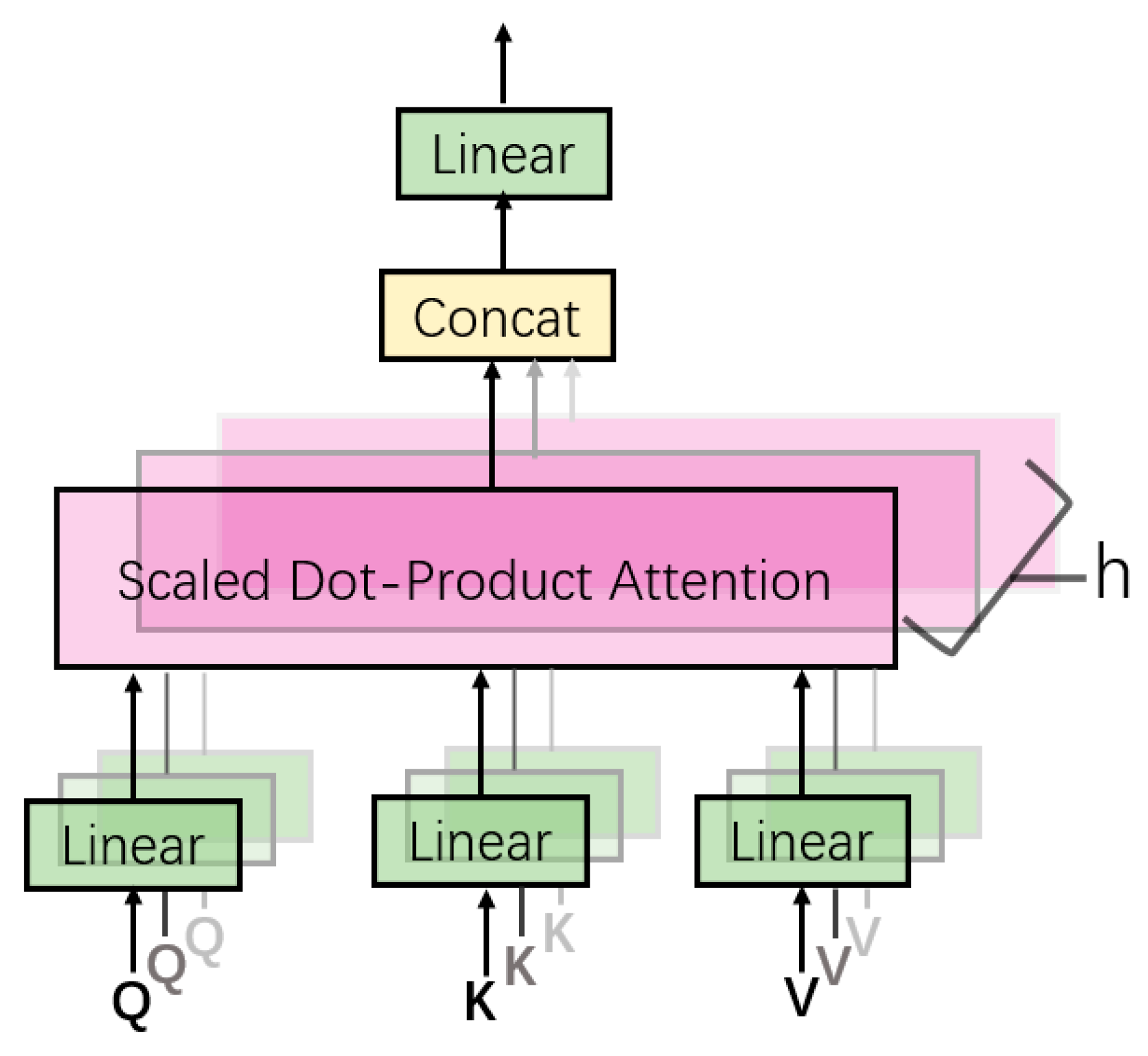
3.2. Classifier Design
4. Experiment
4.1. Experiment Environment
4.2. Dataset Construction
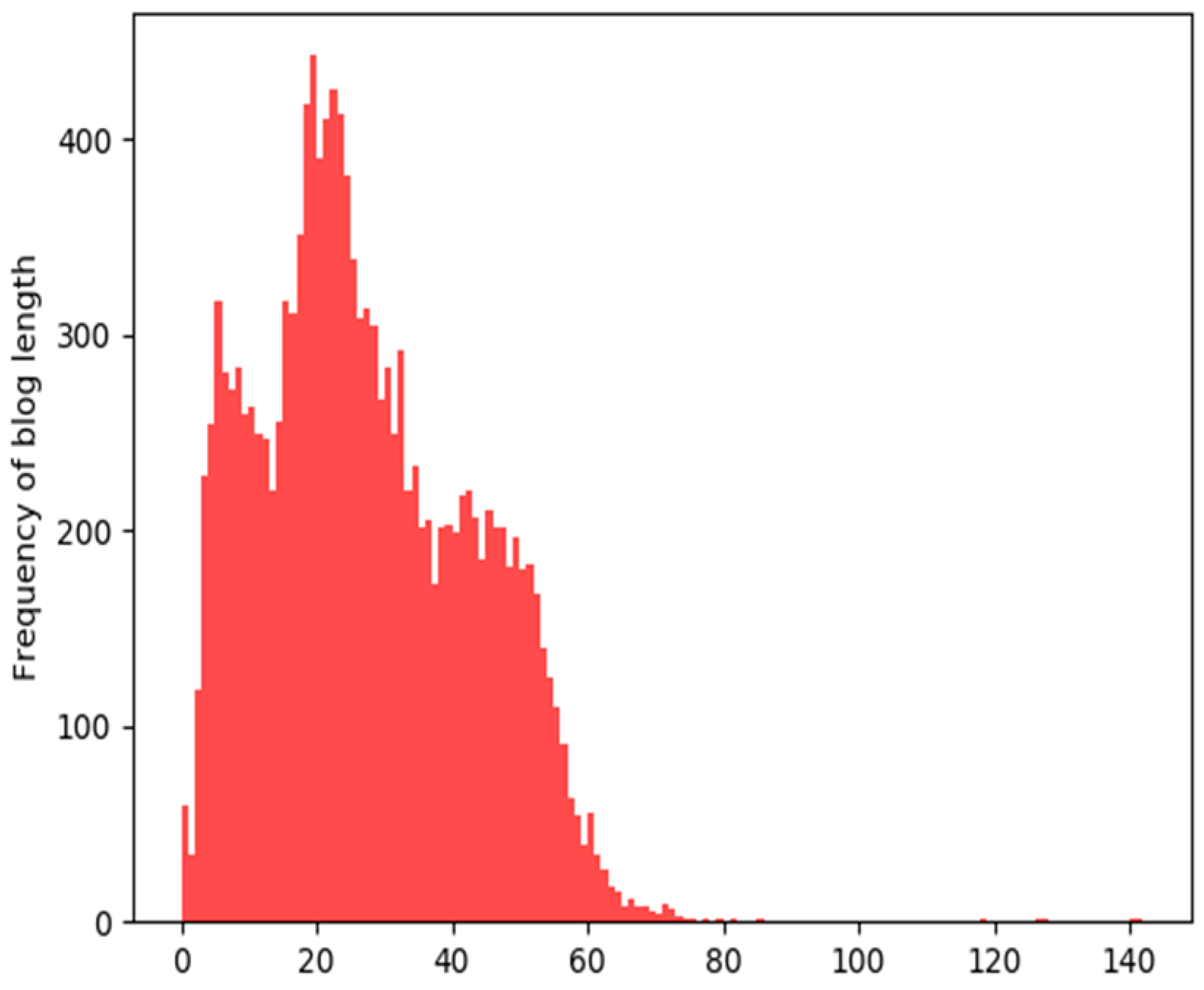
4.3. Experimental Preprocessing
4.4. Comparative Experiment
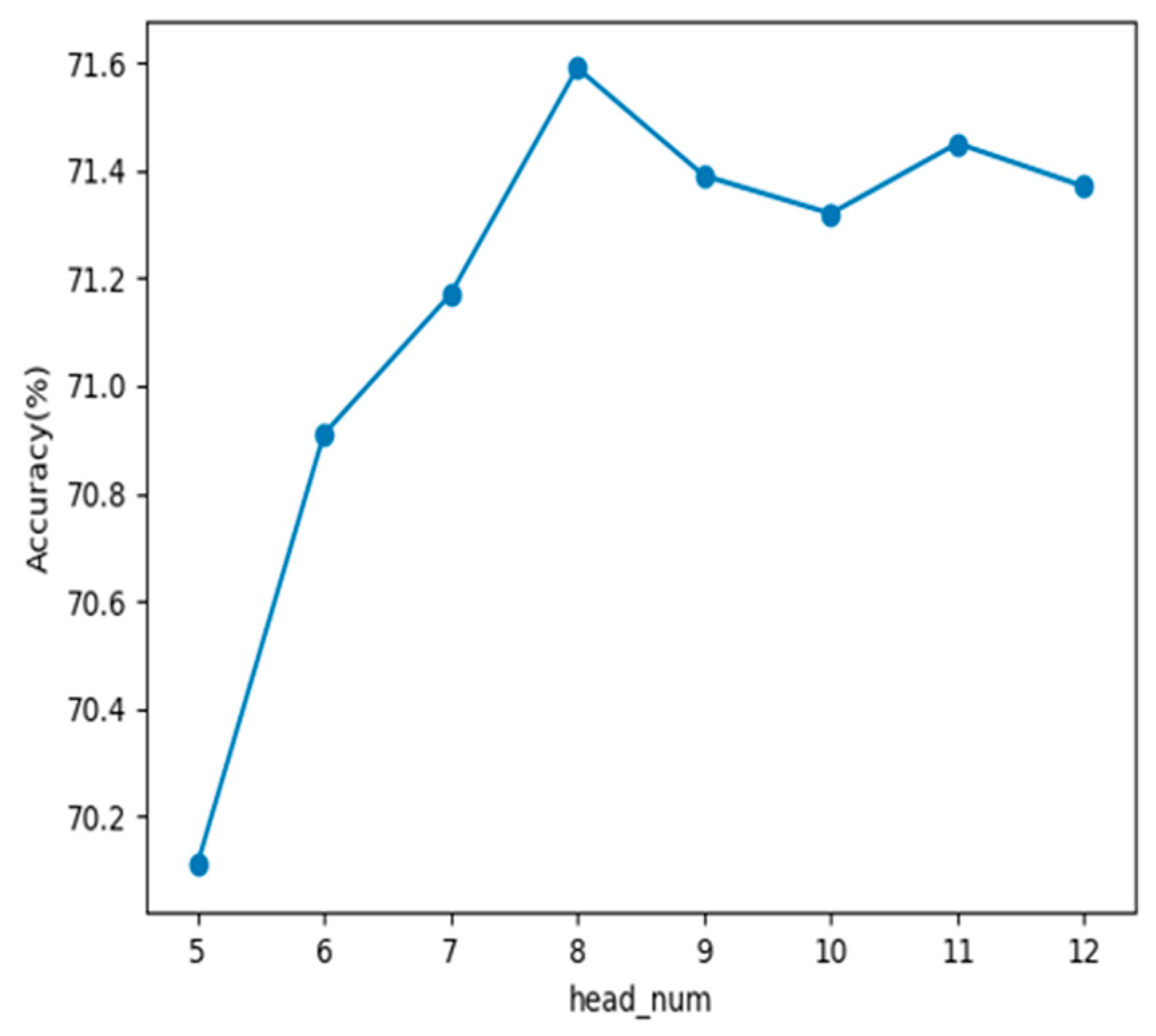
4.5. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Parameters of the Baseline Methods
References
- Peng, H.; Cambria, E. CSenticNet: A Concept-Level Resource for Sentiment Analysis in Chinese Language; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 10762 LNCS; Springer: Berlin/Heidelberg, Germany, 2018; Volume 10762, pp. 90–104. [Google Scholar]
- Hatzivassiloglou, V.; Mckeown, K.R. Predicting the Semantic Orientation of Adjectives. In Proceedings of the 35th Annual Meeting of the Association for Computational Linguistics and Eighth Conference of the European Chapter of the Association for Computational Linguistics, Madrid, Spain, 7–12 July 1997; pp. 174–181. [Google Scholar]
- Liu, K.; Xu, L.; Zhao, J. Co-extracting opinion targets and opinion words from online reviews based on the word alignment model. IEEE Trans. Knowl. Data Eng. 2015, 27, 636–650. [Google Scholar] [CrossRef]
- Hao, Z.; Cai, R.; Yang, Y.; Wen, W.; Liang, L. A Dynamic Conditional Random Field Based Framework for Sentence-level Sentiment Analysis of Chinese Microblog. In Proceedings of the 20th IEEE International Conference on Computational Science and Engineering and 15th IEEE/IFIP International Conference on Embedded and Ubiquitous Computing, CSE and EUC 2017, Guangzhou, China, 21–24 July 2017. [Google Scholar]
- Rehman, Z.U.; Bajwa, I.S. Lexicon-based Sentiment Analysis for Urdu Language. In Proceedings of the 2016 Sixth International Conference on Innovative Computing Technology (INTECH 2016), Dublin, Ireland, 24–26 August 2016; pp. 497–501. [Google Scholar]
- Che, W.; Zhao, Y.; Guo, H.; Su, Z.; Liu, T. Sentence Compression for Aspect-Based Sentiment Analysis. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 2111–2124. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, H.; Jiang, B.; Li, K. Aspect-based sentiment analysis with alternating coattention networks. Inf. Process. Manag. 2019, 56, 463–478. [Google Scholar] [CrossRef]
- Zhou, X.; Wan, X.; Xiao, J. CMiner: Opinion Extraction and Summarization for Chinese Microblogs. IEEE Trans. Knowl. Data Eng. 2016, 28, 1650–1663. [Google Scholar] [CrossRef]
- Ma, Y.; Peng, H.; Cambria, E. Targeted aspect-based sentiment analysis via embedding commonsense knowledge into an attentive LSTM. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence, AAAI 2018, New Orleans, LA, USA, 2–7 February 2018; pp. 5876–5883. [Google Scholar]
- Peng, H.; Ma, Y.; Li, Y.; Cambria, E. Learning multi-grained aspect target sequence for Chinese sentiment analysis. Knowl.-Based Syst. 2018, 148, 167–176. [Google Scholar] [CrossRef]
- Lu, Y.; Zhou, J.; Dai, H.-N.; Wangt, H.; Xiao, H. Sentiment Analysis of Chinese Microblog Based on Stacked Bidirectional LSTM. IEEE Access 2019, 7, 38856–38866. [Google Scholar]
- Tai, Y.-J.; Kao, H.-Y. Automatic Domain-Specific Sentiment Lexicon Generation with Label. In Proceedings of the IIWAS’13: Proceedings of International Conference on Information Integration and Web-based Applications & Services, Vienna, Austria, 2–4 December 2013; pp. 53–62. [Google Scholar]
- Su, M.-H.; Wu, C.-H.; Huang, K.-Y.; Hong, Q.-B. LSTM-based Text Emotion Recognition using semantic and emotional word vector. In Proceedings of the 2018 First Asian Conference on Affective Computing and Intelligent Interaction (ACII Asia), Beijing, China, 20–22 May 2018. [Google Scholar]
- Yang, G.; He, H.; Chen, Q. Emotion-Semantic-Enhanced Neural Network. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 531–543. [Google Scholar] [CrossRef]
- De Almeida, A.M.G.; Barbon, S.; Paraiso, E.C. Multi-class Emotions Classification by Sentic Levels as Features in Sentiment Analysis. In Proceedings of the 5th Brazilian Conference on Intelligent Systems (BRACIS), Pernambuco, Brazil, 2 February 2016. [Google Scholar]
- Wang, J.; Yu, L.-C.; Lai, K.R.; Zhang, X. Community-Based Weighted Graph Model for Valence-Arousal Prediction of Affective Words. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 1957–1968. [Google Scholar] [CrossRef]
- Huang, S.; Niu, Z.; Shi, C. Automatic Construction of Domain-specific Sentiment Lexicon Based on Constrained Label Propagation. Knowl.-Based Syst. 2014, 56, 191–200. [Google Scholar] [CrossRef]
- Teng, Z.; Ren, F.; Kuroiwa, S. Recognition of emotion with SVMs. In Proceedings of the International Conference on Intelligent Computing, ICIC 2006, Kunming, China, 16–19 August 2006; pp. 701–710. [Google Scholar]
- Xia, R.; Zong, C.; Li, S. Ensemble of feature sets and classification algorithms for sentiment-classification. Inf. Sci. 2011, 181, 1138–1152. [Google Scholar] [CrossRef]
- Chen, T.; Xu, R.; He, Y.; Wang, X. Improving sentiment analysis via sentence type classification using BiLSTM-CRF and CNN. Expert Syst. Appl. 2017, 72, 221–230. [Google Scholar] [CrossRef]
- Meisheri, H.; Ranjan, K.; Dey, L. Sentiment Extraction from Consumer-generated Noisy Short Texts. In Proceedings of the 2017 IEEE International Conference on Data Mining Workshops (ICDMW), New Orleans, LA, USA, 18–21 November 2017. [Google Scholar]
- Deng, D.; Jing, L.; Yu, J.; Sun, S. Sparse Self-Attention LSTM for Sentiment Lexicon Construction. IEIEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 1777–1790. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, J.; Wang, Y. Sentiment Lexicon Construction Method Based on Label Propagation. Comput. Eng. 2018, 44, 168–173. [Google Scholar]
- Zhang, S.; Wei, Z.; Wang, Y.; Liao, T. Sentiment analysis of Chinese microblog text based on extended sentiment dictionary. Future Gener. Comput. Syst. 2018, 81, 395–403. [Google Scholar] [CrossRef]
- Chen, J.; Huang, H.; Tian, S. Feature selection for text classification with Naïve Bayes. Expert Syst. Appl. 2009, 36, 5432–5435. [Google Scholar] [CrossRef]
- Pang, B.; Lillian, L.; Vaithyanathan, S. Thumbs up? Sentiment Classification using Machine Learning Techniques. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Philadelphia, PA, USA, 6–7 July 2002; pp. 79–86. [Google Scholar]
- Liu, X.; Wu, Q.; Pan, W. Sentiment classification of microblog comments based on Random forest algorithm. Concurr. Comput.-Pract. Exp. 2019, 31, e4746. [Google Scholar] [CrossRef]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. In Proceedings of the 1st International Conference on Learning Representations, ICLR 2013, Scottsdale, AZ, USA, 2–4 May 2013. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.; Dean, J. Distributed Representations of Words and Phrases and their Compositionality. arXiv 2013, arXiv:1310.4546. [Google Scholar]
- Sun, Y.; Lin, L.; Yang, N.; Ji, Z.; Wang, X. Radical-Enhanced Chinese Character Embedding; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2014; Volume 8835, pp. 279–286. [Google Scholar]
- Peng, H.; Cambria, E.; Zou, X. Radical-based hierarchical embeddings for Chinese sentiment analysis at sentence level. In Proceedings of the FLAIRS 2017—Proceedings of the 30th International Florida Artificial Intelligence Research Society Conference, Sarasota, FL, USA, 19–22 May 2019; pp. 347–352. [Google Scholar]
- Wang, M.; Hu, G. A novel Method for Twitter Sentiment Analysis Based on Attention-Graph Neural Network. Information 2020, 11, 92. [Google Scholar] [CrossRef]
- Irsoy, O.; Cardie, C. Opinion Mining with Deep Recurrent Neural Networks. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 720–728. [Google Scholar]
- Schlichtkrull, M.S. Learning affective projections for emoticons on Twitter. In Proceedings of the 6th IEEE Conference on Cognitive Infocommunications, CogInfoCom 2015, Szechenyi Istvan University, Gyor, Hungary, 19–21 October 2015; pp. 539–543. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N. Attention Is All You Need. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems, NIPS 2017, Long Beach, FL, USA, 4–9 December 2017. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, FL, USA, 7–9 May 2015. [Google Scholar]
| Relation | Correlation Structures |
|---|---|
| Progressive relation | 不但不……反而……(not only …not…,but also…) |
| 尚且……何况…… (…not to mention…) | |
| 甚至…… (…even…) | |
| Selection relation | 宁可……也不…… (rather ... not ...) |
| 与其……不如…… (It is not as good as…) | |
| ……还是…… (…or…) | |
| Twist relation | 虽然……但是…… (However, although…) |
| 尽管……可是…… (…despite…) | |
| 然而…… (…yet…) |
| Emoticon | Meanings | Emoticon | Meaning | Emoticons | Meaning |
|---|---|---|---|---|---|
 | [Haha] |  | [startle] |  | [contempt] |
 | [love you] |  | [handclap] |  | [shy] |
 | [suffer beating] |  | [ok] |  | [No] |
 | [good] |  | [sad] |  | [hum] |
| Sentiment Polarity | Negative | Positive | Neutral | |||
|---|---|---|---|---|---|---|
| NLPCC emotion type | Anger | 1717 | Happiness | 2000 | None | 5000 |
| Fear | 415 | Like | 4000 | |||
| Sadness | 1003 | Surprise | 700 | |||
| Disgust | 1565 | |||||
| Total | 4700 | 6700 | 17100 | |||
| Sg | Window | Sample | Min_count | Negative | Hs | Workers |
|---|---|---|---|---|---|---|
| 1 | 5 | 0.001 | 10 | 1 | 1 | 4 |
| Parameters | Dimension(d) | Maximum Sentence Length | Dropout Rate | Heads | Batch_Size |
|---|---|---|---|---|---|
| value | 200 | 80 | 0.4 | 8 | 32 |
| Parameters | Patience | Epochs | Conv1D | Kernel size | Pool size |
| value | 7 | 30 | 256 | 3, 4, 5 | 28, 27, 26 |
| Label | Prediction | ||
|---|---|---|---|
| Negative | Positive | ||
| Actual | Negative | TN | FP |
| Positive | FN | TP | |
| Method | Positive | Negative | Neutral | Accuracy (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| P(%) | R(%) | F(%) | P(%) | R(%) | F(%) | P(%) | R(%) | F(%) | ||
| EBILSTM-MH | 76.77 | 63.62 | 69.58 | 76.04 | 73.94 | 74.97 | 65.04 | 77.20 | 70.60 | 71.70 |
| BiLSTM + emj_att | 73.93 | 62.13 | 67.51 | 74.32 | 72.66 | 73.49 | 62.86 | 73.60 | 67.80 | 69.55 |
| BiLSTM + multi-head_att(text_only) | 68.27 | 64.79 | 66.48 | 71.72 | 74.47 | 73.07 | 63.64 | 64.40 | 64.02 | 67.81 |
| SVM | 63.17 | 67.87 | 65.44 | 73.23 | 70.40 | 71.80 | 64.59 | 62.40 | 63.48 | 66.81 |
| CNN | 60.07 | 70.10 | 64.70 | 66.97 | 61.91 | 64.34 | 59.41 | 54.30 | 56.74 | 63.19 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhu, Y.; Gao, W.; Cao, M.; Li, M. Emotion-Semantic-Enhanced Bidirectional LSTM with Multi-Head Attention Mechanism for Microblog Sentiment Analysis. Information 2020, 11, 280. https://doi.org/10.3390/info11050280
Wang S, Zhu Y, Gao W, Cao M, Li M. Emotion-Semantic-Enhanced Bidirectional LSTM with Multi-Head Attention Mechanism for Microblog Sentiment Analysis. Information. 2020; 11(5):280. https://doi.org/10.3390/info11050280
Chicago/Turabian StyleWang, Shaoxiu, Yonghua Zhu, Wenjing Gao, Meng Cao, and Mengyao Li. 2020. "Emotion-Semantic-Enhanced Bidirectional LSTM with Multi-Head Attention Mechanism for Microblog Sentiment Analysis" Information 11, no. 5: 280. https://doi.org/10.3390/info11050280
APA StyleWang, S., Zhu, Y., Gao, W., Cao, M., & Li, M. (2020). Emotion-Semantic-Enhanced Bidirectional LSTM with Multi-Head Attention Mechanism for Microblog Sentiment Analysis. Information, 11(5), 280. https://doi.org/10.3390/info11050280




