Heuristic Analysis for In-Plane Non-Contact Calibration of Rulers Using Mask R-CNN
Abstract
1. Introduction
2. Materials and Methods
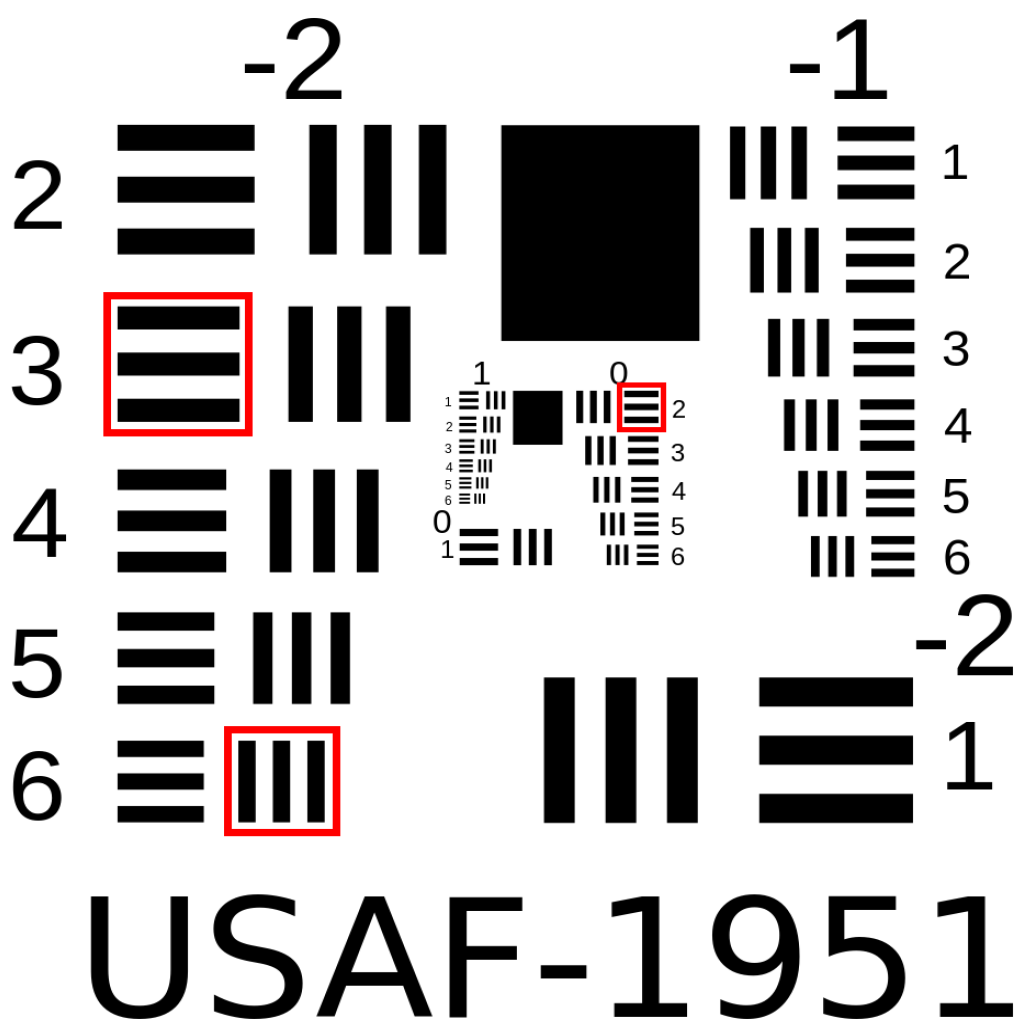
2.1. Resources—Database
2.2. Mask R-CNN Adaptation for Ruler Segmentation
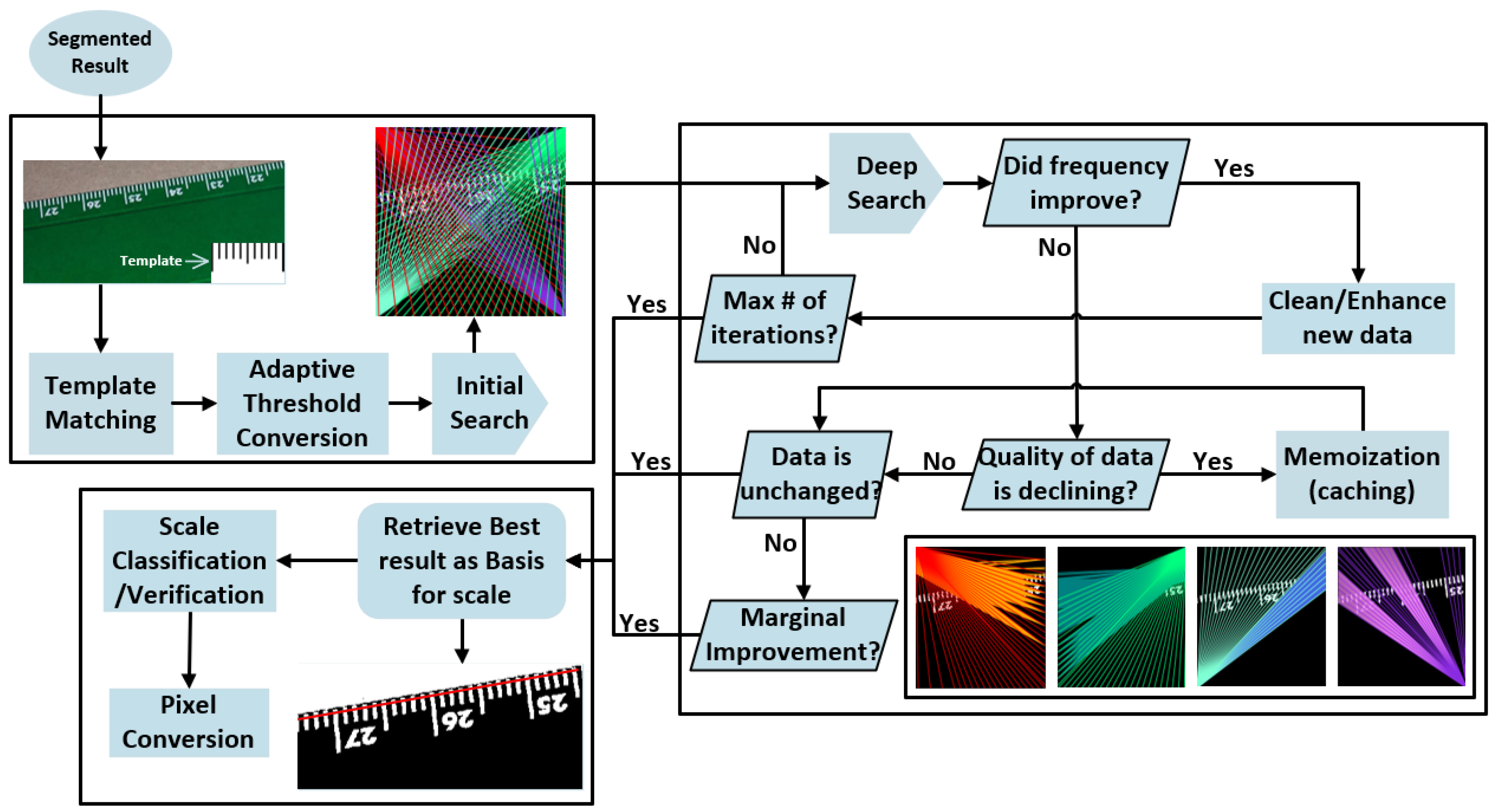
2.3. Heuristic Scale Calibration
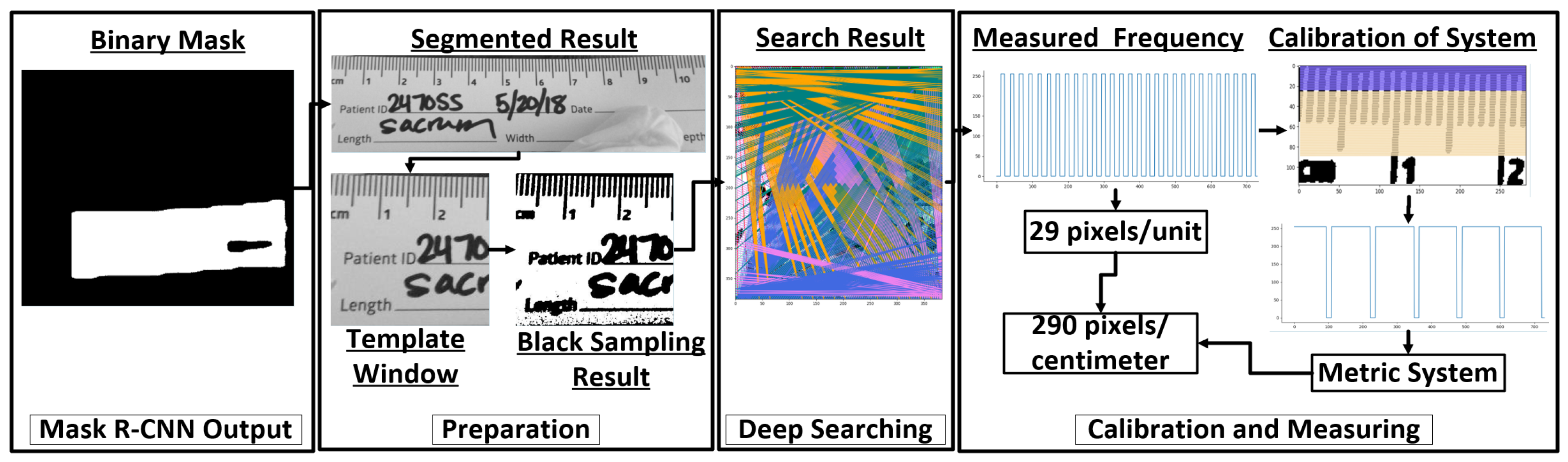
2.3.1. Preparation
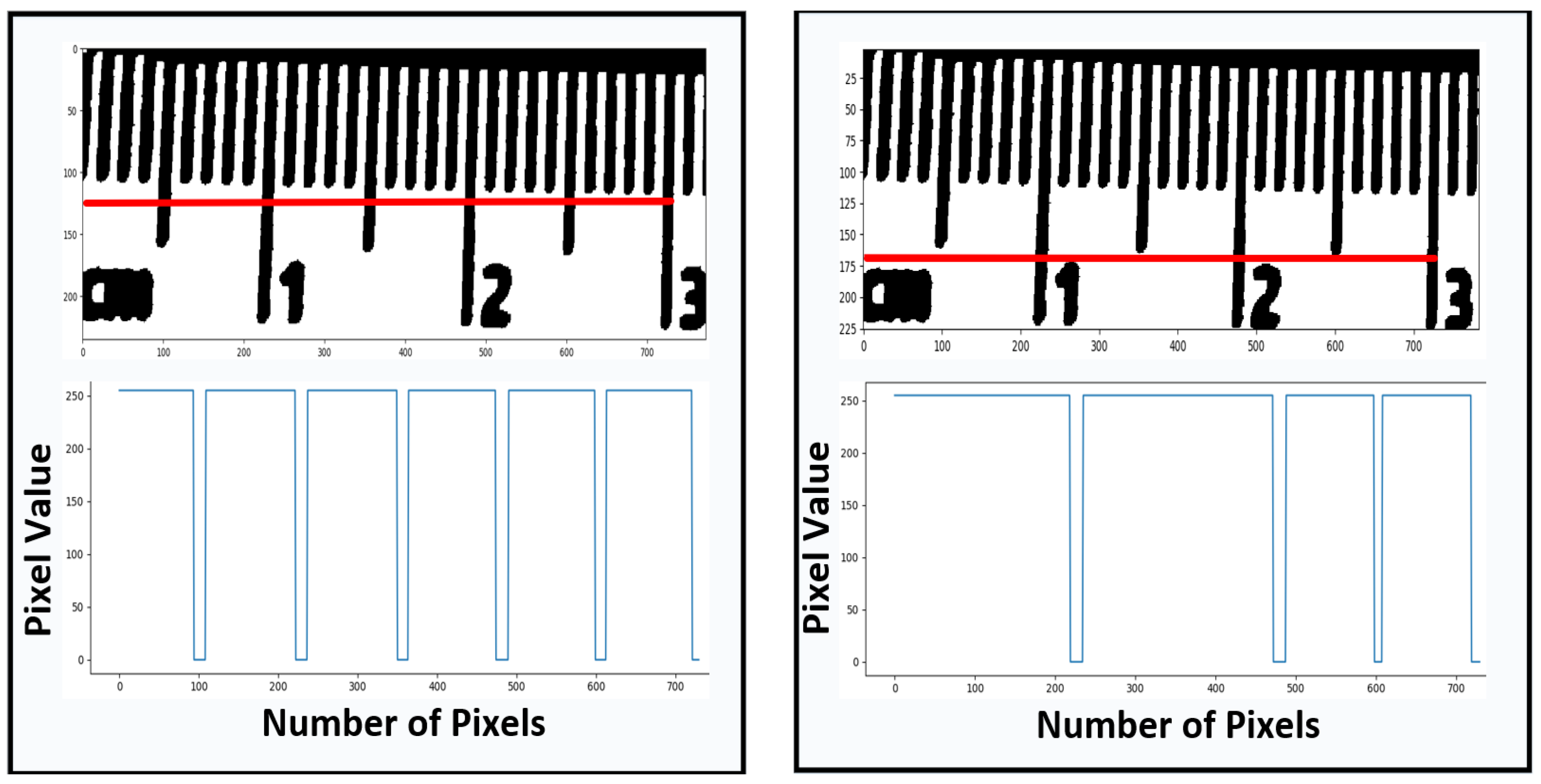
2.3.2. Deep Searching
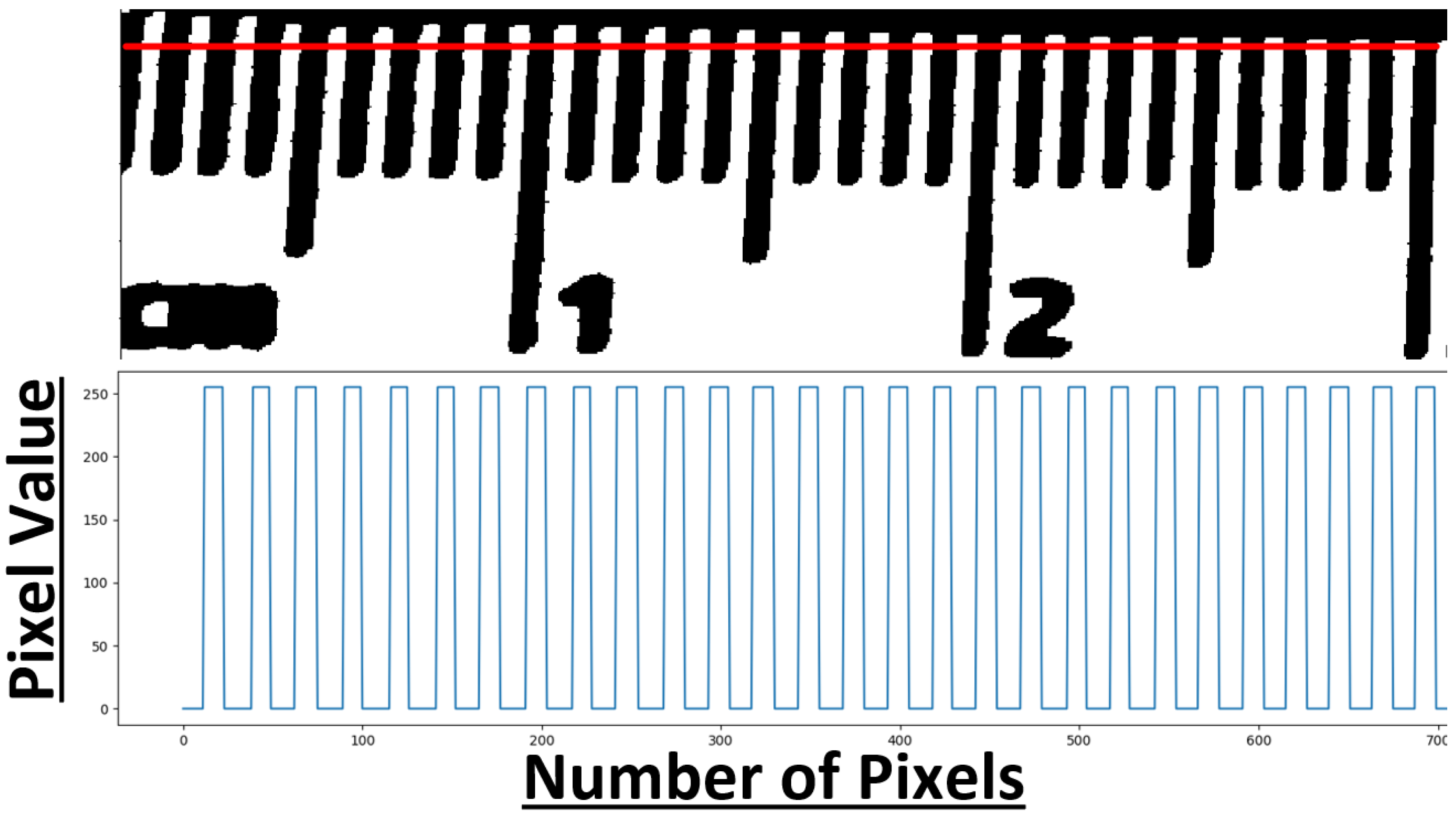
2.3.3. Calibration
3. Results
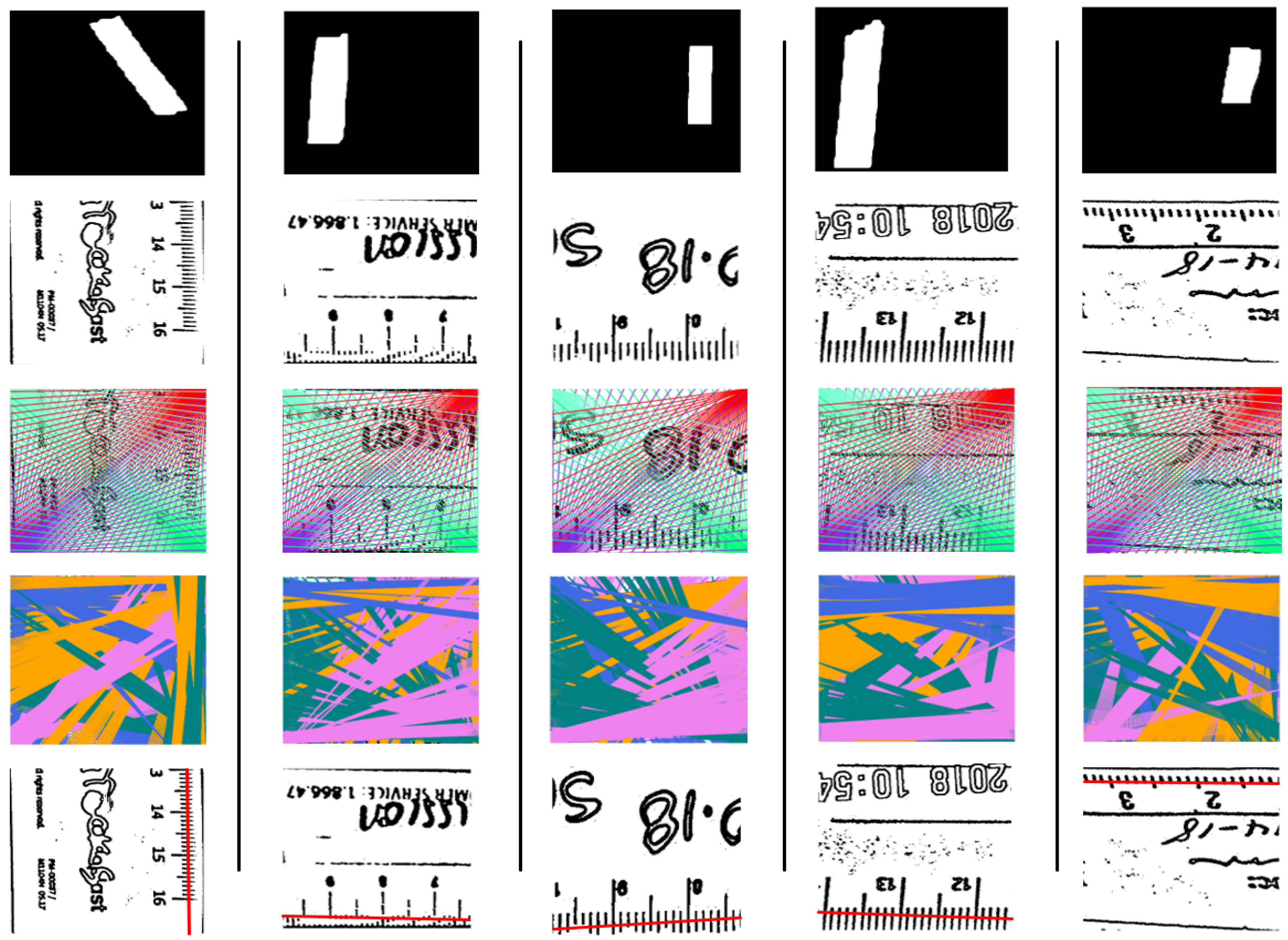
3.1. Segmentation Results
3.2. Heuristic Search Calibration Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Code Availability
References
- Yan, J.; Downey, A.; Cancelli, A.; Laflamme, S.; Chen, A.; Li, J.; Ubertini, F. Concrete crack detection and monitoring using a capacitive dense sensor array. Sensors 2019, 19, 1843. [Google Scholar] [CrossRef] [PubMed]
- Herrera-Téllez, V.I.; Cruz-Olmedo, A.K.; Plasencia, J.; Gavilanes-Ruíz, M.; Arce-Cervantes, O.; Hernández-León, S.; Saucedo-García, M. The protective effect of Trichoderma asperellum on tomato plants against Fusarium oxysporum and Botrytis cinerea diseases involves inhibition of reactive oxygen species production. Int. J. Mol. Sci. 2019, 20, 2007. [Google Scholar] [CrossRef] [PubMed]
- Kekonen, A.; Bergelin, M.; Johansson, M.; Kumar Joon, N.; Bobacka, J.; Viik, J. Bioimpedance Sensor Array for Long-Term Monitoring of Wound Healing from Beneath the Primary Dressings and Controlled Formation of H2O2 Using Low-Intensity Direct Current. Sensors 2019, 19, 2505. [Google Scholar] [CrossRef] [PubMed]
- Nirenberg, M.S.; Ansert, E.; Krishan, K.; Kanchan, T. Two-dimensional linear analysis of dynamic bare footprints: A comparison of measurement techniques. Sci. Justice 2019, 59, 552–557. [Google Scholar] [CrossRef]
- Ortiz-Coder, P.; Sánchez-Ríos, A. A Self-Assembly Portable Mobile Mapping System for Archeological Reconstruction Based on VSLAM-Photogrammetric Algorithm. Sensors 2019, 19, 3952. [Google Scholar]
- Rodriguez-Padilla, I.; Castelle, B.; Marieu, V.; Morichon, D. A Simple and Efficient Image Stabilization Method for Coastal Monitoring Video Systems. Remote Sens. 2020, 12, 70. [Google Scholar] [CrossRef]
- Agapiou, A. Optimal Spatial Resolution for the Detection and Discrimination of Archaeological Proxies in Areas with Spectral Heterogeneity. Remote Sens. 2020, 12, 136. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Calatroni, L.; van Gennip, Y.; Schönlieb, C.B.; Rowland, H.M.; Flenner, A. Graph clustering, variational image segmentation methods and Hough transform scale detection for object measurement in images. J. Math. Imaging Vis. 2017, 57, 269–291. [Google Scholar] [CrossRef]
- Bhalerao, A.; Reynolds, G. Ruler detection for autoscaling forensic images. Int. J. Digit. Crime Forensics (IJDCF) 2014, 6, 9–27. [Google Scholar] [CrossRef][Green Version]
- Belay, B.; Habtegebrial, T.; Meshesha, M.; Liwicki, M.; Belay, G.; Stricker, D. Amharic OCR: An End-to-End Learning. Appl. Sci. 2020, 10, 1117. [Google Scholar] [CrossRef]
- Balado, J.; Martínez-Sánchez, J.; Arias, P.; Novo, A. Road environment semantic segmentation with deep learning from MLS point cloud data. Sensors 2019, 19, 3466. [Google Scholar] [CrossRef]
- Velazquez-Pupo, R.; Sierra-Romero, A.; Torres-Roman, D.; Shkvarko, Y.V.; Santiago-Paz, J.; Gómez-Gutiérrez, D.; Robles-Valdez, D.; Hermosillo-Reynoso, F.; Romero-Delgado, M. Vehicle detection with occlusion handling, tracking, and OC-SVM classification: A high performance vision-based system. Sensors 2018, 18, 374. [Google Scholar] [CrossRef]
- Yang, F.; Kale, A.; Bubnov, Y.; Stein, L.; Wang, Q.; Kiapour, H.; Piramuthu, R. Visual search at ebay. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 2101–2110. [Google Scholar]
- Zhu, Z.; Yin, H.; Chai, Y.; Li, Y.; Qi, G. A novel multi-modality image fusion method based on image decomposition and sparse representation. Inf. Sci. 2018, 432, 516–529. [Google Scholar] [CrossRef]
- Papageorgiou, C.P.; Oren, M.; Poggio, T. A general framework for object detection. In Proceedings of the Sixth International Conference on Computer Vision (IEEE Cat. No. 98CH36271), Bombay, India, 7 January 1998; pp. 555–562. [Google Scholar]
- Viola, P.; Jones, M. Robust real-time object detection. Int. J. Comput. Vis. 2001, 4, 4. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Region-based convolutional networks for accurate object detection and segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 142–158. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Shafiee, M.J.; Chywl, B.; Li, F.; Wong, A. Fast YOLO: A fast you only look once system for real-time embedded object detection in video. arXiv 2017, arXiv:1709.05943. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 21–37. [Google Scholar]
- Zoph, B.; Le, Q.V. Neural architecture search with reinforcement learning. arXiv 2016, arXiv:1611.01578. [Google Scholar]
- Dai, J.; Li, Y.; He, K.; Sun, J. R-fcn: Object detection via region-based fully convolutional networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 379–387. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1440–1448. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 91–99. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Ammirato, P.; Berg, A.C. A Mask-RCNN Baseline for Probabilistic Object Detection. arXiv 2019, arXiv:1908.03621. [Google Scholar]
- Yu, Y.; Zhang, K.; Yang, L.; Zhang, D. Fruit detection for strawberry harvesting robot in non-structural environment based on Mask-RCNN. Comput. Electron. Agric. 2019, 163, 104846. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shapiro, L.G. Image segmentation techniques. Comput. Vis. Graph. Image Process. 1985, 29, 100–132. [Google Scholar] [CrossRef]
- Hong, J.; Cho, B.; Hong, Y.W.; Byun, H. Contextual Action Cues from Camera Sensor for Multi-Stream Action Recognition. Sensors 2019, 19, 1382. [Google Scholar] [CrossRef]
- Jiang, H.; Lu, N. Multi-scale residual convolutional neural network for haze removal of remote sensing images. Remote Sens. 2018, 10, 945. [Google Scholar] [CrossRef]
- Qiu, R.; Yang, C.; Moghimi, A.; Zhang, M.; Steffenson, B.J.; Hirsch, C.D. Detection of Fusarium Head Blight in Wheat Using a Deep Neural Network and Color Imaging. Remote Sens. 2019, 11, 2658. [Google Scholar] [CrossRef]
- Wang, E.K.; Zhang, X.; Pan, L.; Cheng, C.; Dimitrakopoulou-Strauss, A.; Li, Y.; Zhe, N. Multi-path dilated residual network for nuclei segmentation and detection. Cells 2019, 8, 499. [Google Scholar] [CrossRef]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2117–2125. [Google Scholar]
- Bradski, G. The OpenCV Library. Dr. Dobb’S J. Softw. Tools 2000, 25, 120–125. [Google Scholar]
- Zemmour, E.; Kurtser, P.; Edan, Y. Automatic parameter tuning for adaptive thresholding in fruit detection. Sensors 2019, 19, 2130. [Google Scholar] [CrossRef]
- Zhang, T.; Huang, Z.; You, W.; Lin, J.; Tang, X.; Huang, H. An Autonomous Fruit and Vegetable Harvester with a Low-Cost Gripper Using a 3D Sensor. Sensors 2020, 20, 93. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, Z.; Jiao, T.; Wang, M. Defect Detection of Aluminum Alloy Wheels in Radiography Images Using Adaptive Threshold and Morphological Reconstruction. Appl. Sci. 2018, 8, 2365. [Google Scholar] [CrossRef]
- Rueden, C.T.; Schindelin, J.; Hiner, M.C.; DeZonia, B.E.; Walter, A.E.; Arena, E.T.; Eliceiri, K.W. ImageJ2: ImageJ for the next generation of scientific image data. BMC Bioinform. 2017, 18, 529. [Google Scholar] [CrossRef]
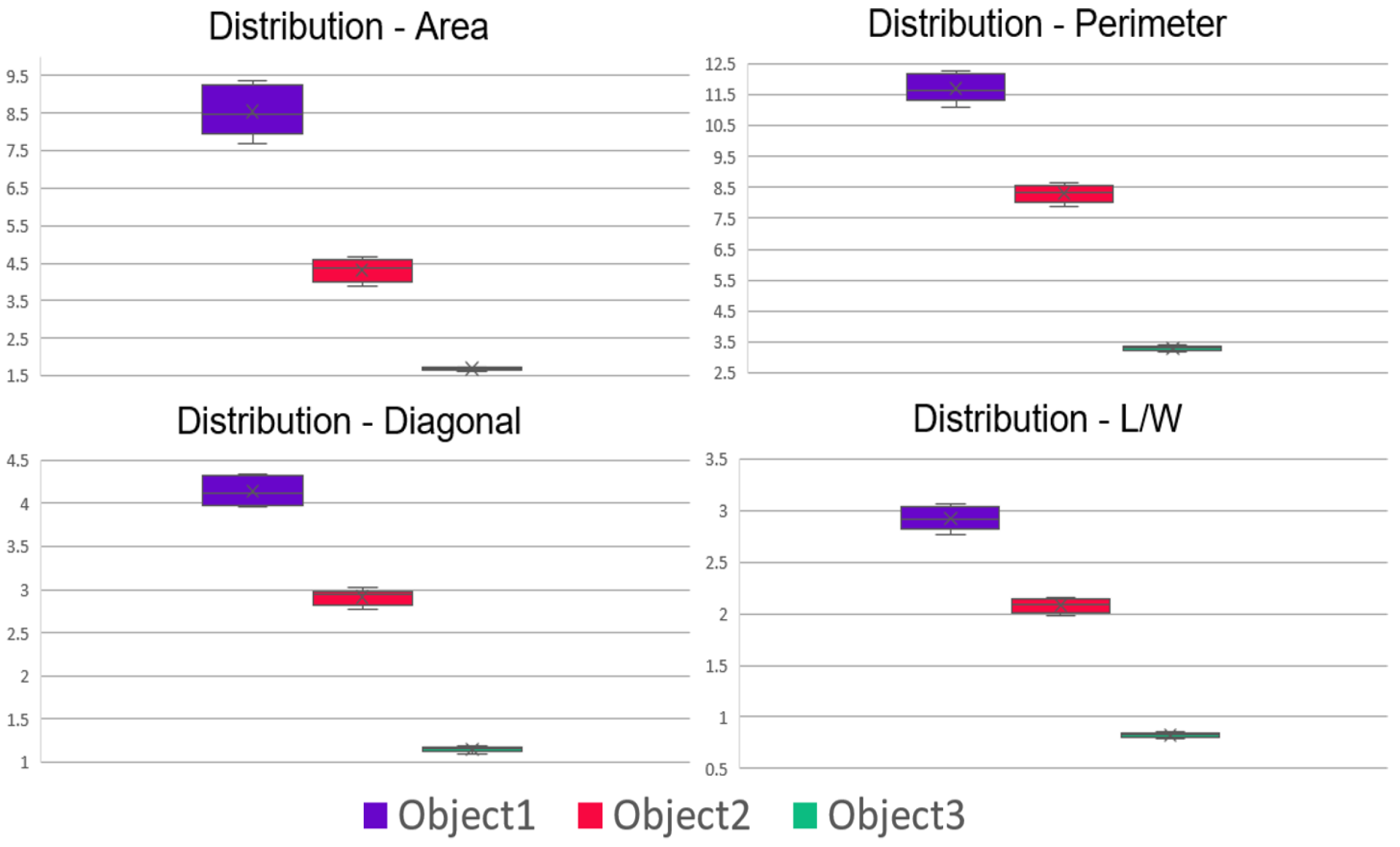
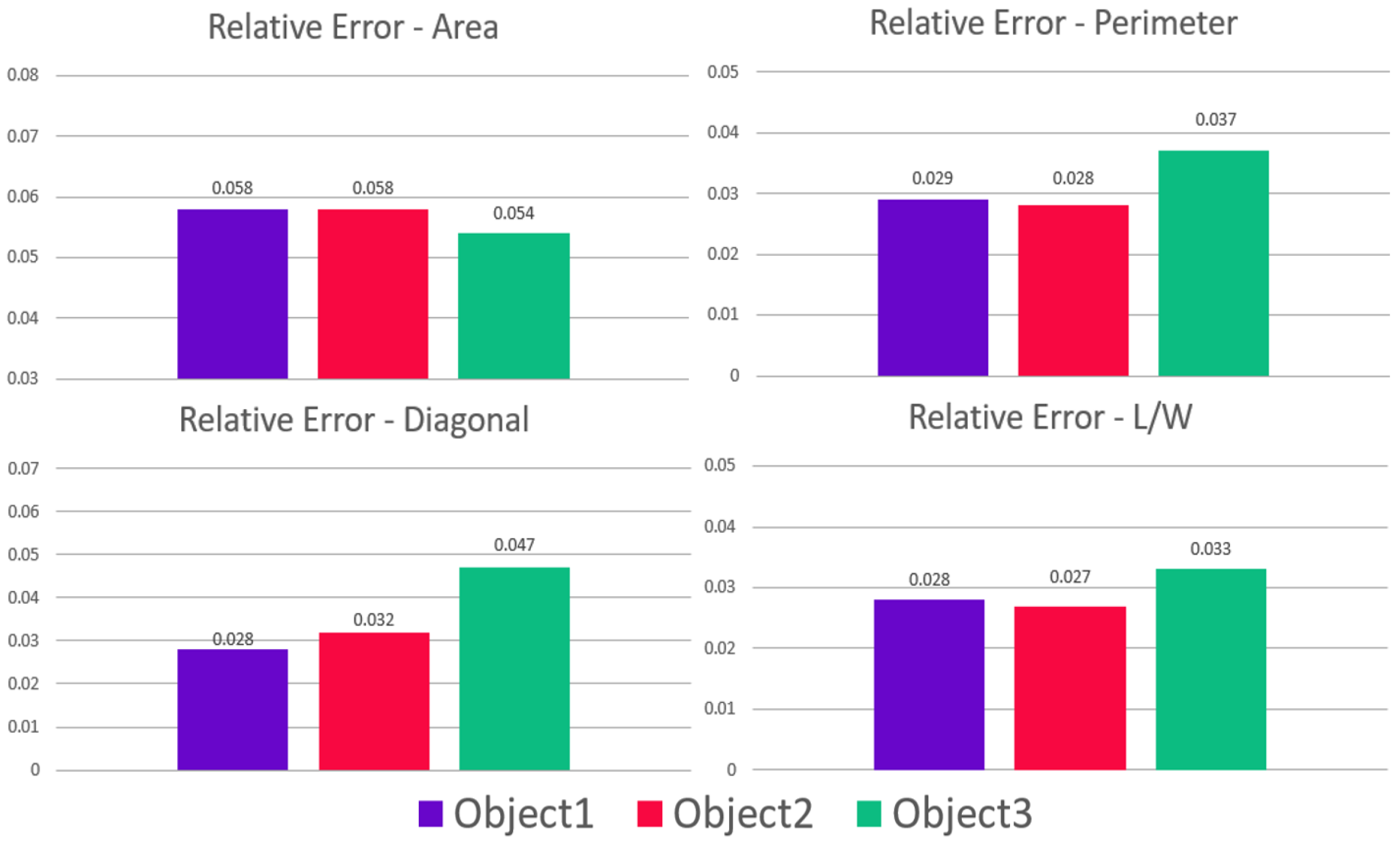
| Measurement (Scale) | Object 1 | Object 2 | Object 3 |
|---|---|---|---|
| Area (cm) | 8.41 | 4.41 | 1.6 |
| Perimeter (cm) | 11.6 | 8.4 | 3.2 |
| Diagonal (cm) | 4.1 | 3.0 | 1.1 |
| Length × Width (cm) | 2.9 × 2.9 | 2.1 × 2.1 | 0.8 × 0.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Telahun, M.; Sierra-Sossa, D.; Elmaghraby, A.S. Heuristic Analysis for In-Plane Non-Contact Calibration of Rulers Using Mask R-CNN. Information 2020, 11, 259. https://doi.org/10.3390/info11050259
Telahun M, Sierra-Sossa D, Elmaghraby AS. Heuristic Analysis for In-Plane Non-Contact Calibration of Rulers Using Mask R-CNN. Information. 2020; 11(5):259. https://doi.org/10.3390/info11050259
Chicago/Turabian StyleTelahun, Michael, Daniel Sierra-Sossa, and Adel S. Elmaghraby. 2020. "Heuristic Analysis for In-Plane Non-Contact Calibration of Rulers Using Mask R-CNN" Information 11, no. 5: 259. https://doi.org/10.3390/info11050259
APA StyleTelahun, M., Sierra-Sossa, D., & Elmaghraby, A. S. (2020). Heuristic Analysis for In-Plane Non-Contact Calibration of Rulers Using Mask R-CNN. Information, 11(5), 259. https://doi.org/10.3390/info11050259






