Abstract
Blockchains such as the bitcoin blockchain depend on reaching a global consensus on the distributed ledger; therefore, they suffer from well-known scalability problems. This paper proposes an algorithm that avoids double-spending in the short term with just O(√n) messages instead of O(n); each node receiving money off-chain performs the due diligence of consulting k√n random nodes to check if any of them is aware of double-spending. Two nodes receiving double-spent money will in this way consult at least one common node with very high probability, because of the ‘birthday paradox’, and any common honest node consulted will detect the fraud. Since the velocity of money in the real world has coins circulating through at most a few wallets per day, the size of the due diligence communication is small in the short term. This ‘k-root-n’ algorithm is suitable for an environment with synchronous or asynchronous (but with fairly low latency) communication and with Byzantine faults. The presented k-root-n algorithm should be practical to avoid double-spending with arbitrarily high probability, while feasibly coping with the throughput of all world commerce. It is resistant to Sybil attacks even beyond 50% of nodes. In the long term, the k-root-n algorithm is less efficient. Therefore, it should preferably be used as a complement, and not a replacement, to a global distributed ledger technology.
1. Introduction
In blockchains such as bitcoin, all n nodes reach Nakamoto consensus [1] on each block of transactions, thereby creating a scalability problem [2,3,4] that notoriously limits the entire bitcoin network to a few transactions per second while consuming massive power [5]. Bitcoin is considered the first digital currency algorithm to solve the double-spending problem without the need for a trusted authority or central server. Additionally, it can cope with Byzantine faults (e.g., [6,7]) including a Sybil attack [8] of up to 50% dishonest nodes. However, it requires O(n) communication messages per transaction that limit its scale.
Practically, bitcoin transactions suffer from a lag time of 15 min to several hours before being included in a block on the bitcoin blockchain [9] (this lag time has a complex dependency on how high a fee is offered by the transaction participants to the miner [10]). It then takes an hour longer to reach the generally desired threshold of 6-block confirmation [11]. Thus, before received bitcoin transfers are confirmed, and are safe to re-spend, there is typically a latency of several hours.
At the time of writing, the typical fee paid to the miner for a single bitcoin transaction is tens of thousands of Satoshi or about US $0.50–$5 [9]; this is higher than many fiat currency domestic bank transaction fees.
Therefore, efforts are being made to redesign the blockchain algorithm itself to ensure greater scalability, such as SCP [12], Algorand [13], bitcoin next generation (bitcoin-NG) [14], which all involve selecting a subset of users (committees or a rotating leader) in various configurations to reduce the number of messages required to reach consensus. In an alternative approach, a subset of nodes transacts with each other off-chain for a time, [15] as in the lightning network [16].
In this paper we consider an approach for protecting against double-spending [17] even if combined with a Sybil attack, without the need for a global ledger consensus. In this paper, we did not consider other forms of attacks, such as eclipse attacks [18], routing attacks [19], attacks based on time advantage [20], incentive attacks [21] and quantum computing attacks [22]. Relevant surveys of other attack types are [23,24]. Some previous research on avoiding double-spending are [25,26]. This study focuses on the protection against the most central vulnerability of cryptocurrencies, namely double-spending covered up by a Sybil attack of malicious nodes.
We propose a scalable low-latency algorithm that can run off-chain in parallel to a global ledger consensus mechanism, such as blockchain, protecting against double-spending in the short term. Thus, commerce may continue at a high pace even while the n nodes are working to reach consensus on transactions possibly with a lag of some hours from the transaction time. By applying this algorithm, we can accept a situation where consensus is achieved infrequently. Therefore, we can accept longer blockchain blocks that are created every hour, or every few hours, instead of bitcoin’s current average of 10 min, thereby increasing blockchain’s throughput of transactions per second [27], while compensating for longer latency with our complementary off-chain algorithm for preventing short-term double-spending.
For example, each morning the nodes may reach a consensus on the valid transaction histories and wallet balances as of the preceding midnight Greenwich Mean Time, and they may do so asynchronously, reaching the consensus by, say, 6 a.m. the next morning. For example, in the particular case of bitcoin, by 6 a.m. all the transactions from the previous day would typically have achieved six-block verification and may be considered final. In this case, the role of our algorithm is to allow fast and safe transactions in the 30 h say from Sunday midnight to Tuesday 6 a. m., when consensus is finalized for the ledger as of Monday midnight. Thus, in this example, our algorithm allows the configuration of the distributed ledger to be relaxed relative to the current configuration of bitcoin, to reach a consensus only every 24 h with a 6-h lag. Therefore, this enables the transaction rate of the ledger to increase. Our proposed solution allows people to trade, particularly to safely pass on the received coins, with next to zero latency.
The proposed algorithm, which is called ‘k√n’ or ‘k-root-n’, avoids double-spending in the short to medium term, while there is no global ledger consensus with an arbitrarily high probability of detecting double-spending, requiring just O(√n) messages per transaction. This is based on the assumption that specific money balances only circulate through O(constant) wallets in 24 h. This assumption is realistic since money circulates in the real economy with a velocity measured in one or two transactions per month [28], and bitcoin is already practically constrained by the transaction confirmation lag times to circulate a few times per day, and in practice rarely more than once or twice a day.
In this algorithm, every transaction should eventually be on-chain. The initial transaction verification is off-chain, thereby allowing transactions to continue off-chain at high speed and waiting for the blockchain to catch up. The algorithm only involves O(√n) nodes and messages per transaction; we typically choose 10√n.
2. Overview of k√n Random Double-Spending Detection
Suppose there are n nodes, in which each node is also a wallet, connected to a network, and they have achieved consensus on the global distributed ledger (or at least on the balance of each node) using blockchain (or another algorithm) sometime recently, a time we shall call the global ledger consensus (in the example above that would occur at 6 a.m. daily for the previous midnight).
For now, we assume that every wallet is also a node, which is usually online and available, and which also provides basic verification services to the network. The central idea is that any honest node that wants to verify whether the funds it receives have not been double-spent, will demand that the sender disclose the pedigree of the transferred funds, namely the sender’s transaction history since the last global ledger consensus. In case the sender depends on incoming funds to have sufficient balance to cover the current transaction, the receiver shall recursively demand disclosure of the source of funds, right back to funds that were available as of the last global ledger consensus.
Since querying all the nodes to verify each transaction is prohibitively expensive, an honest node will perform its due diligence on the pedigree of each inbound transaction with only a random k√n other nodes. The idea is that if two nodes query k√n random nodes, we will show that the probability of zero common queried nodes is extremely small for suitable k, even if a substantial proportion of nodes are failing or malicious. Therefore, if two honest nodes receive the same double-spent coins, they will almost certainly consult at least one common node and detect the fraud. This is the main concept of the algorithm, and it is based on the famous birthday paradox [29], where for example just 40 people (which is of order where n is the number of possible birthdays, 366) have about a 90% chance that at least two of them have the same birthday.
Each honest node provides verification services by keeping a history of all the transaction pedigrees it has been asked to verify. When two honest nodes query random nodes, any common queried honest node can immediately raise the alarm if the two receiving nodes are victims of a double-spending attempt, i.e., if they were given inconsistent transaction histories.
Let k be a small number greater than 1. We will generally choose k = 10. Assume that we are in an environment with Byzantine faults, say about 10% of nodes may not respond at any time because of node or network failure; assume that about 50% of the nodes are malicious, we would then have an effective k = 4.5, i.e., k√n responsive, honest nodes. When each of two honest nodes receives funds and successfully each query 4.5√n responsive, honest nodes, this k = 4.5 is sufficient to ensure an expected value of more than twenty common, honest and responsive nodes. There is a probability of just approximately 10−9 of zero common, honest and responsive nodes. Therefore, the chances of getting away with double-spending are negligible, and there is a probability very close to 1 that any double-spending will be detected as soon as both branches of the spend reach honest nodes.
The penalty for double-spending is at least forfeiting the wallet, so if each wallet has a minimum stake m of $1 and each transaction is limited to well under $1 billion, say to a maximum M = $1,000,000, then there is a negative expected return from any double-spending attempt, since there is a probability of just approximately 10−9 of not being caught.
Now a dishonest node may not be checking its inbound transactions, and may be maliciously collaborating with other nodes. This is why the receiving honest node must check not only the transaction history of the immediate sender for forked history/double-spending, but also to recursively check any of the sender’s transactions, to the extent that the immediate sender depends on the sender’s sender (recursively) payment to have balance for covering the current transaction. This recursive tree of inbound transactions is called the pedigree of the transaction, that is the recursive list of transactions that the current transaction depends on. This recursion is why the k-root-n algorithm is less efficient for long term use since the recursive pedigree of transactions may become large over a long time period.
Figure 1 shows node C receiving a transaction from node B. Before accepting it, node C consults k√n random nodes and checks that they have not seen an alternative history for B, i.e., that B has not been double spending. For illustration only, k = 2, thus C consults two rows of the other nodes when randomly arranged in a square of √n x √n. The diagram shows that a proportion (one) of these nodes fails to respond (dashed thin arrow), and of some may be responding dishonestly (not shown). In case B did not have cover for this transaction as of the last global ledger consensus, and is relying on incoming funds from A, C will recursively validate the A→B transaction too with the same network nodes.
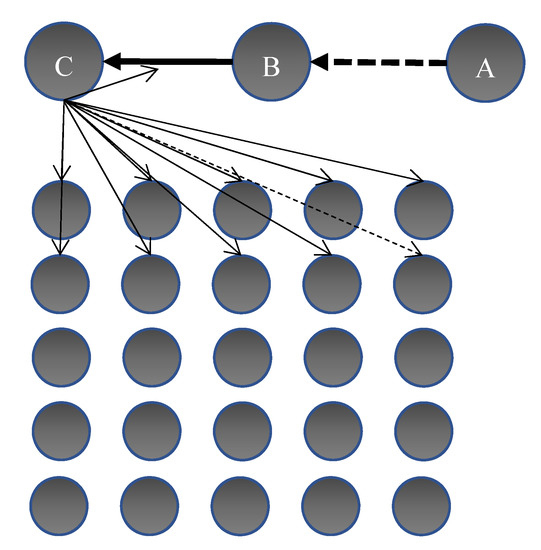
Figure 1.
Simple illustration of node C receiving coin from B, and verifying with a random selection of 2√n nodes that the coin is not double spent; if B is relying on a previous payment from A, C verifies that transaction too with the same nodes.
As a motivation for the O(√n) algorithm, we briefly explore how a 10√n algorithm scales by assuming n = 10 billion people (the projected world population for 2050 [30] and much more than bitcoin’s current 32 m wallets [31]). Suppose people are each transacting once per hour on the average, i.e., 24-h per day (higher than the average rate of commerce). Each transaction involves messages to 10√n = 106 nodes. We will see that this gives a probability of just p ≈ 10−9 of getting away with double-spending, even if half of the nodes are fraudulent and 10% of the nodes are unavailable (i.e., 4.5√n honest, responsive validating nodes). Thus, each transaction only burdens 1 out of 10,000 nodes, a performance improvement of four decimal orders of magnitude. With 10 billion transactions per hour globally, or 2.77 million transactions per second globally, each node should be involved in just 278 transactions per second. This transaction throughput is feasible for a modern computer (especially in 2050).
Thus, it seems practical that the algorithm could securely handle not only Visa/Mastercard volumes, but in fact all the commerce in today’s world and the foreseeable future. Visa’s volumes have been widely misquoted in bitcoin articles as 24,000 per second, although that appears to be mythical [32] with apparently more reliable sources estimating about 78.95 billion Visa transactions in the first half of 2018 [33] which averages 5000 per second, although peak transaction rates would presumably be higher. In any event, the current algorithm could feasibly handle transaction volumes orders of magnitude larger than Visa.
Whilst the idea of depending on probability to secure commerce may at first seem strange, it is noteworthy that all commerce already depends on probability. For example, every credit card transaction is accepted based on a probabilistic evaluation that it is not fraudulent.
We now introduce some definitions and formally present the k-root-n algorithm.
3. Preliminaries
Definition 1.
A Transaction T = (x, t, S, R, ss, sr) is an agreement to transfer a balance from a sender node/wallet to a receiver node/wallet; the tuple comprises a positive monetary amount, that is a quantity of coin, x = x[T], a time stamp t = t[T], identifiers (public keys) of the sender user S = S[T] and the receiver user R = R[T]. Additionally, ss and sr are the respective digital signatures of S and R of the data tuple (x, t, S, R) evidencing their agreement to the transaction.
A transaction T is only valid if the sender S had a balance (see next definition) of at least m + x immediately before the transaction, where m denotes the agreed minimum wallet balance. No sender or receiver may participate in two transactions with identical time stamps t.
A potential transaction T is a transaction that has not yet been signed by the receiver, that is T = (x, t, S, R, ss).
Definition 2.
The Balance b[S, t1] of a user S at time t1, given that s/he had a balance of b0 at the time t0 of the last known global ledger consensus, is defined by
i.e., the last known global ledger consensus balances plus all received amounts, minus all spent amounts.
Definition 3.
The Lineage LIN[T] of a transaction or potential transaction T is the transaction history for the sender S[T] from the last known global ledger consensus at time t0 before t[T] and up to the time of T:
These are the transactions relevant to establishing that the sender S has sufficient balance to afford T. However, not all of this history is necessarily required to establish sufficient balance, so for the sake of efficiency we now introduce a narrower transaction history.
Definition 4.
The Critical Lineage CLIN[T] of a transaction or potential transaction T is a set of transactions whose elements are a subset of LIN[T], comprising a minimal subset of inbound transactions critical to provide the balance that allows the sender to afford T. Formally, suppose that a sender S makes a payment of amount x in a transaction or potential transaction T; suppose that S’s last known global ledger consensus balance was b0. Suppose that the set of transactions in which S participated since the last global ledger consensus, LIN[T], includes inbound payments, T1...Tn, in descending order of amount (and ordered chronologically when amounts are equal) and outbound payments, U1...Um. Now, the critical inbound payments are the subset CLIN[T] = {T1...Tj} of inbound payments with j minimal such that
Thus, given that the sender has opening balance b and has spent the Ui, then, {T1...Tk} is a minimal subset of inbound transactions that are enough to provide balance coverage for this payment of x. Even if any of the other inbound payments, Tj+1...Tn, is derived directly or indirectly from fraud, the validation by the receiver of these critical inbound payments CLIN[T] of the sender is sufficient due diligence to ensure that the sender can afford x. Therefore, the minimum due diligence of the receiver R[T] is to check the following: (A) LIN[T] is complete and (B) the lineage of each transaction in CLIN[T] is complete. We now formalize this recursive set of transactions.
Definition 5.
The Pedigree PED[T] of a transaction or potential transaction T is the recursive closure of the set {T} under the CLIN operator. To compute this:
- Start with the set of PED[T] = {T}.
- For each T1 in PED[T], add any element of CLIN[T1] which is not already in PED[T] to PED[T]. Repeat until there is nothing to add.
- PED[T] = PED[T].
It is also helpful to think of PED[T] as the nodes of a directed acyclic graph for each transaction, recursively showing the inbound transactions that the sender depended on to cover the transaction since the last known global ledger consensus. Figure 2 depicts a $10 transaction and its PED pedigree. Here, the opening balances are shown on the nodes, and we assume an agreed minimum node balance of $1. The $10 transaction depends on $2 that the sender already had (over and above the $1 minimum) plus two received amounts of $4 each, of which one, in turn, depended on a received $3. The dashed lines represent other received amounts that are not critical to covering the transaction balances so are excluded from the PED.
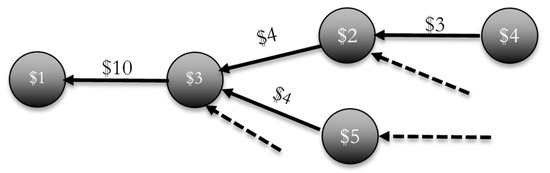
Figure 2.
An example of the PED[T] pedigree of a $10 transaction.
Definition 6.
A Disclosure DIS[T] for a potential transaction T is a communication from sender S[T] to receiver R[T] of PED[T] and LIN[T1] for every T1 in PED[T].
Definition 7.
A Fraudulent Transaction T is any transaction wherein the sender S[T] provides the receiver with an incomplete LIN[T] in the disclosure. Additionally, a transaction is considered a fraudulent transaction in retrospect if, at some time between t[T] and the next global ledger consensus, the same sender S[T] is the sender of another transaction T1 and fails to disclose T when disclosing LIN[T1].
Thus, if Malory sends money to Alice and later double spends by sending the same money to Bob without disclosing to Bob the earlier payment made to Alice, then both payments are considered fraudulent. It is insufficient to cancel the second transaction; the one that was directly involved in the fraud, as Alice may be a co-conspirator of Malory, while Bob is the only victim. The cancellation of both transactions ensures there is a significant penalty for fraud. In theory, this does mean that Bob would lose out since he was a victim of double-spending in retrospect, but practically this arrangement ensures that double-spending has a negative expected value and is very unlikely to occur at all.
Definition 8.
An Invalid transaction is a transaction that is not fraudulent, but wherein the sender in retrospect did not have balance to cover the transaction after removing fraudulent transactions. Equivalently, these are transactions that turn out to have a fraudulent transaction in their pedigree.
Definition 9.
Due diligence for a potential transaction T is the process of receiver R[T] communicating the offered disclosure DIS[T] with a random selection of (strictly i.e., rounded up to the nearest integer) nodes, called the validating nodes, and confirming that none of them has seen an alternative version of LIN[T1] for any T1 in PED[T].
4. k-root-n Algorithm
Suppose we have n nodes, each of which is also a wallet, connected to a network, and the nodes achieved consensus on the global ledger (or at least on the balance of each node) at some time t0 in the recent past; we call this time the global ledger consensus. Each global ledger consensus may become known at time t1 > t0, that is, with some latency after the time t0 which it relates to (e.g., in bitcoin, we may wait some hours for transactions to be included in a block and then for 6-block confirmation, before trusting that consensus was achieved). When we refer to the last global ledger consensus before time t, we mean the last one known before time t.
The nodes transfer balances to each other by mutually digitally signing transactions. Based on the algorithm, each receiving honest node will perform the following steps before accepting and signing a potential transaction T.
- Demand that the sender transmits the disclosure DIS[T], that includes the recursive list of dependent transactions PED[T] and the transaction history LIN[T1], for each T1 in PED[T].
- Validate that each transaction T1 in PED[T] was properly formed and signed by known nodes, and that each node had the balance to cover T1 based on the last known global ledger consensus balance of S[T1] plus the provided LIN[T1].
- Due diligence: Randomly choose validating nodes on the network; send each (directly or by communicating through a cascading tree of nodes) the disclosure DIS[T], and ask the validating nodes to validate that they have not seen any alternative LIN history for any transaction in PED[T].
- Any honest node receiving this due diligence request will validate that they have never previously seen a contradictory LIN history for any of the transactions T1 in PED[T]. If all is well, they will confirm their validation by digitally signing DIS[T] and transmitting that validation back to the receiver R[T]. Each validating node must then store every LIN transaction history they are asked to validate until the next achieved global ledger consensus, for future validation.
- If any validating node has in fact seen an alternative LIN transaction history for some T1 in PED[T], it informs the receiver R[T] who rejects potential transaction T. Proof of fraud, which comprises two alternative histories LIN[T1] and LIN’[T1], should be broadcast to all nodes on the network by the validating node. The double-spending wallet S[T1] will be blacklisted and any balance forfeited.
- The receiver R[T] should also broadcast the list of any of the other validating nodes that failed to raise an alarm. That is, in case R[T1] or any other nodes had previously disclosed LIN’[T1] to one of these same validating nodes V, then this node should also be blacklisted with proof of validation fraud, that is proof that V validated the current potential transaction, even though the disclosure included LIN[T1] while the same V has previously validated a transaction disclosure that included a forked lineage LIN’ for the same sender. Thus, the nodes are also held accountable for providing validation services honestly.
- If on the other hand all the validating nodes validate the transaction, the transaction is accepted and signed by the receiver.
All nodes periodically take time to reach a global ledger consensus on the distributed ledger, e.g., using Nakamoto consensus. All recipients will request that the transactions they received should be added to the global ledger. In the case that a node was caught in a fraudulent transaction, it will be disqualified. All fraudulent transactions are iteratively removed from the ledger.
After removing fraudulent transactions, invalid transactions must be iteratively identified until they are excluded from the global ledger. This process must be iterative since invalidating one transaction may cause the receiver to not have had cover for subsequent spends, thereby invalidating further transactions.
In the k-root-n algorithm, there is a need for honest nodes to be online almost all the time. It is recommended to have a protocol wherein an honest node commits to a service level agreement (SLA) (e.g., [34,35]) of say u = 90% uptime, and a node that does not comply should receive warnings, and eventually financial penalties or disqualification, by consensus of all the nodes. A node that tries to consult k√n nodes and receives less than uk√n responses in a specified target latency time should pick other nodes and retry until it receives the target uk√n validations.
5. An Example of Detection of Double-Spending Using the k-Root-n Algorithm
Suppose during Monday morning the network reaches a consensus that as of Sunday midnight the balances on the distributed ledger after all valid transactions were added, were as follows:
- Chuck (malicious) $100
- Mallory (malicious) $100
- Alice (honest) $100
- Bob (honest) $100
The ledger also showed that there was a total of n valid nodes, each having at least a minimum stake of m = $1.
We analyse the scenario where Chuck conspires with Mallory to double-spend, by transmitting the same money to Alice and also to Bob. To conceal the double-spend, the payment to Bob is passed by Chuck via co-conspirator Mallory.
As shown in Figure 3 transaction #1, Mallory sends $99 to Bob (in exchange for some goods, services or another currency). Mallory discloses her transaction history since the last consensus, which is empty, so she has $99 to spend. Bob first confirms that Mallory had $100 as of the last known global ledger consensus. Then, Bob, being honest, performs his due diligence and queries k√n network nodes (either directly or through a cascading tree of nodes) to confirm that none of them has seen Mallory signing any other transactions since consensus. They have not, and Bob, therefore, accepts the $99 and counter-signs the transaction, and submits it for eventual inclusion on the main distributed ledger.
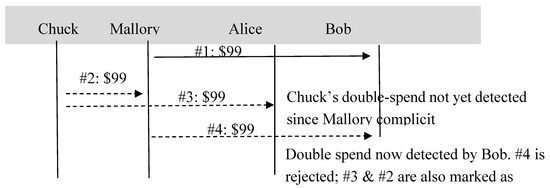
Figure 3.
An example of transactions between two dishonest and two honest nodes, including attempted double-spending.
In transaction #2, Chuck sends $99 to Mallory. Mallory being malicious and complicit with Chuck tells no one about this transaction. They both sign the transaction and may or may not submit it to the main ledger. Chuck is sending this $99 through Mallory attempting to mask the double-spending he is planning. He might potentially pass this money through further nodes.
In transaction #3, Chuck now sends $99 to Alice in exchange for some value. This is a fraudulent double-spend. He informs Alice fraudulently that he has no other transactions since the last consensus. Alice being honest does her due diligence and queries k√n random validating nodes with the declared disclosure. They all inform Alice that they are unaware of any forked transaction lineages (since transaction #2 was not broadcast) for Chuck, and so Alice accepts the payment. Thus, the double-spend is not yet detected (until both instances of double-spent money reach honest nodes).
In transaction #4, Mallory sends another $99 to Bob in exchange for some value. Bob being honest demands disclosure, and Mallory provides Bob with a copy of her transaction history since consensus, namely transaction #1 (-$99 that Bob already knows about) and transaction #2 (+$99), thereby evidencing Mallory’s balance of $100 allowing Mallory to spend $99. At this juncture, Chuck’s double-spent money has, via Mallory, reached the honest Bob.
- Bob notices that Mallory’s $100 balance is contingent on the money from Chuck (so transaction #2 is in the critical lineage CLIN[#4] and therefore in PED[#4]). Thus, Bob validates transaction #2 by requiring Mallory to provide Chuck’s transaction history LIN[#2] as part of the pedigree. In this case no further recursion is required.
- Chuck now does his due diligence and queries k√n random network nodes by asking them to validate the pedigree, which includes both LIN[#4] and LIN[#2].
- Some of these nodes (k2 on average, but at least 1 with an extremely high probability) had previously been told about Chuck’s alternative transaction history of transaction #3 in which he gave $99 to Alice. This triggers the following actions.
- ○
- The common validating nodes raise the alarm of double-spending, and broadcast a fraud-proof, namely that transaction #3 was not disclosed in LIN[#4]. The fraud-proof comprises two divergent transaction histories that were both signed by Chuck.
- ○
- Bob rejects the fraudulent transaction.
- ○
- Chuck has his wallets blacklisted and forfeits his $1 minimum stake.
- ○
- The fraudulent transaction #2 from Chuck to Mallory (which was later hidden from Alice) is also rejected from the distributed ledger. Therefore, transaction #4 is invalid since it depends on a fraudulent transaction #2.
- ○
- The network preferably should ask Mallory to show that she queried k√n validating nodes. When she fails to do so, Mallory may also be blacklisted and forfeit her balance. (This is optional extra protection which we might call no due diligence fraud, although this is not required for the algorithm to work and cannot be enforced in case Mallory had k√n co-conspirators and pretends to select them at random).
- ○
- Alice and Bob compare notes and find all the ~k2 common validating nodes they had consulted in #3 and #4. If any common node failed to raise the alarm, then such node would also be blacklisted for validation fraud, with the fraud-proof showing that the node received two alternative lineages from Chuck and in both cases approved and digitally signed them.
The next morning consensus is established again around the following end balances:
- Chuck (malicious) $100 (blacklisted with balance forfeited for double-spending)
- Mallory (malicious) $1 (may be blacklisted for failing to do due diligence on #2)
- Alice (honest) $100
- Bob (honest) $199
Once this new global ledger consensus is known, future senders only need to provide shorter transaction histories back to the newer global ledger consensus. In this scenario, Alice who is honest has lost out as a victim of fraud, but the algorithm ensures that the fraudsters have significant losses with very high probability, meaning that such fraud is very unlikely.
6. Algorithm Correctness
Theorem 1.
For any two honest nodes receiving and successfully validating payments with k√n random nodes each, there are an average of k2 common nodes queried by both honest nodes (any one of which can detect double-spending and raise the alarm).
Proof of Theorem 1.
The first honest node randomly queries k√n nodes representing a proportion k/√n of all n nodes. Therefore, when the second honest node queries k√n random nodes, a proportion of k√n * (k/√n) = k2 on average will overlap. □
This result is the key strength of the algorithm. Since both transactions involve only O(√n) validating nodes, but the expected value of the number of overlapping nodes is significant, thereby allowing any double-spending to be detected.
However, since it only requires one common node to detect fraud, what we are really interested in is the probability of at least one node in common, versus the probability of zero common nodes, which we require to be very small.
Lemma 2.
The probabilityof zero clashes (zero common nodes) between two random sets of r = k√n nodes satisfieswithfor large n and.
Proof of Lemma 2.
First, since there are ways for the second node to choose r validating nodes from n nodes, in which combinations involve zero of the same r validating nodes that the first node chose. Thus,
Now, let . Then, we can approximate
again with for the limit of large n. □
Therefore, is a safe upper bound for and a good approximation in the realistic case of large n and small k. By substitution, we see that k= 4.5 gives p0 ~ 10−9 for all large n. For convenience, we typically recommend that k = 4.5. k must be large enough to allow for the level of Byzantine faults in the network. As we saw a typical practical value would be k = 10 to allow for 10% unavailable nodes and 50% fraudulent nodes, so we have k = 4.5 of honest available nodes. 10% unavailability seems generous for most modern networks, while 50% of fraudulent nodes is typically the maximum supported by the distributed ledger technology used for global ledger consensus.
Appendix A shows values of and confirms that the approximation is excellent for large n and small k while providing a valid upper bound in all cases.
Now, double-spending with co-conspirators is in itself of no value, as the co-conspirators will not provide any value in return for a payment that they know is fraudulent, and may be later rejected from the global ledger. Therefore, the algorithm depends on ensuring a negative expected value once double-spent money directly or indirectly arrives at honest nodes, and the algorithm must catch the fraud in time before honest nodes naively provide value in exchange for fraudulent payments.
Theorem 3.
Let M be the maximum allowed transaction amount, m be the minimum wallet balance, n be the number of valid nodes as of the last global ledger consensus, h be the proportion of nodes assumed to be honest and u be the proportion of uptime required from nodes. Assume that the network is designed such that
where. Then, the expected return on any combination of double-spending to honest nodes is negative.
Proof of Theorem 3.
The maximum amount of a double-spend transaction is the maximum transaction amount M. By utilizing Lemma 2, the probability of two honest nodes not detecting a double-spend transaction is , in which case there is a gain of M. In the case that a double-spend transaction is detected, the double-spender will at least forfeit the minimum wallet balance m.
Therefore, the maximum expected gain is given by
Given , this expected value is negative. □
As discussed, practical values are m = $1, M = $1,000,000 and k = 4.5 which give . Assuming h = 50% honest nodes (the algorithm can handle even fewer than 50% honest nodes but the blockchain cannot) and u = 90% uptime, we need k = 10 to ensure a negative expected value of any double-spend.
7. Algorithm Message Space Complexity
The number of messages per transactions is k√n. These may be transmitted directly or cascaded through a tree of nodes to avoid the receiving node becoming a network bottleneck.
Before discussing message size, we present some definitions.
Definition 10.
The critical inbound transaction size j[T] is the number of inbound transactions (since the last global ledger consensus) which a sender depends on for their balance when spending money in a transaction t, that is j[T] = |CLIN[T]|.
An upper bound for j[T] is the total number of inbound transactions |LIN[T]| that the node has participated in since the last global ledger consensus. In most transactions, j will likely be zero. A person spending money most often already had the money that morning. However, in extreme cases, v may be large. For example, a grocery store may start the day with zero balance, accept hundreds of small transactions, and spend all their accumulated money on a large capital item or payroll that same evening. The large spend may depend on every one of the small inbound transactions.
Definition 11.
The critical velocity of money v[T] of a transaction T, is the maximum depth of the recursion in PED[T].
v[T] denotes the number of nodes that the specific balance of coin circulated through in the period between the last global ledger consensuses until it landed in transaction T, where it is only considered circulation if the nth transaction depended to cover its balance on the (n−1)th. v is generally assumed to be small, most often 1 and rarely more than 2. It is defined more narrowly than the economic concept of the velocity of money [36] that includes all circulation of currency whether critical to the spender’s balance or not. The velocity of fiat money tends to average a very modest rate of 4–11 per year [37], so v > 2 in a single day between global ledger consensuses would be rather rare. That is, in say 24 h of real commerce, a specific banknote will rarely change hands more than once or twice and at most a few times.
The number of transactions in the pedigree of a transaction T is the size of all transactions in the pedigree, so |PED[T]| = , where and denote the maximum values of j and v for transactions in the pedigree recursion, respectively.
In the majority of the transactions, we expect v = 1 and occasionally v = 2 but rarely more, while j is most often 0 but may occasionally hit a few hundred. Thus, the message sizes in realistic commerce may typically be small; on rare occasions, we may have tens of thousands of transactions and require some megabytes of message size, which is still quite a practical message size for a modern network.
However, if the algorithm is continuously used for days and weeks without a global ledger consensus, v may cause the message size to grow prohibitively large.
8. Sybil Attack
In a Sybil attack, a fraudster develops numerous fraudulent nodes hoping to reduce the chance of two honest nodes detecting the fraudster’s double-spending. We already saw that a 50% attack does not provide a positive expected value of double-spending with the recommended network parameters. What about a still larger attack?
It is noteworthy that the global ledger consensus algorithm will typically fail with a 51% attack [38]; regardless we investigate whether such an attack could pay off in the k-root-n algorithm.
Suppose again that m = $1, M = $106 and k = 10. Assume that there are initially n honest nodes, and the fraudster creates another n fraudulent nodes, to control 50%, and suppose further that 10% of the nodes are unavailable. We already saw that k = 4.5 and the fraudster has successfully reduced p010−44 to p010−9. But with M/m=106 there is no incentive to double-spend with p010−9.
In fact, the appendix shows that the fraudster needs to get approximately k < 3.5 to obtain p010−6 and achieve a positive expected value for double-spending. Therefore, the criminal would need approximately 2n fraudulent nodes. However, the fraudster then faces another challenge. The loss from a single unsuccessful double-spending is not limited to forfeiting the double-spending wallet, but also the loss of all the nodes that failed to detect the double-spend and thereby committed a verification fraud. According to Theorem 1 the expected number of common nodes is (10 − 3.5)2 = 42.25 nodes for an average loss of at least 42.25 m. Thus, even in this case, double-spending will have a negative expected value.
Consider more generally that a fraudster creates (f − 1)n fraudulent nodes for a total of n = fn nodes. When a user consults k√n = k√(fn) nodes, a proportion of 1/f of the nodes or k√(n/f) nodes, will be genuine, this being a proportion k/√(fn) of all the n honest nodes. Two honest nodes will therefore have an expectation of consulting common honest nodes, i.e., k = k/√f. They will also consult on average k2- k2/f dishonest nodes, and if the double-spending is caught these k2 (1-1/f) nodes will be disqualified.
Therefore, the expected payoff from a single double-spending is p0(k, n)M , against the expected cost of (k2 (1 − 1/f) + 1)m ≈ k2m (the fraudulent nodes that fail to report the double-spending, plus one for the double-spending wallet) for every unsuccessful transaction against a setup cost of (f − 1)nm.
Practically, an extremely large number of fraudulent nodes are required for the double-spending to payoff. Since k = 10, we can find numerically that we need approximately f > 10.5 for a positive payoff. Suppose f = 11; the fraudster has to create a massive 10n fake nodes to control ~91% of the network. This is done at a cost of $10nm, assuming $10m for n = 1 million. Now, k = k/√f ≈ 3 and p0 = . Thus, a double-spending of M = $1,000,000 would have an expected value of $120, while the expected cost would be losing k2(1 − 1/f) + 1 = 91 nodes at a cost of 91m = $91, giving an expected profit of $29. After such an extreme attack, a single fraudulent transaction would have a positive expected value.
However, even this strategy is doomed to fail. If n = 106, it costs $10 million to setup 10 million nodes. The user would have to repeat the double-spending three hundred thousand times to recoup the initial investment. However, they would lose 91 nodes, on average, each time they fail, meaning that they would lose the vast majority of the fraudulent nodes before recovering their investment, so the whole scheme is not feasible.
Now, if we increase f further say f ≈ k2 = 100, then the fraud can pay off. p0 gets closer to 1 and the fraudster earns a payback that tends to M as f increases. However, this requires creating O(100n) nodes to dominate ~99% of the network. Various strategies that can help to defend against such an extreme attack include the following.
- Reducing M/m: Reducing M can force honest people to have more wallets that increase n.
- Increasing k.
- Biasing the k√n random nodes towards the nodes that have been around for longer or have higher balances.
- Monitoring for suspicious behaviour such as the creation a huge number of wallets with close to a minimum stake.
In summary, with the recommended parameters of k, m and M, the algorithm is immune to 51% attacks and even 90% attacks, and in fact resilient to all but the most extreme of Sybil attacks.
9. Variations on the Algorithm for Further Research
9.1. k-root-n without Global Ledger Consensus
There would be an option of running k-root-n as the sole algorithm without any common consensus on a ledger. As time goes on, j increases, and the verifications become exponentially heavier. However, each node should cache everything it knows about other nodes’ verified transaction histories. Over time, if money circulates throughout the entire network, every node will end up verifying every transaction at some time or another just once with k√n other nodes, creating in the long term a complexity of kn√n per transaction, that seems unattractive. However, there is room for optimizations that could make this approach of standalone k-root-n feasible.
9.2. Nodes Versus Wallets
The assumption so far is that every wallet is a node, and the provision of node verification services is part of the cost of being a wallet. This may be feasible as we rapidly move to a world where all devices are online almost all the time, but it could also be a limitation.
There could be an alternative variation of the algorithm in which not every wallet is a node. This may be helpful since people may want their wallets to be offline or to be stored on a machine with limited processing power, bandwidth or memory. In this scenario, nodes may be paid a fee to provide verification services. Moreover, the nodes could be the same machines as the nodes of the underlying blockchain. Further research is required to formally define such a network.
9.3. Forced Validation
An alternative idea may be considered where even dishonest nodes are forced to consult O(√n) nodes. In this situation, nodes should not be given the opportunity to select which validating nodes they consult, since they could pick collaborating dishonest nodes. Therefore, we may introduce a pseudorandom formula to dictate the nodes that are consulted. This would also ensure balancing the load between all nodes. In this situation, the idea is that if Alice sends money to Bob and Bob sends the same money to Charlie, then Charlie will again ask k√n nodes to validate that Bob did not double-spend. However, Charlie will not need to ask the network to validate the transaction from Alice to Bob. Charlie can instead ask Bob to see the k√n digital signatures for the appropriate nodes that signed off on the transaction with Alice. Thus, Charlie can verify that Bob indeed consulted the prescribed set of k√n nodes, and received all their approval, creating less traffic and processing demands on the network.
In this approach, when two people agree on a transaction, they must notify a formulaically determined pseudorandom selection of k√n other nodes and obtain each of their digitally signed approval. Moreover, the pseudorandom selection is based on a predetermined formula which is known to all, and takes as input e.g., sender’s ID and the time of the transaction. To reduce the sender’s ability to pick and choose a specific time, we preferably take time stamps to be at a resolution of a second or a minute (rather than a more fine-grained time slot) so they have limited choices to try to find a time slot at which the pseudorandom formula happens to choose all their co-conspirators. As before, each of those nodes that are honest will check that the sender has not double-spent.
Now for the recursive check of sender’s sender and so on, the receiver can check that all the recursive transactions have the necessary sign-off from all the nodes as determined by the pseudorandom formula. Thus, the receiver does not have to burden the network by validating the recursive transactions. Such an algorithm would scale better over longer periods.
This type of algorithm suffers from some clear vulnerabilities. In a real network, there is a high chance that some nodes may not be available, so the sender could feasibly calculate which k2 nodes would detect his double-spending and simply claim that those particular nodes were not available. This would have to be mitigated by common monitoring of node availability, or honest nodes may self-monitor, so that anyone can later validate any claim that a certain node was unavailable at a certain time.
The sender may also have multiple wallets and multiple available time slots allowing them some choice of the sending node and time slot, giving them some leeway to plan a double-spend without any clashes of verifying nodes, by choosing the particular sending wallet and time slot wherein the pseudorandom formula happens to pick many of their complicit nodes. If we choose k large enough, we can make this infeasible, for example with k = 10 and p0 = 3.70 × 10−44, the user must consider O(1044) combinations of wallets and time slots to obtain one with no clashes to an earlier transaction, which is not feasible.
Therefore, it should be possible to design an algorithm wherein each node (honest or not) is forced to consult a particular set of k√n nodes based on a function of the sender and time slot, and wherein there is no feasible way to create a positive expected value of double-spending.
10. Conclusions
For a distributed ledger, reaching consensus is expensive and may involve a long lag time. In this paper, we have explored a two-tier system in which the primary algorithm ensures that the global ledger consensus is reached for the distributed ledger, but perhaps only periodically and with high latency. In the meantime, a secondary k-root-n algorithm allows parties to transact rapidly and protect against double-spending with a more efficient O(√n) probabilistic algorithm which involves validating each transaction, and recursively the transactions it depends on (the transaction’s pedigree) with a random selection of k√n nodes. It seems feasible for such a network to handle all the world’s commerce, while always having a negative expected value of double-spending, and being resistant to even aggressive Sybil attacks.
Further research is required to investigate the practicality of each wallet being a highly available node, or develop the idea of separating wallets and nodes. Further research is also required on the feasibility of the alternative idea of formulaically dictating validating nodes.
Funding
This research received no external funding.
Acknowledgments
My thanks to Joshua Fox, Benjamin Fox, Aviv Zohar, for their valuable, constructive feedback.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Table of k and p0
This table shows p0, the chances of zero clashes when two honest nodes each consult k√n random nodes for various values of k and a couple of values of n.

Table A1.
Values of p0(n,k√n).
Table A1.
Values of p0(n,k√n).
| k | p0(n = 104, k√n) | p0(n = 1010, k√n) | |
|---|---|---|---|
| 1 | 0.36 | 0.37 | 0.37 |
| 1.5 | 0.1 | 0.11 | 0.11 |
| 2 | 0.017 | 0.018 | 0.018 |
| 2.5 | 0.0016 | 0.0019 | 0.0019 |
| 3 | 9.30 × 10−05 | 1.20 × 10−04 | 1.20 × 10−04 |
| 3.5 | 3.10 × 10−06 | 4.80 × 10−06 | 4.80 × 10−06 |
| 4 | 5.80 × 10−08 | 1.10 × 10−07 | 1.10 × 10−07 |
| 4.5 | 6.10 × 10−10 | 1.60 × 10−09 | 1.60 × 10−09 |
| 5 | 3.70 × 10−12 | 1.40 × 10−11 | 1.40 × 10−11 |
| 5.5 | 1.20 × 10−14 | 7.30 × 10−14 | 7.30 × 10−14 |
| 6 | 2.30 × 10−17 | 2.30 × 10−16 | 2.30 × 10−16 |
| 6.5 | 2.30 × 10−20 | 4.50 × 10−19 | 4.50 × 10−19 |
| 7 | 1.30 × 10−23 | 5.20 × 10−22 | 5.20 × 10−22 |
| 7.5 | 3.70 × 10−27 | 3.70 × 10−25 | 3.70 × 10−25 |
| 8 | 5.60 × 10−31 | 1.60 × 10−28 | 1.60 × 10−28 |
| 8.5 | 4.60 × 10−35 | 4.20 × 10−32 | 4.20 × 10−32 |
| 9 | 1.90 × 10−39 | 6.60 × 10−36 | 6.60 × 10−36 |
| 9.5 | 4.10 × 10−44 | 6.30 × 10−40 | 6.40 × 10−40 |
| 10 | 4.40 × 10−49 | 3.70 × 10−44 | 3.70 × 10−44 |
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 15 January 2020).
- Chohan, U. The Limits to Blockchain? Scaling vs. Decentralization. SSRN/3338560. 2019. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3338560 (accessed on 15 January 2020).
- Scalability. Bitcoin Wiki, 2015. Available online: https://en.bitcoin.it/wiki/Scalability (accessed on 15 January 2020).
- Garzik, J. Making Decentralized Economic Policy. 2015. Available online: http://gtf.org/garzik/bitcoin/BIP100-blocksizechangeproposal.pdf (accessed on 15 January 2020).
- Vries, A.D. Bitcoin’s Growing Energy Problem. Joule 2018, 2, 801–805. [Google Scholar] [CrossRef]
- Canneti, R.; Rabin, T. Optimal Asynchronous Byzantine Agreement; Technical Report #92-15; Computer Science Department, Hebrew University: Jerusalem, Israel, 1992. [Google Scholar]
- Castro, M.; Liskov, B. Practical Byzantine Fault Tolerance. In Proceedings of the Third Symposium on Operating Systems Design and Implementation, New Orleans, LA, USA, 22–25 February 1999. [Google Scholar]
- Douceur, J.R. The Sybil Attack, Peer-to-Peer Systems. Lect. Notes Comput. Sci. 2002, 2429, 251–260. [Google Scholar]
- Live Bitcoin Transactions. Blockchain Unconfirmed Transactions. Available online: https://www.blockchain.com/btc/unconfirmed-transactions (accessed on 15 January 2020).
- Azzolini, D.; Riguzzi, F.; Lamma, E. Studying Transaction Fees in the Bitcoin Blockchain with Probabilistic Logic Programming. Information 2019, 10, 335. [Google Scholar] [CrossRef]
- Irreversible Transactions. Available online: https://en.bitcoin.it/wiki/Irreversible_Transactions (accessed on 15 January 2020).
- Luu, L.; Narayanan, V.; Baweja, K.; Zheng, C.; Gilbert, S.; Saxena, P. SCP: A Computationally-Scalable Byzantine Consensus Protocol for Blockchains. IACR Cryptol. 2016, 20. Available online: https://www.weusecoins.com/assets/pdf/library/SCP (accessed on 15 January 2020).
- Gilad, Y.; Hemo, R.; Micali, S.; Vlachos, G.; Zeldovich, N. Algorand: Scaling Byzantine Agreements. In Proceedings of the SOSP 17 26th Symposium on Operating Systems Principles, Shanghai, China, 28–31 October 2017; pp. 51–68. [Google Scholar]
- Eyal, I.; Gencer, A.E.; Sirerr, E.G.; van Renesse, R. Bitcoin-NG: A Scalable Blockchain Protocol. In Proceedings of the 13th USENIX Symposium on Networked Systems Design and Implementation (NSDI 16), Santa Clara, CA, USA, 16–18 March 2016. [Google Scholar]
- Apeltsin, L. A CryptoCubic Protocol for Hacker-Proof Off-Chain Bitcoin Transactions; Cornell University: Ithaca, NY, USA, 2014. [Google Scholar]
- Dryja, J.; Poon, T. The Bitcoin Lightning Network: Scalable Off-Chain Instant Payments. 2016. Available online: https://www.bitcoinlightning.com/wp-content/uploads/2018/03/lightning-network-paper.pdf (accessed on 15 January 2020).
- Chohan, U.W. The Double Spending Problem and Cryptocurrencies. Bank. Insur. J. Soc. Sci. Res. Netw. 2017. [Google Scholar] [CrossRef]
- Heilman, E.; Kendler, A.; Zohar, A.; Goldberg, S. Eclipse Attacks on Bitcoin’s Peer-to-Peer Network, SEC’15. In Proceedings of the 24th USENIX Conference on Security Symposium, Washington, DC, USA, 12–14 August 2015; pp. 129–144. [Google Scholar]
- Apostolaki, M.; Zohar, A.; Vanbever, L. Hijacking Bitcoin: Routing Attacks on Cryptocurrencies. IEEE Symp. Secur. Priv. 2017. [Google Scholar] [CrossRef]
- Pinzón, C.; Rocha, C. Double-spend Attack Models with Time Advantange for Bitcoin. Electron. Notes Theor. Comput. Sci. 2016, 329, 79–103. [Google Scholar] [CrossRef]
- Ittay, E.; Peter, G.; Aljosha, J.; Sarah, M.; Nicholas, S.; Itay, T.; Edgar, W.; Alexei, Z. Pay-To-Win: Incentive Attacks on Proof-of-Work Cryptocurrencies. IACR Cryptol. ePrint Arch. 2019, 775. [Google Scholar]
- Stewart, I.; Ilie, D.; Zamyatin, A.; Werner, S.; Torshizi, M.F.; Knottenbelt, W.J. Committing to quantum resistance: A slow defence for Bitcoin against a fast quantum computing attack. R. Soc. Open Sci. 2018, 5, 180410. [Google Scholar] [CrossRef] [PubMed]
- Saad, M.; Spaulding, J.; Njilla, L.; Kamhoua, C.; Shetty, S.; Nyang, D.; Mohaisen, A. Exploring the Attack Surface of Blockchain: A Systematic Overview. arXiv 2019, 1904, 3487. [Google Scholar]
- Karame, G.O.; Androulaki, E.; Roeschlin, M.; Gervais, A.; Čapkun, S. Misbehavior in Bitcoin: A Study of Double-Spending and Accountability. ACM Trans. Inf. Syst. Secur. 2015, 18, 1. [Google Scholar] [CrossRef]
- Pérez-Solà, C.; Delgado-Segura, S.; Navarro-Arribas, G.; Herrera-Joancomartí, J. Double-spending prevention for Bitcoin zero-confirmation transactions. Int. J. Inf. Secur. 2019, 18, 451–463. [Google Scholar] [CrossRef]
- Kang, K.-Y. Cryptocurrency and Double Spending History: Transactions with Zero Confirmation. Munich Pers. RePEc Arch. 2019, 16, 48. [Google Scholar]
- Göbel, J.; Krzesinski, A.E. Increased Block Size and Bitcoin Blockchain Dynamics. In Proceedings of the 27th International Telecommunication Networks and Applications Conference (ITNAC), Melbourne, Australia, 22–24 November 2017. [Google Scholar]
- Ericsson, N.R.; Hendry, D.F.; Hood, S.B. Milton Friedman and Data Adjustment. In IFDP Notes; Board of Governors of the Federal Reserve System: Washington, DC, USA, 2017. [Google Scholar]
- Ball, W.W.R. Probability. In Mathematical Recreations and Essays; Macmillan: New York, NY, USA, 1960; p. 45. [Google Scholar]
- UNDESA. The World Population Prospects 2019: Highlights; Population Division of the UN Department of Economic and Social Affairs: New York, NY, USA, 2019. [Google Scholar]
- Lielacher, A. How Many People Use Bitcoin in 2019? Bitcoin Mark. J. 2019, 643, 32. [Google Scholar]
- Sedgwick, K. No, Visa Doesn’t Handle 24,000 TPS and Neither Does Your Pet Blockchain. Available online: https://news.bitcoin.com/no-visa-doesnt-handle-24000-tps-and-neither-does-your-pet-blockchain/ (accessed on 15 January 2020).
- Global General Purpose Cards—Midyear 2018, The Nilsen Report. Available online: https://nilsonreport.com/upload/issues/1140_0321.pdf (accessed on 15 January 2020).
- Skene, J.; Lamanna, D.D.; Emmerich, W. Precise Service Level Agreements ICSE ’04. In Proceedings of the 26th International Conference on Software Engineering, Edinburgh, UK, 28 May 2004; pp. 179–188. [Google Scholar]
- Lamanna, D.; Skene, J.; Emmerich, W. SLAng: A Language for Defining. In Proceedings of the Ninth IEEE Workshop on Future Trends of Distributed Computing Systems (FTDCS), San Juan, PR, USA, 30 May 2003. [Google Scholar]
- Fisher, I.; Gunnison Brown, H. The Purchasing Power of Money, its Determination and Relation to Credit, Interest and Crises; Nabu Press: Charleston, SC, USA, 2010; pp. 377–381. [Google Scholar]
- Federal Reserve Bank of St. Louis, Velocity of M1 Money Stock, Fred Economic Data, No.2019. Available online: https://fred.stlouisfed.org/series/M1V (accessed on 15 January 2020).
- Bastiaan, M. Preventing the 51%-Attack: A Stochastic Analysis of Two Phase Proof of Work in Bitcoin. Available online: https://www.hmbastiaan.nl/martijn/docs/2015/preventing-the-majority.pdf (accessed on 15 January 2020).
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).