Abstract
Since fuzzy -covering was proposed, few papers have focused on how to calculate the reduct in fuzzy -covering and how to update the reduct while adding and deleting some objects of the universe. Here, we propose a matrix-based approach for computing the reduct in a fuzzy -covering and updating it dynamically using a matrix. First, matrix forms for computing the reduct in a fuzzy -covering are proposed. Second, properties of the matrix-based approaches are studied while adding and deleting objects. Then, matrix-based algorithms for updating the reduct in a fuzzy -covering are proposed. Finally, the efficiency and validity of the designed algorithms are verified by experiments.
1. Introduction
As generalized models of Palawk’s rough sets [1], covering-based rough sets [2]—which were proposed by Zakowski in 1983—have been widely applied in some popular aspects such as decision-making [3], attribute reduction [4], knowledge reduction [5], etc. Since covering-based rough sets have been proposed, research on the lower and upper approximations of covering-based rough sets and their properties attracts much attention, such as in [6,7,8,9]. In order to extend the application field of covering-based rough sets, fuzzy computing [10,11,12,13,14], which can be applied to covering-based rough sets, has been considered by scholars. Some generalized fuzzy rough approximation operators based on fuzzy coverings were proposed by Li et al. [15] in 2008. Fuzzy covering is a generalized model of covering; it extends the application of covering-based rough sets. Moreover, fuzzy neighborhood systems and some virtual issues of fuzzy covering are discussed by D’eer et al. [16]; they proved that only sixteen different fuzzy neighborhood operators can be obtained, and studied the partial order relations among those sixteen operators. Based on fuzzy covering and its operators—including fuzzy neighborhood operators—fuzzy -covering was proposed by Yang et al. [17]. They investigated some properties of a fuzzy -covering and proposed an algorithm to compute the reduct of a fuzzy -covering.
Computing the reduct of a covering via a matrix approach is an efficient way to reduce its computation time. From different viewpoints, scholars have introduced many algorithms that focused on how to compute the reduct of a covering. Some matrix approaches for issues about the minimal and maximal descriptions were proposed by Wang et al. [18]; similar works were done by Lin et al. [19]. Boolean matrix representations of approximation operators and approaches for calculating the approximations in covering-based rough sets were investigated by Ma et al. [20]. There always exists some variation in data sets which induces the variation of a covering, such as variation of attributes [21,22], variation of attribute values [23], variation of universe [24], and variation of covering cardinalities [25]. However, since fuzzy -covering was proposed, few authors have considered how to compute its reduct or how to update the reduct of a fuzzy -covering. Correspondingly to the crisp covering, we assume that there are there types of variation in fuzzy -coverings, namely, variation of granule size, variation of covering cardinalities, and variation of universe. In [17], there is an algorithm to calculate the reduct of a fuzzy -covering, but it is not efficient enough and cannot adapt to the variation of fuzzy -covering. In order to overcome these defects, we propose matrix-based approaches for computing and updating the reduct in a fuzzy -covering. Moreover, updating the reduct in a fuzzy information system can be applied for some relevant aspects such as knowledge acquisition and recommender systems [26,27], but in these applications, data sets often vary over time and need algorithms to implemented in real-time or almost real-time. Incremental computation is required in these applications. To reach these requirements, in this paper, we propose a matrix form of the algorithm in [17], and then propose algorithms based on the improved algorithm, while adding some objects into the universe or deleting some objects from the universe.
This paper is structured as follows: Some main results of fuzzy -covering will be reviewed in Section 2, as well as the improved matrix-based algorithm for computing the reduct of a fuzzy -covering. In Section 3, matrix-based approaches for updating the reduct of fuzzy -covering while adding and deleting some objects are proposed. Several experiments are conducted to verify the efficiency and validity of our proposed algorithms in Section 4, then some conclusions will be given in Section 5.
2. Preliminaries
In this section, we review several basic concepts of fuzzy -covering, as well as the algorithm to compute the reduct in it.
Fuzzy -Covering
In this subsection, some basic concepts of fuzzy -covering are reviewed.
First of all, based on the -levels which were used for characterizations of fuzziness in metric spaces in [28] to investigate some properties of cyclic fuzzy maps in metric spaces, fuzzy -covering approximation space can be defined.
Definition 1
([17,28]). Let U be an arbitrary universal set, and be the fuzzy power set of U. For each , we call , with for any , a fuzzy β-covering of , if for each . We also call a fuzzy β-covering approximation space.
In a fuzzy -covering approximation space, the reducible element of can be defined as follows.
Definition 2
([17]). Let be a fuzzy β-covering of U and . If C is the union of some fuzzy sets in , we say that C is a reducible element of ; otherwise, C is an irreducible element.
For computing the reduct of a fuzzy -covering, there are two properties of a fuzzy -covering approximation space.
Lemma 1
([17]). Let be a fuzzy β-covering of U and let C be a reducible element of ; then, is still a fuzzy β-covering of U.
Lemma 2
([17]). Let be a fuzzy β-covering of U and let C be a reducible element of ; then, is a reducible element of if and only if is a reducible element of .
Then, the reduct of a fuzzy -covering can be defined as follows.
Definition 3
([17]). Let be a fuzzy β-covering of U and is a subset of . If is the set of all reducible elements of , then is called the reduct of , and is denoted as .
A fuzzy -covering of U can be denoted by a -covering character matrix.
Definition 4
([17]). Let be a fuzzy β-covering approximation space of U; the β-covering character matrix on U is denoted by , where
Example 1.
Let be a fuzzy β-covering approximation space of U; the β-covering character matrix on U, where . According to Definition 5, the fuzzy β-covering character matrix on U is as follows:
To transform the algorithm in [17] for computing the reduct of a fuzzy -covering, we define a containing relation character matrix on U.
Definition 5.
Let be a fuzzy β-covering approximation space of U; the containing relation character matrix on U is denoted by , where
Example 2
(Continuation of Example 1). The containing relation character matrix on U is as follows:
By Definitions 4 and 5, we can change the algorithm for computing the reduct of a fuzzy -covering in [17] into a matrix form. The total time complexity of Algorithm 1 is . Steps 1–6 are to ensure that is a fuzzy -covering with time complexity , and Steps 8–16 are to compute with time complexity .
| Algorithm 1: Algorithm to compute the reduct of a fuzzy -covering. |
 |
3. Matrix-Based Approaches for Updating Reducts in Fuzzy -Coverings While Adding or Deleting Some Objects
3.1. Matrix-Based Approach for Updating Reducts in Fuzzy -Coverings While Adding Some Objects into the Universe
In this subsection, we present matrix-based dynamic approaches for updating the reduct in a fuzzy -covering while adding some objects into the universe. We denote as a fuzzy -covering approximation space of U, where and . We denote as a fuzzy -covering approximation space of , where and . In this paper, t denotes an integer greater than 1.
The next theorem indicates the containing relation before and after adding some objects into U.
Theorem 1.
Let be a fuzzy β-covering approximation space of U and let be a fuzzy β-covering approximation space of ; the following result holds.
Proof.
□
Example 3
(Continuation of Example 1). If and are added into U, the changes are as follows. According to Theorem 1, the new β-covering character matrix on is as follows:
By Definition 2, we have and .
Theorem 2.
Let be a fuzzy β-covering approximation space of U and let be a fuzzy β-covering approximation space of . If the relation character matrix on U is denoted by , the relation character matrix on is denoted by , where , the following result holds.
Proof.
□
Example 4
(Continuation of Example 3). By Theorem 2, the containing relation character matrix on can be calculated as follows.
Because and we have ; because and we have ; because and we have ; because and we have ; because and we have ; because and we have . From the above and from Theorem 2, we have
Through Theorems 1 and 2, we can propose Algorithm 2 for updating the reduct in a fuzzy -covering while adding some objects into the universe. If , the total time complexity of Algorithm 2 is . Steps 2–9 are to update with time complexity , and Steps 11–17 are to compute with time complexity . The time complexity of Algorithm 2 is smaller than the time complexity of Algorithm 1, so Algorithm 2 can be applied in real-time data sets. When some objects are added into a data set, we can use Algorithm 2 to update the reduct rather than compute the reduct by Algorithm 1 again on the new data set.
| Algorithm 2: Algorithm to update the reduct of a fuzzy -covering while adding some objects into the universe. |
 |
3.2. Matrix-Based Approach for Updating Reducts in Fuzzy -Coverings While Deleting Some Objects from the Universe
In this subsection, we present matrix-based dynamic approaches for updating the reduct in a fuzzy -covering while deleting some objects from the universe. We denote as a fuzzy -covering approximation space of U, where and . We denote as a fuzzy -covering approximation space of , where and .
The next theorem indicates the containing relation before and after deleting some objects from U.
Theorem 3.
Let be a fuzzy β-covering approximation space of U and let be a fuzzy β-covering approximation space of ; the following result holds.
Proof.
The proof is similar to that of Theorem 1. □
For any reducible element in , whether it is reducible or not can be decided by the next theorem.
Theorem 4.
Let be a fuzzy β-covering approximation space of U and let be a fuzzy β-covering approximation space of . If is a reducible element of , the following result holds.
Proof.
is reducible ⇔ ⇒ ⇔ is reducible. □
Example 5
(Continuation of Example 1). If and are deleted from U, the changes are as follows. According to Theorem 1, the new β-covering character matrix on is as follows:
By Definition 2, and are reducible. By Theorem 4, and are still reducible.
Theorem 5.
Let be a fuzzy β-covering approximation space of U and let be a fuzzy β-covering approximation space of . If the relation character matrix on U is denoted by and the relation character matrix on is denoted by , the following result holds.
Proof.
The proof is similar to that of Theorem 2. □
Example 6
(Continuation of Example 5). The containing relation character matrix on is as follows. By Theorem 5, for , , , , , and , the corresponding positions of still hold. For and , , . For and , , .
Using Theorems 3 and 5, we can propose Algorithm 3 for updating the reduct in a fuzzy -covering while deleting some objects from the universe. If , the total time complexity of Algorithm 3 is . Steps 2–9 are to update with time complexity , and Steps 11–17 are to compute with time complexity . Similarly, the time complexity of Algorithm 3 is smaller than the time complexity of Algorithm 1, so Algorithm 3 can be applied in real-time data sets. When some objects are deleted from a data set, we can use Algorithm 3 to update the reduct rather than compute the reduct by Algorithm 1 again on the new data set.
| Algorithm 3: Algorithm to update the reduct of a fuzzy -covering while deleting objects from the universe |
 |
4. Constructing Data Sets and Experiments
In this section, we construct some fuzzy -covering character matrices and run several experiments on them. The procedure of constructing the matrices is as follows: We construct some elements of a partial matrix; the elements of the partial matrix are randomly chosen from . The remaining elements can be obtained by randomly union of the element in the fuzzy -covering. Several experiments were conducted and the results are shown in Figure 1. We compared the computational time of Algorithm 1 (SA), 2 (IA) and 3 (DA) with different universe sizes, different covering sizes, and different reducible element percentages. All of the experiments were carried out on a personal computer with 64-bit Windows 10, Inter(R) Core(TM) i7 6700HQ CPU @2.60GHz, and 16GB memory. The programming language was Matlab r2015b.
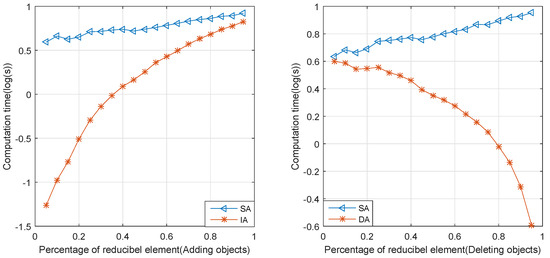
Figure 1.
Comparison of Algorithms 1–3 with different reducible percentages.
To compare the computation time of the three algorithms with different reducible percentages, we set the size of U to 500 and the size of covering to 1000. We conducted the test with different reducible percentage ranges from 0.05% to 0.95%, gradually increasing by a step of 0.05%.
In Figure 1, we can see that with the gradual increase in the reducible percentage, IA is more efficient with a lower reducible percentage, and DA is more efficient with a higher reducible percentage. The different performances with the same reducible percentage are caused by different searching strategies to find out which element of fuzzy -covering is reducible.
To compare the computational time of the three algorithms with different sizes of universe, we set the size of covering to 500 and the percentage of reducible element to 5%, 50%, and 95%, respectively. The size of the universe was increased gradually with a step of 500. The results of the experiments are shown in of Figure 2.
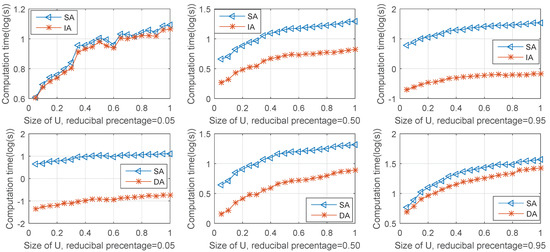
Figure 2.
Comparison of Algorithms 1–3 with different sizes of data sets.
In Figure 2, we can see that with the gradual increase in the size of the universe, the computational time of the three algorithms increases corresponding to the addition to the universe. IA and DA are more efficient than SA. IA is the most efficient with a reducible percentage of 95% DA is the most efficient with a reducible percentage of 0.05%; according to Figure 1, it is within the expected range.
To compare the computational time of the three algorithms with different sizes of fuzzy -covering, we set the size of universe to 500 and the percentage of reducible elements to 5%, 50%, and 95%, respectively. The size of the fuzzy -covering increases gradually with a step of 500. The results of experiments are shown in Figure 3.
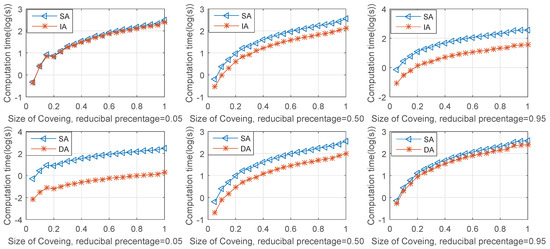
Figure 3.
Comparison of Algorithms 1–3 with different sizes of covering.
In Figure 3, we can see that with the gradual increase in the size of the covering, the computational time of the three algorithms increases. The computational time of IA and DA are less than that of SA, but IA has a great advantage when the size of the covering is small and IA has a great advantage when the size of the covering is big. In Figure 3, we can also observe that IA and DA are more efficient than SA, but have a difference with the variation of the covering size.
5. Conclusions
Variation of data sets induce variation of fuzzy -covering. In this paper, we investigate how to compute and update the reduct of a fuzzy -covering while the universe increases or decreases. Three algorithms have been proposed to ensure that the time complexity of the incremental algorithms is less than that of the static algorithm. Experimental results showed that the computation time of the incremental algorithms is less than that of the static algorithm, which shows that the incremental algorithms are more efficient than the static algorithm. Peiqiu Yu and Weikang Li helped perform the analysis with constructive discussions.
Computing the reduct is a virtual issue of fuzzy -covering. In the future, we will further investigate how to compute the reduct via an incremental approach.
Author Contributions
During the whole process of this work, individual contributions are as follows: conceptualization, J.H.; methodology, J.H.; software, J.H.; validation, J.H., W.L. and P.Y.; formal analysis, J.H.; investigation, J.H.; resources, J.H.; data curation, J.H.; writing—original draft preparation, J.H.; writing—review and editing, P.Y.; visualization, J.H.; supervision, P.Y.; project administration, J.H.; funding acquisition, J.H. All authors have read and agree to the published version of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China grant number 11871259.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pawlak, Z. Rough set. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Zakowski, W. Approximations in the space (u, π). Demonstr. Math. 1983, 16, 761–770. [Google Scholar] [CrossRef]
- Dai, J.; Wang, W.; Xu, Q.; Tian, H. Uncertainty measurement for interval-valued decision systems based on extended conditional entropy. Knowl.-Based Syst. 2012, 27, 443–450. [Google Scholar] [CrossRef]
- Degang, C.; Changzhong, W.; Qinghua, H. A new approach to attribute reduction of consistent and inconsistent covering decision systems with covering rough sets. Inf. Sci. 2007, 177, 3500–3518. [Google Scholar] [CrossRef]
- Li, F.; Yin, Y. Approaches to knowledge reduction of covering decision systems based on information theory. Inf. Sci. 2009, 179, 1694–1704. [Google Scholar] [CrossRef]
- Liu, G. Special types of coverings and axiomatization of rough sets based on partial orders. Knowl.-Based Syst. 2015, 85, 316–321. [Google Scholar] [CrossRef]
- Yao, Y.; Yao, B. Covering based rough set approximations. Inf. Sci. 2012, 200, 91–107. [Google Scholar] [CrossRef]
- Zhu, P. Covering rough sets based on neighborhoods: An approach without using neighborhoods. Int. J. Approx. Reason. 2011, 52, 461–472. [Google Scholar] [CrossRef]
- Zhu, W. Relationship among basic concepts in covering-based rough sets. Inf. Sci. 2009, 179, 2478–2486. [Google Scholar] [CrossRef]
- Dey, A.; Pradhan, R.; Pal, A.; Pal, T. A genetic algorithm for solving fuzzy shortest path problems with Interval type-2 fuzzy arc lengths. Malays. J. Comput. Sci. 2018, 31, 255–270. [Google Scholar] [CrossRef]
- Dey, A.; Pal, A.; Pal, T. Interval type 2 fuzzy set in fuzzy shortest path problem. Mathematics 2016, 4, 62. [Google Scholar] [CrossRef]
- Dey, A.; Son, L.; Kumar, P.; Selvachandran, G.; Quek, S. New concepts on vertex and edge coloring of simple vague graphs. Symmetry 2018, 10, 373. [Google Scholar] [CrossRef]
- Dey, A.; Pal, A.; Long, H.V.; Son, L. Fuzzy minimum spanning tree with interval type 2 fuzzy arc length: Formulation and a new genetic algorithm. Soft Compu. 2019. [Google Scholar] [CrossRef]
- Dey, A.; Pradhan, R.; Pal, A.; Pal, T. The fuzzy robust graph coloring problem. In Proceedings of the 3rd International Conference on Frontiers of Intelligent Computing: Theory and applications (FICTA) 2014, Odisha, India, 14–15 November 2014; Springer: New York, NY, USA, 2015; pp. 805–813. [Google Scholar]
- Li, T.; Leung, Y.; Zhang, W. Generalized fuzzy rough approximation operators based on fuzzy coverings. Int. J. Approx. Reason. 2008, 48, 836–856. [Google Scholar] [CrossRef]
- D’eer, L.; Cornelis, C.; Godo, L. Fuzzy neighborhood operators based on fuzzy coverings. Fuzzy Sets Syst. 2017, 312, 17–35. [Google Scholar] [CrossRef]
- Yang, B.; Hu, B.Q. On some types of fuzzy covering-based rough sets. Fuzzy Sets Syst. 2017, 312, 36–65. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X. Matrix approaches for some issues about minimal and maximal descriptions in covering-based rough sets. Int. J. Approx. Reason. 2019, 104, 126–143. [Google Scholar] [CrossRef]
- Lin, Z.Q.; Wang, J.Q.; Zhu, W. Computing minimal description and maximal description in covering-based rough sets through matrices. J. Shandong Univ. 2014, 49, 97–101. [Google Scholar]
- Ma, L. The investigation of covering rough sets by Boolean matrices. Int. J. Approx. Reason. 2018, 100, 69–84. [Google Scholar] [CrossRef]
- Lang, G.; Miao, D.; Cai, M.; Zhang, Z. Incremental approaches for updating reducts in dynamic covering information systems. Knowl. Based Syst. 2017, 134, 85–104. [Google Scholar] [CrossRef]
- Lang, G.; Cai, M.; Fujita, H.; Xiao, Q. Related families-based attribute reduction of dynamic covering decision information systems. Knowl. Based Syst. 2018, 162, 161–173. [Google Scholar] [CrossRef]
- Chen, H.; Li, T.; Qiao, S.; Ruan, D. A rough set based dynamic maintenance approach for approximations in coarsening and refining attribute values. J. Intell. Syst. 2010, 25, 1005–1026. [Google Scholar] [CrossRef]
- Cai, M.; Lang, G.; Fujita, H.; Li, Z.; Yang, T. Incremental approaches to updating reducts under dynamic covering granularity. Knowl. Based Syst. 2019, 172, 130–140. [Google Scholar] [CrossRef]
- Lang, G.; Miao, D.; Yang, T.; Cai, M. Knowledge reduction of dynamic covering decision information systems when varying covering cardinalities. Inf. Sci. 2016, 346, 236–260. [Google Scholar] [CrossRef]
- Balabanovic, M.; Shoham, Y. Content-Based, Collaborative Recommendation. Commun. ACM 1997, 40, 66–72. [Google Scholar] [CrossRef]
- Stai, E.; Kafetzoglou, S.; Tsiropoulou, E.E.; Papavassiliou, S. A holistic approach for personalization, relevance feedback & recommendation in enriched multimedia content. Multimed. Tools Appl. 2018, 77, 283–326. [Google Scholar]
- La Sen, M.D.; Roldan, A.; Agarwal, R.P. On contractive cyclic fuzzy maps in metric spaces and some related results on fuzzy best proximity points and fuzzy fixed points. Fixed Point Theory Appl. 2015, 2015, 103. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).