Importance Analysis of Components of a Multi-Operational-State Power System Using Fault Tree Models
Abstract
1. Introduction
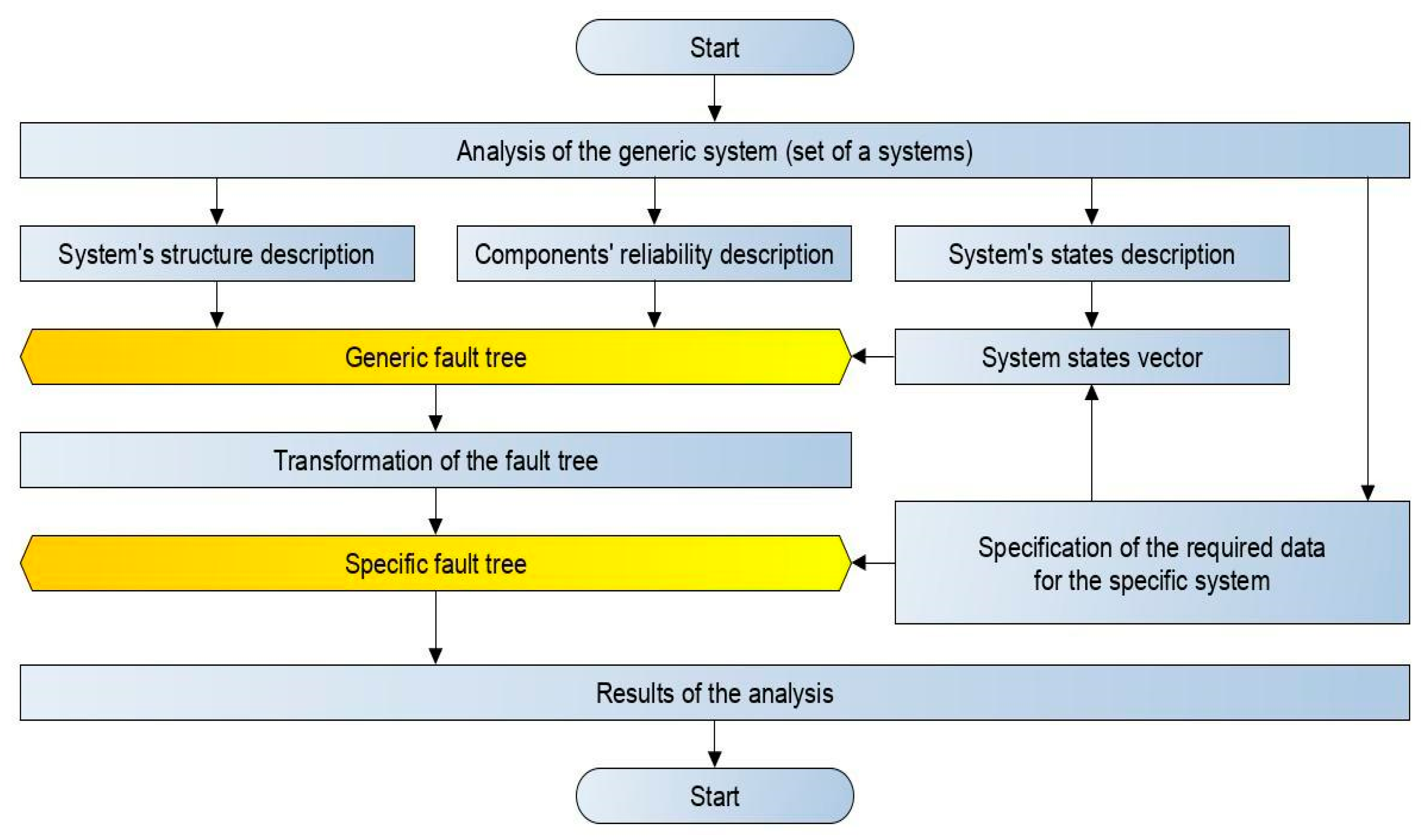
2. Materials and Methods
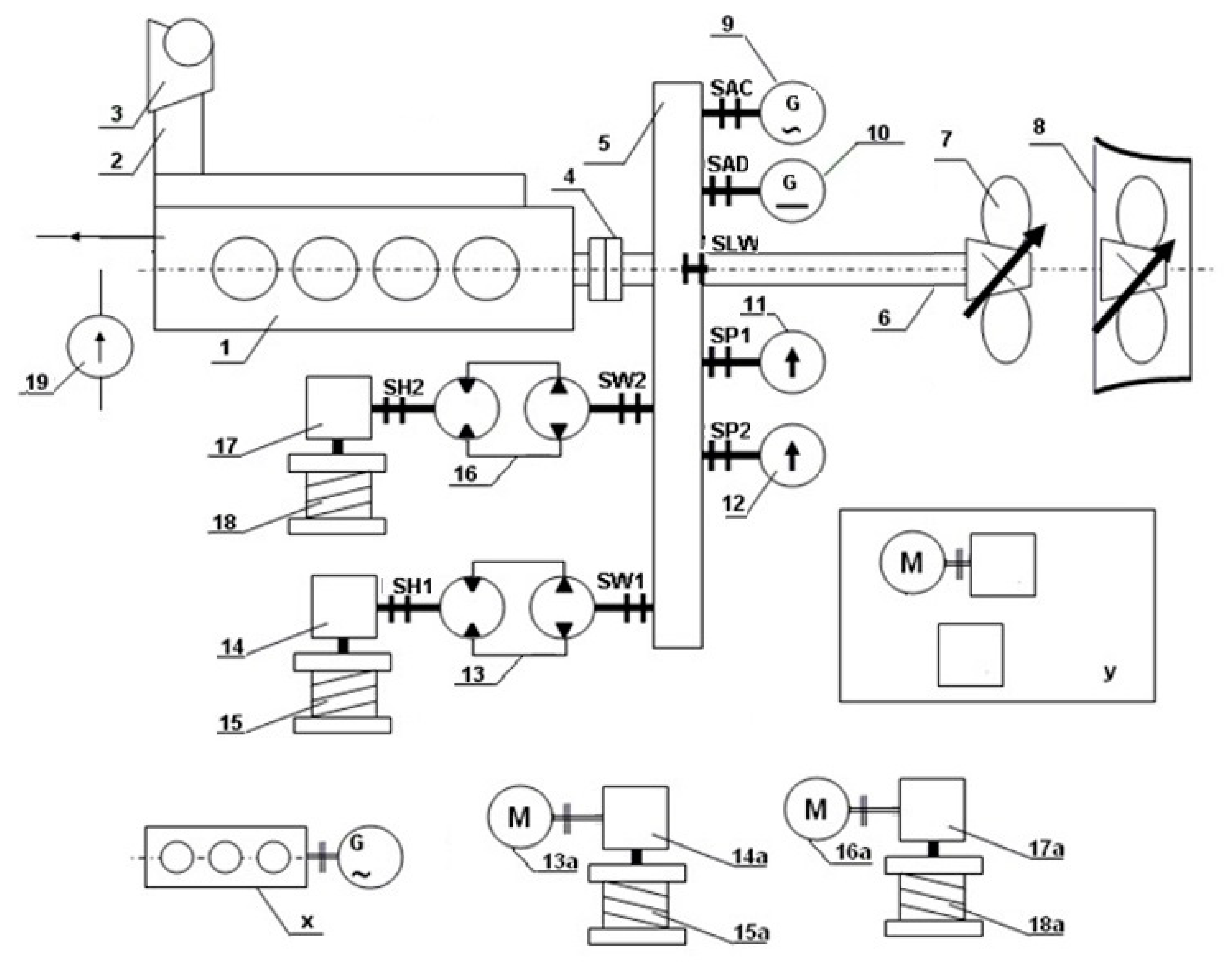
2.1. Object of Analysis
2.2. Modeling Operational State Changes in a System
- Condition w1—Does the propeller have a Kort nozzle?
- Condition w2a—Can the shaft be decoupled?
- Condition w2b—Is the shaft coupled with the engine?
- Condition w3a—Is an AC shaft generator installed?
- Condition w3b—Is the AC generator coupled?
- Condition w4a—Is the DC shaft generator installed?
- Condition w4b—Is the DC generator coupled?
- Condition w5a—Is the shaft pump no. 1 installed?
- Condition w5b—Is the pump no. 1 coupled?
- Condition w6a—Is the shaft pump no. 2 installed?
- Condition w6b—Is the pump no. 2 coupled?
- Condition w7a—Is the trawl winch driven by the main engine installed?
- Condition w7b—Is the trawl winch hydraulic pump coupled?
- Condition w7c—Is the trawl winch hydraulic motor coupled?
- Condition w8a—Is the net winch driven by SG installed?
- Condition w8b—Is the net winch hydraulic pump coupled?
- Condition w8c—Is the net winch hydraulic motor coupled?
- Condition w9—Is the electrical trawl winch installed?
- Condition w10—Is the electrical net winch installed?
2.3. Analysis of the Importance of Components
3. Results and Discussion
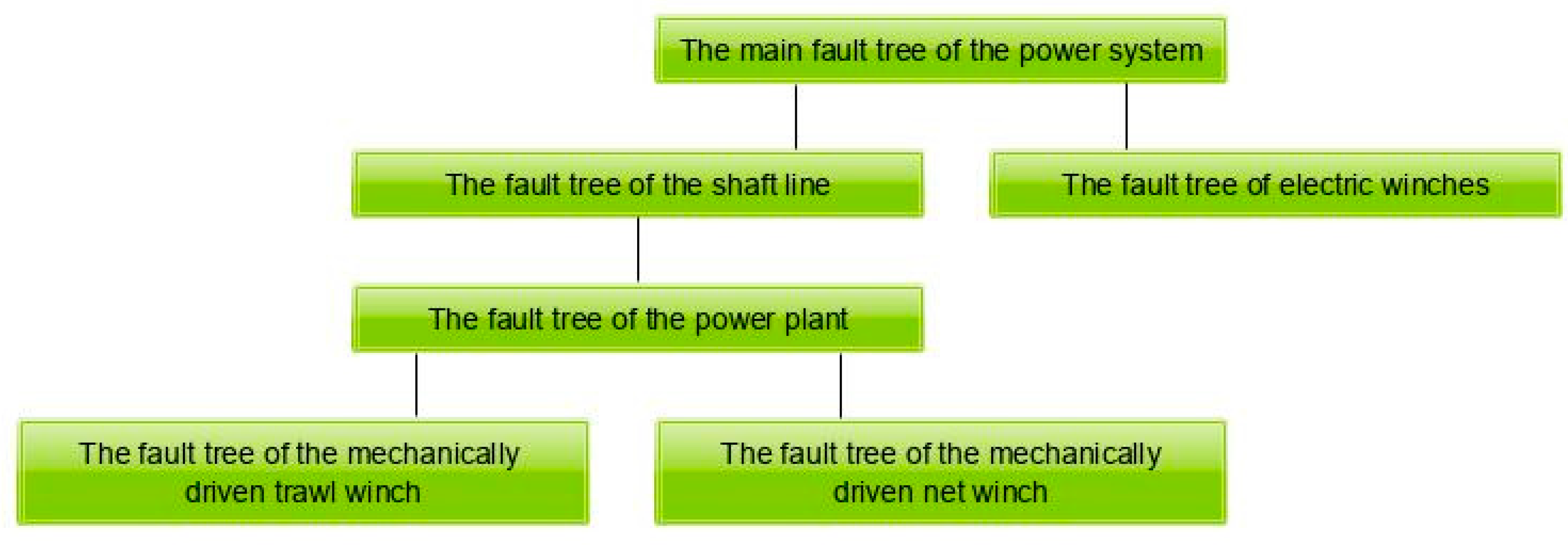
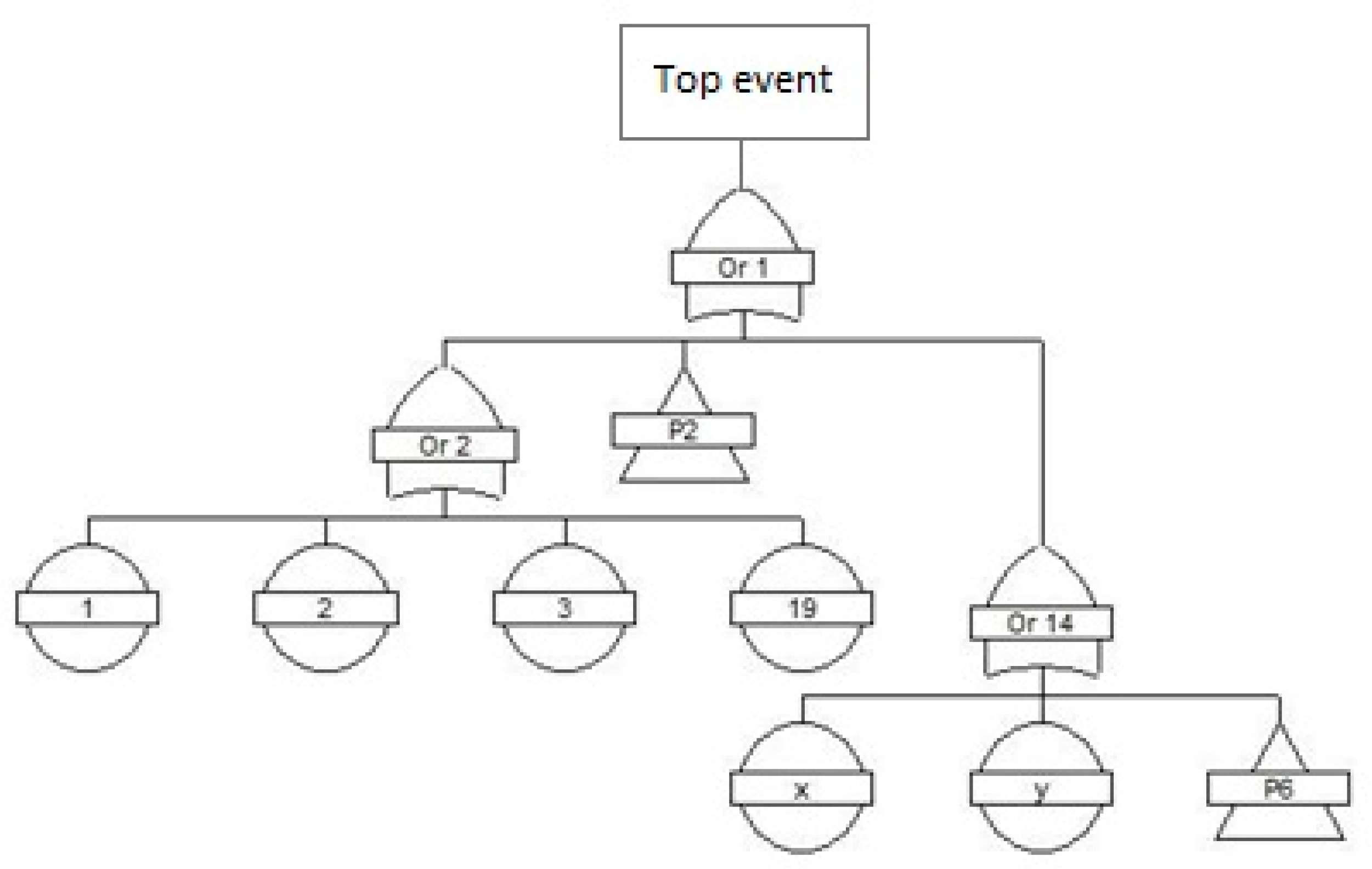
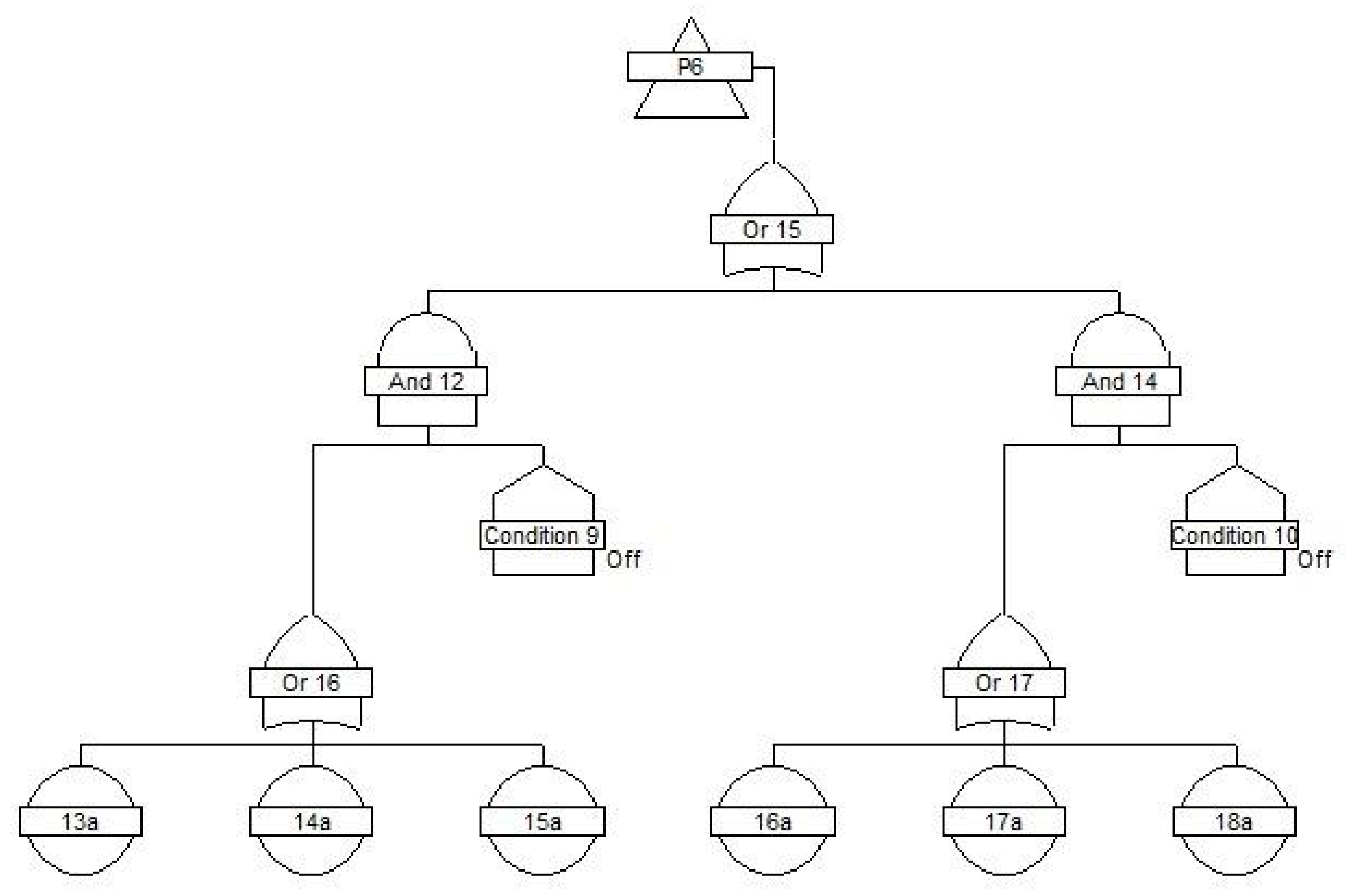
3.1. System Reliability Structure
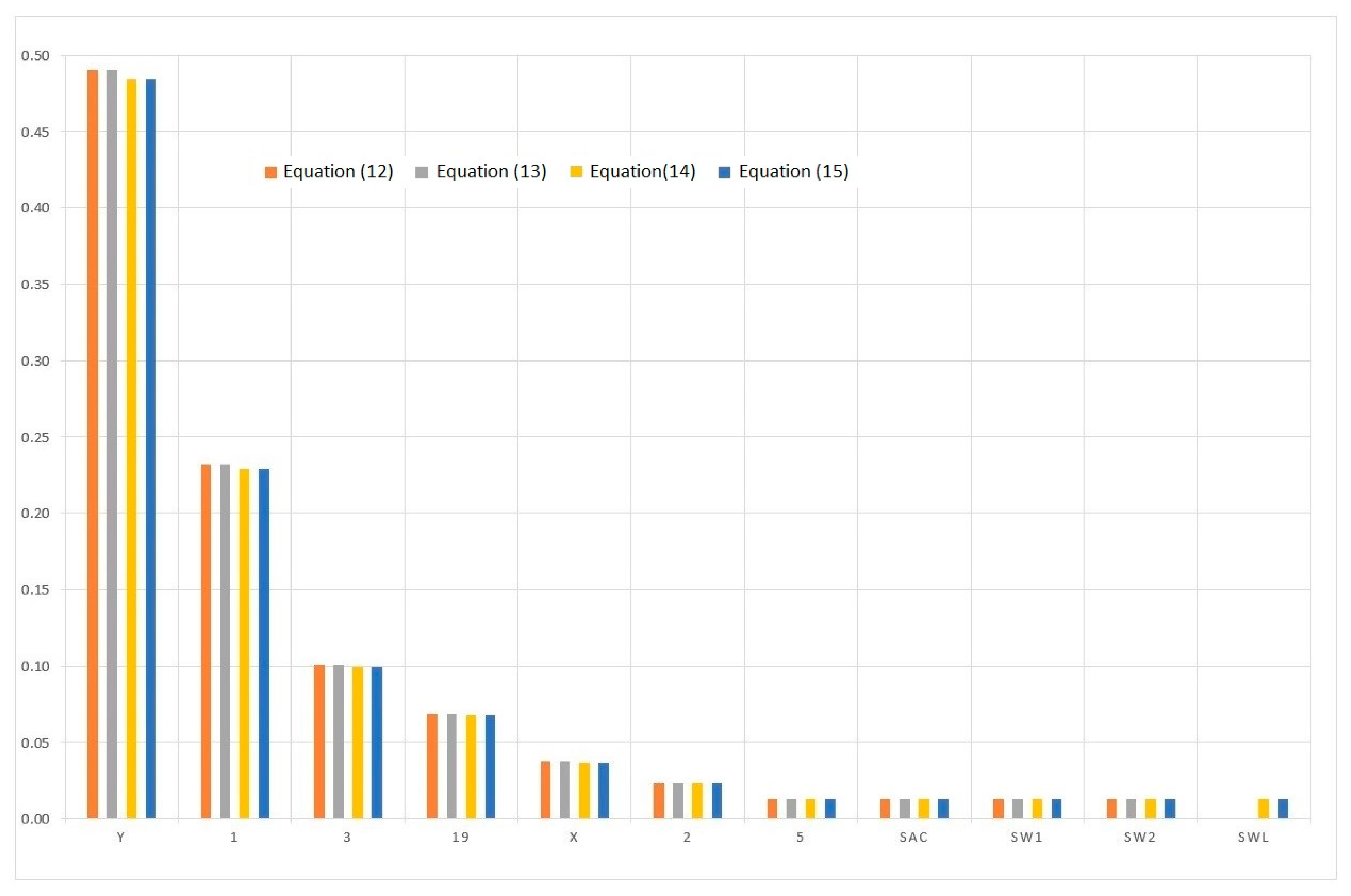
3.2. System Components Importance during Sea Voyage
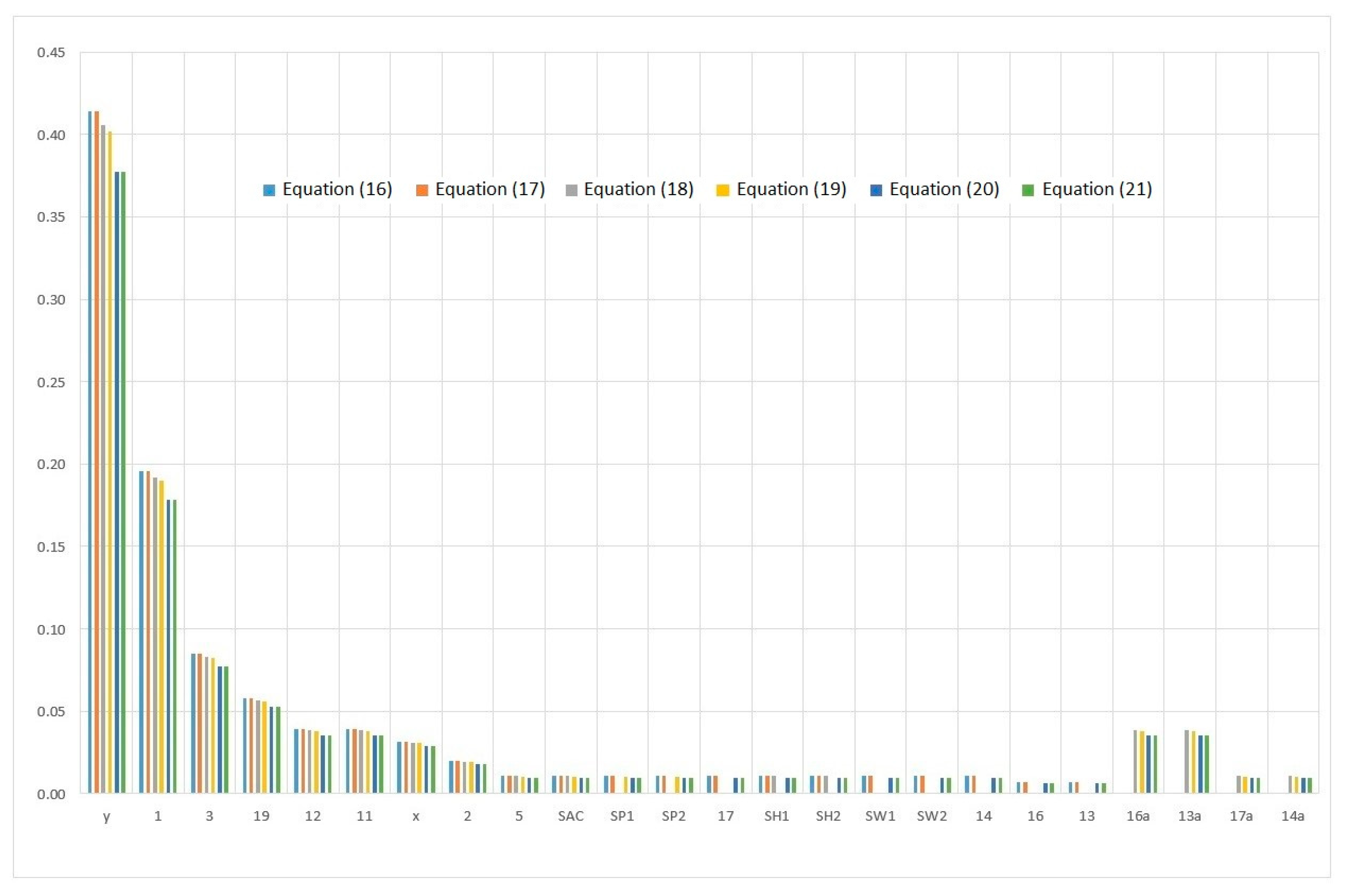
3.3. System Components Importance during Paying out and Hauling in Nets
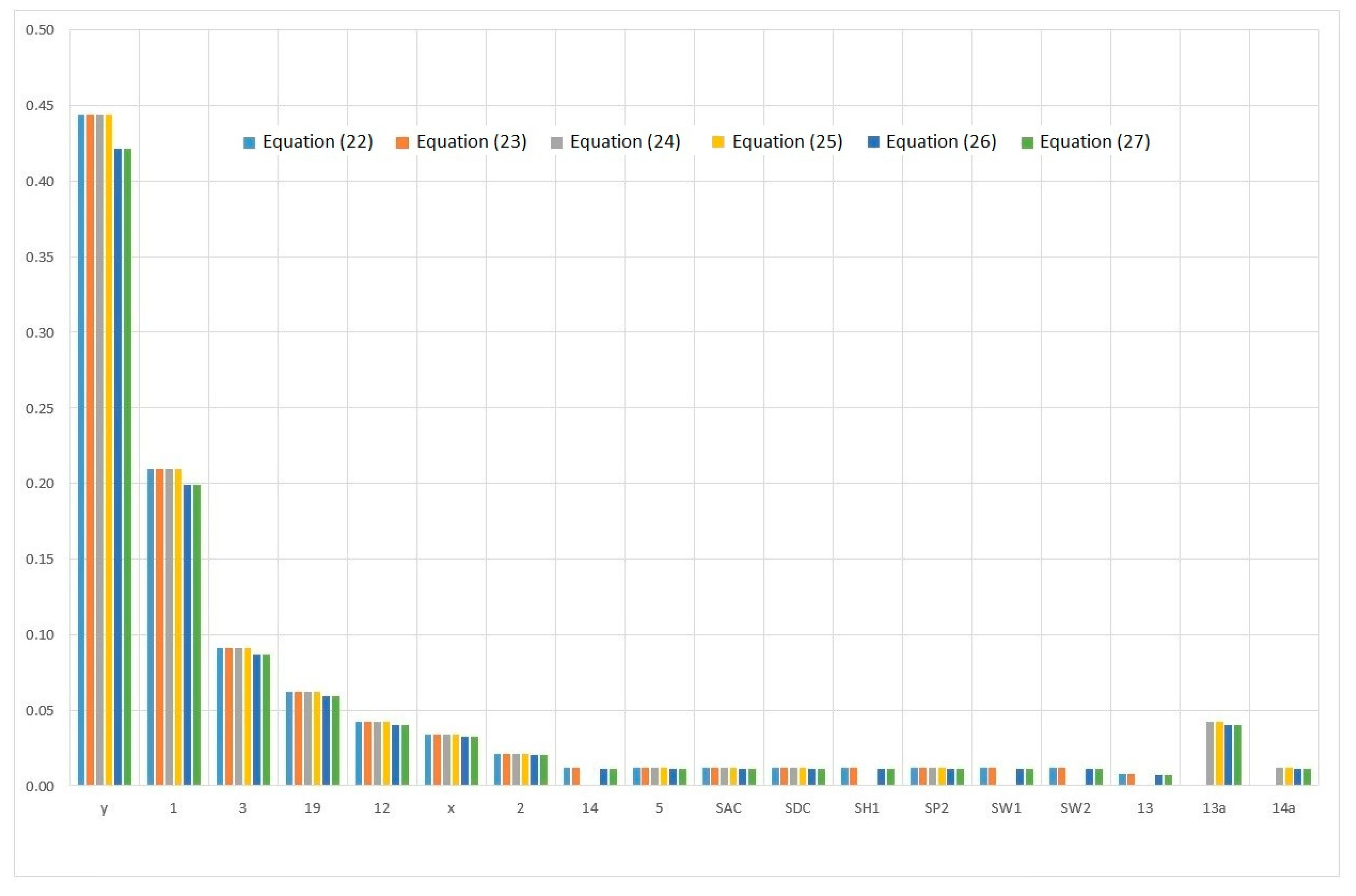
3.4. System Components Importance during Trawling
3.5. System Components Importance during Fishing, When Heaved To, or Staying in a Port
3.6. Quantitative Analysis
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Chybowski, L. Analiza drzewa niezdatności. Podstawy teoretyczne i zastosowania; Wyd. Nauk. Akademii Morskiej w Szczecinie: Szczecin, Radom, 2017; ISBN 978-83-64434-12-9. [Google Scholar]
- Chybowski, L.; Gawdzińska, K.; Ślesicki, O.; Patejuk, K.; Nowosad, G. An engine room simulator as an educational tool for marine engineers relating to explosion and fire prevention of marine diesel engines. Sci. J. Marit. Univ. Szczecin, Zesz. Nauk. Akad. Morskiej w Szczecinie 2016, 43, 15–21. [Google Scholar]
- Chybowski, L.; Twardochleb, M.; Wiśnicki, B. Multi-criteria Decision making in Components Importance Analysis applied to a Complex Marine System. Nase More 2016, 63, 264–270. [Google Scholar] [CrossRef]
- Kim, M.C. Reliability block diagram with general gates and its application to system reliability analysis. Ann. Nucl. Energy 2011, 38, 2456–2461. [Google Scholar] [CrossRef]
- Sharma, G.; Rai, R.N. Reliability modeling and analysis of environmental control and life support systems of space stations: A literature survey. Acta Astronaut. 2019, 155, 238–246. [Google Scholar] [CrossRef]
- Gawdzińska, K.; Chybowski, L.; Przetakiewicz, W.; Laskowski, R. Application of FMEA in the Quality Estimation of Metal Matrix Composite Castings Produced by Squeeze Infiltration. Arch. Metall. Mater. 2017, 62, 2171–2182. [Google Scholar] [CrossRef]
- Chybowski, L. Qualitative and quantitative multi-criteria models of the importance of the components in reliability structure of a complex technical system. J. Konbin 2012, 24, 33–48. [Google Scholar] [CrossRef]
- Gil, M.; Wróbel, K.; Montewka, J. Toward a Method Evaluating Control Actions in STPA-Based Model of Ship-Ship Collision Avoidance Process. J. Offshore Mech. Arct. Eng. 2019, 141, 051105. [Google Scholar] [CrossRef]
- Wróbel, K.; Montewka, J.; Kujala, P. Towards the development of a system-theoretic model for safety assessment of autonomous merchant vessels. Reliab. Eng. Syst. Saf. 2018, 178, 209–224. [Google Scholar] [CrossRef]
- Goerlandt, F.; Montewka, J. A Bayesian network model for accidental oil outflow in double hull oil product tanker collisions. In Proceedings of the PSAM 2014—Probabilistic Safety Assessment and Management, Honolulu, HI, USA, 22–27 June 2014; pp. 1–11. [Google Scholar]
- Goerlandt, F.; Montewka, J. A framework for risk analysis of maritime transportation systems: A case study for oil spill from tankers in a ship-ship collision. Saf. Sci. 2015, 76, 42–66. [Google Scholar] [CrossRef]
- Shafiee, M.; Enjema, E.; Kolios, A. An Integrated FTA-FMEA Model for Risk Analysis of Engineering Systems: A Case Study of Subsea Blowout Preventers. Appl. Sci. 2019, 9, 1192. [Google Scholar] [CrossRef]
- Gucma, L.; Schoeneich, M. Monte carlo method of ship’s underkeel clearance evaluation for safety of ferry approaching to ystad port determination. J. Konbin 2008, 8, 35–44. [Google Scholar] [CrossRef]
- Chybowski, L.; Gawdzińska, K. A stochastic simulation-based component importance analysis for complex technical systems. Probl. Eksploat. Maint. Probl. J. Mach. Constr. Maint. 2017, 17, 47–50. [Google Scholar]
- Ratajczak, M.; Ptak, M.; Chybowski, L.; Gawdzińska, K.; Będziński, R. Material and Structural Modeling Aspects of Brain Tissue Deformation under Dynamic Loads. Materials 2019, 12, 271. [Google Scholar] [CrossRef] [PubMed]
- Girtler, J. The semi-Markov model of the process of appearance of sea-going ship propupsion system ability and inability states in application to determining the reliablity of these systems. Polish Marit. Res. 2013, 20, 18–24. [Google Scholar] [CrossRef]
- Girtler, J. Issue of making decisions with regard to ship traffic safety in different situations at sea. In Marine Navigation and Safety of Sea Transportation: Navigational Problems; Adam, W., Ed.; CRC Press: Boca Raton, FL, USA, 2013; pp. 63–70. [Google Scholar]
- Girtler, J. Application of theory of semi-Markov processes to determining distribution of probabilistic process of marine accidents resulting from collision of ships. Polish Marit. Res. 2014, 1, 9–13. [Google Scholar] [CrossRef]
- Gucma, S.; Ślączka, W. Comprehensive method of formal safety assessment of ship manoeuvring in waterways. Sci. J. Marit. Univ. Szczecin, Zesz. Nauk. Akad. Morskiej w Szczecinie 2018, 54, 110–119. [Google Scholar]
- Gucma, L.; Pietrzykowski, Z. Ship manoeuvring in restricted areas: An attempt to quantify dangerous situations using a probabilistic-fuzzy method. J. Navig. 2006, 59, 251–262. [Google Scholar] [CrossRef]
- Tanaka, H.; Fan, L.T.; Lai, F.S.; Toguchi, K. Fault-Tree Analysis by Fuzzy Probability. IEEE Trans. Reliab. 1983, R-32, 453–457. [Google Scholar] [CrossRef]
- Markowski, A.S.; Mannan, M.S.; Bigoszewska, A. Fuzzy logic for process safety analysis. J. Loss Prev. Process Ind. 2009, 22, 695–702. [Google Scholar] [CrossRef]
- Alves, G.; Marques, D.; Silva, I.; Guedes, L.A.; da Silva, M.d.G. A Methodology for Dependability Evaluation of Smart Grids. Energies 2019, 12, 1817. [Google Scholar] [CrossRef]
- Chybowski, L.; Grzadziel, Z.; Gawdzinska, K. Simulation and experimental studies of a multi-tubular floating sea wave damper. Energies 2018, 11, 1012. [Google Scholar] [CrossRef]
- Nozdrzykowski, K.; Chybowski, L. A Force-Sensor-Based Method to Eliminate Deformation of Large Crankshafts during Measurements of Their Geometric Condition. Sensors 2019, 19, 3507. [Google Scholar] [CrossRef] [PubMed]
- Chybowski, L.; Laskowski, R.; Gawdzińska, K. An overview of systems supplying water into the combustion chamber of diesel engines to decrease the amount of nitrogen oxides in exhaust gas. J. Mar. Sci. Technol. 2015, 20, 393–405. [Google Scholar] [CrossRef]
- Chybowski, L. Ważność elementów w strukturze złożonych systemów technicznych; Wyd. Nauk. Instytutu Technologii Eksploatacji-PIB: Szczecin, Radom, 2014; ISBN 978-83-7789-309-8. [Google Scholar]
- Chybowski, L.; Matuszak, Z. Marine Auxuliary Diesel Engine Turbocharger Damage (Explosion) Cause Analysis. J. Polish CIMAC 2007, 2, 33–40. [Google Scholar]
- Vesely, W.E. A time-dependent methodology for fault tree evaluation. Nucl. Eng. Des. 1970, 13, 337–360. [Google Scholar] [CrossRef]
- Chiacchio, F.; Aizpurua, J.I.; Compagno, L.; Khodayee, S.M.; D’Urso, D. Modelling and Resolution of Dynamic Reliability Problems by the Coupling of Simulink and the Stochastic Hybrid Fault Tree Object Oriented (SHyFTOO) Library. Information 2019, 10, 283. [Google Scholar] [CrossRef]
- Xu, H.; Dugan, J.B. Combining dynamic fault trees and event trees for probabilistic risk assessment. In Proceedings of the Proceedings of the Annual Reliability and Maintainability Symposium, Los Angeles, CA, USA, 26–29 January 2004; pp. 214–219. [Google Scholar]
- Chybowski, L. Assessment of Reliability and Availability of Fishing Vessels Power, Propulsion and Technological Plants Based on Fault Tree Analysis. Polish J. Environ. Stud. 2009, 18, 39–44. [Google Scholar]
- Wu, Y.-C.; Laiwang, B.; Shu, C.-M. Investigation of an Explosion at a Styrene Plant with Alkylation Reactor Feed Furnace. Appl. Sci. 2019, 9, 503. [Google Scholar] [CrossRef]
- Tchórzewska-Cieślak, B.; Pietrucha-Urbanik, K.; Papciak, D. An Approach to Estimating Water Quality Changes in Water Distribution Systems Using Fault Tree Analysis. Resources 2019, 8, 162. [Google Scholar] [CrossRef]
- Chybowski, L. Application of External Events Vectors for Defining Reliability Structure of Fishing Vessels Power, Propulsion and Technological Plants. Polish J. Environ. Stud. 2009, 18, 45–50. [Google Scholar]
- Vesely, W.; Stamatelatos, M.; Dugan, J.; Fragola, J.; Minarick, J.I.; Railsback, J. Fault Tree Handbook with Aerospace Applications; NASA: Washington, DC, USA, 2002. [Google Scholar]
- Woropay, M. Metoda Budowy Wielopoziomowych Systemów do Badania Niezawodności Elementów o Wyznaczonej a Priori Istotności; ATR: Bydgoszcz, Poland, 1983. [Google Scholar]
- Kuo, W.; Zhu, X. Importance measures in reliability, risk and optimization. In Principles and Applications; John Wiley & Sons, Ltd.: New York, NY, USA, 2012. [Google Scholar]
- Chybowski, L.; Gawdzińska, K. On the Possibilities of Applying the AHP Method to a Multi-criteria Component Importance Analysis of Complex Technical Objects. Adv. Intell. Syst. Comput. 2016, 445, 701–710. [Google Scholar]
- Chybowski, L.; Matuszak, Z. Methodology of Fishing Vessels Power Plant Systems Reliability and Availability Evaluation; Report OR 16-61535-OR 1600006/06; Maritime University of Szczecin: Szczecin, Poland, 2008. [Google Scholar]
- Duda-Gwiazda, J. Reliability of Marine Diesel Power Plants; Report RT-95/T-01; Centrum Techniki Okrętowej: Gdańst, Poland, 1995. [Google Scholar]
- Natvig, B. New light on measures of importance of system components. Scand. J. Stat. 1985, 12, 43–54. [Google Scholar]
- Gnedenko, B.V.; Belyayev, Y.K.; Solovyev, A.D. Mathematical Methods of Reliability Theory; Elsevier/Academic Press: Cambridge, MA, USA, 1969; ISBN 9781483230535. [Google Scholar]
- Fussell, J.B. How to Hand-Calculate System Reliability and Safety Characteristics. IEEE Trans. Reliab. 1975, 24, 169–174. [Google Scholar] [CrossRef]
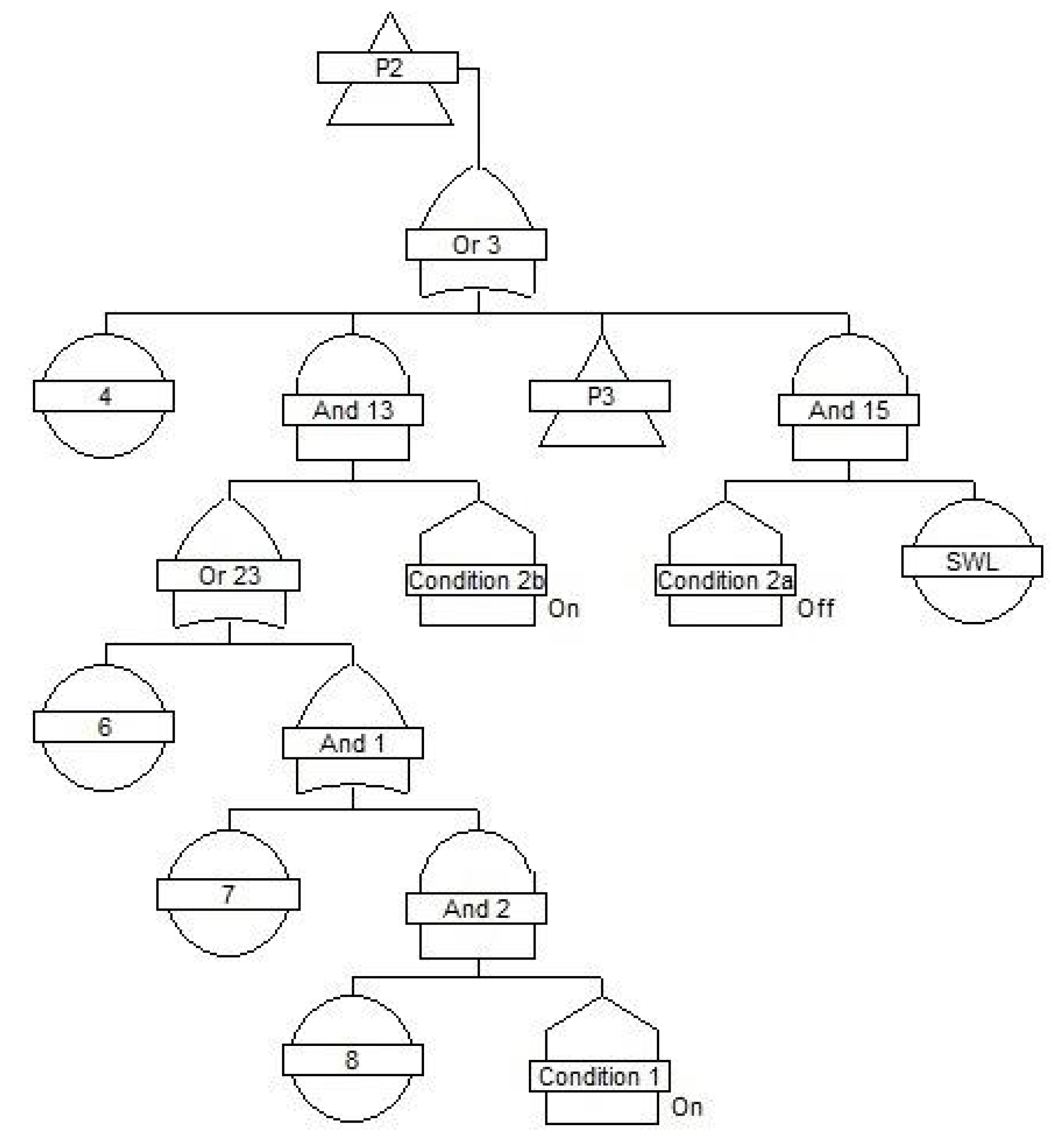
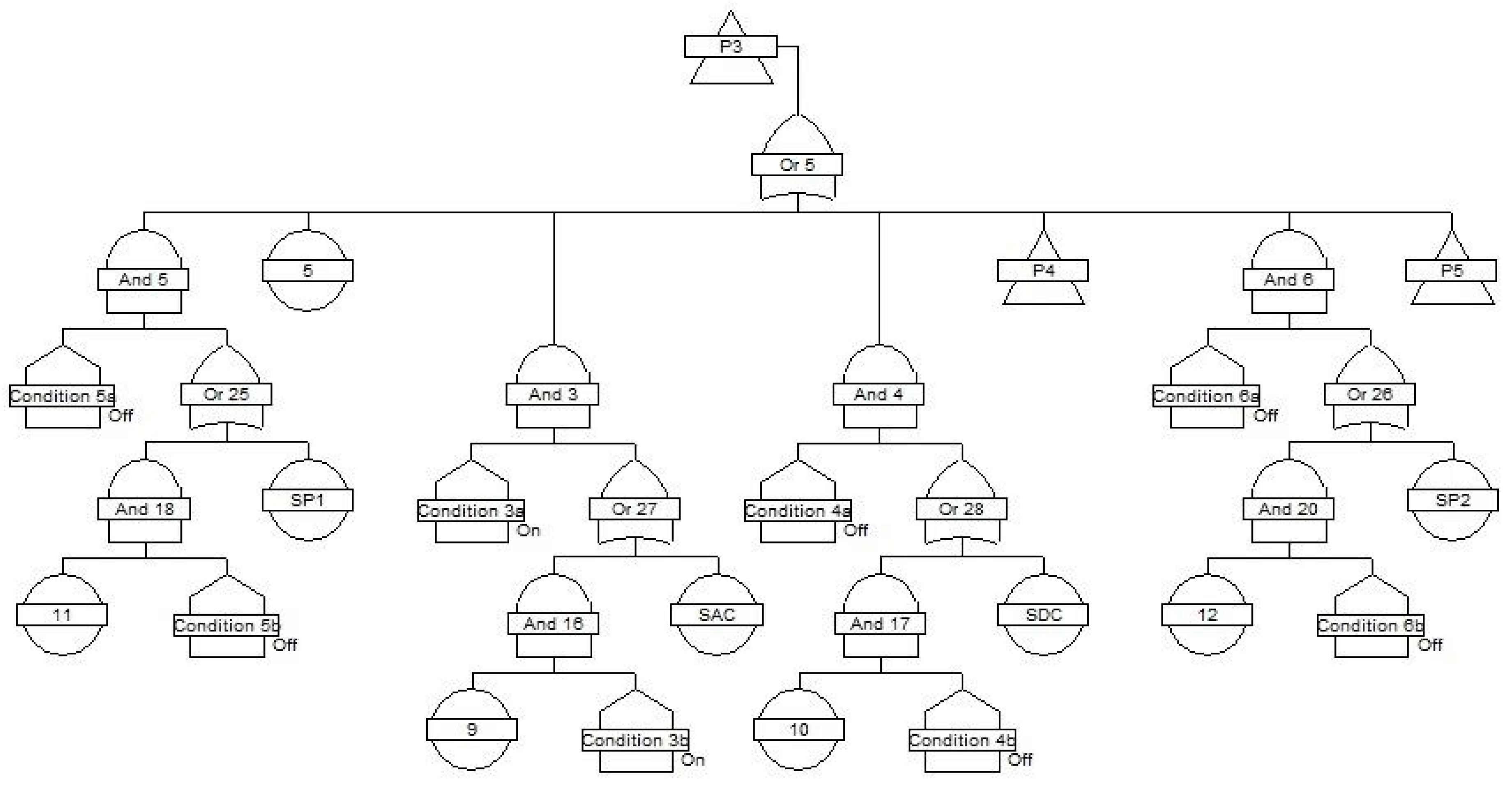
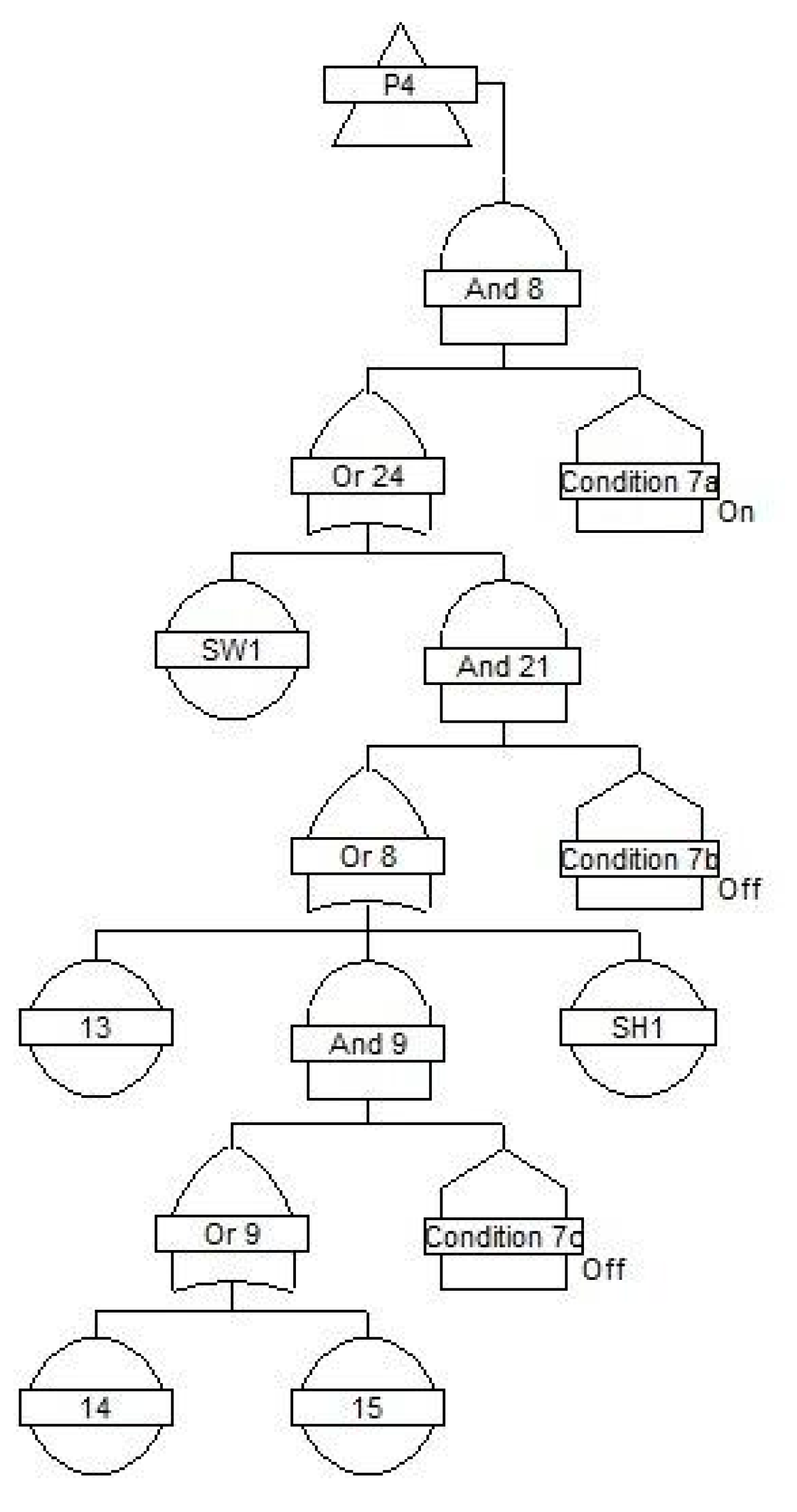
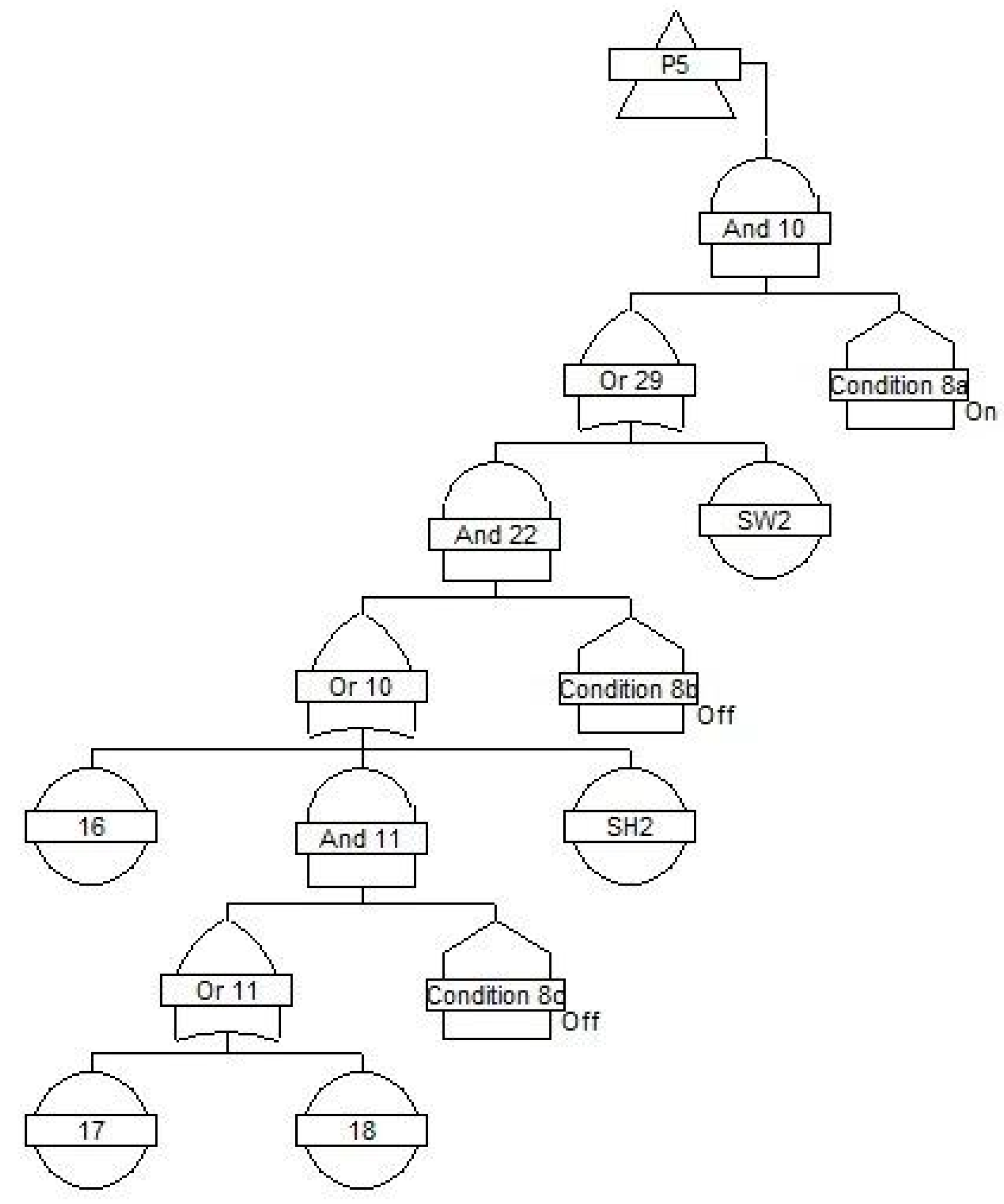
| Symbol | Type of Fault | Availability a [-] | Failure Rate λ [10−6 h] |
|---|---|---|---|
| 1 | Fault of a main propulsion engine and auxiliary systems supporting its operation | 0.995907 | 0.0575 |
| 2 | The fault of an exhaust manifold of the main propulsion engine | 0.999586 | 0.0082 |
| 3 | The fault of the charge exchange system (supercharging air filter, supercharging air cooler, turbocharger) | 0.998221 | 0.0418 |
| 4 | The fault of the countershaft coupling to the engine (coupling locked) | 0.999997 | 0.00033 |
| 5 | The fault of the transmission | 0.999773 | 0.00429 |
| 6 | The fault of line shafting (countershaft and propeller shaft, stern bush bearing and seal); | 0.999983 | 0.00291 |
| 7 | The fault of the screw propeller | 0.999997 | 0.00033 |
| 8 | The fault of the screw propeller nozzle | 0.999999 | 0.00002 |
| 9 | The fault of the alternating current (AC) shaft generator | 0.999972 | 0.00044 |
| 10 | The fault of the direct-current (DC) shaft generator | 0.999972 | 0.00044 |
| 11 | The fault of the pump no. 1 driven by the main propulsion engine through a transmission | 0.999181 | 0.01769 |
| 12 | The fault of the pump no. 2 driven by the main propulsion engine through a transmission | 0.999181 | 0.01769 |
| 13 | The fault of the hydraulic drive system (pump—engine) of the trawl winch driven by the main propulsion engine through the transmission; | 0.999851 | 0.00882 |
| 14 | The fault of the transmission of the trawl winch driven by the main engine | 0.999773 | 0.00429 |
| 15 | The fault of the head of the trawl winch driven by the main engine | 0.999993 | 0.00111 |
| 16 | The fault of the hydraulic drive system (pump—engine) of the net winch driven by the main propulsion engine through the transmission; | 0.999851 | 0.00882 |
| 17 | The fault of the transmission of the net winch driven by the main engine | 0.999773 | 0.00429 |
| 18 | The fault of the head of the net winch driven by the main engine | 0.999993 | 0.00111 |
| 13a | The fault of the electric motor of the trawl winch | 0.999181 | 0.01749 |
| 14a | The fault of the transmission of the trawl winch driven by the main engine | 0.999773 | 0.00429 |
| 15a | The fault of the head of the trawl winch driven by the main engine | 0.999993 | 0.00111 |
| 16a | The fault of the electric motor of the net winch | 0.999181 | 0.01749 |
| 17a | The fault of the transmission of the net winch driven by the main engine | 0.999773 | 0.00429 |
| 18a | The fault of the head of the net winch driven by the main engine | 0.999993 | 0.00111 |
| 19 | The fault of the seawater pump and its system | 0.998787 | 0.02975 |
| SAC | The fault of the disengaging coupling of the AC shaft generator | 0.999773 | 0.00429 |
| SDC | The fault of the disengaging coupling of the DC shaft generator | 0.999773 | 0.00429 |
| SP1 | The fault of the disengaging coupling of the shaft pump no. 1 | 0.999773 | 0.00429 |
| SP2 | The fault of the disengaging coupling of the shaft pump no. 2 | 0.999773 | 0.00429 |
| SW1 | The fault of the disengaging coupling of the hydraulic pump of the trawl winch drive | 0.999773 | 0.00429 |
| SW2 | The fault of the disengaging coupling of the hydraulic pump of the net winch | 0.999773 | 0.00429 |
| SH1 | The fault of the disengaging coupling of the hydraulic motor of the trawl winch drive | 0.999773 | 0.00429 |
| SH2 | The fault of the disengaging coupling of the hydraulic motor of the net winch drive | 0.999773 | 0.00429 |
| SWL | The fault of the disengaging coupling of the ship’s driveshaft | 0.999773 | 0.00429 |
| x | The fault of the ancillary electrical and power unit | 0.999339 | 0.01817 |
| y | The fault of other current-using equipment | 0.991335 | 0.19519 |
| Component | External Events Vector | |||||
|---|---|---|---|---|---|---|
| Equation (12) | Equation (13) | Equation (14) | Equation (15) | Equation (16) | Equation (17) | |
| 1 | 0.23157 | 0.23157 | 0.22869 | 0.22869 | 0.19562 | 0.19562 |
| 2 | 0.02342 | 0.02342 | 0.02313 | 0.02313 | 0.01979 | 0.01979 |
| 3 | 0.10065 | 0.10065 | 0.09940 | 0.09940 | 0.08502 | 0.08502 |
| 4 | 0.00017 | 0.00017 | 0.00017 | 0.00017 | 0.00014 | 0.00014 |
| 5 | 0.01284 | 0.01284 | 0.01268 | 0.01268 | 0.01085 | 0.01085 |
| 6 | 0.00096 | 0.00096 | 0.00095 | 0.00095 | 0.00081 | 0.00081 |
| 7 | 0.00017 | 0.00017 | 0.00017 | 0.00017 | 0.00014 | 0.00014 |
| 8 | 0.00000 | - | 0.00000 | - | 0.00000 | - |
| 9 | 0.00158 | 0.00158 | 0.00156 | 0.00156 | 0.00134 | 0.00134 |
| 10 | - | - | - | - | - | - |
| 11 | - | - | - | - | 0.03914 | 0.03914 |
| 12 | - | - | - | - | 0.03914 | 0.03914 |
| 13 | - | - | - | - | 0.00712 | 0.00712 |
| 14 | - | - | - | - | 0.01085 | 0.01085 |
| 15 | - | - | - | - | 0.00033 | 0.00033 |
| 16 | - | - | - | - | 0.00712 | 0.00712 |
| 17 | - | - | - | - | 0.01085 | 0.01085 |
| 18 | - | - | - | - | 0.00033 | 0.00033 |
| 19 | 0.06863 | 0.06863 | 0.06777 | 0.06777 | 0.05797 | 0.05797 |
| 13a | - | - | - | - | - | - |
| 14a | - | - | - | - | - | - |
| 15a | - | - | - | - | - | - |
| 16a | - | - | - | - | - | - |
| 17a | - | - | - | - | - | - |
| 18a | - | - | - | - | - | - |
| SAC | 0.01284 | 0.01284 | 0.01268 | 0.01268 | 0.01085 | 0.01085 |
| SDC | - | - | - | - | - | - |
| SH1 | - | - | - | - | 0.01085 | 0.01085 |
| SH2 | - | - | - | - | 0.01085 | 0.01085 |
| SP1 | - | - | - | - | 0.01085 | 0.01085 |
| SP2 | - | - | - | - | 0.01085 | 0.01085 |
| SW1 | 0.01284 | 0.01284 | 0.01268 | 0.01268 | 0.01085 | 0.01085 |
| SW2 | 0.01284 | 0.01284 | 0.01268 | 0.01268 | 0.01085 | 0.01085 |
| SWL | 0.00000 | 0.00000 | 0.01268 | 0.01268 | - | - |
| x | 0.03740 | 0.03740 | 0.03693 | 0.03693 | 0.03159 | 0.03159 |
| y | 0.49025 | 0.49025 | 0.48414 | 0.48414 | 0.41412 | 0.41412 |
| Component | External Events Vector | |||||
|---|---|---|---|---|---|---|
| Equation (18) | Equation (19) | Equation (20) | Equation (21) | Equation (22) | Equation (23) | |
| 1 | 0.19174 | 0.18976 | 0.17808 | 0.17808 | 0.20965 | 0.20965 |
| 2 | 0.01939 | 0.01919 | 0.01801 | 0.01801 | 0.02121 | 0.02121 |
| 3 | 0.08334 | 0.08248 | 0.07740 | 0.07740 | 0.09112 | 0.09112 |
| 4 | 0.00014 | 0.00014 | 0.00013 | 0.00013 | 0.00015 | 0.00015 |
| 5 | 0.01063 | 0.01052 | 0.00988 | 0.00988 | 0.01163 | 0.01163 |
| 6 | 0.00080 | 0.00079 | 0.00074 | 0.00074 | 0.00087 | 0.00087 |
| 7 | 0.00014 | 0.00014 | 0.00013 | 0.00013 | 0.00015 | 0.00015 |
| 8 | 0.00000 | - | 0.00000 | - | 0.00000 | - |
| 9 | 0.00131 | 0.00130 | 0.00122 | 0.00122 | 0.00143 | 0.00143 |
| 10 | - | - | - | - | - | - |
| 11 | 0.03837 | 0.03797 | 0.03563 | 0.03563 | - | - |
| 12 | 0.03837 | 0.03797 | 0.03563 | 0.03563 | 0.04195 | 0.04195 |
| 13 | - | - | 0.00648 | 0.00648 | 0.00763 | 0.00763 |
| 14 | - | - | 0.00988 | 0.00988 | 0.01163 | 0.01163 |
| 15 | - | - | 0.00030 | 0.00030 | 0.00036 | 0.00036 |
| 16 | - | - | 0.00648 | 0.00648 | - | - |
| 17 | - | - | 0.00988 | 0.00988 | - | - |
| 18 | - | - | 0.00030 | 0.00030 | - | - |
| 19 | 0.05682 | 0.05624 | 0.05278 | 0.05278 | 0.06213 | 0.06213 |
| 13a | 0.03837 | 0.03797 | 0.03563 | 0.03563 | - | - |
| 14a | 0.01063 | 0.01052 | 0.00988 | 0.00988 | - | - |
| 15a | 0.00033 | 0.00032 | 0.00030 | 0.00030 | - | - |
| 16a | 0.03837 | 0.03797 | 0.03563 | 0.03563 | - | - |
| 17a | 0.01063 | 0.01052 | 0.00988 | 0.00988 | - | - |
| 18a | 0.00033 | 0.00032 | 0.00030 | 0.00030 | - | - |
| SAC | 0.01063 | 0.01052 | 0.00988 | 0.00988 | 0.01163 | 0.01163 |
| SDC | - | - | - | - | 0.01163 | 0.01163 |
| SH1 | 0.01063 | - | 0.00988 | 0.00988 | 0.01163 | 0.01163 |
| SH2 | 0.01063 | - | 0.00988 | 0.00988 | - | - |
| SP1 | - | 0.01052 | 0.00988 | 0.00988 | - | - |
| SP2 | - | 0.01052 | 0.00988 | 0.00988 | 0.01163 | 0.01163 |
| SW1 | - | - | 0.00988 | 0.00988 | 0.01163 | 0.01163 |
| SW2 | - | - | 0.00988 | 0.00988 | 0.01163 | 0.01163 |
| SWL | - | - | - | - | - | - |
| x | 0.03096 | 0.03065 | 0.02876 | 0.02876 | 0.03386 | 0.03386 |
| y | 0.40591 | 0.40173 | 0.37700 | 0.37700 | 0.44383 | 0.44383 |
| Component | External Events Vector | |||||
|---|---|---|---|---|---|---|
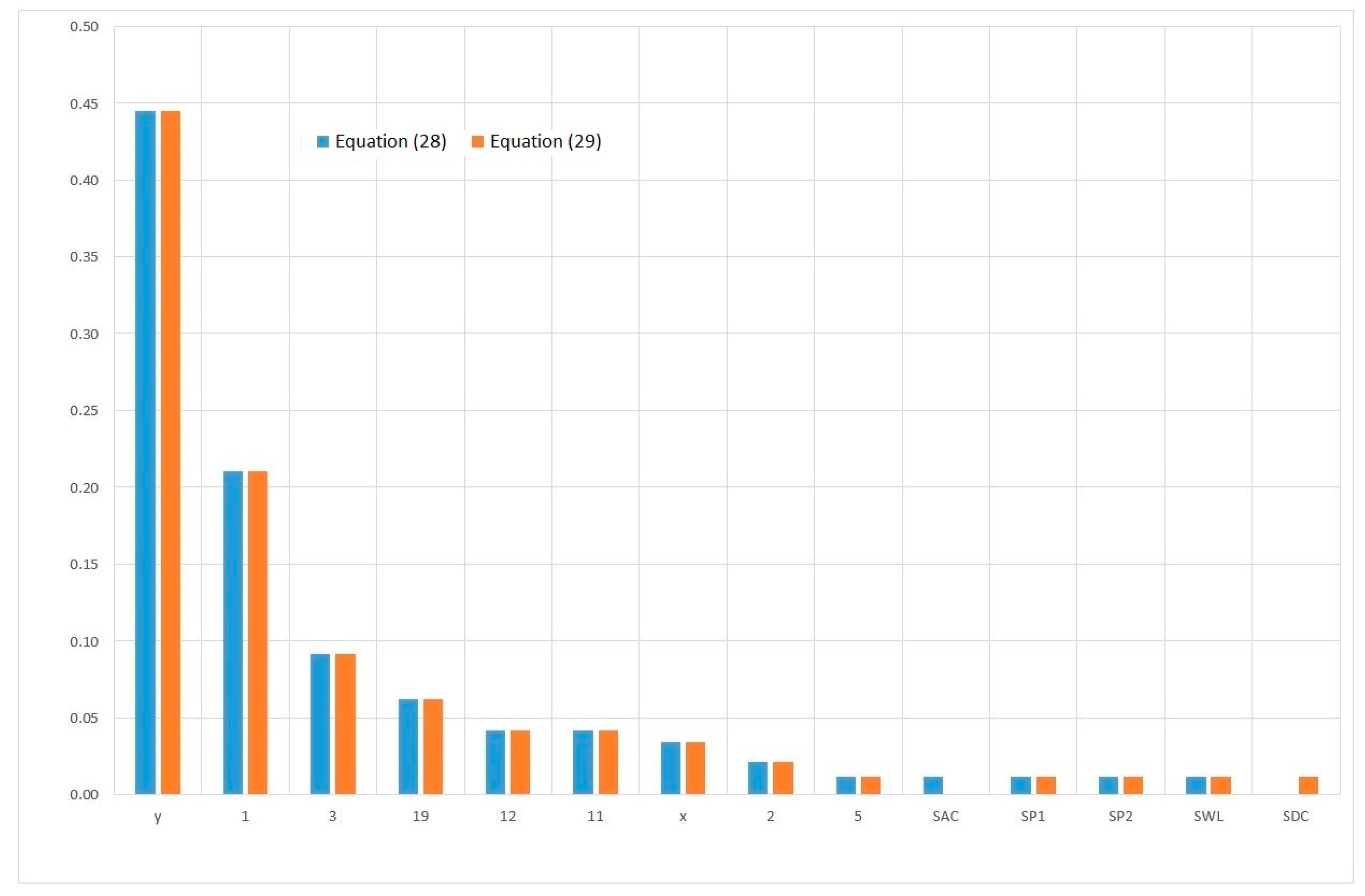
| Equation (24) | Equation (25) | Equation (26) | Equation (27) | Equation (28) | Equation (29) | |
| 1 | 0.20976 | 0.20976 | 0.19912 | 0.19912 | 0.21005 | 0.21005 |
| 2 | 0.02122 | 0.02122 | 0.02014 | 0.02014 | 0.02125 | 0.02125 |
| 3 | 0.09117 | 0.09117 | 0.08655 | 0.08655 | 0.09130 | 0.09130 |
| 4 | 0.00015 | 0.00015 | 0.00015 | 0.00015 | 0.00015 | 0.00015 |
| 5 | 0.01163 | 0.01163 | 0.01104 | 0.01104 | 0.01165 | 0.01165 |
| 6 | 0.00087 | 0.00087 | 0.00083 | 0.00083 | - | - |
| 7 | 0.00015 | 0.00015 | 0.00015 | 0.00015 | - | - |
| 8 | 0.00000 | - | 0.00000 | - | - | - |
| 9 | 0.00144 | 0.00144 | 0.00136 | 0.00136 | 0.00144 | 0.00000 |
| 10 | - | - | - | - | - | 0.00144 |
| 11 | - | - | - | - | 0.04203 | 0.04203 |
| 12 | 0.04197 | 0.04197 | 0.03984 | 0.03984 | 0.04203 | 0.04203 |
| 13 | - | - | 0.00725 | 0.00725 | - | - |
| 14 | - | - | 0.01104 | 0.01104 | - | - |
| 15 | - | - | 0.00034 | 0.00034 | - | - |
| 16 | - | - | - | - | - | - |
| 17 | - | - | - | - | - | - |
| 18 | - | - | - | - | - | - |
| 19 | 0.06217 | 0.06217 | 0.05901 | 0.05901 | 0.06225 | 0.06225 |
| 13a | 0.04197 | 0.04197 | 0.03984 | 0.03984 | - | - |
| 14a | 0.01163 | 0.01163 | 0.01104 | 0.01104 | - | - |
| 15a | 0.00036 | 0.00036 | 0.00034 | 0.00034 | - | - |
| 16a | - | - | - | - | - | - |
| 17a | - | - | - | - | - | - |
| 18a | - | - | - | - | - | - |
| SAC | 0.01163 | 0.01163 | 0.01104 | 0.01104 | 0.01165 | - |
| SDC | 0.01163 | 0.01163 | 0.01104 | 0.01104 | - | 0.01165 |
| SH1 | - | - | 0.01104 | 0.01104 | - | - |
| SH2 | - | - | - | - | - | - |
| SP1 | - | - | - | - | 0.01165 | 0.01165 |
| SP2 | 0.01163 | 0.01163 | 0.01104 | 0.01104 | 0.01165 | 0.01165 |
| SW1 | - | - | 0.01104 | 0.01104 | 0.00000 | 0.00000 |
| SW2 | - | - | 0.01104 | 0.01104 | 0.00000 | 0.00000 |
| SWL | - | - | - | - | 0.01165 | 0.01165 |
| x | 0.03388 | 0.03388 | 0.03216 | 0.03216 | 0.03392 | 0.03392 |
| y | 0.44407 | 0.44407 | 0.42154 | 0.42154 | 0.44467 | 0.44467 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chybowski, L. Importance Analysis of Components of a Multi-Operational-State Power System Using Fault Tree Models. Information 2020, 11, 29. https://doi.org/10.3390/info11010029
Chybowski L. Importance Analysis of Components of a Multi-Operational-State Power System Using Fault Tree Models. Information. 2020; 11(1):29. https://doi.org/10.3390/info11010029
Chicago/Turabian StyleChybowski, Leszek. 2020. "Importance Analysis of Components of a Multi-Operational-State Power System Using Fault Tree Models" Information 11, no. 1: 29. https://doi.org/10.3390/info11010029
APA StyleChybowski, L. (2020). Importance Analysis of Components of a Multi-Operational-State Power System Using Fault Tree Models. Information, 11(1), 29. https://doi.org/10.3390/info11010029





