Low-Cost, Low-Power FPGA Implementation of ED25519 and CURVE25519 Point Multiplication

Abstract

Twisted Edwards curves have been at the center of attention since their introduction by Bernstein et al. in 2007. The curve ED25519, used for Edwards-curve Digital Signature Algorithm (EdDSA), provides faster digital signatures than existing schemes without sacrificing security. The CURVE25519 is a Montgomery curve that is closely related to ED25519. It provides a simple, constant time, and fast point multiplication, which is used by the key exchange protocol X25519. Software implementations of EdDSA and X25519 are used in many web-based PC and Mobile applications. In this paper, we introduce a low-power, low-area FPGA implementation of the ED25519 and CURVE25519 scalar multiplication that is particularly relevant for Internet of Things (IoT) applications. The efficiency of the arithmetic modulo the prime number $2^{255}-19$, in particular the modular reduction and modular multiplication, are key to the efficiency of both EdDSA and X25519. To reduce the complexity of the hardware implementation, we propose a high-radix interleaved modular multiplication algorithm. One benefit of this architecture is to avoid the use of large-integer multipliers relying on FPGA DSP modules.

1. Introduction

Based on Euler and Gauss works, Edwards introduced a normal form of elliptic curves in 2007 [1]. He generalized the curve as:

$$y^2+x^2=a^2(1+x^2{y}^2)$$

(1)

over the field K, where $a\in K$, such that: $a^5\ne a$.

As Edwards stated in his paper, every curve of the form given in (1) is birationally equivalent to an elliptic curve in Weierstrass form. Bernstein et al. [2] generalized Edwards’ original curves. For a fixed field K of odd characteristic and arbitrary integers $c,d\in K$ such that $cd(1-d{c}^4)\ne 0$, they introduced the curves:

$$y^2+x^2=c^2(1+d{x}^2{y}^2).$$

(2)

This definition covers “more than $1/4$ of all isomorphism classes of elliptic curves over a finite field”. They showed that every elliptic curve over a non-binary field is birationally equivalent to a curve in Edwards form over an extension of the field and in many cases over the original field [2]. In [3], Bernstein et al. introduced a generalization of Edwards curves named twisted Edwards curves. These include more curves, including Edwards curves and every elliptic curve in Montgomery form [4]. As explained in [3], the curve name comes from the fact that the set of twisted Edwards curves is invariant under quadratic twists while a quadratic twist of an Edwards curve is not necessarily an Edwards curve. A quadratic twist of a curve is an isomorphic curve over a field extension of degree two.

For a field K of odd characteristic, and nonzero elements $a,d\in K$, the twisted Edwards curve $E_{T,a,d}\left(K\right)$ is defined as:

$$E_{T,a,d}\left(K\right):a{x}^2+y^2=1+d{x}^2{y}^2.$$

(3)

If $a=1$, then $E_{T,a,d}$ is an Edwards curve with $c=1$. Moreover, $E_{T,a,d}$ is a quadratic twist of the Edwards curve $E_{\mathcal{O},1,d/a}$ with the map: $(\overline{x},\overline{y})\to (x,y)=(\frac{\overline{x}}{\sqrt{a}},\overline{y})$ over the field extension $K\left(\sqrt{a}\right)$:

$${\overline{x}}^2+{\overline{y}}^2=1+(d/a){\overline{x}}^2{\overline{y}}^2$$

(4)

Twisted Edwards curves and Montgomery curves are closely related. As shown in [3], every twisted Edwards curve $E_{T,a,d}$ on the Field K with $char\left(K\right)\ne 2$, is birationally equivalent to a Montgomery curve $E_{M,A,B}:B{v}^2=u^3+A{u}^2+u$ using the map:

$$\begin{array}{c}\hfill (x,y)\to (u,v)=\left({\displaystyle \frac{(1+y)}{(1-y)}},{\displaystyle \frac{(1+y)}{(1-y)x}}\right)\end{array}$$

(5)

where $A={\displaystyle \frac{2(a+d)}{(a-d)}}$, and $B={\displaystyle \frac{4}{(a-d)}}$.

If a is a square in K, then these curves are isomorphic over K itself. From the operation counts of the point arithmetic given in [5], it is easy to see that twisted Edwards curves outperform curves in Weierstrass form in terms of speed (despite the binary form of Edwards curve that is a bit slower than its Weierstrass counterpart [6]). However twisted Edwards curves are appealing for another reason. Their group laws are unified and complete; that leads to safer implementations against certain types of attacks [3].

The Edwards-curve Digital Signature Algorithm (EdDSA) is the most significant application of twisted Edwards curves. The ED25519 is a twisted Edwards curve used for EdDSA, where its parameters are defined as [7]:

• $a=-1$,
• $d=-\frac{121665}{121666}$,
• $p=2^{255}-19$.

The corresponding Montgomery curve of ED25519 is CURVE25519 that is defined as [8]:

$$y^2=x^3+486662x^2+x$$

(6)

Point multiplication is fast and efficient on Montgomery curves. It efficiently uses differential point addition and point doubling [5] and uniform Montgomery ladder algorithm to perform a point multiplication [9]. The uniform Montgomery ladder algorithm is performed in constant time that makes its implementations robust to timing attacks. The CURVE25519 has been used in many software implementations since its introduction by Bernstein in 2006 [8]. It has also become a promising candidate for Internet of Things (IoT) applications due to its 128-bit security level and efficient arithmetic. Recently, a number of hardware implementations have been introduced [10,11,12,13] with a focus on IoT applications. All these works use FPGA DSP slices to implement modular multipliers. High-performance cryptographic processors that can be implemented on low-cost FPGAs or ASICs are in demand for mobile applications such as the Internet of Things (IoT) and Intelligent Transport Systems (ITS) [14]. Low-cost FPGAs (including anti-fused-based FPGAs) are namely restricted in the number of hardware resources. A portable low-power design that uses minimum hardware resources without losing its performance is then the most appealing. In the following, we propose an area-efficient, low-power hardware implementation of the CURVE25519 and ED25519 on FPGA. Our design is not using multipliers and DSP units of FPGA resources. We introduce a high speed interleaved modular multiplier tailored for this application. Section 2 provides a background on Elliptic Curve Discrete Logarithm Problem (ECDLP) and the arithmetic of curves ED25519 and CURVE25519, used in this work. Section 3 introduces hardware design of the point multiplication core and Section 4 shows implementation results and comparisons with previous work.

2. Background

Like any elliptic curve cryptosystem, the security of ED25519 and CURVE25519 is based on the elliptic curve discrete logarithm problem (ECDLP). Let E be an elliptic curve defined over the prime field ${\mathbb{F}}_p$ and let the group of rational points on the curve E denoted by $E\left({\mathbb{F}}_p\right)$. Now, consider a point $P\in E\left({\mathbb{F}}_p\right)$ of order n and the cyclic subgroup of $E\left({\mathbb{F}}_p\right)$ generated by point P, i.e., $⟨P⟩=\{\mathcal{O},P,2P,\cdots ,(n-1\left)P\right\}$. Take a random integer $k\in [1,n-1]$ and let $Q=k·P$. The point Q is defined by adding point P to itself $k-1$ times.

$$Q=k·P=\underset{k\mathrm{times}}{\underbrace{P+P+\cdots +P}}.$$

(7)

Given the domain parameters and Q, the problem of determining the integer k is called ECDLP [15]. The point Q can be easily computed with a given k using the one-way function $Q=k·P$ (called elliptic curve point multiplication or scalar multiplication). However, it is computationally difficult to calculate k from known points Q and P.

Optimized explicit point addition and point doubling formulae for twisted Edwards curves and Montgomery curves are presented in [5]. Projective coordinates are used in this work. The input Z-coordinate for the point P is set to $Z=1$. So, transformation from affine to projective coordinates can be done at no cost.

$$\begin{array}{c}\hfill P(x,y)\to P(X,Y,Z),\\ \hfill x=\frac{X}{Z},y=\frac{Y}{Z}.\\ \hfill P(x,y)\to P(x,y,1)\end{array}$$

(8)

We did minor modifications in the Elliptic Curve Point Doubling (ECPD) formulae (9) and Elliptic Curve Point Addition (ECPA) (10) to minimize the number of holding registers and optimize hardware implementation. Data flow diagram of ECPD and ECPA are shown in Figure 1 and Figure 2, respectively. At each level one modular multiplication is performed. Modular addition and/or modular subtraction is performed in parallel with modular multiplication whenever possible.

$$\begin{array}{cccc}\hfill A& =2·{Z_1}^2\hfill & \hfill B& =X_1+Y_1\hfill \\ \hfill C& ={X_1}^2\hfill & \hfill D& ={Y_1}^2\hfill \\ \hfill E& =p-(C+D)\hfill & \hfill F& =(C-D)\hfill \\ \hfill J& =F-A\hfill & \hfill K& =B^2+E\hfill \\ \hfill X_2& =J·K\hfill \\ \hfill Y_2& =F·E\hfill \\ \hfill Z_2& =F·J\hfill \end{array}$$

(9)

$$\begin{array}{cccc}\hfill B& ={Z_2}^2\hfill & \hfill C& =X_1·X_2\hfill \\ \hfill D& =Y_1·Y_2\hfill & \hfill E& =d·C·D\hfill \\ \hfill F& =B-E\hfill & \hfill G& =B+E\hfill \\ \hfill H& =(X_1+Y_1)·(X_2+Y_2)\hfill & \hfill I& =H-(C+D)\hfill \\ \hfill J& =F·Z_2\hfill & \hfill K& =G·Z_2\hfill \\ \hfill X_3& =J·I\hfill \\ \hfill Y_3& =K·(C+D)\hfill \\ \hfill Z_3& =F·G\hfill \end{array}$$

(10)

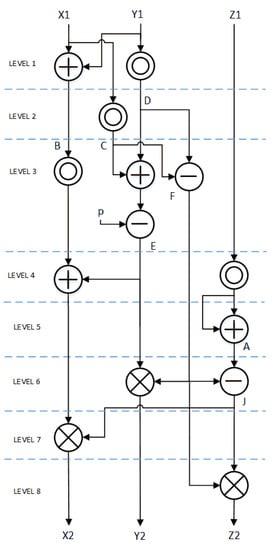
Figure 1. ED25519 Point doubling flow diagram.

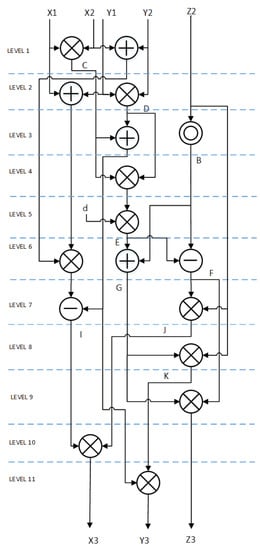
Figure 2. ED25519 Point addition flow diagram.

Point multiplication on the Montgomery curve CURVE25519 can be done by using efficient uniform differential point addition and doubling for X and Z in projective coordinates. This allows low latency, low-power hardware implementations. Explicit formulae can be found in [5]. We have rearranged these formulae as in (11) for hardware optimized implementation. Similar to ED25519, at every level one modular multiplication in parallel to possible modular addition and/or modular subtraction is performed. Data flow diagram of differential point addition and doubling on CURVE25519 is shown in Figure 3.

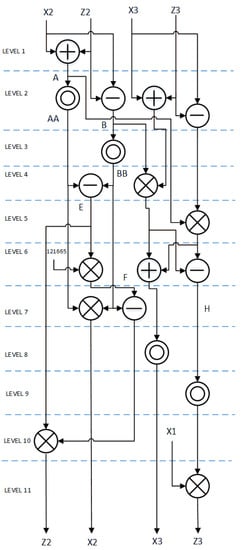
Figure 3. CURVE25519 differential point addition and point doubling flow diagram.

The legend of Figure 1, Figure 2 and Figure 3 is given separately in Figure 4.

Figure 4. Legend for Figure 1, Figure 2 and Figure 3.

3. Hardware Design

3.1. Interleaved Modular Multiplication Algorithm

Modular multiplication is a basic operation of crucial importance in elliptic curve cryptography. The interleaved modular multiplication algorithm, unlike other modular multiplication methods, does not employ actual multipliers. The basic interleaved modular multiplication algorithm [16] is shown in Algorithm 1. The idea of this algorithm is to interleave the accumulation steps of the multiplication with the steps of a division operation. An operand is multiplied by a bit of the other operand in a loop and followed by a division by the modulus to control the size of the intermediate values. A multiple of the modulus is then subtracted from the value of the accumulator and a new partial product is added. It is essential to start with the most significant bit to avoid gradually increasing digits when adding the shifted version of the multiplicand. Direct implementation of this algorithm is not efficient due to the carry propagation delay of the long bit adder and the sequential steps that add delay to the circuit and increase the clock period. Bunimov et al. [17] proposed an architecture to solve these problems. A carry save adder (CSA) is used to eliminate carry propagation delay.

$$\begin{array}{cccc}\hfill A& =X_2+Z_2\hfill & \hfill B& =X_2-Z_2\hfill \\ \hfill AA& =A^2\hfill & \hfill BB& =B^2\hfill \\ \hfill C& =X_3+Z_3\hfill & \hfill D& =X_3-Z_3\hfill \\ \hfill E& =AA-BB\hfill & \hfill F& =121665·E\hfill \\ \hfill DA& =D·A\hfill & \hfill CB& =C·B\hfill \\ \hfill G& =DA+CB\hfill & \hfill H& =DA-CB\hfill \\ \hfill X_2& =AA·BB\hfill & \hfill Z_2& =E·(BB-F)\hfill \\ \hfill X_3& =G^2\hfill & \hfill Z_3& =H^2·X_1\hfill \end{array}$$

(11)

Instead of comparing with the modulus, they compared intermediate values with $2^n$ and precomputed and saved the difference in a look-up table. This precomputed difference is added to the intermediate value at the next iteration. Figure 5 shows their proposed hardware architecture. To reduce the number of cycles the High-Radix technique has been proposed [18,19,20,21].

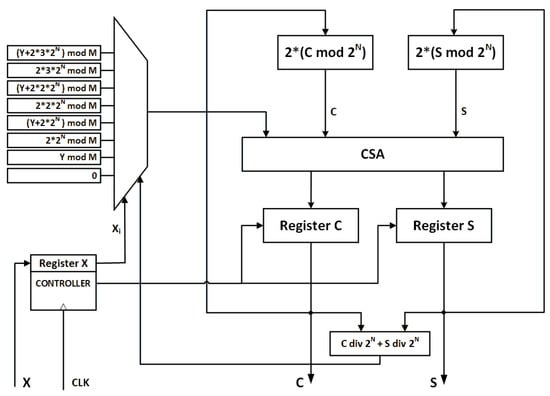
Figure 5. Basic Interleaved modular multiplication unit proposed by [17].

Algorithm 1: Basic interleaved modular multiplication algorithm [16]

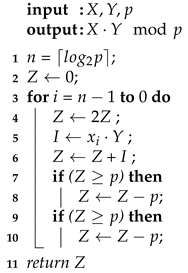Algorithm 2 presents our proposed radix-8 interleaved modular multiplier. The values $\{2Ymodp,\dots ,7Ymodp\}$ are precomputed before the start of shift cycles and stored in a look-up table ($LUT1$). To complete the for loop in the algorithm, 85 clock cycles are required. Three bits of the multiplicand X are read at every clock cycle and decide the output of $LUT1$. At the end of the loop, the accumulator value is not greater than $12p$. The algorithm is proofed with 10,000 random 255-bit integers using MAPLE. The MAPLE implementation of Algorithm 2 is suggested in Appendix A. The hardware implementation is very efficient. Figure 6 depicts the hardware implementation of the proposed Radix-8 algorithm 2. The loop logic has maximum net and logic delay of 1.8 ns. So maximum clock frequency of 550 MHz is achievable. The weakness of this algorithm is the latency of calculating $LUT1$ for every new run. However, taking this latency into account, the overall improvement is notable compared to similar works. The first ten clock cycles are treated as waiting cycles to complete $LUT1$ table. The modular multiplication is then completed in 95 clock cycles. In case of using 550 MHz clock frequency, that is equivalent to 172.7 ns. A reducer logic is used to output a complete modulo reduction at the end of last clock cycle that costs one comparison and one subtraction and imposes 7.2 ns delay to output. So, the complete reduction latency is 180 ns.

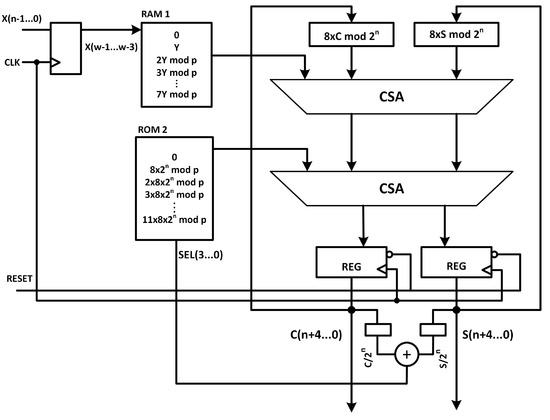
Figure 6. Radix-8 Interleaved modular multiplication unit.

In this architecture, the high-frequency logic is very small (900 FPGA LUTs or 22% of total area), hence the dynamic power consumption is very low. Table 1 compares our design performance with some similar works in the literature. It must be noted that the circuit area/latency reported in [19,21] are related to partial reduction and the final reduction logic is not taken into account. We estimated the power consumption of the designs presented in [19,21] with Xilinx power estimator tool. These estimates are based on the reported used FPGA resources, clock frequency, average signal toggle rate, and default average fan-out.

Table 1. Comparing our Radix-8 256-bit interleaved modular multiplication design performance with other works.

Design	Platform	Area	Latency @Clk Freq	Clock Cycles	Power
		Slices	ns @ MHz		(Static/Dynamic) mW
Ours	VIRTEX 7	983	180 @ 550	95	178/57
Ours	ZYNQ7000	983	180 @ 550	95	101/51
[21]	VIRTEX 5	1042	303 @ 422	128	1808/503 1
[19] EIMM	VIRTEX 4	2559	1171.66 @ 437.12	512	1828/728 1
[20] R4 MIM	VIRTEX 6	4630	1487 @ 86.6	129	1990/419 1
[20] R8 MIM	VIRTEX 6	5657	930 @ 71	66	1996/450 1

¹ Our estimation using Xilinx Power Estimator tool.

Algorithm 2: New Radix-8 Interleaved Modular multiplication algorithm

3.2. Modular Addition and Subtraction

Figure 7 and Figure 8 show the proposed fast and area-efficient modular addition and subtraction units, respectively. The Carry Propagate Adders (CPA) and a Carry Save Adder(CSA) resources are shared and the implementation is fast and very area-efficient. ($\overline{B}$ and $\overline{p}$ denotes bitwise not$\left(B\right)$ and not$\left(p\right)$ respectively.)

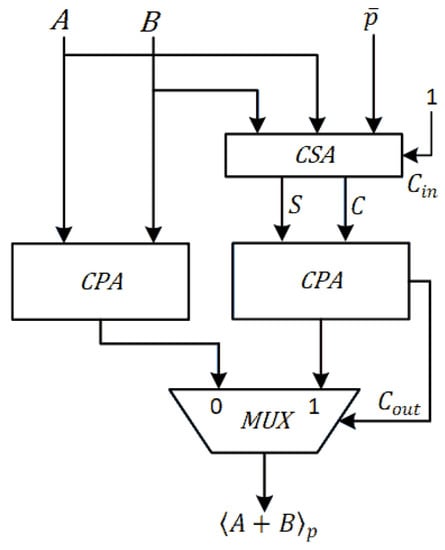
Figure 7. Hardware implementation of modular addition ($A+Bmodp$).

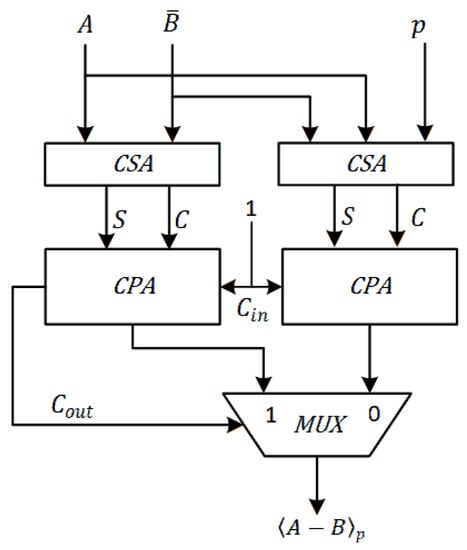
Figure 8. Hardware implementation of modular subtraction ($A-Bmodp$).

3.3. ED25519 and CURVE25519 Point Multiplication Core

Point multiplication unit uses an Arithmetic Logic Unit (ALU) that consists of a point addition and a point doubling state machine. As shown in Figure 9, the state machines share the modular multiplication and modular add/subtract arithmetic units as well as register bank resources.

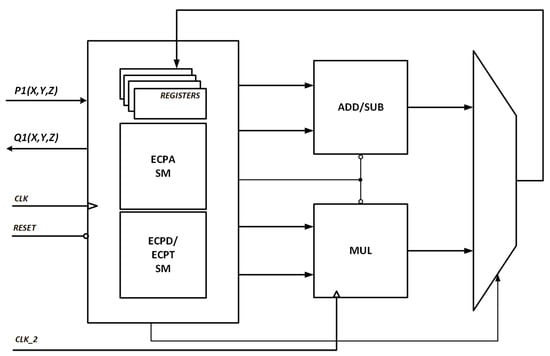
Figure 9. ALU unit configuration.

Figure 10 shows the point multiplication core configuration. Projective coordinates are used to avoid modular inversions. Finally, one modular inversion is required at the end of the computation to convert projective coordinates back to affine.

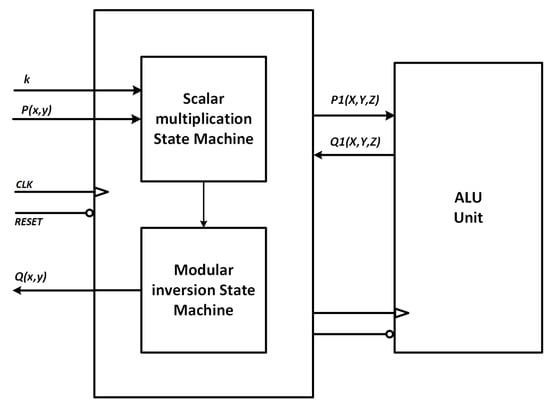
Figure 10. Point multiplication core.

3.4. Modular Inversion

There are basically two methods to calculate the modular inverse of an integer in the field ${\mathbb{F}}_p$. Euclidean algorithm and Fermat’s little theorem [15]. The Euclidean algorithm is a recursive method that needs multiplications, additions/subtractions and maintaining intermediate results at every iteration. Implementation of the Euclidean algorithm requires a new hardware that contrasts with our low-area design approach. Based on Fermat’s little theorem, ${⟨a^{-1}⟩}_p={⟨a^{p-2}⟩}_p$. The modular field inversion unit can be implemented by sharing the interleaved modular multiplication with the point multiplication unit. As mentioned in [8], 254 squaring and 11 multiplications are required to complete a field inversion for $p=2^{255}-19$. However, the actual sequence of operations is not provided. Our design uses the chain in (12) to return a modular inversion using 265 modular multiplications.

$$\begin{array}{c}\hfill a^2\\ \hfill {\left(a^2\right)}^{2^2}\\ \hfill a^8·a\\ \hfill a^9·a^2\\ \hfill {\left(a^{11}\right)}^2·a^9\\ \hfill {\left(a^{2^5-1}\right)}^{2^5}·a^{2^5-1}\\ \hfill {\left(a^{2^{10}-1}\right)}^{2^{10}}·a^{2^{10}-1}\\ \hfill {\left(a^{2^{20}-1}\right)}^{2^{20}}·a^{2^{20}-1}\\ \hfill {\left(a^{2^{40}-1}\right)}^{2^{10}}·a^{2^{10}-1}\\ \hfill {\left(a^{2^{50}-1}\right)}^{2^{50}}·a^{2^{50}-1}\\ \hfill {\left(a^{2^{100}-1}\right)}^{2^{100}}·a^{2^{100}-1}\\ \hfill {\left(a^{2^{200}-1}\right)}^{2^{50}}·a^{2^{50}-1}\\ \hfill {\left(a^{2^{250}-1}\right)}^{2^5}·a^{2^{11}}\end{array}$$

(12)

4. Results and Comparison

Our design implementation results on ZYNQ 7000 series FPGAs are presented in Table 2. We used minimum hardware resources to achieve low-area/low-power goals, which are very appealing for IoT applications. Point multiplication of ED25519 uses Double and Add and NAF (Non-Adjacent Form) algorithms [15]. The average core latency is calculated using one thousand 255-bit random scalars. Several implementations of CURVE25519 and ED25519 are presented in [10,11,12,13]. Table 3 summarizes the outcome of these works for comparison. The focus of all these works has been on the speed of point multiplication operation by adding arithmetic resources to the hardware. Heuristic methods presented in [12,13] to optimize the modular multiplication that is the critical arithmetic unit. All known works employed FPGA DSP modules for implementation of modular multipliers. However, in our design, no DSP module is used. We estimated the power consumption of these works with the Xilinx power estimator tool. The power consumption shown in Table 3 is calculated based on the FPGA resources used in each work. These include clock frequency, default average fan-out, and considering 100% toggle rate for the DSP modules. We implemented multipliers using LUT resources only, to provide a baseline comparison. In [10,13], fifteen 17-bit × 17-bit multipliers are used to implement a 255-bit modular multiplier. This implementation requires 345 LUT resources for each multiplier. As a comparison, a 64-bit × 64-bit multiplier needs 4256 LUT and a 127-bit × 127-bit multiplier uses 24335 LUTs on a 7-Series Xilinx FPGA. Table 3 gives an estimate of cores area in [10,11,12,13] assuming that no DSP slice is used.

Table 2. Implementation results of ED25519 and CURVE25519 point multiplication cores on ZYNQ 7000 Series.

Platform	Area	Latency @Clk Freq	Power
	KLUT/FF/DSP/BRAM	ns @ MHz	Static/Dynamic (mW)
ED25519 (Double and add Method)	8.68/3472/0/0	627985 @ 137.5	104/172
ED25519 (NAF Method)	8.77/3729/0/0	543874 @ 137.5	105/180
CURVE25519	7.38/3141/0/0	511780 @ 137.5	103/145
CURVE25519 (using 2 modular mult.)	12.95/4194/0/0	280640 @ 137.5	106/236

Table 3. Other works implementation results.

Reference	Area	Latency @Clk Freq	Power	Equivalent Area 2
	KLUT/FF/DSP/BRAM	µs @ MHz	Static/Dynamic (mW)	KLUT/FF/BRAM
[10] Single core	2.783/3592/20/2	397 @ 100	105/189 1	9.683/3592/2
[10] Multi core	34.009/43875/210/2	340 @ 200	185/1738 1	106.459/43875/2
[11]	21.107/26483/260/0	118 @ 115	150/789	45.442/26483/0
[12]	17.94/21107/175/0	97 @ 115	134/709 1	42.275/21107/0
[13] (CURVE25519)	2.707/962/15/0	608 @ 105	104/141 1	7.875/962/0
[13] (ED25519)	11.15/2656/16/0	1467 @ 82	107/298 1	16.670/2656/0

¹ Our estimation using Xilinx Power Estimator tool. ² Area estimation in case of using FPGA LUTs for multiplier implementation.

5. Side-Channel Attacks Considerations

Resistance against side-channel attacks can be easily provided to ED25519 and CURVE25519 point multiplication cores by different approaches. The Montgomery powering ladder algorithm [22] can be employed for ED25519 point multiplication hardware to hide the power spectrum patterns of ECPD and ECPA and provide resistance against SPA (Simple Power Analysis) attacks. At every single step, both ECPD and ECPA operations are performed, then it must be decided which result should be used for the next step. The latency of the Montgomery ladder algorithm is constant equal to the latency of 255-point doublings and 254-point additions. The constant calculation time provides immunity to timing attacks. The disadvantage of the Montgomery ladder algorithm is its larger latency compared to other point multiplication methods. Curve25519, however, uses the uniform differential point addition and point doubling method. To implement resistance to DPA (Differential Power Analysis) attacks, a random factor $\lambda$ is injected to the projective coordinates of the initial point $P(x,y)$ [23]. Then randomized projective coordinated point $P(\lambda X_1,\lambda Y_1,\lambda Z_1)$ is used. The algorithm starts with: $X_2=\lambda$, $Z_2=0$, $X_3=X_1$, $Z_3=\lambda$. The formulae (11) and Figure 3 must be revised by replacing $X_3=\lambda ·G^2$. The DPA attack cannot be successful as it is not possible to predict any specific bit of $4P$ (or other multiples of P in randomized projective coordinates [15]. The timing costs of this approach is 256 more modular multiplications, two initial and 254 in loop modular multiplications.

6. Conclusions

Interleaved modular multipliers are very efficient in terms of area and power consumption and work at high clock frequencies. We introduced a radix-8 interleaved modular multiplier algorithm to reduce the number of clock cycles required to achieve one modular multiplication. We implemented ED25519 and CURVE 25519-point multiplication cores using the interleaved modular multiplier as a primitive arithmetic unit. Comparing our results to the most recent works listed in Table 3, reveals that we achieved a low-power/area-efficient design. The modular multiplier is the critical arithmetic unit that determines the overall performance of the hardware. Research on the improvement of the modular multiplier performance is recommended as future works.