A Novel Approach to Component Assembly Inspection Based on Mask R-CNN and Support Vector Machines
Abstract
:1. Introduction
2. Research Method
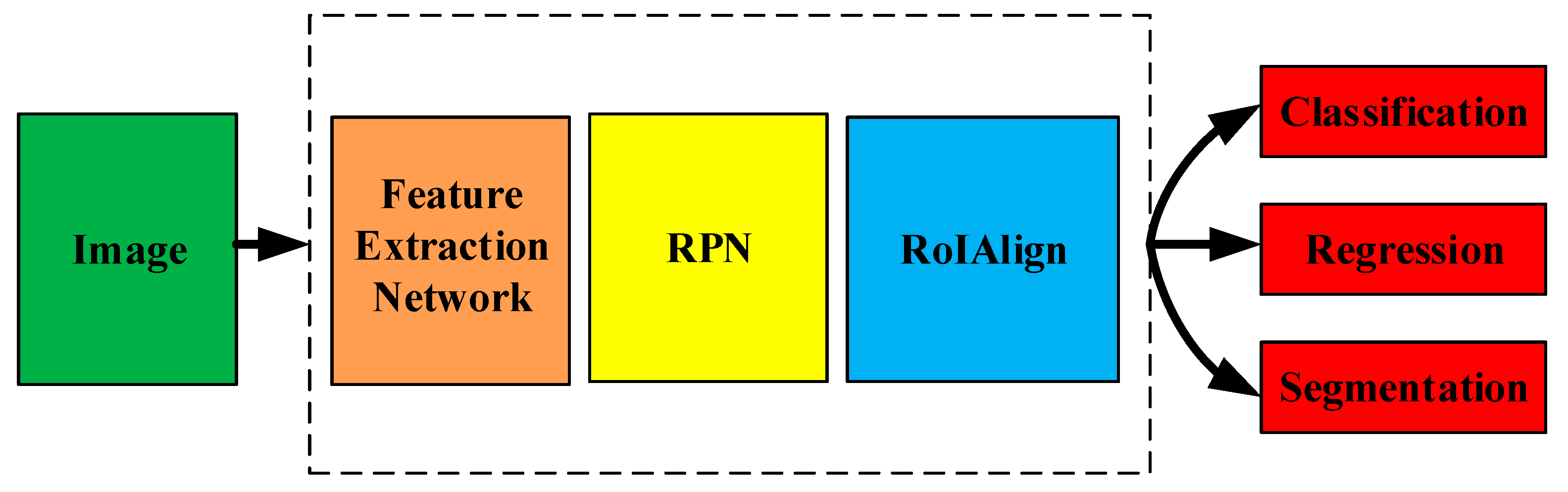
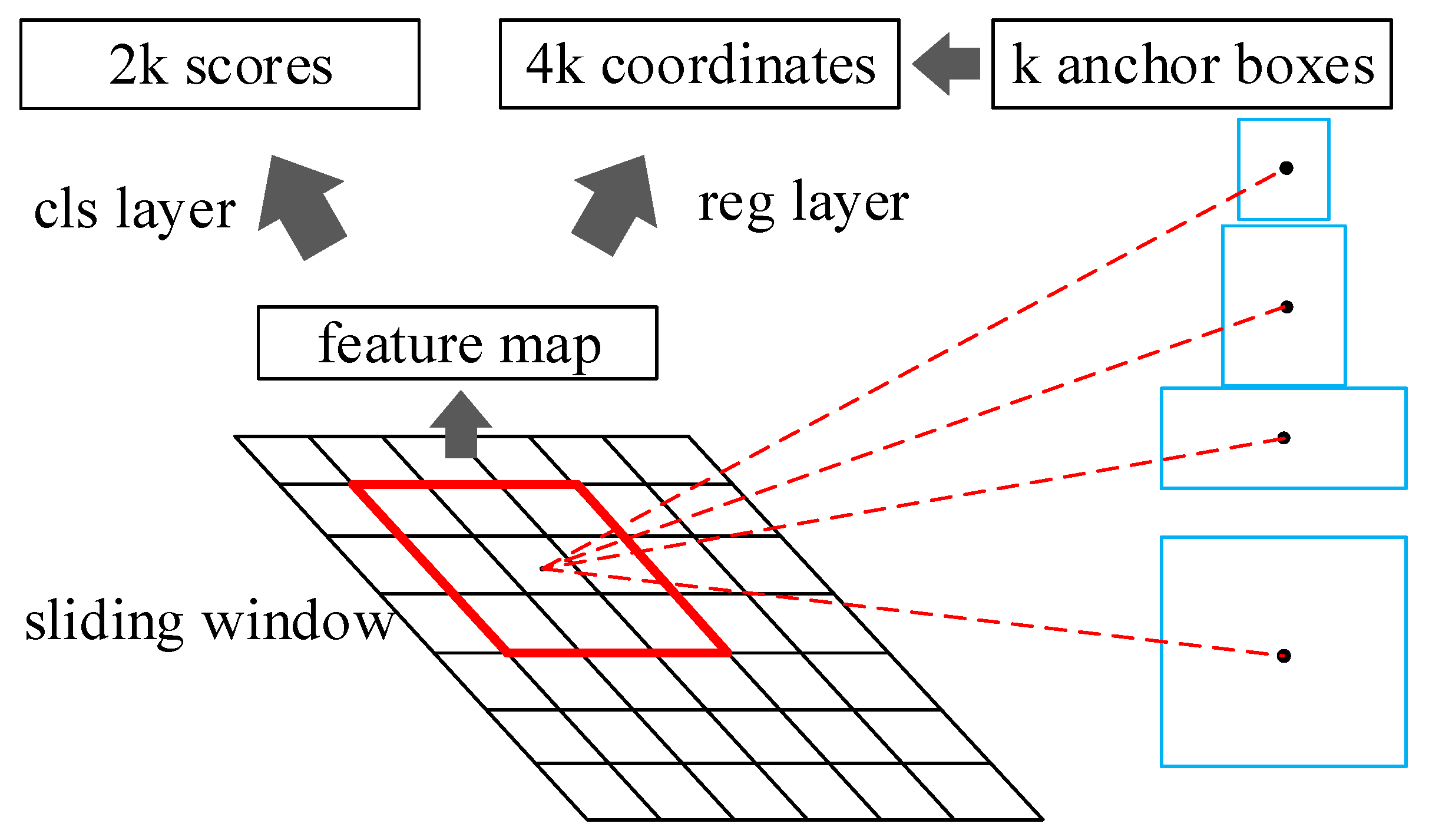
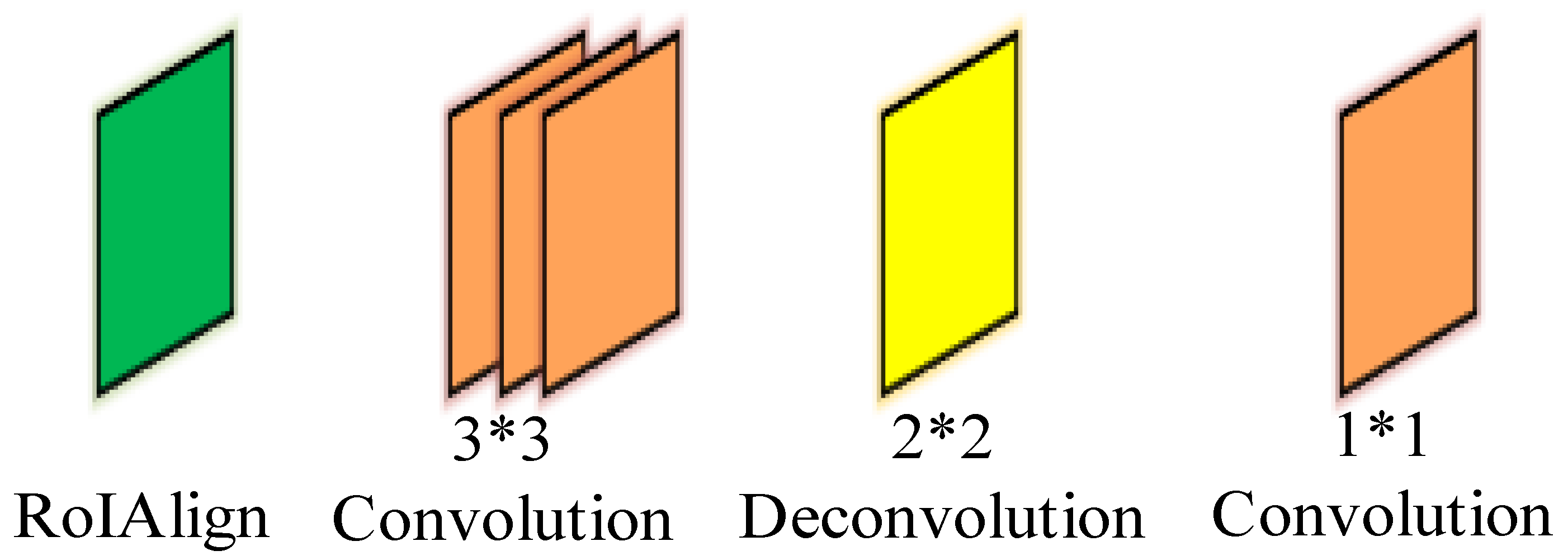
2.1. Instance Segmentation Based on Mask R-CNN
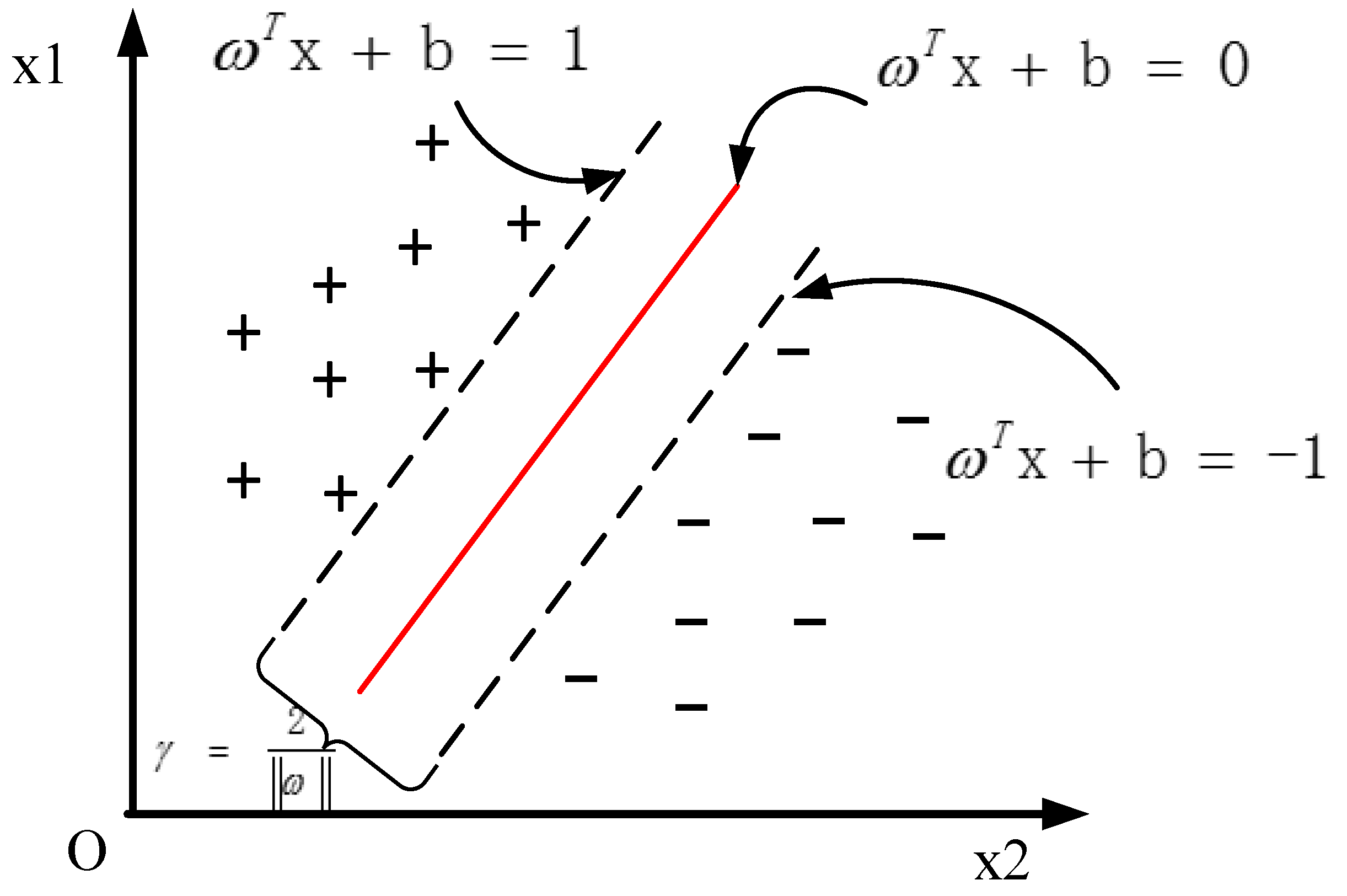
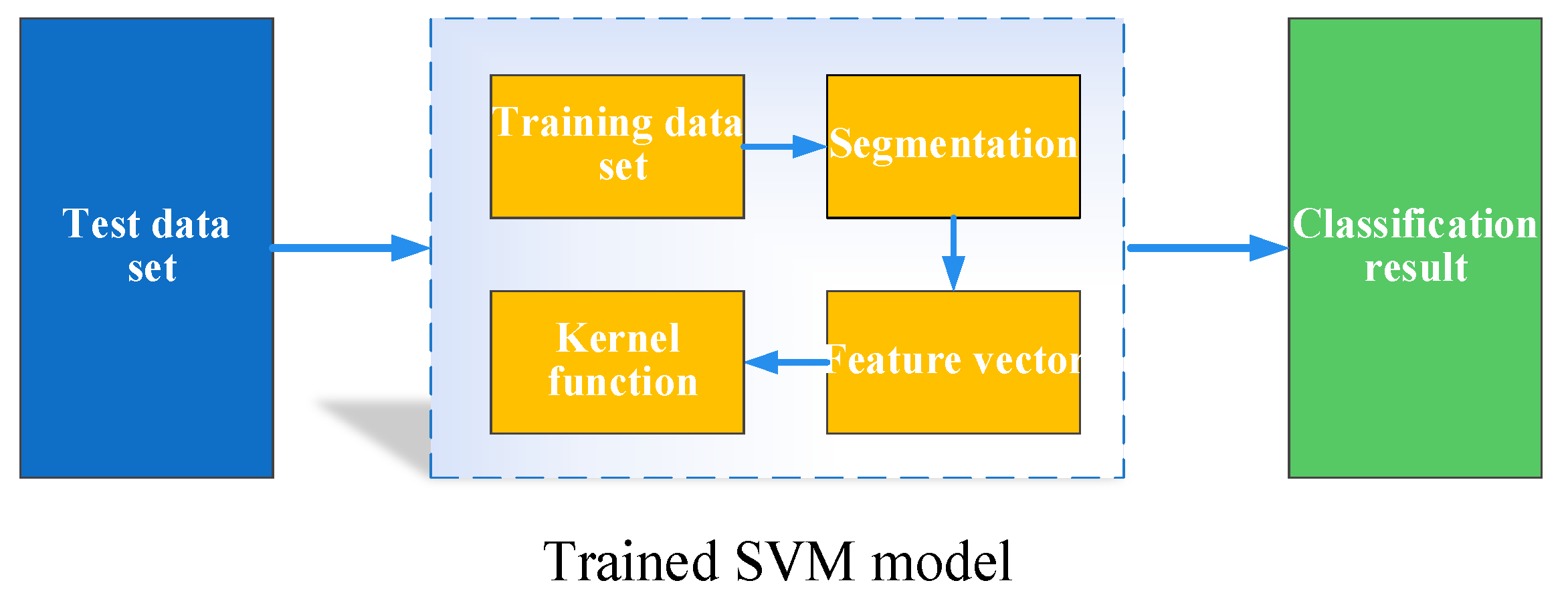
2.2. Component Assembly Inspection Based on SVM
3. Data Preparation and Training
3.1. Data Preparation
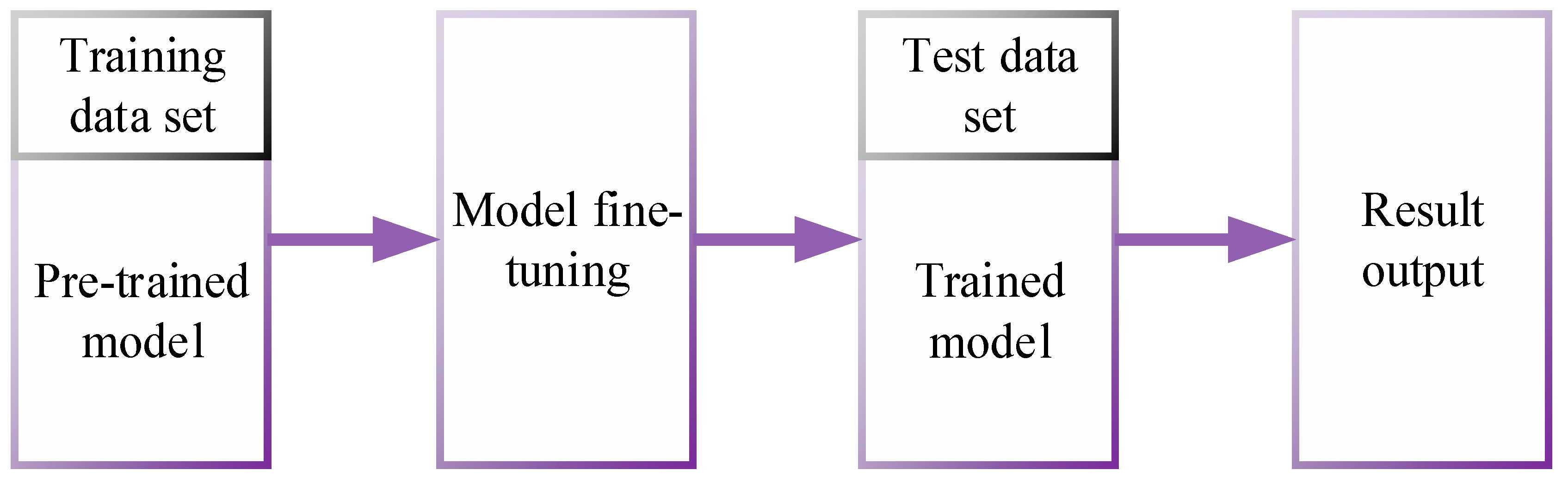
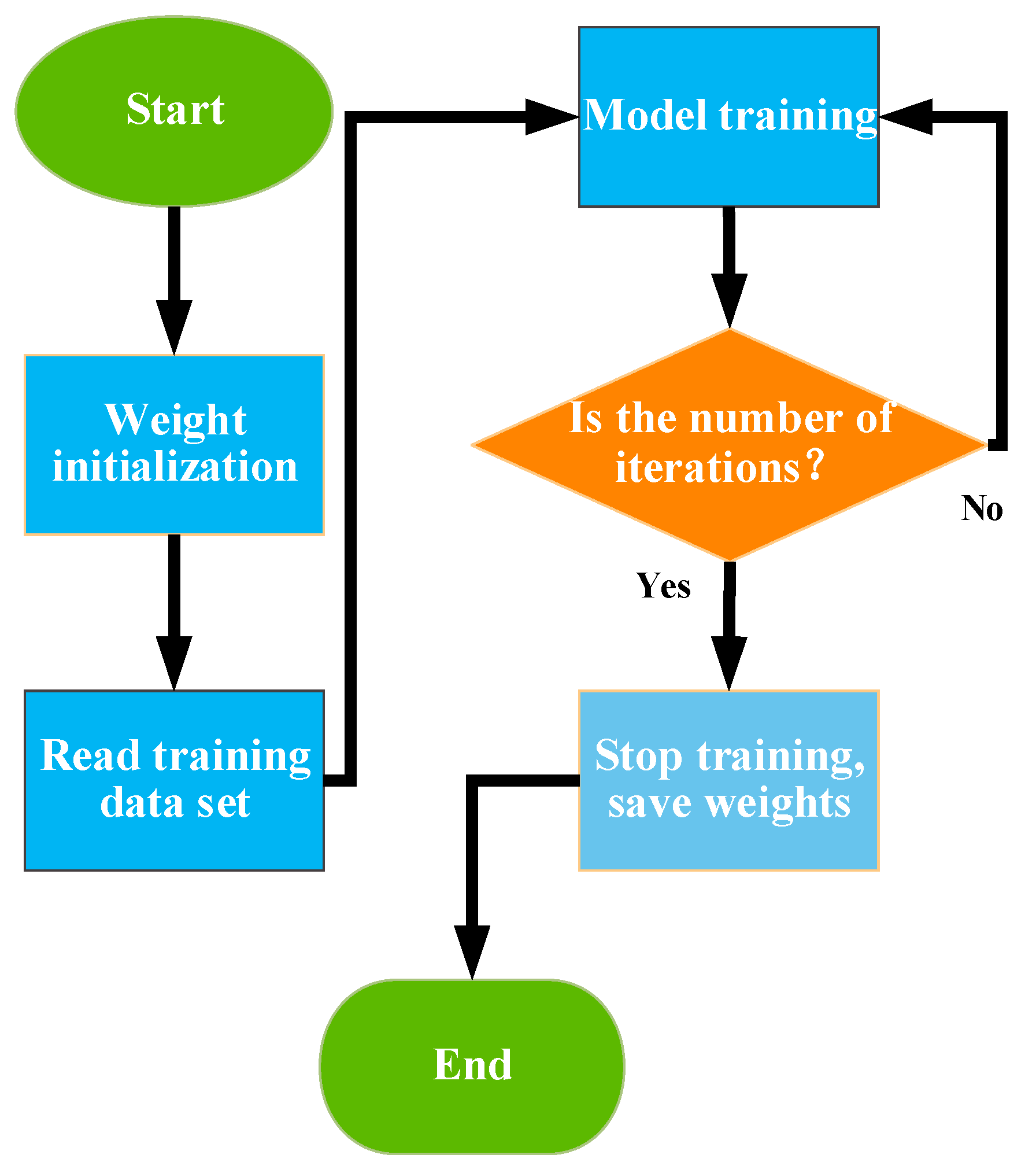
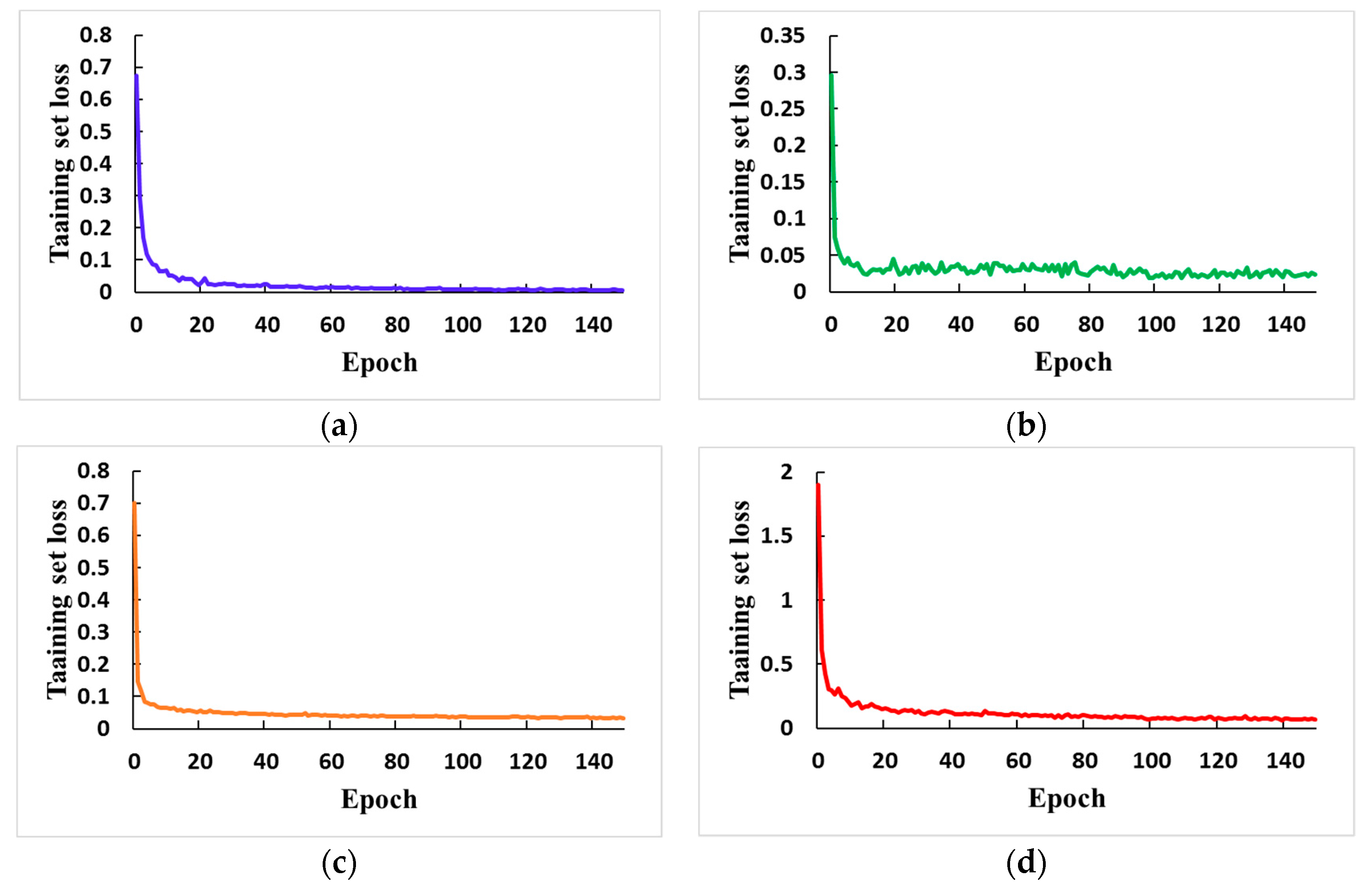
3.2. Training Methods and Details
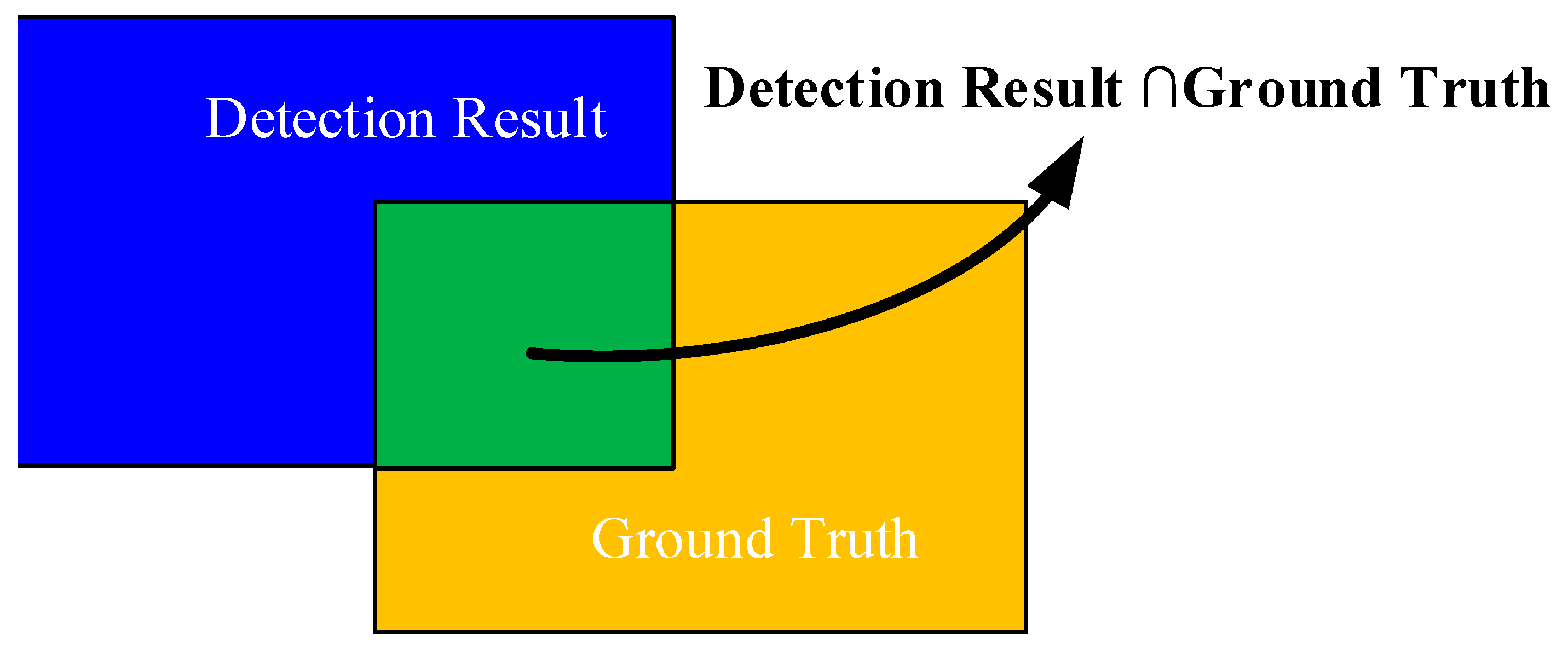
4. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Del Fabbro, E.; Santarossa, D. Ergonomic analysis in manufacturing process. A real time approach. Procedia CIRP 2016, 41, 957–962. [Google Scholar] [CrossRef]
- Chauhan, V.; Surgenor, B. A comparative study of machine vision based methods for fault detection in an automated assembly machine. Procedia Manuf. 2015, 1, 416–428. [Google Scholar] [CrossRef]
- Nee, A.Y.C. Handbook of Manufacturing Engineering Technology; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Chauhan, V.; Surgenor, B. Fault detection and classification in automated assembly machines using machine vision. Int. J. Adv. Manuf. Technol. 2017, 90, 2491–2512. [Google Scholar] [CrossRef]
- Bhuvanesh, A.; Ratnam, M.M. Automatic detection of stamping defects in leadframes using machine vision: Overcoming translational and rotational misalignment. Int. J. Adv. Manuf. Technol. 2007, 32, 1201–1210. [Google Scholar] [CrossRef]
- Teck, L.; Sulaiman, M.; Shah, H.; Omar, R. Implementation of Shape-Based Matching Vision System in Flexible Manufacturing System. J. Eng. Sci. Technol. Rev. 2010, 3, 128–135. [Google Scholar] [CrossRef]
- Kim, S.; Lee, M.H.; Woo, K.-B. Wavelet analysis to fabric defects detection in weaving processes. In Proceedings of the ISIE’99 IEEE International Symposium on Industrial Electronics (Cat. No. 99TH8465), Bled, Slovenia, 12–16 July 1999; pp. 1406–1409. [Google Scholar]
- Andres, N.S.; Jang, B.-C. Development of a machine vision system for automotive part car seat frame inspection. J. Korea Acad. Ind. Coop. Soc. 2011, 12, 1559–1564. [Google Scholar]
- Jiang, L.; Sun, K.; Zhao, F.; Hao, X. Automatic detection system of shaft part surface defect based on machine vision. In Visual Inspection and Machine Vision; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; p. 95300G. [Google Scholar]
- Wu, J.; Bin, H. Subpixel edge detection of machine vision image for thin sheet part. China Mech. Eng. 2009, 20, 297–299. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ferreira, A.J.; Figueiredo, M.A. Boosting algorithms: A review of methods, theory, and applications. In Ensemble Machine Learning; Springer: Berlin/Heidelberg, Germany, 2012; pp. 35–85. [Google Scholar]
- Felzenszwalb, P.F.; Girshick, R.B.; McAllester, D.; Ramanan, D. Object detection with discriminatively trained part-based models. Ieee Trans. Pattern Anal. Mach. Intell. 2009, 32, 1627–1645. [Google Scholar] [CrossRef] [PubMed]
- Bohlool, M.; Taghanaki, S.R. Cost-efficient Automated Visual Inspection System for small manufacturing industries based on SIFT. In Proceedings of the 2008 23rd International Conference Image and Vision Computing New Zealand, Christchurch, New Zealand, 26–28 November 2008; pp. 1–6. [Google Scholar]
- Sinkar, S.V.; Deshpande, A.M. Object recognition with plain background by using ANN and SIFT based features. In Proceedings of the 2015 International Conference on Information Processing (ICIP), Pune, India, 16–19 December 2015; pp. 575–580. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Kavukcuoglu, K.; Farabet, C. Convolutional networks and applications in vision. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 253–256. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, NIPS 2012, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition, Columbus, OH, USA, 24–27 June 2014; pp. 580–587. [Google Scholar]
- Uijlings, J.R.; Van De Sande, K.E.; Gevers, T.; Smeulders, A.W. Selective search for object recognition. Int. J. Comput. Vis. 2013, 104, 154–171. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. you only look once: Unified, real-time object detection. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2015), Boston, MA, USA, 7–12 June 2015; pp. 779–788. [Google Scholar]
- He, K.; Gkioxari, G.; Doll á r, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International. Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.B.; He, K. Feature Pyramid Networks for Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6230–6239. [Google Scholar]






| Kernel Function Name | Mathematical Expression |
|---|---|
| Linear Kernel | |
| Polynomial Kernel | |
| Gaussian Kernel | |
| Sigmoid Kernel |
| Dataset Name | Image Size | Number of Classes | Total Number | Format |
|---|---|---|---|---|
| A | 256 × 256 | 4 | 1000 | .jpg |
| Sample Size | Qualified | Missing | Misaligned |
|---|---|---|---|
| Number of samples | 15 | 15 | 15 |
| Correct test result | 12 | 13 | 13 |
| Accuracy | 80% | 86.6% | 86.6% |
| Category | Linear Kernel | Polynomial Kernel | Gaussian Kernel | Sigmoid Kernel |
|---|---|---|---|---|
| 75% | 76.25% | 86.25% | 71.25% | |
| 74.1% | 72.5% | 88.75% | 68.5% | |
| 76.7 | 74.4% | 87.5% | 70% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Wei, Z.; Yao, L. A Novel Approach to Component Assembly Inspection Based on Mask R-CNN and Support Vector Machines. Information 2019, 10, 282. https://doi.org/10.3390/info10090282
Huang H, Wei Z, Yao L. A Novel Approach to Component Assembly Inspection Based on Mask R-CNN and Support Vector Machines. Information. 2019; 10(9):282. https://doi.org/10.3390/info10090282
Chicago/Turabian StyleHuang, Haisong, Zhongyu Wei, and Liguo Yao. 2019. "A Novel Approach to Component Assembly Inspection Based on Mask R-CNN and Support Vector Machines" Information 10, no. 9: 282. https://doi.org/10.3390/info10090282
APA StyleHuang, H., Wei, Z., & Yao, L. (2019). A Novel Approach to Component Assembly Inspection Based on Mask R-CNN and Support Vector Machines. Information, 10(9), 282. https://doi.org/10.3390/info10090282




