Constructing and Visualizing High-Quality Classifier Decision Boundary Maps †
Abstract
1. Introduction
- How do the depicted decision boundaries differ as a function of the chosen DR technique?
- Which DR techniques are best for a trustworthy depiction of decision boundaries?
2. Background
2.1. Preliminaries
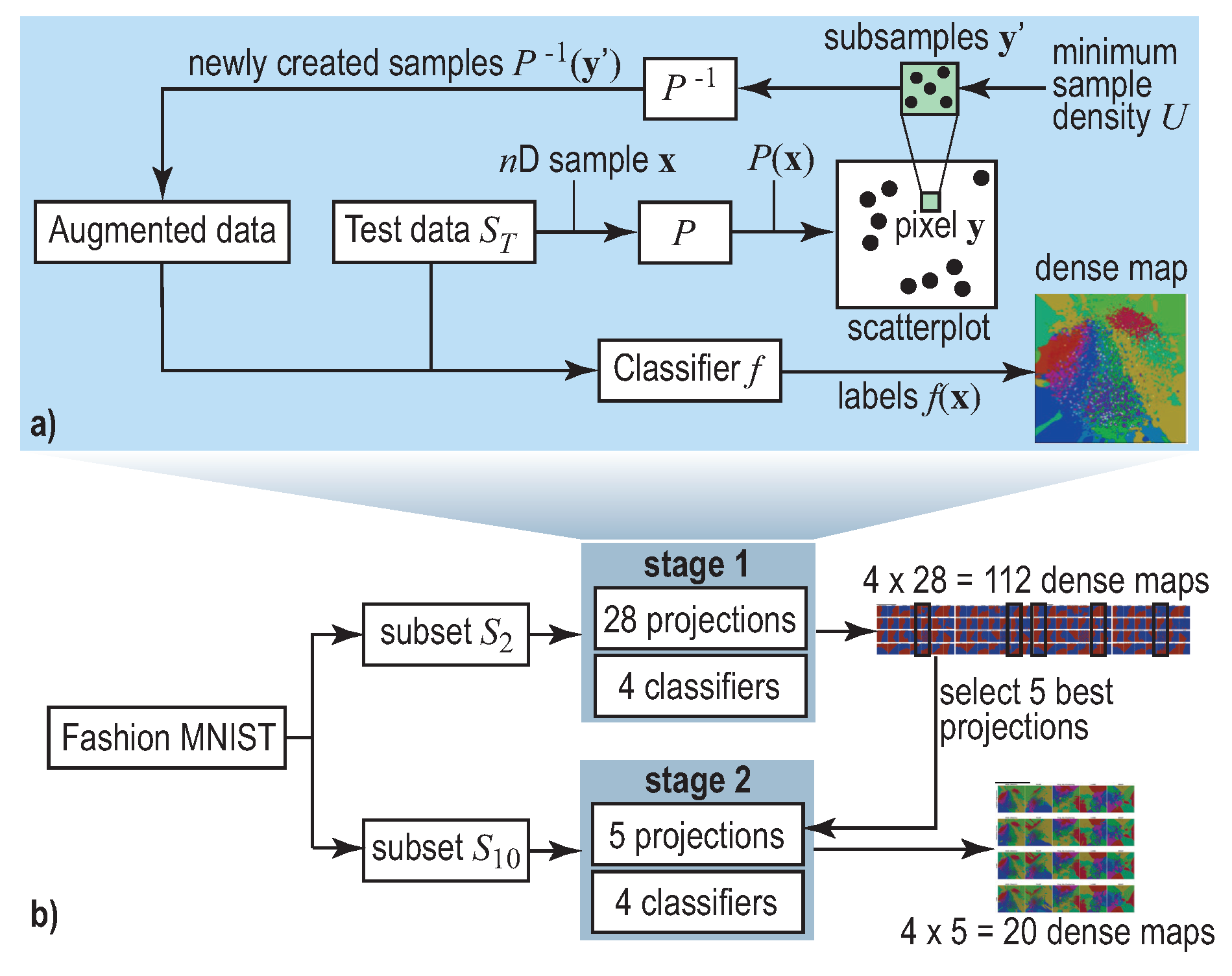
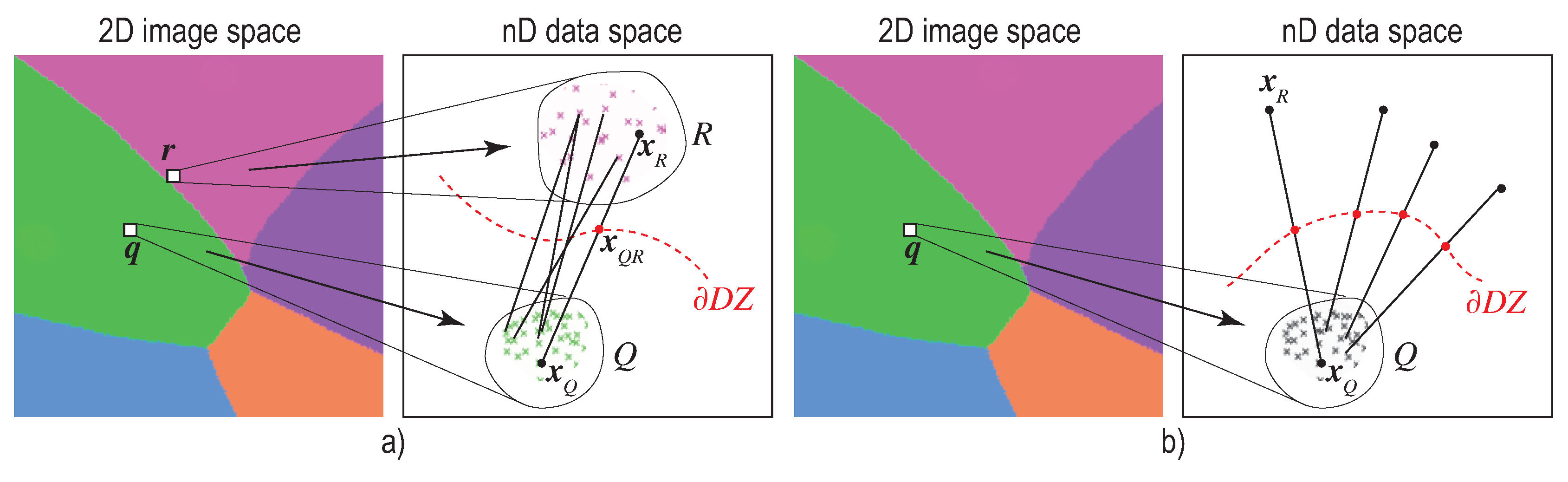
2.2. Decision Boundary Maps
3. Experiment Setup
- : A two-class subset (classes T-Shirt and Ankle Boot) that we hand-picked to be linearly-separable;
- : An all-class subset (T-Shirt, Trouser, Pullover, Dress, Coat, Sandal, Shirt, Sneaker, Bag and Ankle Boot). This is a non-linearly-separable dataset.
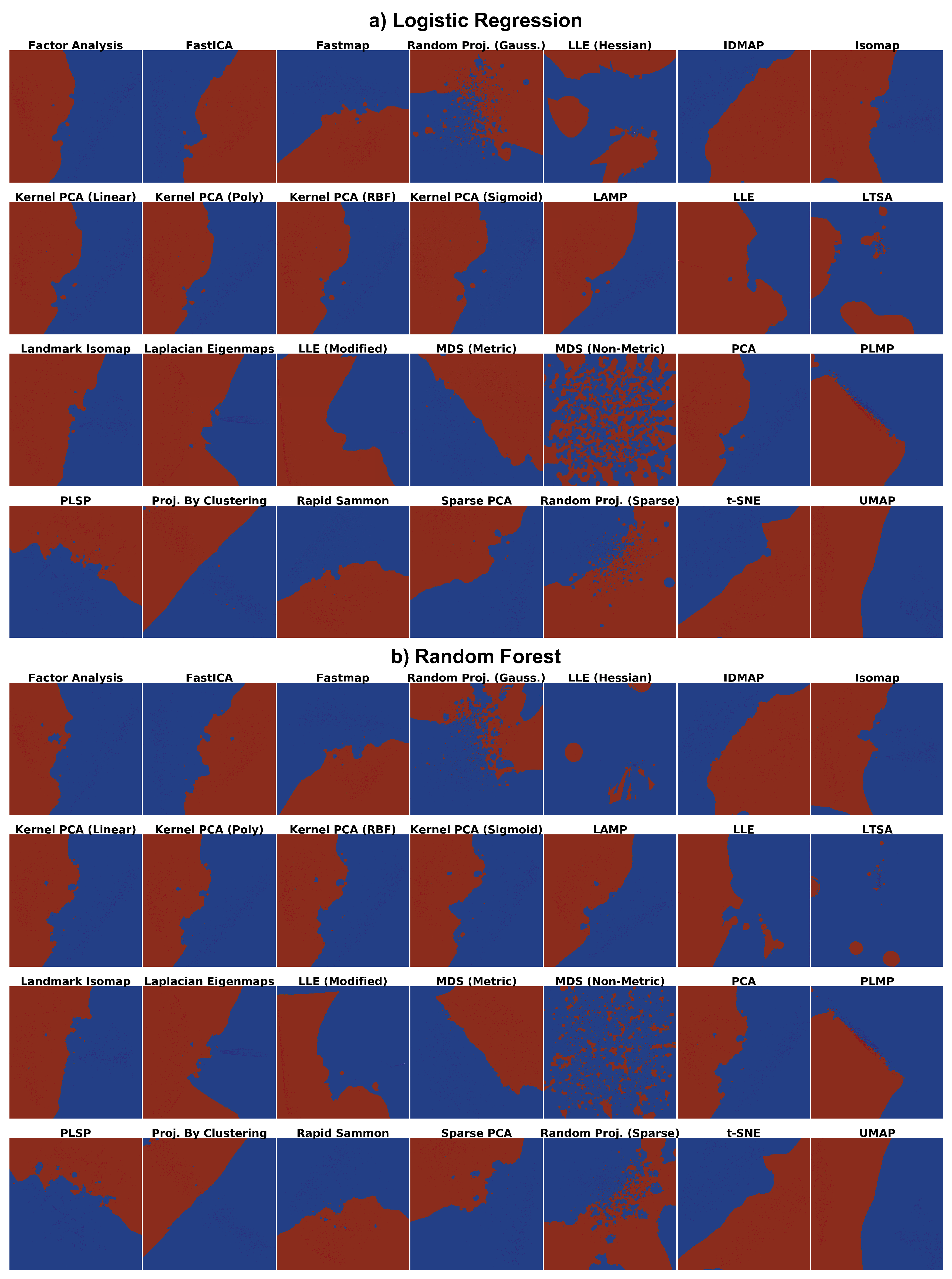
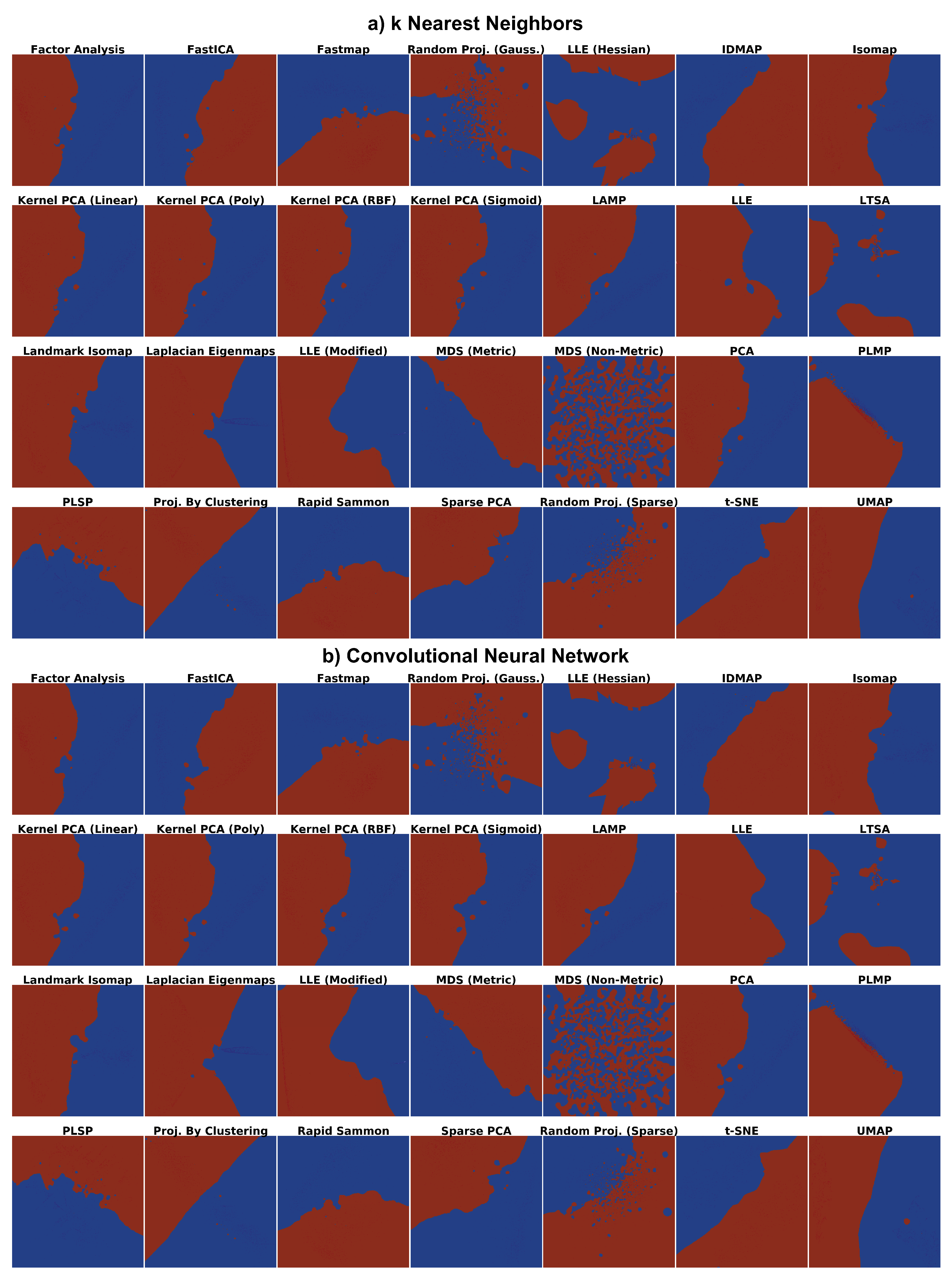
4. Analysis of Evaluation Results
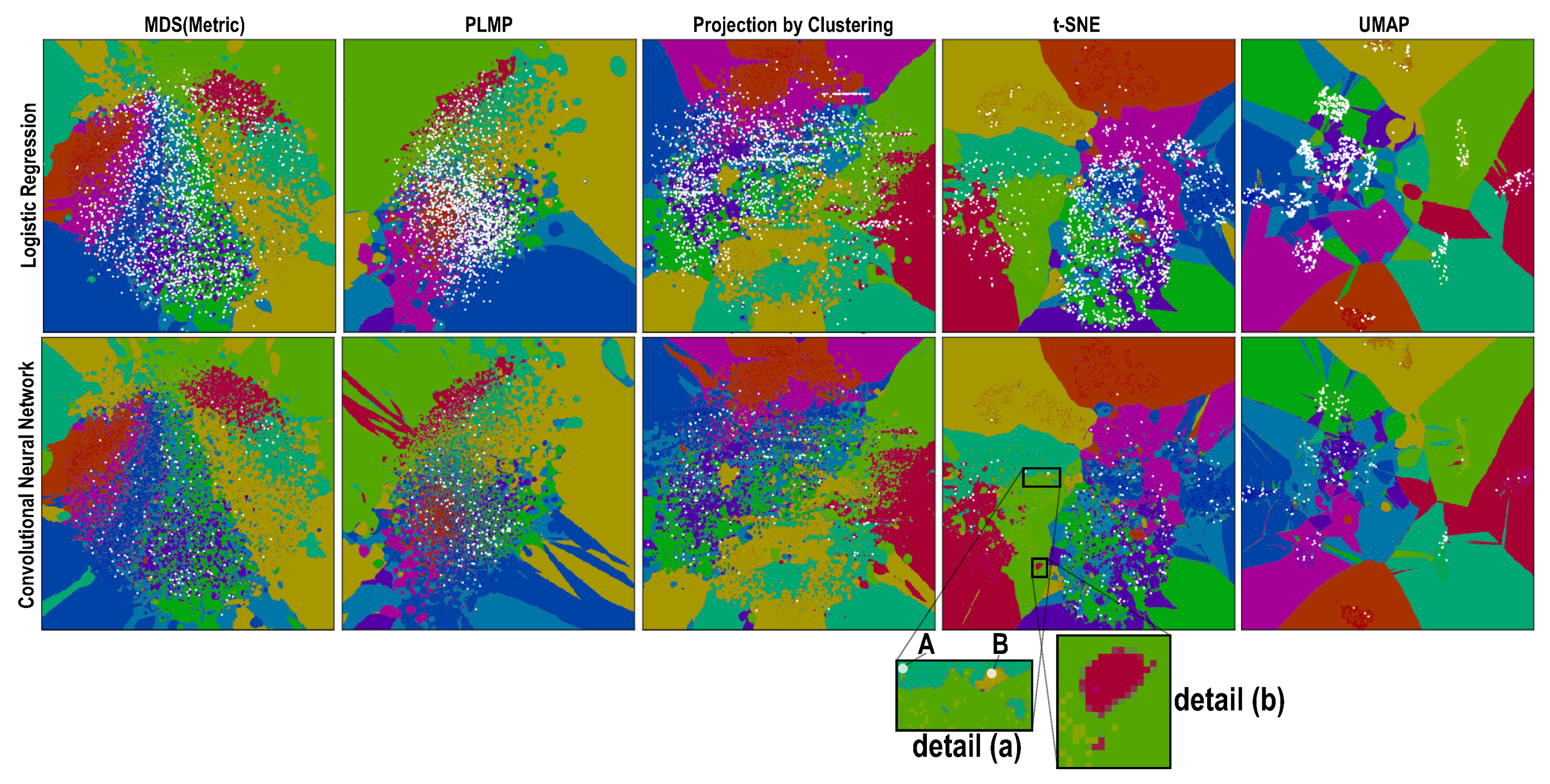
4.1. Phase 1: Picking the Best Projections
4.2. Phase 2: Refined Insights on Complex Data
- (a)
- the island does not actually exist in the high-dimensional space D, so the projection P did a bad job in distance preservation when mapping nD points to 2D; or
- (b)
- the island may exist in D, that is, there exist very similar samples that get assigned different labels. This case can be further split into
- (b1)
- the island actually exists in D, that is, similar points in D do indeed have different labels and the classifier did a good job capturing this; or
- (b2)
- the island does not exist in D, that is, the classifier misclassified points which are similar in the feature space but actually have different labels.
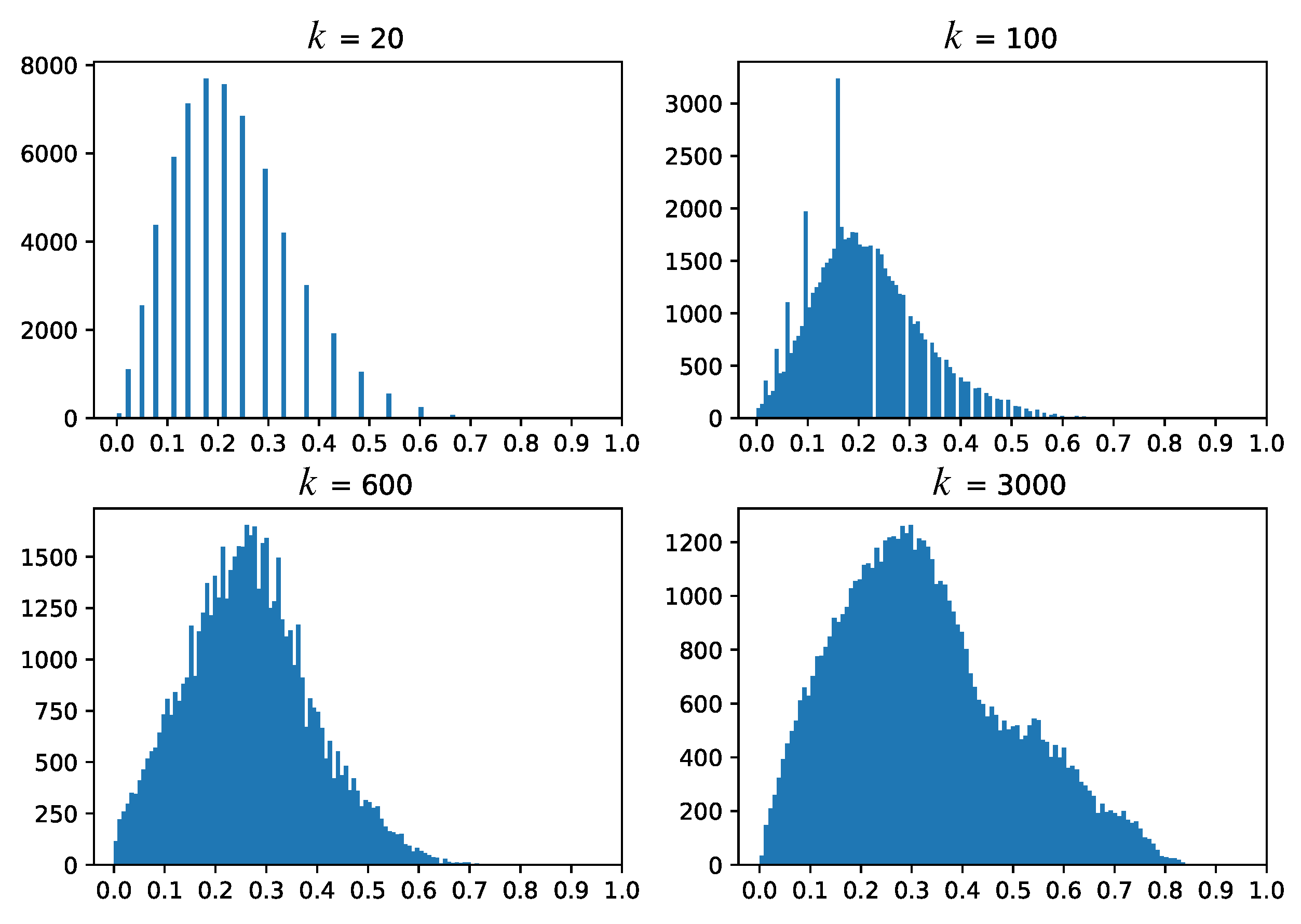
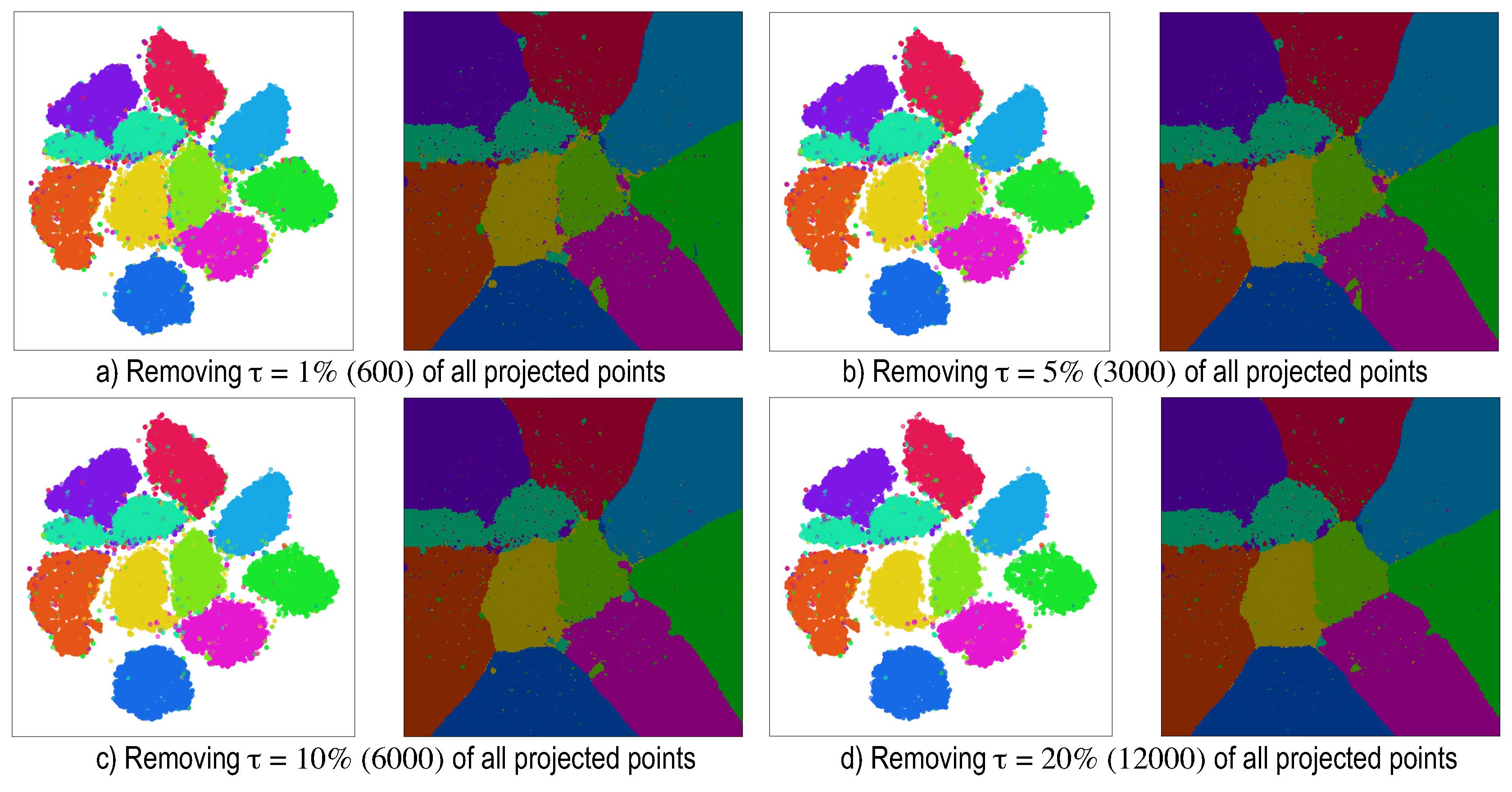
5. Dense Map Filtering
- we need to interpret such maps also in actual inference mode (after testing), when no ground-truth labels are available;
- having to visually filter dense map artifacts like decision boundary jaggies and small islands is tedious.
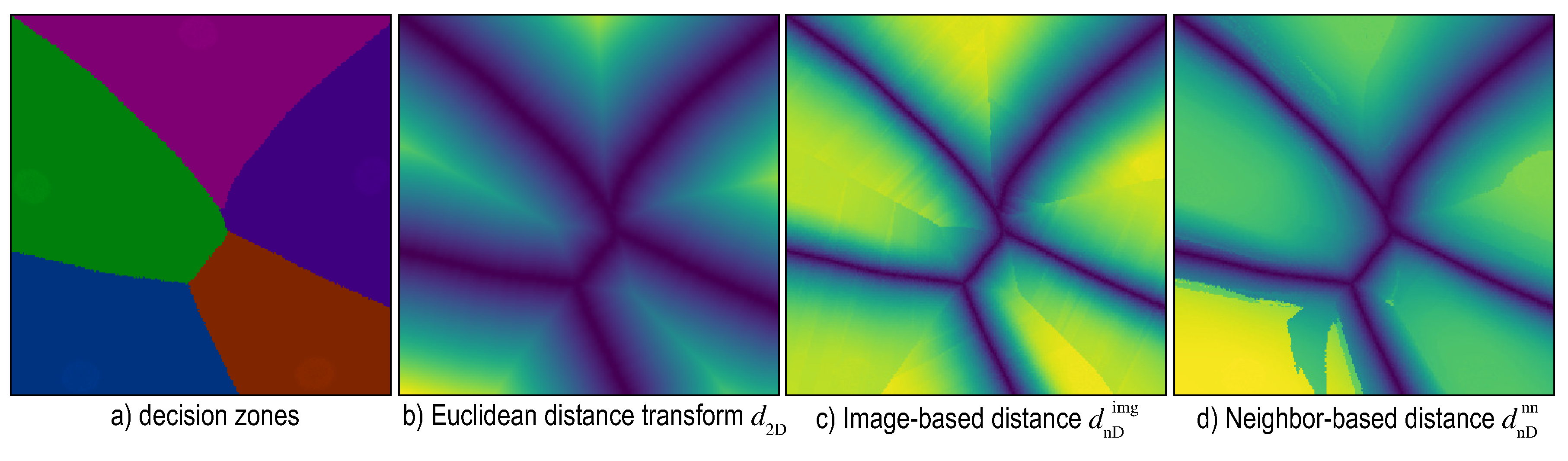
6. Distance-Enriched Dense Maps
6.1. Image-Based Distance Estimation
6.2. Nearest-Neighbor Based Distance Estimation
6.3. Adversarial Based Distance Estimation
6.4. Visualizing Boundary Proximities
Enridged Distance Maps
7. Discussion
- Computation of inverse projection : In Reference [10], this is done by extending non-parametric projections P to parametric forms, by essentially modeling P as the effect of several fixed-bandwidth Gaussian interpolation kernels. This is very similar to the way iLAMP works. However, as shown in Reference [12], iLAMP is far less accurate and far slower than other inverse projection approaches such as NNinv. In our work, we let one freely choose how is implemented, regardless of P. In particular, we use the deep-learning inverse projection NNinv which is faster and more accurate than iLAMP;
- Supervised projections P: In Reference [10], the projection P is implemented using so-called discriminative dimensionality reduction which selects a subset of the nD samples to project, rather than the entire set, so as to reduce the complexity of DR and thus make its inversion more well posed. More precisely, label information for the nD samples is used to guide the projection construction. While this, indeed, makes P easier to invert, we argue that it does not parallel the way typical practitioners work with DR in machine learning. Indeed, in most cases, one has an nD dataset and projects it fully, to reason next about how a classifier trained on that dataset will behave. Driving P by class label is, of course, possible but risky, since P next does not visualize the actual data space. Moreover, discriminative DR is quite expensive to implement ( for N sample points). Note that our outlier filtering (Section 5) achieves roughly the same effect as discriminative DR but at a lower computational cost and with a very simple implementation;
- Distance to boundary: In Reference [10], this quantity, which is next essential for creating dense decision boundary maps, is assumed to be given by the projection algorithm P. Quoting from Reference [10]: “We assume that the label is accompanied by a nonnegative real value which scales with the distance from the closest class boundary.” Obviously, not all classifiers readily provide this distance. Moreover, getting hold of this information (for classifiers which provide it) implies digging into the classifier’s internals and implementation. We avoid such complications by providing ways to estimate the distance to boundary generically, that is, considering the classifier as a black box (Section 6).
- Computational scalability: Reference [10] does not discuss the scalability of their proposal, only hinting that the complexity is squared in the number of input samples. Complexity in the resolution of the decision maps is not discussed. In contrast, we detail our complexity (see Scalability below).
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Why should I trust you?: Explaining the predictions of any classifier. In Proceedings of the ACM SIGMOD KDD, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199. [Google Scholar]
- Féraud, R.; Clérot, F. A methodology to explain neural network classification. Neural Netw. 2002, 15, 237–246. [Google Scholar] [CrossRef]
- Rauber, P.E.; Falcão, A.X.; Telea, A.C. Projections as Visual Aids for Classification System Design. Inf. Vis. 2017, 17, 282–305. [Google Scholar] [CrossRef] [PubMed]
- Rauber, P.E.; Fadel, S.G.; Falcao, A.X.; Telea, A.C. Visualizing the hidden activity of artificial neural networks. IEEE TVCG 2017, 23, 101–110. [Google Scholar] [CrossRef] [PubMed]
- Cutura, R.; Holzer, S.; Aupetit, M.; Sedlmair, M. VisCoDeR: A tool for visually comparing dimensionality reduction algorithms. In Proceedings of the ESANN Université Catholique de Louvain, Bruges, Belgium, 25–27 April 2018. [Google Scholar]
- Hamel, L. Visualization of Support Vector Machines with Unsupervised Learning. In Proceedings of the 2006 IEEE Symposium on Computational Intelligence and Bioinformatics and Computational Biology (CIBCB’06), Toronto, ON, Canada, 28–29 September 2006. [Google Scholar]
- Migut, M.A.; Worring, M.; Veenman, C.J. Visualizing multi-dimensional decision boundaries in 2D. Data Min. Knowl. Discov. 2015, 29, 273–295. [Google Scholar] [CrossRef]
- Rodrigues, F.C.M.; Hirata, R.; Telea, A.C. Image-based visualization of classifier decision boundaries. In Proceedings of the 2018 31st SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Paraná, Brazil, 29 October–11 November 2018; pp. 353–360. [Google Scholar]
- Schulz, A.; Gisbrecht, A.; Hammer, B. Using Discriminative Dimensionality Reduction to Visualize Classifiers. Neural Process. Lett. 2015, 42, 27–54. [Google Scholar] [CrossRef][Green Version]
- Espadoto, M.; Rodrigues, F.C.M.; Telea, A.C. Visual Analytics of Multidimensional Projections for Constructing Classifier Decision Boundary Maps. In Proceedings of the IVAPP. SCITEPRESS, Prague, Czech Republic, 25–27 February 2019; pp. 132–144. [Google Scholar]
- Espadoto, M.; Rodrigues, F.C.M.; Hirata, N.S.T.; Hirata, R., Jr.; Telea, A.C. Deep Learning Inverse Multidimensional Projections. In Proceedings of the EuroVis Workshop on Visual Analytics (EuroVA), Porto, Portugal, 3 June 2019; The Eurographics Association: Geneva, Switzerland, 2019. [Google Scholar]
- LeCun, Y.; Cortes, C. MNIST Handwritten Digits Dataset. 2018. Available online: http://yann.lecun.com/exdb/mnist (accessed on 7 September 2019).
- Krizhevsky, A.; Sutskever, I.; Hinton, G. Imagenet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Manning, C.D.; Schütze, H.; Raghavan, P. Introduction to Information Retrieval; Cambridge University Press: Cambridge, UK, 2008; Volume 39. [Google Scholar]
- Hoffman, P.; Grinstein, G. A survey of visualizations for high-dimensional data mining. In Information Visualization in Data Mining and Knowledge Discovery; Fayyad, U., Grinstein, G., Wierse, A., Eds.; Morgan Kaufmann: Burlington, MA, USA, 2002; pp. 47–82. [Google Scholar]
- Liu, S.; Maljovec, D.; Wang, B.; Bremer, P.T.; Pascucci, V. Visualizing High-Dimensional Data: Advances in the Past Decade. IEEE TVCG 2015, 23, 1249–1268. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. JMLR 2008, 9, 2579–2605. [Google Scholar]
- Joia, P.; Coimbra, D.; Cuminato, J.A.; Paulovich, F.V.; Nonato, L.G. Local Affine Multidimensional Projection. IEEE TVCG 2011, 17, 2563–2571. [Google Scholar] [CrossRef]
- Amorim, E.; Brazil, E.; Daniels, J.; Joia, P.; Nonato, L.; Sousa, M. iLAMP: Exploring high-dimensional spacing through backward multidimensional projection. In Proceedings of the IEEE VAST, Seattle, WA, USA, 14–19 October 2012. [Google Scholar]
- Nonato, L.; Aupetit, M. Multidimensional Projection for Visual Analytics: Linking Techniques with Distortions, Tasks, and Layout Enrichment. IEEE TVCG 2018. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Postma, E. Dimensionality Reduction: A Comparative Review; Tech. Report TiCC TR 2009-005; Tilburg University: Tilburg, The Netherlands, 2009. [Google Scholar]
- Sorzano, C.; Vargas, J.; Pascual-Montano, A. A survey of dimensionality reduction techniques. arXiv 2014, arXiv:1403.2877. [Google Scholar]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv 2017, arXiv:1708.07747v2. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. (JMLR) 2011, 12, 2825–2830. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980v9. [Google Scholar]
- Jolliffe, I.T. Principal Component Analysis and Factor Analysis. In Principal Component Analysis; Springer: Berlin, Germany, 1986; pp. 115–128. [Google Scholar]
- Hyvarinen, A. Fast ICA for noisy data using Gaussian moments. In Proceedings of the IEEE ISCAS, Orlando, FL, USA, 30 May–2 June 1999; Volume 5, pp. 57–61. [Google Scholar]
- Faloutsos, C.; Lin, K. FastMap: A fast algorithm for indexing, data-mining and visualization of traditional and multimedia datasets. ACM SIGMOD Newsl. 1995, 24, 163–174. [Google Scholar] [CrossRef]
- Minghim, R.; Paulovich, F.V.; Lopes, A.A. Content-based text mapping using multi-dimensional projections for exploration of document collections. In Proceedings of the SPIE. Intl. Society for Optics and Photonics, San Jose, CA, USA, 15–19 January 2006; Volume 6060. [Google Scholar]
- Tenenbaum, J.B.; Silva, V.D.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef] [PubMed]
- Schölkopf, B.; Smola, A.; Müller, K. Kernel Principal Component Analysis. In International Conference on Artificial Neural Networks; Springer: Berlin, Germany, 1997; pp. 583–588. [Google Scholar]
- Chen, Y.; Crawford, M.; Ghosh, J. Improved nonlinear manifold learning for land cover classification via intelligent landmark selection. In Proceedings of the IEEE IGARSS, Denver, CO, USA, 31 July–4 August 2006; pp. 545–548. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 9–14 December 2002; pp. 585–591. [Google Scholar]
- Roweis, S.T.; Saul, L.L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- Donoho, D.L.; Grimes, C. Hessian Eigenmaps: Locally Linear Embedding techniques for high-dimensional data. Proc. Natl. Acad. Sci. USA 2003, 100, 5591–5596. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wang, J. MLLE: Modified Locally Linear Embedding using multiple weights. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 3–6 December 2007; pp. 1593–1600. [Google Scholar]
- Zhang, Z.; Zha, H. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment. SIAM J. Sci. Comput. 2004, 26, 313–338. [Google Scholar] [CrossRef]
- Kruskal, J.B. Multidimensional Scaling by optimizing goodness of fit to a nonmetric hypothesis. Psychometrika 1964, 29, 1–27. [Google Scholar] [CrossRef]
- Paulovich, F.V.; Silva, C.T.; Nonato, L.G. Two-phase mapping for projecting massive data sets. IEEE TVCG 2010, 16, 1281–1290. [Google Scholar] [CrossRef] [PubMed]
- Paulovich, F.V.; Eler, D.M.; Poco, J.; Botha, C.P.; Minghim, R.; Nonato, L.G. Piecewise Laplacian-based Projection for Interactive Data Exploration and Organization. Comput. Graph. Forum 2011, 30, 1091–1100. [Google Scholar] [CrossRef]
- Paulovich, F.V.; Minghim, R. Text map explorer: A tool to create and explore document maps. In Proceedings of the International Conference on Information Visualisation (IV), London, UK, 5–7 July 2006; pp. 245–251. [Google Scholar]
- Dasgupta, S. Experiments with Random Projection. In Proceedings of the of the Sixteenth Conference on Uncertainty in Artificial Intelligence, San Francisco, CA, USA, 30 June–3 July 2000; Morgan Kaufmann: Burlington, MA, USA, 2000; pp. 143–151. [Google Scholar]
- Pekalska, E.; de Ridder, D.; Duin, R.P.W.; Kraaijveld, M.A. A new method of generalizing Sammon mapping with application to algorithm speed-up. In Proceedings of the ASCI, Heijen, The Netherlands, 15–17 June 1999; Volume 99, pp. 221–228. [Google Scholar]
- Zou, H.; Hastie, T.; Tibshirani, R. Sparse Principal Component Analysis. J. Comput. Graph. Stat. 2006, 15, 265–286. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2018, arXiv:1802.03426v1. [Google Scholar]
- Aupetit, M. Visualizing distortions and recovering topology in continuous projection techniques. Neurocomputing 2007, 10, 1304–1330. [Google Scholar] [CrossRef]
- Martins, R.M.; Minghim, R.; Telea, A.C. Explaining Neighborhood Preservation for Multidimensional Projections. In Proceedings of the CGVC, London, UK, 16–17 September 2015; pp. 7–14. [Google Scholar]
- Martins, R.; Coimbra, D.; Minghim, R.; Telea, A. Visual Analysis of Dimensionality Reduction Quality for Parameterized Projections. Comput. Graph. 2014, 41, 26–42. [Google Scholar] [CrossRef]
- Amorim, E.; Brazil, E.V.; Mena-Chalco, J.; Velho, L.; Nonato, L.G.; Samavati, F.; Sousa, M.C. Facing the high-dimensions: Inverse projection with radial basis functions. Comput. Graph. 2015, 48, 35–47. [Google Scholar] [CrossRef]
- Schreck, T.; von Landesberger, T.; Bremm, S. Techniques for precision-based visual analysis of projected data. Inf. Vis. 2010, 9, 181–193. [Google Scholar] [CrossRef]
- Fabbri, R.; Costa, L.; Torellu, J.; Bruno, O. 2D Euclidean distance transform algorithms: A comparative survey. ACM Comput. Surv. 2008, 40, 2. [Google Scholar] [CrossRef]
- Cao, T.T.; Tang, K.; Mohamed, A.; Tan, T.S. Parallel Banding Algorithm to Compute Exact Distance Transform with the GPU. In Proceedings of the ACM I3D, Washington, DC, USA, 19–21 February 2010; pp. 83–90. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Van Wijk, J.J.; Telea, A. Enridged contour maps. In Proceedings of the IEEE Visualization 2001 (VIS’01), San Diego, CA, USA, 21–26 October 2001; pp. 69–543. [Google Scholar]
- Benato, B.; Telea, A.; Falcão, A. Semi-Supervised Learning with Interactive Label Propagation guided by Feature Space Projections. In Proceedings of the SIBGRAPI, Paraná, Brazil, 29 October–11 November 2018; pp. 144–152. [Google Scholar]




| Classifier Technique | 2-Class | 10-Class |
|---|---|---|
| Logistic Regression (LR) | 1.0000 | |
| Random Forest (RF) | 1.0000 | 0.8332 |
| k-Nearest Neighbors (KNN) | 0.9992 | 0.8613 |
| Conv. Neural Network (CNN) | 1.0000 | 0.9080 |
| Projection | Parameters |
|---|---|
| Factor Analysis [27] | iter: 1000 |
| Fast Independent Component Analysis (FastICA) [28] | fun: exp, iter: 200 |
| Fastmap [29] | default parameters |
| IDMAP [30] | default parameters |
| Isomap [31] | neighbors: 7, iter: 100 |
| Kernel PCA (Linear) [32] | default parameters |
| Kernel PCA (Polynomial) | degree: 2 |
| Kernel PCA (RBF) | default parameters |
| Kernel PCA (Sigmoid) | default parameters |
| Local Affine Multidimensional Projection (LAMP) [19] | iter: 100, delta: 8.0 |
| Landmark Isomap [33] | neighbors: 8 |
| Laplacian Eigenmaps [34] | default parameters |
| Local Linear Embedding (LLE) [35] | neighbors: 7, iter: 100 |
| LLE (Hessian) [36] | neighbors: 7, iter: 100 |
| LLE (Modified) [37] | neighbors: 7, iter: 100 |
| Local tangent space alignment (LTSA) [38] | neighbors: 7, iter: 100 |
| Multidimensional Scaling (MDS) (Metric) [39] | init: 4, iter: 300 |
| MDS (Non-Metric) | init: 4, iter: 300 |
| Principal Component Analysis (PCA) [27] | default parameters |
| Part-Linear Multidimensional Projection (PLMP) [40] | default parameters |
| Piecewise Least-Square Projection (PLSP) [41] | default parameters |
| Projection By Clustering [42] | default parameters |
| Random Projection (Gaussian) [43] | default parameters |
| Random Projection (Sparse) [43] | default parameters |
| Rapid Sammon [44] | default parameters |
| Sparse PCA [45] | iter: 1000 |
| t-Stochastic Neighbor Embedding (t-SNE) [18] | perplexity: 20, iter: 3000 |
| Uniform Manifold Approximation (UMAP) [46] | neighbors: 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodrigues, F.C.M.; Espadoto, M.; Hirata, R., Jr.; Telea, A.C. Constructing and Visualizing High-Quality Classifier Decision Boundary Maps. Information 2019, 10, 280. https://doi.org/10.3390/info10090280
Rodrigues FCM, Espadoto M, Hirata R Jr., Telea AC. Constructing and Visualizing High-Quality Classifier Decision Boundary Maps. Information. 2019; 10(9):280. https://doi.org/10.3390/info10090280
Chicago/Turabian StyleRodrigues, Francisco C. M., Mateus Espadoto, Roberto Hirata, Jr., and Alexandru C. Telea. 2019. "Constructing and Visualizing High-Quality Classifier Decision Boundary Maps" Information 10, no. 9: 280. https://doi.org/10.3390/info10090280
APA StyleRodrigues, F. C. M., Espadoto, M., Hirata, R., Jr., & Telea, A. C. (2019). Constructing and Visualizing High-Quality Classifier Decision Boundary Maps. Information, 10(9), 280. https://doi.org/10.3390/info10090280





