Correlations and How to Interpret Them
Abstract
1. Correlations
2. Diachronic Correlations
2.1. Predictive Yet Not Causal Models
2.2. Causal Models
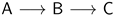
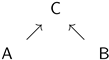
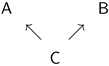
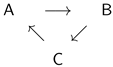
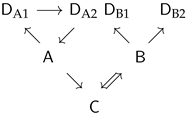
3. Synchronic Correlations
3.1. Data Mining
3.2. Correlations Across Domains
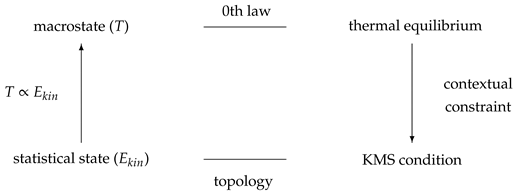
3.3. Nonlocal Quantum Correlations
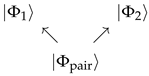
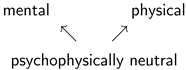
3.4. Mind–Matter Correlations
4. Some Conclusions
I hope that no one still maintains that theories are deduced by strict logical conclusions from laboratory-books, a view which was still quite fashionable in my student days. Theories are established through an understanding inspired by empirical material, an understanding which is best construed ... as an emerging correspondence of internal images and external objects and their behavior. The possibility of understanding demonstrates again the presence of typical dispositions regulating both inner and outer conditions of human beings.
Funding
Acknowledgments
Conflicts of Interest
References
- Hume, D. A Treatise of Human Nature; Norton, D.F., Norton, M.J., Eds.; Clarendon: Oxford, UK, 2007. [Google Scholar]
- Pearson, K. Notes on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar]
- Asuero, A.G.; Sayago, A.; Gonzalez, A.G. The correlation coefficient. An Overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Anscombe, F.J. Graphs in statistical analysis. Am. Stat. 1973, 27, 17–21. [Google Scholar]
- Kantz, H.; Schreiber, T. Nonlinear Timer Series Analysis; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Lyons, L. Open statistical issues in particle physics. Ann. Appl. Stat. 2008, 2, 887–915. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical Methods for Research Workers; Oliver and Boyd: Edinburgh, UK, 1925; p. 43. [Google Scholar]
- Ramsey, F.P. On a problem of formal logic. Proc. Lond. Math. Soc. 1930, s2-30, 264–286. [Google Scholar] [CrossRef]
- Erdös, P.; Rényi, A.; Sós, V.T. On a problem of graph theory. Stud. Sci. Math. Hung. 1966, 1, 215–235. [Google Scholar]
- Calude, C.S.; Longo, G. The deluge of spurious correlations in big data. Found. Sci. 2017, 22, 595–612. [Google Scholar] [CrossRef]
- Vygen, T. Spurious Correlations. Available online: http://www.tylervigen.com/spurious-correlations (accessed on 22 August 2019).
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Champaign, IL, USA, 1949. [Google Scholar]
- Atmanspacher, H. On macrostates in complex multiscale systems. Entropy 2016, 18, 426. [Google Scholar]
- AMS. Statement of the American Meterological Society. 2015. Available online: www.ametsoc.org/ams/index.cfm/about-ams/ams-statements/statements-of-the-ams-in-force/weather-analysis-and-forecasting/ (accessed on 22 August 2019).
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 3, 424–438. [Google Scholar] [CrossRef]
- Reichenbach, H. The Direction of Time; University of California Press: Berkeley, CA, USA, 1956. [Google Scholar]
- Rao, R.P.N.; Ballard, D.H. Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 1999, 2, 79–87. [Google Scholar] [CrossRef]
- Friston, K. Learning and inference in the brain. Neural Netw. 2003, 16, 1325–1352. [Google Scholar] [CrossRef] [PubMed]
- Wiese, W.; Metzinger, T. Vanilla PP for philosophers: A primer on predictive processing. In Philosophy and Predictive Processing; Metzinger, T., Wiese, W., Eds.; MIND Group: Frankfurt, Germany, 2017. [Google Scholar]
- Hinton, G.E. Learning multiple layers of representation. Trends Cognit. Sci. 2007, 11, 428–434. [Google Scholar] [CrossRef] [PubMed]
- Wilson, R.J. Introduction to Graph Theory; Oliver & Boyd: Edinburgh, UK, 1972. [Google Scholar]
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Woodward, J.; Causation and Manipulability. Stanford Encyclopedia of Philosophy. 2016. Available online: https://plato.stanford.edu/entries/causation-mani/#InteCoun (accessed on 22 August 2019).
- Gomez-Marin, A. Causal circuit explanations of behavior: Are necessity and sufficiency necessary and sufficient? In Decoding Neural Circuit Structure and Function; Çelik, A., Wernet, M.F., Eds.; Springer: Berlin, Germany, 2017; pp. 283–306. [Google Scholar]
- Aristotle. Physics; Hackett Publishing: Cambridge, UK, 2018; pp. b17–b20. [Google Scholar]
- Falcon, A.; Aristotle on Causality. Stanford Encyclopedia of Philosophy. 2019. Available online: https://plato.stanford.edu/entries/aristotle-causality/ (accessed on 22 August 2019).
- Hitchcock, C.; Causal Models. Stanford Encyclopedia of Philosophy. 2018. Available online: https://plato.stanford.edu/entries/causal-models/ (accessed on 22 August 2019).
- Atmanspacher, H.; Filk, T. Determinism, causation, prediction and the affine time group. J. Conscious. Stud. 2012, 19, 75–94. [Google Scholar]
- El Hady, A. (Ed.) Closed-Loop Neuroscience; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Harary, F. On the notion of balance of a signed graph. Mich. Math. J. 1953, 2, 143–146. [Google Scholar] [CrossRef]
- Nagel, E. The Structure of Science; Harcourt, Brace & World: New York, NY, USA, 1961. [Google Scholar]
- Cios, K.J.; Pedrycz, W.; Swiniarski, R.W.; Kurgan, L.A. Data Mining. A Knowledge Discovery Approach; Springer: Berlin, Germany, 2010. [Google Scholar]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques; Morgan Kaufmann: Waltham, MA, USA, 2011. [Google Scholar]
- Xu, R.; Wunsch, D.C. Clustering; Addison-Wesley: Reading, UK, 2009. [Google Scholar]
- Lange, T.; Roth, V.; Braun, M.L.; Buhmann, J.M. Stability-based validation of clustering solutions. Neural Comput. 2004, 16, 1299–1323. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R.; Walther, G. Cluste validation by prediction strength. J. Comput. Gr. Stat. 2005, 14, 511–528. [Google Scholar] [CrossRef]
- Cartwright, N. The Dappled World; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Kim, J. Supervenience as a philosophical concept. Metaphilosophy 1990, 21, 1–27. [Google Scholar] [CrossRef]
- Bishop, R.C.; Atmanspacher, H. Contextual emergence in the description of properties. Found. Phys. 2006, 36, 1753–1777. [Google Scholar] [CrossRef]
- Haag, R.; Kastler, D.; Trych-Pohlmeyer, E.B. Stability and equilibrium states. Commun. Math. Phys. 1974, 3, 173–193. [Google Scholar] [CrossRef]
- Kossakowski, A.; Frigerio, A.; Gorini, V.; Verri, M. Quantum detailed balance and the KMS condition. Commun. Math. Phys. 1977, 57, 97–110. [Google Scholar] [CrossRef]
- Sewell, G.L. Quantum Mechanics and Its Emergent Macrophysics; Princeton University Press: Princeton, NJ, USA, 2002. [Google Scholar]
- Poeppel, D. The maps problem and the mapping problem: Two challenges for a cognitive neuroscience of speech and language. Cognit. Neuropsychol. 2012, 29, 34–55. [Google Scholar] [CrossRef] [PubMed]
- Butterfield, J. Laws, causation and dynamics at different levels. Interface Focus 2012, 2, 101–114. [Google Scholar] [CrossRef] [PubMed]
- Ellis, G.F.R. On the nature of causation in complex systems. Trans. R. Soc. S. Afr. 2008, 63, 69–84. [Google Scholar] [CrossRef]
- Atmanspacher, H.; beim Graben, P. Contextual emergence. Scholarpedia 2009, 4, 7997. Available online: http://www.scholarpedia.org/article/Contextual_emergence (accessed on 22 August 2019). [CrossRef]
- Shalizi, C.R.; Moore, C. What is a macrostate? Subjective observations and objective dynamics. arXiv 2003, arXiv:cond-mat/0303625. [Google Scholar]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein-Podolsky-Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Aspect, A.; Grangier, P.; Roger, G. Experimental realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A new violation of Bell’s inequalities. Phys. Rev. Lett. 1982, 49, 91–94. [Google Scholar] [CrossRef]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880–884. [Google Scholar] [CrossRef]
- Gilder, L. The Age of Entanglement; Vintage: New York, NY, USA, 2009. [Google Scholar]
- Maudlin, T. Non-Locality and Relativity; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Giustina, M.; Versteegh, M.A.M.; Wengerowsky, S.; Handsteiner, J.; Hochrainer, A.; Phelan, K.; Steinlechner, F.; Kofler, J.; Larsson, J.-A.; Abellán, C.; et al. Significant-loophole-free test of Bell’s theorem with entangled photons. Phys. Rev. Lett. 2015, 115, 250401. [Google Scholar] [CrossRef]
- Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.L.; Schouten, R.N.; Abellán, C.; et al. Experimental loophole-free violation of a Bell inequality using entangled electron spins separated by 1.3 km. Nature 2015, 526, 682–686. [Google Scholar] [CrossRef] [PubMed]
- Shalm, L.K.; Meyer-Scott, E.; Christensen, B.G.; Bierhorst, P.; Wayne, M.A.; Stevens, M.J.; Gerrits, T.; Glancy, S.; Hamel, D.R.; Allman, M.S.; et al. A strong loophole-free test of local realism. Phys. Rev. Lett. 2015, 115, 250402. [Google Scholar] [CrossRef] [PubMed]
- Li, M.-H.; Wu, C.; Zhang, Y.; Liu, W.-Z.; Bai, B.; Liu, Y.; Zhang, W.; Zhao, Q.; Li, H.; Wang, Z.; et al. Test of local realism into the past without detection and locality loopholes. Phys. Rev. Lett. 2018, 121, 080404. [Google Scholar] [CrossRef] [PubMed]
- Rauch, D.; Handsteiner, J.; Hochrainer, A.; Gallicchio, J.; Friedman, A.S.; Leung, C.; Liu, B.; Bulla, L.; Ecker, S.; Steinlechner, F.; et al. Cosmic Bell test using random measurement settings from high-redshift quasars. Phys. Rev. Lett. 2018, 121, 080403. [Google Scholar] [CrossRef] [PubMed]
- Popescu, S. Nonlocality beyond quantum mechanics. Nat. Phys. 2014, 10, 264–270. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J. The Undivided Universe; Routledge: London, UK, 1993. [Google Scholar]
- Myrvold, W. Philosophical Issues in Quantum Theory. 2016. Available online: https://plato.stanford.edu/entries/qt-issues/#MeasProbForm (accessed on 22 August 2019).
- Atmanspacher, H.; Primas, H. Epistemic and ontic quantum realities. In Time, Quantum, and Information; Castell, L., Ischebeck, O., Eds.; Springer: Berlin, Germany, 2003; pp. 301–321. [Google Scholar]
- Harrigan, N.; Spekkens, R.W. Einstein, incompleteness, and the epistemic view of quantum states. Found. Phys. 2010, 4, 125–157. [Google Scholar] [CrossRef]
- Ismael, J.; Schaffer, J. Quantum holism: Nonseparability as common ground. Synthese 2016. [Google Scholar] [CrossRef]
- Allen, J.-M.A.; Barrett, J.; Horsman, D.C.; Lee, C.M.; Spekkens, R.W. Quantum common causes and quantum causal models. Phys. Rev. X 2017, 7, 031021. [Google Scholar] [CrossRef]
- Bieri, P. Analytische Philosophie des Geistes; Anton Hain Publisher: Königstein, Germany, 1981. [Google Scholar]
- Harbecke, J. Mental Causation; Walter de Gruyter: Berlin, Germany, 2008. [Google Scholar]
- Atmanspacher, H. 20th century variants of dual-aspect thinking (with commentaries and replies). Mind Matter 2014, 12, 245–288. [Google Scholar]
- Atmanspacher, H.; Fuchs, C.A. (Eds.) The Pauli-Jung Conjecture and Its Impact Today; Andrews UK Limited: Luton, UK, 2017. [Google Scholar]
- Schaffer, J. Monism: The priority of the whole. Philos. Rev. 2010, 119, 31–76. [Google Scholar] [CrossRef]
- Jung, C.G.; Pauli, W. The Interpretation of Nature and the Psyche; Pantheon: New York, NY, USA, 1955. [Google Scholar]
- Atmanspacher, H.; Fach, W. A structural-phenomenological typology of mind-matter correlations. J. Anal. Psychol. 2013, 58, 218–243. [Google Scholar] [CrossRef] [PubMed]
- Fach, W.; Atmanspacher, H.; Landolt, K.; Wyss, T.; Rössler, W. A comparative study of exceptional experiences of clients seeking advice and of subjects in an ordinary population. Front. Psychol. 2013, 4, 65. [Google Scholar] [CrossRef] [PubMed]
- Atmanspacher, H.; Fach, W. Exceptional experiences of stable and unstable mental states, understood from a dual-aspect point of view. Philosophies 2019, 4, 7. [Google Scholar] [CrossRef]
- Curie, P. Sur la symétrie dans les phénomènes physiques, symétrie d’un champ électrique et d’un champ magnétique. J. Phys. Theor. Appl. 1894, 3, 393–415. [Google Scholar] [CrossRef]
- Pauli, W. Phänomen und physikalische Realität. Dialectica 1957, 11, 36–48. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atmanspacher, H.; Martin, M. Correlations and How to Interpret Them. Information 2019, 10, 272. https://doi.org/10.3390/info10090272
Atmanspacher H, Martin M. Correlations and How to Interpret Them. Information. 2019; 10(9):272. https://doi.org/10.3390/info10090272
Chicago/Turabian StyleAtmanspacher, Harald, and Mike Martin. 2019. "Correlations and How to Interpret Them" Information 10, no. 9: 272. https://doi.org/10.3390/info10090272
APA StyleAtmanspacher, H., & Martin, M. (2019). Correlations and How to Interpret Them. Information, 10(9), 272. https://doi.org/10.3390/info10090272



