Understanding the Propagation and Control Strategies of Congestion in Urban Rail Transit Based on Epidemiological Dynamics Model
Abstract
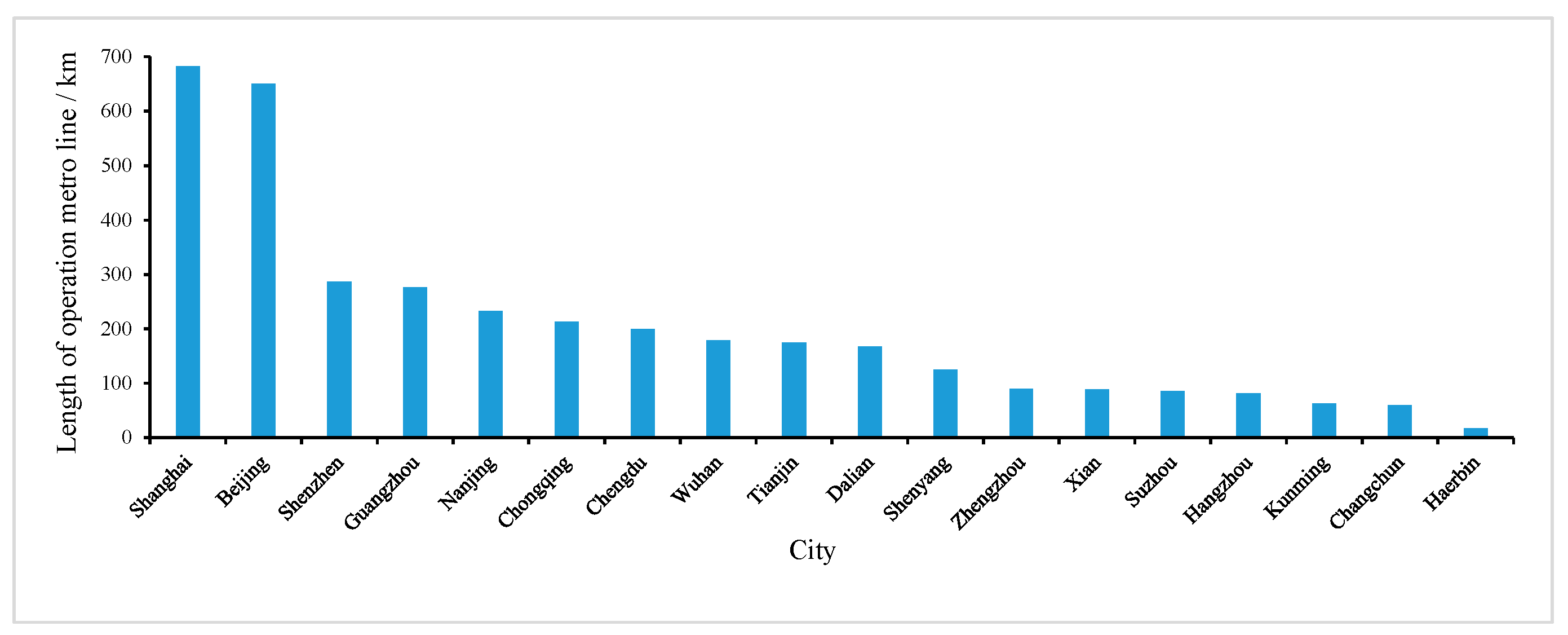
1. Introduction
2. Literature Review
2.1. Passenger Flow Congestion Propagation and Control Strategy
2.2. Epidemiological Dynamics
3. Mathematical Model
3.1. Model Constructing
3.2. Parameter Analysis
4. Numerical Experiment
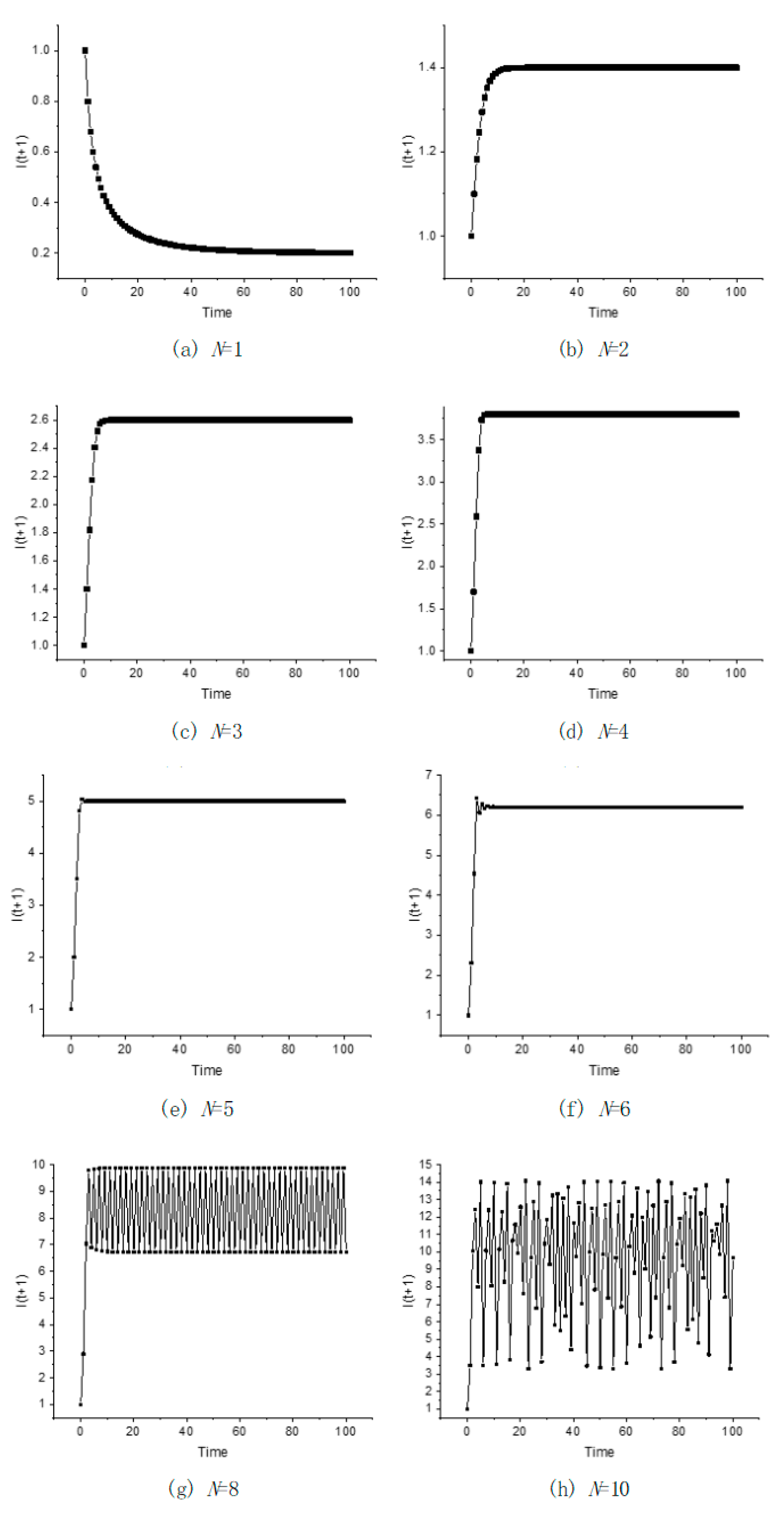
4.1. Sensitivity to Station Degree
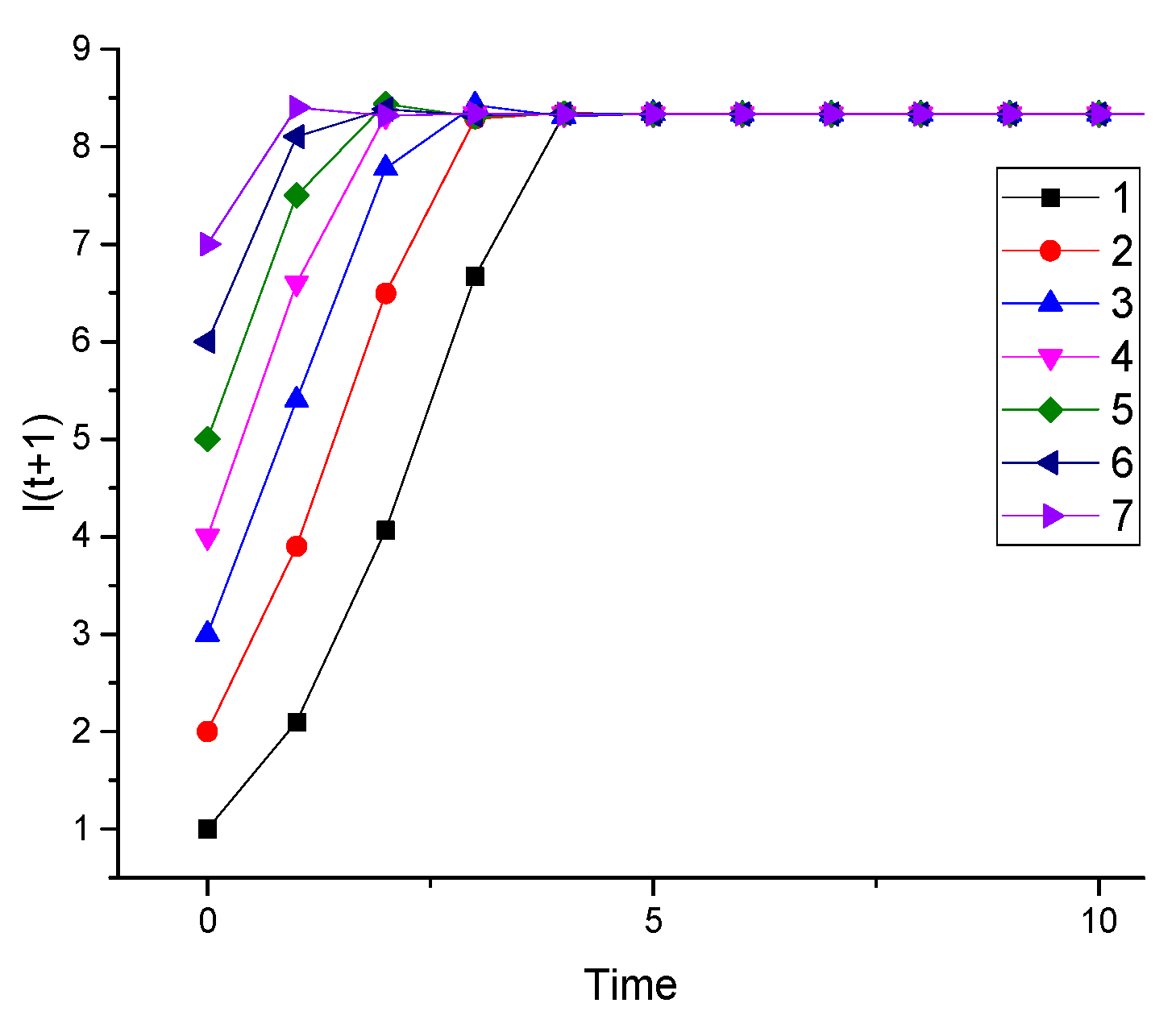
4.2. Sensitivity to Initial Congested Stations
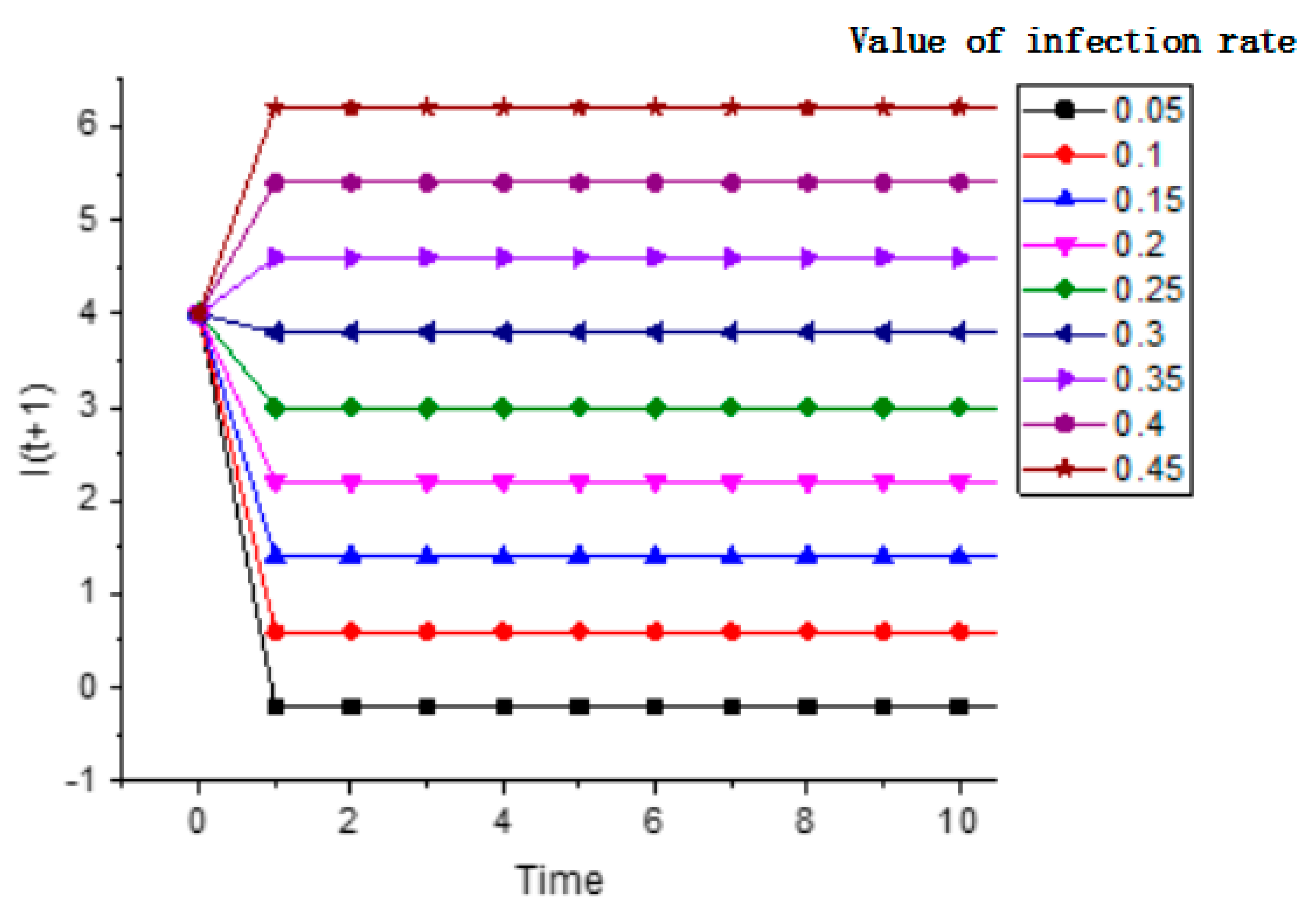
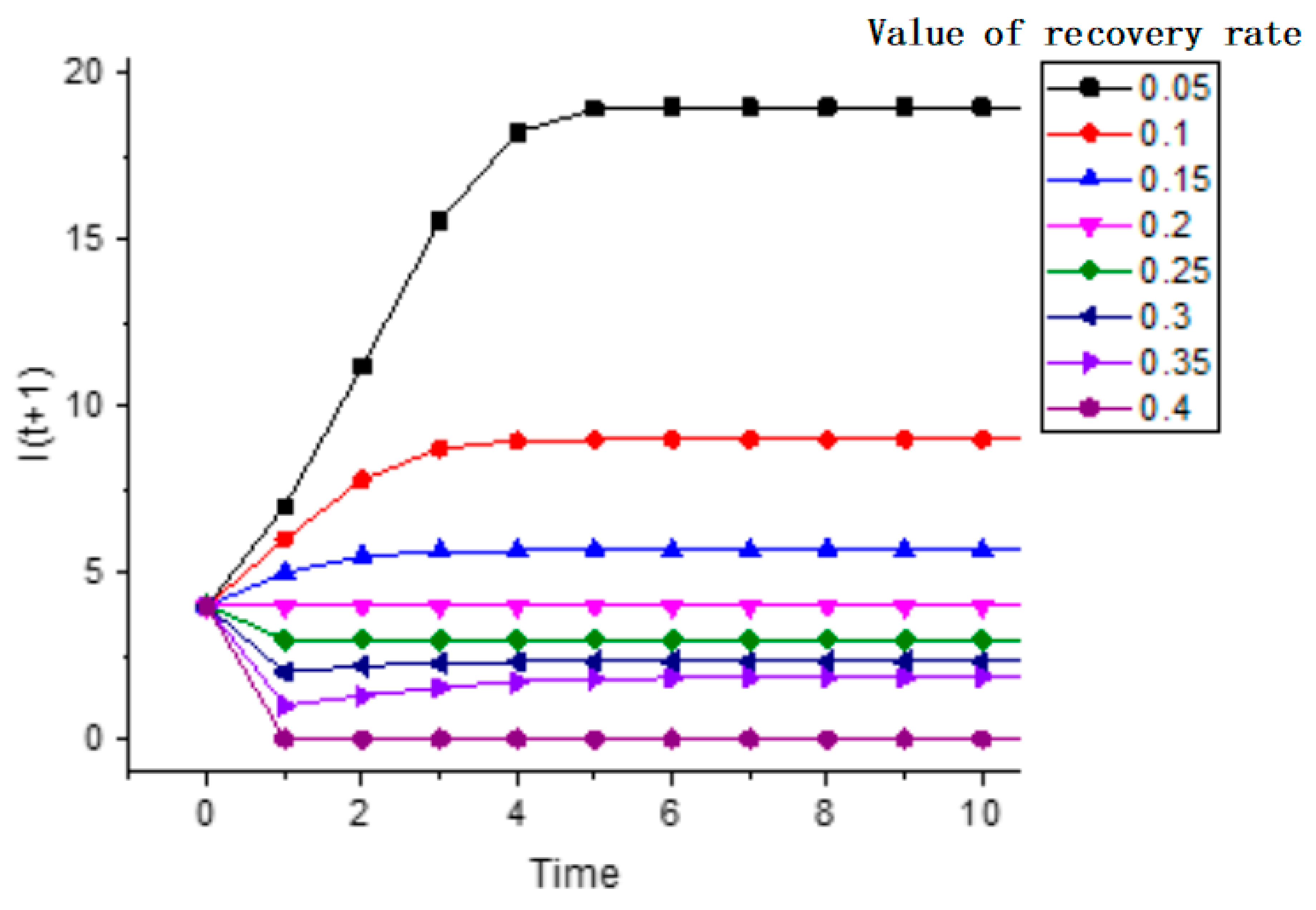
4.3. Sensitivity to Infection Rate and Recovery Rate
5. Control Strategy
5.1. Supply Control
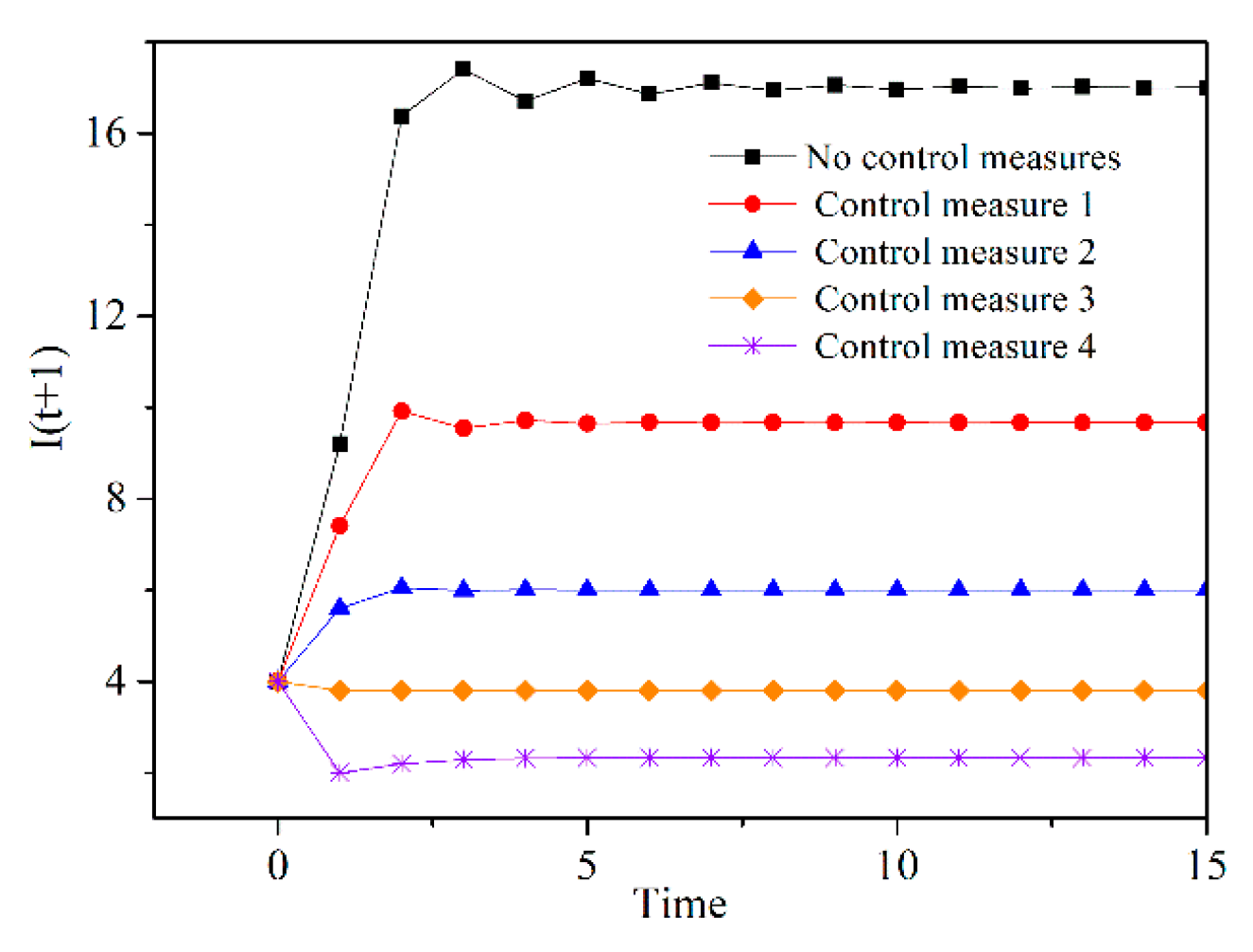
5.2. Demand Control
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Statistical Analysis Report on Urban Rail Transit in 2016; Message of China Association of Metros; China Association of Metros: Beijing, China, 2016; Volume 2.
- Shi, C.; Zhong, M.; Nong, X.; He, L.; Shi, J.; Feng, G. Modeling and safety strategy of passenger evacuation in a metro station in china. Saf. Sci. 2012, 50, 1319–1332. [Google Scholar]
- Trozzi, V.; Gentile, G.; Bell, M.; Kaparias, I. Dynamic user equilibrium in public transport networks with passenger congestion and hyperpaths. Transp. Res. Part B Methodol. 2013, 57, 266–285. [Google Scholar]
- Nuzzolo, A.; Crisalli, U.; Rosati, L. A schedule-based assignment model with explicit capacity constraints for congested transit networks. Transp. Res. Part C Emerg. Technol. 2012, 20, 16–33. [Google Scholar] [CrossRef]
- Mehran, R.; Oyama, A.; Shah, M. Abnormal Crowd Behavior Detection using Social Force Model. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2009), Miami, FL, USA, 20–25 June 2009; Volume 1–4, pp. 935–942. [Google Scholar]
- Van Landegen, D.L.; Chen, X.W. Microsimulation of large-scale evacuations utilizing metrorail transit. Appl. Geogr. 2012, 32, 787–797. [Google Scholar] [CrossRef]
- Kittelson & Associates, Transit Cooperative Research Program, and Transit Development Corporation. Transit Capacity and Quality of Service Manual; No. 100; Transportation Research Board: Washington, DC, USA, 2003. [Google Scholar]
- Mokhtarian, P.L. Reducing road congestion: A reality check—A comment. Transp. Policy 2004, 11, 183–184. [Google Scholar] [CrossRef]
- Oliveira, D.E.L.; Portugal, S.L.D.; Junior, P.W. Determining critical links in a road network: Vulnerability and congestion indicators. Proc. Soc. Behav. Sci. 2014, 162, 158–167. [Google Scholar] [CrossRef]
- Ministry of Construction of the PRC. Urban Rail Transit Project Construction Standards; China Planning Press: Beijing, China, 2008.
- Zhang, Y.; Yan, K. Traffic Congestion Mechanism Analysis Based on Economic Theory. J. Tongji Univ. Nat. Sci. 2006, 34, 359–362. [Google Scholar]
- Zhang, J.G.; Hua, C.C. An appraisal model for the status and solving strategy of traffic jam in Kunming city. J. Yunnan Norm. Univ. 2007, 27, 14–19. [Google Scholar]
- Wu, J.J.; Gao, Z.Y.; Sun, H.J.; Huang, H.J. Congestion in different topologies of traffic networks. Europhys. Lett. 2006, 74, 560–566. [Google Scholar] [CrossRef]
- Long, C.J.; Gao, Y.Z.; Ren, L.H.; Lian, P.A. Urban traffic congestion propagation and bottleneck identification. Sci. China 2008, 51, 948. [Google Scholar] [CrossRef]
- Meloni, S.; Arenas, A.; Moreno, Y.; Stanley, H.E. Traffic-driven epidemic spreading in finite-size scale-free networks. Proc. Natl. Acad. Sci. USA 2009, 106, 897–902. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Gao, Z.; Sun, H. Simulation of traffic congestion with sir model. Mod. Phys. Lett. B 2004, 18, 1537–1542. [Google Scholar] [CrossRef]
- Liu, Z.; Hu, M.B.; Jiang, R.; Wang, W.X.; Wu, Q.S. Method to enhance traffic capacity for scale-free networks. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2007, 76, 037101. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.Q.; Wang, D.; Li, G.J. Enhancing the transmission efficiency by edge deletion in scale-free networks. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2007, 76, 017101. [Google Scholar] [CrossRef] [PubMed]
- Orski, C.K. TDM trends in the United States. IATSS Res. 1998, 22, 25–32. [Google Scholar]
- Wang, W.X.; Yin, C.Y.; Yan, G.; Wang, B.H. Integrating local static and dynamic information for routing traffic. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2006, 74, 016101. [Google Scholar] [CrossRef]
- Wei, L.; Yuan, Z. A Robust Timetabling Model for a Metro Line with Passenger Activity Information. Information 2017, 8, 102. [Google Scholar] [CrossRef]
- Zhao, H.; Gao, Z.Y. Cascade defense via navigation in scale free networks. Eur. Phys. J. B 2007, 57, 95–101. [Google Scholar] [CrossRef]
- Pastorsatorras, R.; Castellano, C.; Mieghem, P.V.; Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 2014, 87, 120–131. [Google Scholar]
- Pu, C.; Li, S.; Yang, X.X.; Xu, Z.; Ji, Z.; Yang, J. Traffic-driven sir epidemic spreading in networks. Phys. A Stat. Mech. Its Appl. 2016, 446, 129–137. [Google Scholar] [CrossRef]
- Code, J.R.; Zaparyniuk, N.E. Transportation dynamics on networks of mobile agents. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2011, 83, 016102. [Google Scholar]
- Yang, H.X.; Wu, Z.X. Suppressing traffic-driven epidemic spreading by use of the efficient routing protocol. J. Stat. Mech. Theory Exp. 2014, 3, 03018. [Google Scholar] [CrossRef]
- Yang, H.X.; Wu, Z.X.; Wang, B.H. Suppressing traffic-driven epidemic spreading by edge-removal strategies. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2013, 87, 064801. [Google Scholar] [CrossRef]
- Kermack, W.O.; Mckendrick, A.G. Contributions to the mathematical theory of epidemics: IV. Analysis of experimental epidemics of the virus disease mouse ectromelia. J. Hyg. 1937, 37, 172. [Google Scholar] [CrossRef]




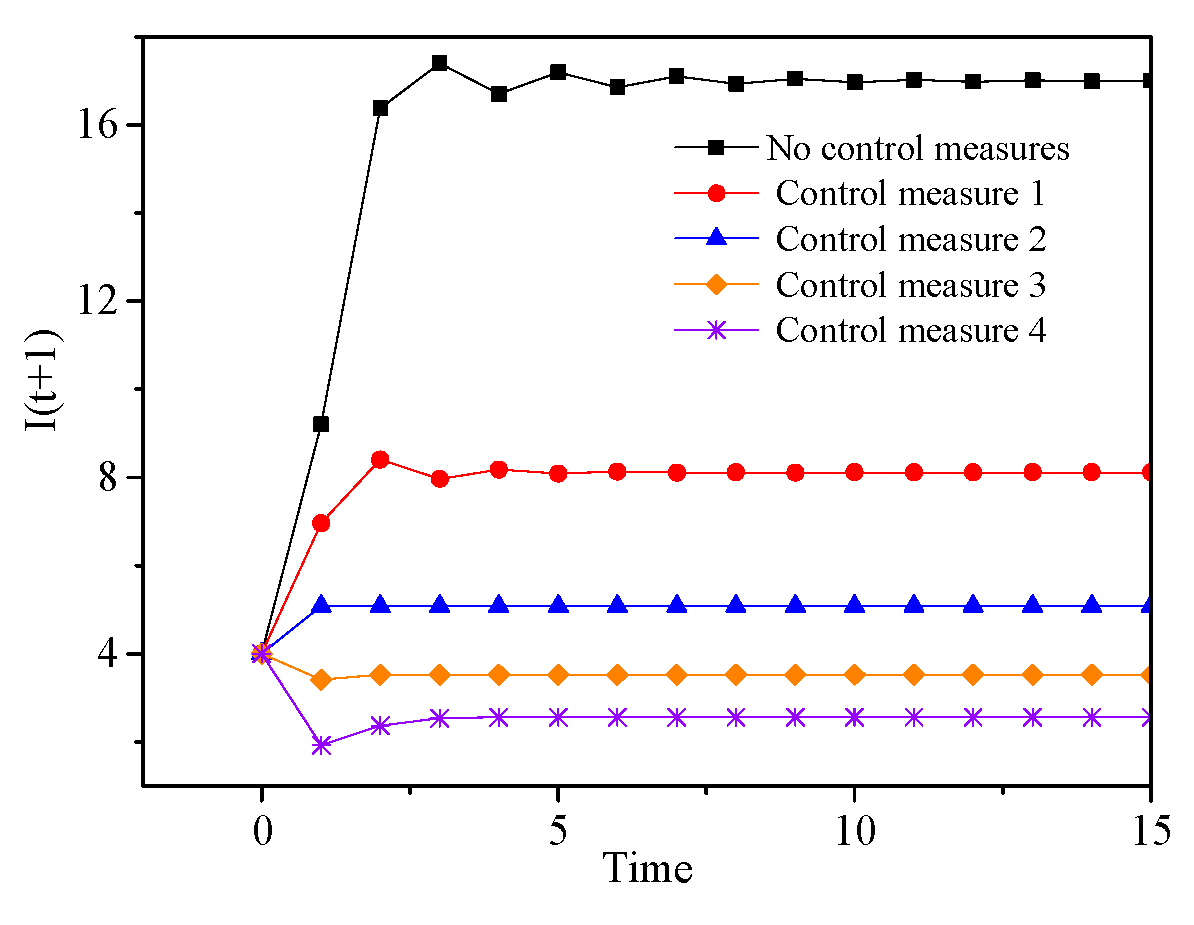
| Supply Control Measures | Max I (t + 1) | ||
|---|---|---|---|
| Without control measure | 0.45 | 0.10 | 17.40 |
| Control measure 1 | 0.41 | 0.18 | 8.40 |
| Control measure 2 | 0.38 | 0.25 | 5.08 |
| Control measure 3 | 0.35 | 0.31 | 3.52 |
| Control measure 4 | 0.32 | 0.36 | 2.56 |
| Level of Restriction | Action Position | Detailed Content |
|---|---|---|
| Level I | Platform/Platform channel | Intercept passenger flow, close channel or change escalator running direction |
| Level II | Subway hall/Gate | Control passenger flow continued to enter the payment area |
| Level III | Station entrances | Control passenger flow into the station |
| Demand Control Measures | Infection Rate β | Max I (t + 1) | |
|---|---|---|---|
| No control measure | 0.45 | 0.10 | 17.40 |
| Control measure 1 | 0.40 | 0.15 | 9.92 |
| Control measure 2 | 0.35 | 0.20 | 6.05 |
| Control measure 3 | 0.30 | 0.25 | 3.80 |
| Control measure 4 | 0.25 | 0.30 | 2.33 |
| Demand Control Measures | Infection Rate β | Recovery Rate λ | Max I (t + 1) |
|---|---|---|---|
| No control measure | 0.45 | 0.10 | 17.40 |
| Control measure 1 | 0.45 | 0.20 | 8.35 |
| Control measure 2 | 0.45 | 0.30 | 5.20 |
| Control measure 3 | 0.45 | 0.40 | 3.58 |
| Control measure 4 | 0.45 | 0.50 | 2.61 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Z.; Zhang, N.; Zhu, L. Understanding the Propagation and Control Strategies of Congestion in Urban Rail Transit Based on Epidemiological Dynamics Model. Information 2019, 10, 258. https://doi.org/10.3390/info10080258
Shi Z, Zhang N, Zhu L. Understanding the Propagation and Control Strategies of Congestion in Urban Rail Transit Based on Epidemiological Dynamics Model. Information. 2019; 10(8):258. https://doi.org/10.3390/info10080258
Chicago/Turabian StyleShi, Zhuangbin, Ning Zhang, and Lei Zhu. 2019. "Understanding the Propagation and Control Strategies of Congestion in Urban Rail Transit Based on Epidemiological Dynamics Model" Information 10, no. 8: 258. https://doi.org/10.3390/info10080258
APA StyleShi, Z., Zhang, N., & Zhu, L. (2019). Understanding the Propagation and Control Strategies of Congestion in Urban Rail Transit Based on Epidemiological Dynamics Model. Information, 10(8), 258. https://doi.org/10.3390/info10080258





