A Template Generation and Improvement Approach for Finger-Vein Recognition
Abstract
1. Introduction
2. Weighted Least Square Regression for Template Generation
2.1. Template Quality Definition for Verification
2.2. Weight Computation
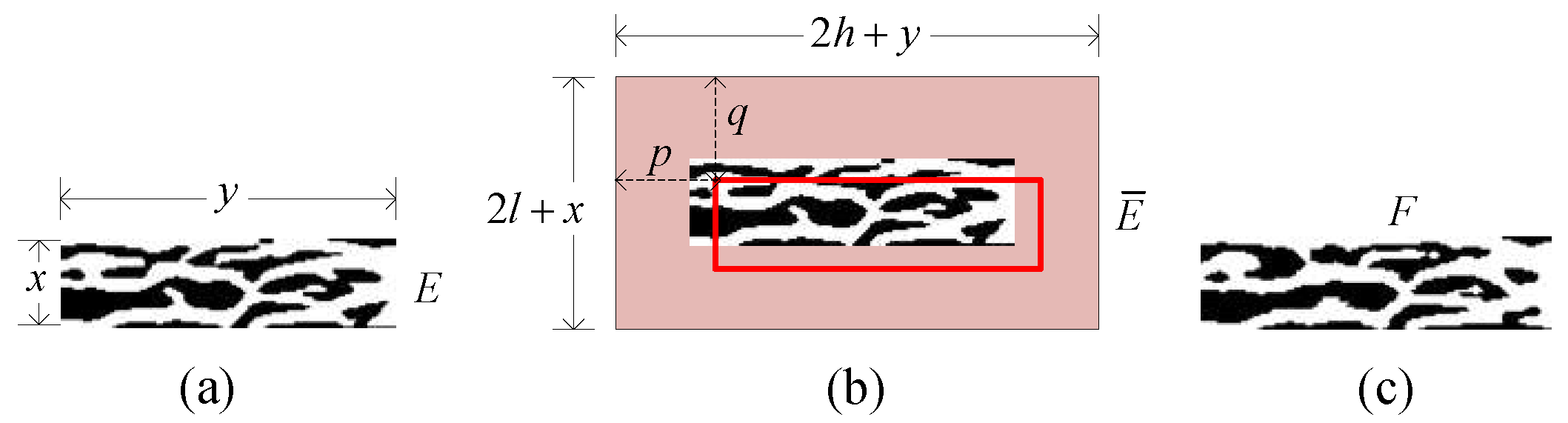
2.2.1. Similarity Computation
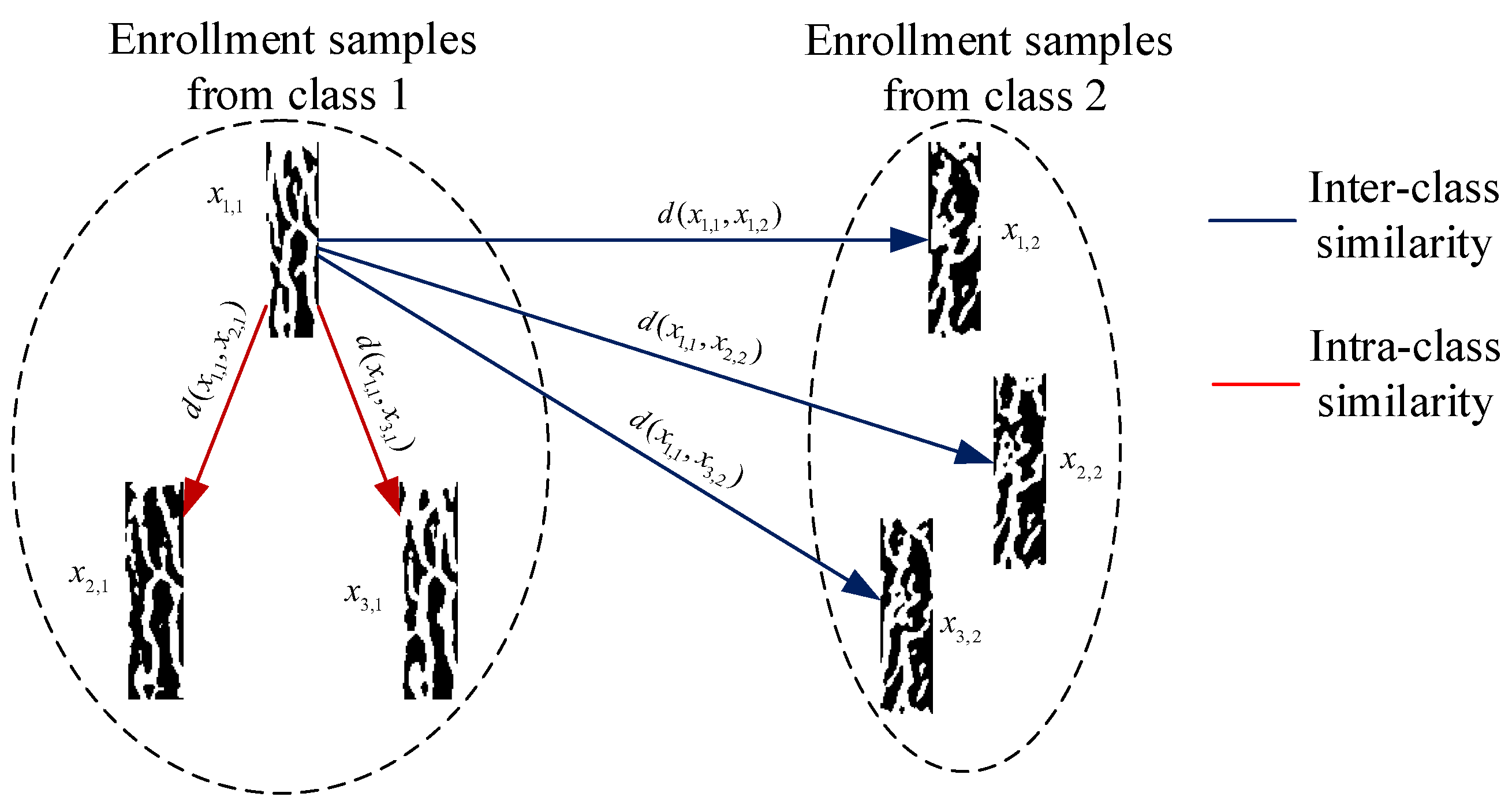
2.2.2. Intra-Class Similarity Computation
2.2.3. Inter-Class Similarity Computation
2.2.4. Similarity Fusion
2.3. Template Generation
3. Finger-Vein Template Improvement
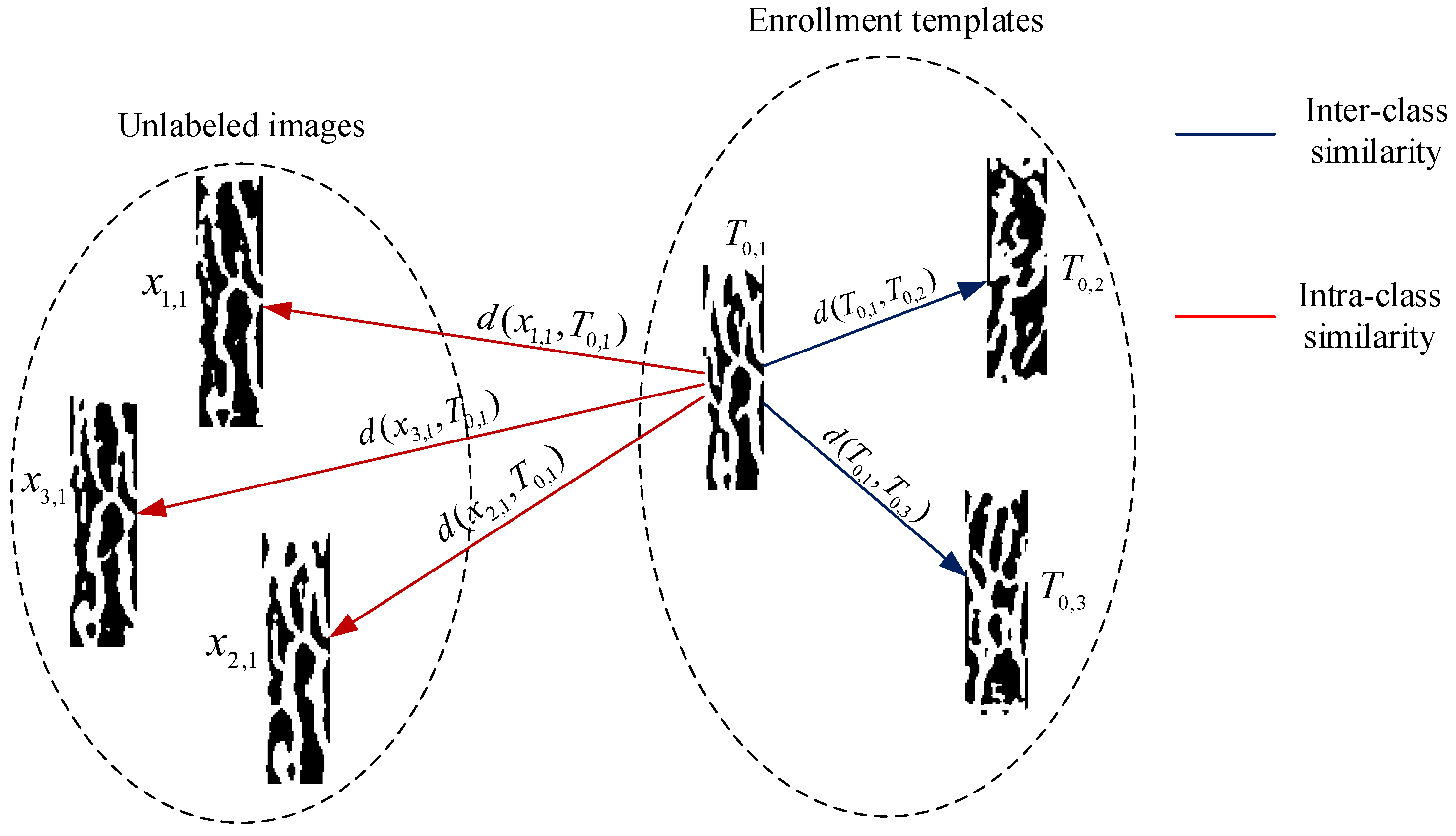
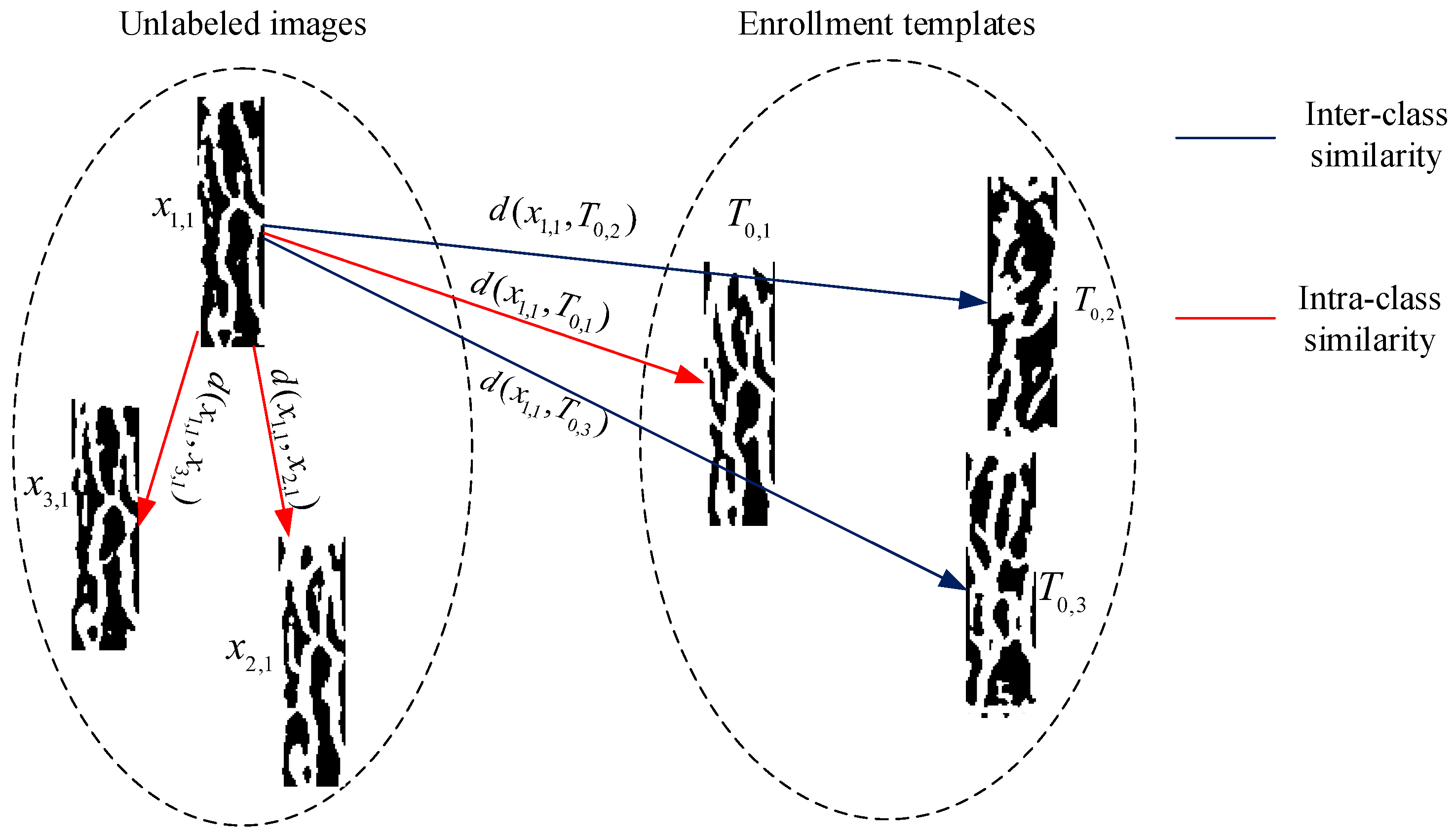
3.1. Weight Computation
3.2. Template Improvement
4. Experiments and Results
4.1. Database
4.1.1. Hkpu Database
4.1.2. Fv-Usm Database
4.1.3. Finger-Vein Feature Extraction and Matching
4.1.4. Experiment Settings for Template Generation and Improvement
4.2. Visual Assessment
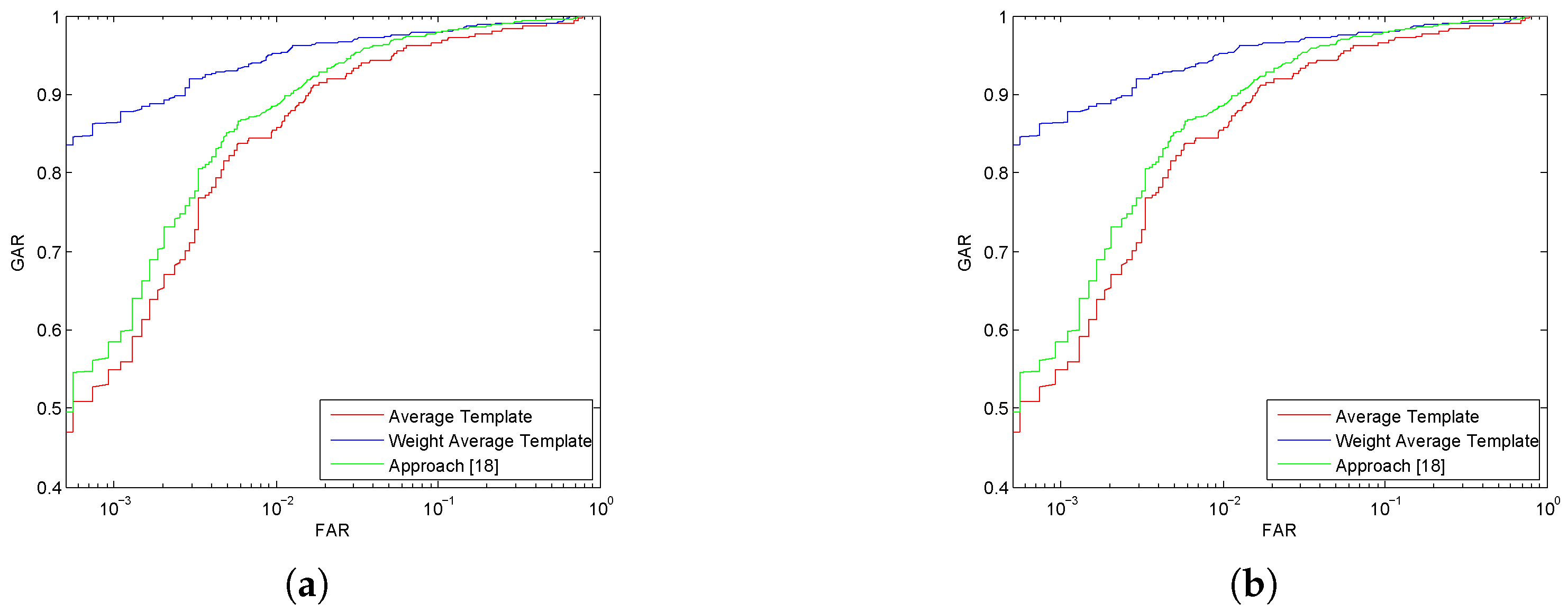
4.3. Experiments Results with Template Generation
4.3.1. Experiments Results with Template Generation for Verification
4.3.2. Experiments Results with Template Generation for Identification
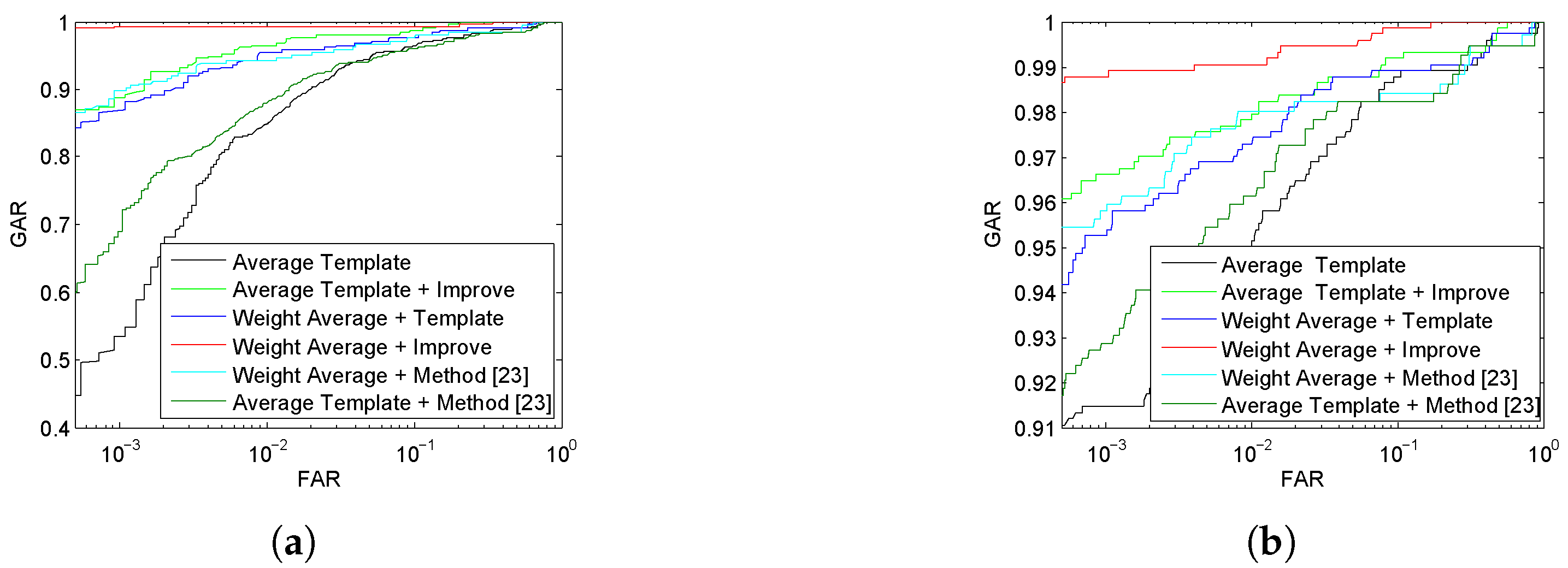
4.4. Experiment Results with Template Improvement
4.4.1. Experiment Results with Template Improvement for Verification
4.4.2. Experiment Results with Template Improvement for Identification
5. Conclusions and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Daugman, J. How iris recognition works. IEEE Trans. Circuits Syst. Video Technol. 2004, 14, 21–30. [Google Scholar] [CrossRef]
- Jain, A.; Hong, L.; Bolle, R. On-line fingerprint verification. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 302–314. [Google Scholar] [CrossRef]
- Turk, M.A.; Pentland, A.P. Face recognition using eigenfaces. In Proceedings of the 1991 IEEE Computer Society Conference on Computer Vision and Pattern Recognition CVPR, Maui, HI, USA, 3–6 June 1991; pp. 586–591. [Google Scholar]
- Kumar, A.; Prathyusha, K.V. Personal authentication using hand vein triangulation and knuckle shape. IEEE Trans. Image Process. 2009, 18, 2127–2136. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Zhou, Y. Human identification using finger images. IEEE Trans. Image Process. 2012, 21, 2228–2244. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Kumar, A. Human identification using palm-vein images. IEEE Trans. Inf. Forensics Secur. 2011, 6, 1259–1274. [Google Scholar] [CrossRef]
- Hashimoto, J. Finger vein authentication technology and its future. In Proceedings of the 2006 Symposium on VLSI Circuits, Honolulu, HI, USA, 15–17 June 2006; pp. 5–8. [Google Scholar]
- Huang, B.; Dai, Y.; Li, R.; Tang, D.; Li, W. Finger-vein authentication based on wide line detector and pattern normalization. In Proceedings of the 2010 20th International Conference on Pattern Recognition ICPR, Istanbul, Turkey, 23–26 August 2010; pp. 1269–1272. [Google Scholar]
- Song, W.; Kim, T.; Kim, H.C.; Choi, J.H.; Kong, H.J.; Lee, S.R. A finger-vein verification system using mean curvature. Pattern Recognit. Lett. 2011, 32, 1541–1547. [Google Scholar] [CrossRef]
- Yang, J.; Shi, Y. Towards finger-vein image restoration and enhancement for finger-vein recognition. Inf. Sci. 2014, 268, 33–52. [Google Scholar] [CrossRef]
- Lee, E.C.; Park, K.R. Image restoration of skin scattering and optical blurring for finger vein recognition. Opt. Lasers Eng. 2011, 49, 816–828. [Google Scholar] [CrossRef]
- Miura, N.; Nagasaka, A.; Miyatake, T. Extraction of finger-vein patterns using maximum curvature points in image profiles. IEICE Trans. Inf. Syst. 2007, 90, 1185–1194. [Google Scholar] [CrossRef]
- Miura, N.A.; Miyatake, T. Feature extraction of finger-vein patterns based on repeated line tracking and its application to personal identification. Mach. Vis. Appl. 2004, 15, 194–203. [Google Scholar] [CrossRef]
- Liu, T.; Xie, J.; Yan, W.; Li, P.; Lu, H. An algorithm for finger-vein segmentation based on modified repeated line tracking. Imaging Sci. J. 2013, 61, 491–502. [Google Scholar] [CrossRef]
- Gupta, P.; Gupta, P. An accurate finger vein based verification system. Digit. Signal Process. 2015, 38, 43–52. [Google Scholar] [CrossRef]
- Yin, Y.; Ning, Y.; Ren, C.; Liu, L. A framework of multitemplate ensemble for fingerprint verification. EURASIP J. Adv. Signal Process. 2012, 1, 1–11. [Google Scholar] [CrossRef]
- Abboud, A.J.; Jassim, S.A. Biometric templates selection and update using quality measures. Mob. Multimedia Image Process. Secur. Appl. 2012, 8406, 7. [Google Scholar] [CrossRef]
- Lumini, A.; Nanni, L. A clustering method for automatic biometric template selection. Pattern Recognit. 2006, 39, 495–497. [Google Scholar] [CrossRef]
- Uludag, U.; Ross, A.; Jain, A. Biometric template selection and update: A case study in fingerprints. Pattern Recognit. 2004, 37, 1533–1542. [Google Scholar] [CrossRef]
- Prabhakar, S.; Jain, A.K. Decision-level fusion in fingerprint verification. Pattern Recognit. 2002, 35, C861–C874. [Google Scholar] [CrossRef]
- Yang, C.; Zhou, J. A comparative study of combining multiple enrolled samples for fingerprint verification. Pattern Recognit. 2006, 39, 2115–2130. [Google Scholar] [CrossRef]
- Hu, Z.; Li, D.; Isshiki, T.; Kunieda, H. Narrow Fingerprint Template Synthesis by Clustering Minutiae Descriptors. IEICE Trans. Inf. Syst. 2017, 100, 1290–1302. [Google Scholar] [CrossRef]
- Jiang, X.; Ser, W. Online fingerprint template improvement. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1121–1126. [Google Scholar] [CrossRef]
- Ryu, C.; Han, Y.; Kim, H. Super-template Generation Using Successive Bayesian Estimation for Fingerprint Enrollment. In Proceedings of the 5th International Conference on Audio- and Video-Based Biometric Person Authentication, Hilton Rye Town, NY, USA, 20–22 July 2005; pp. 710–719. [Google Scholar]
- Uz, T.; Bebis, G.; Erol, A.; Prabhakar, S. Minutiae-based template synthesis and matching for fingerprint authentication. Comput. Vis. Image Underst. 2009, 113, 979–992. [Google Scholar] [CrossRef]
- Marcialis, G.L.; Granger, E.; Didaci, L.; Pisano, A.; Roli, F. Why template self-update should work in biometric authentication systems? In Proceedings of the International Conference on Information Science, Signal Processing and Their Applications, Montreal, QC, Canada, 2–5 July 2012; pp. 1086–1091. [Google Scholar]
- Akhtar, Z.; Ahmed, A.; Erdem, C.E.; Foresti, G.L. Biometric template update under facial aging. In Proceedings of the 2014 IEEE Symposium on Computational Intelligence in Biometrics and Identity Management, Orlando, FL, USA, 9–12 December 2014; pp. 9–15. [Google Scholar]
- Wang, C.; Zhang, J.; Wang, L.; Pu, J.; Yuan, X. Human identification using temporal information preserving gait template. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2164–2176. [Google Scholar] [CrossRef] [PubMed]
- Tolosana, R.; Vera-Rodriguez, R.; Ortega-Garcia, J.; Fierrez, J. Update strategies for HMM-based dynamic signature biometric systems. In Proceedings of the International Workshop on Information Forensics and Security, Rome, Italy, 16–19 November 2016; pp. 1–6. [Google Scholar]
- Nandakumar, K.; Jain, A.K. Biometric template protection: Bridging the performance gap between theory and practice. IEEE Signal Process. Mag. 2015, 32, 88–100. [Google Scholar] [CrossRef]
- Ratha, N.K.; Chikkerur, S.; Connell, J.H.; Bolle, R.M. Generating cancelable fingerprint templates. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 561–572. [Google Scholar] [CrossRef] [PubMed]
- Menotti, D.; Chiachia, G.; Pinto, A.; Schwartz, W.R.; Pedrini, H.; Falcao, A.X.; Rocha, A. Deep representations for iris, face, and fingerprint spoofing detection. IEEE Trans. Inf. Forensics Secur. 2015, 10, 864–879. [Google Scholar] [CrossRef]
- Tome, P.; Vanoni, M.; Marcel, S. On the vulnerability of finger vein recognition to spoofing. In Proceedings of the 2014 International Conference of the Biometrics Special Interest Group (BIOSIG), Darmstadt, Germany, 10–12 September 2014; pp. 1–10. [Google Scholar]
- Liu, Y.; Ling, J.; Liu, Z.; Shen, J.; Gao, C. Finger vein secure biometric template generation based on deep learning. Soft Comput. 2018, 22, 2257–2265. [Google Scholar] [CrossRef]
- Yang, W.; Hu, J.; Wang, S. A finger-vein based cancellable bio-cryptosystem. In Proceedings of the International Conference on Network and System Security, Madrid, Spain, 3–4 June 2013; pp. 784–790. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Seber, G.A.; Lee, A.J. Linear Regression Analysis; John Wiley and Sons: Hoboken, NJ, USA, 2012; Volume 329. [Google Scholar]
- Nagar, A.; Nandakumar, K.; Jain, A.K. Biometric template transformation: A security analysis. In Media Forensics and Security II, Proceedings of the IS&T/SPIE Electronic Imaging, San Jose, CA, USA, 17–21 January 2010; International Society for Optics and Photonics: Bellingham, WA, USA, 2010; Volume 7541, p. 75410O. [Google Scholar]
- Wang, Y.; Rane, S.; Draper, S.C.; Ishwar, P. A theoretical analysis of authentication, privacy, and reusability across secure biometric systems. IEEE Trans. Inf. Forensics Secur. 2012, 7, 1825–1840. [Google Scholar] [CrossRef]
- Lu, J.; Tan, Y.P. Nearest feature space analysis for classification. IEEE Signal Process. Lett. 2011, 18, 55–58. [Google Scholar] [CrossRef]
- Naseem, I.; Togneri, R.; Bennamoun, M. Linear regression for face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2106–2112. [Google Scholar] [CrossRef]
- Chai, X.; Shan, S.; Chen, X.; Gao, W. Locally linear regression for pose-invariant face recognition. IEEE Trans. Image Process. 2007, 16, 1716–1725. [Google Scholar] [CrossRef]
- Asaari, M.S.M.; Suandi, S.A.; Rosdi, B.A. Fusion of band limited phase only correlation and width centroid contour distance for finger based biometrics. Expert Syst. Appl. 2014, 41, 3367–3382. [Google Scholar] [CrossRef]
- Qin, H.; El-Yacoubi, M.A. Deep representation-based feature extraction and recovering for finger-vein verification. IEEE Trans. Inf. Forensics Secur. 2017, 12, 1816–1829. [Google Scholar] [CrossRef]

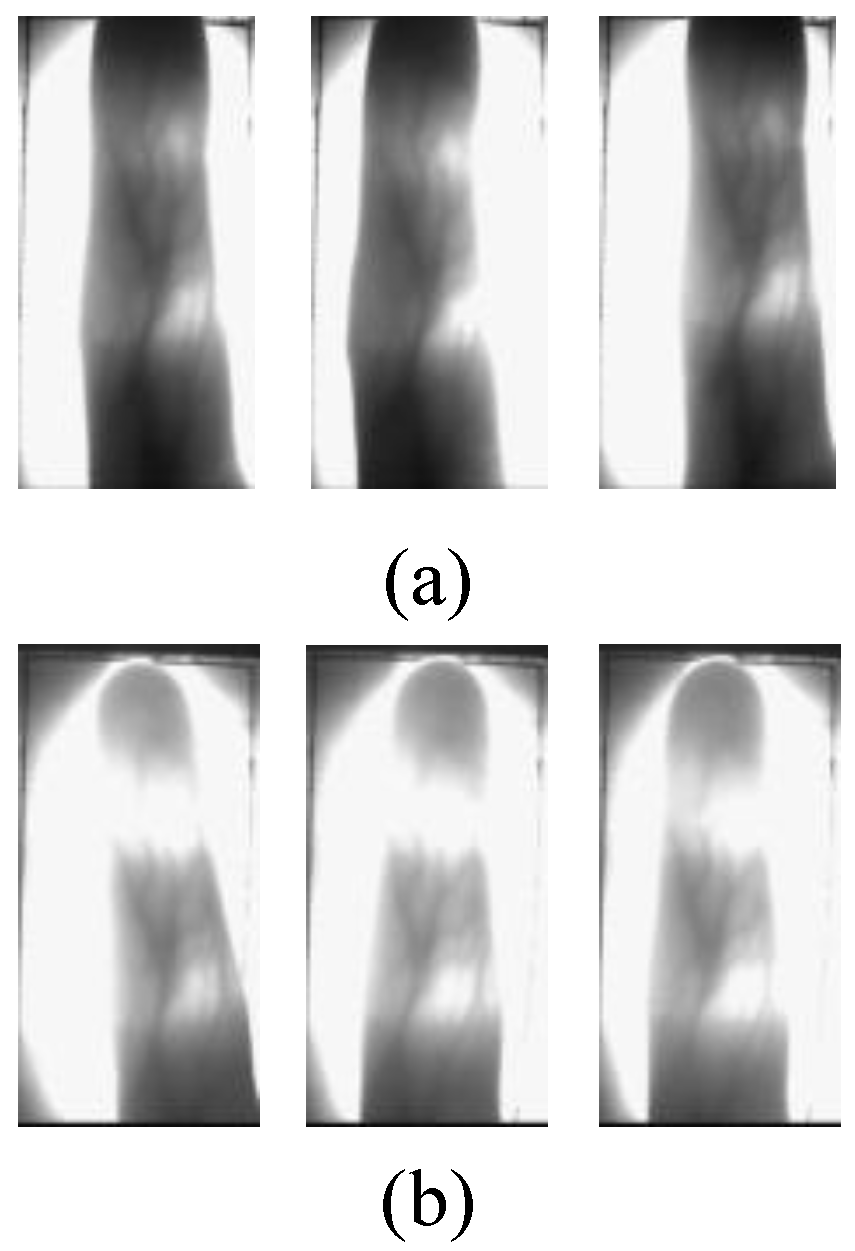






| Methods | HKPU Database | FV-USM Database |
|---|---|---|
| Approach [18] | 4.64 | 2.88 |
| Average template | 5.18 | 2.91 |
| Weight average template | 3.02 | 2.30 |
| Methods | HKPU Database | FV-USM Database |
|---|---|---|
| Approach [18] | 94.44 | 97.56 |
| Average template | 94.29 | 97.49 |
| Weight average template | 95.71 | 97.70 |
| Methods | HKPU Database | FV-USM Database |
|---|---|---|
| Average template | 5.13 | 2.98 |
| Average template + improve | 2.22 | 2.30 |
| Weight average template | 3.49 | 1.90 |
| Weight average template + improve | 0.63 | 0.95 |
| Average template + Method [23] | 3.26 | 2.54 |
| Weight average template + Method [23] | 1.28 | 1.43 |
| Methods | HKPU Database | FV-USM Database |
|---|---|---|
| Average template | 94.92 | 97.29 |
| Weight average template | 95.56 | 97.56 |
| Average template + improve | 98.73 | 99.45 |
| Weight average template + improve | 99.37 | 99.59 |
| Average template + Method [23] | 95.23 | 97.83 |
| Weight average template + Method [23] | 96.19 | 97.97 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, H.; Wang, P. A Template Generation and Improvement Approach for Finger-Vein Recognition. Information 2019, 10, 145. https://doi.org/10.3390/info10040145
Qin H, Wang P. A Template Generation and Improvement Approach for Finger-Vein Recognition. Information. 2019; 10(4):145. https://doi.org/10.3390/info10040145
Chicago/Turabian StyleQin, Huafeng, and Peng Wang. 2019. "A Template Generation and Improvement Approach for Finger-Vein Recognition" Information 10, no. 4: 145. https://doi.org/10.3390/info10040145
APA StyleQin, H., & Wang, P. (2019). A Template Generation and Improvement Approach for Finger-Vein Recognition. Information, 10(4), 145. https://doi.org/10.3390/info10040145





