Youla–Kučera Parametrization with no Coprime Factorization—Single-Input Single-Output Case

Abstract

We present a generalization of the Youla—Kučera parametrization to obtain all stabilizing controllers for single-input and single-output plants. This uses three parameters and can be applied to plants that may not admit coprime factorizations. In this generalization, at most two rational expressions of plants are required, while the Youla–Kučera parametrization requires precisely one rational expression.

1. Introduction

So far, the coprime factorization has played a central role to obtain stabilizing controllers in the factorization approach [1]. The factorization approach to control systems has the advantage that it includes, within a single framework, numerous linear systems such as continuous-time as well as discrete-time systems, lumped as well as distributed systems, one-dimensional as well as multidimensional systems, etc. [1,2]. A transfer function of this approach is considered as the ratio of two stable causal transfer functions. One of the attractive points of the factorization approach is the fact that all stabilizing controllers can be obtained by the Youla–Kučera parametrization with coprime factorization [3,4,5]. This Youla–Kučera parametrization has been used in a wide variety of applications for a long time (e.g., [6,7,8,9,10]).

Unfortunately, the Youla–Kučera parametrization cannot be applied to the plants that do not admit coprime factorizations. Mori, so far, gave the method to obtain part of stabilizing controllers by some different factorizations [11,12]. The objective of this paper is to generalize the Youla–Kučera parametrization to be applicable even for single-input single-output plants that may not admit the coprime factorization. This generalization employs three parameters and requires at most two rational expressions of plant, while the Youla–Kučera parametrization requires only one parameter and one rational expression of plant. The generalization will be expressed with an extension of Bézout identity. We will show that this generalization is equivalent to the parameterization method of [13], which does not require coprime factorization.

This paper is started with preliminaries from Section 2 to recall the notion of the factorization approach. We next state the main results of this paper, generalization of the Bézout identity and the Youla–Kučera parametrization, in Section 3. Then we review, in Section 4, the parametrization of stabilizing controllers of plants which may not admit coprime factorizations [13]. The proofs of the main results are given in Section 5. In Section 6, we give examples for the main results of Section 3. First example will be the plants that admit coprime factorizations. The next one will be Anantharam’s example [14]. Third one will be the discrete-time systems without the unit-delay element.

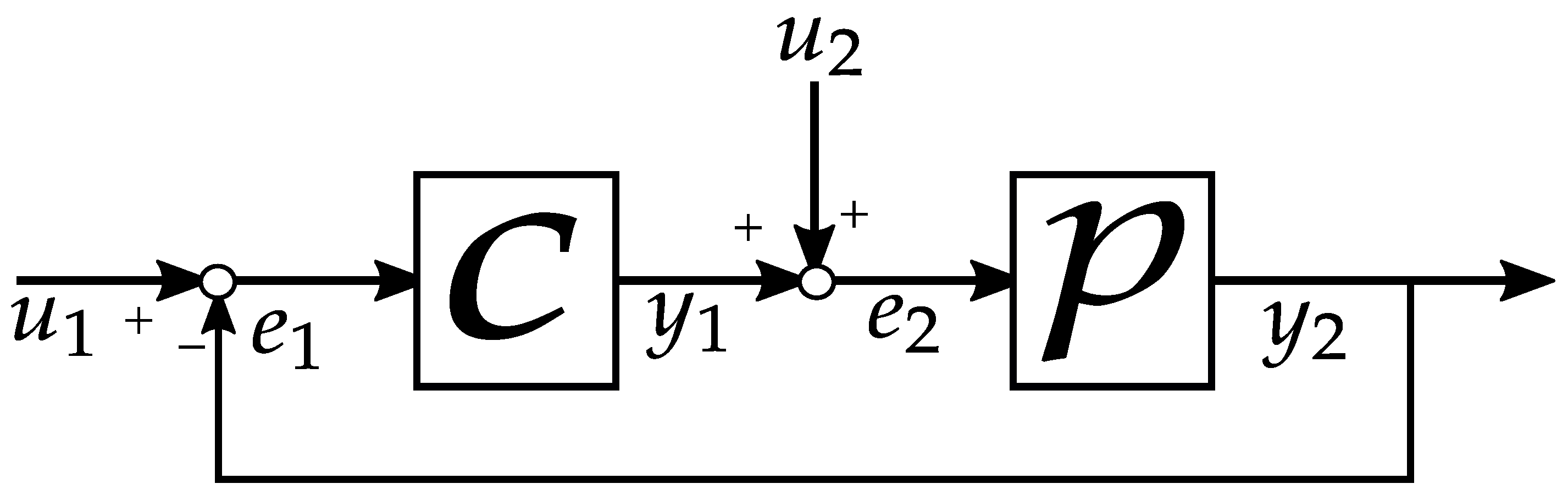
2. Preliminaries

The stabilization problem considered in this paper follows that of [15,16], shown in Figure 1. In the figure, $u_1$ and $u_2$ are inputs, $y_1$ and $y_2$ outputs, and $e_1$ and $e_2$ errors. We employ the symbols used in [13,15] in general. For further details, the reader is referred to [1,2,3,4,5,6,7,8,9,10,11,12,13].

We consider that the set of stable causal transfer functions is an integral domain with identity, denoted by $\mathcal{A}$. The total field of fractions of $\mathcal{A}$ is denoted by $\mathcal{F}$; that is, $\mathcal{F}=\{n/d|n,d\in \mathcal{A},d\ne 0\}$. This $\mathcal{F}$ is considered as the set of all possible transfer functions. Let $\mathcal{Z}$ be a prime ideal of $\mathcal{A}$ with $\mathcal{Z}\ne \mathcal{A}$. Define the subsets $\mathcal{P}$ and ${\mathcal{P}}_{\mathrm{s}}$ of $\mathcal{F}$ as follows: $\mathcal{P}=\{a/b\in \mathcal{F}|a\in \mathcal{A},b\in \mathcal{A}\backslash \mathcal{Z}\}$, ${\mathcal{P}}_{\mathrm{s}}=\{a/b\in \mathcal{F}|a\in \mathcal{Z},b\in \mathcal{A}\backslash \mathcal{Z}\}$. Then, a transfer function in $\mathcal{P}$ (${\mathcal{P}}_{\mathrm{s}}$) is called causal (strictly causal).

Throughout the paper, the plant we consider has single-input and single-output, and its transfer function, which is also called a plant itself simply, is denoted by p and belongs to $\mathcal{P}$ (that is, p is causal).

For $p\in \mathcal{P}$ and $c\in \mathcal{F}$, a matrix $H(p,c)\in {\mathcal{F}}^{2\times 2}$ is defined as

$$H(p,c)=\left[\begin{array}{cc}{(1+pc)}^{-1}& -p{(1+pc)}^{-1}\\ c{(1+pc)}^{-1}& {(1+pc)}^{-1}\end{array}\right]$$

(1)

provided that $1+pc$ is nonzero. This $H(p,c)$ is the transfer matrix from ${\left[u_1{u}_2\right]}^t$ to ${\left[e_1{e}_2\right]}^t$ of the feedback system of Figure 1. If $1+pc$ is nonzero and $H(p,c)\in {\mathcal{A}}^{2\times 2}$, then we say that the plant p is stabilizable, p is stabilized by c, and c is a stabilizing controller of p. In the definition above, we do not mention the causality of the stabilizing controller. Even so, it is known that if a causal plant is stabilizable, there always exists a causal stabilizing controller of the plant, and further if a strictly causal plant is stabilizable, any stabilizing controller of the plant is causal [16] [Propositions 6.1 and 6.2].

We denote by $\mathcal{S}\left(p\right)$ the set of all stabilizing controllers of the plant p, and by $\mathcal{H}\left(p\right)$ the set of $H(p,c)$’s with all stabilizing controllers c of p. The relationship between $\mathcal{S}\left(p\right)$ and $\mathcal{H}\left(p\right)$ is as follows [17]:

$$\mathcal{H}\left(p\right)=\{H(p,c)\in {\mathcal{A}}^{2\times 2}|c\in \mathcal{S}\left(p\right)\},$$

(2)

$$\mathcal{S}\left(p\right)=\left\{h_{11}^{-1}{h}_{21}\in \mathcal{F}|\left[\begin{array}{cc}{h}_{11}& h_{12}\\ h_{21}& h_{11}\end{array}\right]\in \mathcal{H}\left(p\right)\right\}.$$

(3)

Thus, obtaining $\mathcal{S}\left(p\right)$ and obtaining $\mathcal{H}\left(p\right)$ are equivalent to each other.

3. Main Results

We present three main results. The first one is a generalization of the notions of Bézout identity and coprime factorization. The others are generalizations of the Youla–Kučera parametrization that can be applied to stabilizable plants even with no coprime factorization.

Theorem 1.

Let p be a causal plant ($p\in \mathcal{P}$). Then p is stabilizable if and only if there exist $n_1$ and $n_2$ of $\mathcal{A}$, and $d_1$ and $d_2$ of $\mathcal{A}-\left\{0\right\}$ such that

$$\begin{array}{cc}\hfill & p=n_1/d_1=n_2/d_2,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & y_1{n}_1+x_1{d}_1+y_2{n}_2+x_2{d}_2=1\hfill \end{array}$$

(5)

with $y_1$, $x_1$, $y_2$, $x_2$ of $\mathcal{A}$.

Theorem 2.

Let p be a stabilizable causal plant of $\mathcal{P}$ with symbols in Theorem 1 satisfying (4) and (5). Then the set $\mathcal{S}\left(p\right)$ of all stabilizing controllers of p is given as

$$\begin{array}{c}\mathcal{S}\left(p\right)=\{\frac{y_1{d}_1+y_2{d}_2+r{d}_1^2+s{d}_1{d}_2+t{d}_2^2}{x_1{d}_1+x_2{d}_2-r{n}_1{d}_1-s{n}_1{d}_2-t{n}_2{d}_2}\hfill \\ \hfill |r,s,t\in \mathcal{A},(x_1{d}_1+x_2{d}_2-r{n}_1{d}_1-s{n}_1{d}_2-t{n}_2{d}_2\left)isnonzero\right\}.\end{array}$$

(6)

Theorem 3.

Let p be a stabilizable causal plant of $\mathcal{P}$ and c its stabilizing controller. Denote

$$\left[\begin{array}{cc}{h}_{11}& h_{12}\\ h_{21}& h_{11}\end{array}\right]=H(p,c).$$

Then the set $\mathcal{S}\left(p\right)$ of stabilizing controllers of p is given as

$$\begin{array}{c}\mathcal{S}\left(p\right)=\{\frac{h_{21}+h_{11}^{2}r+h_{11}{h}_{21}s+h_{21}^{2}t}{h_{11}+h_{11}{h}_{12}r+h_{12}{h}_{21}s-(1-h_{11})h_{21}t}\hfill \\ \hfill |r,s,t\in \mathcal{A},(h_{11}+h_{11}{h}_{12}r+h_{12}{h}_{21}s-(1-h_{11})h_{21}t\left)isnonzero\right\}.\end{array}$$

(7)

Remark 1.

The fraction in (6) can be rewritten as

$$\frac{(y_1+r{d}_1+s{d}_2)d_1+(y_2+t{d}_2)d_2}{(x_1-r{n}_1)d_1+(x_2-t{n}_2-s{n}_1)d_2}$$

(8)

and, by noting that $n_1{d}_2=n_2{d}_1$,

$$\frac{(y_1+r{d}_1)d_1+(y_2+t{d}_2+s{d}_1)d_2}{(x_1-r{n}_1-s{n}_2)d_1+(x_2-t{n}_2)d_2}.$$

(9)

Observing the fractions above, we might add new parameter $s^{\prime }$ of $\mathcal{A}$ as follows:

$$\frac{(y_1+r{d}_1+s{d}_2)d_1+(y_2+t{d}_2+s^{\prime }{d}_1)d_2}{(x_1-r{n}_1-s^{\prime }{n}_2)d_1+(x_2-t{n}_2-s{n}_1)d_2},$$

where s and $s^{\prime }$ are s of (8) and (9), respectively. Even so, rearranging the numerator and denominator, we have

$$\frac{y_1{d}_1+y_2{d}_2+r{d}_1^2+(s+s^{\prime })d_1{d}_2+t{d}_2^2}{x_1{d}_1+x_2{d}_2-r{n}_1{d}_1-(s+s^{\prime })n_1{d}_2-t{n}_2{d}_2}.$$

Since s and $s^{\prime }$ appear as in the form $s+s^{\prime }$ only, we can remove the parameter $s^{\prime }$ and consider s only.

Remark 2.

Even without considering the coprimeness, any stabilizable plant must satisfy (4) and (5) of Theorem 1. Otherwise, the plant is not stabilizable.

Remark 3.

An attractive point of Theorem 2 is that the set of stabilizing controllers can be obtained in the generalization form of the Youla–Kučera parametrization without the computation of coprime factorization, once the Equations (4) and (5) are obtained. On the other hand, Theorem 3 has the same attractive point once exactly one stabilizing controller is obtained.

Remark 4.

Theorems 1 and 2 are generalizations of Corollary 3.1.11 and Theorem 3.1.13 of [1], respectively.

Remark 5.

Suppose that a plant $p\in \mathcal{P}$ has two rational representations $n_1/d_1$ and $n_2/d_2$ with $n_1$, $n_2$, $d_1$, $d_2\in \mathcal{A}$. Suppose further that we have found $y_1$ and $x_2$ of $\mathcal{A}$ such that

$$y_1{n}_1+x_2{d}_2=1.$$

(10)

In this case, we can apply Theorems 1 and 2 to the plant with $y_2=x_1=0$ as special cases of Theorems 1 and 2, so that a stabilizing controller can be obtained and the set of stabilizing controllers can also be obtained. See Section 6.2 and Section 6.3 for examples.

Note that, in (10), we consider only numerator and denominator of (possibly) different rational expressions. Also, (10) does not mean the coprimeness of the plant. Evan so, once we have (10), we can obtain all stabilizing controllers.

4. Parametrization without Coprime Factorizability

Here, we briefly review the parameterization method of [13], which does not require coprime factorization. This is used to give the proof of Theorem 2.

Theorem 4.

(Single-input single-output version of Theorem 4 and Corollary 1 of [13]) Let p be a stabilizable causal plant of $\mathcal{P}$. Let $H_0$ be $H(p,c)\in {\mathcal{A}}^{2\times 2}$, where c is a fixed stabilizing controller of p. Let $\Omega \left(Q\right)$ be a matrix defined as

$$\Omega \left(Q\right)=\left(H_0-\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]\right)Q\left(H_0-\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]\right)+H_0$$

(11)

with a stable causal and square matrix Q in ${\mathcal{A}}^{2\times 2}$. Then we have the identity

$$\mathcal{H}\left(p\right)=\{\Omega \left(Q\right)|Q\in {\mathcal{A}}^{2\times 2}anddet(\Omega \left(Q\right))isnonzero\}.$$

(12)

Then, any stabilizing controller has the form ${\omega }_{21}{\omega }_{22}^{-1}$, where ${\omega }_{21}$ and ${\omega }_{22}$ are the (2,1)- and (2,2)-entries of $\Omega \left(Q\right)$, provided that ${\omega }_{22}$ is nonzero.

This theorem gives the parameterization with a parameter matrix Q without coprime factorizability of the plant. The parameterization by $\Omega \left(Q\right)$ is independent of the choice of stabilizing controller c.

Decompose Q, $\Omega \left(Q\right)$, and $H(p,c)$ in Theorem 4 as follows:

$$\left[\begin{array}{cc}{q}_{11}& q_{12}\\ q_{21}& q_{22}\end{array}\right]=Q,\left[\begin{array}{cc}{\omega }_{11}& {\omega }_{12}\\ {\omega }_{21}& {\omega }_{22}\end{array}\right]=\Omega \left(Q\right),\left[\begin{array}{cc}{h}_{11}& h_{12}\\ h_{21}& h_{11}\end{array}\right]=H(p,c).$$

(13)

Then, by noting that $-h_{12}{h}_{21}=(1-h_{11})h_{11}$, we have

$$\begin{array}{cc}\hfill {\omega }_{11}={\omega }_{22}& =h_{11}+(h_{11}-1)h_{11}(q_{11}+q_{22})+(h_{11}-1)h_{21}{q}_{12}+h_{11}{h}_{12}{q}_{21},\hfill \\ \hfill {\omega }_{12}& =h_{12}+(h_{11}-1)h_{12}(q_{11}+q_{22})+{(h_{11}-1)}^2{q}_{12}+h_{12}^2{q}_{21},\hfill \\ \hfill {\omega }_{21}& =h_{21}+h_{11}{h}_{21}(q_{11}+q_{22})+h_{21}^2{q}_{12}+h_{11}^2{q}_{21}.\hfill \end{array}$$

In the equations above, $q_{11}$ and $q_{22}$ appears always in the form $(q_{11}+q_{22})$. Thus, the parameter $q_{22}$ can be removed with keeping the parameter $q_{11}$ effective, so that ${\omega }_{11}$, ${\omega }_{12}$, ${\omega }_{21}$, and ${\omega }_{22}$ can be given as

$${\omega }_{11}={\omega }_{22}=h_{11}+(h_{11}-1)h_{11}{q}_{11}+(h_{11}-1)h_{21}{q}_{12}+h_{11}{h}_{12}{q}_{21},$$

(14)

$${\omega }_{12}=h_{12}+(h_{11}-1)h_{12}{q}_{11}+{(h_{11}-1)}^2{q}_{12}+h_{12}^2{q}_{21},$$

(15)

$${\omega }_{21}=h_{21}+h_{11}{h}_{21}{q}_{11}+h_{21}^2{q}_{12}+h_{11}^2{q}_{21}.$$

(16)

Hence, noting that ${\omega }_{11}={\omega }_{22}$, we can express $\mathcal{H}\left(p\right)$ and $\mathcal{S}\left(p\right)$ as follows:

$$\begin{array}{c}\hfill \mathcal{H}\left(p\right)=\left\{\left[\begin{array}{cc}{\omega }_{11}& {\omega }_{12}\\ {\omega }_{21}& {\omega }_{11}\end{array}\right]\right|{\omega }_{11},{\omega }_{12},{\omega }_{21}\mathrm{are}\mathrm{of}\left(14\right),\left(15\right),\left(16\right),\mathrm{respectively},\mathrm{and}{\omega }_{11}\mathrm{is}\mathrm{nonzero}.\},\end{array}$$

(17)

$$\begin{array}{c}\hfill \mathcal{S}\left(p\right)=\left\{{\displaystyle \frac{{\omega }_{21}}{{\omega }_{11}}}|{\omega }_{11},{\omega }_{21}\mathrm{are}\mathrm{of}\left(14\right),\left(16\right),\mathrm{respectively},\mathrm{and}{\omega }_{11}\mathrm{is}\mathrm{nonzero}.\right\},\end{array}$$

(18)

in which the parameters are $q_{11}$, $q_{12}$, and $q_{21}$. In the proof of Theorem 2, we will show that the parametrization of (17) is equal to the set of $H(p,c)$’s based on the right-hand side of (6).

5. Proofs of Theorems 1, 2 and 3

Proof of Theorem 1.

(Only If). Suppose that p is stabilizable. Then, there exists a stabilizing controller c. Thus, $H(p,c)$ of (1) is over $\mathcal{A}$. Let

$$\left[\begin{array}{cc}{h}_{11}& h_{12}\\ h_{21}& h_{11}\end{array}\right]:=H(p,c)=\left[\begin{array}{cc}{(1+pc)}^{-1}& -p{(1+pc)}^{-1}\\ c{(1+pc)}^{-1}& {(1+pc)}^{-1}\end{array}\right]$$

(19)

((1,1)- and (2,2)-entries of $H(p,c)$ are identical).

If c is zero, then p is in $\mathcal{A}$ because of $-h_{12}=p$. Letting $n_1=n_2=p$, $y_1=y_2=x_2=0$, $d_1=d_2=x_1=1$, we have (4) and (5).

In the case where c is nonzero, both $h_{11}$ and $h_{21}$ are nonzero. Letting $n_1=-h_{12}$, $d_1=h_{11}$, $n_2=p{h}_{21}$ ($=1-h_{11}$), $d_2=h_{21}$, $x_1=y_2=1$, $y_1=x_2=0$, we have (4) and (5).

(If). Suppose that there exist $n_1$, $d_1$, $y_1$, $x_1$, $n_2$, $d_2$, $y_2$, $x_2$ of $\mathcal{A}$ with (4) and (5).

Consider the case where $x_1{d}_1+x_2{d}_2$ is zero. This is equal to $1-(y_1{n}_1+y_2{n}_2)$, so that $y_1{n}_1+y_2{n}_2=1$. It follows that at least one of $y_1{n}_1$ and $y_2{n}_2$ is nonzero. Assume, without loss of generality, that $y_1{n}_1$ is nonzero, which means that both $y_1$ and $n_1$ are nonzero. Because $d_1$ is nonzero, $n_1{d}_1$ is a nonzero. Thus, $x_1{d}_1+x_2{d}_2+n_1{d}_1$ is nonzero.

From the previous paragraph, we observe that the expression

$$x_1{d}_1+x_2{d}_2+r_0{n}_1{d}_1+t_0{n}_2{d}_2$$

(20)

is nonzero by appropriate choice of $(r_0,t_0)$ from $(0,0)$, $(1,0)$, $(0,1)$. In the following, we suppose that (20) is nonzero with $(r_0,t_0)$ being one of $(0,0)$, $(1,0)$, $(0,1)$.

From now, we show that the following c is a stabilizing controller of p:

$$c=\frac{y_1{d}_1+y_2{d}_2-r_0{d}_1^2-t_0{d}_2^2}{x_1{d}_1+x_2{d}_2+r_0{n}_1{d}_1+t_0{n}_2{d}_2}.$$

(21)

This is done by showing that $H(p,c)$ with c of (21) is over $\mathcal{A}$, which consists of $h_{11}$, $h_{12}$, $h_{21}$ of (19). Observe that

$$\begin{array}{cc}\hfill h_{11}& =x_1{d}_1+x_2{d}_2+r_0{n}_1{d}_1+t_0{n}_2{d}_2,\hfill \\ \hfill h_{12}& =-(x_1{n}_1+x_2{n}_2+r_0{n}_1^2+t_0{n}_2^2),\hfill \\ \hfill h_{21}& =y_1{d}_1+y_2{d}_2-r_0{d}_1^2-t_0{d}_2^2,\hfill \end{array}$$

which are all in $\mathcal{A}$, so that $H(p,c)$ is over $\mathcal{A}$. Further, $1+pc$ is $1/(x_1{d}_1+x_2{d}_2+r_0{n}_1{d}_1+t_0{n}_2{d}_2)$, which is nonzero. Hence, c is a stabilizing controller of p. Therefore, p is stabilizable. □

Remark 6.

Analogously to the construction of (20), we can make $x_1{d}_1+x_2{d}_2+r_0{n}_1{d}_1+t_0{n}_2{d}_2$ not in $\mathcal{Z}$ with $(r_0,t_0)$ being one of $(0,0)$, $(1,0)$, $(0,1)$, so that c of (21) is causal. This fact can be shown by discussion analogous to the proof above.

Proof of Theorem 2.

Suppose that p is stabilizable.

We denote by $\overline{\mathcal{S}}\left(p\right)$ the right-hand side of (6). We also introduce $\overline{\mathcal{H}}\left(p\right)$, by virtue of the relation (2), as follows:

$$\overline{\mathcal{H}}\left(p\right)=\left\{H(p,c)\right|c\in \overline{\mathcal{S}}\left(p\right)\}.$$

This $\overline{\mathcal{H}}\left(p\right)$ is expressed as follows:

$$\begin{array}{c}\overline{\mathcal{H}}\left(p\right)=\{\left[\begin{array}{cc}{x}_1{d}_1+x_2{d}_2-r{n}_1{d}_1-s{n}_1{d}_2-t{n}_2{d}_2& -(x_1{n}_1+x_2{n}_2-r{n}_1^2-s{n}_1{n}_2-t{n}_2^2)\\ y_1{d}_1+y_2{d}_2+r{d}_1^2+s{d}_1{d}_2+t{d}_2^2& x_1{d}_1+x_2{d}_2-r{n}_1{d}_1-s{n}_1{d}_2-t{n}_2{d}_2\end{array}\right]\hfill \\ \hfill |r,s,t\in \mathcal{A},x_1{d}_1+x_2{d}_2-r{n}_1{d}_1-s{n}_1{d}_2-t{n}_2{d}_2\mathrm{is}\mathrm{nonzero}\}\end{array}$$

(22)

(The determinant of the matrix in (22) is equal to $x_1{d}_1+x_2{d}_2-r{n}_1{d}_1-s{n}_1{d}_2-t{n}_2{d}_2$).

Thus, the proof of Theorem 2 is achieved by showing $\overline{\mathcal{H}}\left(p\right)=\mathcal{H}\left(p\right)$, which is done by showing $\overline{\mathcal{H}}\left(p\right)\supset \mathcal{H}\left(p\right)$ and $\overline{\mathcal{H}}\left(p\right)\subset \mathcal{H}\left(p\right)$.

In the following, based on the proof of Theorem 1, we assume, without loss of generality, that $x_1{d}_1+x_2{d}_2+r_0{n}_1{d}_1+t_0{n}_2{d}_2$ is nonzero, where $(r_0,t_0)$ is one of $(0,0)$, $(1,0)$, $(0,1)$.

($\overline{\mathcal{H}}\left(p\right)\supset \mathcal{H}\left(p\right)$). Let

$$c=\frac{y_1{d}_1+y_2{d}_2-r_0{d}_1^2-t_0{d}_2^2}{x_1{d}_1+x_2{d}_2+r_0{n}_1{d}_1+t_0{n}_2{d}_2},$$

which is a stabilizing controller of p. Then $H(p,c)$ is as follows:

$$H(p,c)=\left[\begin{array}{cc}{h}_{11}& h_{12}\\ h_{21}& h_{11}\end{array}\right]=\left[\begin{array}{cc}{x}_1{d}_1+x_2{d}_2+r_0{n}_1{d}_1+t_0{n}_2{d}_2& -(x_1{n}_1+x_2{n}_2+r_0{n}_1^2+t_0{n}_2^2)\\ y_1{d}_1+y_2{d}_2-r_0{d}_1^2-t_0{d}_2^2& x_1{d}_1+x_2{d}_2+r_0{n}_1{d}_1+t_0{n}_2{d}_2\end{array}\right].$$

(23)

Based on this c, we consider an element of $\mathcal{H}\left(p\right)$, that is, a matrix below in the set of the right-hand side of (17) with the equations of (14), (15), and (16):

$$\left[\begin{array}{cc}{\omega }_{11}& {\omega }_{12}\\ {\omega }_{21}& {\omega }_{11}\end{array}\right].$$

(24)

Now we let

$$\begin{array}{cc}\hfill q_{11}=& (d_1{n}_1+d_1^2{n}_1(x_1+r_0{n}_1)+d_1^2{n}_2(x_2+t_0{n}_2))(r+r_0)+2d_1{n}_{2}s\hfill \\ & +(d_2{n}_2+d_2^2{n}_1(x_1+r_0{n}_1)+d_2^2{n}_2(x_2+t_0{n}_2))(t+t_0),\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill q_{12}=& (n_1^2+d_1{n}_1^2(x_1+r_0{n}_1)+d_1{n}_1{n}_2(x_2+t_0{n}_2))(r+r_0)+n_1{n}_{2}s\hfill \\ & +(n_2^2+d_2{n}_1{n}_2(x_1+r_0{n}_1)+d_2{n}_2^2(x_2+t_0{n}_2))(t+t_0),\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill q_{21}& =d_1^2(r+r_0)+d_1{d}_{2}s+d_2^2(t+t_0).\hfill \end{array}$$

(27)

Then, a straightforward but tedious computation shows that the matrix of (24) becomes equal to the matrix in the right-hand side of (22). Hence we have $\overline{\mathcal{H}}\left(p\right)\supset \mathcal{H}\left(p\right)$.

($\overline{\mathcal{H}}\left(p\right)\subset \mathcal{H}\left(p\right)$). Suppose an element of $\overline{\mathcal{H}}\left(p\right)$ of (22). Then we let

$$\begin{array}{cc}\hfill r& =(y_1-r_0{d}_1)(x_1+r_0{n}_1)q_{11}+{(y_1-r_0{d}_1)}^2{q}_{12}+{(x_1+r_0{n}_1)}^2{q}_{21}-r_0,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill s=& ((y_1-r_0{d}_1)(x_2+t_0{n}_2)+(y_2-t_0{d}_2)(x_1+r_0{n}_1))q_{11}\hfill \\ & +2(y_1-r_0{d}_1)(y_2-t_0{d}_2)q_{12}+2(x_1+r_0{n}_1)(x_2+t_0{n}_2)q_{21},\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill t& =(y_2-t_0{d}_2)(x_2+t_0{n}_2)q_{11}+{(y_2-t_0{d}_2)}^2{q}_{12}+{(x_2+t_0{n}_2)}^2{q}_{21}-t_0.\hfill \end{array}$$

(30)

By a straightforward but tedious computation again, the matrix in the right-hand side of (22) becomes equal to $\Omega \left(Q\right)$ of (11) with

$$\begin{array}{cc}\hfill Q& =\left[\begin{array}{cc}{q}_{11}& q_{12}\\ q_{21}& 0\end{array}\right],\hfill \\ \hfill c& =\frac{y_1{d}_1+y_2{d}_2+r_0{d}_1^2+t_0{d}_2^2}{x_1{d}_1+x_2{d}_2+r_0{n}_1{d}_1+t_0{n}_2{d}_2},\mathrm{and}\hfill \\ \hfill H_0& =H(p,c).\hfill \end{array}$$

Therefore, we have $\overline{\mathcal{H}}\left(p\right)\subset \mathcal{H}\left(p\right)$. □

Proof of Theorem 3.

We consider two cases: $c=0$ and $c\ne 0$.

($c=0$). In this case, p is in $\mathcal{A}$. Then, $h_{11}=1$, $h_{12}=-p$, and $h_{21}=0$. The fraction in (7) is expressed as $\frac{r}{1-rp}$ provided $1-rp$ is nonzero. This is just the Youla–Kučera parametrization of the plant p in $\mathcal{A}$ by noting that the coprime factorization of $p\in \mathcal{A}$ is $p=n/d$ with $n=p$, $d=1$, and the Bézout identity $0·n+1·d=1$.

($c\ne 0$). As in the proof of Theorem 1, letting $n_1=-h_{12}$, $d_1=h_{11}$, $n_2=1-h_{11}$, $d_2=h_{21}$, $x_1=y_2=1$, $y_1=x_2=0$, we obtain (4) and (5). Applying Theorem 2 to them, we have (7). □

6. Example

6.1. Coprime Factorization

Suppose that a plant admits a coprime factorization, say $p=n/d$ and $yn+xd=1$ with n, d, y, $x\in \mathcal{A}$. Letting $n_1=n_2=n$, $d_1=d_2=d$, $y_1=y$, $x_1=x$, $y_2=x_2=0$, one can apply Theorems 1 and 2 to the plant in order to obtain stabilizing controllers. The expression in the right-hand side of (6) is expressed as

$$\frac{y+(r+s+t)d}{x-(r+s+t)n}.$$

By replacing $(r+s+t)$ by new parameter u of $\mathcal{A}$, we have

$$\frac{y+ud}{x-un},$$

which is equivalent to the Youla–Kučera parametrization.

6.2. Anantharam’s Example

Let us consider an example given by Anantharam in [14]. He considered the case $\mathcal{A}=\mathbb{Z}\left[\sqrt{-5}\right]=\{u+v\sqrt{-5}|u,v\in \mathbb{Z}\}$, where $\mathbb{Z}$ denotes the set of integers. We also let $\mathcal{Z}$ be $\left\{0\right\}$. The ring $\mathcal{A}$ is isomorphic to $\mathbb{Z}\left[x\right]/(x^2+5)$ and is an integral domain but not a unique factorization domain [18] (pp. 134–135). In fact, $6\in \mathcal{A}$ has two factorizations, $2·3$ and $(1+\sqrt{-5})·(1-\sqrt{-5})$. He showed, in [14], that a plant $p=(1+\sqrt{-5})/2$ does not admit a coprime factorization but is stabilizable and $c=(1-\sqrt{-5})/(-2)$ is a stabilizing controller. Then, $H(p,c)$ is as follows:

$$H(p,c)=\left[\begin{array}{cc}-2& 1+\sqrt{-5}\\ 1-\sqrt{-5}& -2\end{array}\right].$$

Based on Theorem 3, the set of stabilizing controllers of p, $\mathcal{S}\left(p\right)$ of (7), is given as

$$\begin{array}{c}\mathcal{S}\left(p\right)=\{\frac{(1-\sqrt{-5})+4r-2(1-\sqrt{-5})s-2(2+\sqrt{-5})t}{-2-2(1+\sqrt{-5})r+6s-3(1-\sqrt{-5})t}\hfill \\ \hfill |r,s,t\in \mathcal{A},(-2-2(1+\sqrt{-5})r+6s-3(1-\sqrt{-5})t\left)\mathrm{is}\mathrm{nonzero}\right\}.\end{array}$$

(31)

By replacing $r\to -u$, $s\to -u$, $t\to -u$ with new parameter u of $\mathcal{A}$, we have

$$\mathcal{S}\left(p\right)=\left\{\frac{2u+(1-\sqrt{-5})}{-(1+\sqrt{-5})u-2}|u\in \mathcal{A},(-(1+\sqrt{-5})u-2)\mathrm{is}\mathrm{nonzero}\right\},$$

which is the same result as one shown in [19].

We can also obtain alternative parametrization from Theorem 2 based on Note 5. The plant $p=(1+\sqrt{-5})/2$ has alternative representation $3/(1-\sqrt{-5})$. From 3 and 2, which are the numerator of $3/(1-\sqrt{-5})$ and the denominator of $(1+\sqrt{-5})/2$, respectively, we can see $1·3+(-1)·2=1$, so that letting $n_1=3$, $n_2=(1+\sqrt{-5})$, $d_1=(1-\sqrt{-5})$, $d_2=2$, $y_1=1$, $x_1=0$, $y_2=0$, $x_2=-1$, we have (4) and (5). Thus, (6) results

$$\begin{array}{c}\{\frac{(1-\sqrt{-5})-2(2+\sqrt{-5})r+2(1-\sqrt{-5})s+4t}{-2-3(1-\sqrt{-5})r-6s-2(1+\sqrt{-5})t}\hfill \\ \hfill |r,s,t\in \mathcal{A},(-2-3(1-\sqrt{-5})r-6s-2(1+\sqrt{-5})t\left)\mathrm{is}\mathrm{nonzero}\right\}.\end{array}$$

(32)

This set (32) is equal to (31) by appropriate changes of parameters r, s, t.

6.3. Discrete-Time Systems without Unit-Delay Element

Mori [16] considered the case $\mathcal{A}=\mathbb{R}[z^2,z^3]$, where $\mathbb{R}$ denotes the set of real numbers. We also let $\mathcal{Z}$ be $\{f\in \mathcal{A}|f\mathrm{has}\mathrm{zero}\mathrm{constant}\mathrm{term}.\}$. This ring is an integral domain but not a unique factorization domain. In fact, $z^6\in \mathcal{A}$ has two factorizations, $z^2·z^2·z^2$ and $z^3·z^3$.

Let us consider the plant $p=(1-z^2)/(1-z^3)\in \mathcal{P}$. Now we let

$$n_1=1-z^2,d_1=1-z^3,n_2=1+z^3,d_2=1+z^2+z^4$$

of $\mathcal{A}$ with $p=n_1/d_1=n_2/d_2$. Then we have $y_1=(2+z^2)/3$, $x_1=0$, $y_2=0$, and $x_2=1/3$ with $n_1{y}_1+d_1{x}_1+n_2{y}_2+d_2{x}_2=1$. Thus, the plant p is stabilizable by Theorem 1.

Based on Theorem 2, the set of stabilizing controllers of p, $\mathcal{S}\left(p\right)$ of (6), is given as

$$\mathcal{S}\left(p\right)=\{n_c/d_c|r,s,t\in \mathcal{A},d_c\mathrm{is}\mathrm{nonzero}\},$$

where

$$\begin{array}{cc}\hfill n_c& =\frac{1}{3}(2+z^2)(1-z^3)+{(1-z^3)}^{2}r+(1-z^3)(1+z^2+z^4)s+{(1+z^2+z^4)}^{2}t,\hfill \\ \hfill d_c& =\frac{1}{3}(1+z^2+z^4)-(1-z^2)(1-z^3)r-(1-z^6)s-(1+z^3)(1+z^2+z^4)t.\hfill \end{array}$$

7. Conclusions and Future Work

This paper has presented a generalization of the Youla–Kučera parametrization to obtain all stabilizing controllers without coprime factorization. This is based on two rational expressions of a given plant. Alternative parametrization is also given by one stabilizing controller.

As future work, we will aim to investigate further generalization of the Youla–Kučera parametrization for multi-input multi-output plants with no coprime factorizations as well. Also, the possibility to extend Theorems 1–3 will be investigated.