Abstract
Selecting representative objects from a large-scale database is an essential task to understand the database. A skyline query is one of the popular methods for selecting representative objects. It retrieves a set of non-dominated objects. In this paper, we consider a distributed algorithm for computing skyline, which is efficient enough to handle “big data”. We have noticed the importance of “big data” and want to use it. On the other hand, we must take care of its privacy. In conventional distributed algorithms for computing a skyline query, we must disclose the sensitive values of each object of a private database to another for comparison. Therefore, the privacy of the objects is not preserved. However, such disclosures of sensitive information in conventional distributed database systems are not allowed in the modern privacy-aware computing environment. Recently several privacy-preserving skyline computation frameworks have been introduced. However, most of them use computationally expensive secure comparison protocol for comparing homomorphically encrypted data. In this work, we propose a novel and efficient approach for computing the skyline in a secure multi-party computing environment without disclosing the individual attributes’ value of the objects. We use a secure multi-party sorting protocol that uses the homomorphic encryption in the semi-honest adversary model for transforming each attribute value of the objects without changing their order on each attribute. To compute skyline we use the order of the objects on each attribute for comparing the dominance relationship among the objects. The security analysis confirms that the proposed framework can achieve multi-party skyline computation without leaking the sensitive attribute value to others. Besides that, our experimental results also validate the effectiveness and scalability of the proposed privacy-preserving skyline computation framework.
1. Introduction
Data is an integral part of the current business and technology world. Every day, different organizations are producing a massive amount of data also known as “big data”. This “big data” analysis has attracted much attention to many organizations and researchers because it can assist in making strategic decisions and creating new knowledge. Product pricing for the open market place, investment risk estimation, mining customers’ spending/buying behaviors, credit card usage patterns, health issues, and so on are some common example of big data analytics. Designing a new framework for collecting, storing and analyzing this “big data” is undoubtedly a challenging task.
In the current IT era, multiple organizations dealing with similar kind of services want to perform analysis on their joint databases. It is often referred to as multi-party computation or analysis. This analysis may involve data-mining, querying over the joint dataset, data classification, statistical decision making, etc. [1,2]. Since the business applications contain sensitive data, such as personal health-related data or financial data, unveiling these data can potentially violate individual privacy and lead to significant financial loss to the organizations. Therefore, organizations do not want to disclose their data to anyone. However, when multiple organizations want to conduct a data-mining operation jointly, they are willing to get the result from the union of their databases without disclosing their sensitive data.
On the other hand, the skyline query is one of the popular methods for selecting representative objects from a large dataset. It retrieves a set of representative objects, each of which is not dominated by any other object within the database. For example, let us consider the issue of financial investment: an investor usually wants to purchase the stock that can minimize the commission costs and predicted risks. As a result, the target can be formalized as finding the skyline stock with minimal cost and minimal risk. Figure 1 shows a sample plot diagram of stock records along with their costs and risks. If we want to provide a suitable suggestion list for our clients using skyline query, the result will be . From Figure 1, it is obvious that no other object, within the given sample dataset, can dominate those seven objects. Therefore, they are in the skyline result. The skyline query attracts consistent attention in database research, due to its applications in decision making as well as analytics.
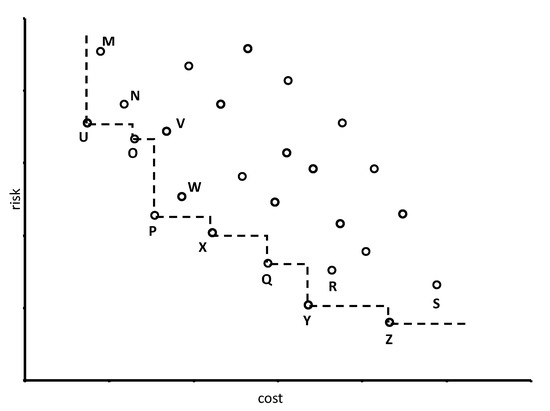
Figure 1.
A skyline Problem.
Like other data analysis applications, the distributed skyline computation certainly can benefit the participating organizations by producing skyline objects set from the joint database of the organizations. However, such computation also depends on managing data security and privacy challenges, especially for the skyline computation from the distributed multi-party databases. So far, several algorithms have been proposed for skyline computation, some of them are designed in a distributed computing environment and able to handle “big data” [3,4,5]. However, none of them considered database privacy issues.
Let us assume that several organizations have done surveys about commission cost and risk prediction where each of the organization has collected the same kind of privacy information from their customers/clients. This information is sensitive since the privacy of client information is a vital responsibility for each organization. Therefore, one organization does not want to disclose the dataset to other organization. Hence one organization cannot compute global skyline on organizations’ union databases but only compute skyline query of its own, although all parties (organizations) are willing to get the skyline result from their combined databases. In conventional skyline computation algorithm, it is not possible to get skyline query result without disclosing the objects’ attributes value to others.
When concerning the privacy of the database objects in a distributed multi-party computation environment, most of the existing work on privacy-preserving skyline computation focused on the secure comparison of encrypted values owned by participating organizations [6,7,8,9]. Although these frameworks can preserve the data objects privacy, they are not much suitable concerning computational efficiency. In our previous work [10], we introduced MapReduce framework-based secure ordering of database objects on each attribute in a semi-honest computation environment. Then computes the skyline by using the dominance relationship among the order of multi-party’s objects on each attribute. Although it is more efficient compared to secure comparison-based skyline query, it requires several rounds of ID encryption and decryption by the individual parties on each attribute of the database objects for creating the order of the objects. It also needs several rounds of data sorting by the coordinator on each dimension of the database objects. In this regard, our previous work consumes a significant amount of time for preparing the secure object order on each attribute. We also included the MapReduce framework only for sorting numeric values. However, using the MapReduce framework just for object ordering does not seem to be wise, since the framework itself requires a significant amount of time for inter-node communication and managing the process execution among multiple nodes.
In this work, we introduced an extended approach of [10] that can process the distributed object order more efficiently in a semi-honest computation environment; at the same time, it preserves the privacy of individual objects. In this extended work, we incorporate Paillier cryptosystem [11] for transforming the objects attributes value without changing the order of the objects on each attribute; where each participating party securely prepare encrypted object order on each attribute in collaboration with other participating parties. Then computes skyline from the order of the objects attribute value on each dimension without obtaining the original attributes’ value of the objects.
The remaining part of this paper is organized as follows. Section 2 reviews the related work. Section 3 discusses the notions and basic properties of skyline and Paillier cryptosystem. We briefly explain our secure skyline computation problem and proposed system model in Section 4. In Section 5, we specify the detailed algorithm with proper examples and analysis. Next, we discuss the privacy and security of our proposed framework in Section 6. We experimentally explain the efficiency of our algorithms in Section 7 under a variety of settings. Finally, Section 8 concludes this work.
Throughout this paper, we have used the hexadecimal number system for describing our proposed algorithm.
2. Related Work
Our previous research [10], as well as current research work, are motivated by earlier studies of skyline query processing, secure multi-party computation, and privacy-preserving secure skyline computation. Following Section 2.1 focuses on skyline query and Section 2.2 discuses about multi-party secure computation. Lastly, we highlighted on privacy-preserving secure skyline in Section 2.3.
2.1. Skyline Query
Borzsonyi et al., the original introducer of the skyline operator, proposed three algorithms for computing skyline from a large dataset: Block-Nested-Loops (BNL), Divide-and-Conquer (D&C), and B-tree-based schemes [12]. The BNL algorithm compares each object of the database with every other object and lists an object as a skyline object when any other object within the database does not dominate it. The D&C algorithm noticed the problem of memory limitation of a system. It divides the large dataset into several partitions and computes the skyline objects set for each partition by using a main-memory skyline algorithm. The skyline computation on the merged set of the skyline objects of each partition produces the final skyline. Later Kossmann et al. improved the D&C algorithm and proposed the Nearest Neighbor (NN) algorithm for pruning out dominated objects efficiently by iteratively partitioning the data space based on the nearest objects in the domain space [13]. Similarly, Chomicki et al. improved BNL by presorting, known as Sort-Filter-Skyline (SFS) [14]. The current most efficient algorithm is Branch-and-Bound Skyline (BBS) [15,16], which is a progressive algorithm based on the Fest-First Nearest Neighbor (BF-NN) algorithm proposed by Papadias et al. [17].
Presently, the distributed skyline computation becomes very popular. Balke et al. introduced skyline queries in distributed environments [18]. In their study, they presented several models for computing distributed skyline queries from the vertically partitioned web information. Wang et al. and Chen et al. both researched skyline query in structured P2P networks, named BATON networks, where peers are responsible for a partial region of data space [19,20]. Alternatively, a grid-based approach for distributed skyline processing (AGiDS) proposed by Rocha-Junior et al. [21] assuming that each peer maintains a grid-based data summary structure for describing its data distribution. Arefin et al. [22] worked on agent-based privacy skyline-set for the distributed database, but their query is different from us.
2.2. Multi-Party Secure Computation
The story of secure multi-party computation problem is widespread. Yao, who is the first introducer of this problem, presented a secure function evaluation process [23]. The process allows a set of m players/parties to compute an arbitrary agreed function of their private data. The function preserves the privacy of data even if an adversary may corrupt and control some players/parties in various ways. After that, Goldreich, Micali, and Wigderson [24] and many others extended the research. According to Goldreich et al. [24], Security in Multi-party Computation means that the parties’ data remain secret except the intended results of the computation. Fundamentally, secure multi-party computation protocols are relatively less efficient than specific purpose protocols.
Privacy-preserving data-mining problems are another example of secure multi-party computation problem. We addressed it in this literature. Lindell et al. and Agrawal et al. proposed two different privacy-preserving data-mining approach [1,25]. Lindell defines the problem considering two parties; each of them has a nonpublic database, where the parties want to conduct a data-mining operation jointly on the union of their databases without disclosing their database to other parties, or any third party. In Agrawal’s paper, the problem was defined in another way, assuming two parties: Alice and Bob. The problem is to allow Alice to conduct data-mining operation on a private database owned by Bob, where Bob wants to prevent Alice from accessing precise information in individual data records. Although the problems are quite similar, the solution of these two similar problems proposed by Lindell and Agrawal are different: Lindell and Pinkas adopted secure multi-party computation protocols to solve their problem, while Agrawal applied the data perturbation method.
Most of the existing solutions used homomorphic encryption for secure comparison [26,27,28] although these protocols are highly expensive concerning computation and communication complexity [29]. Lin et al. introduced an efficient comparison protocol based on homomorphic encryption [30]. They have improved the secure comparison protocol by comparing two secret values in two rounds of data communication between two participating parties. However, this protocol is only limited to comparing secure attribute values owned by two parties, and it is not scalable.
Besides that, several multi-party computation tasks could be performed over the sorting order of the objects’ attributes. Such as skyline computation, querying with aggregation function, statistical analysis, and so on [10,31,32,33]. The oblivious radix sort is a renowned protocol for sorting privacy-preserving multi-party objects, proposed by Hamada et al. [31]. However, it demands multiple rounds of computation and communication between the participating parties for sorting multi-party objects based on attribute value. Recently Xin et al. also proposed a solution for secure multi-party sorting problem [34]. However, their protocol is based on the assumption that the attributes’ value are elements of a universal set, which is known by all participating parties and the computational complexity of the protocol will become high when the size of the universal set is large.
2.3. Secure Skyline Query
Due to the information privacy and security awareness of the present era, privacy-preserving secure data analysis is considered to be one of the major research areas in “big data” processing. The privacy-preserving secure skyline query is also being researched for multi-criteria data analysis considering different application aspect. Liu et al. have proposed secure skyline queries on cloud platform [7]. On the other hand, Hua et al. have proposed another privacy-preserving skyline computation model, called CINEMA [8]. They have considered computing skyline based on the user’s dynamic query. Using their proposed framework, they have considered keeping the privacy of the user’s dynamic query point and keep the database objects secret from the users, so that the users cannot access the secure database objects, and the database owner cannot obtain the user’s query point during computation. Although their proposed model produces a secure computation environment concerning data privacy, their circumstances are entirely different from us. Moreover, both models involve computationally expensive secure comparison protocols. Where Liu et al. integrates secure comparison and secure bit-decomposition protocols proposed by Veugen et al. [27] and Samanthula et al. [35]. On the other hand, Hua et al. reduced the communication overhead of secure comparison by using 0-encoding and 1-encoding scheme proposed by Lin et al. [30].
Liu et al. proposed another privacy-preserving skyline computation framework [6], which can be deployable in a multi-party computation platform. They also improved the efficiency of multi-party secure skyline computation by using secure comparison protocol based on the 0-encoding and 1-encoding scheme proposed by [30] and Lightweight Additive Homomorphic Public Key Encryption(LAHE) Scheme. They also reduce the number of secure comparisons by using the additivity property of skyline [36]. They considered that each party computes local skyline objects set at first. Then the global skyline object set could be computed by using secure dominance relationship computation among each party’s local skyline objects. However, their proposed framework is based on pairwise secure skyline computation for computing global skyline. So, the computational complexity increases rapidly with the number of participating parties. Moreover, the complexity of 0-encoding and 1-encoding scheme used by their framework for comparing two private attributes value increase with the length of the attribute value in the number of binary bits.
Recently, Liu et al. also proposed a new framework for privacy-preserving user-centric dynamic skyline query over multi-party databases, called PUSC [9]. Although it is a new framework for dynamic skyline query over distributed multi-party databases, it is not efficient enough since it requires a massive time for execution due to the complexity of different protocols integrated with the computation process. And the skyline computation time of PUSC increases with the total number of encrypted data objects supplied by data providers.
Besides that, our previous work introduced secure objects’ ordering-based skyline computation framework [10]. In this framework, the participating parties jointly construct their database objects’ order in collaboration with a semi-honest third party, called the coordinator. It requires several rounds of ID encryption and decryption by individual parties and requires several rounds of data sorting by the coordinator for generating objects’ order securely on each attribute. In this regard, our previous work consumes a significant time for preparing a secure object order. We also deployed the MapReduce framework for sorting the numeric values there. However, employing the MapReduce framework just for sorting values does not improve the efficiency of the computation, since the framework requires significant time for inter-node communication and controlling the task execution using multiple computing nodes.
3. Preliminaries
This section defines related properties of the proposed algorithm.
3.1. Dominance and Skyline
Given a dataset with d-dimensions and n objects . We use . to denote the j-th dimension value of object . We assume that the smaller value in each attribute is better, without loss of generality.
Dominance: An object is said to dominate another object , denoted as , if () for all d dimensions and () for at least one dimension. We call such as dominant object and such as dominated object between and . For example, in Figure 2 object W is dominated by object P.
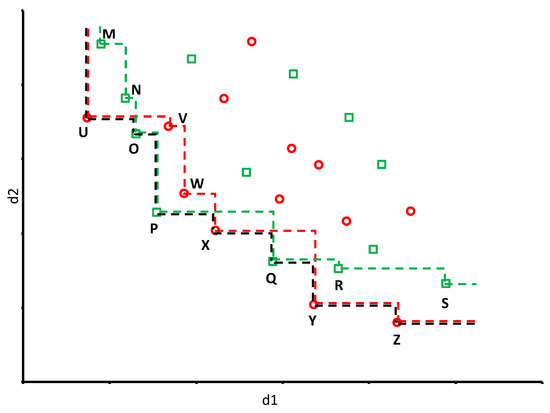
Figure 2.
A multi-party skyline Problem. Green Squares and Dotted-Line represent the objects and skyline of . Red Bubbles and Dotted-Line represent the objects and skyline of . Black Dotted-Line represents the global skyline of and .
Skyline: An object is said to be a skyline object of , if and only if there is no such object () that dominates . The skyline of , denoted by , is the set of skyline objects in . For dataset shown in Figure 2, objects are not dominated by any other objects. Thus, skyline query retrieves .
Additivity of Skyline Computation [36]: Given a dataset and p datasets such that , the following equation holds: . In Figure 2, if we consider that the red bubbles represent the objects of and green squares represents the objects of . Then the skyline objects set of and can be given by and . However, the common skyline objects set can be given by , where and .
3.2. Paillier Cryptosystem
In our proposed approach we use the Paillier cryptosystem, which is a probabilistic asymmetric algorithm for public key cryptography [11]. In Paillier cryptosystem both the public and private key consists of two integers, where the public key is given by and the private key is given by . The scheme is additive homomorphic encryption; this means that given the public key and the encryption of plain messages and , one can compute the encryption of .
Let us consider two plain messages and and their corresponding cipher messages and , where and .
Then, the following equations give the homomorphic addition and multiplication properties of Paillier cryptosystem.
- Homomorphic Addition
- Homomorphic Multiplication
At the above equations, n is the part of Paillier public key and k is a positive integer constant.
4. Multi-Party Secure Skyline Computation Problem and Proposed System Model
In this section, we formalize privacy-preserving multi-party secure skyline computation problem and our proposed system model.
4.1. Multi-Party Secure Skyline Problem
Let us consider a situation where several organizations have done some surveys about commission cost and risk prediction. We assume that each of the organizations has collected similar private information of their customers. Also, assume that all the organizations computed the local skyline from their private dataset. Now each organization wants to find the resultant skyline from the union of these local skyline result also termed as the organizations’ global database. However, none of them is allowed to disclose the attributes’ value of their database objects to other organizations. We call participant organizations of the skyline computation as parties. Due to additivity property of skyline computation, it is apparent that the result of skyline query computed from the union of each party’s dataset must be equal to the skyline query result obtained from the merged results of individual skyline.
To simplify the problem, we keep the number of participant parties is equivalent to 2. They are denoted as and , respectively. To describe the proposed algorithm, assume that Figure 2 represent the union dataset of these two parties. Where “Green Square” symbol represents that the objects come from and “Red Circle” symbol means objects comes from . Table 1 and Table 2 represents the two-dimensional secure skyline objects set of and .

Table 1.
Secure skyline objects set, of .

Table 2.
Secure skyline objects set, of .
4.2. System Model
In our proposed system model, we introduced a skyline computation procedure from secure multi-party databases in an efficient and privacy-preserving way. Like some existing model of privacy-preserving multi-party computation [7,8,9,10], we also adopted the semi-honest adversary model in our study, as defined in [37], and included a semi-honest third party adversary, called the coordinator, which will be trusted by all participating parties. We considered that the coordinator is honest-but-curious. Specifically, all participating parties along with the coordinator strictly executes the protocol but intend to extract the private data from the computation. Therefore, any participating party will not expose their object directly to the coordinator or other participating parties. Therefore, we consider that all parties securely transform their objects’ attributes’ value without changing their order on each dimension and the coordinator computes the multi-party skyline objects set from the order of the objects’ attributes value. The detailed process of this skyline query, which does not use actual attributes’ value but the order of the attributes, can be found in [32]. The sorting order generation process should need to be secure enough so that nothing could be obtained by the coordinator other than the relative order of objects’ secret attributes’ value on each dimension. The proposed framework also needs to confirm that the participating parties should be unable to guess the value of the secret objects’ attributes of other party’s objects during computation. Therefore, the transformed order information should need to be secret to all participating parties. In this regard, we consider using the Paillier cryptosystem, and its properties for transforming the objects’ attributes’ value. As a semi-honest model, our proposed framework implicitly assumes that there will be no collude among the coordinator and some of the corrupted parties.
5. Privacy-Preserving Multi-Party Secure Skyline Computation Algorithm
In this section, we provide details of the proposed algorithm. It consists of eight steps.
- Local skyline computation.
- Fix the bit-slice length and maximum bit-length of substitute vector element.
- Paillier key-pair generation.
- Generate and share the encrypted substitute vectors.
- Combine the encrypted substitute vectors.
- Encrypt the object order and resultant dataset generation.
- Decrypt the objects order and global skyline computation.
- Qualified global skyline objects identification.
Figure 3 describes the simplified block-diagram of our proposed privacy-preserving skyline computation model. Where we use one coordinator and p is the number of participating parties. Each represents the substitute vector generated by , and represents the encrypted substitute vector of , where each element of is encrypted using the Paillier public key.
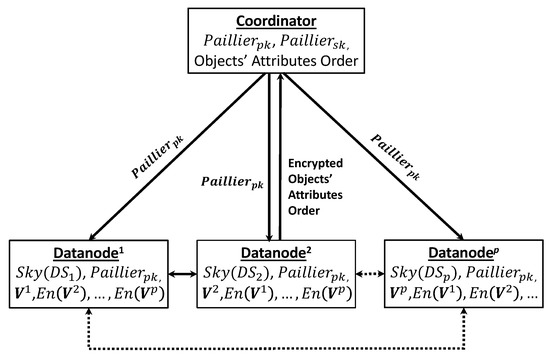
Figure 3.
Privacy-preserving multi-party skyline computation model.
5.1. Local Skyline Computation
Due to the additivity property of skyline computation, we can say that each global skyline object must be a member of any one of the local skyline objects set of the participating parties. So, we consider that each participating party initially computes respective local skyline objects set from their secure private dataset to compute global skyline. The local skyline query minimizes the risk of database disclosure by analyzing the objects’ attributes’ order information by the coordinator. This process also reduces the complexity of skyline computation from the combined large database of multi-party objects’ attributes’ order.
5.2. Fix the Bit-Slice Length and Maximum Bit-Length of Substitute Vector Element
We admitted that the objects’ attribute value could be significantly large. Therefore, we need to split the attribute value into multiple slices for substituting the attribute value with the substitute vector element. These substitute vectors replace the attribute value without changing their order. We also need to keep the vector size within the acceptable memory capacity during computation. For example, if we consider the attribute value could have a variation from 0 to , it is not feasible to create a single vector of length for replacing the attribute value. However, it could be possible to use three substitute vectors of length to substitute the attribute value without changing their sorting order. In this regard, at the beginning of our proposed framework, all participating parties mutually fix the bit-slice length for splitting the attributes’ value of each dimension to substitute it with substitute vector element. After that, it generates a separate objects order on each attribute. Each party also mutually fix the maximum bit-length of substitute vector element. The maximum bit-length of substitute vector element must need to be higher than the corresponding bit-slice length. It is also essential that the bit-slice length for splitting the attributes’ value should be long enough, since the coordinator may try to assume the actual attribute value by analyzing the incidence of the bit pattern of the transformed value of the objects’ attributes, while the bit-slice length is small.
Our proposed algorithm considered the most straightforward way for fixing the bit-slice length and maximum bit-length of substitute vector element without any concern of the coordinator. At first, each participating party recommend bit-slice length and maximum bit-length and shares it with other parties. Finally, each participating party computes the rounded-up integer average of all participating parties’ recommendation. All participating parties must follow this rounded-up integer average bit-slice length and maximum bit-length of the corresponding vector element for generating encrypted substitute vector.
Assume that two participating party recommendations are shown in Table 3 and Table 4 respectively, for generating encrypted substitute vector to substitute their two-dimensional integer dataset. Here each indicates the bit-slice length of attribute and slice, where j is indexed from less significant bits slice to most significant bits slice of the corresponding attribute value. Similarly, each indicates the maximum bit-length of substitute vector element for attribute and slice. Table 5 represent the computed common bit-slice length for splitting the attribute value and common maximum bit-length of the corresponding vector element.

Table 3.
Bit-slice length, and maximum bit-length, recommended by .

Table 4.
Bit-slice length, and maximum bit-length, recommended by .

Table 5.
Determined bit-slice length, and maximum bit-length, .
Although we have considered 8-bit integer attribute values for our running example and 4 or 5-bit bit-slice length for splitting the attribute value, in the real experiment, we have examined our proposed protocol for 32-bit integer attribute value and bit-slice length higher than 10.
5.3. Paillier Key-Pair Generation
The coordinator generates Paillier public key, for data encryption and private key, for data decryption. The detail Paillier key construction process is explained in [11]. After generating the key-pair, the coordinator shares the public key with all participating parties.
5.4. Generate and Share the Encrypted Substitute Vectors
To conceal the actual attribute value from the coordinator, all participating parties generate unique values between 0 to for substituting slice of dimension. Then each participating party sort the generated random values into a vector table, . After that, each element of sorted vector table multiplied with , except the sorted vector table constructed for the less significant bit-slice of each attribute (i.e., ). Value of can be computed using the following equation.
After multiplying with , the participating parties encrypt each element of their generated vector table using Paillier public key, to construct encrypted substitute vector table, . Assume that all parties has determined to construct an encrypted substitute vector table for substituting the attributes’ value of dimension and slice of a dataset, where the bit-slice length, and the maximum bit-length, . The construction of encrypted substitute vector, for described in Table 6.

Table 6.
Example of Encrypted Substitute Vector Generation for and .
Following this way, all participating parties generate encrypted substitute vector for all attributes and slices according to Table 5. After encrypted substitute vectors generation, each participating party shares their generated vectors to other parties except the coordinator. The Paillier encryption hides the value of the sorted vector element from the other participating parties, while they shared the vector among each other. It allows homomorphic addition and multiplication on the encrypted vector elements.
5.5. Combine the Encrypted Substitute Vectors
After receiving the encrypted substitute vector from all participating parties, each party adds (using homomorphic addition property) all the encrypted substitute vectors supplied by the individual parties to obtain the ultimate consolidated encrypted substitute vectors. Table 7 illustrates this process, where we consider two participating parties and .

Table 7.
Example of Combined Encrypted Substitute Vector Construction for Ni,j = 4.
5.6. Encrypt the Object Order and Resultant Dataset Generation
All participating parties split each local skyline objects set attribute values according to predetermined bit-slice length. For our running example bit-slice is shown in Table 5. The split value should be used as the index of the combined encrypted vector elements corresponds to their respective attributes and slices. Finally, the corresponding encrypted vector elements for each attribute value added together using homomorphic addition to generate encrypted order sequence of the object on that attribute. For self-blinding, each party also add the encryption of 0 with the value of encrypted sorting order.
Consider that both parties agreed to split the attribute value with slices and represent the corresponding encrypted vector elements of the split pieces of that attribute value. Then the transformation to encrypted object order by using the encrypted substitute vector elements can be computed by the following equation:
The coordinator may assume the individual skyline object identity by identifying the object provider. To avoid such situation, we consider that the individual parties do not send their locally computed skyline objects attributes order separately to the coordinator. In this regard, each party anonymizes their local skyline object’s IDs as follows: (1) Each party adds redundant bits with their local skyline objects’ IDs by using CRC scheme [38]. (2) The IDs with padded CRC bits are then encrypted by the corresponding party’s symmetric encryption key. Let us consider the original of a local skyline object belongs to is and is the symmetric encryption key of . If represents the encrypted of that object, then can be computed by using the following equation:

Table 8.
Encrypted disguised object order generation by .

Table 9.
Encrypted disguised object order generation by .
Finally, all participating parties send the encrypted local skyline objects order on each attribute along with their encrypted s to a common participating party. This party is also responsible for merging all encrypted skyline objects order on each attribute. After that, it sends the merged set of encrypted local skyline objects order to the coordinator.
5.7. Decrypt the Objects Order and Global Skyline Computation
After receiving the dataset with the encrypted disguised order of the local skyline objects on each attribute, the coordinator decrypts them by using Paillier private key, and obtain the transformed value of local skyline objects without changing their relative order.
Table 10 illustrates the sample database with encrypted data obtained from individual parties. The transformed order value of the objects’ attributes on each dimension after decryption, where each value in column for obtained by decrypting each encrypted value in column . This process can be represented by the following equation:

Table 10.
Disguised Object Order Decryption by the coordinator.
Here we discuss the procedure of obtaining for , where the original attribute value is . Let’s assume the value of substitute vector elements and for hexadecimal value generated by and are and , respectively. Similarly, and for .
After encrypting with , and obtain and . Therefore, using homomorphic addition property, both parties can obtain the combine encrypted substitute vector element for as .
Since, for our running example. Hence, for , . By using the same equation computes . Proceeding in the same way of obtaining combine encrypted substitute vector element for , both parties can get for .
Finally, by adding the encrypted substitute vector elements for original attribute value , can produce the encrypted order value as .
After decryption, the coordinator uses the object order on each attribute for computing global skyline query. From Table 10, we observe that according to the transformed value of the objects secure attribute value, any other objects within the dataset do not dominate the dataset objects with IDs . It can be confirmed from column and . Therefore, the coordinator computes the skyline result as . Since each representing the object with ID, hence the result is also correct according to their original attributes value, as illustrated in Figure 2. After computing the global skyline objects set the coordinator sends the encrypted IDs of qualified objects to all participating parties.
5.8. Qualified Global Skyline Objects Identification
After receiving the encrypted s of the global skyline objects each party tries to decrypt the encrypted s using their symmetric encryption key. If the party owns that skyline object, the party can quickly identify it by the decrypted s and CRC code checking. Proceeding in a similar way each participating party recognizes their respective globally qualified skyline objects.
6. Privacy and Security
Our proposed framework of privacy-preserving secure multi-party skyline computation is based on transforming the attributes’ value without changing the order of the objects‘ attributes on each dimension. As a semi-honest adversary model, this framework implicitly assumes that all participating parties trust the coordinator and the coordinator honestly executes the processes and does not make an alliance with any of the corrupted party for obtaining the combined encrypted substitute vector.
Since only the coordinator has the private decryption key, no other party can obtain the transformed order information of the objects’ attributes. So, the data privacy of honest parties will not be affected by the dishonesty of some of the corrupted parties. On the other hand, since the participating parties only share the attributes order of their local skyline objects set computed from their secure database, it is not possible to guess the attribute value by analyzing the frequency of the limited number of objects’ attributes order value. However, if the coordinator and any corrupted party make any conspiracy by sharing substitute vectors, those are used for transforming the objects’ attributes, then the proposed framework cannot meet the privacy and security expectation.
Therefore, now we can claim that the proposed framework secures the privacy of the objects during multi-party skyline computation.
7. Experiments
In this section, we evaluate the performance and effectiveness of our proposed framework. We used four identical computers connected with Cisco Catalyst 2960-X Series Gigabit Switch for the experimental setup. Out of the four computers one was considered to be the coordinator and other three computers as individual parties containing private datasets. Each of the computers has an Intel® Core™ i5-6500 3.20 GHz CPU and 8 GB memory. We used the 64-bit Ubuntu 16.04 operating system for our experiment. We compiled the source codes of the program under Java V8 and executed the program under Java™ 1.8.0 Runtime Environment. We generated synthetic datasets for evaluating the performance of our proposed framework. Each attribute value of the synthetic datasets was randomly picked from 32-bit unsigned integer. For the proposed study, we put our focus on the performance of generating secure object order targeting skyline computation from the privacy-preserved multi-party databases without unveiling the original attributes’ value of the objects to anyone. For evaluating the efficiency of our model, we considered that all participating parties begin to generate the encrypted substitute vectors and compute there local skyline objects set simultaneously after obtaining the Pallier public key, Paillierpk from the coordinator.
From our experiment, we found that the significant time consumes for computing the local skyline objects set, for generating encrypted substitute vector and for combining the vectors generated by individual parties. However, since the individual parties compute the local skyline objects set from their plain dataset without any security protocol, the local skyline computation time remain same either for non-secured distributed skyline computation or for privacy-preserved multi-party skyline computation. We also comprehensively compared the complexity of our proposed framework with the frameworks proposed in [6,10].
A. Encrypted Substitute Vector Generation and Combining: We studied the runtime for encrypted substitute vector generation process according to the algorithm described in Section 5.4, which will be executed by each participating party simultaneously. Since the length of the substitute vector increases twice with each increase of the bit-slice length, the process runtime of generating the unique random numbers within a given range and encrypting the substitute vector elements also increases. However, using the larger bit-slice length reduces the number of partitions for splitting the attribute value to transform the attribute value and thus also reduces the number of the required substitute vector. For example, a 32-bit attribute value can be substitutable by using two vectors of 16-bit-slice length, but it requires three vectors to substitute using the vector of 11-bit-slice length. We examined runtime with varied bit-slice length from 10 to 16. Figure 4a shows the effect of encrypted substitute vector generation process with different bit-slice length.
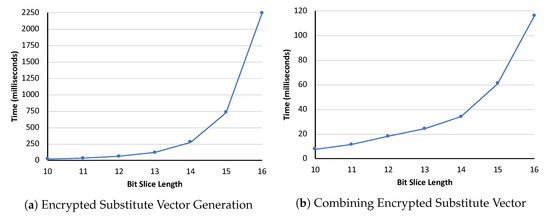
Figure 4.
Bit-slice length effect on encrypted substitute vector generation process.
We also studied the process execution time for joining the encrypted substitute vectors using homomorphic addition property according to Section 5.5. In this regard, we examined the runtime of combining three substitute vectors generated by three participating parties for varied bit-slice length. Our experimental result is illustrated in Figure 4b.
B. Privacy-Preserving Multi-Party Skyline Computation: To evaluate the performance of our proposed framework, we assumed that each participating party computes local skyline from the equal amount of data tuples. We evaluate the performance of our proposed framework for different data distribution and the varied number of objects’ dimension. For both experiments, we varied each participating parties’ tuples number from 10 k to 50 k.
To conduct this experiment, we used three different types of data distribution. They are correlated, anti-correlated, and independent distributions. As shown in Figure 5, this framework is affected by data distribution. We found that the framework is more efficient for the correlated dataset and less efficient for the anti-correlated dataset. However, the performance for independent dataset lies in between the performance for the anti-correlated and correlated dataset.
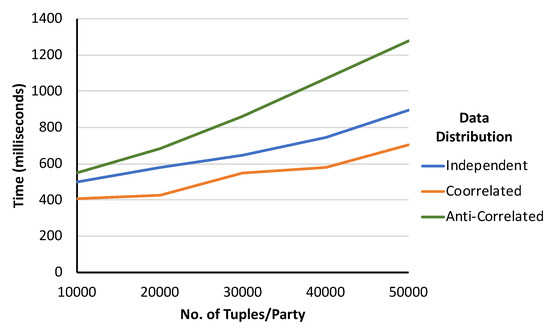
Figure 5.
Running time varies with data distribution. [Dimension: 2; Bit-slice length: 11-bit; Slices/Attribute: 3].
Figure 6 illustrates the effect of data dimension for computing skyline. We varied the data dimension from 2 to 6. Since the number of required encrypted substitute vector along with the number of comparisons and the amount of qualified local skyline objects increases with the vector dimension, the process execution time also increases. The results of our experiment also reflect it.
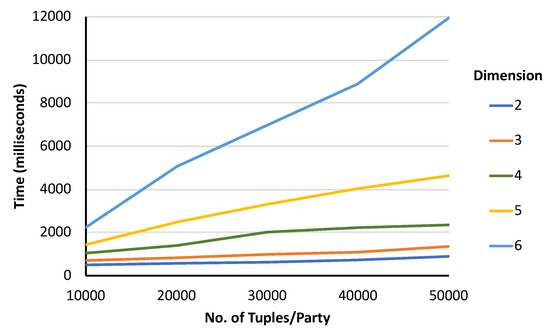
Figure 6.
Running time varies with data dimension. [Data Distribution: Independent; Bit-slice length: 11-bit; Slices/Attribute: 3].
C. Comparison with Existing Privacy-Preserving Multi-party Skyline Computation Frameworks: The framework proposed in [6] applies the pairwise secure comparison of the objects’ attributes for computing dominance relationship between two participating parties’ objects. Therefore, the complexity of the algorithm increases with the number of participating parties, since each local skyline object of a party needs to be securely compared with other parties local skyline objects set separately. The author proposed to generate the homomorphic encryption key-pair twice for each comparison of the two private objects using the LAHE scheme. The complexity of the Fast Secure Integer Comparison (FSIC) protocol used by the framework depends on the maximum length of the attribute value in the number of bits. Furthermore, it also requires five rounds of information exchange between each pair of the participating parties for each comparison of their local skyline objects.
On the other hand, our proposed framework is comparatively less dependent on the number of participating parties. The coordinator generates the homomorphic encryption key-pair only for one time for the whole process. And our framework does not employ secure comparison protocol like [6]. Moreover, it just requires six rounds of data exchange for the entire computation process: at the beginning between the coordinator and the participating parties for sharing the public encryption key. After that, three rounds communication requires between the participating parties for fixing the bit-slice length, for sharing the encrypted substitute vector and merging the individual parties’ local skyline objects’ encrypted order on each attribute. Then, another round of communication required for sending the merged set of local skyline objects’ encrypted order to the coordinator. The final round of data communication needed between the coordinator and the participating parties, for sharing the encrypted s of the globally qualified skyline objects. Although it requires to transmit a large amount of data during the sharing of each party’s encrypted substitute vector, it is negligible compared to five rounds of information exchange for each dominance relationship comparison of two parties’ objects.
The method proposed in [10] is also scalable for any number of participating parties, although it requires multiple rounds of data interchange between the participating parties with the coordinator based on the number of slices of each attribute value and the number of dimension of the objects for preparing the order of the objects on each attribute. It also requires multiple rounds of sorting by the coordinator, and partial order merging by the individual parties for generating objects’ order securely on each attribute. On the other hand, our present work does not need several rounds of data exchange, data sorting and partial order merging like [10]. Besides that, we consider using homomorphic encrypted substitute vector to transform the objects’ attributes value securely without altering their order on each attribute.
Therefore, we claim that the proposed algorithm is more efficient and robust in terms of computation and communication complexity.
8. Conclusions
Our proposed approach addresses the problem of privacy-preserving skyline query in distributed multi-party databases. Considering privacy awareness, we must take the issue of data privacy during multi-party computation into account. We offered a secured but straightforward and efficient approach for skyline query in distributed multi-party databases without unveiling the objects’ attributes’ value, where most of the existing proposed framework for privacy-preserving multi-party skyline query requires time-consuming, expensive, and complex computation. We demonstrated the effectiveness and scalability of the proposed algorithm through intensive examples and experiments. It can also be possible to consider our proposed algorithm for the secure computation of the other variant of skyline query, such as k-dominant skyline and k-skyband. Besides that, the proposed algorithm of secured object ordering can also be applicable for retrieving the number of tuples with some given criteria of the database attributes from the privacy-preserved distributed multi-party databases.
Author Contributions
M.Q., A.Z., M.A.S., Annisa and Y.M. conceived the original idea for the study, analyzed the experiment results and revised the manuscript. M.Q. and A.Z. designed the system model. M.Q. performed the experiments and wrote the initial manuscript. All authors have confirmed and approved the submitted manuscript.
Funding
This work is supported by KAKENHI (16K00155, 23500180) Japan. Mahboob Qaosar is supported by the Japanese Government MEXT Scholarship. Asif Zaman was supported by the Japanese Government MEXT Scholarship. Annisa was supported by the Indonesian Government DG-RSTHE Scholarship.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Agrawal, R.; Srikant, R. Privacy-preserving Data Mining. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 439–450. [Google Scholar]
- Pathak, F.A.N.; Pandey, S.B.S. An efficient method for privacy preserving data mining in secure multiparty computation. In Proceedings of the 2013 Nirma University International Conference on Engineering (NUiCONE), Ahmedabad, India, 28–30 November 2013; pp. 1–3. [Google Scholar] [CrossRef]
- Afrati, F.N.; Koutris, P.; Suciu, D.; Ullman, J.D. Parallel Skyline Queries. In Proceedings of the International Conference on Database Theory (ICDT), Berlin, Germany, 26–28 March 2012; pp. 274–284. [Google Scholar]
- Mullesgaard, K.; Pedersen, J.L.; Lu, H.; Zhou, Y. Efficient Skyline Computation in MapReduce. In Proceedings of the International Conference on Extending Database Technology (EDBT), Athens, Greece, 24–28 March 2014; pp. 37–48. [Google Scholar]
- Park, Y.; Min, J.K.; Shim, K. Parallel Computation of Skyline and Reverse Skyline Queries Using MapReduce. J. Proc. VLDB Endow. 2013, 6, 2002–2013. [Google Scholar] [CrossRef]
- Liu, X.; Lu, R.; Ma, J.; Chen, L.; Bao, H. Efficient and privacy-preserving skyline computation framework across domains. Future Gen. Comput. Syst. 2016, 62, 161–174. [Google Scholar] [CrossRef]
- Liu, J.; Yang, J.; Xiong, L.; Pei, J. Secure Skyline Queries on Cloud Platform. In Proceedings of the 2017 IEEE 33rd International Conference on Data Engineering (ICDE), San Diego, CA, USA, 19–22 April 2017; pp. 633–644. [Google Scholar] [CrossRef]
- Hua, J.; Zhu, H.; Wang, F.; Liu, X.; Lu, R.; Li, H.; Zhang, Y. CINEMA: Efficient and Privacy-Preserving Online Medical Primary Diagnosis with Skyline Query. IEEE Internet Things J. 2018. [Google Scholar] [CrossRef]
- Liu, X.; Choo, K.R.; Deng, R.H.; Yang, Y.; Zhang, Y. PUSC: Privacy-Preserving User-Centric Skyline Computation Over Multiple Encrypted Domains. In Proceedings of the 2018 17th IEEE International Conference On Trust, Security and Privacy In Computing And Communications/12th IEEE International Conference on Big Data Science And Engineering (TrustCom/BigDataSE), New York, NY, USA, 1–3 August 2018; pp. 958–963. [Google Scholar] [CrossRef]
- Zaman, A.; Siddique, M.A.; Annisa; Morimoto, Y. Secure Computation of Skyline Query in MapReduce. In Advanced Data Mining and Applications (ADMA) 2016; Li, J., Li, X., Wang, S., Li, J., Sheng, Q.Z., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 345–360. [Google Scholar]
- Paillier, P. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes. In Advances in Cryptology, Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques (EUROCRYPT)’99, Prague, Czech Republic, 2–6 May 1999; Stern, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 223–238. [Google Scholar]
- Borzsonyi, S.; Kossmann, D.; Stocker, K. The skyline operator. In Proceedings of the IEEE International Conference on Data Engineering (ICDE), Heidelberg, Germany, 2–6 April 2001; pp. 421–430. [Google Scholar]
- Kossmann, D.; Ramsak, F.; Rost, S. Shooting stars in the sky: An online algorithm for skyline queries. In Proceedings of the International Conference on Very Large Data Bases (VLDB), Hong Kong, China, 20–23 August 2002; pp. 275–286. [Google Scholar]
- Chomicki, J.; Godfrey, P.; Gryz, J.; Liang, D. Skyline with Presorting. In Proceedings of the IEEE International Conference on Data Engineering (ICDE), Bangalore, India, 5–8 March 2003; pp. 717–719. [Google Scholar]
- Jin, W.; Han, J.; Ester, M. Mining Thick Skylines over Large Databases. In Knowledge Discovery in Databases: PKDD 2004; Boulicaut, J.F., Esposito, F., Giannotti, F., Pedreschi, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 255–266. [Google Scholar]
- He, W.; Li, C.; Chen, H. Maintaining the Dominant Representatives on Data Streams. In Database and Expert Systems Applications; Bhowmick, S.S., Küng, J., Wagner, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 704–718. [Google Scholar]
- Papadias, D.; Tao, Y.; Fu, G.; Seeger, B. Progressive skyline computation in database systems. ACM Trans. Database Syst. 2005, 30, 41–82. [Google Scholar] [CrossRef]
- Balke, W.T.; Güntzer, U.; Zheng, J.X. Efficient Distributed Skylining for Web Information Systems. In Advances in Database Technology, Proceedings of the EDBT 2004: 9th International Conference on Extending Database Technology, Heraklion, Crete, Greece, 14–18 March 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 256–273. [Google Scholar]
- Wang, S.; Ooi, B.C.; Tung, A.K.H.; Xu, L. Efficient Skyline Query Processing on Peer-to-Peer Networks. In Proceedings of the 2007 IEEE 23rd International Conference on Data Engineering, Istanbul, Turkey, 15–20 April 2007; pp. 1126–1135. [Google Scholar]
- Chen, L.; Cui, B.; Lu, H.; Xu, L.; Xu, Q. iSky: Efficient and Progressive Skyline Computing in a Structured P2P Network. In Proceedings of the 2008 the 28th International Conference on Distributed Computing Systems, Beijing, China, 17–20 June 2008; pp. 160–167. [Google Scholar] [CrossRef]
- Rocha, J.B.; Vlachou, A.; Doulkeridis, C.; Nørvåg, K. AGiDS: A Grid-Based Strategy for Distributed Skyline Query Processing. In Data Management in Grid and Peer-to-Peer Systems: Second International Conference, Globe 2009 Linz, Austria Proceedings; Springer: Berlin/Heidelberg, Germany, 2009; pp. 12–23. [Google Scholar]
- Arefin, M.S.; Morimoto, Y. Privacy Aware Parallel Computation of Skyline Sets Queries from Distributed Databases. In Proceedings of the 2013 International Conference on Computing, Networking and Communications (ICNC), Osaka, Japan, 30 November–2 December 2011; pp. 186–192. [Google Scholar] [CrossRef]
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd Annual IEEE Symposium on Foundations of Computer Science, Chicago, IL, USA, 3–5 November 1982; pp. 160–164. [Google Scholar]
- Goldreich, O.; Micali, S.; Wigderson, A. How to Play ANY Mental Game. In Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing STOC’87, New York, NY, USA, 25–27 May 1987; pp. 218–229. [Google Scholar]
- Lindell, Y.; Pinkas, B. Privacy Preserving Data Mining. In Advances in Cryptology, Proceedings of the CRYPTO 2000: 20th Annual International Cryptology Conference Santa Barbara, CA, USA, 20–24 August 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 36–54. [Google Scholar]
- Lin, Z.; Jaromczyk, J.W. An efficient secure comparison protocol. In Proceedings of the 2012 IEEE International Conference on Intelligence and Security Informatics, Washington, DC, USA, 11–14 June 2012; pp. 30–35. [Google Scholar] [CrossRef]
- Veugen, T.; Blom, F.; de Hoogh, S.J.A.; Erkin, Z. Secure Comparison Protocols in the Semi-Honest Model. IEEE J. Sel. Top. Signal Process. 2015, 9, 1217–1228. [Google Scholar] [CrossRef]
- Nishide, T.; Ohta, K. Multiparty Computation for Interval, Equality, and Comparison Without Bit-Decomposition Protocol. In Public Key Cryptography—PKC 2007; Okamoto, T., Wang, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 343–360. [Google Scholar]
- Kerschbaum, F.; Biswas, D.; de Hoogh, S. Performance Comparison of Secure Comparison Protocols. In Proceedings of the 2009 20th International Workshop on Database and Expert Systems Application, Linz, Austria, 31 August–4 September 2009; pp. 133–136. [Google Scholar] [CrossRef]
- Lin, H.Y.; Tzeng, W.G. An Efficient Solution to the Millionaires’ Problem Based on Homomorphic Encryption. In Applied Cryptography and Network Security; Ioannidis, J., Keromytis, A., Yung, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 456–466. [Google Scholar]
- Hamada, K.; Ikarashi, D.; Chida, K.; Takahashi, K. Oblivious Radix Sort: An Efficient Sorting Algorithm for Practical Secure Multi-party Computation. IACR Cryptol. ePrint Arch. 2014, 2014, 121. [Google Scholar]
- Siddique, M.A.; Tian, H.; Morimoto, Y. Distributed Skyline Computation of Vertically Splitted Databases by Using MapReduce. In Database Systems for Advanced Applications (DASFAA); Springer: Berlin/Heidelberg, Germany, 2014; pp. 33–45. [Google Scholar]
- Sepehri, M.; Cimato, S.; Damiani, E. Privacy-Preserving Query Processing by Multi-Party Computation. Comput. J. 2015, 58, 2195–2212. [Google Scholar] [CrossRef]
- Liu, X.; Li, S.; Chen, X.; Xu, G.; Zhang, X.; Zhou, Y. Efficient Solutions to Two-Party and Multiparty Millionaires’ Problem. Secur. Commun. Netw. 2017, 2017, 11. [Google Scholar] [CrossRef]
- Samanthula, B.K.K.; Chun, H.; Jiang, W. An Efficient and Probabilistic Secure Bit-decomposition. In Proceedings of the 8th ACM SIGSAC Symposium on Information, Computer and Communications Security (ASIA CCS ’13), Hangzhou, China, 8–10 May 2013; pp. 541–546. [Google Scholar] [CrossRef]
- Hose, K.; Vlachou, A. A survey of skyline processing in highly distributed environments. VLDB J. 2012, 21, 359–384. [Google Scholar] [CrossRef]
- Hazay, C.; Lindell, Y. Semi-honest Adversaries. In Efficient Secure Two-Party Protocols: Techniques and Constructions; Springer: Berlin/Heidelberg, Germany, 2010; pp. 53–80. [Google Scholar] [CrossRef]
- Williams, R. A Painless Guide to CRC Error Detection Algorithms. 1993. Available online: http://www.ross.net/crc/download/crc_v3.txt (accessed on 27 December 2018).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).