Application of Machine Learning Models for Survival Prognosis in Breast Cancer Studies †
Abstract
1. Background
2. Problem Description
3. Related Work
4. Data Description
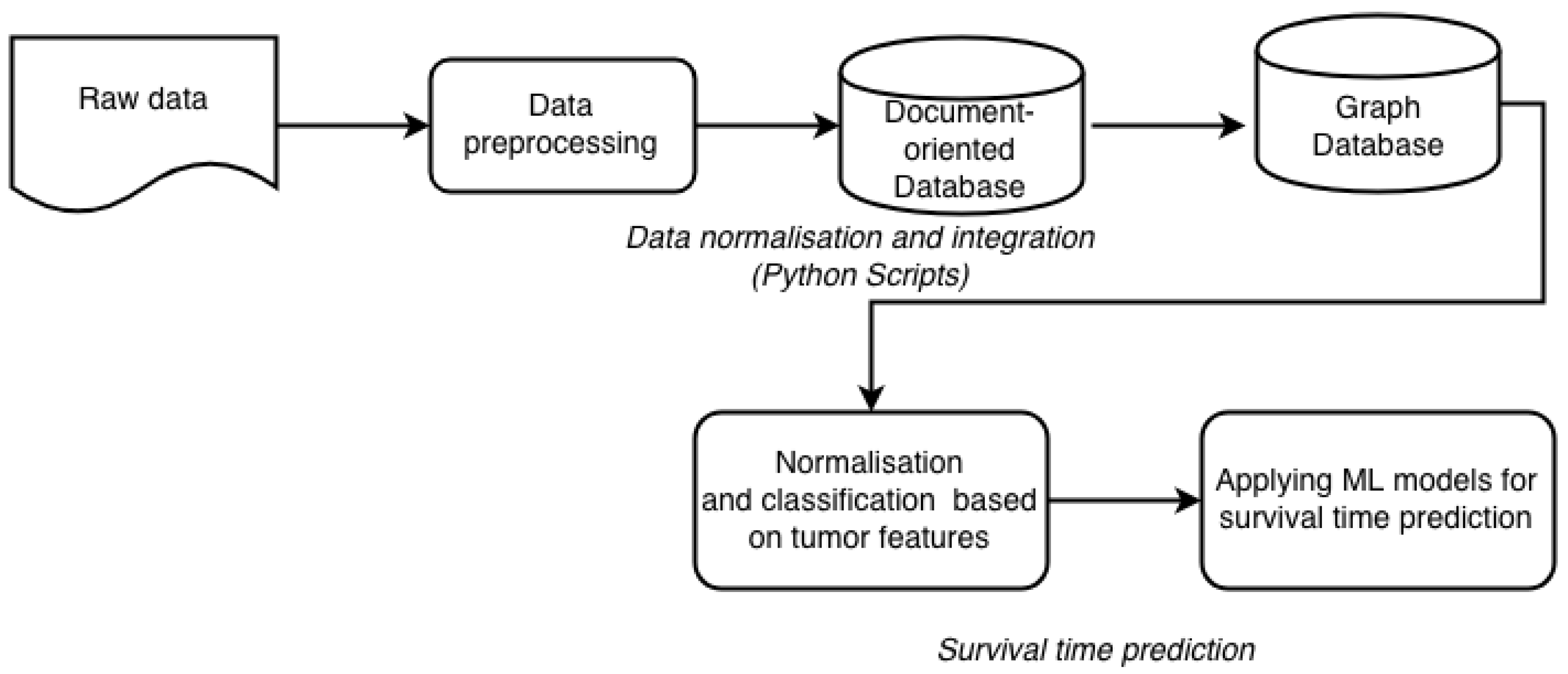
4.1. Data Preprocessing
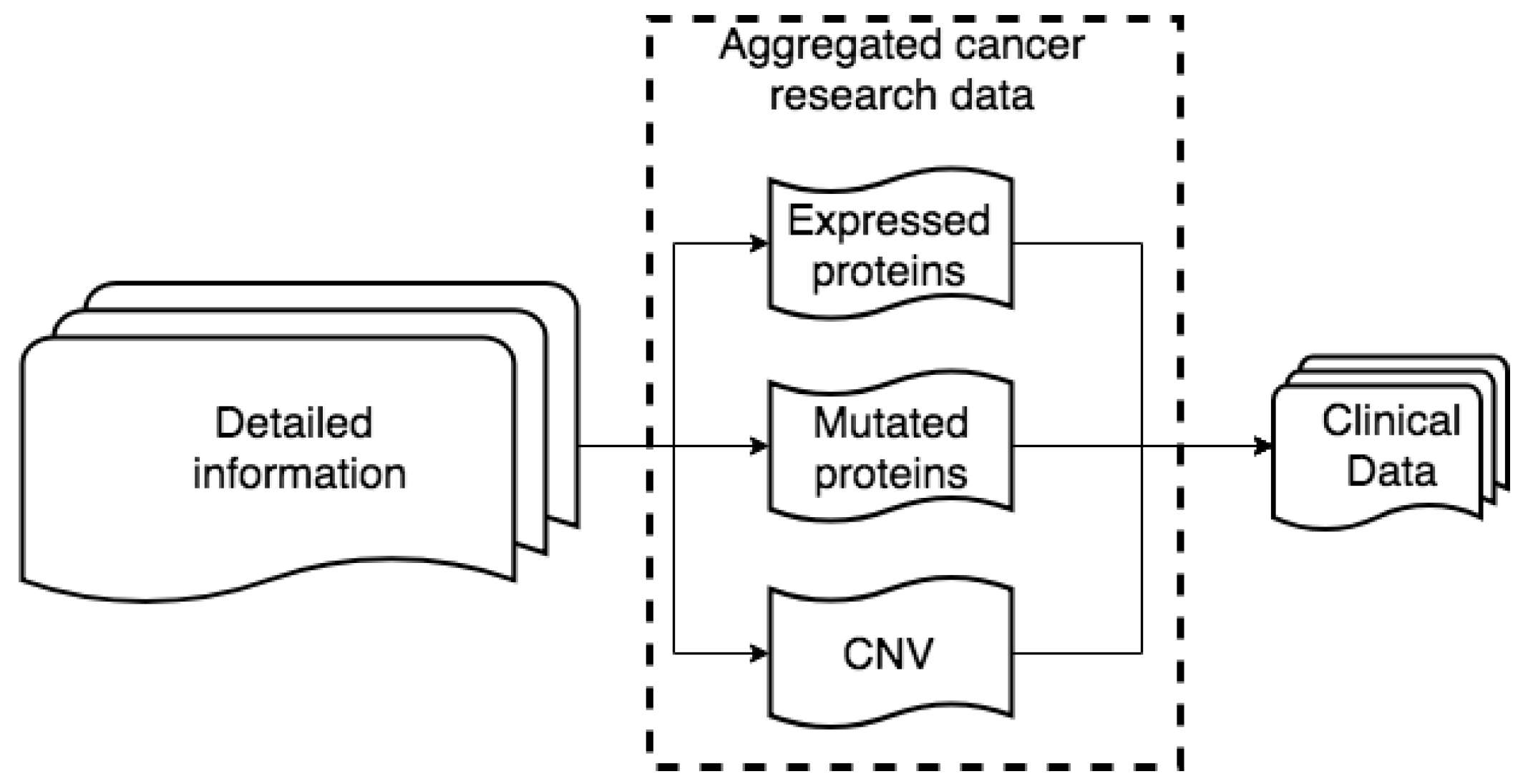
4.2. Data Integration
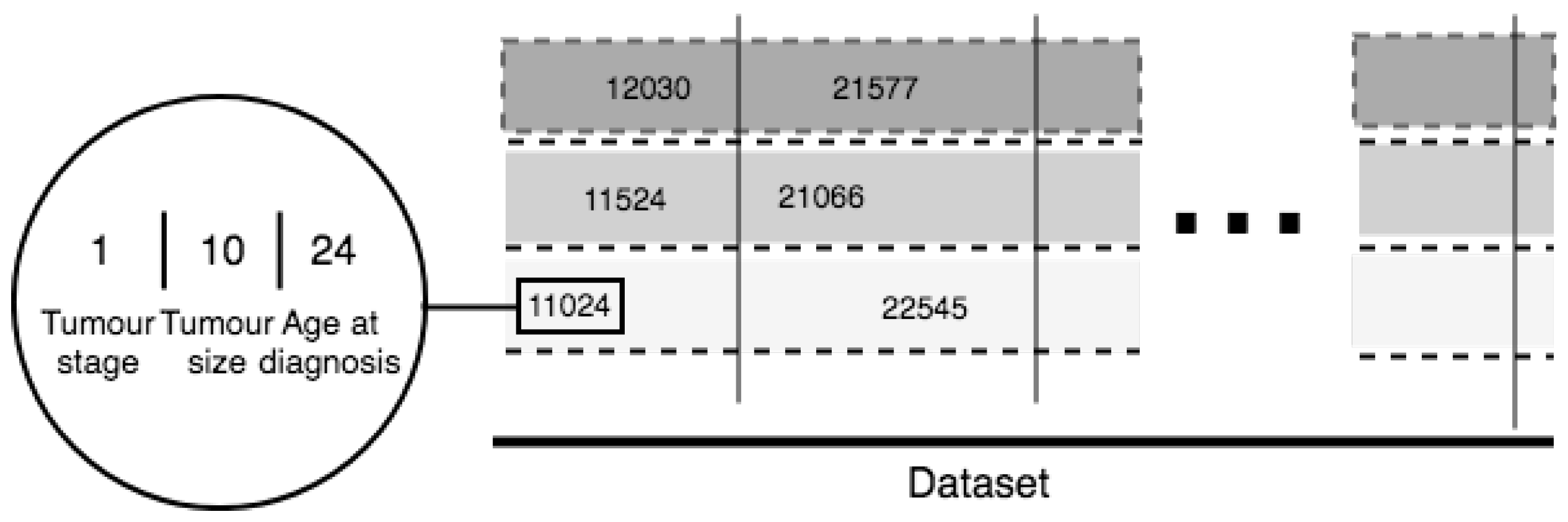
5. Novel Feature
6. Suggested Methodology
- Leave One Out—data are split each time in one chunk of training data and only one element falls into the test set
- Leave P Out—provides train/test datasets. This results in testing on all distinct samples of size p, while the remaining n-p samples form the training set in each iteration
- K-fold cross-validation—provides train/test indices to split data in train/test sets. Splits the dataset into k consecutive folds (without shuffling by default). Each fold is then used once as a validation parameter while the k-1 remaining folds form the training set. The advantage of this method is that all observations are used for both training and validation, and each observation is used for validation exactly once. 10-fold cross-validation is commonly used, but in general k remains an unfixed parameter
- ShuffleSplit—returns random chosen data for the training and testing sets. Such validation models can be used to estimate any quantitative measure of fit that is appropriate for both the data and the model.
7. Results and Discussion
8. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Hull, R.; Wodtke, W.D.; Weissenfels, J.; Weikum, G.; Patil, R.S.; Fikes, R.E.; Patel-schneider, P.F.; Mckay, D.; Finin, T.; Gruber, T.R.; et al. Managing Semantic Heterogeneity in Databases: A Theoretical Perspective. In Proceedings of the Sixteenth ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems, Tucson, AZ, USA, 11–15 May 1997; pp. 51–61. [Google Scholar]
- Ullman, J. Information Integration Using Logical Views. In Proceedings of the International Conference on Database Theory, Delphi, Greece, 8–10 January 1997; Springer: Berlin/Heidelberg, Germany, 1997; pp. 19–40. [Google Scholar]
- DeSantis, C.E.; Ma, J.; Goding Sauer, A.; Newman, L.A.; Jemal, A. Breast cancer statistics, 2017, racial disparity in mortality by state. CA Cancer J. Clin. 2017, 67, 439–448. [Google Scholar] [CrossRef] [PubMed]
- Cruz, J.A.; Wishart, D.S. Applications of Machine Learning in Cancer Prediction and Prognosis. Cancer Inform. 2006, 2. [Google Scholar] [CrossRef]
- Weston, A.D.; Hood, L. Systems Biology, Proteomics, and the Future of Health Care: Toward Predictive, Preventative, and Personalized Medicine. J. Proteome Res. 2004, 3, 179–196. [Google Scholar] [CrossRef] [PubMed]
- Tattersall, M.H.N.; Ellis, P.M.; Butow, P.N.; Hagerty, R.G.; Dimitry, S. Communicating prognosis in cancer care: A systematic review of the literature. Ann. Oncol. 2005, 16, 1005–1053. [Google Scholar]
- Futschik, M.E.; Sullivan, M.; Reeve, A.; Kasabov, N. Prediction of clinical behaviour and treatment for cancers. Appl. Bioinform. 2003, 2, 53–58. [Google Scholar]
- Kourou, K.; Exarchos, T.P.; Exarchos, K.P.; Karamouzis, M.V.; Fotiadis, D.I. Machine learning applications in cancer prognosis and prediction. Comput. Struct. Biotechnol. J. 2015, 13, 8–17. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wang, C.; Zhang, L. Decision Tree Based Predictive Models for Breast Cancer Survivability on Imbalanced Data. In Proceedings of the 3rd International Conference on Bioinformatics and Biomedical Engineering, iCBBE 2009, Beijing, China, 11–13 June 2009; pp. 1–4. [Google Scholar]
- Delen, D.; Walker, G.; Kadam, A. Predicting breast cancer survivability: A comparison of three data mining methods. Artif. Intell. Med. 2005, 34, 113–127. [Google Scholar] [CrossRef] [PubMed]
- Djebbari, A.; Liu, Z.; Phan, S.; Famili, F. An ensemble machine learning approach to predict survival in breast cancer. Int. J. Comput. Biol. Drug Des. 2008, 1, 275–294. [Google Scholar] [CrossRef] [PubMed]
- Lisboa, P.; Wong, H.; Harris, P.; Swindell, R. A Bayesian neural network approach for modelling censored data with an application to prognosis after surgery for breast cancer. Artif. Intell. Med. 2003, 28, 1–25. [Google Scholar] [CrossRef]
- Seker, H.; Odetayo, M.O.; Petrovic, D.; Naguib, R.N.; Bartoli, C.; Alasio, L.; Lakshmi, M.S.; Sherbet, G.V. Assessment of nodal involvement and survival analysis in breast cancer patients using image cytometric data: Statistical, neural network and fuzzy approaches. Anticancer Res. 2002, 22, 433–438. [Google Scholar] [PubMed]
- Halevy, A.Y. Answering queries using views: A survey. VLDB J. 2001, 10, 270–294. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, Y.; Li, Q.; George, T.J.; Shenkman, E.A.; Bian, J. Data Integration through Ontology-Based Data Access to Support Integrative Data Analysis: A Case Study of Cancer Survival. In Proceedings of the IEEE International Conference on Bioinformatics and Biomedicine, Kansas City, MO, USA, 13–16 November 2017; pp. 1300–1303. [Google Scholar]
- Liang, M.; Li, Z.; Chen, T.; Zeng, J. Integrative Data Analysis of Multi-Platform Cancer Data with a Multimodal Deep Learning Approach. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 12, 928–937. [Google Scholar] [CrossRef] [PubMed]
- Chaudhary, K.; Poirion, O.B.; Lu, L.; Garmire, L.X. Deep Learning–Based Multi-Omics Integration Robustly Predicts Survival in Liver Cancer. Clin. Cancer Res. 2018, 24, 1248–1259. [Google Scholar] [CrossRef] [PubMed]
- Abreu, P.H.; Santos, M.S.; Abreu, M.H.; Andrade, B.; Silva, D.C. Predicting Breast Cancer Recurrence Using Machine Learning Techniques: A Systematic Review. ACM Comput. Surv. 2016, 49, 52. [Google Scholar] [CrossRef]
- Aloraini, A. Different Machine Learning Algorithms for Breast Cancer Diagnosis. Int. J. Artif. Intell. Appl. 2012, 3, 21–30. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Python Release Python 3.7.0. Available online: https://www.python.org/downloads/release/python-370/ (accessed on 2 March 2019).
- Nayak, A.; Poriya, A.; Poojary, D. Article: Type of NOSQL databases and its comparison with relational databases. Int. J. Appl. Inf. Sys. 2013, 5, 16–19. [Google Scholar]
- Mihaylov, I.; Nisheva, M.; Vassilev, D. Machine Learning Techniques for Survival Time Prediction in Breast Cancer. In Proceedings of the 18th International Conference on Artificial Intelligence: Methodology, Systems, Applications, AIMSA 2018, Varna, Bulgaria, 12–14 September 2018; Springer: Cham, Switzerland; pp. 186–194. [Google Scholar]
- Gupta, S.; Tran, T.; Luo, W.; Phung, D.; Kennedy, R.L.; Broad, A.; Campbell, D.; Kipp, D.; Singh, M.; Khasraw, M.; et al. Machine-learning prediction of cancer survival: A retrospective study using electronic administrative records and a cancer registry. BMJ Open 2014, 4. [Google Scholar] [CrossRef] [PubMed]
- Have, C.T.; Jensen, L.J. Are graph databases ready for bioinformatics? Bioinformatics 2013, 29, 3107–3108. [Google Scholar] [CrossRef] [PubMed]
- McLachlan, G.; Do, K.; Ambroise, C. Analyzing Microarray Gene Expression Data; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Lindqvist, N.; Price, T. Evaluation of Feature Selection Methods for Machine Learning Classification of Breast Cancer; Degree Project in Computer Science; KTH Royal Institute of Technology: Stockholm, Sweden, 2018. [Google Scholar]
- Akay, M.F. Support vector machines combined with feature selection for breast cancer diagnosis. Expert Syst. Appl. 2009, 36, 3240–3247. [Google Scholar] [CrossRef]
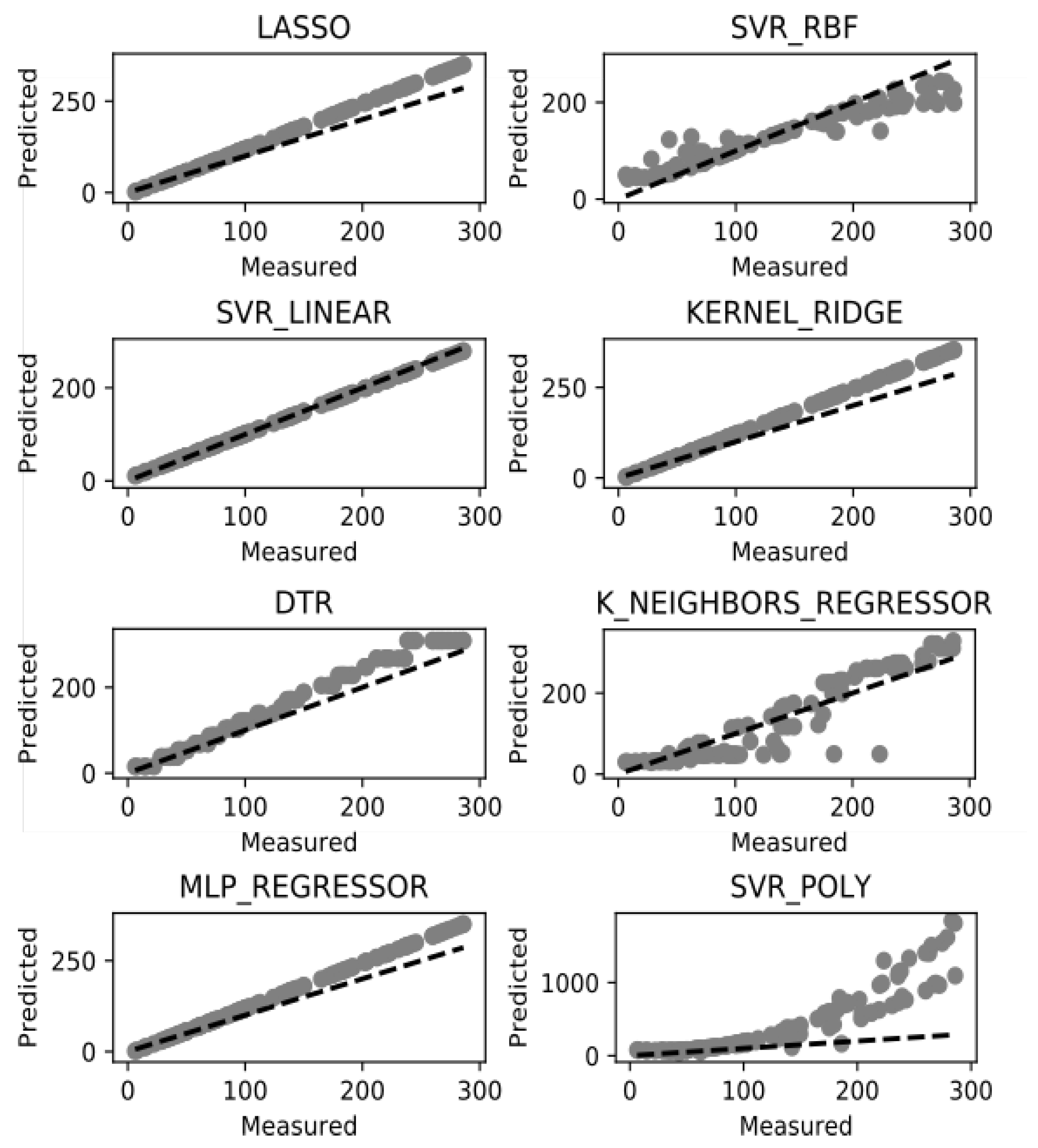
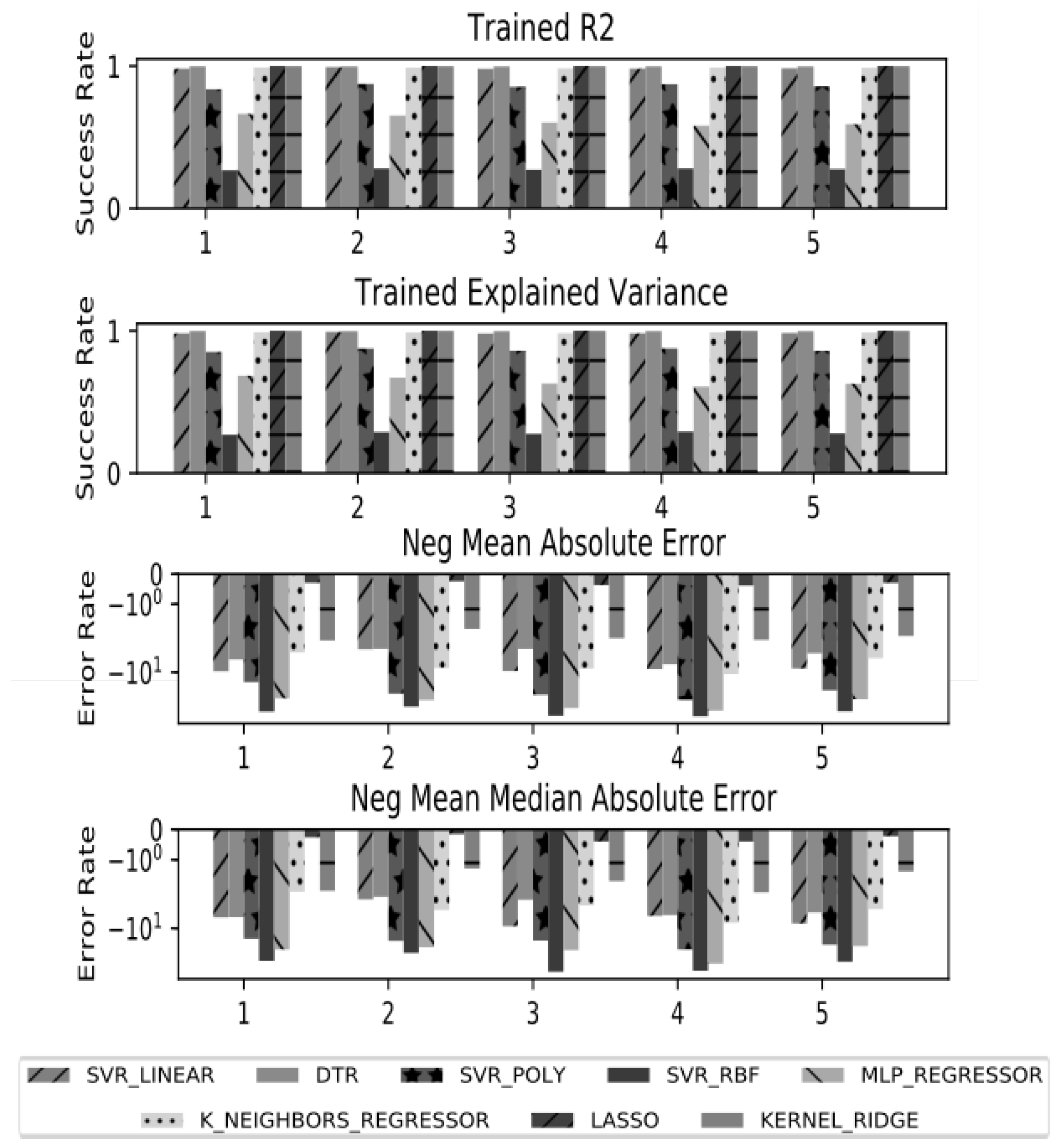
| ML Model | Train R2 | Explained Variance | Negative Mean Absolute Error | Negative Median Absolute Error | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | StD | Mean | StD | Mean | StD | Mean | StD | |
| LASSO | 1.000 | 0.000 | 1.000 | 0.000 | −0.356 | 0.020 | −0.326 | 0.025 |
| SVR-RBF | 0.318 | 0.038 | 0.341 | 0.032 | −45.742 | 5.224 | −34.455 | 5.594 |
| SVR-LINEAR | 0.983 | 0.007 | 0.986 | 0.006 | −7.288 | 1.935 | −6.109 | 1.509 |
| KERNEL RIDGE | 0.999 | 0.000 | 0.999 | 0.000 | −1.853 | 0.340 | −1.686 | 0.454 |
| DTR | 0.996 | 0.000 | 0.996 | 0.427 | −5.624 | 0.427 | −4.636 | 0.467 |
| KNR | 0.988 | 0.001 | 0.988 | 0.001 | −7.007 | 1.384 | −4.725 | 0.744 |
| ML REGRESSION | 0.603 | 0.029 | 0.607 | 0.028 | −39.592 | 7.001 | −34.549 | 10.064 |
| SVR-POLY | 0.884 | 0.007 | 0.887 | 0.009 | −20.354 | 3.290 | −15.581 | 5.382 |
| ML Model | Train (s) | Predict (s) | Total (s) |
|---|---|---|---|
| LASSO | 0.027842999 | 0.000209093 | 0.028052092 |
| SVR-RBF | 0.070589066 | 0.001976013 | 0.072565079 |
| SVR-LINEAR | 0.050335884 | 0.000173092 | 0.050508976 |
| KERNEL RIDGE | 0.106621981 | 0.002275944 | 0.108897924 |
| DTR | 0.028145075 | 0.000221968 | 0.028367043 |
| KNR | 0.070935965 | 0.001635075 | 0.072571039 |
| ML REGRESSION | 3.409966946 | 0.00106287 | 3.411029816 |
| SVR-POLY | 0.479592085 | 0.001157999 | 0.480750084 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mihaylov, I.; Nisheva, M.; Vassilev, D. Application of Machine Learning Models for Survival Prognosis in Breast Cancer Studies. Information 2019, 10, 93. https://doi.org/10.3390/info10030093
Mihaylov I, Nisheva M, Vassilev D. Application of Machine Learning Models for Survival Prognosis in Breast Cancer Studies. Information. 2019; 10(3):93. https://doi.org/10.3390/info10030093
Chicago/Turabian StyleMihaylov, Iliyan, Maria Nisheva, and Dimitar Vassilev. 2019. "Application of Machine Learning Models for Survival Prognosis in Breast Cancer Studies" Information 10, no. 3: 93. https://doi.org/10.3390/info10030093
APA StyleMihaylov, I., Nisheva, M., & Vassilev, D. (2019). Application of Machine Learning Models for Survival Prognosis in Breast Cancer Studies. Information, 10(3), 93. https://doi.org/10.3390/info10030093






