Abstract
The increase in demand for clean, safe, and environmentally friendly renewable energy sources faces several challenges such as system design and reliable operations. DC microgrid (MG) is a promising system due to higher efficiency and natural interface to renewable sources. In the hierarchical control of DC Microgrid, the V-I droop control is deployed usually in primary control level for common load sharing between converters. However, conventional droop control causes improper current sharing, voltage variations, and circulating current regulation due to the presence of droop and line resistance between converters. The aim of this paper is to presents the primary control level design of buck converters in current mode control according to the concepts of time constant and time delay, and secondary control design for parallel operations in distributed manners by combining methods, namely, low bandwidth communication (LBC), circulating current minimization techniques, and average voltage/current control. Moreover, different time delays are used for two converters to testify the effects of communication delays on current sharing and voltage restoration. The simulation is done for 2 × 2.5 KWdc parallel buck converters in PLECS (a Simulation software used for high speed simulation for power electronics) environment which shows excellent results in minimizing circulation currents, enhancing proportional current sharing, and restoring the grid voltage.
1. Introduction
The blackouts, usual shutdown of centralized grids, CO2 emission, damage to the Ozone layer, dependency on biomass fuel and its increasing price, global warming, etc. brought the concept of a safe, renewable, environmental friendly, clean and green energy source to the fore. In the last decade, the use of renewable energies such as photovoltaic, wind, tidal, etc. has increased dramatically due to a lot of advantages such as low dependency on biomass, decrease in CO2 emission, fuel prices, and unusual shutdown of centralized grids. The concept of these green energies also brought the idea of a Microgrid (MG) which is unique, diverse, controllable, interactive, as well as independent.
A Microgrid is the parallel interconnection of different distributed energy sources such as photovoltaic arrays, wind turbines, Micro CHP (Combined heat and power), diesel generators etc.; different loads, a control and communication system for energy sharing within the MG or other grids; as well as an Energy storage system (ESS) and Electric vehicle (EV) station. The concept of the Microgrid was presented by CERTS of USA in their whitepaper which further provides the information of Distributed energy resources (DERs) within a Microgrid [1]. A microgrid is an essential system for a future Smart grid [2]. Big brand companies such as SMA Solar Tech. of USA and Fronius GMBH provide AC microgrid solutions with DERs. The devices used by these manufacturers are, namely, a Cluster controller and data logger for control and communication of multiple DERs or Microgrid. However, these devices act as central controllers which could possibly be a single point of failure. Recently, a new trend in Microgrids for energy trading and sharing is introduced, called peer to peer (P2P) energy trading which is based on DERs. A small scale DERs owner using P2P technology can become a prosumer of energy as P2P trading allows prosumers to sell or purchase electricity directly from their neighbors which means this technology can provide bidirectional energy exchange within a microgrid. A good explanation of P2P energy trading is proposed and discussed in [3,4].
A lot of research has been conducted on MGs’ architecture, control, and communication and still many things are needed to develop truly distributed and independent MGs with several distributed DERs. Microgrids are basically of two types according to the nature of electric current, namely AC MG and DC MG, respectively. A hierarchical control of droop controlled AC and DC Microgrids consisting of primary, secondary, and tertiary level control is proposed in [5], and because the nature of electronic interfaces are DC and generation of DC power by most renewable sources, DC MG is considered better than AC MG as the DC system does not associate with problems such as harmonic current, injection current from the transformer, reactive power flow etc. However, ESS and super capacitors are naturally DC sources, and conversion power efficiency from AC to DC decreased by at least 5%. Eneko et al. [6] compared and analyzed autonomous primary control strategies in AC and DC microgrids using the virtual synchronous machine (VSM) technique for ACMG and a virtual impedance based algorithm for DC MG, respectively. Moreover, DC MG also does not need synchronization as well as AC–DC–AC power conversion as required in AC MG [6].
A detailed discussion about architecture, design, communication networks, AC interfaces grounding schemes, challenges, and standardization aspects for DC MG is presented in [7] and a DC MG diagram is shown in Figure 1.
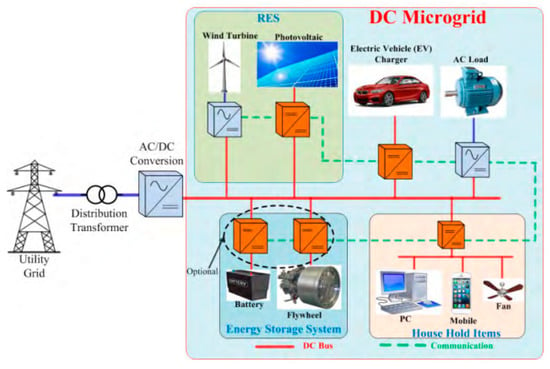
Figure 1.
Distributed energy resources (DERs) connected in a DC Microgrid (MG) [7].
Manoj et al. [8] provided a literature overview of DC MG control and operation which explains that the main causes of power disturbance in DC MG are power variations between ESS and DERs, sudden load changes, and exchange of power between other grids and the DC MG, respectively. The DC bus voltage variation control is needed in a protective scheme suggesting hierarchical control in case of large number of DC MGs. Authors in [9,10] presented a detailed overview of hierarchical control where primary control is lower level control and is responsible for direct control of local voltage and the current of the converter; secondary is on top of primary which is responsible for power regulation; and tertiary is the top level management control which controls energy balance of ESS, energy sharing to other grids, and overall system regulations. Droop index based adaptive droop controller is proposed for load sharing in [11,12]. Using input-to-state theory, a non-linear current limiting droop controller is proposed in [13] by limiting the inductor’s current when the output power demand exceeds the converter’s capacity. Communication based logical switch in distributed secondary control is presented in [14]. An average voltage and current are utilized in distributed secondary control using low bandwidth communication (LBC) as presented in [15]. A hybrid dynamic controller is proposed [16] in distributed secondary control via discrete time interaction. Daniel et al. [17] presented a centralized secondary control in parallel operation of buck converters. Energy storage system, vehicle to grid (V2G) control, tertiary or management level control, and entire energy management in DC Microgrids are well presented in [18,19,20,21,22,23].
This paper presents a combined way to design distributed secondary controllers for buck converters in DC Microgrid using low bandwidth communication, average voltage, and controllers for maximizing current sharing and circulation current minimization theory. Section 2 discusses the modeling for the buck converter, issues in parallel connecting converters for load sharing and primary control. Section 3 provides the detail of the distributed secondary control. Section 4 and Section 5 analyzes the details of simulation results in PLECS, and conclusion, respectively.
2. Modeling and Paralleling of the Buck Converters
2.1. Buck Converters
A buck converter is the basic switch mode non-isolated step down converter which converts a high voltage DC to low output DC voltage. Figure 2 shows the practical power conversion PLECS model of the Buck converter where
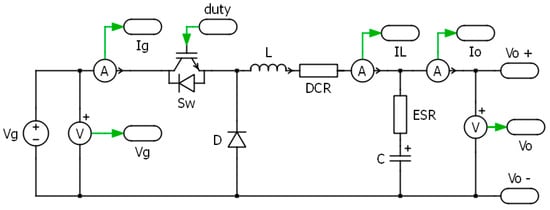
Figure 2.
Power Conversion stage of Buck converter modeled in PLECS.
- Vg = the source voltage
- Vo = the output voltage
- Sw = the switch (IGBT)
- Ig = Input Current
- IL = Inductor’s current
- IO = Output current
- D = the diode
- L = inductor
- C = Capacitor
- DCR = Inductor’s resistance
- ESR = Equivalent series resistance
In the continuous conduction mode (CCM), the switching frequency is fS = 1/TS, where TS = TON + TOFF is sampling time. TON is the time when the switch is closed or ON while TOFF is the time when switch is open or off. The duty cycle of Buck converter is given by
The values of inductor and capacitor can be found using the following equations:
where and represent desired peak ripple of inductor current and output voltage, respectively. Table 1 shows Buck converter parameter given in [17].

Table 1.
Buck converter parameters and values.
2.2. Small Signal Modeling of Open Loop Buck Converters
A small signal equivalent model of open loop Buck converter (s-domain) is shown in Figure 3. which is essential to find the transfer functions for closed loop operation. In order to work on the practical model and considering the converter’s internal losses cause by inductor and capacitor internal resistances (DCR and ESR), we have considered an internal resistance = DCR + ESR as shown in Figure 3. This consideration can simplify the equation such as becomes as well as this assumption avoids working on 3rd order transfer function in s-domain [24].
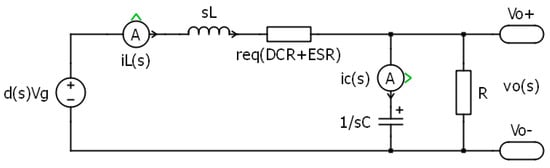
Figure 3.
A small signal equivalent open loop Buck converter.
Based on Kirchhoff’s voltage and current laws, we can get following equations from Figure 3:
where , , and are small ac perturbations in values of inductor current , output voltage , and duty cycle , respectively.
In order to work on CCM, the transfer function from duty cycle to output voltage is necessary in voltage mode control and vital for describing the voltage loop in current mode control [25]. In current mode control, we assume the perturbation in input voltage is negligible.
The transfer function from duty cycle to output voltage is given by
The transfer function from duty cycle to inductor current is necessary in current control mode to find out the effect of change in duty cycle on inductor current. The transfer function from duty cycle to inductor current is given by
where represents the voltage conversion ratio for Buck converter with energy losses and is the efficiency for buck converter. and are the time constant and damping time constant, respectively. Theories of these time constants are well explained by Dr. Luo and Dr. Yeinin Digital Power Electronics and application [26]. For converters with internal power loss, time constant is given by
In (8) and (9), is the energy factor and is the capacitor-inductor ratio given by (10) and (11), respectively.
where and are the storage and pumping energy, and represents number of inductors and capacitors in the circuit, and are stored energy in inductor and capacitor, and is the input current to the system according to digital power electronics, respectively.
Transfer function for outer voltage loop in current control mode is necessary which is used to obtain the effect of inductor current on output voltage and is given by (12).
2.3. Issues in Parallel Connected Converters
Figure 4 shows two converters are connected in parallel and sharing a common load . Let us suppose and are output voltages of converter No. 1 and converter No. 2. Similarly, are output currents of converter No. 1 and converter No. 2, respectively. and are the load current and voltage, and are line resistances of converter No. 1 and 2 to load, respectively. Applying KVL, we get following equations:
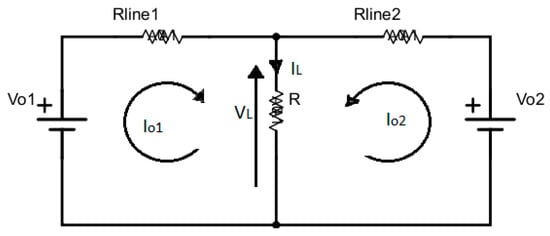
Figure 4.
Parallel connected converters sharing a common load.
According to [26], the output voltage equations of the open-loop buck converters with internal energy losses are given by
Droop resistor is normally used in primary level control of converters for current sharing and avoiding voltage deviation. Considering reference voltage source , as mentioned in [15], (15) and (16) become
where and are the droop resistances of converter No. 1 and 2, respectively.
All the above Equations (13)–(18) clearly show that the output voltage of converters must influenced by the line resistances, droop resistors, as well as the efficiency of converter. Similarly, whenever there is change in load or output power of parallel converters, it generates circulating currents from one converter to another which eventually affects the output voltage. The equation for circulating current considering Figure 4 is given by
3. Primary and Secondary Control Design in Current Control Mode
3.1. Primary Control Design
Figure 5 shows the block diagram of primary control of the Buck converter in current control mode. The control system consists of two loops, namely, an inner and outer loop. Both loops are designed using PI controllers, i.e., Current and voltage PI controllers. In order to make the design stable, the inner current controller should be faster as compared to outer voltage controller. Transfer functions from the duty cycle to the inductor current (7) and from the inductor current to output voltage (12) are used in inner current control loop and outer voltage control loop, respectively, and the transfer function of pulse width modulator (PWM) block is given by
where is peak to peak amplitude of triangular waveform and is used by PWM block in comparison to control voltage (s). The transfer functions for both voltage and current PI (Proportional–Integral) controllers are given by
where , are the proportional and integral gains, respectively. is a constant.

Figure 5.
The Secondary controller design: (a) The proposed Secondary controller, (b) The average voltage and average proportional current controller, (c) Internal view of average voltage and average proportional current controller, (d) The circulating current and voltage deviation controller.
The current PI controller gains i.e., and can be found using Cohein-Hrones-Reswick (CHR) method for PID tuning which is the modification of the Ziegler-Nichols method. The CHR method uses time constant to dead time constant ratio, i.e., of the plant explicitly. CHR tuning formula for set point regulation with 0% overshoot is given in Table 2 [27], where “K” is the steady state level of voltage waveform. The voltage PI controller gains can be found by transforming the equations and into time domain using inverse Laplace transformation and then equating both equations.

Table 2.
With 0% overshoot Cohein-Hrones-Reswick (CHR) formula for Proportional-Integral (PI) tuning [27].
The above equations after transforming into time domain would be in the form given by (24) and (25), respectively.
a1-2, b1-2, and c1-2 are the residue of partial fraction. and represents damping factor and frequency, respectively. The transfer function in (6) and (7) are 2nd order functions with couple of conjugated poles located at the left hand side in s-domain. The values of and can be found using (26) and (27), respectively.
3.2. Secondary Control Design
Secondary control is used on the top of primary control in distributed system. It controls the power regulation, power quality, and coordination in connecting or disconnecting to and from the main grid. It is necessary in a DC Microgrid to maintain the grid level voltage in each single distributed system as well as minimizing the circulating currents. The secondary controller must take rapid action if there is any disturbance within system level such as change in load resistance. Therefore, the proposed secondary control design mainly focuses on the average voltage and proportional current controller [15], and additionally the circulating current minimizing technique.
Figure 5a shows the external view of proposed secondary controller in PLECS, where Vo1 and Io1 are the local voltage and current parameters, respectively. Vo2 and Io2 are the voltage and current of nth converter, respectively. The local secondary controller obtains Vo2 and Io2 through a low bandwidth communication channel with the time delay transfer of as proposed in [15], where represents communication delay. VMG in Figure 5a represents the Microgrid’s reference voltage. Figure 5b,c shows the design of average voltage and average proportional current controller where K1 and K2 are the proportion used in current sharing for converter 1 and converter 2, respectively, which is given by , where, and are the output currents of converter 1 and converter 2, respectively.
Droop resistance or controller is normally adopted in primary level control for energy sharing. Unlike conventional or other secondary controllers presented in the literature, the fixed droop resistance ( is maximum output voltage deviation and is maximum output current) is added with circulating current minimizing loop in the proposed secondary control shown in Figure 5d, where Rline1 and Rline2 represent line resistances of converter 1 and converter 2, respectively. Hence, a combined average voltage, proportional current and circulating current minimizing control with fixed droop resistance using low bandwidth communication in secondary control is proposed in this research. The proposed secondary controller provides voltage restoration “Vres” (Figure 5a) which eventually controls the local primary controller.
4. The Simulation Results and Discussion
Figure 6 shows the complete simulation of a parallel Buck converter modeled in PLECS. Normally, the line resistance is much lesser than the droop resistance. However, the line resistances are still considered in this research. Different scenarios such as proportional current sharing, different line resistances, and change in common load resistance and different communication delays have been apprehended in this simulation. The controller design and simulation parameters of each converter are shown in Table 3.
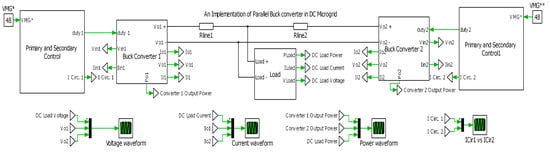
Figure 6.
Complete simulation model of parallel Buck converters in DC Microgrid in PLECS.

Table 3.
Controller design and simulation parameter.
4.1. Scenario 1
Scenario 1 is considered as the best case scenario in this simulation where equal current sharing K1 = K2, equal line resistances Rline1 = Rline2 = 0.001 Ω and, no communication delay are considered. Initially, the load resistance was 0.4608Ω, however, at t = 0.99 s the load was changed to 0.9216 Ω, and again changed to 0.4608 Ω at t = 1.48 s. Figure 7a shows the output voltages of each converter and load. It took about 0.064 s to restore the voltage to 48V during each step change in load resistance. Current waveforms are shown in Figure 7b and the reaction times during step changes are found to be about t = 0.06 s. It is worth mentioning that current sharing is equal after the reaction time. Similarly, the power waveforms are shown in Figure 7c and circulating currents are shown in Figure 7d. The circulating currents in each converter in scenario 1 are nearly zero except during step changes.
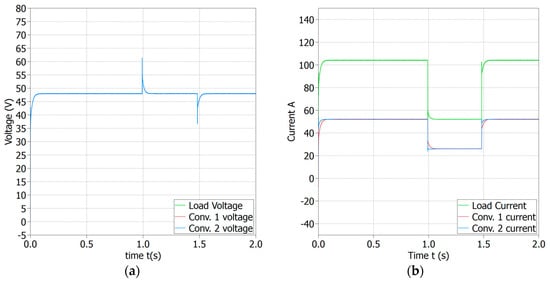
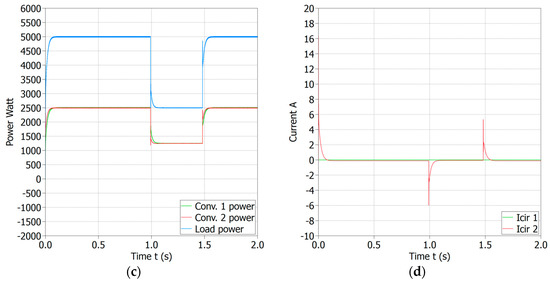
Figure 7.
Scenario 1 outputs with load resistance of 0.4608 Ω, K1 = K2 = 1, Rline1 = Rline2 = 0.001 Ω, , (a) Converters’ output voltages and the load voltage, (b) Converters’ output currents and the load current, (c) Converters’ output power and the load power, (d) Circulating currents.
4.2. Scenario 2
In scenario 2, equal line resistances but unequal current sharing, i.e., K1 = 1 and K2 = 2, and communication delay of are introduced. Initially in this case, the load of 2.5 KW (0.9216 Ω) was used and then changed to 2 KW (1.152 Ω) at t = 1.02 s. In Figure 8a, it took t = 0.03 s to stabilize the grid voltage of 48 V as the LBC starts after and also during the step change in the load resistance. Figure 8b shows the proportional current sharing of each converter. Converter 2 provides twice the current of converter 1, i.e., and and, after the load change, converter 2 provides and converter 1 shares , respectively. Figure 8c shows the power waveform of scenario 2 where two loads of 2500 W and 2000 W are visible. The circulating current minimization is shown in Figure 8d. It is worth mentioning that after the communication delay of 5 ms and the load change at t = 1.02 s, the controller took almost 0.03 s and 0.05 s, respectively, to minimize the circulating currents.
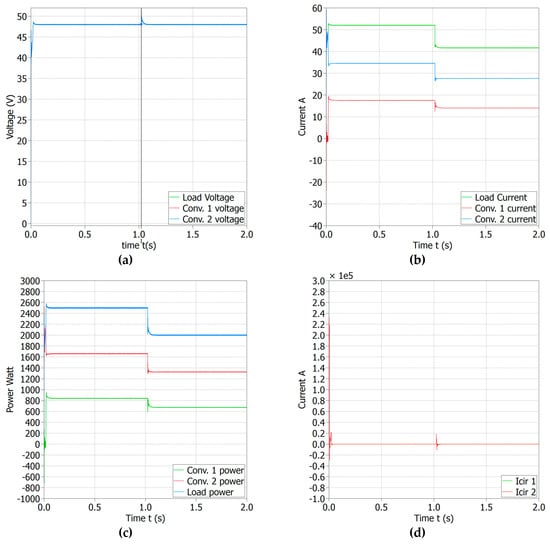
Figure 8.
Scenario 2 outputs with load resistance of 0.9216 Ω, K1 = 1 and K2 = 2, Rline1 = Rline2 = 0.0001 Ω, , (a) Converters’ output voltages and the load voltage, (b) Converters’ output currents and the load current, (c) Converters’ output power and the load power, (d) Circulating currents.
4.3. Scenario 3
This scenario is considered as the worst case scenario of the simulation. Different line resistances Rline1 = 0.0001 Ω and Rline2 = 0.00015 Ω, communication delays for two converters and , current proportion of K1 = 1 and K2 = 3 are considered, respectively. However, a fixed load of 0.9216 Ω is used. Because of huge communication delays, different line resistances, and different current sharing proportions, the controllers took t = 0.8 s to stabilize the grid voltage to 48 V shown in Figure 9a. Similarly, the current, power, and circulating current waveforms are shown in Figure 9b,c,d, respectively. Conversely, the controllers still work and gain stability even after the large communication gap.
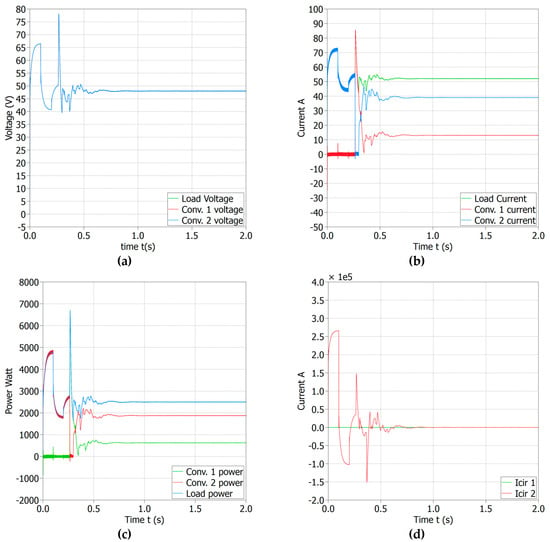
Figure 9.
Scenario 3 outputs with load resistance of 0.9216 Ω, K1 = 1 and K2 = 3, Rline1 = 0.0001 Ω, Rline2 = 0.00015 Ω, , . (a) Converters’ output voltages and the load voltage, (b) Converters’ output currents and the load current, (c) Converters’ output power and the load power, (d) Circulating currents.
5. Conclusions
In this paper, paralleling of buck converters is done. The theory of time constant and damping time constant is utilized in primary control design. A simply combined average voltage and proportional current sharing controller and a circulating current minimization technique with fixed droop resistance based on LBC in secondary control is proposed and implemented in PLECS software. The system is analyzed by different scenarios such as different line resistances between parallel converters, different time delays in communication for each converter, change in load, and proportional current sharing. A general guideline for implementing the proposed method and the results obtained from simulation is presented. The line resistances should be less than the droop resistance, i.e., Rline << Rdroop, for proper operation. The tested system shows rapid response during the transient state in restoring the grid and output voltages of converters during a sudden change in load. The proposed system also shows stability in communication delays of each neighboring converter up to 100 ms and circulating current minimization. For best system operation, it is suggested to select scenario 1. However, the proposed system design guarantees fulfilling the worst case scenario as well.
In the future work, tertiary or management level control must be added and a large number of buck converters would be considered with practical implementation. Furthermore, tertiary control would not only guarantee the energy sharing to other grids but would also detect/disconnect abnormal connected distributed converters because of communication link failure or insufficient energy balance.
Author Contributions
Investigation, Z.J.; Resources, A.A. and A.N.; Supervision, T.S.; Writing—original draft, S.A.
Funding
The project is supported by “The National Natural Science Foundation of China” (Grant No. 51477040).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhou, X.; Guo, T.; Ma, Y. An overview on microgrid technology. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Beijing, China, 2–5 August 2015; pp. 76–81. [Google Scholar]
- Zhou, X.; Cui, L.; Ma, Y. Research on smart grid technology. In Proceedings of the International Conference on Computer Application and System Modeling, Taiyuan, China, 22–24 October 2010; pp. 599–603. [Google Scholar]
- Zhang, C.; Wu, J.; Zhou, Y.; Cheng, M.; Long, C. Peer-to-Peer energy trading in a Microgrid. Applied Energy 2018, 220, 1–12. [Google Scholar] [CrossRef]
- Jogunola, O.; Ikpehai, A.; Anoh, K.; Adebisi, B.; Hammoudeh, M.; Gacanin, H.; Harris, G. Comparative analysis of P2P architectures for energy trading and sharing. Energies 2017, 11, 62. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Unamuno, E.; Barrena, J.A. Equivalence of primary control strategies for AC and DC microgrids. Energies 2017, 10, 91. [Google Scholar] [CrossRef]
- Kumar, D.; Zare, F.; Ghosh, A. DC microgrid technology: System architectures, AC grid interfaces, grounding schemes, power quality, communication networks, applications and standardizations aspects. IEEE Access 2017, 5, 12230–12256. [Google Scholar] [CrossRef]
- Lonkar, M.; Ponnaluri, S. An overview of DC microgrid operation and control. In Proceedings of the 2015 Sixth International Renewable Energy Congress (IREC), Sousse, Tunisia, 24–26 March 2015. [Google Scholar]
- Meng, L.; Shafiee, Q.; Ferrari-Trecate, G.; Karimi, H.; Fulwan, D.; Lu, X.; Zapata, J.M.G. Review on Control Methods of DC Microgrid. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 928–948. [Google Scholar]
- Sahoo, S.K.; Sinha, A.K.; Kishore, N.K. Control techniques in AC, DC, and Hybrid AC–DC Microgrid: A review. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 738–759. [Google Scholar] [CrossRef]
- Thomas, R.M.; Jose, D. Control method for Parallel DC-DC converters used in standalone Photovoltaic power Systems. Int. J. Energy Res. Technol. 2015, 4, 784–789. [Google Scholar]
- Babu, J.; Mathew, B.K. Decentralized Control Method for load sharing and circulating current minimizaion in standalone DC Microgrid. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2016, 5, 7170–7178. [Google Scholar]
- Braitor, A.C.; Konstantopoulos, G.C.; Kadirkamanathan, V. Power sharing of parallel operated DC-DC converters using current-limiting droop control. In Proceedings of the 25th Mediterranean Conference on Control and Automation (MED), Valletta, Malta, 3–6 July 2017. [Google Scholar]
- Shahid, M.; Khan, M.; Hashmi, K.; Habib, S.; Jiang, H.; Tang, H. A control methodology for load sharing system restoration in islanded DC micro grid with faulty communication links. Electronics 2018, 7, 90. [Google Scholar] [CrossRef]
- Lu, X.; Guerrero, J.M.; Sun, K. Distributed secondary control for dc microgrid applications with enhanced current sharing accuracy. In Proceedings of the 2013 IEEE International Symposium on Industrial Electronics, Taipei, Taiwan, 28–31 May 2013. [Google Scholar]
- Liu, X.K.; He, H.; Wang, Y.W.; Xu, Q.; Guo, F. Distributed Hybrid Secondary Control for a DC Microgrid via Discrete-Time Interaction. IEEE Trans. Energy Convers. 2018, 33, 1865–1875. [Google Scholar] [CrossRef]
- Zammit, D.; Staines, C.S.; Apap, M.; Micallef, A. Paralleling of buck converters for DC microgrid operation. In Proceedings of the IEEE-3rd International Conference on Control, Decision and Information Technologies, Saint Julian’s, Malta, 6–8 April 2016. [Google Scholar]
- Gunasekaran, M.; Mohamed Ismail, H.; Chokkalingam, B.; Mihet-Popa, L.; Padmanaban, S. Energy Management Strategy for Rural Communities’ DC Micro Grid Power System Structure with Maximum Penetration of Renewable Energy Sources. Appl. Sci. 2018, 8, 585. [Google Scholar] [CrossRef]
- Phurailatpam, C.; Sangral, R.; Rajpurohit, B.S.; Singh, S.N.; Longatt, F.G. Design and analysis of a dc microgrid with centralized battery energy storage system. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015. [Google Scholar]
- Khoucha, F.; Benbouzid, M.; Amirat, Y.; Kheloui, A. Integrated energy management of a plug-in electric vehicle in residential distribution systems with renewables. In Proceedings of the 24th IEEE International Symposium on Industrial Electronics, Búzios, Rio de Janeiro, Brazil, 3–5 June 2015. [Google Scholar]
- Wang, H.; Han, M.; Guerrero, J.M.; Vasquez, J.C.; Teshager, B.G. Distributed secondary and tertiary controls for I–V droop-controlled-paralleled DC–DC converters. IET Gener. Transm. Distrib. 2017, 12, 1538–1546. [Google Scholar] [CrossRef]
- Kato, M.; Imura, T.; Hori, Y. Study on maximize efficiency by secondary side control using DC-DC converter in wireless power transfer via magnetic resonant coupling. World Electr. Veh. J. 2013, 6, 858–862. [Google Scholar] [CrossRef]
- Zhong, W.; Huang, Z.; Zhu, T.; Gu, Y.; Zhang, Q.; Yi, P.; Jiang, D.; Xiao, S. IDES: Incentive-driven distributed energy sharing in sustainable microgrids. In Proceedings of the International Green Computing Conference (IGCC), Dallas, TX, USA, 3–5 November 2014. [Google Scholar]
- Luo, F.L.; Ye, H. Small signal analysis of energy factor and mathematical modeling for power dc–dc converters. IEEE Trans. Power Electron. 2007, 22, 69–79. [Google Scholar] [CrossRef]
- Wang, F.; Ma, K. Transfer function modeling and analysis of the open-loop Buck converter using the fractional calculus. Chin. Phys. B 2013, 22, 030506. [Google Scholar] [CrossRef]
- Luo, F.; Ye, H.; Muhammad, R. Digital Power Electronics and Operation; Elsevier Academic Press: San Diego, CA, USA, 2005. [Google Scholar]
- Salem, F.A.; Rashed, A.A. PID controllers and algorithms: Selection and design techniques applied in mechatronics systems design-Part II. Int. J. Eng. Sci. 2013, 2, 191–203. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).