Abstract
This work addresses the question of explaining changes in the desired timescales of the stock market. Tangled string is a sequence visualization tool wherein a sequence is compared to a string and trends in the sequence are compared to the appearance of tangled pills and wires bridging the pills in the string. Here, the tangled string is extended and applied to detecting stocks that trigger changes and explaining trend changes in the market. Sequential data for 11 years from the First Section of the Tokyo Stock Exchange regarding top-10 stocks with weekly increase rates are visualized using the tangled string. It was found that the change points obtained by the tangled string coincided well with changes in the average prices of listed stocks, and changes in the price of each stock are visualized on the string. Thus, changes in stock prices, which vary across a mixture of different timescales, could be explained in the time scale corresponding to interest in stock analysis. The tangled string was created using a data-driven innovation platform called Innovators Marketplace on Data Jackets, and is extended to satisfy data users here, so this study verifies the contribution of data market to data-driven innovation.
1. Introduction: Problem Definition
Stock analysts are often classified simply into fundamentalists and technical analysts, i.e., chartists. The former considers the basic effects of events that significantly affect stock investors’ decisions, whereas the latter analyze charts, i.e., the time series of stock prices. Although these two groups tend to be regarded differently, it is quite natural that a chartist may also consider the effects of social events not shown in charts [1] and that a fundamentalist may also refer to sequential data regarding stock prices [2,3]. The existence of these two approaches is partially analogous to the positioning of real (human) analysts and machine learning. Machine learning tools have been recently adopted to forecast market demand [4,5,6,7] from data, and this can be regarded as the partial automation of the thoughts of a technical analyst. However, changes in the market due to external events are hard to explain by learning from data, because the consideration of external events indicates that these fundamental causes of investor behaviors are not included in available data. Not only investors, but also policy-makers related to the market need to explain the changes in the market resulting from external events.
The main goal of this study is to enable the detection and the explanation of changes in the stock market from available sequential data on stock prices. We aim to detect changes in investor preferences that influence the market and to explain the associated causality, i.e., why investors showed positive preference for a certain group of stocks, and why the positive attitude was subsequently overwhelmed by the appearance of a new trend. Here, we define a trend as the enhancement of various investor preferences for a certain set of stocks for a certain period. We simply regard the stock market as a place where the trends of investor preferences compete, which reflects complex social dynamics because each trend is a mixture of various causalities across different timescales. On the other hand, negative effects such as the downpricing/disappearance of stocks, or chained downpricing/bankruptcies are excluded from our scope in order to reduce the complexity in modeling the interaction of both positive (to buy stocks) and negative (to sell or not to buy) motivations.
So far, event studies have been applied to validate the effects of focused information generating events such earnings announcements or discount rate changes, estimates of earnings, and news events [8,9] on the changes in stock prices in the period following the events. Machine learning was also applied for the prediction of changes using the results of event studies as teaching signals [10]. On the other hand, in this study we aim to aid analysts in the detection and explanation of changes in the market and in the price of each stock, in such a long-term sequence of 10 years or more. Furthermore, we aim to enable the explanation based on real and available data that includes events occurring under the action of several different causalities. Regarding the availability of data, professional analysts working for asset companies may have elaborate data that are classified into categories of stocks and also include downpriced stocks that may not be listed anymore in the stock exchange market. We, on the other hand, use the sequential data on stock prices, which is available to the public, where timescales are mixed and information about the worst companies are typically unavailable.
Suppose we have data D on the increase in stock prices designated as }, where Bt stands for a basket, i.e., a set of members of itemset I, forming a co-occurring set of top-rank, up-pricing stocks. D is regarded as the data corresponding to the high-rank preference of investors at time t, which corresponds to the research interest in the positive preference of investors as mentioned above, and T is the sequence length of the data. This type of basket data has been used for explaining patterns and changes in the market [11,12,13]. For example, suppose the weekly average stock prices of firms in healthcare businesses show the greatest increase for a month, whereas those in electronics registered a greater increase last year. The cause of this new trend may be the interest intensified by investors in healthcare due to a famous movie at the end of the previous year that dealt with the negative effect of daily foods on human health. This causality may be explained if stock analysts, who broadcasted the analysis to investors, were also interested in the movie (certainly not in the set I) during the corresponding period. Furthermore, policy-makers can plan ahead to support healthcare businesses if the new trend is regarded as sustainable on a long timescale.
Using machine learning, change points of the features (parameters in parametric models) of time series models have also been detected. By projecting the data to the principal components, for example, the sensitivity of change detection was improved using the method for detecting the changes in the correlation, variance, and mean of the components with time [14]. Changes in model parameters that capture the structure of the latent causality have been detected in discrete [15,16,17] and continuous [18] time series. Here, suppose the changes in the values of the parameter set Θ from time t−δt to t is learned as Θ [t−Δt, t]−Θ [t−δt−Δt, t−δt], where Δt is the length of the training time of the data to learn Θ from and δt is the given time step from before (t−δt) to the present (t). The precision of change detection is expected to improve for larger values of Δt that can be regarded as a part of the tolerant delay, i.e., the length of time that analysis should wait to detect a change. In [12], the author pointed out that a large value of Δt is not convenient for capturing the variations accurately. On the other hand, the focus of this study is to detect events that explain the changes in the timescale that is in accordance with the interest of the analyst or investor. This corresponds to the detection of change points for δt that fits the users’ purpose, to relate with external information that can explain the changes in a time scale corresponding to δt. In machine learning for price forecasting using an adaptive timescale, a mixture of patterns across various timescales has been fitted to real data to analyze the price dynamics on different granularities and different abstraction levels and a high accuracy classification into patterns of decision opportunities in stock investment was realized [7]. On the other hand, in this paper we aim to aid an analyst’s explanation of a complex, mixed timescale sequence. Like a tangle on a string (to be illustrated as “a complex part” in Figure 1), the complexity of each subsequence where the behavior of different investors are mixed may be grasped without separating or reducing into simple patterns, as long as the abstract of each complex part and the ending/starting points of each complex part can be used for explaining the changes in the sequence.
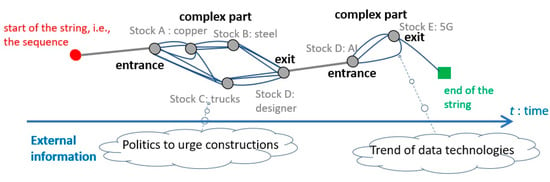
Figure 1.
Visualization of a sequence by a string with complex tangled parts.
In order to explain a change, in addition to detecting it, we may consider employing methods to learn latent topics from sequential data. Consecutive time segments, each of which corresponds to a vector in the space of a limited dimension of latent topics (without labels corresponding to the meaning of the topics) are obtained by the dynamic topic model (DTM) [19]. By applying DTM to sales data, the changes in consumers’ interests can be detected as the boundaries between the obtained time segments corresponding to discontinuous changes in the topic vector. The topic tracking model (TTM) has been also presented to analyze the change in each consumer if consumer behavior c is reflected on the data of Bt,c, instead of Bt above [13]. The hierarchical structure of topics has also been learned [20], which indicates the potential to explain the changes behind observed events by considering latent events, i.e., deep causes not covered by the data in hand. On the other hand, we aim to obtain different explanations where trends (corresponding to topics in the sequence) in the explained scenarios change at different times, and for different timescales, by introducing external information about latent events. For example, the sequence of stock prices for a decade can be explained as the shifts in trending business domains if we think in terms of an annual timescale, but we may observe different change points such as the effects of analysts’ or firm managers’ predictions if we consider a monthly timescale. Thus, we regard D as in place of } mentioned above, where i stands for a timescale and Bt is the union of Bi,t for all i in {1, 2, …, n}, where n is the number of mixed timescales. To further the understanding, the problem here is to obtain and , where enti,t and exti,t represent events at time t that play the role of an entrance to and exit from a trend in the i-th timescale considered, respectively. If no event at time t plays the role, enti,t and exti,t should take a null value.
In this study, for the main goal mentioned above, we consider the subgoal of aiding the human in linking parts of a sequence that is difficult to explain, to other parts and external information. Here we assume that an essential part of the difficulty in explanation comes from the complexity of event-to-event causality, where an event may occur in the mixture of various subsequences. From this assumption, we extend the tangled string (TS), as in Section 2, which deals with a sequence where patterns of different timescales coexist. Such a sequence is usual for data on the behavior of participants in a society who may not share the same interest in topics or trends. Behind the sequence of stock prices, various investors really have different reasons for buying and/or selling stocks, reflecting their various interests in the market dynamics in various timescales. In TS, a sequence is visualized as a string as in Figure 1 where a node and an edge represent an event and the temporal order of events, respectively, and each tangled part corresponds to a complex mixture of different subsequences in various timescales corresponding to the different interests of investors if applied to a stock price sequence shown in Section 2.1. Each tangled part corresponds to a trend of included stocks, and the multiple paths meet at entrances (stocks A and E) and exits (stocks E and F) of a tangled part, as stated above regarding enti,t and exti,t. The choice of method for data visualization becomes key for integrating the approaches of fundamentalist and technical analysts, by providing both classes of (if we can so classify) investors with links to information that they should refer to via the procedure to be shown in Section 2.3. For example, a simple stock price chart may turn out to be a useful visualization if the essential tipping points of price transition are marked so that an investor can link them with external information about events affecting the stock market. In addition, the graphical visualization of the map of stocks and the news provide hints about sentiments in the market relevant to stocks [21,22]. In Section 3, we show the coincidence found in the results of TS with the beginning of the increasing value of stocks in the market and with major changes in stock prices. In Section 4, we discuss the qualitative explanations of trend shifts given by stock analysis experts based on the output of TS. The conclusions relate these results to our future work.
2. TS for a Stock Price Sequence
In this section, we introduce the tangled string (TS hereafter [23,24]) as a method for the analysis and visualization of sequential data. This tool is expected to fulfill the purpose stated in the previous section, i.e., to explain the changes in a sequence where different timescales coexist.
2.1. Origins of TS and the Data Market
The original version of TS was a product of the Innovators Marketplace on Data Jackets (IMDJ), a market-like creativity support system [25,26]. On IMDJ, data providers make available the data that they have and/or possible methods for data analysis, while data users post requirements for data and analysis technologies or methods. Events in the given sequential data are analyzed and visualized by TS as nodes on a string, where the importance of each event is computed according to their positions on the string. This visualization has been designed to fit the user’ requirements presented in IMDJ; that is, in order to realize the method M1 below for satisfying the requirement R1. TS was originally invented for detecting the message with the highest social impact from a log of human communication (DJ1) by considering the trends of topics in the preceding and subsequent messages. After choosing such words, additional information about disasters (DJ2) should be used for validating the credibility of the message corresponding to the chosen messages.
- Requirement R1: collect information useful for decision making
- Method M1: obtain a high impact message in a sequence and relate it to external information
- Data for realizing M1: {DJ1: log text of communication, DJ2: information about disasters}
The performance of TS has been shown to satisfy the requirement R1 above and others in the analysis of the text in timelines and the sensor-based log of human’s movements in office [23]. After TS was invented as a response to R1, it came to be required in the following set.
- Requirement R2: explain events in the tipping points of consumer behaviors in the market
- Method M2: detect a high impact event by TS and relate it with external information to explain the causality
- Data for realizing M2: {DJ3: log of consumptions or purchase history, DJ4: social events and news}
In this paper, we take the stock market as the target market in R2 and investors as consumers. That is, R2, as listed above, is expected to be solved by TS in this paper (challenged since [24]), by an analogy from R1, as shown in the Discussions section of this paper, where the detected events are explained by an expert with links to external information and news such as Prime Minister Abe’s policy for the national economy. Although the obtained explanation is not guaranteed to be the only one or the best, we can say that the changes corresponding to the complex parts in the sequence came to be linked to real social events in the explanations, as illustrated in Figure 1. The novelty here is that we introduce the analogy from DJ1 (log text of communication) to DJ3 (log of consumptions or purchase history) and from the relation of requirement(R1)-method(M1)-data(DJ1, DJ2) to requirement(R2)-method(M2)-data(DJ3, DJ4).
2.2. TS Algorithm
As shown in Figure 1, the tangled string (TS) visualizes a string corresponding to a sequence, where each complex part corresponds to a tangled substring as in Figure 2. In TS, a sequence is modeled by a string of which each tangled substring is called a pill. A pill is defined as a sequence of events beginning from a particular event to the appearance of the same event in the sequence. Events in the sequence are classified into two components: (1) events in pills and (2) others on wires that are substrings connecting pills.
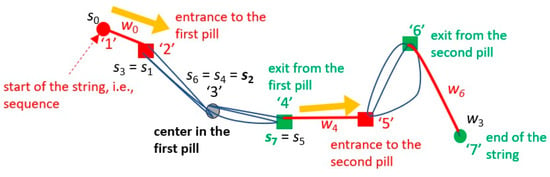
Figure 2.
Tangled string TS applied for String. si is the i-th event in the sequence, corresponding to the token “x” beside it.
In order to reduce ambiguity, the symbol expressing an event (in this study, the pricing up of a stock) is called a token. In natural language, the same token may mean different items, and the same item may be represented by different tokens. On the other hand, the token representing a stock ID (a number representing a unique stock) is the event that the increase in the stock price ranked in the top-10 (or top-5, depending on the target data) in the market. Therefore, a token corresponds uniquely to an event at a certain time in the target sequence. Pills formed in the sequence may meet each other, due to their sharing the same tokens. As a result, a string having pills may cross itself to make a larger pill. For example, in Figure 2, the pill including {s2 (=“3”), s3 (=“2”), s4 (=“3”)} and the pill including {s5 (=“4”), s6 (=“3”)} meet at s2, s4, and s6 because they include the same token “3” and form one pill. Thus, a pill may include other pills; a maximum pill (a pill not properly included by any other pill) is called just a pill hereafter. The same token may appear multiple times in a pill within a constant time window, which means that a pill corresponds to a trend where the included items appear repeatedly.
On the other hand, events on wires represent the changes from a trend represented by a pill to the next trend. In this sense, the connections of pills via wires are expected to be used to explain changes in the sequence. By the connection of pills and wires, we aim to visualize sequential data to explain the changes in the trends and their causes. The TS algorithm is given below as Algorithm 1.
| Algorithm 1. Original version algorithm of TS algorithm (Revised from [23] without changing the meaning) |
| Initial setting: String = {s1, …, … si, …sj, …, …, sL}, Wires = {w1-w2-w3-…-wL−1} where wi = si−si+1 represents the edge connecting the adjacent pair of tokens for i = 1 to L: pill(si) = si where pill(s) represents the pill including event s. weight(si) = 0 For W, a preset window, execute the cycles below: For i = W + 1 to L: Neighbors (si, W) = {si-W, si-W+1, …, …, si-1} if ∃sj(<i) ∈ Neighbors(si, W) {token(si) = token(sj)}: j = min{j|sj ∈ Neighbors(si, W), token(si) = token(sj)} r(si) = r(sj) #place si at r(sj), the same position as sj Wires = Wires\{wj-wj+1-…-wi-2} # cut the subsequence from sj to si-1 from Wires pill(si) = … = pill (sj+1) = pill (sj) # put all the events on the loop made by si and sj in the same pill pill_weight(sj) += i − j # the length of the loop is added to the weight of event sj in the pill else r(si) = r(si-1) + a {r(si-1)−r(si-2)} # place si in the extension of the line from si-1 to si (a: a real constant) end if End For For each pill sent, sext = the first and the last event in pill weight(sent) =weight(sext) = ext – ent # assign the pill size as the weight of each event on a wire End For |
Here, si denotes an event that the symbol token(si) appeared at the i-th position in the given string String, rather than the symbol itself. That is, token(si) is unique to a symbol, and si for multiple i’s may correspond to the same symbol. In the initial setting, no pill but only a single wire exists as a string corresponding to the given sequence of length L. After the initial setting, each event si in the string is considered one by one in the ascending order. For each si, the event sj of the same token as si is searched from the events preceding si within the window of the time interval W in weeks (e.g., W = 3 implies that the interval is 3 weeks), represented by Neighbors(si) in the backward search for events, i.e., for the time range [i−W, i−1]. If such an event sj is found, si and all the events between sj and si are considered to belong to the same pill as sj (i.e., pill(sj) = pill(sj)); so, the trend in this pill appears as repeated tokens (as token(si) = token(sj)). A pill may later become a part of a larger pill if a token in the succeeding W baskets matches with a token in the pill. The substring between sj and si is pruned from Wires, which represents the set of all the wires if sj and si join the same pill. On the other hand, if no event such as sj for which the token (token(sj)) is equal to token(si) is found within the window of W baskets before si, then si and all the events in Neighbors(si) stay as a wire. After the cycles, a position (position i) is assigned to each si.
When a new event si is added as a node in a pill, the size of the pill is increased by the number of events added. After all the cycles are completed, the weights of sent and sext, which are the first and last events (i.e., st of the smallest and the largest t) in each pill, denoted by weight(sent) and weight(sext), respectively, take the values of the size of the pill. This means that the size of a pill is counted as the weight loaded on the edges of the wires connected to the pill. We call sent the entrance to the pill and sext the exit from the pill. The events at the entrance and the exit of a pill are visualized as a red and a green node, respectively, on the string. Each of these events having a large value of weight is visualized by a large letter. These events play an important role in explaining the changes in the trends in the sequence, such as trend shifts in the market. For example, if TS is applied to the sequence String as Equation (1).
String = 1, 2, 3, 2, 3, 4, 3, 4, 5, 6, 2, 5, 6, 7.
In this case, as shown in Figure 2 and Figure 3a, the event of the appearance of an item represented by token “2” starts the first pill including itself, along with “3” and “4”, because “2” is the first token revisited by the other nodes in the string. The first item ”1” in the sequence is assigned to the event s0, and “2” is to s1 as well as s3. The token “3” is visited thrice, i.e., as {s2, s4, s6}, and “4” is visited twice as {s5, s7}. In this pill, “4” is the last token repeated, so it is regarded as the exit of the pill. Then “4” is the beginning of the wire that connects to the next pill. Here, TS visualizes the flow of the sequence, highlighting the nodes where each wire is connected to the preceding and following pills. Events on the wires may not look outstanding because they are not frequent in pills that are repeated. However, an on-wire node possibly plays an essential role in the mainstream of the sequence because the connection in the whole structure is cut off if such an event is lost. Although in this sense, the event of token “3” in Figure 2 and Figure 3a may be suitable to be on a wire as the structure gets destroyed by deleting “3”; here “3” is regarded not as an on-wire, but the main event in the first pill as the other events in the first pill are connected to “3”.
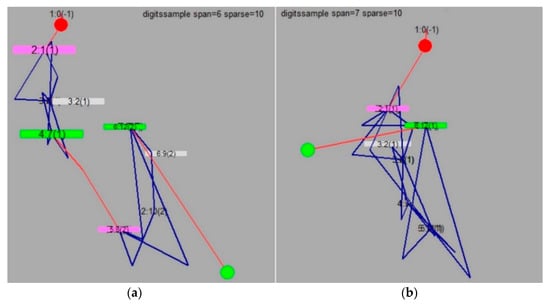
Figure 3.
TS employed for the widths (W) of 6 and 7 (the unit of W is a week). (a) is for W = 6, (b) for W = 7. The overlapping letters are visualized as they are in order to show tokens revisited multiple times.
The window width W plays an important role because setting W to a larger value means aiming at the detection of the entrances to and the exits from pills in a longer timescale. Although the obtained time length of a pill is not in proportion to W, we can obtain an obvious change in the structure of the TS by changing W and can find different change points for different timescales. In Figure 3a, “2” appears twice because the distance from the first and the second “2” is 7 in the sequence and the window width W is set to 5. As in Figure 3b, the change in W causes a radical change in the structure if W is set larger than the distance between the appearances of the same item. The structure changes considerably from Figure 3a,b, losing the wire from “4” to “3” and unifying the two clusters in (a) into one in (b). The structure does not change more for a further increase in W. An additional advantage of the algorithm is that the computational time is in the order of O(L), i.e., linear to the length of the sequence.
In the extension below (Algorithm 2), si in the initial setting denotes the i-th event in the data except “#n” in String, where String is the given data on a sequence and “#n” denotes delimiters between baskets. Other settings are similar to the original TS shown earlier.
| Algorithm 2. An extension of TS for dealing with basket data; TS for basket-set data |
| Initial setting: String = {#n1, s1, s2, …, #n2, s.., …, s.., …, #nT, …, sL}, where #n: the delimiter for each time t. Wires = {w1-w2-w3-…-wT} where wj is {#nj-s … -smj (just before #nj+1)} for each s in String: pill(s) = wj where sj is a member of wj weight(s) = 0 For W, a preset window, execute the cycles below: For each si in String/{#n1, #n2, …, #nT}: Neighbors (si, W) = ∪ wk-W+1, …, wk where si is a member of wk. if ∃sj (<i) ∈Neighbors(si, W) s.t. token(si) = token(sj): j = min{j|sj ∈Neighbors(si, W), s.t. token(si) = token(sj)} r(si) = r(sj) #place si at r(sj), the same position as sj Wires = Wires\{wp-…-wk-1} where sj is a member of wp. pill(s) = pill (sj) for all s in {si} ∪ all s in {wp, …, wk-1} pill_weight(sj) += i−j # the length of the loop is added to the weight of event sj in the pill else r(si) = r(si-1) + a {r(si-1)−r(si-2)} #place si in the extension of the line from si-1 to si (a: a real constant) end if End For For each pill sent, sext = the first and the last event in pill weight(sent) = weight(sext) = ext−ent # assign the pill size as the weight of each event on a wire End For |
In this extended TS for sequential basket data, for the newest event si, sj of the same token as si is searched from the preceding W baskets before si. If such an event as sj is found, all the events between sj and si and their constituent baskets form a pill. The entrance to the combined pill thus obtained is sj if sj is the first event revisited in the pill, and si becomes the exit if sj is the last event revisited in the pill.
2.3. Explanation by TS Approach
It is recommended that the user of the visualized string finds the association between the string and external information about real events using the following procedure, for explaining the changes in the sequence. It is assumed that the user is a domain expert, i.e., a stock analyst, with respect to this study. The string is visualized, not only to obtain the entrances and exits from the pills automatically.
- (1)
- Find nodes (s of “s : t” in Figure 4, Figure 5 and Figure 6) at entrances or exits, shown in large letters in the string compared to the surrounding items, indicating that a larger letter means the entrance to or the exit from a larger trend of some set of stocks.
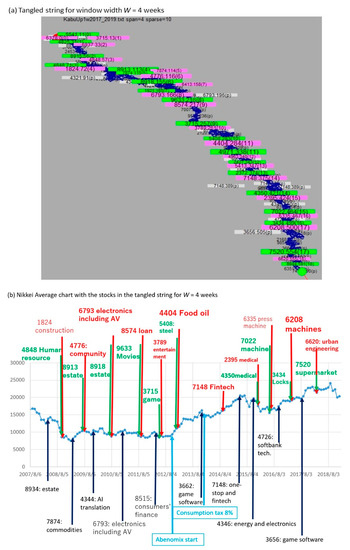 Figure 4. Results of TS for W = 4 (weeks) for the top-10 data. In (a), each red (pill entrance) or green (pill exit) node show X:Y:Z where X, Y, and Z represent the stock ID, its time (the week counted from the start of the sequence), and the number of pills counted from the beginning, respectively. The white node in (a) shows the most frequent token in each pill. (b) shows the timing of the nodes in (a) on the curve of the average price of all stocks (Nikkei Average).
Figure 4. Results of TS for W = 4 (weeks) for the top-10 data. In (a), each red (pill entrance) or green (pill exit) node show X:Y:Z where X, Y, and Z represent the stock ID, its time (the week counted from the start of the sequence), and the number of pills counted from the beginning, respectively. The white node in (a) shows the most frequent token in each pill. (b) shows the timing of the nodes in (a) on the curve of the average price of all stocks (Nikkei Average).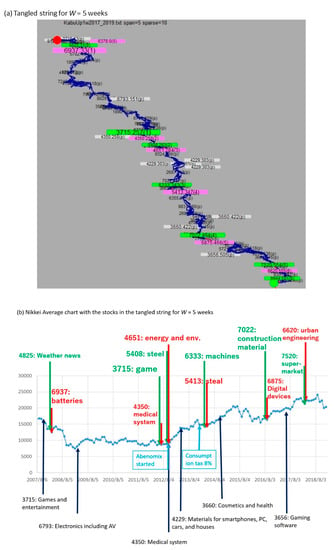 Figure 5. Result of TS for W = 5 (weeks) for the top-10 data. (a,b) mean the same as in Figure 4, respectively.
Figure 5. Result of TS for W = 5 (weeks) for the top-10 data. (a,b) mean the same as in Figure 4, respectively.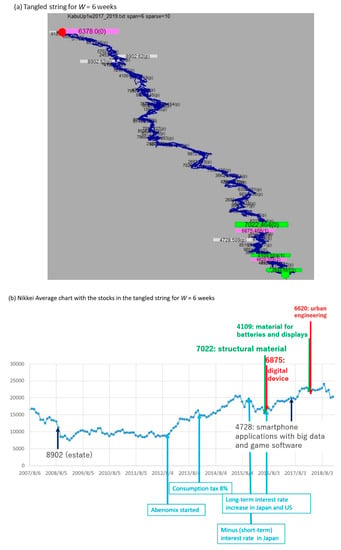 Figure 6. Result of TS for W = 6 (weeks) for the top-10 data. (a,b) mean the same as in Figure 4, respectively.
Figure 6. Result of TS for W = 6 (weeks) for the top-10 data. (a,b) mean the same as in Figure 4, respectively. - (2)
- From the string, choose large pills that have a tangled structure as complex parts in Figure 1. This is because a large complex pill corresponds to a trend that includes a set of frequent events occurring under various subsequences.
- (3)
- Explain the events at the nodes found in (1) above and the complex pills chosen in (2) above, correlating closely located events in the string with real events in the external information such as the user’s experience, common sense, and news. This part should be a free externalization of subjective ideas, rather than adherence to objective facts, in order to collect various explanations of possible causalities.
Such a simple procedure enables easy usage of the string. However, the authors assume that this human–machine interaction process should be regarded as the essence of TS, and the high performance of TS stated in Section 3 should be positioned as the evidence to support the user’s belief in this procedure where TS is employed in positioning entrances and exits of pills in the explanation.
3. Results
The performance of TS as a tool for change detection is experimentally evaluated here. In Section 3.1, the outline of the weekly data on high-rank price-increasing stocks is shown. Then, the results presented here are two-fold. In Section 3.2, we show the coincidence of the entrances and exits of the pills obtained by TS with the beginning of the up-pricing of stocks in the market, by setting W to several different values. Subsequently, in Section 3.3., we show the coincidence of the entrances and exits with the major changes in stock prices. Later in Section 4, the qualitative explanation of the trend shifts, provided by an expert of stock analysis and approved by other analysts, is given for the output figures of TS.
3.1. Data on Up-Pricing Stocks
The TS method is applied to the data on stock prices, of which the stocks with the highest price increase rate are considered every week (http://www.kabu-data.info/neagari/neagari_hizuke_w_1.htm). These data were taken from the First Section of the Tokyo Stock Market for 592 weeks from 6th July 2007 till 4th January 2019. The original data included the names of each company but here we consider just the stock ID number of each firm as shown in Table 1. Each set of top-10 stocks per week are collected as basket data as in Table 1, and a similar collection is done for top-5 stocks per week to make a comparison. We also used data on Japan’s stock price trend (Nikkei Average) for evaluating the performance of TS in detecting the up/downward price changes in the entire stock market. The data on each stock were collected as described in Data Availability in the Supplementary Materials section.

Table 1.
Weekly data on top up-pricing stocks. The white cells show the data content, where “#n” represents the beginning of each basket of top up-pricing stocks for each week, and each 4-digit integer shows a stock ID. This table shows a sequence of top-10 up-pricing stocks. A row includes five stock IDs for top-5 up-pricing stocks.
We include experiments for only the top (up-pricing) stocks, and not for the worst (downpricing) stocks, for three reasons. First, this study aims to enable the detection and the explanation of changes in a sequence in available data. In comparison with data on the top five or ten stocks, it is not easy to collect or get approval to use data on the worst stocks. Second, there are firms in even worse situations than the worst among the listed companies in the stock market—that is, being at the end of a list does not mean that the situation of the firm is exceptionally bad. The third and most essential point is that, in this study, the explanation is aimed at changes in the investors’ preferences, i.e., why they preferred positively to buy some stocks rather than act upon negative motivations to sell stocks (See Section 1).
3.2. TS Visualization with Changing the Window Width W
The TS visualizations are shown in Figure 4, Figure 5 and Figure 6. In (a) of each figure, the letters in red and green show sent and sext, respectively, which are the events that start and end a pill. The letter size shows the weight, i.e., the number of items in the pill that are started or ended by the event. The node other than red or green (white node marked by “(p)”) shows the most frequent token in each pill. In each figure, the curve in (b) shows the average price of all the stocks (Nikkei Average mentioned in Data Availability). In (b), the larger letters of s in “s:t” in (a) is shown in larger letters at time t. This procedure can be automatically executed, but has been executed by the authors after discarding smaller letters such as 4825 that could not be included in (b) due to the space constraint. Note that each (b) is just for making the discussion in Section 4 understandable and is not the result of the procedure in Section 2.3. For example, the pill ending at 4825 in Figure 4a was discarded, although 4848 was as small as 4825 in (a). Thus, (b) of Figure 4, Figure 5 and Figure 6 does not include sent and sext but just relatively larger letters in (a). However, from the viewpoint of aiding the human explanation of changes as mentioned in Section 1 with such a figure as Figure 1, the visualization of the letter sizes together with their connections with the tangled parts is meaningful. For example, a small-sized red token in (a) should not be ignored if it is larger than other letters nearby on the string and is an entrance to a small but complex pill. In such a case, the human should link his/her experiences or common sense to the entrance stock and to stocks in the pills connected to this entrance stock. The position of nodes and edges in the output of TS are coordinated just for simplifying the string shape [27], and the structure is not changed.
For the top-10 data, in the sequence visualized by TS in Figure 4a, setting window width W to 4 corresponds to the time series of the Nikkei Average in Figure 4b. Because 19 pills were obtained by TS here for 11 years, setting W to 4 implies investigating the pills for the timescale of approximately 0.58 y, which indicates the minimum required time resolution to distinguish two consecutive pills. For this W value, we do not find an obvious coincidence between the timing of the red/green nodes and the long-term change points in the stock prices of Nikkei Average in Figure 4b as far as we view the curve. On the other hand, the results in Figure 5a,b are for setting W to 5. Because we obtained seven pills for the 11 y, W = 5 means the timescale of ~1.6 y. In this case, we find a substantial coincidence between the timing of red/green nodes and the long-term changes in the Nikkei Average. That is, five of six red nodes (except the first of the seven red nodes which turned out to be the first of the whole sequence, because the distinction between the first node and its previous nodes is trivial) are within 3 months before the monotonic increase for 6 months or longer in the Nikkei Average in Figure 5b.
Including the results for other settings of W and the data for the top-5 companies, the precisions are shown in Table 2. Here precision means the percentage of the red nodes within three months before the monotonic increase for six months or longer in the Nikkei Average. Note that the number of entrances and exits become larger for top-5 data than top-10 data if W is set equal. This is because each pill becomes smaller if the first same token in [t−W, t−1] as the token at time t appears later due to the lack of information in each basket. All the values in this table are larger than 0.52 (70 weeks within 3 months before the monotonic increase for 6 months, among all 134 weeks) for a random choice of alarm. Additionally, coinciding with intuition, the richer data of top-10 comments achieves higher precision than top-5 as in Table 2.

Table 2.
The precision of the entrances to pills in Nikkei Average.
The stock IDs and the timing of their appearance as entrances or exits of pills are shared in the Supplementary S1_Data. For a qualitative explanation of the changes considering the red/green nodes by experts, kindly refer to the next chapter.
3.3. Change in Stock Price and the Two Types of Change Points in TS
Next, we evaluated the coincidence of the entrances and the exits from pills to the change, i.e., increase and decrease, in stock prices. As in Figure 7, the entrances and the exits are viewed intuitively to coincide with the starting and halting of the periods of the high-price trend. Figure 7 exemplifies some of the cases where the prices of the stocks increased visually at (from before to after) the entrance. On the other hand, the price of the stock that started (appeared at the entrance of) a pill tended to decrease at the time of the exit from the started pill. To evaluate these tendencies, as in the left half of Table 3, let us compare the trend of the period of length Δt before and after the entrances of pills, for stocks that appeared as entrances (red letters in TS: see Figure 8a for an intuitive understanding). The comparison is shown in the right half of Table 3 for stocks that appeared at exits (green letters in TS, Figure 8b). It can be noted that we did not include cases where W is less than 3 for top-10 data or less than 7 for top-5 data in Table 3, because the number of pills came to 50 or more, meaning the average pill lengths were 2.8 months or shorter, i.e., shorter than any Δt we chose (3 months at least) for this evaluation. In these results, the prices of both change point stocks, i.e., stocks appearing as entrances and exits, tend to increase after their appearance. Although the percentage of increase is larger for the top-5 for all Δt, the significance of the increase (a larger increase than the standard deviation σ) is substantially smaller for top-5 than top-10. Here, similar to the results in Section 3.2, the results for top-10 data are finer than for top-5 in detecting high impact changes.
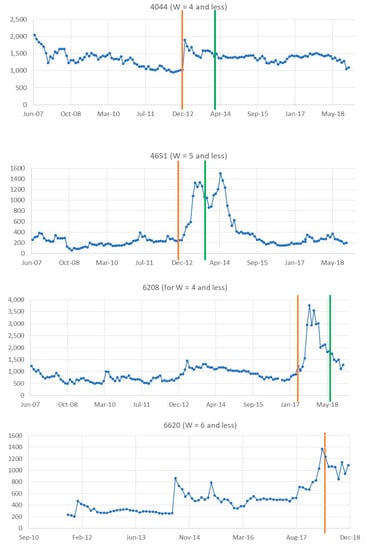
Figure 7.
Examples of entrances and exits of pills for top-10 data, located on the time axis of price changing.

Table 3.
Rates (and the counted numbers in the brackets) of the in/decrease of stock prices at (i.e., from the period of length Δt before to Δt after each entrance/exit) the entrances or the exits of pills, unifying the counts for W = 3, 4, 5, 6 for top-10, W = 7, 8, 9, 10 for top-5. The pair “stock ID: the time” in a red/green node in Figure 4, Figure 5 and Figure 6 are counted uniquely (one time for each pair). σ indicates the standard deviation of the price of each stock for the period of length Δt before t.
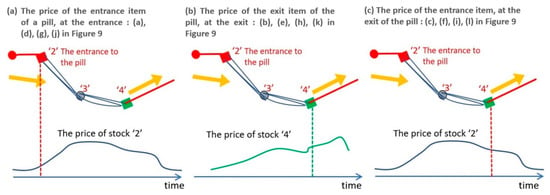
Figure 8.
Price changes of stocks at pill entrance/pill-exit, at the entrance/exit. (a–c) show the price of an item that appeared at the entrance or the exit that changed as shown in the curve, respectively. The price was evaluated at the time shown by the dotted vertical line.
On the other hand, let us investigate the dependence of the precision of the detection of price increase on the value of W. The probability of price increase of a pill entrance stock is high at (from Δt before and Δt after) the time that it appeared at the entrance (Figure 9a,d,g,j corresponding to Figure 8a). These probabilities tend to be higher than a pill-exit stock at the time it appears at the exit (Figure 9b,e,h,k corresponding to Figure 8b). On the other hand, the probability by which the price of the stock that appeared at an entrance increased is relatively smaller at the time of the exit from the pill (as in Figure 9c,f,i,l corresponding to Figure 8c) than the probability at the time it appeared at the entrance. These tendencies are found especially for larger values of W. This tendency is interpreted as in the discussions later.
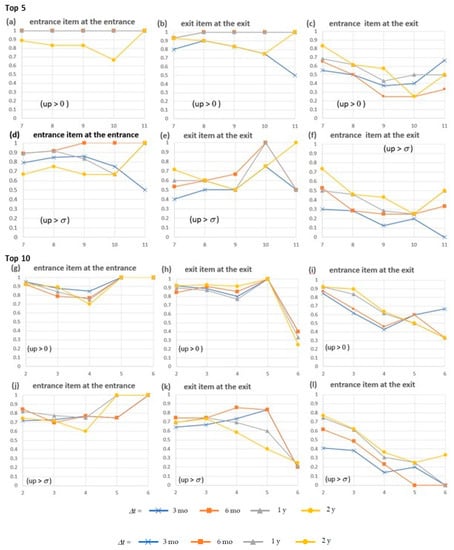
Figure 9.
Price rates (vertical) for entrance/exit items at the entrance/exits. The horizontal axes show the values of W. See Figure 8 and the main text for the meaning of panel (a–l), and the Supplementary S2_Data for the real values. For example, (c,f,I,l) show the price-up rates (i.e., increase rate in price) of the stock item that appeared at the entrance of a pill, evaluated at the exit of the same pill, corresponding to Figure 8c, respectively.
In this paper, we do not compare these results experimentally with methods for prediction using machine learning as in [4,5,6,7], because both the aims of (1) detection of the change points based on which the future increase/decrease trend can be forecasted in various time scales and (2) to explain or predict the long-term (e.g., 6 months) trend from a change point both in the entire stock market and of each stock, by the same visualization method, has not been challenged by an existing method. Furthermore, the precisions in Table 3 are higher than those associated with the prediction of up/downpricing by such machine learning techniques (e.g., 65% in [4]), even though changes in the long-term trend are difficult to predict because of the uncertainty in the long-term future. In the face of this difficulty, the precision of TS in the worst case to predict a middle/long-term (3 months or longer) increase in Table 3 is 81% for pill entrance events, 71% for increase larger than the standard deviation and for richer data, i.e., the top-10 up-pricing stocks. These percentages are higher than those obtained by existing methods that achieved high accuracy in finding precursors to drawdowns of the market average [28], or the rate of change oscillators as indicators for buying/selling [29]. On the other hand, the precision of classification into patterns of decision opportunities in stock investment exceeds 90% by the machine learning method [7]. Although the performance criterion differs from ours due to the difference in the goal, we plan toward the future to borrow this strength so that the explanation of each complex mixture can be made more efficient if the mixture can be reduced into simple structures or patterns using machine learning.
We also checked the tolerant delay in obtaining a changing point (entrance/exit) by entering a part of the original data, which do not include the entire target sequence of 11 y, but each tested sequence, having all the times before the evaluated event and the subsequence of length dt following the event, is available for various values of dt. This tolerant delay dt means the time we await after the appearance of a token s, for distinguishing if s is in a pill or on a wire. The tolerant delay in this sense includes both Δt and δt in the introduction. As a result, for all the pill entrances and exits for W > 3 for top-10 and W > 6 for top-5, we found the same entrances and exits are obtained for dt set to 3 months or larger. This result, however, needs no experimental verification because this is mathematically supported. That is, we can say that dt is upper-bounded by W−1 for the following reason. Here, let us count the time using an integer. Suppose the current time t is τ (>0) after the exit from the last pill (i.e., t−τ). Note there is no pair of same tokens in the time range [t−τ, t] at time t because this range is not in a pill. When a new token st+1 is added at the next time t+1, it is impossible to find the same token as st+1 in the time range of [t−τ, t−τ] if τ > W−1, because the time range [t+1−W, t] is the scope in searching the same token as st+1 and t+1−W is later than t−τ. That is, st−τ cannot be in the same pill as st+1 as far as τ > W−1, which means that st−τ is on a wire (note: the exit of a pill is on a wire linked to the next pill) forever if it is on a wire for time length W−1 after its appearance. In addition, st−τ+1 is on a wire (note: the entrance to a pill is on a wire). Further, it is trivially true that st−τ+1 is on a pill once it is on a pill. Thus, the tolerant delay is W−1 at the longest. From this principle, under the condition where the span W is set to shorter than 3 months for all the experimental cases, the tolerant delay is shorter than 3 months.
4. Discussions
Let us discuss the meaning of the results summarized above from the perspective of attaining the goal of this study, i.e., explanation of changes in various timescales by following the procedure in Section 2.3. In Figure 4 and Figure 5, an expert stock analyst, who has been a significant figure in investors’ voting in Japan (listed by Nikkei Veritas) for 16 years (2002 through 2017), found a high impact change in the period near December 2012 (stock no. 4404 in Figure 4 and no. 4651 in Figure 5, viewed as large letters as in Section 2.3(1)), corresponds to the political decision by Japan’s Prime Minister Abe who started to promote the economy for the upward trend through a policy called Abenomics. Abenomics is a complex mixture of various strategies to activate the Japanese economy, associated with the substrings viewed to be tangled (as in Section 2.3(2)) between 3789 and 4403 in Figure 4 and between 4651 and 6333 in Figure 5. The following explanations are given by the same expert. The stock IDs below were chosen as they were relatively large letters in Section 2.3(1), tangled substrings in Section 2.3(2), or stocks relevant to them in the market in Section 2.3(3). Three other experts also agreed with the explanations below, although they had various additional comments. Although the comments below can be regarded as a consensus of a couple of experts, we position this section as a discussion about the subjective explanation given by humans regarding visualized strings rather than objective facts, mainly because it is difficult to collect a sufficiently large number of experts to obtain statistically significant explanation.
After December 2012, the upward trend was reinforced by investors who preferred to buy the stocks of stable industries such as healthcare (3660, 4350), energy (4651), and established IT (4229) that have been generally regarded as low-risk investments, i.e., low volatility [30], because the governmental bonds fell into distrust due to the lowered interest rate introduced by the Bank of Japan since April 2013. Although software for smartphones (diverting technologies for games) and urban development based on big data became trendy according to the frequent tokens in pills in Figure 4, Figure 5 and Figure 6, investors lead the market with their preference for low-risk stocks. Here the larger letters (red: entrances of pills, green: exits) show events of larger weight. The low-volatility stocks did not cause new long-term trends immediately but contributed to the foundation of innovative industries by the opening of pills, according to the expert.
In Figure 6, the largest green node 7022 is placed in July 2016 rather than the end of 2012. Coincidentally, the long-term interest rate came to be increased in Japan [31] from July 2016 and in the US [32] from August 2016 from the low interest rate since April 2013 above. From the aspect of stock analysis, this is informative in explaining the general movements in investor interest. That is, after the inception of Abenomics in 2012, due to the low rate (negative at the beginning of 2016) of interest introduced by the government of Japan, investors who had been investing in governmental bonds shifted to buying low-volatility stocks such as specific electric/precision machineries, healthcare, and medical systems. These low-volatility stocks increased in price since the end of 2012 and priced up further in 2014 and 2016 according to the expert’s comments. Stocks of construction firms were also bought at a similar interest rate. On the other hand, because of the increase in the long-term interest rate in Japan and US since the July of 2016, as an effect opposite to the price-up of low-risk stocks as discussed before for the reduced interest rate due to Abenomics, high-risk stocks came to be bought relative to low-risk (i.e., low-volatility) stocks. As a result, stocks of new industries such as digital devices for ultra-highspeed telecommunication, software for smartphones with the integrated use of big data (on maps and healthcare) and artificial intelligence, and urban engineering for cities embracing innovative firms such as Shenzhen came to rise recently, such as stock 6875, which is one of the few entrances of long (W=6) time scale pills in Figure 6.
On the other hand, given below is about the objective results in Table 3 rather than the human-based explanations above. These results are understandable for a stock appearing at a pill entrance because the entrance indicates the beginning of the trend that stock is to be bought frequently. In contrast, the exit stock may be intuitively felt to price down. However, the stock at an exit means it is of high enough impact enough to break the trend so far, so this tends to be a new focus of attention of investors. Rather, the tendency of decrease is found at the exit of a pill for the stock that appeared as the entrance of the same pill. The tendencies found in Figure 9, in summary, are as follows.
- (1)
- A trend starts at the entrance of a pill and continues during the pill. As a result, the price of the stock at the entrance of a pill continues to increase during the trend (Figure 9a,d,g,i).
- (2)
- The impact of the stock that appears at the exit fades in a short time because the trend disappears when the pill disappears. As a result, the price of the stock at the exit of a pill increases once but decreases sooner than the stock at the entrance (Figure 9b,e,h,k).
- (3)
- A trend ends at the exit of a pill. As a result, the price of the stock at the entrance of a pill decreases soon after the exit of the same pill (Figure 9c,f,I,l).
- (4)
- The stock tends to increase more for the shorter W because a short W means a reduced capacity to detect repeating events. Thus, only the entrances/exits of an especially high frequency of repetition in pills are obtained. However, even for a long W, the price of stocks appearing at the entrance increases continuously during the period of the trend (all in Figure 9).
Thus, we propose that investors consider positioning all the stocks at the time that they appear at entrances or at exits, and sell the entrance stock by the time of the pill’s exit or within the delay of length that is in a negative correlation to the length of the window width W.
5. Conclusions
Here, we extended and applied TS to the data on stocks with increasing value, where various timescales are mixed corresponding to various investors’ reasons for the buying and/or selling of stocks. By the use of TS, the connections to/from trends in the market came to be visualized, to aid in explaining the changes in the market at the desired time scale, associated with middle-term changes caused by political decisions, and long-term ones due to innovations in the industry. The change points found as entrances to pills by TS coincide with high precision with the increase in each stock price. This precision varies by the timescale and the positioning (e.g., at the entrances/exits of pills or elsewhere) of the stocks in the string presented by TS, and the timing of measuring the increase after the entrance of a pill. For the time being, the success in selling a stock at the exit of a pill is not as certain as buying the same stock when it started a pill, according to the probabilities of up/downpricing that we obtained. In our future work, we plan to assign external knowledge or data to refine this certainty, as expected in the method M2 in IMDJ.
The strength of TS is also in that the trend shifts in both (1) the overall stock market and (2) the price of each stock can be explained with one string, whereas (1) and (2) have been analyzed or discussed separately in the previous work and the literature (e.g., [28,29] above). The direction taken to enable analysis about the interrelationship between the global dynamics of the market and the local change in each stock is thus consistent with the fact that the former is composed of the latter and the latter is affected by the former. Thus, the ability to predict both with a single visualization fits analysts’ requirement of efficiency. As TS has been created from the requirement shown in IMDJ, this paper presents evidence that the product of the data market is of practical utility.
Supplementary Materials
The following are available online at https://www.mdpi.com/2078-2489/10/3/118/s1, S1_data (obtained events): The events obtained as the entrances to or exits from pills as results, with the corresponding dates. S2_data (up-pricing rates): The price-up rates, showing the rates of cases where the period of length Δt after t was larger than before t for each event at t that meant the time of (1) the entrance of a pill, (2) the exit of a pill, and (3) the exit of a pill (but the evaluated price is of the stock that appeared at the entrance).
Author Contributions
Conceptualization of TS: IMDJ, Y.O., and T.H.; Methodology and Software: Y.O.; Validation: Y.O. and T.Y.
Funding
This work was funded by JST CREST No. JPMJCR1304 and JSPS KAKENHI JP16H01836 and JP16K12428.
Acknowledgments
We appreciate for the stock analysts who provided comments on the results and the method of TS adopted to stock analysis. We would like to thank Editage for English language editing.
Conflicts of Interest
The authors declare no conflict of interest.
Data Availability
We used data on Japan’s stock price trend chart (Nikkei Average: https://indexes.nikkei.co.jp/en) for evaluating the performance of TS in detecting the up/downward price changes in the stock market. Such a scientific use of the data is allowed in https://indexes.nikkei.co.jp/nkave/archives/file/license_agreement_jp.pdf. The monthly data from 2007 till 2019 are taken, and the average of the max and min prices are taken for each month. The data on each stock has been collected using http://kabubegin.web.fc2.com/kabu052.html. However, due to the disallowance to copy the data in the publication, we show only the analysis result below. We also provide the supplementary data below.
References
- Jagtiani, J.; Lemieux, C. The Roles of Alternative Data and Machine Learning in Fintech Lending: Evidence from the Lending Club Consumer Platform; WP18-15; Lemieux Federal Reserve Bank of Chicago: Chicago, IL, USA, 2018. [Google Scholar] [CrossRef]
- Lux, T. The socio-economic dynamics of speculative markets: Interacting agents, chaos, and the fat tails of return distributions. J. Econ. Behav. Organ. 1998, 33, 143–165. [Google Scholar] [CrossRef]
- Lespagnol, V.; Rouchie, J. Trading Volume and Market Efficiency: An Agent Based Model with Heterogenous Knowledge about Fundamentals. HAL Archives-Ouvertes. 2014. Available online: https://halshs.archives-ouvertes.fr/halshs-00997573 (accessed on 15 March 2019).
- Ding, X.; Zhang, Y.; Liu, T.; Duan, J. Deep Learning for Event-Driven Stock Prediction. In Proceedings of the 24th International Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015; pp. 2327–2333. [Google Scholar]
- Dash, R.; Dash, P.K. A hybrid stock trading framework integrating technical analysis with machine learning techniques. J. Financ. Data Sci. 2016, 2, 42–57. [Google Scholar] [CrossRef]
- Rajput, V.; Sarika Bobde, S. Stock market forecasting technique literature survey. Int. J. Comput. Sci. Mob. Comput. 2016, 5, 500–506. [Google Scholar]
- Cimino, M.G.C.A.; Bona, F.D.; Foglia, P.; Monaco, M.; Prete, C.A.; Vaglini, G. Stock price forecasting over adaptive timescale using supervised learning and receptive fields. In Proceedings of the 6th International Conference on Mining Intelligence and Knowledge Exploration, Cluj-Napoca, Romania, 20–22 December 2018; pp. 279–288. [Google Scholar] [CrossRef]
- Fama, E.F.; Fisher, L.; Jensen, M.C.; Roll, R. The Adjustment of Stock Prices to New Information. Int. Econ. Rev. 1969, 10, 1–21. [Google Scholar] [CrossRef]
- Foster, G. Stock Market Reaction to Estimates of Earnings per Share by Company Officials. J. Account. Res. 1973, 11, 25–27. [Google Scholar] [CrossRef]
- Yoon, S.; Suge, A.; Takahashi, H. Do news articles have an impact on trading?—Korean market studies with high frequency data. In New Frontiers in Artificial Intelligence, Proceedings of the JSAI-isAI Workshops, JURISIN, Tsukuba, Tokyo, 30 June 2018; Springer: Berlin, Germany, 2018; pp. 129–139. [Google Scholar] [CrossRef]
- Kaura, M.; Kanga, S. Market Basket Analysis: Identify the changing trends of market data using association rule mining. Procedia Comput. Sci. 2016, 85, 78–85. [Google Scholar] [CrossRef]
- Ohsawa, Y. Graph-Based Entropy for Detecting Explanatory Signs of Changes in Market. Rev. Socionetwork Strat. 2018, 12, 183–203. [Google Scholar] [CrossRef]
- Iwata, T.; Watanabe, S.; Yamada, T.; Ueda, N. Topic tracking model for analyzing consumer purchase behavior. In Proceedings of the 21st International Joint Conference on Artificial Intelligence (IJCAI), Pasadena, CA, USA, 22 July 2009; pp. 1427–1432. [Google Scholar]
- Abdulhakim, Q.; Alharbi, B.; Wang, S.; Zhang, X. A PCA-Based Change Detection Framework for Multidimensional Data Streams: Change Detection in Multidimensional Data Streams. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 935–944. [Google Scholar] [CrossRef]
- Kleinberg, J. Bursty and hierarchical structure in streams. Data Min. Knowl. Discov. 2003, 7, 373–397. [Google Scholar] [CrossRef]
- Fearnhead, P.; Liu, Z. Online Inference for Multiple Changepoint Problems. J. R. Stat. Soc. Ser. B 2007, 69, 589–605. [Google Scholar] [CrossRef]
- Hayashi, Y.; Yamanishi, K. Sequential network change detection with its applications to ad impact relation analysis. Data Min. Knowl. Discov. 2015, 29, 137–167. [Google Scholar] [CrossRef]
- Miyaguchi, K.; Yamanishi, K. Online detection of continuous changes in stochastic processes. Int. J. Data Sci. Anal. 2017, 3, 213–229. [Google Scholar] [CrossRef]
- Blei, D.; Lafferty, J.D. Dynamic Topic Models. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; Volume 23, pp. 113–120. [Google Scholar] [CrossRef]
- Li, W.; McCallum, A. Pachinko Allocation: DAG-Structured Mixture Models of Topic Correlations. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006. [Google Scholar] [CrossRef]
- Hua, J.; Huang, M.L.; Wang, G.; Zreika, M. Applying Data Visualization Techniques for Stock Relationship Analysis. Filomat 2018, 32, 1931–1936. [Google Scholar] [CrossRef]
- Shoemate, B. Stock Market Visualizations. 2015. Available online: https://www.benshoemate.com /2015/08/20/stock-market-visualizations/ (accessed on 20 March 2019).
- Ohsawa, Y.; Hayashi, T. Tangled string for sequence visualization as fruit of ideas in innovators marketplace on data jackets. Intell. Decis. Technol. 2016, 10, 235–247. [Google Scholar] [CrossRef]
- Ohsawa, Y. Tangled String Diverted for Evaluating Stock Risks: A by Product of Innovators Marketplace on Data Jackets. In Proceedings of the 2015 IEEE International Conference on Data Mining Workshop (ICDMW), Atlantic City, NJ, USA, 14–17 November 2015. [Google Scholar] [CrossRef]
- Ohsawa, Y.; Liu, C.; Hayashi, T.; Kido, H. Data jackets for externalizing use value of hidden datasets. Procedia Comput. Sci. 2014, 35, 946–953. [Google Scholar] [CrossRef]
- Ohsawa, Y.; Liu, C.; Suda, Y.; Kido, H. Innovators Marketplace on Data Jackets for Externalizing the Value of Data via Stakeholders’ Requirement Communication. In Proceedings of the AAAI 2014 Spring Symposium on Big Data Becomes Personal: Knowledge into Meaning, Stanford, CA, USA, 24 March 2014; Available online: https://www.aaai.org/ocs/index.php/SSS/SSS14/paper/viewFile/7676/7775 (accessed on 20 March 2019).
- Ohsawa, Y.; Ji, Q. Wire stretching for noise reduction in a visualized tangled string. In Proceedings of the Workshop on Chance Discovery, Data Synthesis, Curation and Data Market, IJCAI, Buenos Aires, Argentina, 26 July 2015; pp. 1–4. [Google Scholar]
- Chong, T.T.; Leung, K.W.; Yuen, A.H. Is the Rate-of-Change Oscillator Profitable? J. Investig. 2011, 20, 72–74. [Google Scholar] [CrossRef]
- Kritzman, M.; Li, Y.; Page, S.; Rigobon, R. Principal Components as a Measure of Systemic Risk. J. Portf. Manag. 2011, 37, 112–126. [Google Scholar] [CrossRef]
- Matsuura, N. Low Volatility Funds as the Focus of Investors’ Interest. Morningstar 2014. Available online: https://www.morningstar.co.jp/fund/analyst/2014/4q/MFA120141028 (accessed on 20 March 2019). (In Japanese).
- Japan Bond Tradikng, Co., Ltd. Long-Term JGB Yield. 2018. Available online: http://www.bb.jbts.co.jp/english/ marketdata/marketdata01 (accessed on 20 March 2019).
- Baklanova, V.; Berg, T.; Stemp, D. U.S. Long-Term Interest Rates Rise, But Remain Low; OFR Financial Markets Monitor; Office of Financial Research: Washington, DC, USA, 2017. Available online: https://www.financialresearch.gov/financial-markets-monitor/files/OFR-FMM-2017-01-13_Long-Term-Rates-Rise-But-Remain-Low.pdf (accessed on 20 March 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).