Studying Transaction Fees in the Bitcoin Blockchain with Probabilistic Logic Programming †
Abstract
1. Introduction
2. Blockchain, Bitcoin, and Fees
3. Probabilistic Logic Programming
Approximate Inference and Conditional Approximate Inference
- Sample a head for each ground clause to sample a world,
- Check if the query is true in the world,
- Compute the probability of the query as the fraction of samples where the query is true,
- Repeat the three previous steps until convergence or for a fixed number of steps.
4. Modelling Transaction Fee with Probabilistic Logic Programming
- The total mining (hashing) power in the network is constant. The attacker has a fraction of the total power (hence, the rest of the network has 1-)
- All miners except for the attacker are honest (i.e., they mine on the main chain)
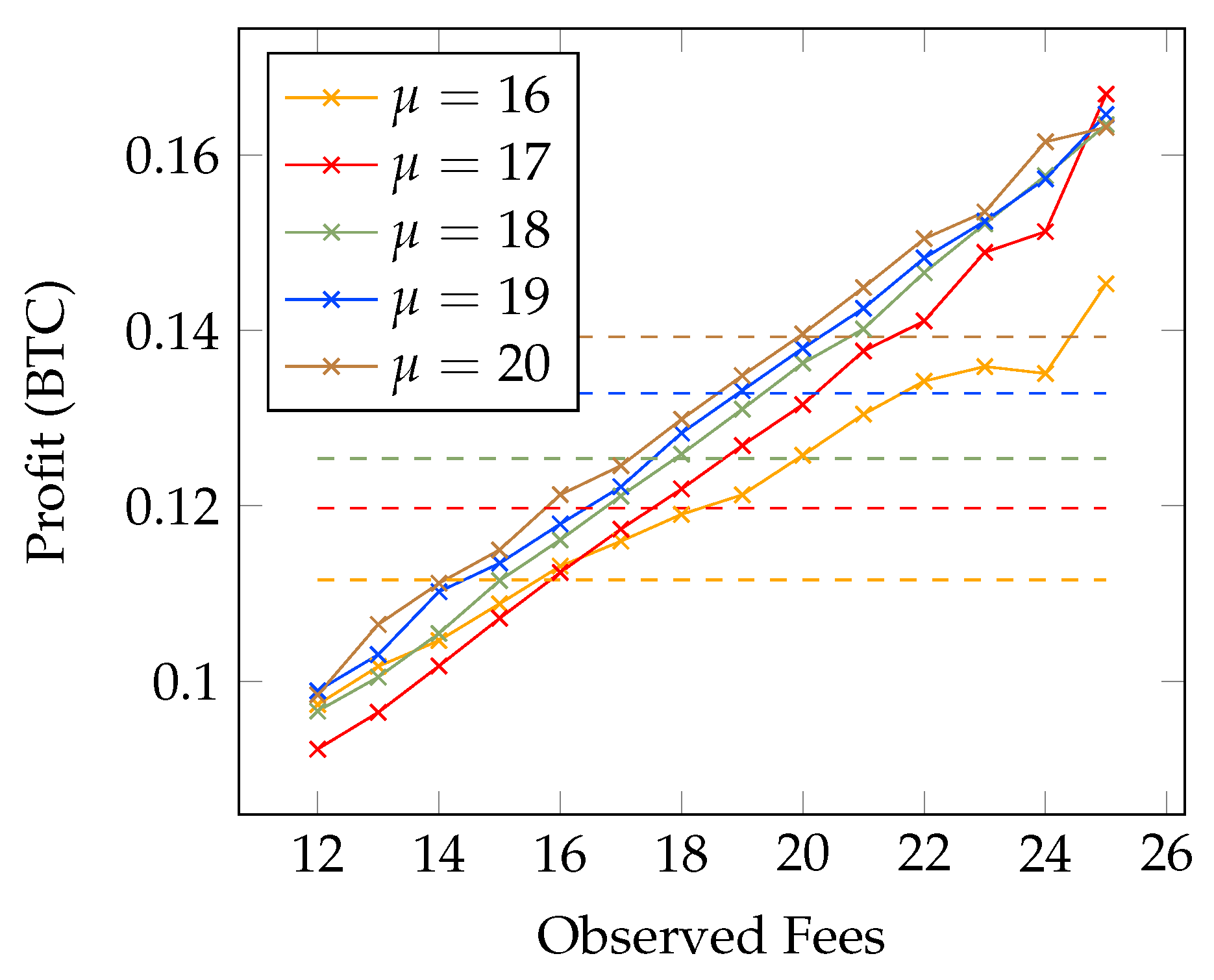
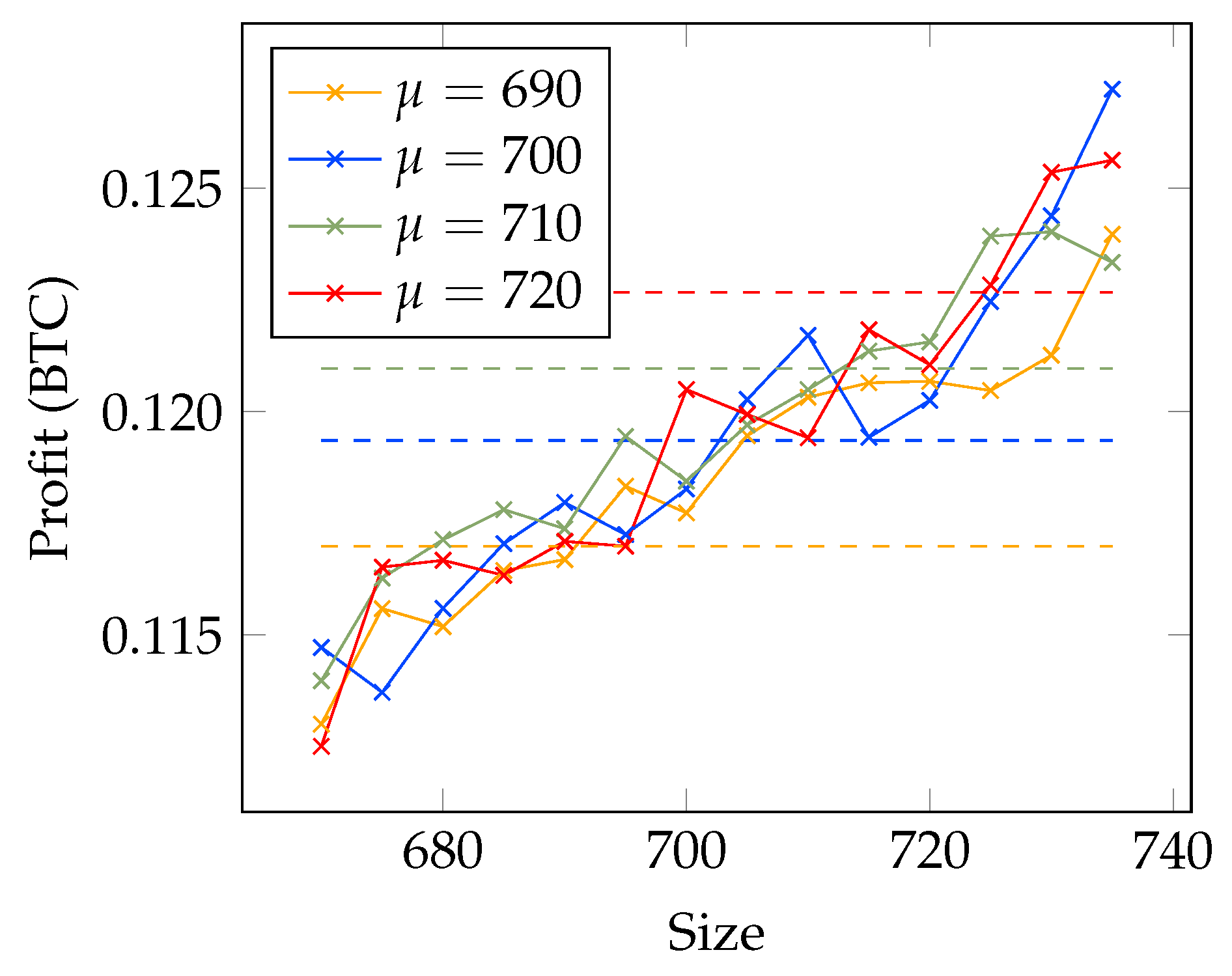
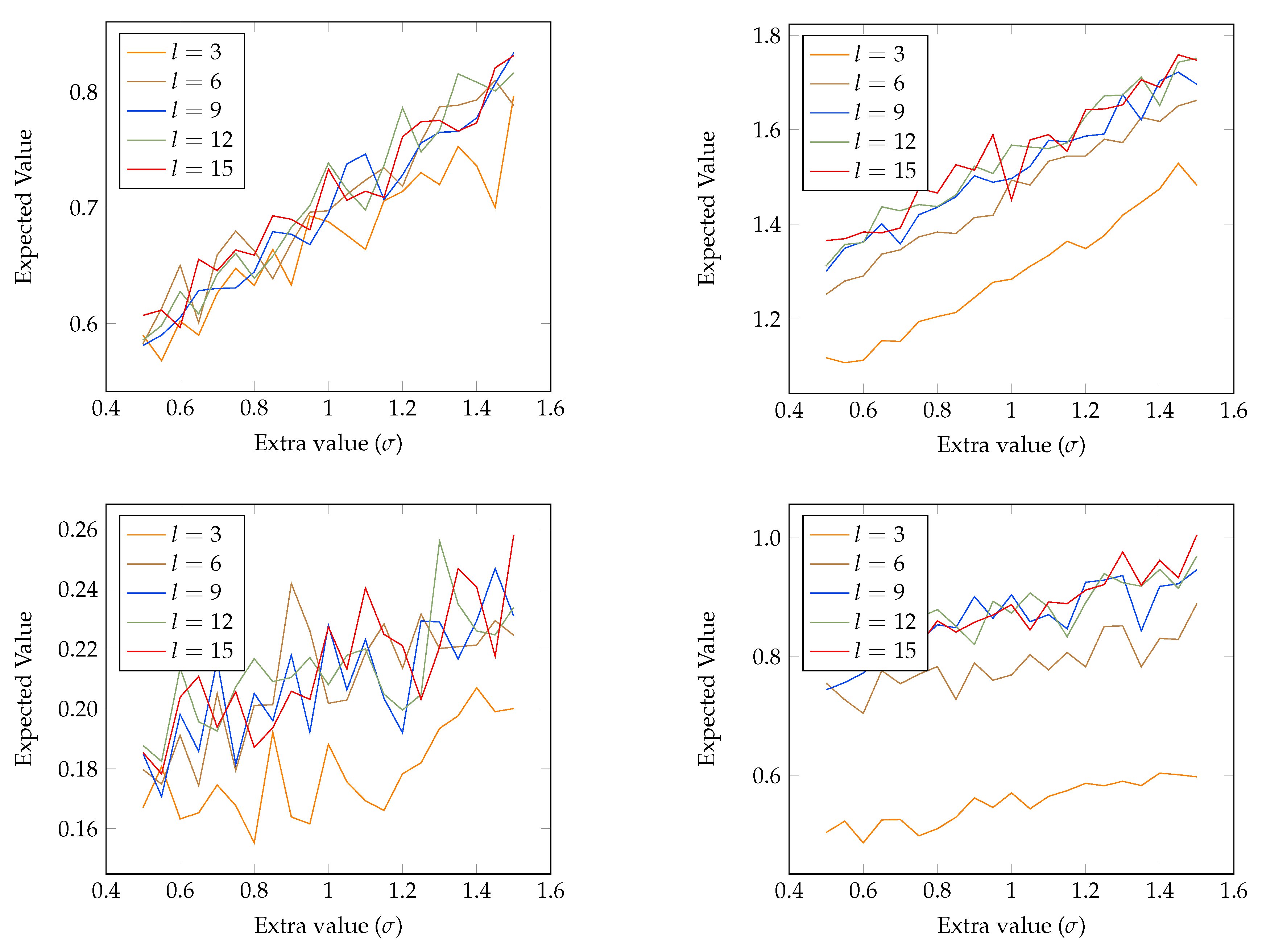
4.1. Analyzing Transaction Fees
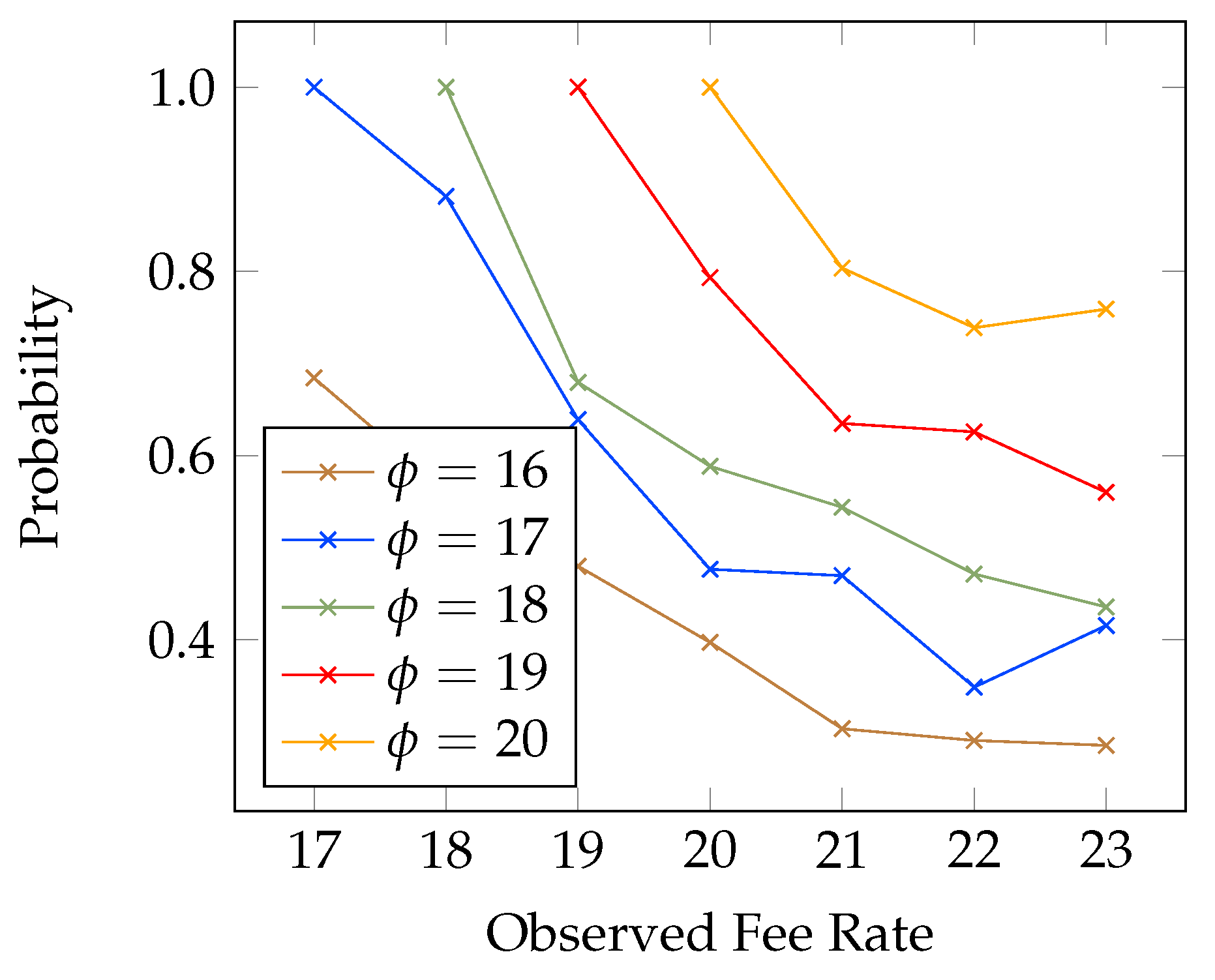
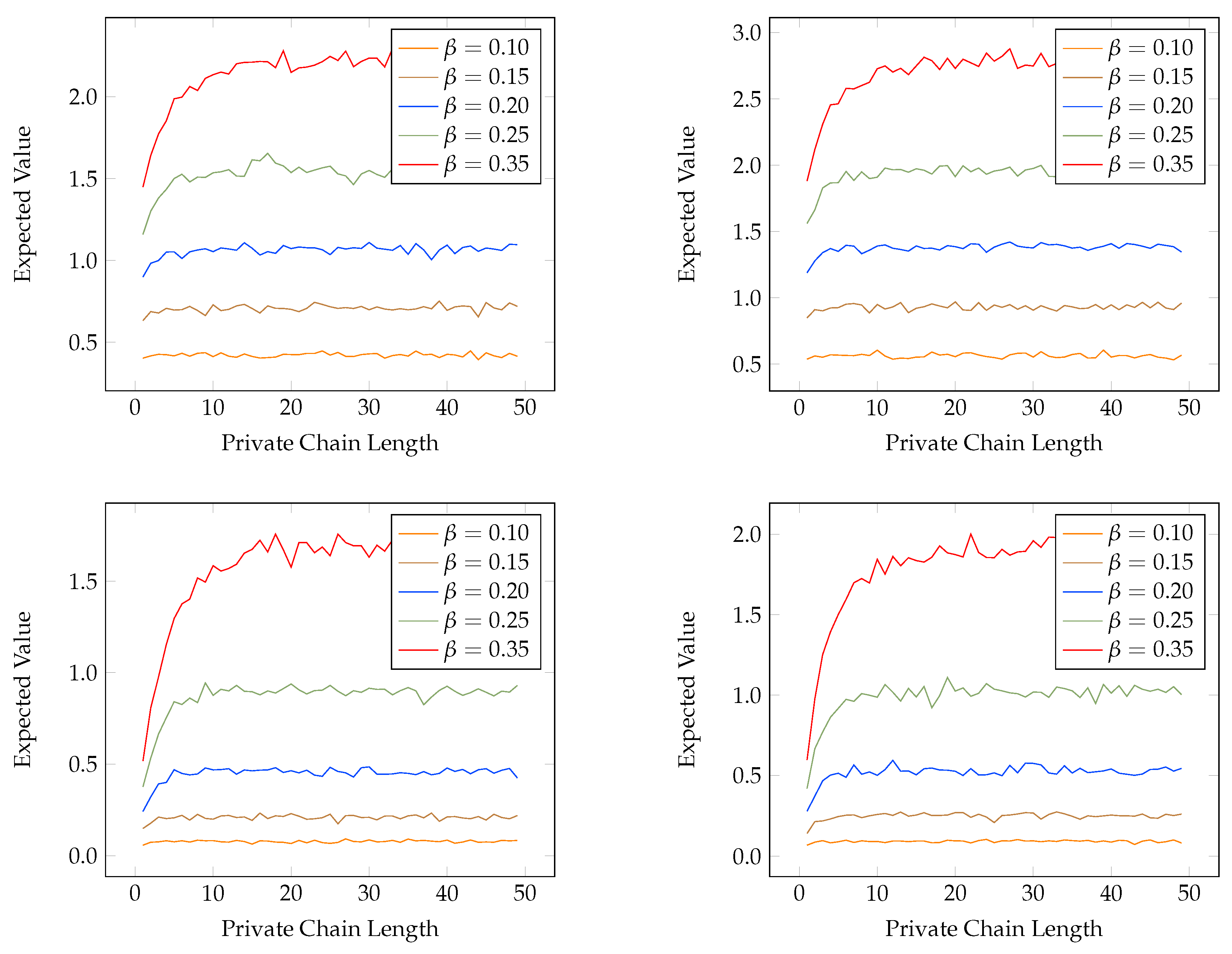
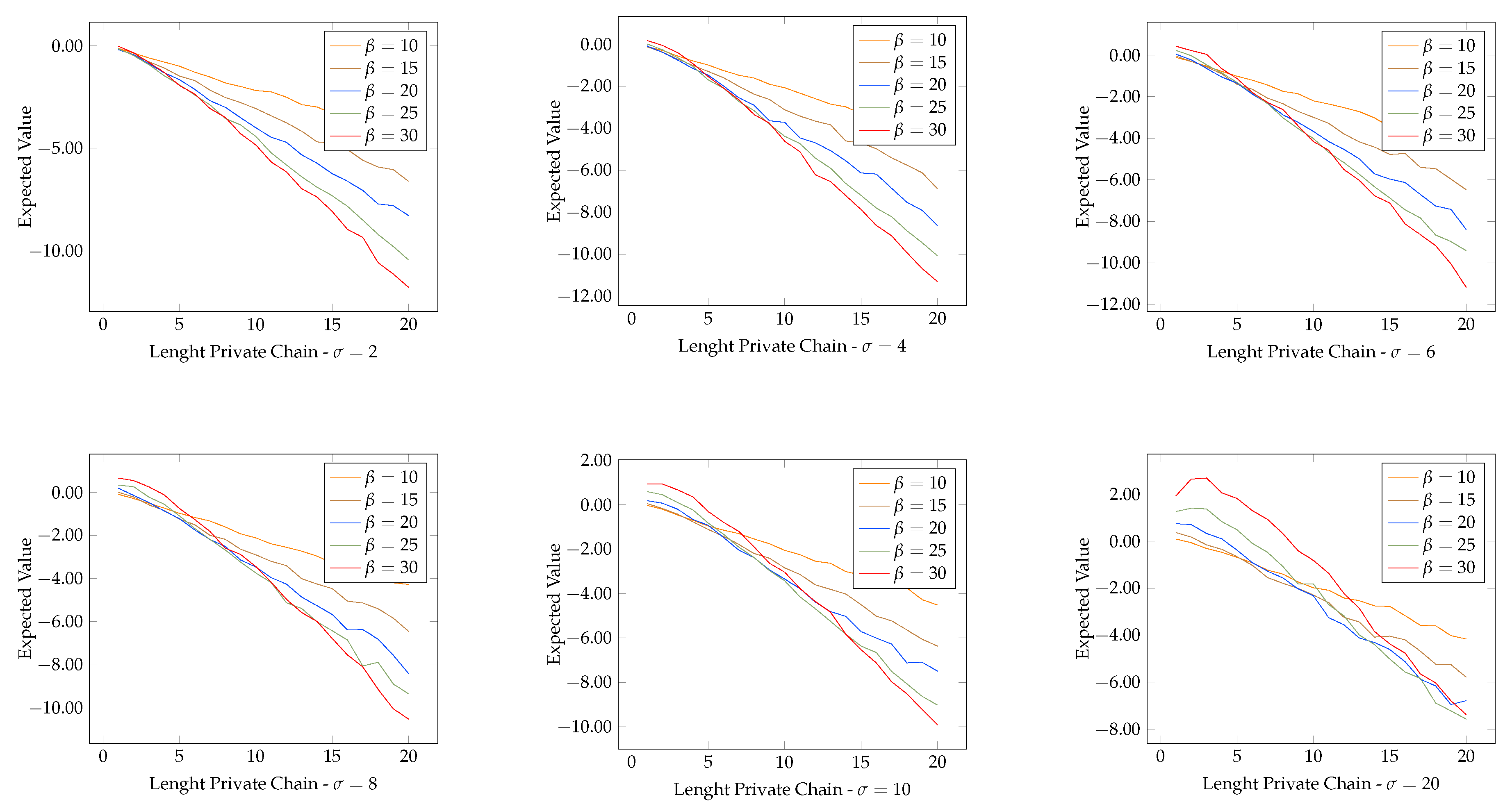
4.2. Probability of Profitable Forks
| Listing 3: Code used for the experiments in Section 4.2. |
5. Related Works
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 29 October 2019).
- Swan, M. Blockchain: Blueprint for A New Economy; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2015. [Google Scholar]
- Buterin, V. A Next,-Generation Smart Contract and Decentralized Application Platform. 2014. Available online: https://github.com/ethereum/wiki/wiki/White-Paper (accessed on 29 October 2019).
- Wood, G. Ethereum: A secure decentralised generalised transaction ledger. Ethereum Proj. Yellow Pap. 2014, 151, 1–32. [Google Scholar]
- EOSIO—An Introduction by Ian Grigg. Available online: https://eos.io/introduction (accessed on 29 October 2019).
- Hyperledger. Available online: https://www.hyperledger.org/ (accessed on 29 October 2019).
- Cardano. Available online: https://whycardano.com/ (accessed on 29 October 2019).
- De Raedt, L.; Kimmig, A. Probabilistic (Logic) Programming Concepts. Mach. Learn. 2015, 100, 5–47. [Google Scholar] [CrossRef]
- Nguembang Fadja, A.; Riguzzi, F. Probabilistic Logic Programming in Action. In Towards Integrative Machine Learning and Knowledge Extraction; Holzinger, A., Goebel, R., Ferri, M., Palade, V., Eds.; Springer: New York, NY, USA, 2017; Volume 10344. [Google Scholar] [CrossRef]
- Azzolini, D.; Riguzzi, F.; Lamma, E.; Bellodi, E.; Zese, R. Modeling Bitcoin Protocols with Probabilistic Logic Programming. In Proceedings of the 5th International Workshop on Probabilistic Logic Programming, PLP 2018, Co-Located with the 28th International Conference on Inductive Logic Programming (ILP 2018), Ferrara, Italy, 1 September 2018; Bellodi, E., Schrijvers, T., Eds.; CEUR-WS.org: Tilburg, The Netherlands, 2018; Volume 2219, pp. 49–61. [Google Scholar]
- Haber, S.; Stornetta, W.S. How to time-stamp a digital document. In Proceedings of the Conference on the Theory and Application of Cryptography, Santa Barbara, CA, USA, 11–15 August 1990; Springer: New York, NY, USA, 1990; pp. 437–455. [Google Scholar]
- Rosenfeld, M. Analysis of Hashrate-Based Double Spending. arXiv 2014, arXiv:1402.2009. [Google Scholar]
- Pinzón, C.; Rocha, C. Double-spend Attack Models with Time Advantange for Bitcoin. Electr. Notes Theor. Comput. Sci. 2016, 329, 79–103. [Google Scholar] [CrossRef]
- Alberti, M.; Cota, G.; Riguzzi, F.; Zese, R. Probabilistic Logical Inference On the Web. In AI*IA 2016; Adorni, G., Cagnoni, S., Gori, M., Maratea, M., Eds.; Springer: Cham, Switzerland, 2016; Volume 10037, pp. 351–363. [Google Scholar] [CrossRef]
- Riguzzi, F.; Bellodi, E.; Lamma, E.; Zese, R.; Cota, G. Probabilistic Logic Programming on the Web. Softw.-Pract. Exper. 2016, 46, 1381–1396. [Google Scholar] [CrossRef]
- Alberti, M.; Bellodi, E.; Cota, G.; Riguzzi, F.; Zese, R. cplint on SWISH: Probabilistic Logical Inference with a Web Browser. Intell. Artif. 2017, 11, 47–64. [Google Scholar] [CrossRef]
- Sato, T. A Statistical Learning Method for Logic Programs with Distribution Semantics. In ICLP 1995; Sterling, L., Ed.; MIT Press: Cambridge, MA, USA, 1995; pp. 715–729. [Google Scholar]
- Riguzzi, F. Foundations of Probabilistic Logic Programming; River Publishers: Gistrup, Denmark, 2018. [Google Scholar]
- Van Gelder, A.; Ross, K.A.; Schlipf, J.S. The Well-founded Semantics for General Logic Programs. J. ACM 1991, 38, 620–650. [Google Scholar] [CrossRef]
- Vennekens, J.; Verbaeten, S.; Bruynooghe, M. Logic Programs With Annotated Disjunctions. In ICLP 2004; Springer: New York, NY, USA, 2004; Volume 3132, pp. 431–445. [Google Scholar]
- Riguzzi, F. The Distribution Semantics for Normal Programs with Function Symbols. Int. J. Approx. Reason. 2016, 77, 1–19. [Google Scholar] [CrossRef]
- Poole, D. The Independent Choice Logic for Modelling Multiple Agents under Uncertainty. Artif. Intell. 1997, 94, 7–56. [Google Scholar] [CrossRef]
- Riguzzi, F.; Swift, T. Tabling and Answer Subsumption for Reasoning on Logic Programs with Annotated Disjunctions. In ICLP TC 2010. Schloss Dagstuhl—Leibniz-Zentrum fuer Informatik; Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2010; Volume 7, pp. 162–171. [Google Scholar] [CrossRef]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; Adaptive computation and machine learning; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Riguzzi, F. MCINTYRE: A Monte Carlo System for Probabilistic Logic Programming. Fund. Inform. 2013, 124, 521–541. [Google Scholar] [CrossRef]
- Bragaglia, S.; Riguzzi, F. Approximate Inference for Logic Programs with Annotated Disjunctions. In ILP 2011; Springer: Florence, Italy, 2011; Volume 6489, pp. 30–37. [Google Scholar]
- Azzolini, D.; Riguzzi, F.; Lamma, E.; Masotti, F. A Comparison of MCMC Sampling for Probabilistic Logic Programming. In Proceedings of the 18th Conference of the Italian Association for Artificial Intelligence (AI*IA2019), Rende, Italy, 19–22 November 2019; Alviano, M., Greco, G., Scarcello, F., Eds.; Springer: Heidelberg, Germany, 2019. [Google Scholar]
- Nitti, D. Hybrid Probabilistic Logic Programming. Ph.D. Thesis, KU Leuven, Leuven, Belgium, 2016. [Google Scholar]
- Bowden, R.; Keeler, H.P.; Krzesinski, A.E.; Taylor, P.G. Block arrivals in the Bitcoin blockchain. arXiv 2018, arXiv:1801.07447. [Google Scholar]
- Yli-Huumo, J.; Ko, D.; Choi, S.; Park, S.; Smolander, K. Where is current research on blockchain technology?—A systematic review. PLoS ONE 2016, 11, e0163477. [Google Scholar] [CrossRef] [PubMed]
- Risius, M.; Spohrer, K. A blockchain research framework. Bus. Inf. Syst. Eng. 2017, 59, 385–409. [Google Scholar] [CrossRef]
- Koops, D.T. Predicting the confirmation time of Bitcoin transactions. arXiv 2018, arXiv:1809.10596. [Google Scholar]
- Kasahara, S.; Kawahara, J. Priority Mechanism of Bitcoin and Its Effect on Transaction-Confirmation Process. arXiv 2016, arXiv:1604.00103, 2016. [Google Scholar]
- Basu, S.; Easley, D.; O’Hara, M.; Sirer, E.G. Towards a Functional Fee Market for Cryptocurrencies. arXiv 2019, arXiv:1901.06830. [Google Scholar] [CrossRef]
- Tsabary, I.; Eyal, I. The gap game. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; pp. 713–728. [Google Scholar]
- Carlsten, M.; Kalodner, H.; Weinberg, S.M.; Narayanan, A. On the instability of bitcoin without the block reward. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austri, 24–28 October 2016; pp. 154–167. [Google Scholar]
- Liao, K.; Katz, J. Incentivizing blockchain forks via whale transactions. In Proceedings of the International Conference on Financial Cryptography and Data Security, Sliema, Malta, 3–7 April 2017; Springer: New York, NY, USA, 2017; pp. 264–279. [Google Scholar]
- Möser, M.; Böhme, R. Trends, tips, tolls: A longitudinal study of Bitcoin transaction fees. In Proceedings of the International Conference on Financial Cryptography and Data Security, San Juan, Puerto Rico, 26–30 January 2015; pp. 19–33. [Google Scholar]
- Corbet, S.; Lucey, B.; Urquhart, A.; Yarovaya, L. Cryptocurrencies as a financial asset: A systematic analysis. Int. Rev. Financ. Anal. 2019, 62, 182–199. [Google Scholar] [CrossRef]
- Williams, M.T. Virtual currencies–Bitcoin risk. In Proceedings of the World Bank Conference, Washington, DC, USA, 21 October 2014. [Google Scholar]
- Katsiampa, P. Volatility estimation for Bitcoin: A comparison of GARCH models. Econ. Lett. 2017, 158, 3–6. [Google Scholar] [CrossRef]
- Iwamura, M.; Kitamura, Y.; Matsumoto, T.; Saito, K. Can we stabilize the price of a Cryptocurrency?: Understanding the design of Bitcoin and its potential to compete with Central Bank money. Hitotsubashi J. Econ. 2019, 60, 41–60. [Google Scholar] [CrossRef][Green Version]
- Bouri, E.; Gupta, R.; Tiwari, A.K.; Roubaud, D. Does Bitcoin hedge global uncertainty? Evidence from wavelet-based quantile-in-quantile regressions. Financ. Res. Lett. 2017, 23, 87–95. [Google Scholar] [CrossRef]
- Garcia, D.; Tessone, C.J.; Mavrodiev, P.; Perony, N. The digital traces of bubbles: Feedback cycles between socio-economic signals in the Bitcoin economy. J. R. Soc. Interface 2014, 11, 20140623. [Google Scholar] [CrossRef] [PubMed]
- Kristoufek, L. BitCoin meets Google Trends and Wikipedia: Quantifying the relationship between phenomena of the Internet era. Sci. Rep. 2013, 3, 3415. [Google Scholar] [CrossRef] [PubMed]
- Van den Broeck, G.; Thon, I.; van Otterlo, M.; De Raedt, L. DTProbLog: A Decision-Theoretic Probabilistic Prolog. In Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; Fox, M., Poole, D., Eds.; AAAI Press: Menlo Park, CA, USA, 2010; pp. 1217–1222. [Google Scholar]
- Salah, K.; Rehman, M.H.U.; Nizamuddin, N.; Al-Fuqaha, A. Blockchain for AI: Review and open research challenges. IEEE Access 2019, 7, 10127–10149. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azzolini, D.; Riguzzi, F.; Lamma, E. Studying Transaction Fees in the Bitcoin Blockchain with Probabilistic Logic Programming. Information 2019, 10, 335. https://doi.org/10.3390/info10110335
Azzolini D, Riguzzi F, Lamma E. Studying Transaction Fees in the Bitcoin Blockchain with Probabilistic Logic Programming. Information. 2019; 10(11):335. https://doi.org/10.3390/info10110335
Chicago/Turabian StyleAzzolini, Damiano, Fabrizio Riguzzi, and Evelina Lamma. 2019. "Studying Transaction Fees in the Bitcoin Blockchain with Probabilistic Logic Programming" Information 10, no. 11: 335. https://doi.org/10.3390/info10110335
APA StyleAzzolini, D., Riguzzi, F., & Lamma, E. (2019). Studying Transaction Fees in the Bitcoin Blockchain with Probabilistic Logic Programming. Information, 10(11), 335. https://doi.org/10.3390/info10110335





