Moderate Impact of Increasing Temperatures on Food Intake in Human Populations
Abstract
1. Introduction
2. Materials and Methods
2.1. Analytical Approach
2.2. Separation of Variables in State and Non-State Variables
2.3. Extraction of Reaction Norms and AIC Values from Time Series
2.4. The Applicability and Quality of Assessment Models
2.5. Data Sets for Extraction Models
2.6. Data Sets for Assessment Models
2.7. Validation by Standard Cross-Sectional Analysis
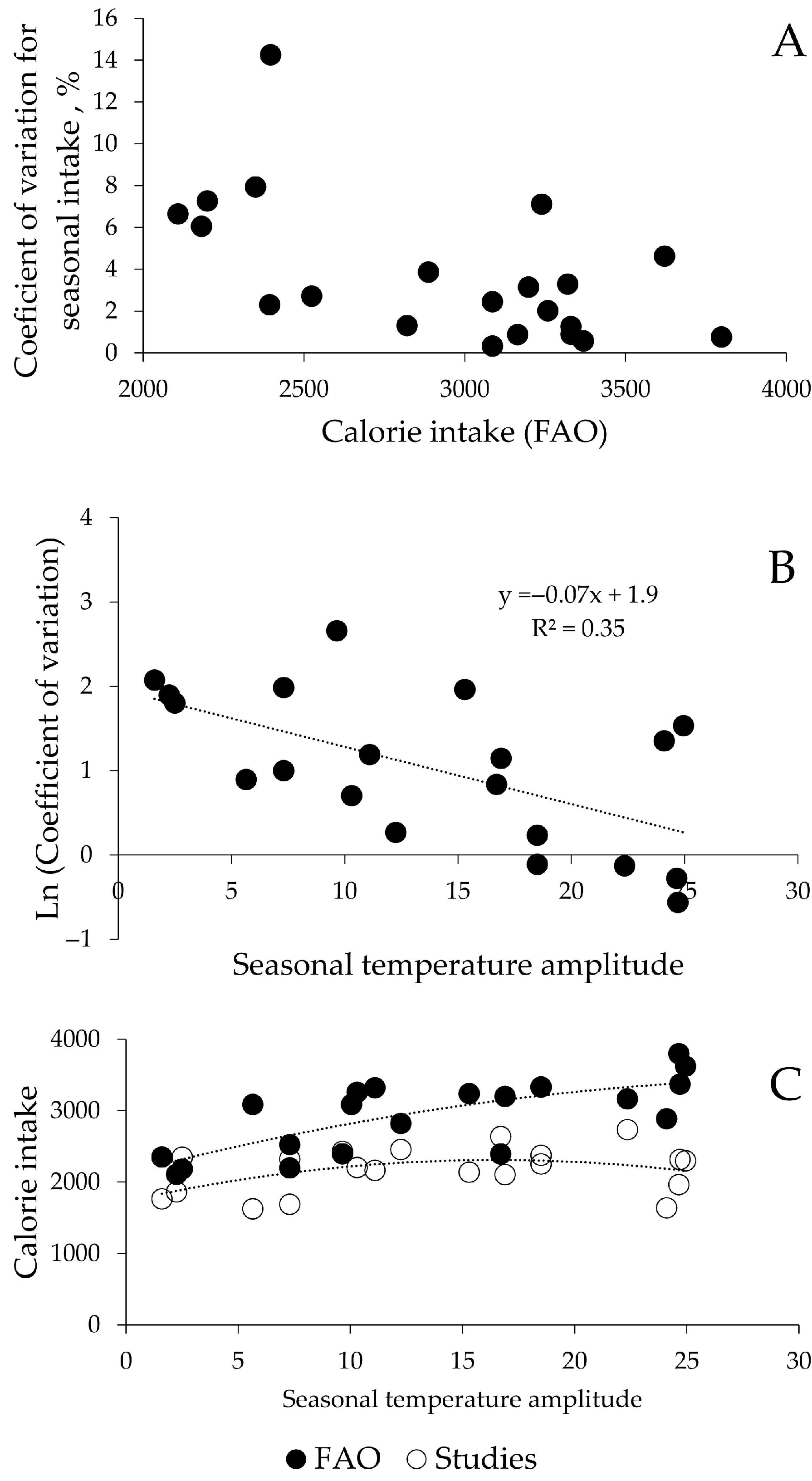
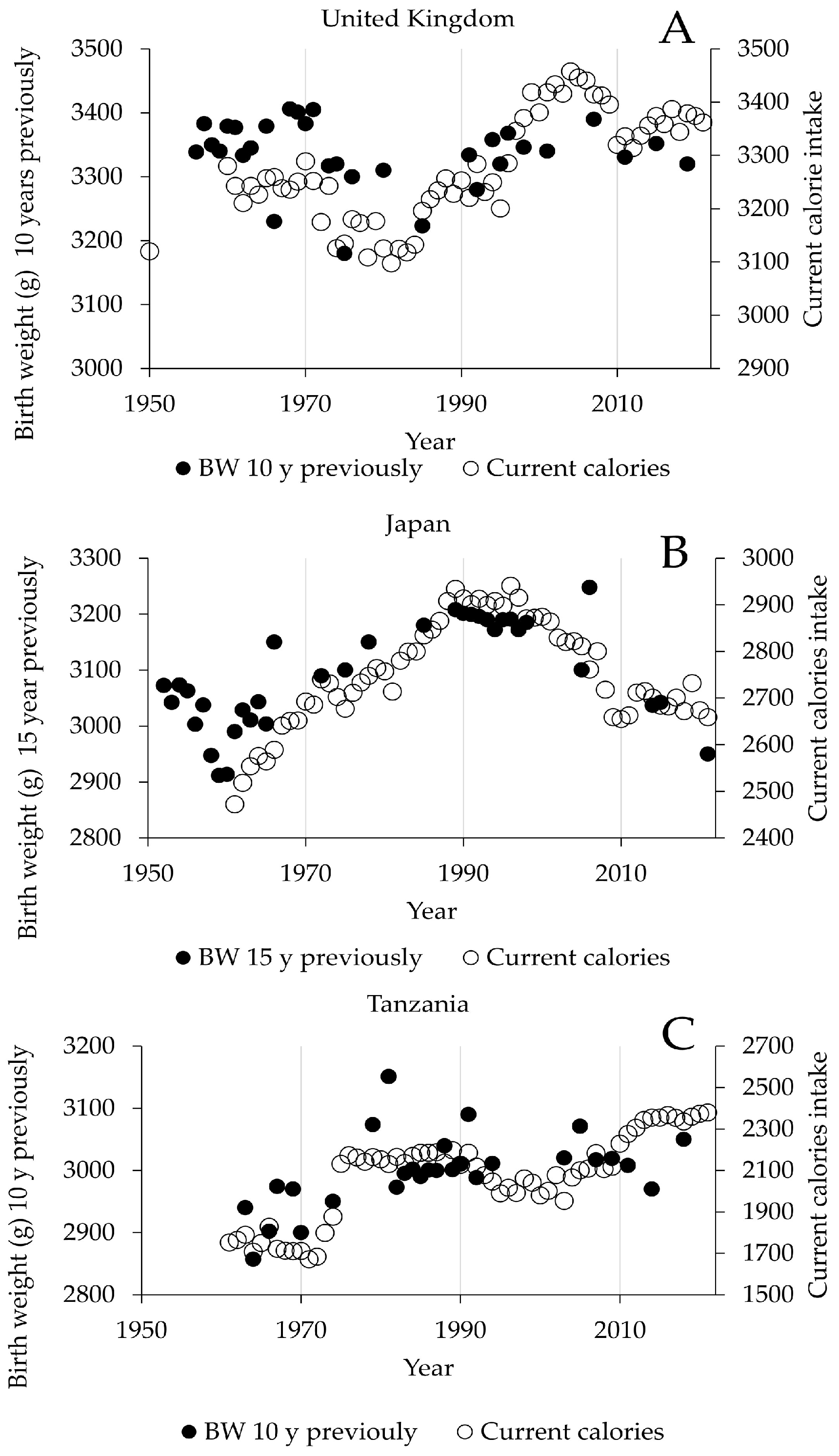
3. Results
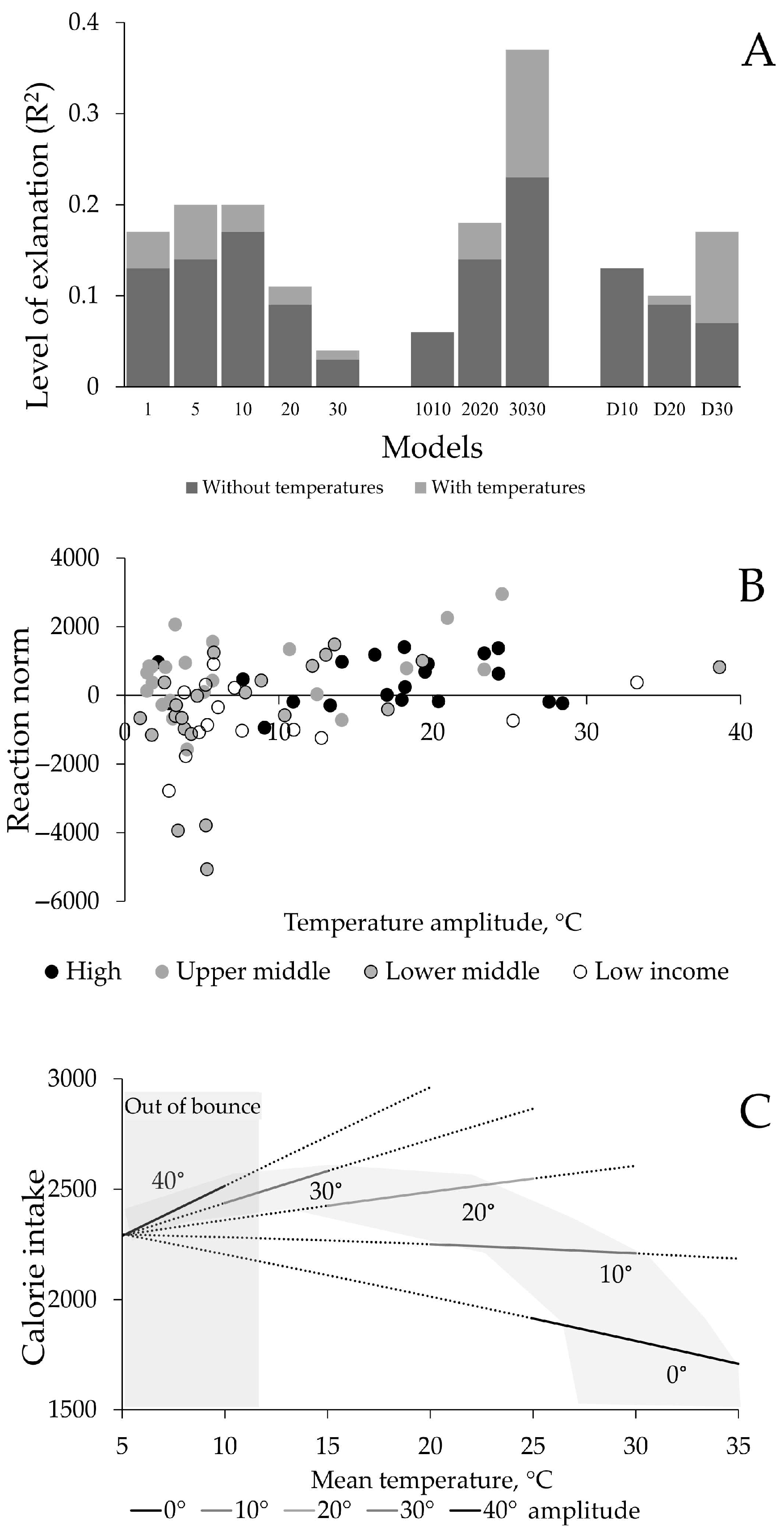
4. Discussion
Strengths and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2023: Synthesis Report, Summary for Policymakers. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023. [Google Scholar]
- Rocque, R.J.; Beaudoin, C.; Ndjaboue, R.; Cameron, L.; Poirier-Bergeron, L.; Poulin-Rheault, R.A.; Fallon, C.; Tricco, A.C.; Witteman, H.O. Health effects of climate change: An overview of systematic reviews. BMJ Open 2021, 11, e046333. [Google Scholar] [CrossRef]
- Iizumi, T.; Ramankutty, N. Changes in yield variability of major crops for 1981–2010 explained by climate change. Environ. Res. Lett. 2016, 11, 034003. [Google Scholar] [CrossRef]
- Katona, P.; Katona-Apte, J. The interaction between nutrition and infection. Clin. Infect. Dis. 2008, 46, 1582–1588. [Google Scholar] [CrossRef] [PubMed]
- Ebi, K.L.; Capon, A.; Berry, P.; Broderick, C.; de Dear, R.; Havenith, G.; Honda, Y.; Kovats, S.; Ma, W.; Malik, A.; et al. Hot weather and heat extremes: Health risks. Lancet 2021, 398, 698–708. [Google Scholar] [CrossRef] [PubMed]
- Diniz, F.R.; Gonçalves, F.L.T.; Sheridan, S. Heat wave and elderly mortality: Historical analysis and future projection for metropolitan region of São Paulo, Brazil. Atmosphere 2020, 11, 933. [Google Scholar] [CrossRef]
- Hansen, P.J. Effects of heat stress on mammalian reproduction. Philos. Trans. R. Soc. B: Biol. Sci. B 2009, 364, 3341–3350. [Google Scholar] [CrossRef]
- Jensen, P.M.; Sørensen, M.; Weiner, J. Human total fertility rate affected by ambient temperatures in both the present and previous generations. Int. J. Biometeorol. 2021, 65, 1837–1848. [Google Scholar] [CrossRef]
- Choudhari, R.H. Multidimensional Impact of Climate Change on Human Reproduction and Fertility: A Medical Perspective on Changing Dynamics. In Research Anthology on Environmental and Societal Impacts of Climate Change: 1672–1709; IGI Global: Hershey, PA, USA, 2022. [Google Scholar] [CrossRef]
- Johnson, R.E.; Kark, R.M. Environment and food intake in man. Science 1947, 105, 378–379. [Google Scholar] [CrossRef]
- Fuquay, J.W. Heat stress as it affects animal production. J. Anim. Sci. 1981, 52, 164–174. [Google Scholar] [CrossRef]
- Nienaber, J.A.; Hahn, G.L.; Yen, J.T. Thermal environment effects on growing-finishing swine Part I—Growth, feed intake and heat production. Trans. ASAE 1987, 30, 1772–1775. [Google Scholar] [CrossRef]
- Renaudeau, D.; Gourdine, J.L.; St-Pierre, N.R. A meta-analysis of the effects of high ambient temperature on growth performance of growing-finishing pigs. J. Anim. Sci. 2011, 89, 2220–2230. [Google Scholar] [CrossRef] [PubMed]
- Thornton, P.; Nelson, G.; Mayberry, D.; Herrero, M. Increases in extreme heat stress in domesticated livestock species during the twenty-first century. Glob. Change Biol. 2021, 27, 5762–5772. [Google Scholar] [CrossRef] [PubMed]
- Bergmann, C. Uber die Verhaltniesse der Warmeokonomie der Thiere zu ihrer Grosse. Gott. Stud. 1847, 1, 595–708. [Google Scholar]
- Allen, J.A. The influence of physical conditions in the genesis of species. Radic. Rev. 1877, 1, 108–140. [Google Scholar]
- Bindon, J.R.; Baker, P.T. Bergmann’s rule and the thrifty genotype. Am. J. Phys. Anthropol. 1997, 104, 201–210. [Google Scholar] [CrossRef]
- Foster, F.; Collard, M. A reassessment of Bergmann’s rule in modern humans. PLoS ONE 2013, 8, e72269. [Google Scholar] [CrossRef]
- Leonard, W.R.; Sorensen, M.V.; Galloway, V.A.; Spencer, G.J.; Mosher, M.J.; Osipova, L.; Spitsyn, V.A. Climatic influences on basal metabolic rates among circumpolar populations. Am. J. Hum. Biol. 2002, 14, 609–620. [Google Scholar] [CrossRef]
- Yurkevicius, B.R.; Alba, B.K.; Seeley, A.D.; Castellani, J.W. Human cold habituation: Physiology, timeline, and modifiers. Temperature 2022, 9, 122–157. [Google Scholar] [CrossRef]
- Brobeck, J.R. Food intake as a mechanism of temperature regulation. Obes. Res. 1997, 5, 641–645. [Google Scholar] [CrossRef]
- McCue, M.D. Specific dynamic action: A century of investigation. Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 2006, 144, 381–394. [Google Scholar] [CrossRef]
- Secor, S.M. Specific dynamic action: A review of the postprandial metabolic response. J. Comp. Physiol. B 2009, 179, 1–56. [Google Scholar] [CrossRef] [PubMed]
- Kingma, B.; Frijns, A.; van Marken Lichtenbelt, W. The thermoneutral zone: Implications for metabolic studies. Front. Biosci.-Elite 2012, 4, 1975–1985. [Google Scholar] [CrossRef] [PubMed]
- Pallubinsky, H.; Schellen, L.; van Marken Lichtenbelt, W.D. Exploring the human thermoneutral zone—A dynamic approach. J. Therm. Biol. 2019, 79, 199–208. [Google Scholar] [CrossRef] [PubMed]
- Taylor, N.A. Ethnic differences in thermoregulation: Genotypic versus phenotypic heat adaptation. J. Therm. Biol. 2006, 31, 90–104. [Google Scholar] [CrossRef]
- Hanna, J.M.; Brown, D.E. Human heat tolerance: An anthropological perspective. Annu. Rev. Anthropol. 1983, 12, 259–284. [Google Scholar] [CrossRef]
- Roberts, D.F. Body weight, race and climate. Am. J. Phys. Anthropol. 1953, 11, 533–558. [Google Scholar] [CrossRef]
- Roberts, D.F. Climate and Human Variability, 2nd ed.; Cummings: Menlo Park, CA, USA, 1978. [Google Scholar]
- Tontisirin, K.; de Haen, H. Human Energy Requirements; Report of a Joint FAO/WHO/UNU Expert Consultation 17–24; FAO: Rome, Italy, 2001; Available online: https://www.fao.org/3/y5686e/y5686e.pdf (accessed on 13 March 2024).
- Stelmach-Mardas, M.; Kleiser, C.; Uzhova, I.; Peñalvo, J.L.; La Torre, G.; Palys, W.; Boeing, H. Seasonality of food groups and total energy intake: A systematic review and metaanalysis. Eur. J. Clin. Nutr. 2016, 70, 700–708. [Google Scholar] [CrossRef]
- FAO. Food and Agriculture Organization of the United Nations; 2021 Caloric Intake Per Day Per Capita. 2021. Available online: http://www.fao.org/faostat/en/#data/FBSH (accessed on 23 April 2021).
- Westerterp-Plantenga, M.S. Effects of extreme environments on food intake in human subjects. Proc. Nutr. Soc. 1999, 58, 791–798. [Google Scholar] [CrossRef]
- Ma, Y.; Olendzki, B.C.; Li, W.; Hafner, A.R.; Chiriboga, D.; Hebert, J.R.; Campbell, M.; Sarnie, M.; Ockene, I.S. Seasonal variation in food intake, physical activity, and body weight in a predominantly overweight population. Eur. J. Clin. Nutr. 2006, 60, 519–528. [Google Scholar] [CrossRef]
- Bernstein, S.; Zambell, K.; Amar, M.J.; Arango, C.; Kelley, R.C.; Miszewski, S.G.; Tryon, S.; Courville, A.B. Dietary intake patterns are consistent across seasons in a cohort of healthy adults in a metropolitan population. J. Acad. Nutr. Diet. 2016, 116, 38–45. [Google Scholar] [CrossRef]
- Westerterp, K.R. Seasonal variation in body weight: An experimental case study. J. Therm. Biol. 2001, 26, 525–527. [Google Scholar] [CrossRef]
- Keys, A.; Henschel, A.; Mickelsen, O.; Taylor, H.L. The Biology of Human Starvation; University of Minnesota Press: Minneapolis, MN, USA, 1950; pp. 1–2. [Google Scholar]
- Dulloo, A.G. Physiology of weight regain: Lessons from the classic Minnesota Starvation Experiment on human body composition regulation. Obes. Rev. 2021, 22, e13189. [Google Scholar] [CrossRef]
- Roberts, D.F. Race, genetics and growth. J. Biosoc. Sci. Suppl. 1969, 1, 43–67. [Google Scholar] [CrossRef]
- Wells, J.C.; Cole, T.J. Birth weight and environmental heat load: A between-population analysis. Am. J. Phys. Anthropol. 2002, 119, 276–282. [Google Scholar] [CrossRef] [PubMed]
- Jensen, P.M.; Sørensen, M. Differences in human birth weight and corollary attributes as a result of temperature regime. Ann. Hum. Biol. 2013, 40, 385–395. [Google Scholar] [CrossRef] [PubMed]
- Hales, C.N.; Barker, D.J. The thrifty phenotype hypothesis: Type 2 diabetes. Br. Med. Bull. 2001, 60, 5–20. [Google Scholar] [CrossRef] [PubMed]
- Grzęda, E.; Matuszewska, J.; Ziarniak, K.; Gertig-Kolasa, A.; Krzyśko-Pieczka, I.; Skowrońska, B.; Sliwowska, J.H. Animal Foetal Models of Obesity and Diabetes–From Laboratory to Clinical Settings. Front. Endocrinol. 2022, 13, 63. [Google Scholar] [CrossRef]
- Prentice, A.M.; Jebb, S.A.; Goldberg, G.R.; Coward, W.A.; Murgatroyd, P.R.; Poppitt, S.D.; Cole, T.J. Effects of weight cycling on body composition. Am. J. Clin. Nutr. 1992, 56, 209S–216S. [Google Scholar] [CrossRef]
- Yang, Z.; Huffman, S.L. Nutrition in pregnancy and early childhood and associations with obesity in developing countries. Matern. Child Nutr. 2013, 9, 105–119. [Google Scholar] [CrossRef]
- Kroke, A.; Liese, A.D.; Schulz, M.; Bergmann, M.M.; Klipstein-Grobusch, K.; Hoffmann, K.; Boeing, H. Recent weight changes and weight cycling as predictors of subsequent two year weight change in a middle-aged cohort. Int. J. Obes. 2002, 26, 403–409. [Google Scholar] [CrossRef]
- Zou, H.; Yin, P.; Liu, L.; Duan, W.; Li, P.; Yang, Y.; Li, P.; Yang, Y.; Li, W.; Zong, Q.; et al. Association between weight cycling and risk of developing diabetes in adults: A systematic review and meta-analysis. J. Diabetes Investig. 2021, 12, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Tanner, J.M. Growth as a target-seeking function: Catch-up and catch-down growth in man. In Human Growth: A Comprehensive Treatise Volume 1 Developmental Biology Prenatal Growth; Springer: Boston, MA, USA, 1986; pp. 167–179. [Google Scholar] [CrossRef]
- van Wesenbeeck, C.F.; Keyzer, M.A.; Nubé, M. Estimation of undernutrition and mean calorie intake in Africa: Methodology, findings and implications. Int. J. Health Geogr. 2009, 8, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Kramer, M.S. Determinants of low birth weight: Methodological assessment and metaanalysis. Bull. World Health Organ. 1987, 65, 663–737. [Google Scholar] [PubMed]
- Buklijas, T.; Al-Gailani, S. A fetus in the world: Physiology, epidemiology, and the making of fetal origins of adult disease. Hist. Philos. Life Sci. 2023, 45, 44. [Google Scholar] [CrossRef]
- Hollstein, T.; Basolo, A.; Ando, T.; Votruba, S.B.; Walter, M.; Krakoff, J.; Piaggi, P. Recharacterizing the metabolic state of energy balance in thrifty and spendthrift phenotypes. J. Clin. Endocrinol. Metab. 2020, 105, 1375–1392. [Google Scholar] [CrossRef]
- Wells, J.C. Natural selection and human adiposity: Crafty genotype, thrifty phenotype. Philos. Trans. R. Soc. B 2023, 378, 20220224. [Google Scholar] [CrossRef]
- Del Giudice, M. Early stress and human behavioral development: Emerging evolutionary perspectives. J. Dev. Orig. Health Dis. 2014, 5, 270–280. [Google Scholar] [CrossRef]
- Wells, J.C.; Cole, T.J.; Cortina-Borja, M.; Sear, R.; Leon, D.A.; Marphatia, A.A.; Murray, J.; Wehrmeister, F.C.; Oliveira, P.D.; Goncalves, H.; et al. Low maternal capital predicts life history trade-offs in daughters: Why adverse outcomes cluster in individuals. Front. Public Health 2019, 7, 206. [Google Scholar] [CrossRef]
- Tanner, J.M. Foetus into Man: Physical Growth from Conception to Maturity; Harvard University Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Santos, J.L.; Martinez, J.A.; Martinez-Gonzalez, M.A.; Gibney, M.J.; Irala, J.; Kearney, J.; Varo-Cenarruzabeitia, J.J. Prevalence of Physical Activity During Leisure Time in the European Union. 2001. Available online: https://hdl.handle.net/10171/17570 (accessed on 22 March 2024).
- Andersen, L.G.; Ängquist, L.; Gamborg, M.; Byberg, L.; Bengtsson, C.; Canoy, D. NordNet Study Group. Birth weight in relation to leisure time physical activity in adolescence and adulthood: Meta-analysis of results from 13 Nordic cohorts. PLoS ONE 2009, 4, e8192. [Google Scholar] [CrossRef]
- Wakimoto, P.; Block, G. Dietary intake, dietary patterns, and changes with age: An epidemiological perspective. J. Gerontol. Ser. A Biol. Sci. Med. Sci. 2001, 56 (Suppl. S2), 65–80. [Google Scholar] [CrossRef]
- Kogan, M.D. Social causes of low birth weight. J. R. Soc. Med. 1995, 88, 611–615. [Google Scholar] [CrossRef] [PubMed]
- Jensen, P.M.; Sørensen, M. In Search of Environmental Factors Associated with Global Differences in Birth Weight and BMI. Am. J. Hum. Biol. 2025, 37, e70038. [Google Scholar] [CrossRef] [PubMed]
- Kuzawa, C.W.; Eisenberg, D.T. Intergenerational Predictors of Birth Weight in the Philippines: Correlations with Mother’s and Father’s Birth Weight and Test of Maternal Constraint. PLoS ONE 2012, 7, e40905. [Google Scholar] [CrossRef] [PubMed]
- Kuzawa, C.W.; Fried, R.L. Intergenerational memories of past nutritional deprivation: The phenotypic inertia model. In The Arc of Life: Evolution and Health Across the Life Course; Springer: Berlin/Heidelberg, Germany, 2017; pp. 7–20. [Google Scholar] [CrossRef]
- OECD. Age of Mothers at Childbirth and Age-Specific Fertility (SF2.3) 2023. Available online: https://www.oecd.org/els/soc/SF_2_3_Age_mothers_childbirth.pdf (accessed on 7 April 2023).
- WHO. World Health Organization. Human Energy Requirements: Report of a Joint FAO/WHO/UNU Expert Consultation: Rome, 17-24 October 2001; Food & Agriculture Org.: Rome, Italy, 2004; Volume 1.
- Perkins, J.M.; Subramanian, S.V.; Davey Smith, G.; Özaltin, E. Adult height, nutrition, and population health. Nutr. Rev. 2016, 74, 149–165. [Google Scholar] [CrossRef]
- Langhans, W. Bacterial products and the control of ingestive behavior: Clinical implications. Nutrition 1996, 12, 303–315. [Google Scholar] [CrossRef]
- Brown, W.E.; Bradford, B.J. Invited review: Mechanisms of hypophagia during disease. J. Dairy Sci. 2021, 104, 9418–9436. [Google Scholar] [CrossRef]
- Rosen, S.L.; Shapouri, S.; Global Economic Crisis Threatens Food Security in Lower Income Countries. Amber Waves: The Economics of Food, Farming, Natural Resources, and Rural America. 2009. Available online: https://ageconsearch.umn.edu/record/122562/files/06GlobalEconomic.pdf (accessed on 11 April 2024).
- Waibel, H.; Hohfeld, L. Poverty and nutrition: A case study of rural households in Thailand and Viet Nam. In The Asian ‘Poverty Miracle; Edward Elgar Publishing: Cheltenham, UK, 2016; pp. 215–250. [Google Scholar] [CrossRef]
- Emanuel, I.; Filakti, H.; Alberman, E.; Evans, S.J. Intergenerational studies of human birthweight from the 1958 birth cohort. 1. Evidence for a multigenerational effect. BJOG Int. J. Obstet. Gynaecol. 1992, 99, 67–74. [Google Scholar] [CrossRef]
- Lummaa, V.; Clutton-Brock, T. Early development, survival and reproduction in humans. Trends Ecol. Evol. 2002, 17, 141–147. [Google Scholar] [CrossRef]
- Barber, N. On the relationship between fertility and geographic latitude: A cross-national study. Cross-Cult. Res. 2002, 36, 3–15. [Google Scholar] [CrossRef]
- Tamashiro, K.L.; Hegeman, M.A.; Sakai, R.R. Chronic social stress in a changing dietary environment. Physiol. Behav. 2006, 89, 536–542. [Google Scholar] [CrossRef]
- Singh, D.S.N.; Sridharan, K.; Selvamurthy, W. Human nutrition at high altitude. Nutr. Bull. 1999, 24, 195–202. [Google Scholar] [CrossRef]
- Morel, O.E.; Aubert, R.; Richalet, J.P.; Chapelot, J.P. Simulated high altitude selectively decreases protein intake and lean mass gain in rats. Physiol. Behav. 2005, 86, 145–153. [Google Scholar] [CrossRef]
- Atkin, D. The caloric costs of culture: Evidence from Indian migrants. Am. Econ. Rev. 2016, 106, 1144–1181. [Google Scholar] [CrossRef]
- Gapminder. Median Age in Years. Available online: https://www.gapminder.org/data/ (accessed on 23 April 2021).[Green Version]
- FAO. Food and Agriculture Organization of the United Nations. An Introduction to the Basic Concepts of Food Security. Italy, Rome. 2008. Available online: https://www.fao.org/3/al936e/al936e00.pdf (accessed on 12 February 2023).[Green Version]
- FAO. Food and Agriculture Organization of the United Nations. Food Balance Sheets—A Handbook. Rome Italy. 2001. Available online: https://www.fao.org/documents/card/en/c/7d49abaa-eccf-5412-878a-8c190c46748a (accessed on 12 February 2023).[Green Version]
- Cialfa, E.; Turrini, A.; Lintas, C. A National Food Survey: Food Balance Sheets and Other Methodologies: A Critical Overview. In Monitoring Dietary Intakes; ILSI Monographs; Macdonald, I., Ed.; Springer: London, UK, 1991. [Google Scholar] [CrossRef]
- Thar, C.M.; Jackson, R.; Swinburn, B.; Mhurchu, C.N. A review of the uses and reliability of food balance sheets in health research. Nutr. Rev. 2020, 78, 989–1000. [Google Scholar] [CrossRef] [PubMed]
- TWBC. The World Bank Climate Knowledge Portal. Historical Data Covering 1901 to 2016. 2020. Available online: https://climateknowledgeportal.worldbank.org/download-data (accessed on 1 June 2020).
- Gapminder. Geographic Territories Frequently Used by Gapminder. Includes Geographical Regions and National Income Level as Given by World Bank Income Group in 2017. 2018. Available online: https://www.gapminder.org/data/ (accessed on 19 June 2018).
- OWD. Our World in Data (OWD). Height by Year of Birth 1896 to 1996. 2019. Available online: https://ourworldindata.org/human-height (accessed on 3 February 2019).
- Tremblay, J.C.; Ainslie, P.N. Global and country-level estimates of human population at high altitude. Proc. Natl. Acad. Sci. USA 2021, 118, e2102463118. [Google Scholar] [CrossRef] [PubMed]
- FAO. Food and Agriculture Organization of the United Nations. FAO Statistics Division. 2020. Available online: http://www.fao.org/faostat/foodsecurity/Files/FoodConsumptionNutrients.xls (accessed on 11 September 2020).
- Depenbusch, L.; Klasen, S. The effect of bigger human bodies on the future global calorie requirements. PLoS ONE 2019, 14, e0223188. [Google Scholar] [CrossRef]
- Grasgruber, P.; Sebera, M.; Hrazdíra, E.; Cacek, J.; Kalina, T. Major correlates of male height: A study of 105 countries. Econ. Hum. Biol. 2016, 21, 172–195. [Google Scholar] [CrossRef]
- Jensen, P.M.; Sørensen, M. Spatiotemporal variations in human birth weight are associated with multiple thermal indices. Atmosphere 2025, 16, 569. [Google Scholar] [CrossRef]
- Jang, Y.S.; Shen, S.F.; Juang, J.Y.; Huang, C.Y.; Lo, M.H. Discontinuity of diurnal temperature range along elevated regions. Geophys. Res. Lett. 2022, 49, e2021GL097551. [Google Scholar] [CrossRef]
- Marshall, W.A. Evaluation of growth rate in height over periods of less than one year. Arch. Dis. Child. 1971, 46, 414–420. [Google Scholar] [CrossRef]
- Kościński, K.; Krenz-Niedbała, M.; Kozłowska-Rajewicz, A. Month-of-birth effect on height and weight in Polish rural children. Am. J. Hum. Biol. 2004, 16, 31–42. [Google Scholar] [CrossRef]
- Pomeroy, E.; Stock, J.T.; Wells, J.C.K. Population history and ecology, in addition to climate, influence human stature and body proportions. Sci. Rep. 2021, 11, 274. [Google Scholar] [CrossRef] [PubMed]
- Macdiarmid, J.I.; Whybrow, S. Nutrition from a climate change perspective. Proc. Nutr. Soc. 2019, 78, 380–387. [Google Scholar] [CrossRef] [PubMed]
- Ray, D.K.; Gerber, J.S.; MacDonald, G.K.; West, P.C. Climate variation explains a third of global crop yield variability. Nat. Commun. 2015, 6, 5989. [Google Scholar] [CrossRef] [PubMed]
- Frieler, K.; Schauberger, B.; Arneth, A.; Balkovič, J.; Chryssanthacopoulos, J.; Deryng, D.; Elliott, J.; Folberth, C.; Khabarov, N.; Müller, C.; et al. Understanding the weather signal in national crop-yield variability. Earth’s Future 2017, 5, 605–616. [Google Scholar] [CrossRef]
- Myers, S.S. Planetary health: Protecting human health on a rapidly changing planet. Lancet 2017, 390, 2860–2868. [Google Scholar] [CrossRef]

| Model Name | Calculated As | Understood As | For a 35-Year-Old Person, the Years Refer to. |
|---|---|---|---|
| 1 | Minimum and maximum temperatures in the given year | An impact of temperatures in the current year | Current year |
| 5 | Average minimum and maximum temperatures for the past 5 years | A general impact of temperature given by the mean over past years. | Recent years |
| 10 | Average minimum and maximum temperatures for the past 10 years | A general impact of temperature given by the mean over the past decade | Last decade |
| 20 | Average minimum and maximum temperatures for the past 20 years | A general impact of temperature given by the mean over past decades | Last decades |
| 30 | Average minimum and maximum temperatures for the past 30 years | A general impact of temperature from childhood to adulthood | Current generation |
| 1010 | Average minimum and maximum temperatures for the past 10 years 10 years previously | An impact of temperatures over a decade, a decade ago (in recent past) | Young adulthood |
| 2020 | Average minimum and maximum temperatures for the past 20 years 20 years previously | An impact of temperatures over decades, decades ago (in the past) | Young adulthood and some years prior to birth |
| 3030 | Average minimum and maximum temperatures for the past 30 years 30 years previously | A general impact of temperature on childhood and on the parents. | Effects on parents and some years after birth. |
| D10 | Model 10 and 1010 combined | A general impact of temperature given by the mean over past years | Last decades |
| D20 | Model 20 and 2020 combined | A general impact of temperature given by the mean over past decades | Current generation and some years prior to birth |
| D30 | Model 30 and 3030 combined | An impact of temperature on both current and past generations. | A lifetime and parental youth and adulthood |
| Model | Parameter (Temperatures) | Estimate | SE | t Value | p-Value | R2 |
|---|---|---|---|---|---|---|
| 1 | Minimum | −1.06 | 2.04 | −0.52 | 0.61 | 0.17 |
| Maximum | 7.70 | 4.11 | 1.87 | 0.07 | ||
| 5 | Minimum | −2.24 | 4.88 | −0.46 | 0.65 | 0.20 |
| Maximum | 22.35 | 9.82 | 2.28 | 0.03 | ||
| 10 | Minimum | 0.26 | 7.92 | 0.03 | 0.97 | 0.20 |
| Maximum | 19.53 | 15.95 | 1.22 | 0.23 | ||
| 20 | Minimum | 11.78 | 14.32 | 0.82 | 0.41 | 0.11 |
| Maximum | −25.32 | 28.82 | −0.88 | 0.38 | ||
| 30 | Minimum | 9.29 | 18.10 | 0.51 | 0.61 | 0.04 |
| Maximum | −21.92 | 36.44 | −0.60 | 0.55 | ||
| 1010 | Minimum | 3.42 | 9.72 | 0.35 | 0.73 | 0.06 |
| Maximum | −6.83 | 19.58 | −0.35 | 0.73 | ||
| 2020 | Minimum | −29.18 | 15.51 | −1.88 | 0.06 | 0.18 |
| Maximum | 47.48 | 31.23 | 1.52 | 0.13 | ||
| 3030 | Minimum | −50.24 | 16.99 | −2.96 | 0.004 | 0.37 |
| Maximum | 127.92 | 34.19 | 3.74 | 0.0004 | ||
| D10 | Minimum | 5.27 | 13.48 | 0.39 | 0.69 | 0.13 |
| Maximum | −9.78 | 27.13 | −0.36 | 0.72 | ||
| D20 | Minimum | −16.36 | 23.14 | −0.71 | 0.48 | 0.10 |
| Maximum | 34.91 | 46.58 | 0.75 | 0.46 | ||
| D30 | Minimum | −56.39 | 30.38 | −1.86 | 0.07 | 0.17 |
| Maximum | 164.23 | 61.16 | 2.69 | 0.009 | ||
| 30 within D30 | Minimum | −17.19 | 15.56 | −1.10 | 0.27 | 0.07 |
| Maximum | 41.83 | 31.33 | 1.34 | 0.19 | ||
| 3030 within D30 | Minimum | −39.20 | 18.19 | −2.15 | 0.03 | 0.24 |
| Maximum | 122.40 | 36.62 | 3.34 | 0.001 |
| Variable | Parameter | Estimate | SE | t-Value | Pr > |t| | R2 |
|---|---|---|---|---|---|---|
| Mean temperature Reaction norm | Intercept | 10,437.59 | 6703.92 | 1.56 | 0.12 | 0.37 |
| Minimum temperature | −50.24 | 16.99 | −2.96 | 0.004 | ||
| Maximum temperature | 127.92 | 34.19 | 3.74 | 0.0004 | ||
| Low-altitude populations | −4.52 | 4.69 | −0.96 | 0.34 | ||
| Height | −84.96 | 41.13 | −2.07 | 0.04 | ||
| High income | 1422.31 | 569.69 | 2.50 | 0.02 | ||
| Upper middle income | 1403.03 | 424.27 | 3.31 | 0.002 | ||
| Lower middle income | 51.19 | 384.51 | 0.13 | 0.89 | ||
| Low income | 0.00 | |||||
| Daily calorie intake | 0.23 | 0.49 | 0.47 | 0.64 | ||
| Relative AIC value | Intercept | 0.9588 | 0.2180 | 4.4 | <0.0001 | 0.11 |
| Minimum temperature | −0.0001 | 0.0006 | −0.1 | 0.92 | ||
| Maximum temperature | −0.0015 | 0.0011 | −1.37 | 0.18 | ||
| Low-altitude populations | 0.0003 | 0.0002 | 2.16 | 0.03 | ||
| Height | 0.0006 | 0.0013 | 0.43 | 0.66 | ||
| High income | −0.0177 | 0.0185 | −0.95 | 0.34 | ||
| Upper middle income | −0.0073 | 0.0138 | −0.53 | 0.60 | ||
| Lower middle income | −0.0012 | 0.0125 | −0.1 | 0.92 | ||
| Low income | 0 | |||||
| Daily calorie intake | −1.7 × 10−5 | 1.6 × 10−5 | −1.06 | 0.29 |
| Variable | Parameters | Estimate | SE | t-Value | Pr > |t| | R2 |
|---|---|---|---|---|---|---|
| Mean temperature Reaction norm | Intercept | −1766.52 | 831.69 | −2.12 | 0.037 | 0.13 |
| Minimum temperature | −54.48 | 16.38 | −3.33 | 0.001 | ||
| Maximum temperature | 101.44 | 37.48 | 2.71 | 0.008 | ||
| Maximum Temperature Reaction norm | Intercept | −1638.26 | 836.67 | −1.96 | 0.054 | 0.13 |
| Minimum temperature | −53.54 | 16.48 | −3.25 | 0.002 | ||
| Maximum temperature | 100.00 | 37.70 | 2.65 | 0.009 | ||
| Minimum Temperature Reaction norm | Intercept | −128.26 | 776.71 | −0.17 | 0.87 | 0.00 |
| Minimum temperature | −0.94 | 15.30 | −0.06 | 0.95 | ||
| Maximum temperature | 1.44 | 35.00 | 0.04 | 0.97 |
| Parameter | Estimate | SE | t Value | Pr > |t| | R2 |
|---|---|---|---|---|---|
| Intercept | 2049.7 | 339.5 | 6.04 | <0.0001 | 0.75 |
| Mean temperature | −244.6 | 58.3 | −4.19 | <0.0001 | |
| Maximum temperature | 105.3 | 32.9 | 3.2 | 0.002 | |
| Mean × maximum temp. | 1.6 | 0.8 | 1.98 | 0.04 | |
| Minimum temperature | 121.7 | 26.9 | 4.53 | <0.0001 | |
| Mean × minimum temp. | −1.6 | 0.4 | −4.27 | <0.0001 | |
| Median Age | 13.5 | 6.5 | 2.09 | 0.04 | |
| Low-altitude populations | 2.0 | 0.8 | 2.32 | 0.02 | |
| High income | 552.5 | 102.4 | 5.39 | <0.0001 | |
| Upper middle income | 447.2 | 73.1 | 6.11 | <0.0001 | |
| Lower middle income | 211.6 | 64.3 | 3.29 | 0.001 | |
| Low income | 0.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jensen, P.M.; Sørensen, M. Moderate Impact of Increasing Temperatures on Food Intake in Human Populations. Challenges 2025, 16, 34. https://doi.org/10.3390/challe16030034
Jensen PM, Sørensen M. Moderate Impact of Increasing Temperatures on Food Intake in Human Populations. Challenges. 2025; 16(3):34. https://doi.org/10.3390/challe16030034
Chicago/Turabian StyleJensen, Per M., and Marten Sørensen. 2025. "Moderate Impact of Increasing Temperatures on Food Intake in Human Populations" Challenges 16, no. 3: 34. https://doi.org/10.3390/challe16030034
APA StyleJensen, P. M., & Sørensen, M. (2025). Moderate Impact of Increasing Temperatures on Food Intake in Human Populations. Challenges, 16(3), 34. https://doi.org/10.3390/challe16030034






