A Finite Element Model for Underwater Sound Propagation in 2-D Environment
Abstract
:1. Introduction
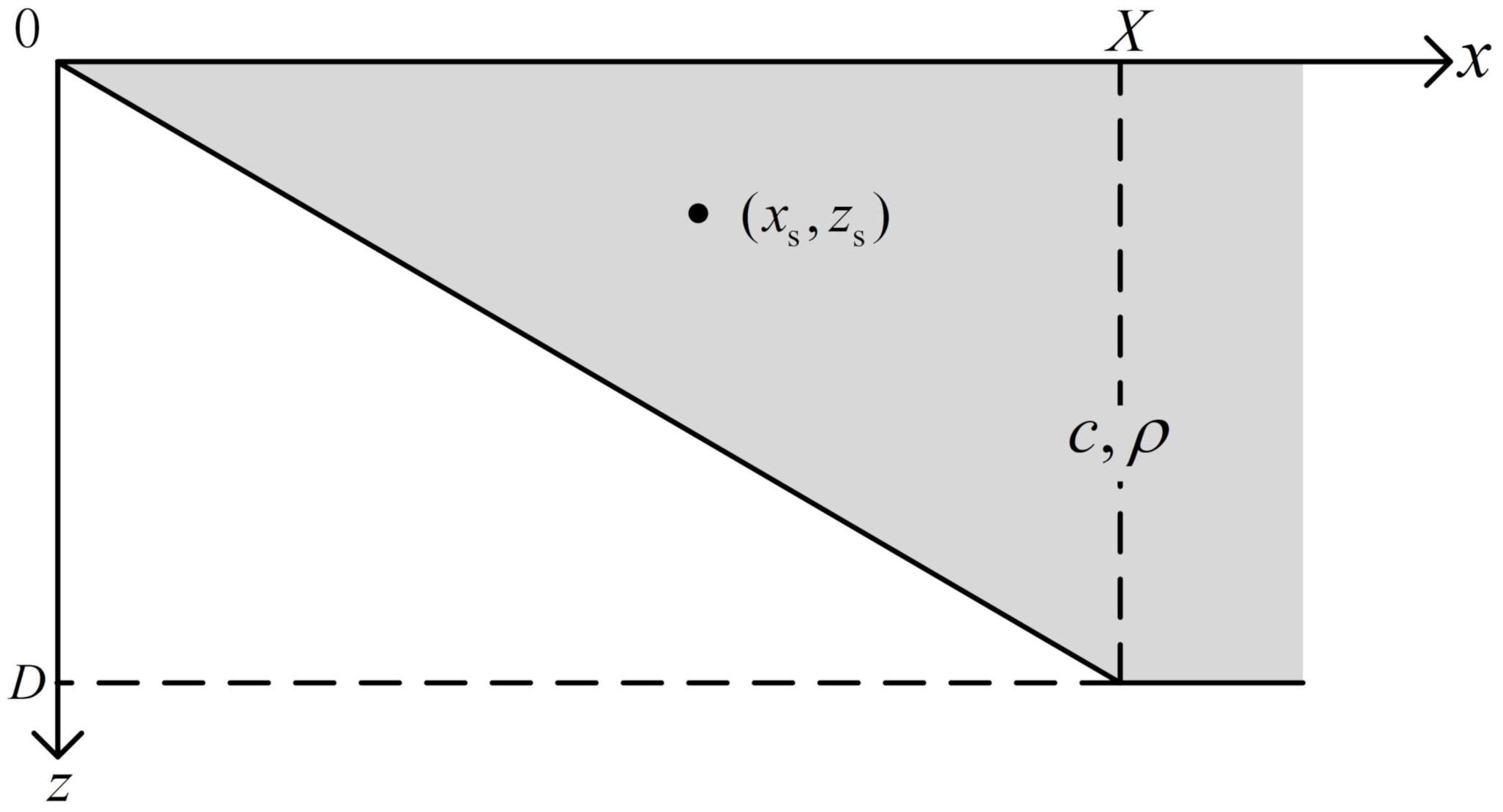
2. Practical Aspects of the Implementation
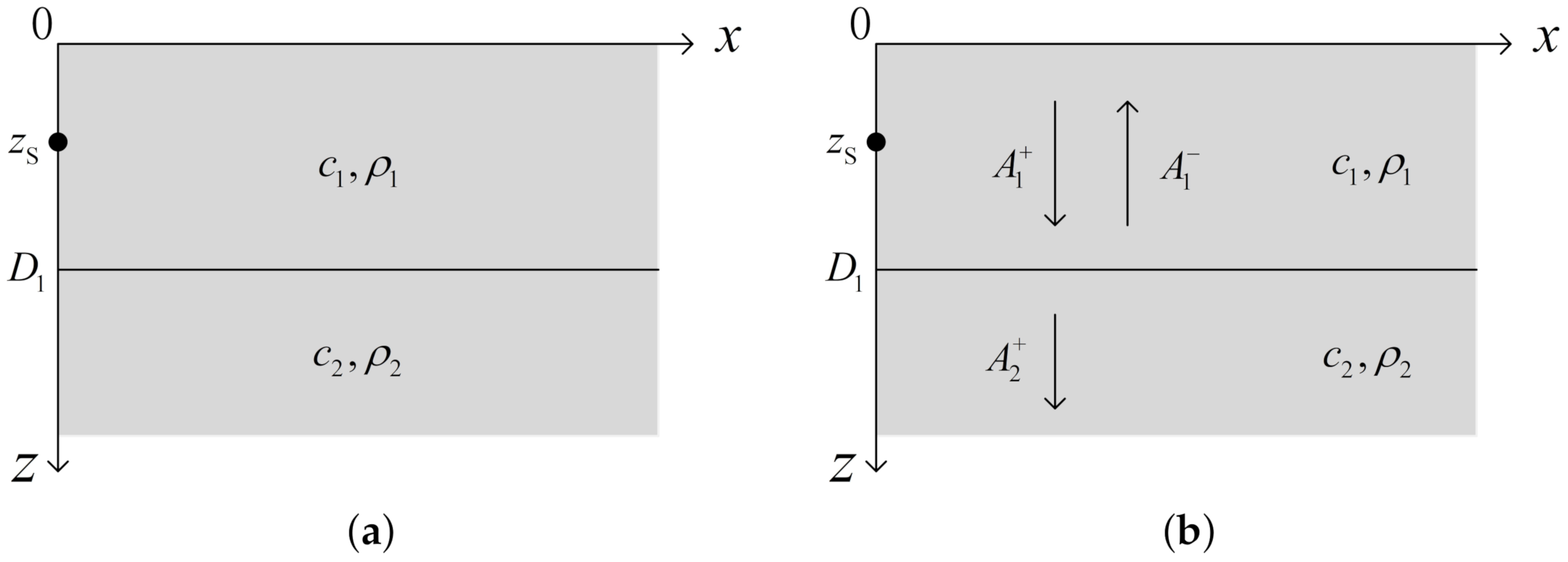
2.1. Weak Form of Helmholtz Equation
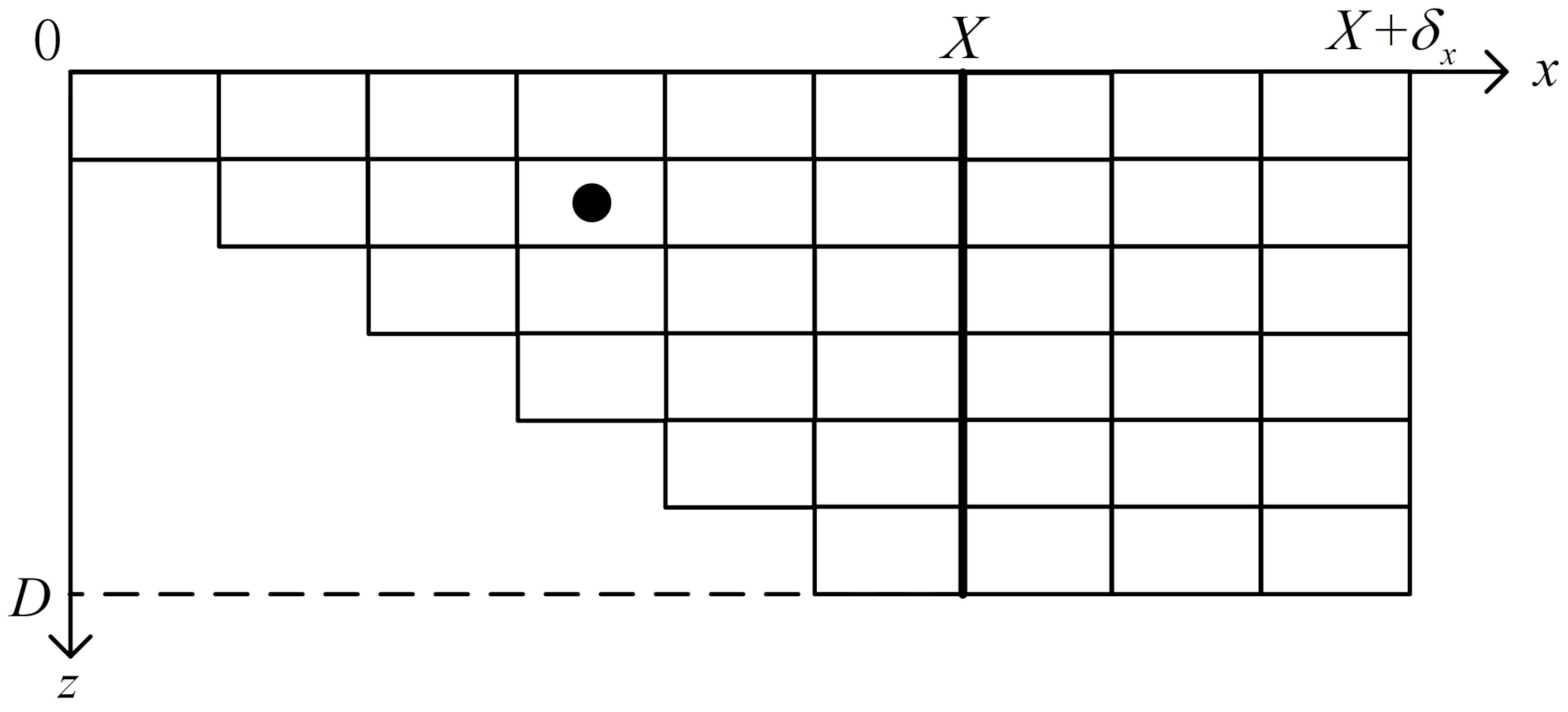
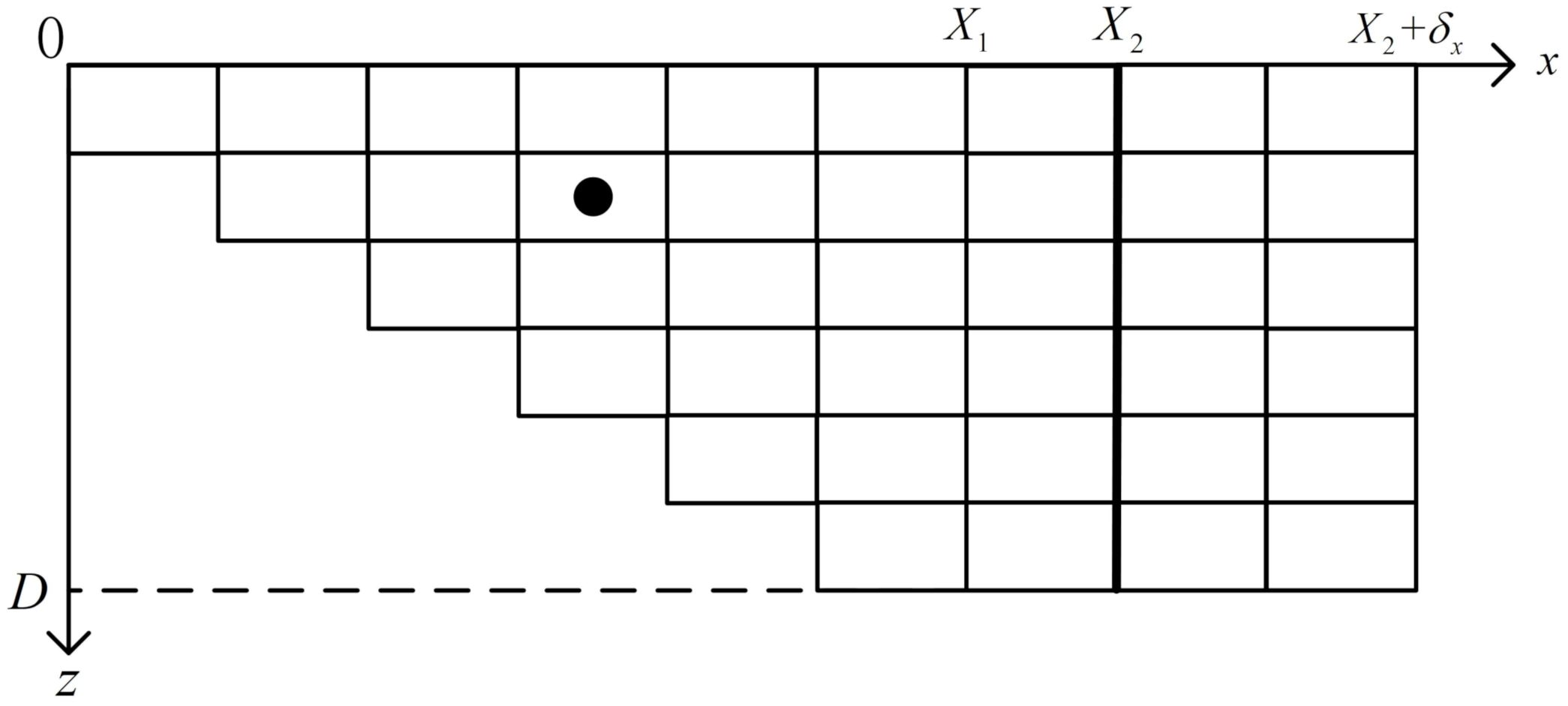
2.2. The Finite Element Discretization
2.3. Finite Element Matrices
2.3.1. Calculation of Local Stiffness Matrices
2.3.2. Assembly of Global Stiffness Matrix
2.4. Boundary Conditions
2.4.1. Dirichlet Boundary
- Define the global stiffness matrix as , the global load vector as , and the sound pressure vector as . They satisfy the linear equation system .
- Subtract the product of the lth column of and the lth element of from .
- Set the elements of the lth row and the lth column of to 0 and the lth diagonal element to 1.
- Set the lth element of to 0.
2.4.2. Neumann Boundary
2.4.3. Free-Space Simulation
3. Numerical Results
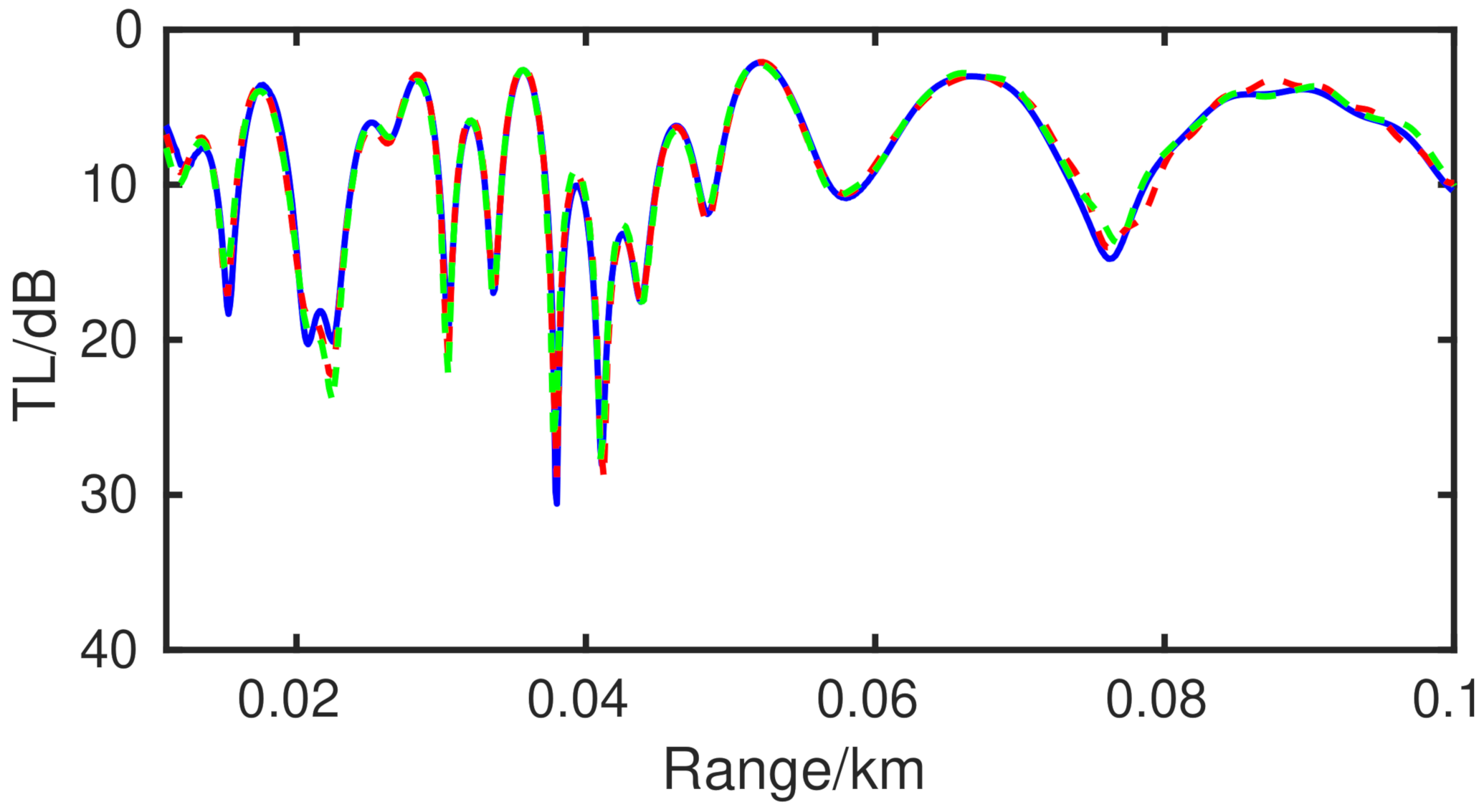
3.1. Range-Dependent Benchmark Problem
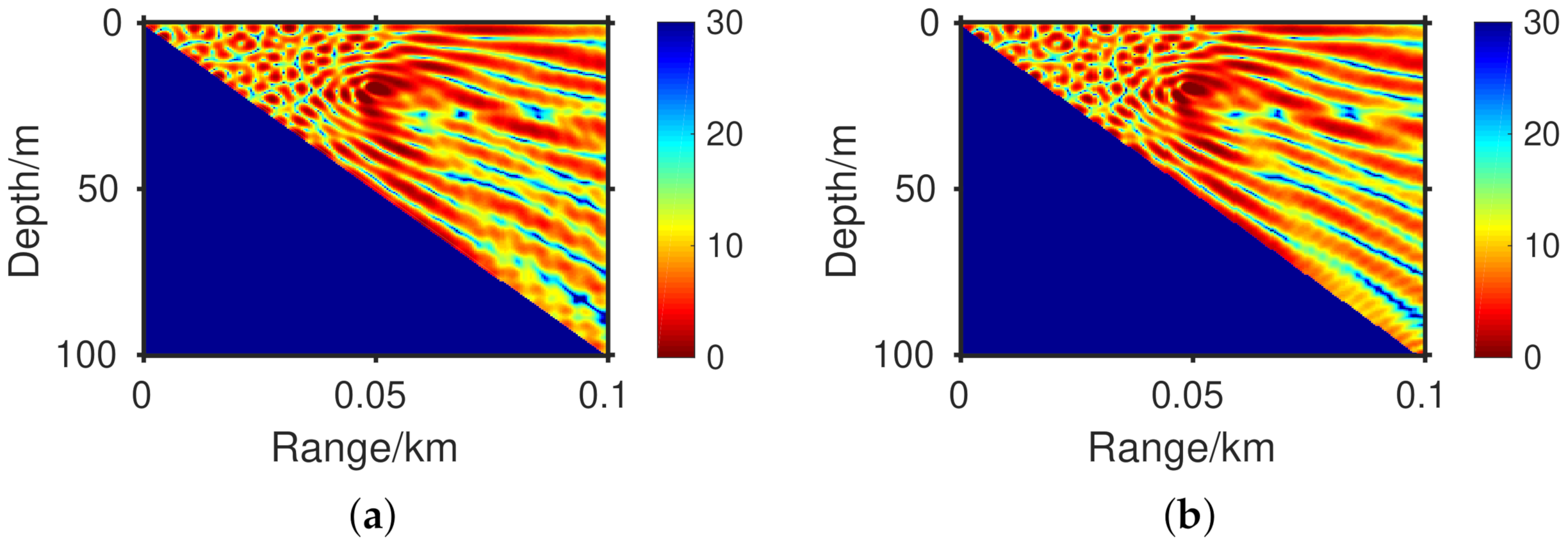
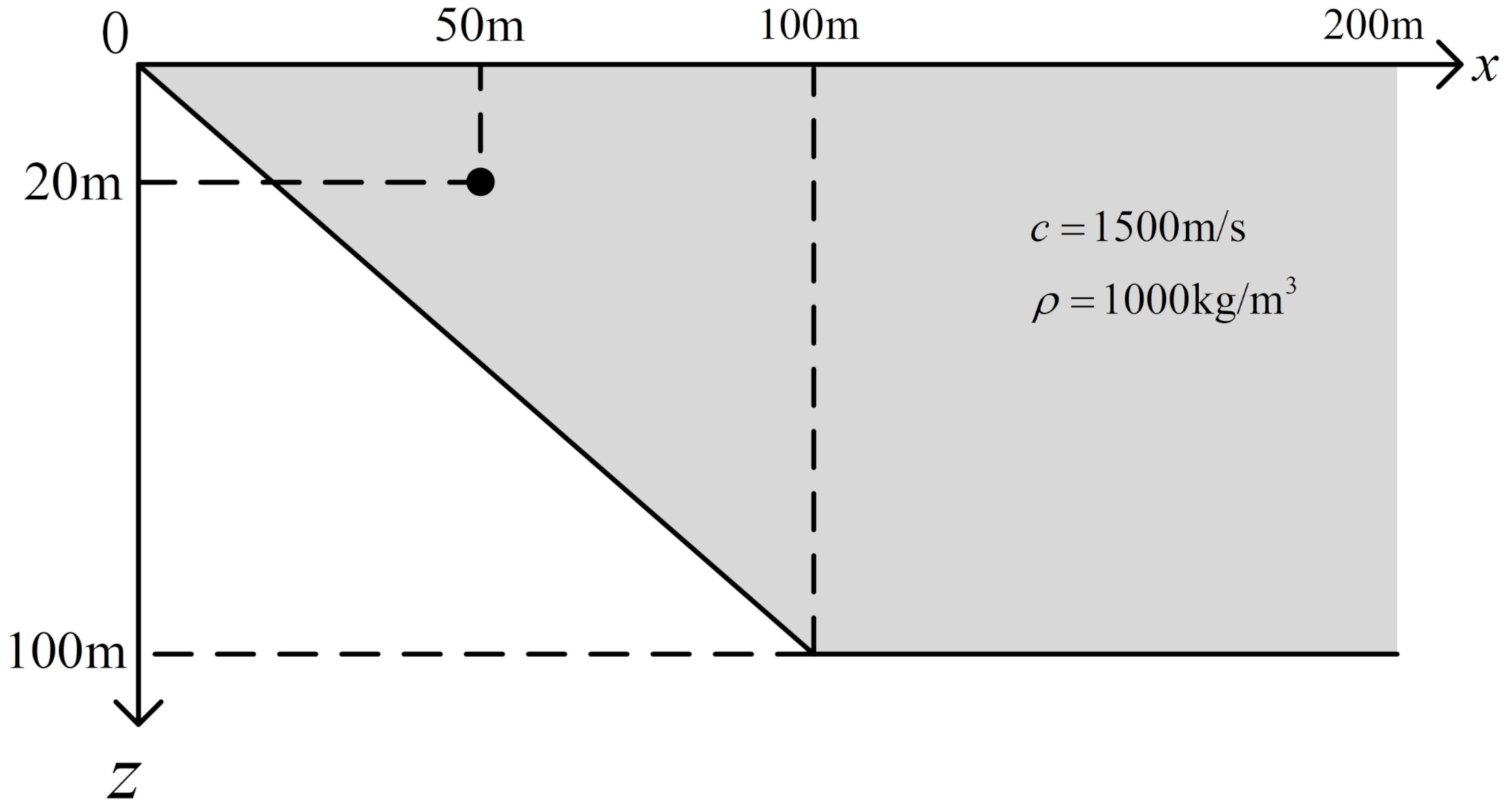
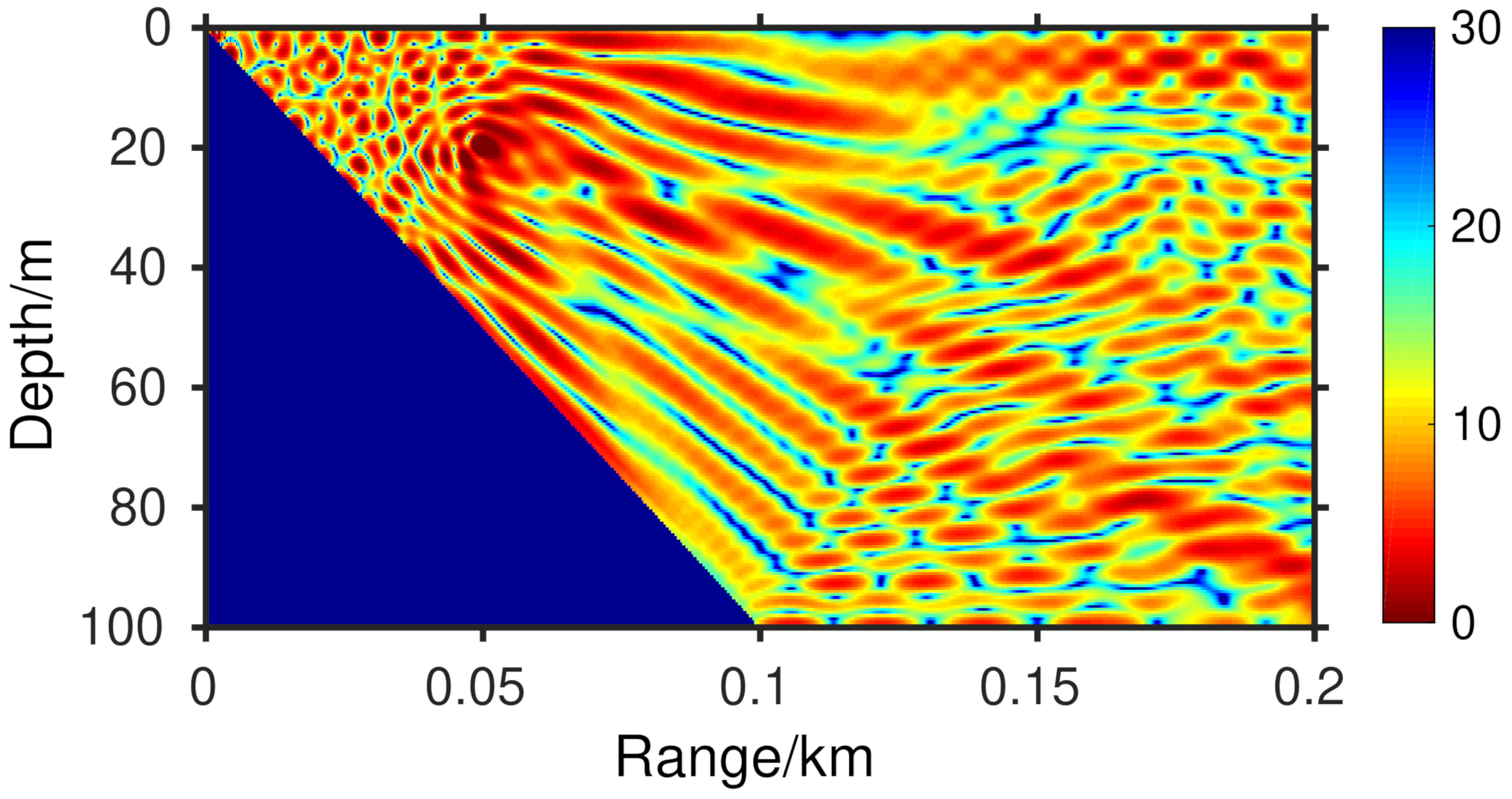
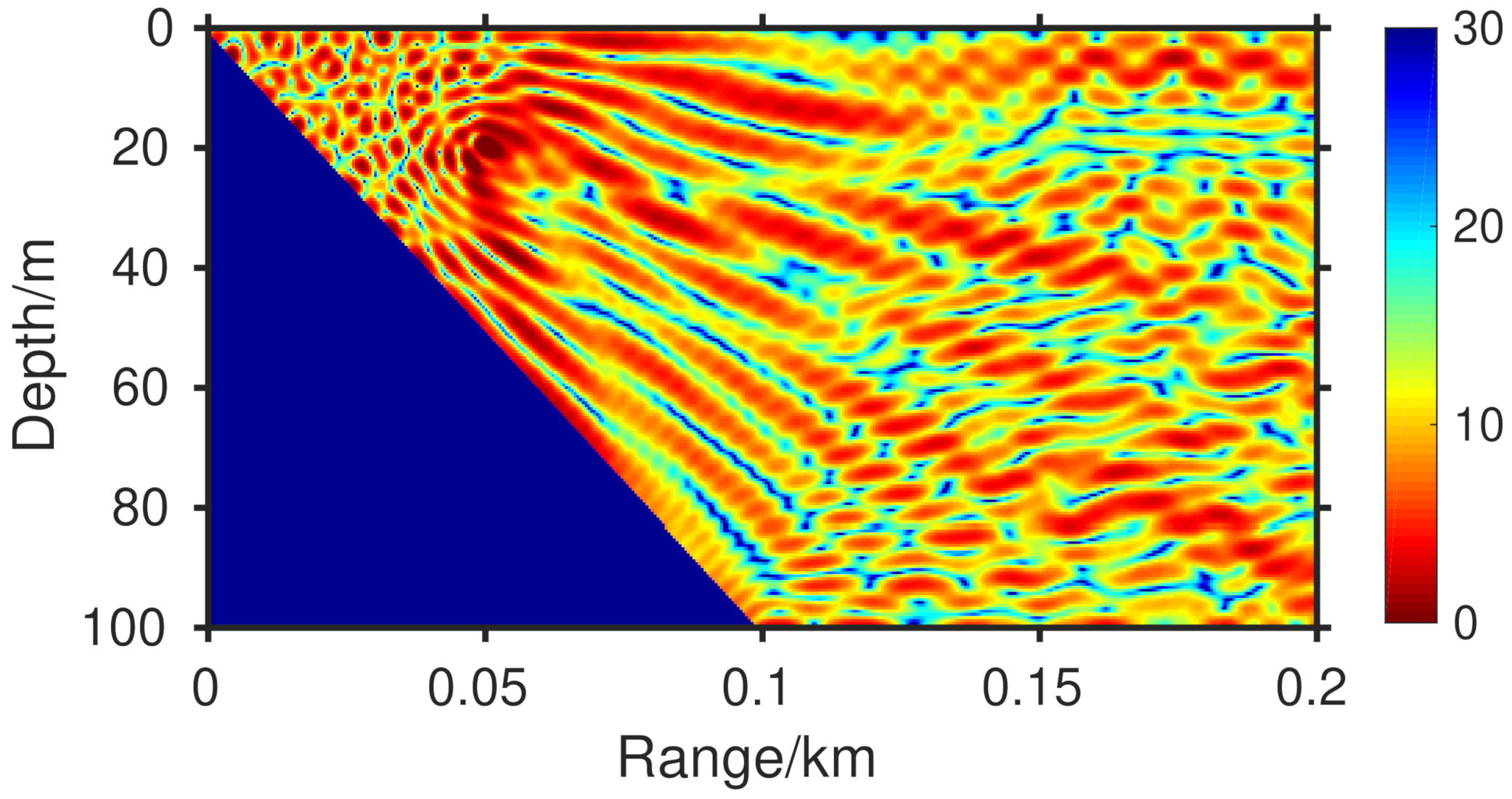
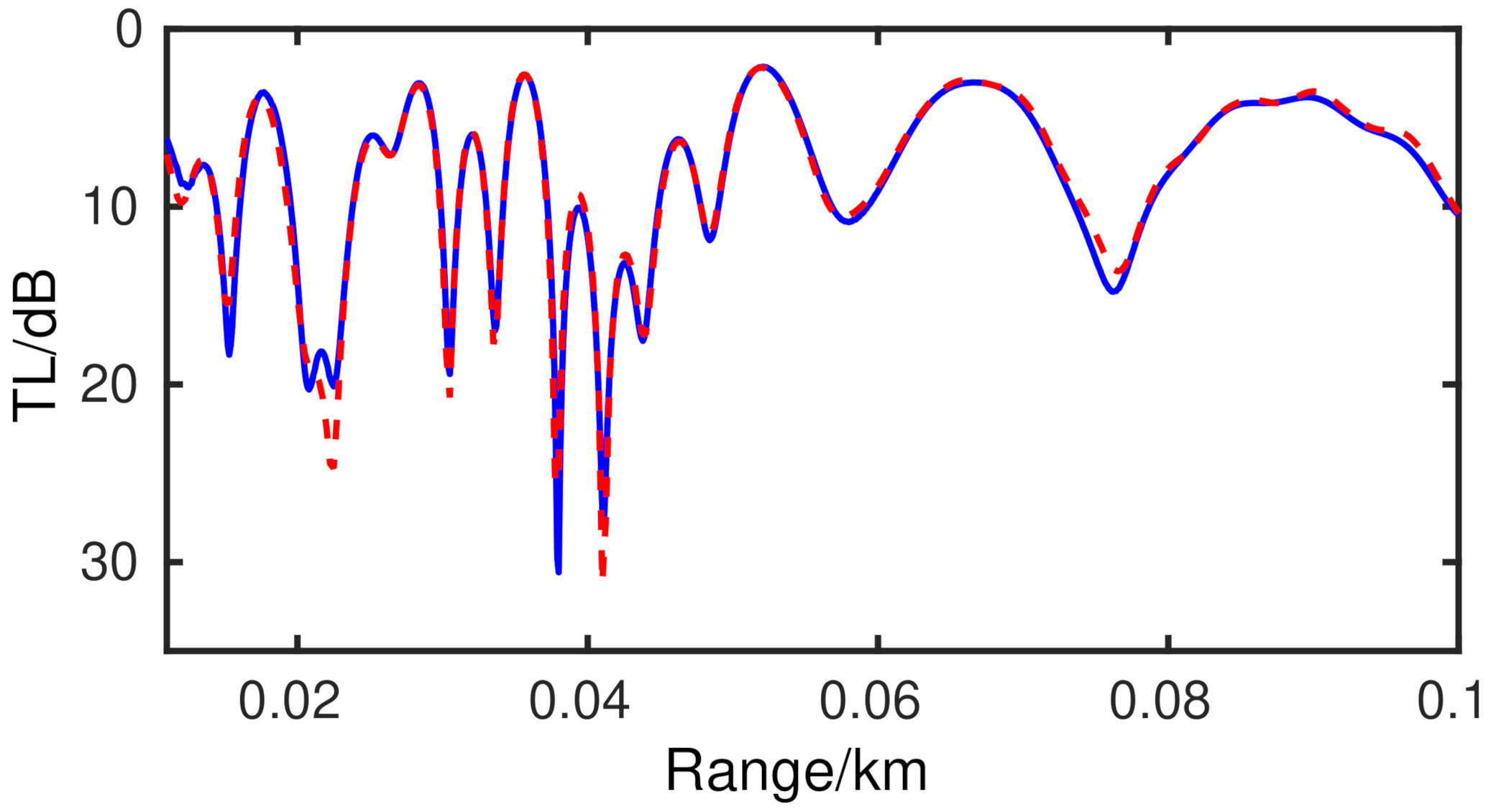
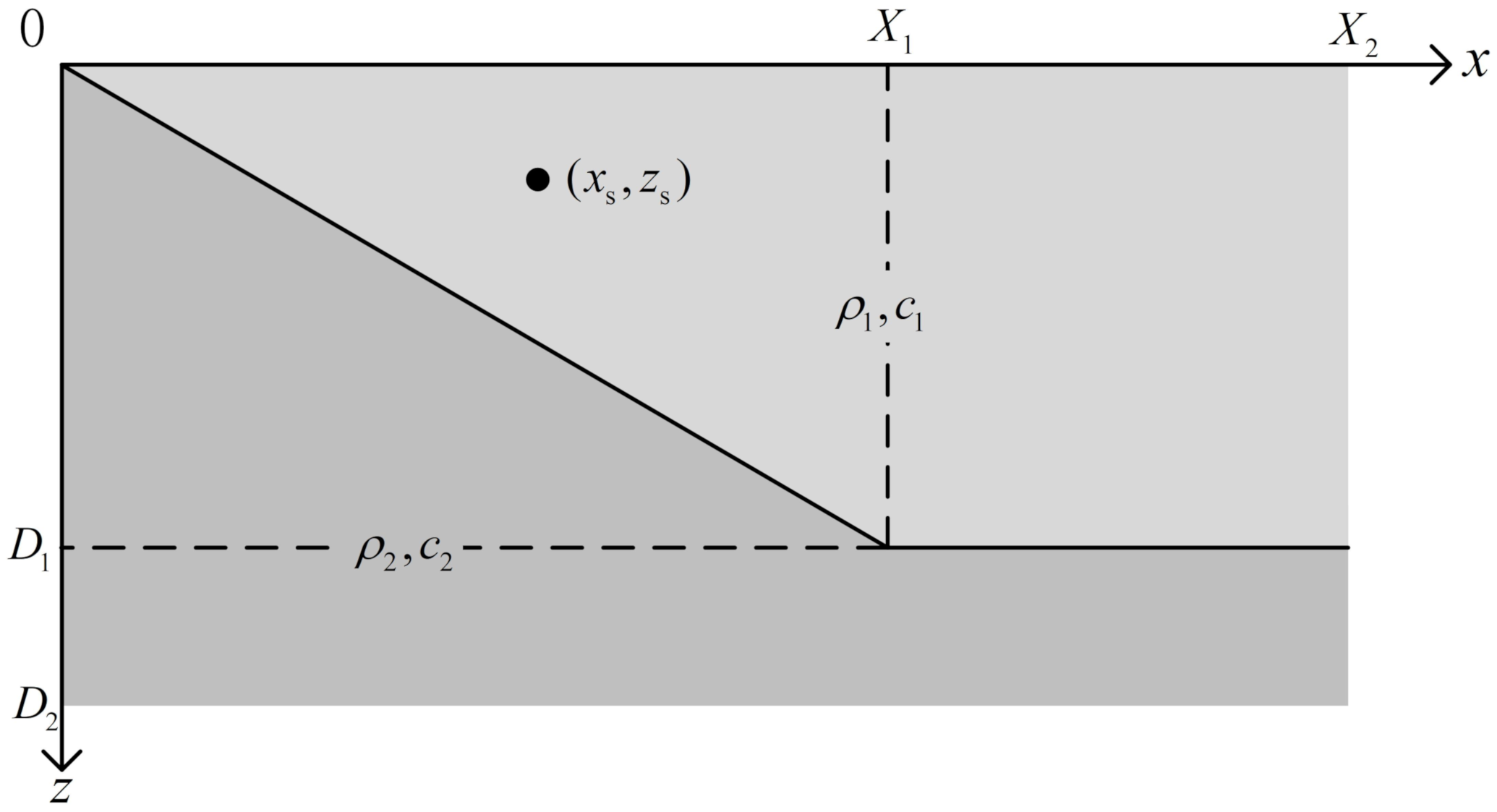
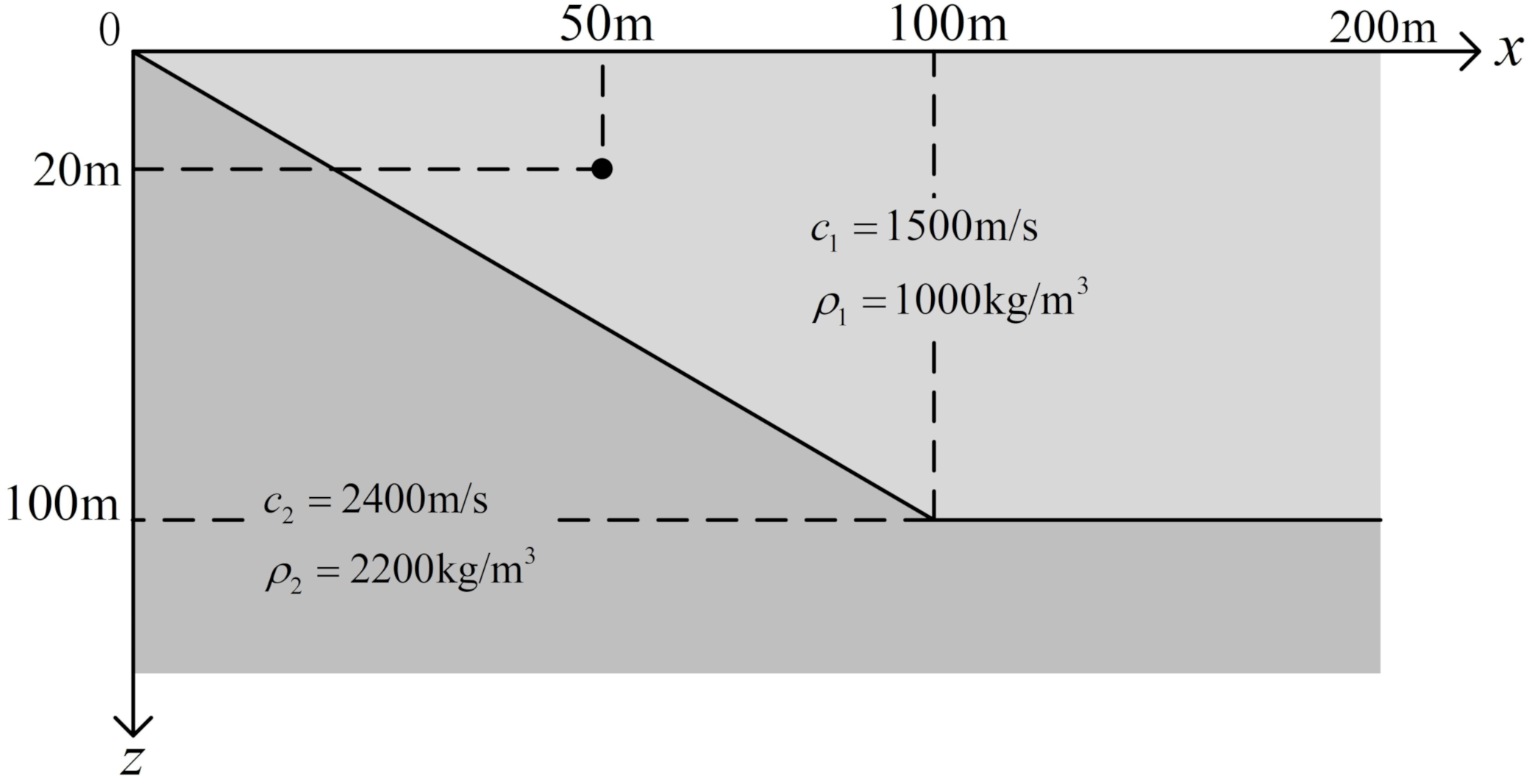
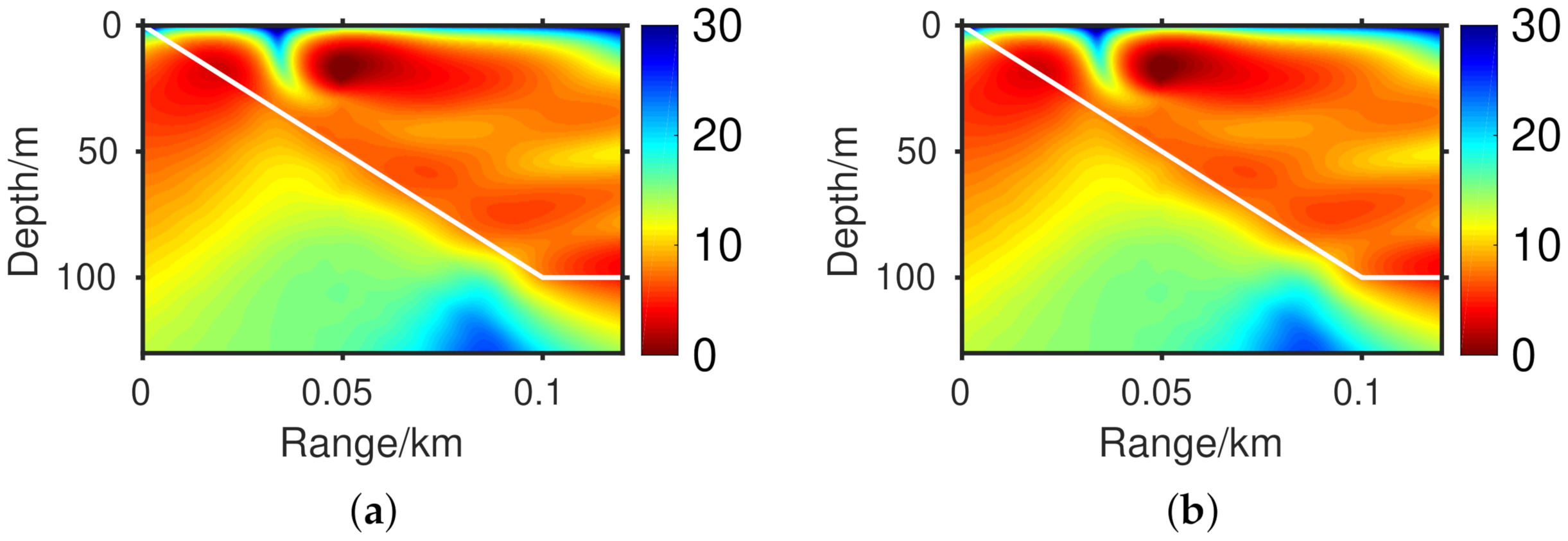
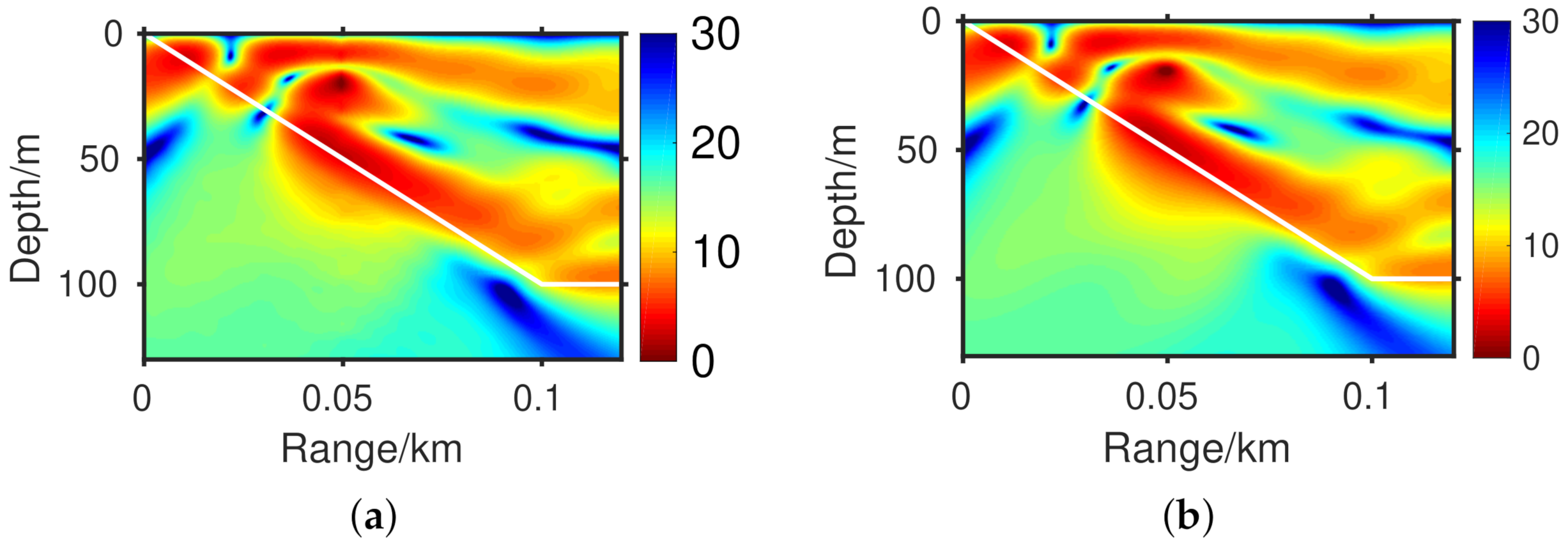
3.2. Slope Problem with Totally Reflected Bottom
3.3. Slope Problem with Penetrable Bottom
3.4. Analysis of Universality
4. Conclusions
- High accuracy. Our finite element model achieves high accuracy in both range-dependent problems and inhomogeneous media problems.
- Great universality. Compared with the popular KRAKEN model, our finite element model has better universality and is well-suited for more complex problems.
- Focused on range-dependent underwater sound propagation problems.
- Flexible. Since our model is entirely developed by ourselves instead of relying on commercial software, it is easier to modify and optimize.
- The integral method. While calculating the elements of stiffness matrices, we used the trapezoid method to evaluate the integral, which is not efficient enough. We will try other methods, such as the Gauss integral method, to improve the accuracy and efficiency.
- The selection of meshes. Only four-node quadrilateral elements are used in this model. As a result, when calculating the sound field in a complex environment especially with complex shape of boundaries, the meshes cannot match the boundaries very well. We plan to optimize the selection of meshes, combining triangular elements and quadrilateral elements to discretize the physical domain.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PML | Perfectly Matched Layer |
References
- Clough, R.W. The finite element method in plane stress analysis. In Proceedings of the 2nd ASCE Conference on Electronic Computation, Pittsburgh, PA, USA, 8–9 September 1960. [Google Scholar]
- Gladwell, G. A variational formulation of damped acousto structural vibration problems. J. Sound Vib. 1966, 4, 172–186. [Google Scholar] [CrossRef]
- Craggs, A. The use of simple three-dimensional acoustic finite elements for determining the natural modes and frequencies of complex shaped enclosures. J. Sound Vib. 1972, 23, 331–339. [Google Scholar] [CrossRef]
- Nefske, D.; Wolf, J., Jr.; Howell, L. Structural-acoustic finite element analysis of the automobile passenger compartment: A review of current practice. J. Sound Vib. 1982, 80, 247–266. [Google Scholar] [CrossRef]
- Hunt, J.T.; Knittel, M.R.; Barach, D. Finite element approach to acoustic radiation from elastic structures. J. Acoust. Soc. Am. 1974, 55, 269–280. [Google Scholar] [CrossRef]
- Hunt, J.T.; Knittel, M.R.; Nichols, C.S.; Barach, D. Finite- element approach to acoustic scattering from elastic structures. J. Acoust. Soc. Am. 1975, 57, 287–299. [Google Scholar] [CrossRef]
- Bettess, P. Infinite elements. Int. J. Numer. Methods Eng. 1977, 11, 53–64. [Google Scholar] [CrossRef]
- Astley, R.; Coyette, J.P. The performance of spheroidal infinite elements. Int. J. Numer. Methods Eng. 2001, 52, 1379–1396. [Google Scholar] [CrossRef]
- Berenger, J.P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Berenger, J.P. Perfectly matched layer for the FDTD solution of wave-structure interaction problems. IEEE Trans. Antennas Propag. 1996, 44, 110–117. [Google Scholar] [CrossRef]
- Givoli, D. High-order local non-reflecting boundary conditions: A review. Wave Motion 2004, 39, 319–326. [Google Scholar] [CrossRef]
- Givoli, D. Recent advances in the DtN FE method. Arch. Comput. Methods Eng. 1999, 6, 71–116. [Google Scholar] [CrossRef]
- Thompson, L.L.; Pinsky, P.M. Encyclopedia of Computational Mechanics: Acoustics; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Harari, I.; Hughes, T.J. A cost comparison of boundary element and finite element methods for problems of time-harmonic acoustics. Comput. Methods Appl. Mech. Eng. 1992, 97, 77–102. [Google Scholar] [CrossRef]
- Harari, I.; Hughes, T.J. Analysis of continuous formulations underlying the computation of time-harmonic acoustics in exterior domains. Comput. Methods Appl. Mech. Eng. 1992, 97, 103–124. [Google Scholar] [CrossRef]
- Chew, W.C.; Song, J.; Cui, T.; Velamparambil, S.; Hastriter, M.; Hu, B. Review of large scale computing in electromagnetics with fast integral equation solvers. CMES-Comput. Model. Eng. Sci. 2004, 5, 361–372. [Google Scholar]
- Fischer, M.; Gaul, L. Fast BEM–FEM mortar coupling for acoustic–structure interaction. Int. J. Numer. Methods Eng. 2005, 62, 1677–1690. [Google Scholar] [CrossRef]
- Van Hal, B.; Desmet, W.; Vandepitte, D.; Sas, P. A coupled finite element–wave based approach for the steady-state dynamic analysis of acoustic systems. J. Comput. Acoust. 2003, 11, 285–303. [Google Scholar] [CrossRef]
- Murphy, J.E.; Chin-Bing, S.A. A finite element model for ocean acoustic propagation. Math. Comput. Model. 1988, 11, 70–74. [Google Scholar] [CrossRef]
- Murphy, J.E.; Chin-Bing, S.A. A finite-element model for ocean acoustic propagation and scattering. J. Acoust. Soc. Am. 1989, 86, 1478–1483. [Google Scholar] [CrossRef]
- Murphy, J.E.; Chin-Bing, S.A. A seismo-acoustic finite element model for underwater acoustic propagation. In Shear Waves in Marine Sediments; Springer: Berlin/Heidelberg, Germany, 1991; pp. 463–470. [Google Scholar]
- Kampanis, N.A.; Dougalis, V.A. A finite element code for the numerical solution of the Helmholtz equation in axially symmetric waveguides with interfaces. J. Comput. Acoust. 1999, 7, 83–110. [Google Scholar] [CrossRef]
- Jun, L. Numerical Solution of Sound Field in Shallow Water by Finite Element Method. Ph.D. Thesis, Peking University, Beijing, China, 2005. [Google Scholar]
- Athanassoulis, G.; Belibassakis, K.; Mitsoudis, D.; Kampanis, N.; Dougalis, V. Coupled mode and finite element approximations of underwater sound propagation problems in general stratified environments. J. Comput. Acoust. 2008, 16, 83–116. [Google Scholar] [CrossRef]
- Junyu, F. Research on Finite Element Method in Ocean Acoustic Propagation Problems. Master’s Thesis, Harbin Engineering University, Harbin, China, 2016. [Google Scholar]
- Jun, Z. Research on Ocean Sound Propagation Characteristics Based on Finite Element Method. Master’s Thesis, Zhejiang Ocean University, Zhoushan, China, 2019. [Google Scholar]
- Goldsberry, B.M.; Isakson, M. Comparison of two-dimensional axial-symmetric and longitudinally invariant methods for three-dimensional shallow water acoustic propagation using finite element methods. In Proceedings of the Meetings on Acoustics ICA2013, Montreal, QC, Canada, 2–7 June 2013; Acoustical Society of America: New York, NY, USA, 2013; Volume 19, p. 070080. [Google Scholar]
- Chai, Y.; Gong, Z.; Li, W.; Li, T.; Zhang, Q.; Zou, Z.; Sun, Y. Application of smoothed finite element method to two-dimensional exterior problems of acoustic radiation. Int. J. Comput. Methods 2018, 15, 1850029. [Google Scholar] [CrossRef]
- Chai, Y.; Li, W.; Gong, Z.; Li, T. Hybrid smoothed finite element method for two-dimensional underwater acoustic scattering problems. Ocean Eng. 2016, 116, 129–141. [Google Scholar] [CrossRef]
- Chai, Y.; You, X.; Li, W.; Huang, Y.; Yue, Z.; Wang, M. Application of the edge-based gradient smoothing technique to acoustic radiation and acoustic scattering from rigid and elastic structures in two dimensions. Comput. Struct. 2018, 203, 43–58. [Google Scholar] [CrossRef]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics; Springer: New York, NY, USA, 2011. [Google Scholar]
- Liu, L.; Qin, Y.; Xu, Y.; Zhao, Y. The uniqueness and existence of solutions for the 3-D Helmholtz equation in a stratified medium with unbounded perturbation. Math. Methods Appl. Sci. 2013, 36, 2033–2047. [Google Scholar] [CrossRef]
- Wen-Yu, L.; Chun-Mei, Y.; Ji-Xing, Q.; Zhang, R.H. Benchmark solutions for sound propagation in an ideal wedge. Chin. Phys. B 2013, 22, 054301. [Google Scholar]
- Luo, W.; Yang, C.; Qin, J.; Zhang, R. A numerically stable coupled-mode formulation for acoustic propagation in rage-dependent waveguides. Sci. China Phys. Mech. Astron. 2012, 55, 572–588. [Google Scholar] [CrossRef]
- Deane, G.; Buckingham, M. An analysis of the three-dimensional sound field in a penetrable wedge with a stratified fluid or elastic basement. J. Acoust. Soc. Am. 1993, 93, 1319–1328. [Google Scholar] [CrossRef]
- Tang, J.; Petrov, P.; Piao, S.; Kozitskiy, S. On the Method of Source Images for the Wedge Problem Solution in Ocean Acoustics: Some Corrections and Appendices. Acoust. Phys. 2018, 64, 228–240. [Google Scholar] [CrossRef]
- Luo, W.Y.; Yu, X.L.; Yang, X.F.; Zhang, R.H. Analytical solution based on the wavenumber integration method for the acoustic field in a Pekeris waveguide. Chin. Phys. B 2016, 25, 044302. [Google Scholar] [CrossRef]





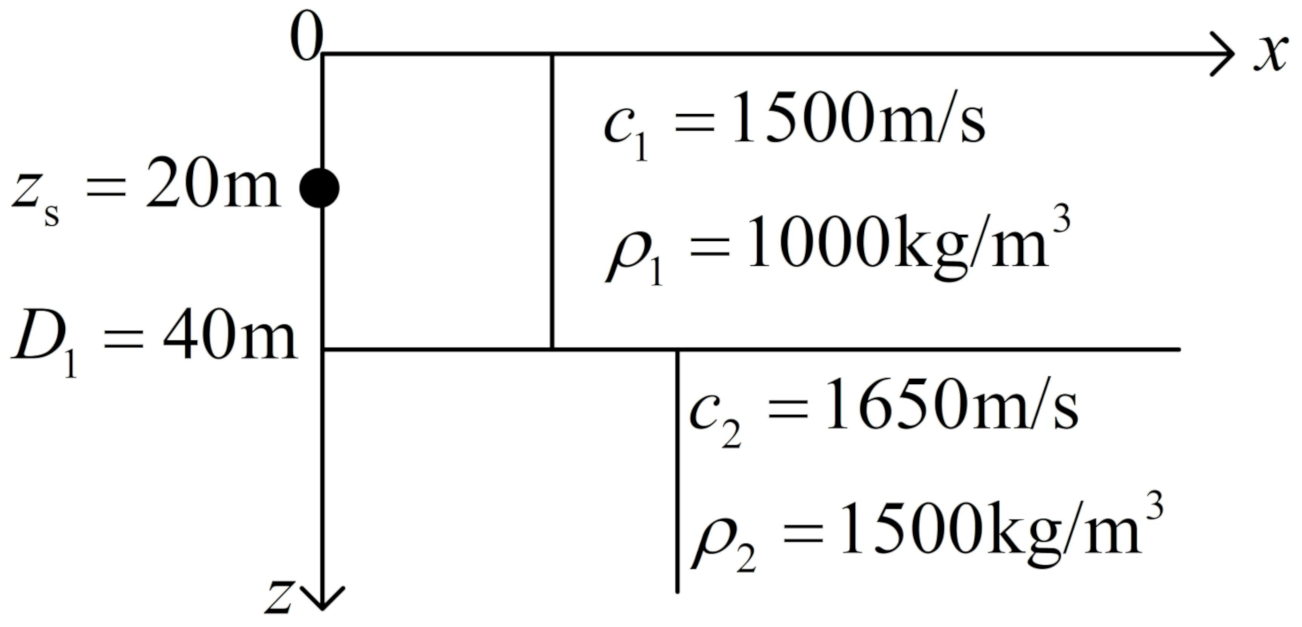


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.-Q.; Luo, W.-Y. A Finite Element Model for Underwater Sound Propagation in 2-D Environment. J. Mar. Sci. Eng. 2021, 9, 956. https://doi.org/10.3390/jmse9090956
Zhou Y-Q, Luo W-Y. A Finite Element Model for Underwater Sound Propagation in 2-D Environment. Journal of Marine Science and Engineering. 2021; 9(9):956. https://doi.org/10.3390/jmse9090956
Chicago/Turabian StyleZhou, Yi-Qing, and Wen-Yu Luo. 2021. "A Finite Element Model for Underwater Sound Propagation in 2-D Environment" Journal of Marine Science and Engineering 9, no. 9: 956. https://doi.org/10.3390/jmse9090956
APA StyleZhou, Y.-Q., & Luo, W.-Y. (2021). A Finite Element Model for Underwater Sound Propagation in 2-D Environment. Journal of Marine Science and Engineering, 9(9), 956. https://doi.org/10.3390/jmse9090956





