A Numerical Study of Sheet Flow Driven by Skewed-Asymmetric Shoaling Waves Using SedWaveFoam
Abstract
:1. Introduction
2. Governing Equations
3. Setup
3.1. Experimental Setup
3.2. Model Setup
4. Model Validation
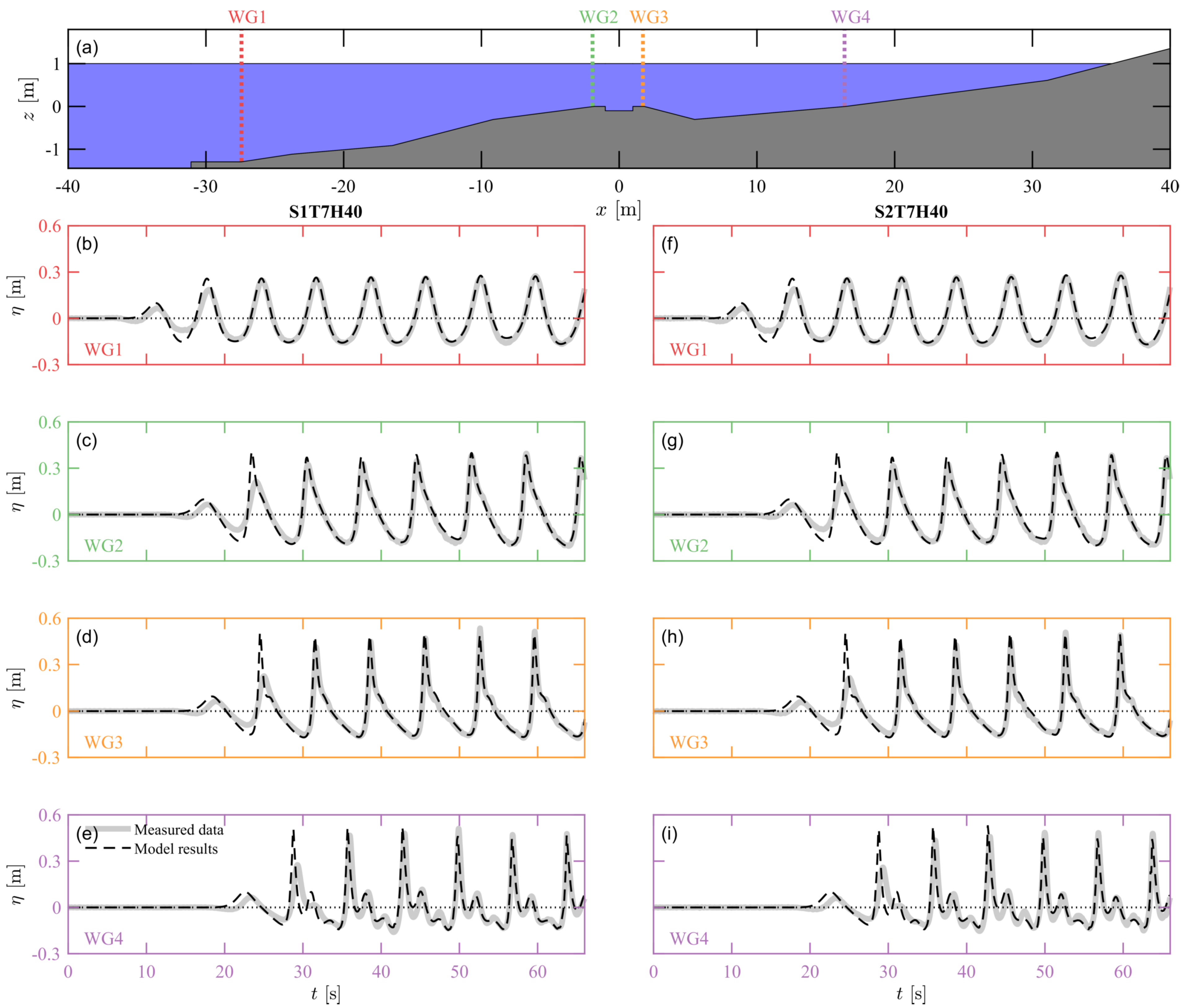
4.1. Wave Height
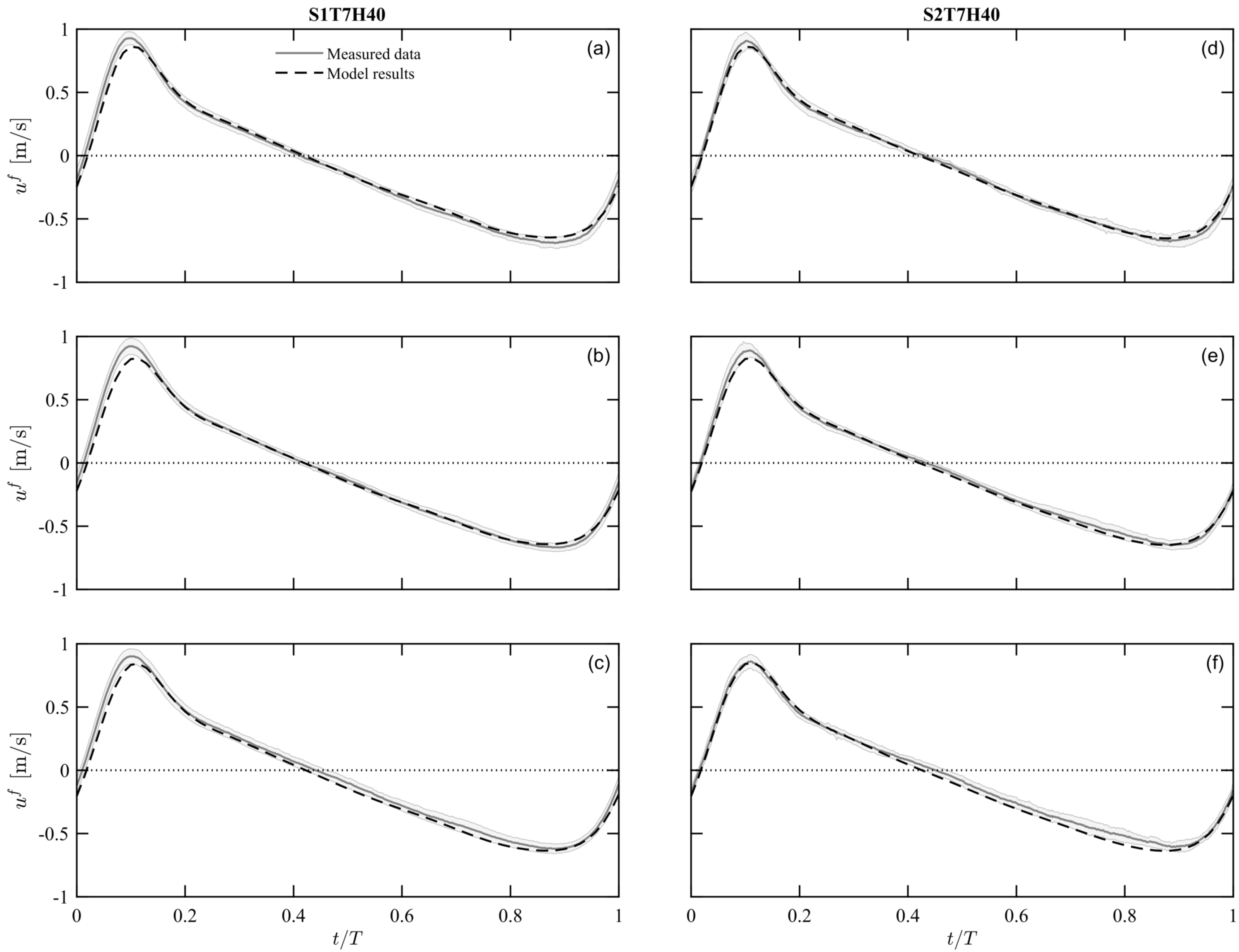
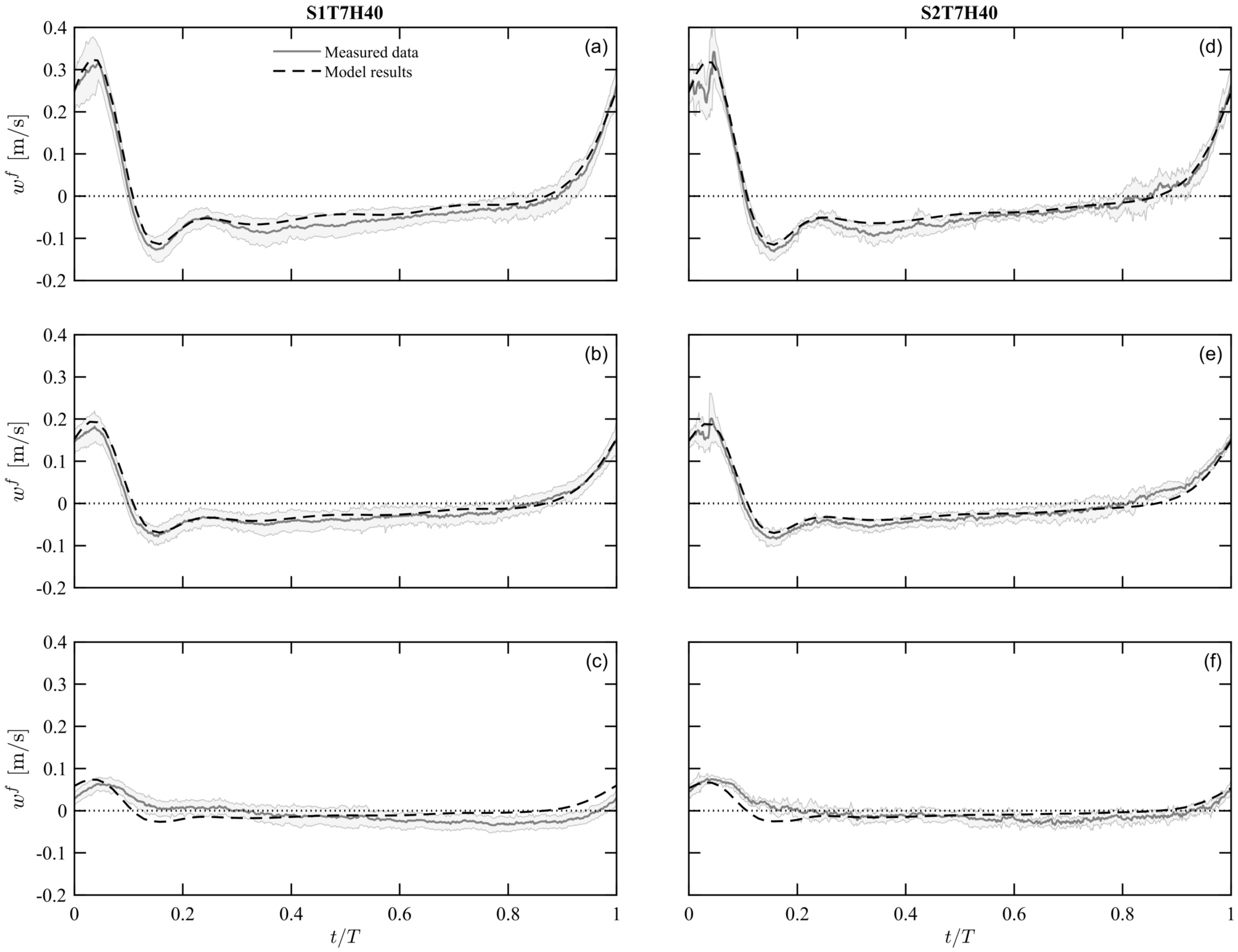
4.2. Fluid Velocity
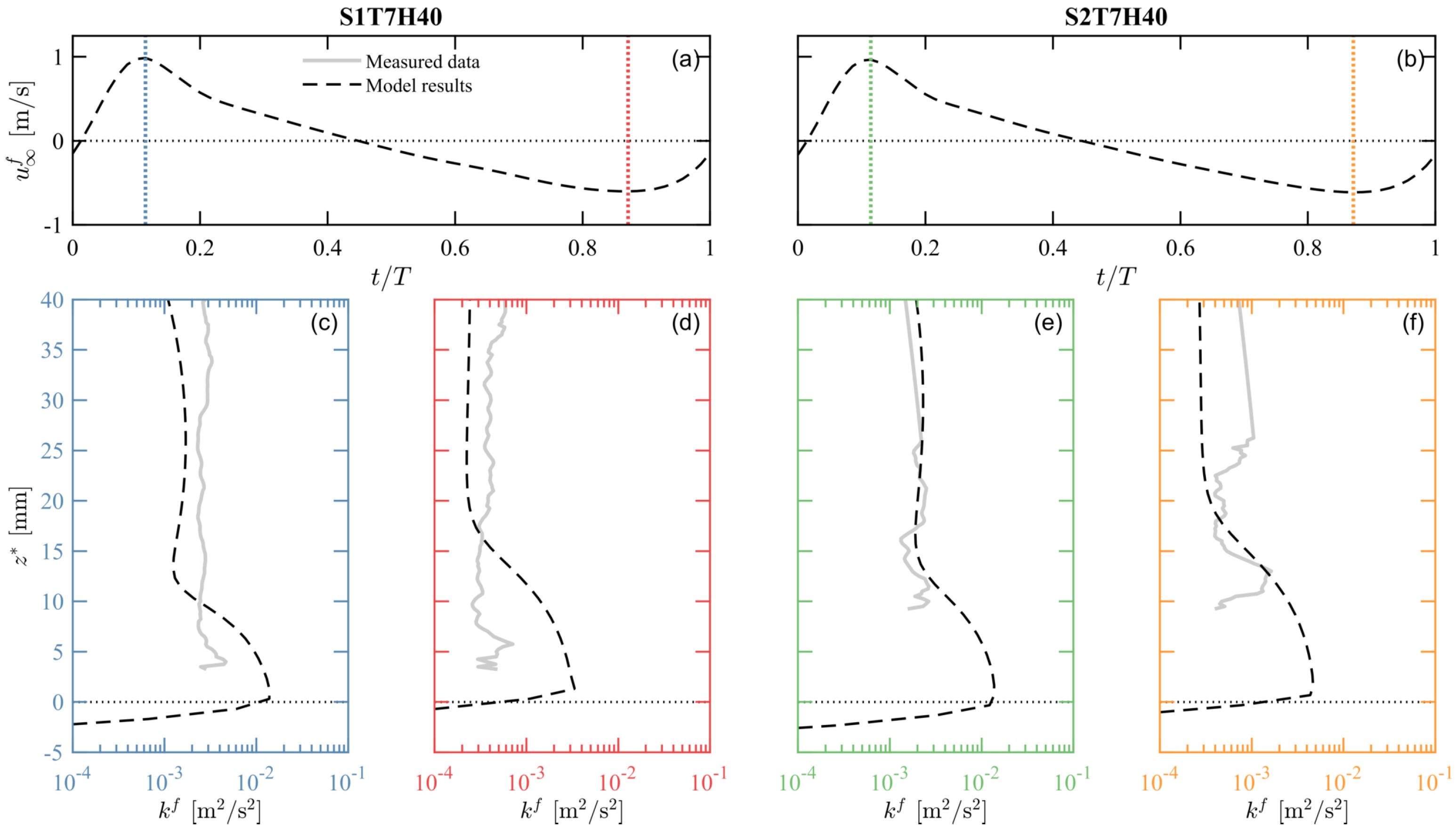
4.3. Turbulent Kinetic Energy
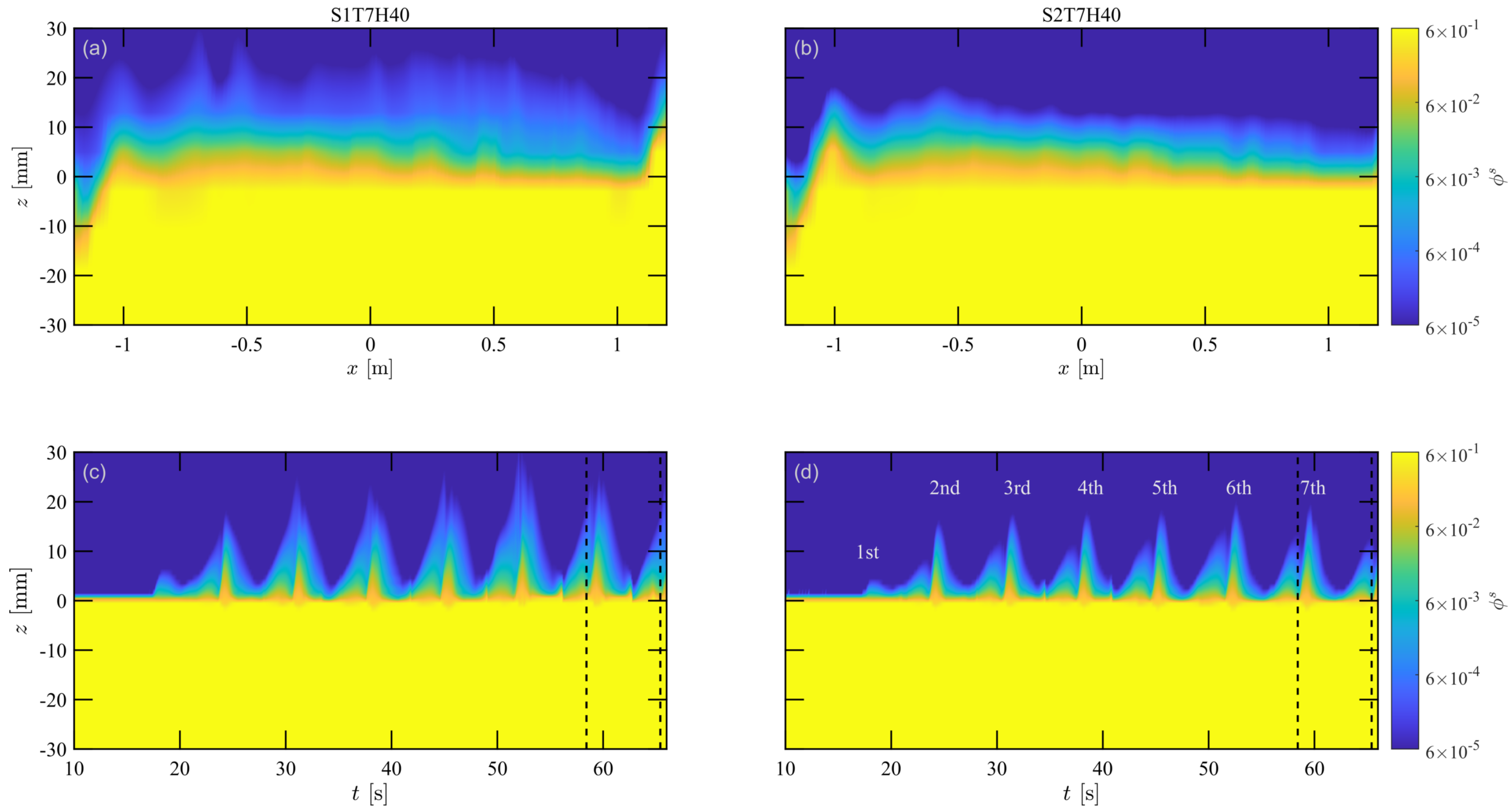
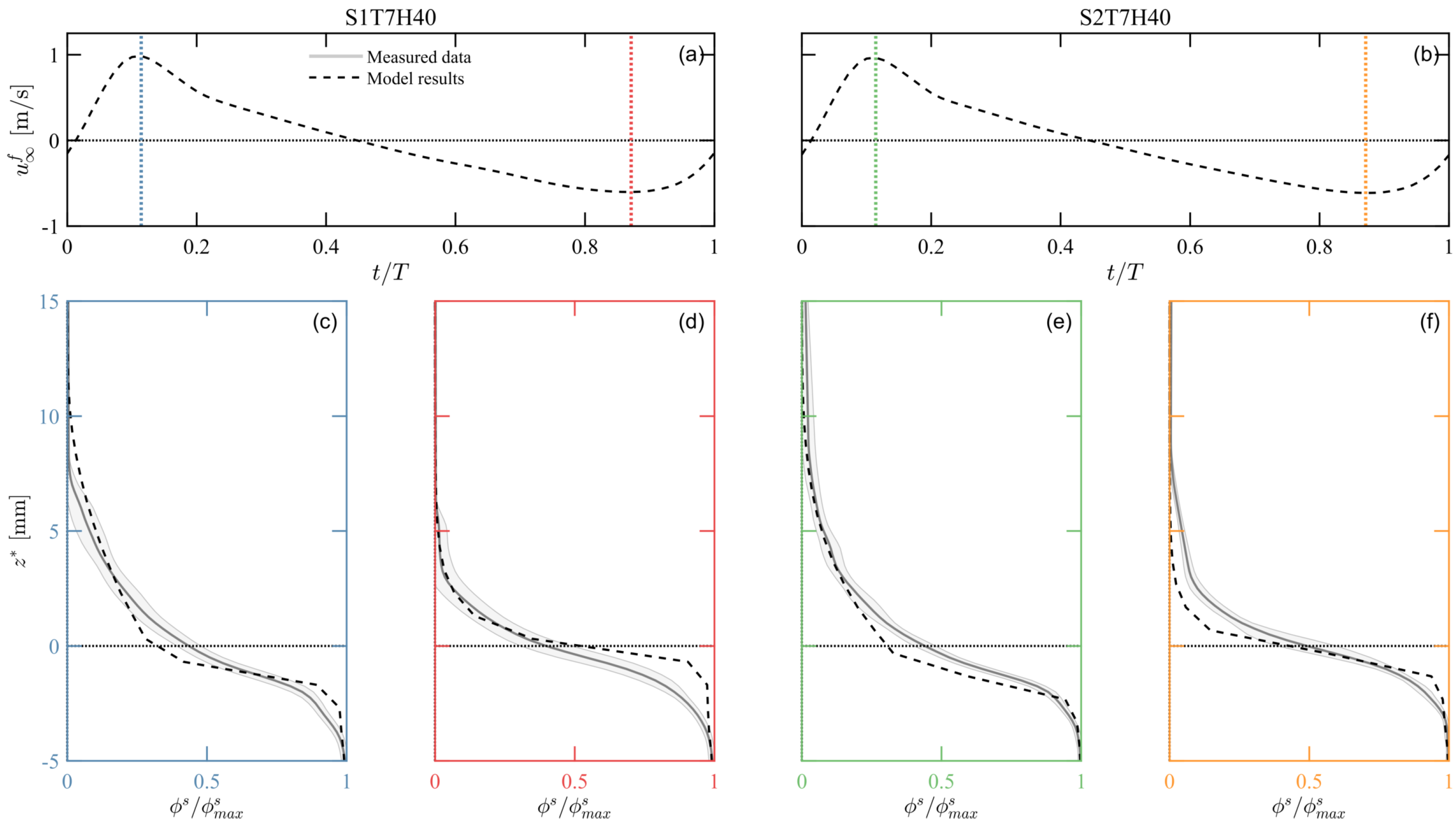
4.4. Volumetric Sediment Concentration
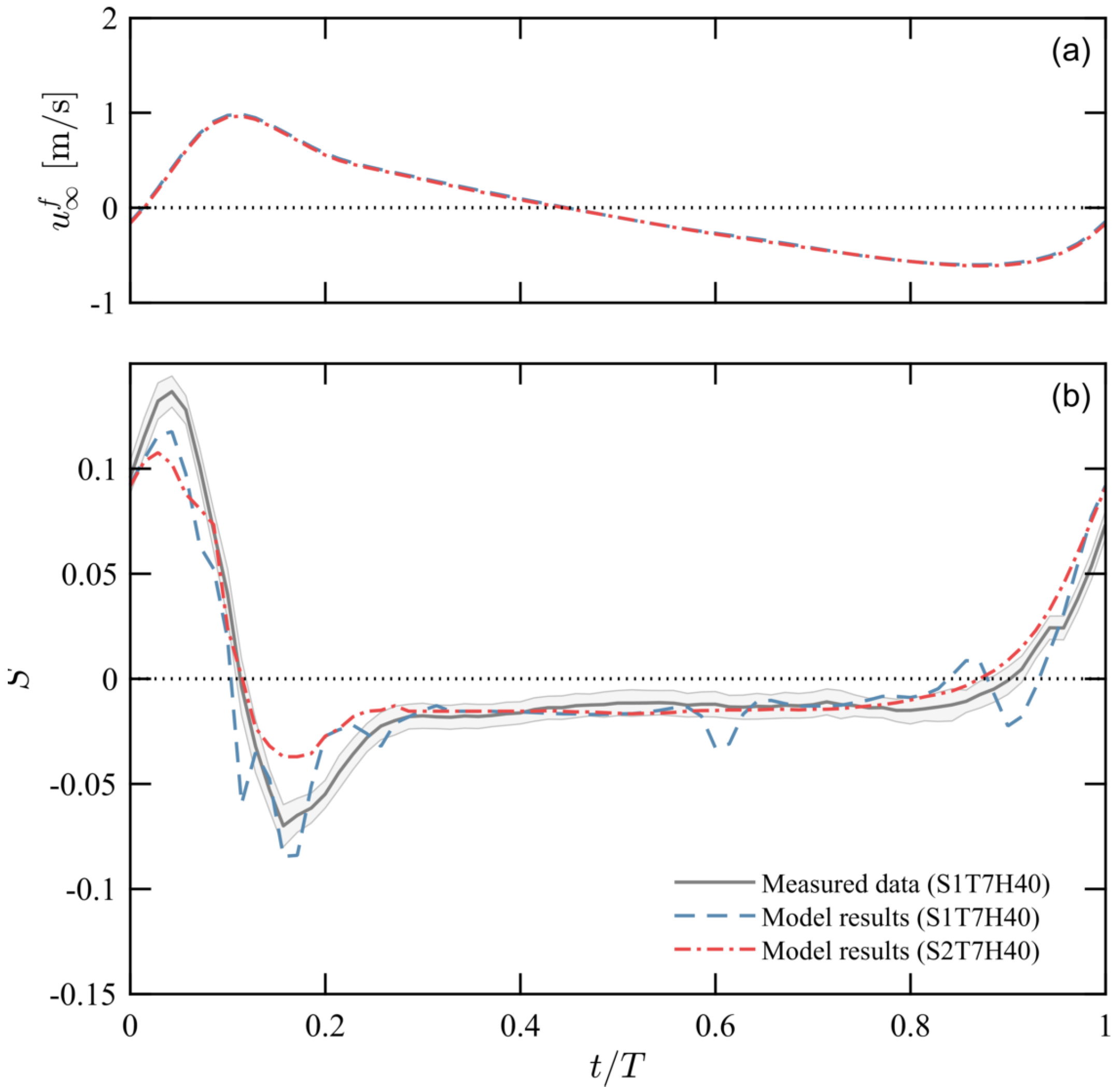
4.5. Horizontal Pressure Gradient
5. Parameterization
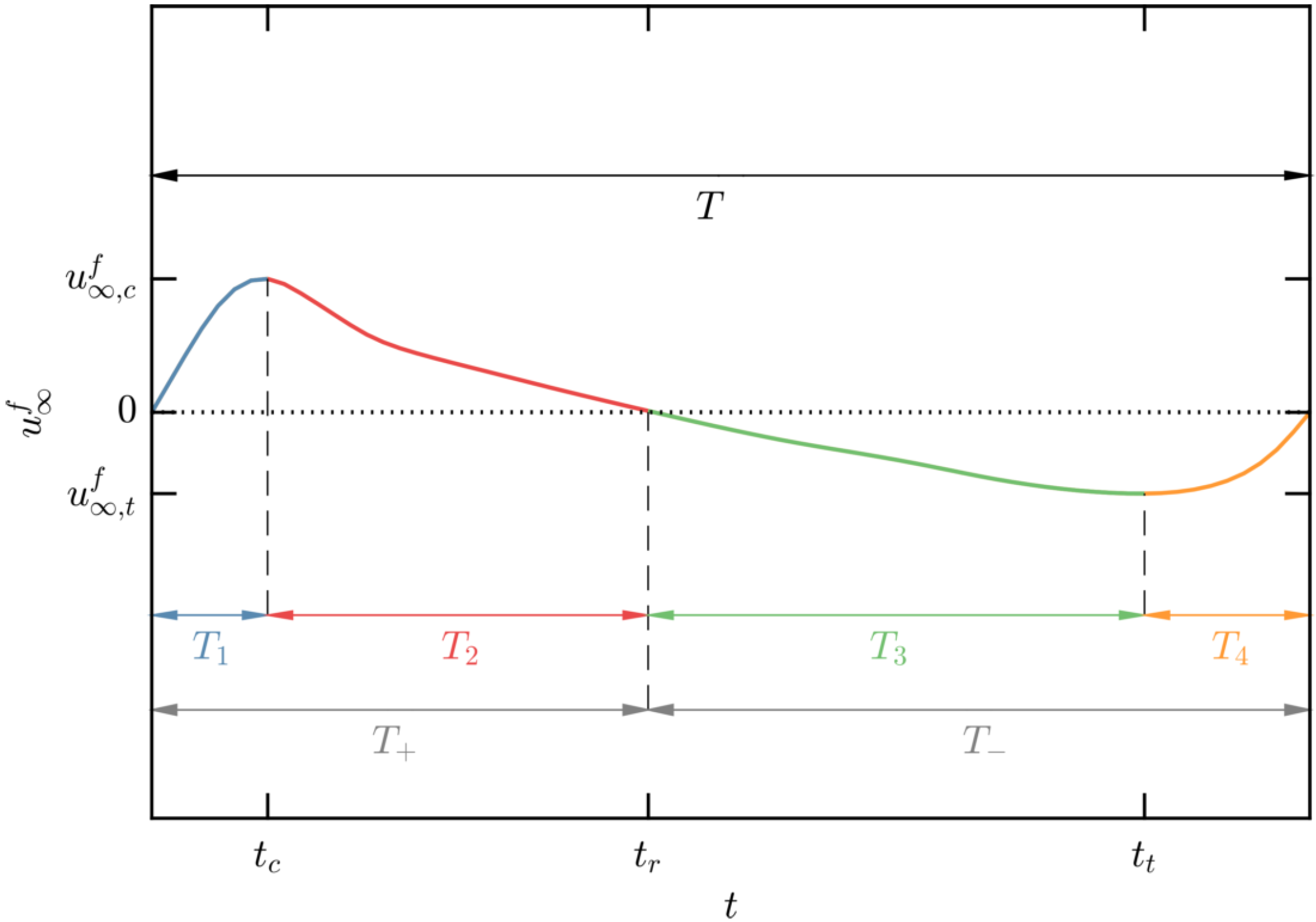
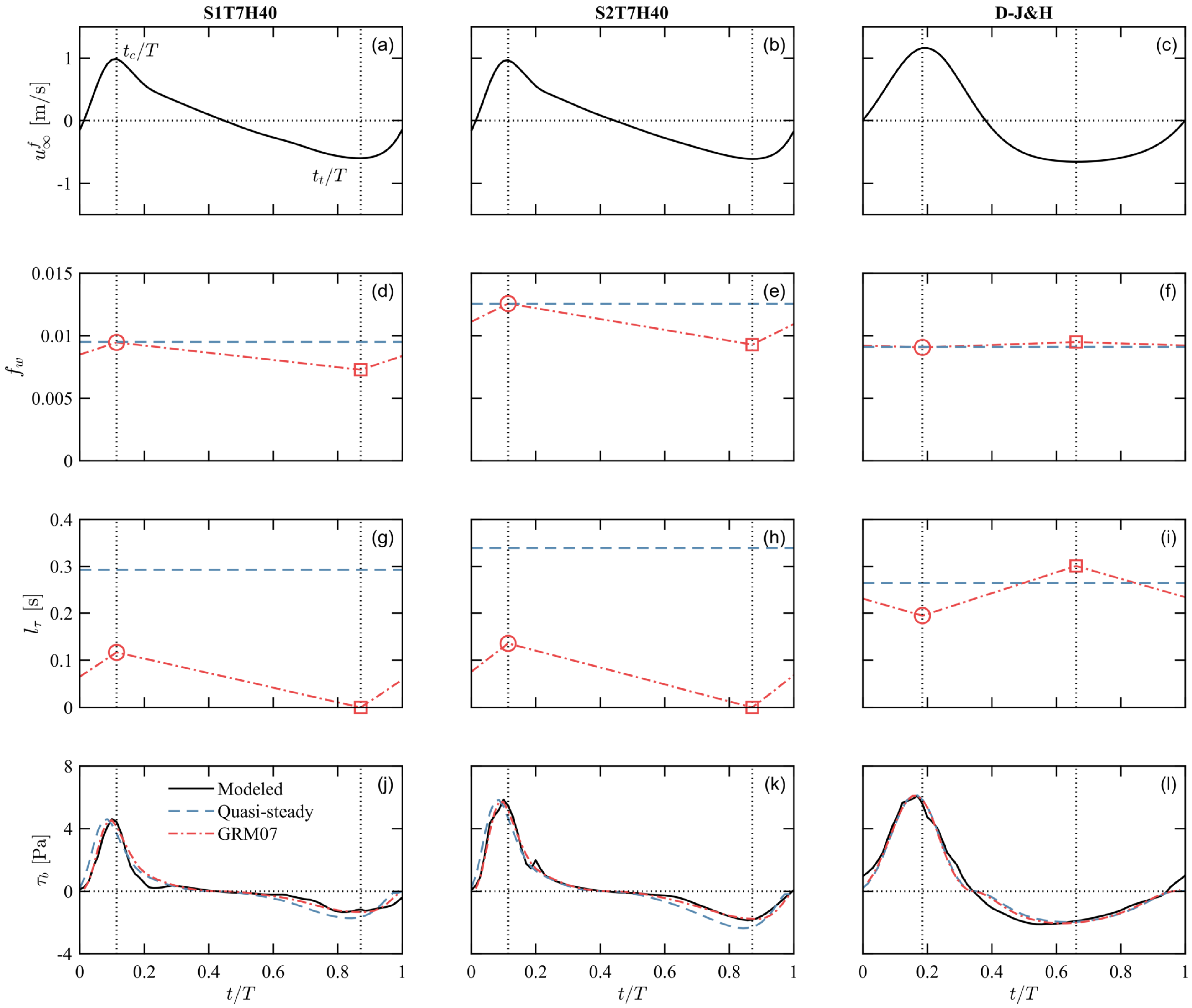
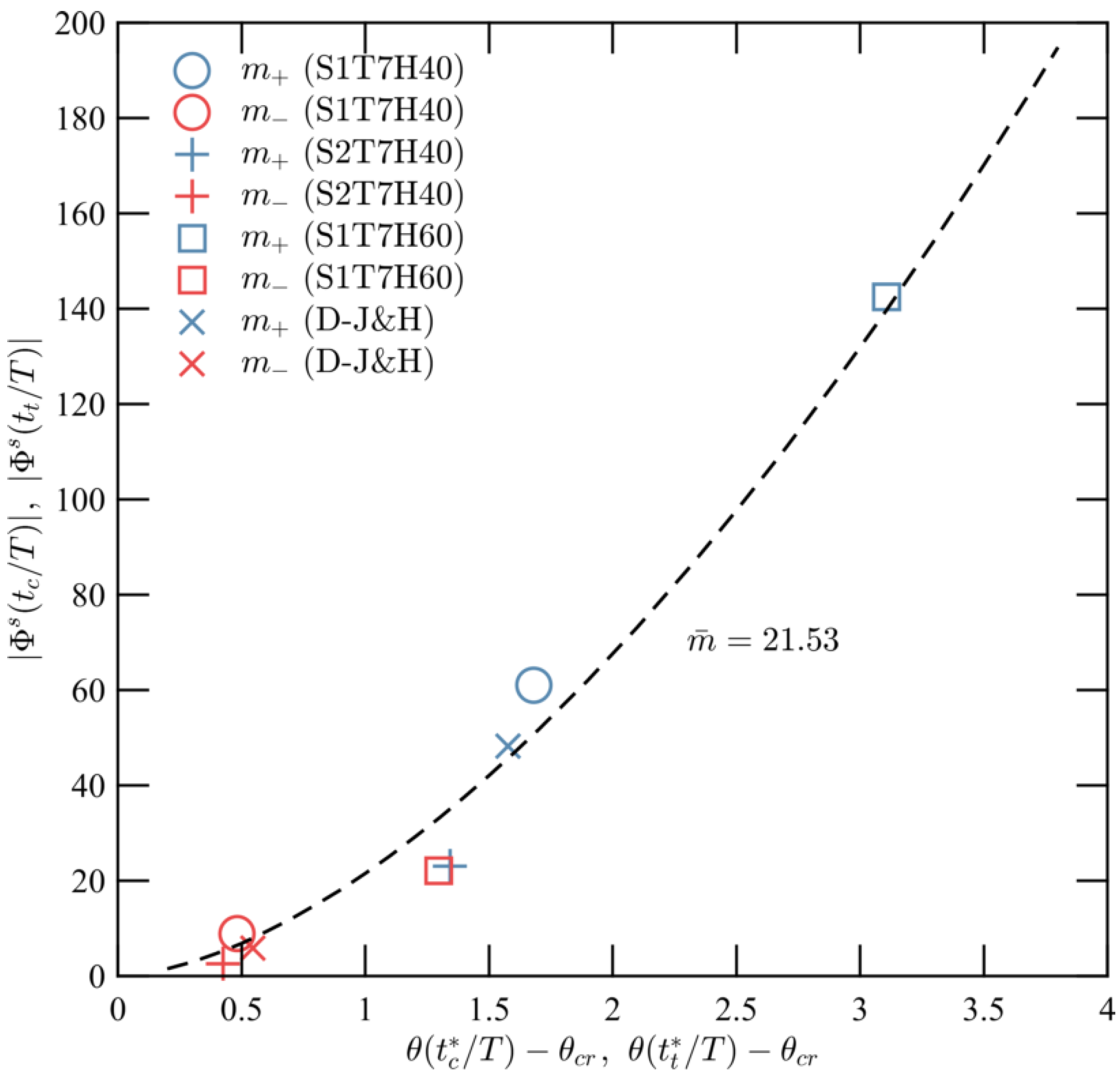
5.1. Bed Shear Stress
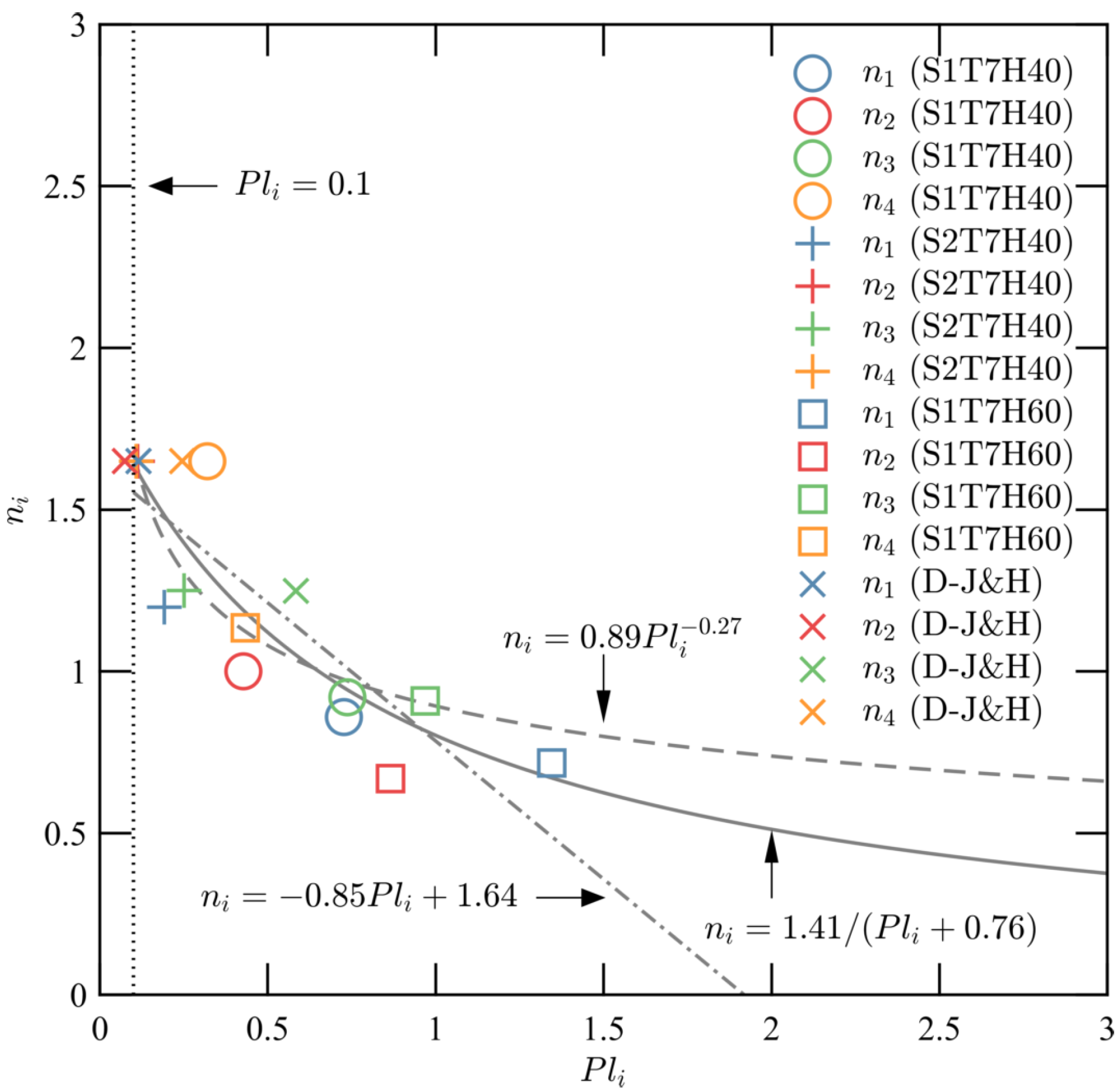
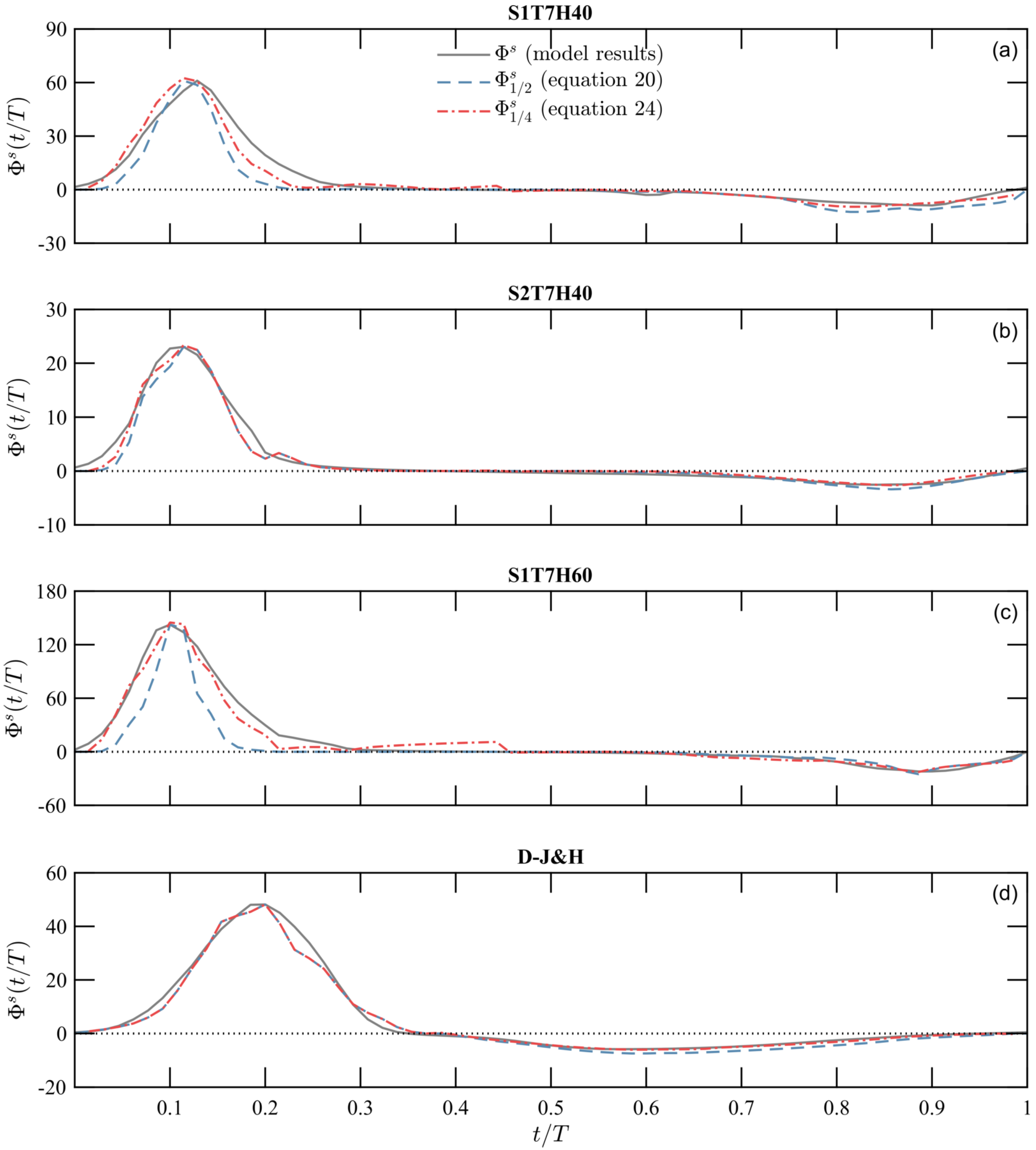
5.2. Sediment Transport
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dally, W.R.; Dean, R.G. Suspended Sediment Transport and Beach Profile Evolution. J. Waterw. Port Coast. Ocean Eng. 1984, 110, 15–33. [Google Scholar] [CrossRef]
- Carter, T.; Liu, P.; Mei, C. Mass Transport by Waves and Offshore Sand Bedforms. J. Waterw. Harb. Coast. Eng. Div. 1973, 99, 165–184. [Google Scholar] [CrossRef]
- Howd, P.A.; Bowen, A.J.; Holman, R.A. Edge waves in the presence of strong longshore currents. J. Geophys. Res. Ocean. 1992, 97, 11357–11371. [Google Scholar] [CrossRef] [Green Version]
- Gallagher, E.L.; Elgar, S.; Guza, R.T. Observations of sand bar evolution on a natural beach. J. Geophys. Res. Ocean. 1998, 103, 3203–3215. [Google Scholar] [CrossRef] [Green Version]
- van Maanen, B.; de Ruiter, P.; Coco, G.; Bryan, K.; Ruessink, B. Onshore sandbar migration at Tairua Beach (New Zealand): Numerical simulations and field measurements. Mar. Geol. 2008, 253, 99–106. [Google Scholar] [CrossRef]
- Thornton, E.B.; Humiston, R.T.; Birkemeier, W. Bar/trough generation on a natural beach. J. Geophys. Res. Ocean. 1996, 101, 12097–12110. [Google Scholar] [CrossRef]
- Bailard, J.A. An energetics total load sediment transport model for a plane sloping beach. J. Geophys. Res. Ocean. 1981, 86, 10938–10954. [Google Scholar] [CrossRef]
- Henderson, S.M.; Allen, J.S.; Newberger, P. Nearshore sandbar migration predicted by an eddy-diffusive boundary layer model. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Hsu, T.J.; Hanes, D.M. Effects of wave shape on sheet flow sediment transport. J. Geophys. Res. Ocean. 2004, 109, C05025. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A.; van Dongeren, A.; van Thiel de Vries, J.; McCall, R.; Lescinski, J. Modelling storm impacts on beaches, dunes and barrier islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- Kalligeris, N.; Smit, P.; Ludka, B.; Guza, R.; Gallien, T. Calibration and assessment of process-based numerical models for beach profile evolution in southern California. Coast. Eng. 2020, 158, 103650. [Google Scholar] [CrossRef] [Green Version]
- Rafati, Y.; Hsu, T.J.; Elgar, S.; Raubenheimer, B.; Quataert, E.; van Dongeren, A. Modeling the hydrodynamics and morphodynamics of sandbar migration events. Coast. Eng. 2021, 103885. [Google Scholar] [CrossRef]
- Ruessink, B.; Kuriyama, Y.; Reniers, A.; Roelvink, J.; Walstra, D. Modeling cross-shore sandbar behavior on the timescale of weeks. J. Geophys. Res. Earth Surf. 2007, 112, F03010. [Google Scholar] [CrossRef] [Green Version]
- Austin, M.; Masselink, G.; O’Hare, T.; Russell, P. Onshore sediment transport on a sandy beach under varied wave conditions: Flow velocity skewness, wave asymmetry or bed ventilation? Mar. Geol. 2009, 259, 86–101. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. Mass transport in water waves. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1953, 245, 535–581. [Google Scholar] [CrossRef]
- Trowbridge, J.; Young, D. Sand transport by unbroken water waves under sheet flow conditions. J. Geophys. Res. Ocean. 1989, 94, 10971–10991. [Google Scholar] [CrossRef]
- Nielsen, P. Sheet flow sediment transport under waves with acceleration skewness and boundary layer streaming. Coast. Eng. 2006, 53, 749–758. [Google Scholar] [CrossRef]
- Yu, X.; Hsu, T.J.; Hanes, D.M. Sediment transport under wave groups: Relative importance between nonlinear waveshape and nonlinear boundary layer streaming. J. Geophys. Res. Ocean. 2010, 115, C02013. [Google Scholar] [CrossRef]
- Flores, N.Z.; Sleath, J.F. Mobile layer in oscillatory sheet flow. J. Geophys. Res. Ocean. 1998, 103, 12783–12793. [Google Scholar] [CrossRef]
- Drake, T.G.; Calantoni, J. Discrete particle model for sheet flow sediment transport in the nearshore. J. Geophys. Res. Ocean. 2001, 106, 19859–19868. [Google Scholar] [CrossRef]
- Foster, D.; Bowen, A.; Holman, R.A.; Natoo, P. Field evidence of pressure gradient induced incipient motion. J. Geophys. Res. Ocean. 2006, 111, C05004. [Google Scholar] [CrossRef]
- Frank, D.; Foster, D.; Sou, I.M.; Calantoni, J. Incipient motion of surf zone sediments. J. Geophys. Res. Ocean. 2015, 120, 5710–5734. [Google Scholar] [CrossRef]
- Anderson, D.; Cox, D.; Mieras, R.; Puleo, J.A.; Hsu, T.J. Observations of wave-induced pore pressure gradients and bed level response on a surf zone sandbar. J. Geophys. Res. Ocean. 2017, 122, 5169–5193. [Google Scholar] [CrossRef]
- Cheng, Z.; Hsu, T.J.; Calantoni, J. SedFoam: A multi-dimensional Eulerian two-phase model for sediment transport and its application to momentary bed failure. Coast. Eng. 2017, 119, 32–50. [Google Scholar] [CrossRef] [Green Version]
- Yuan, J.; Li, Z.; Madsen, O.S. Bottom-slope-induced net sheet-flow sediment transport rate under sinusoidal oscillatory flows. J. Geophys. Res. Ocean. 2017, 122, 236–263. [Google Scholar] [CrossRef]
- Yuan, J.; Tan, W. Modeling net sheet-flow sediment transport rate under skewed and asymmetric oscillatory flows over a sloping bed. Coast. Eng. 2018, 136, 65–80. [Google Scholar] [CrossRef]
- Tan, W.; Yuan, J. Experimental study of sheet-flow sediment transport under nonlinear oscillatory flow over a sloping bed. Coast. Eng. 2019, 147, 1–11. [Google Scholar] [CrossRef]
- Madsen, O.S.; Grant, W.D. Quantitative description of sediment transport by waves. In Proceedings of the 15th International Conference on Coastal Engineering, Honolulu, HI, USA, 11–17 July 1976; pp. 1093–1112. [Google Scholar] [CrossRef]
- Ribberink, J.S. Bed-load transport for steady flows and unsteady oscillatory flows. Coast. Eng. 1998, 34, 59–82. [Google Scholar] [CrossRef]
- Ribberink, J.S.; Al-Salem, A.A. Sheet flow and suspension of sand in oscillatory boundary layers. Coast. Eng. 1995, 25, 205–225. [Google Scholar] [CrossRef]
- O’Donoghue, T.; Wright, S. Flow tunnel measurements of velocities and sand flux in oscillatory sheet flow for well-sorted and graded sands. Coast. Eng. 2004, 51, 1163–1184. [Google Scholar] [CrossRef]
- Horikawa, K.; Watanabe, A.; Katori, S. Sediment transport under sheet flow condition. Coast. Eng. 1982, 1982, 1335–1352. [Google Scholar]
- Gonzalez-Rodriguez, D.; Madsen, O.S. Seabed shear stress and bedload transport due to asymmetric and skewed waves. Coast. Eng. 2007, 54, 914–929. [Google Scholar] [CrossRef]
- Watanabe, A.; Sato, S. A Sheet-flow transport rate formula for asymmetric, forward-leaning waves and currents. Coast. Eng. 2004, 2004, 1703–1714. [Google Scholar] [CrossRef]
- Hassan, W.; Ribberink, J. Modelling of sand transport under wave-generated sheet flows with a RANS diffusion model. Coast. Eng. 2010, 57, 19–29. [Google Scholar] [CrossRef]
- Dohmen-Janssen, C.M.; Kroekenstoel, D.F.; Hassan, W.N.; Ribberink, J.S. Phase lags in oscillatory sheet flow: Experiments and bed load modelling. Coast. Eng. 2002, 46, 61–87. [Google Scholar] [CrossRef]
- O’Donoghue, T.; Wright, S. Concentrations in oscillatory sheet flow for well sorted and graded sands. Coast. Eng. 2004, 50, 117–138. [Google Scholar] [CrossRef]
- van der A, D.A.; Ribberink, J.S.; van der Werf, J.J.; O’Donoghue, T.; Buijsrogge, R.H.; Kranenburg, W.M. Practical sand transport formula for non-breaking waves and currents. Coast. Eng. 2013, 76, 26–42. [Google Scholar] [CrossRef] [Green Version]
- Dibajnia, M.; Watanabe, A. Sheet flow under nonlinear waves and currents. Coast. Eng. Proc. 1992, 1, 2015–2028. [Google Scholar] [CrossRef]
- Camenen, B.; Larson, M. A Total Load Formula for the Nearshore. In Proceedings of the Coastal Sediments ’07, New Orleans, LA, USA, 13–17 May 2007; pp. 56–67. [Google Scholar] [CrossRef]
- Mieras, R.S.; Puleo, J.A.; Anderson, D.; Cox, D.T.; Hsu, T.J. Large-scale experimental observations of sheet flow on a sandbar under skewed-asymmetric waves. J. Geophys. Res. Ocean. 2017, 122, 5022–5045. [Google Scholar] [CrossRef]
- Mieras, R.S.; Puleo, J.A.; Anderson, D.; Hsu, T.J.; Cox, D.T.; Calantoni, J. Relative Contributions of Bed Load and Suspended Load to Sediment Transport Under Skewed-Asymmetric Waves on a Sandbar Crest. J. Geophys. Res. Ocean. 2019, 124, 1294–1321. [Google Scholar] [CrossRef]
- Kim, Y.; Cheng, Z.; Hsu, T.J.; Chauchat, J. A numerical study of sheet flow under monochromatic nonbreaking waves using a free surface resolving Eulerian two-phase flow model. J. Geophys. Res. Ocean. 2018, 123, 4693–4719. [Google Scholar] [CrossRef]
- Berberović, E.; van Hinsberg, N.P.; Jakirlić, S.; Roisman, I.V.; Tropea, C. Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution. Phys. Rev. 2009, E79, 036306. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsøe, J. A wave generation toolbox for the open-source CFD library: OpenFoam®. Int. J. Numer. Meth. Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Kim, Y.; Mieras, R.S.; Cheng, Z.; Anderson, D.; Hsu, T.J.; Puleo, J.A.; Cox, D. A numerical study of sheet flow driven by velocity and acceleration skewed near-breaking waves on a sandbar using SedWaveFoam. Coast. Eng. 2019, 152, 103526. [Google Scholar] [CrossRef]
- Chauchat, J.; Cheng, Z.; Nagel, T.; Bonamy, C.; Hsu, T.J. SedFoam-2.0: A 3-D two-phase flow numerical model for sediment transport. Geosci. Model Dev. 2017, 10, 4367–4392. [Google Scholar] [CrossRef] [Green Version]
- Klostermann, J.; Schaake, K.; Schwarze, R. Numerical simulation of a single rising bubble by VOF with surface compression. Int. J. Numer. Meth. Fluids 2012, 71, 960–982. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Drew, D.A. Mathematical Modeling of Two-Phase Flow. Annu. Rev. Fluid Mech. 1983, 15, 261–291. [Google Scholar] [CrossRef]
- Jenkins, J.T.; Savage, S.B. A theory for the rapid flow of identical, smooth, nearly elastic, spherical particles. J. Fluid Mech. 1983, 130, 187–202. [Google Scholar] [CrossRef]
- Ding, J.; Gidaspow, D. A bubbling fluidization model using kinetic theory of granular flow. AIChE J. 1990, 36, 523–538. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Johnson, P.C.; Jackson, R. Frictional-collisional constitutive relations for granular materials, with application to plane shearing. J. Fluid Mech. 1987, 176, 67–93. [Google Scholar] [CrossRef]
- Mieras, R.S.; Puleo, J.; Cox, D.; Hsu, T.J. Sandbar Sediment Transport; DesignSafe-CI 2018. Available online: https://www.designsafe-ci.org/data/browser/public/designsafe.storage.published/PRJ-1740 (accessed on 9 August 2021). [CrossRef]
- Garcez Faria, A.; Thornton, E.; Stanton, T. Small-Scale morphology related to wave and current parameters over a barred beach. Coast. Eng. Proc. 1996, 1, 3391–3404. [Google Scholar] [CrossRef]
- Scott, C.P.; Cox, D.T.; Maddux, T.B.; Long, J.W. Large-scale laboratory observations of turbulence on a fixed barred beach. Meas. Sci. Technol. 2005, 16, 1903. [Google Scholar] [CrossRef]
- Lanckriet, T.; Puleo, J.A.; Waite, N. A conductivity concentration profiler for sheet flow sediment Transport. IEEE J. Ocean. Eng. 2013, 38, 55–70. [Google Scholar] [CrossRef]
- Beach, R.A.; Sternberg, R.W.; Johnson, R. A fiber optic sensor for monitoring suspended sediment. Mar. Geol. 1992, 103, 513–520. [Google Scholar] [CrossRef]
- Thomas, R.E.; Schindfessel, L.; McLelland, S.J.; Creëlle, S.; Mulder, T.D. Bias in mean velocities and noise in variances and covariances measured using a multistatic acoustic profiler: The Nortek Vectrino Profiler. Meas. Sci. Technol. 2017, 28, 075302. [Google Scholar] [CrossRef]
- Lanckriet, T.; Puleo, J.A.; Masselink, G.; Turner, I.L.; Conley, D.; Blenkinsopp, C.; Russell, P. Comprehensive Field Study of Swash-Zone Processes. II: Sheet Flow Sediment Concentrations during Quasi-Steady Backwash. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 29–42. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, T.; Shin, S.; Cox, D.T.; Mori, N. Spatiotemporal Characteristics of Near-Bed Pressure Gradients on a Barred Beach. J. Waterw. Port Coast. Ocean Eng. 2010, 136, 327–336. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Frankel, S. Numerical Methods for Engineers and Scientists; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Sleath, J. Conditions for plug formation in oscillatory flow. Cont. Shelf Res. 1999, 19, 1643–1664. [Google Scholar] [CrossRef]
- Shields, A. Anwendung der Aehnlichkeitsmechanik und der Turbulenzforschung auf die Geschiebebewegung. Ph.D. Thesis, Technical University Berlin, Berlin, Germany, 1936. [Google Scholar]
- Nielsen, P.; Callaghan, D.P. Shear stress and sediment transport calculations for sheet flow under waves. Coast. Eng. 2003, 47, 347–354. [Google Scholar] [CrossRef]
- Hsu, T.J.; Elgar, S.; Guza, R. Wave-induced sediment transport and onshore sandbar migration. Coast. Eng. 2006, 53, 817–824. [Google Scholar] [CrossRef] [Green Version]
- Madsen, O.S. Spectral wave-current bottom boundary layer flows. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994; pp. 384–398. [Google Scholar] [CrossRef]
- Krumbein, W.C. Size frequency distributions of sediments. J. Sediment. Res. 1934, 4, 65–77. [Google Scholar] [CrossRef]
- Ribberink, J.S.; van der Werf, J.J.; O’Donoghue, T.; Hassan, W.N. Sand motion induced by oscillatory flows: Sheet flow and vortex ripples. J. Turbul. 2008, 9, N20. [Google Scholar] [CrossRef]
- van Rijn, L. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas; Number pt. 1 in Principles of Sediment Transport in Rivers, Estuaries, and Coastal Seas, Aqua Publications; Aqua Publications: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Dohmen-Janssen, C.M.; Hanes, D.M. Sheet flow dynamics under monochromatic nonbreaking waves. J. Geophys. Res. Ocean. 2002, 107, 3149. [Google Scholar] [CrossRef]



| S1T7H40 | S2T7H40 | S1T7H60 | D-J&H | |
|---|---|---|---|---|
| [mm] | 0.17 | 0.27 | 0.17 | 0.24 |
| [m] | 2.448 | 2.448 | 2.448 | 4.25 |
| [m] | 1.001 | 1.001 | 1.001 | 3.5 |
| [m] | 0.40 | 0.40 | 0.60 | 1.6 |
| [m] | 0.59 | 0.59 | 0.94 | 1.55 |
| [m/s] | 0.99 | 0.97 | 1.30 | 1.16 |
| T [s] | 7.0 | 7.0 | 7.0 | 6.5 |
| 0.56 | 0.56 | 0.61 | 0.71 | |
| 1.03 | 1.04 | 1.34 | −0.10 |
| S1T7H40 | S2T7H40 | |
|---|---|---|
| 3.0% ( m) | 3.5% ( m) | |
| 4.2% ( m) | 4.9% ( m) | |
| 4.8% ( m) | 5.5% ( m) | |
| 8.7% ( m) | 9.8% ( m) | |
| 2.2% ( m) | 1.2% ( m) | |
| 2.6% ( m) | 1.7% ( m) | |
| 3.5% ( m) | 2.6% ( m) | |
| 3.5% ( m) | 3.8% ( m) | |
| 4.4% ( m) | 4.5% ( m) | |
| 22.8% ( m) | 15.3% ( m) | |
| 2.5% | 2.2% | |
| 5.9% () | 9.1% () | |
| 6.7% () | 7.5% () | |
| 5.1% () | 4.1% () | |
| 7.8% () | 4.3% () | |
| 10.5% | N/A |
| S1T7H40 | S2T7H40 | S1T7H60 | D-J&H | |
|---|---|---|---|---|
| T [s] | 7.0 | 7.0 | 7.0 | 6.5 |
| [s] | 0.7 | 0.7 | 0.5 | 1.2 |
| [s] | 2.3 | 2.3 | 2.5 | 1.3 |
| [s] | 3.0 | 3.0 | 3.1 | 1.8 |
| [s] | 1.0 | 1.0 | 0.9 | 2.2 |
| 6.6 | 10.2 | 11.0 | 4.4 | |
| 2.6 | 4.1 | 3.1 | 3.2 | |
| 0.010 | 0.013 | 0.010 | 0.009 | |
| 0.010 | 0.013 | 0.010 | 0.010 | |
| 0.007 | 0.009 | 0.007 | 0.009 | |
| [s] | 0.29 | 0.34 | 0.30 | 0.26 |
| [s] | 0.12 | 0.14 | 0.09 | 0.30 |
| [s] | 0 | 0 | 0 | 0.20 |
| [Pa] | 4.62 | 5.86 | 8.54 | 6.12 |
| 1.68 | 1.34 | 3.11 | 1.58 |
| S1T7H40 | S2T7H40 | S1T7H60 | D-J&H | |
|---|---|---|---|---|
| 27.71 | 15.61 | 24.06 | 23.79 | |
| 35.56 | 12.15 | 15.32 | 18.07 | |
| 0.86 () | 1.20 () | 0.72 () | 1.65 () | |
| 1.00 () | 1.65 () | 0.67 () | 1.65 () | |
| 0.92 () | 1.25 () | 0.91 () | 1.25 () | |
| 1.65 () | 1.65 () | 1.13 () | 1.65 () | |
| Modeled | 5.14 | 1.95 | 12.07 | 5.37 |
| Parameterized | 1.96 | 1.56 | 4.78 | 4.23 |
| Parameterized | 4.59 | 1.89 | 11.06 | 4.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Mieras, R.S.; Anderson, D.; Gallien, T. A Numerical Study of Sheet Flow Driven by Skewed-Asymmetric Shoaling Waves Using SedWaveFoam. J. Mar. Sci. Eng. 2021, 9, 936. https://doi.org/10.3390/jmse9090936
Kim Y, Mieras RS, Anderson D, Gallien T. A Numerical Study of Sheet Flow Driven by Skewed-Asymmetric Shoaling Waves Using SedWaveFoam. Journal of Marine Science and Engineering. 2021; 9(9):936. https://doi.org/10.3390/jmse9090936
Chicago/Turabian StyleKim, Yeulwoo, Ryan S. Mieras, Dylan Anderson, and Timu Gallien. 2021. "A Numerical Study of Sheet Flow Driven by Skewed-Asymmetric Shoaling Waves Using SedWaveFoam" Journal of Marine Science and Engineering 9, no. 9: 936. https://doi.org/10.3390/jmse9090936
APA StyleKim, Y., Mieras, R. S., Anderson, D., & Gallien, T. (2021). A Numerical Study of Sheet Flow Driven by Skewed-Asymmetric Shoaling Waves Using SedWaveFoam. Journal of Marine Science and Engineering, 9(9), 936. https://doi.org/10.3390/jmse9090936






