Hydrodynamic Behaviour of Floating Polygonal Platforms under Wave Action
Abstract
:1. Introduction
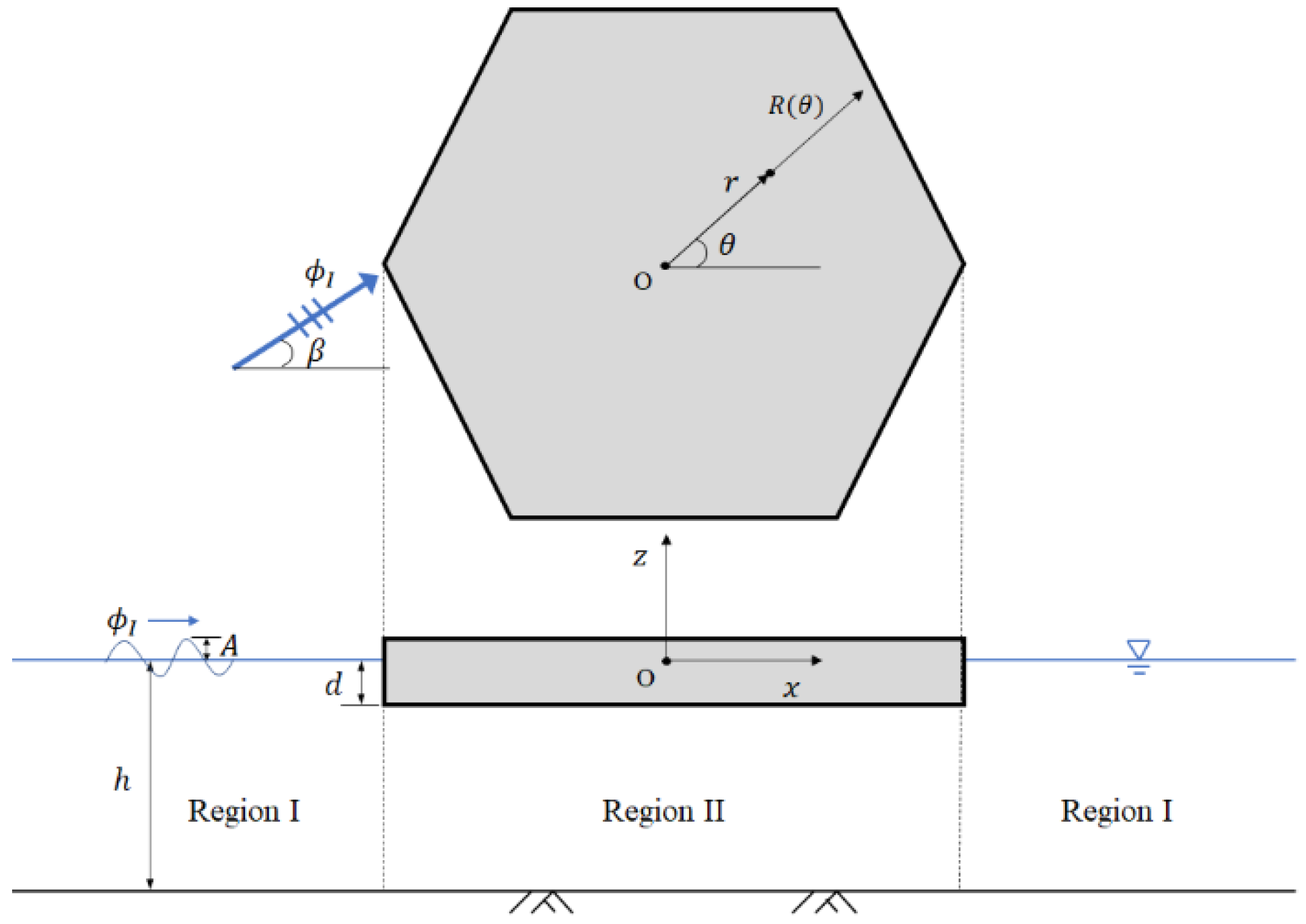
2. Problem Definition
3. Governing Equation and Boundary Conditions
4. Solutions for Diffracted and Radiated Potentials
4.1. Solution for Diffraction Problem
4.2. Solution for Radiation Problem
- the quadruple summation series are required as compared to semi-analytical approach 1, which only requires double summation series;
- the Fourier coefficients must be numerically calculated in advance;
- the convergence analysis is required to determine the truncation numbers of additional series ( and ).
5. Determination of Wave Exciting Force
6. Determination of Radiation Forces
7. Determination of Motion Responses of Floating Platform
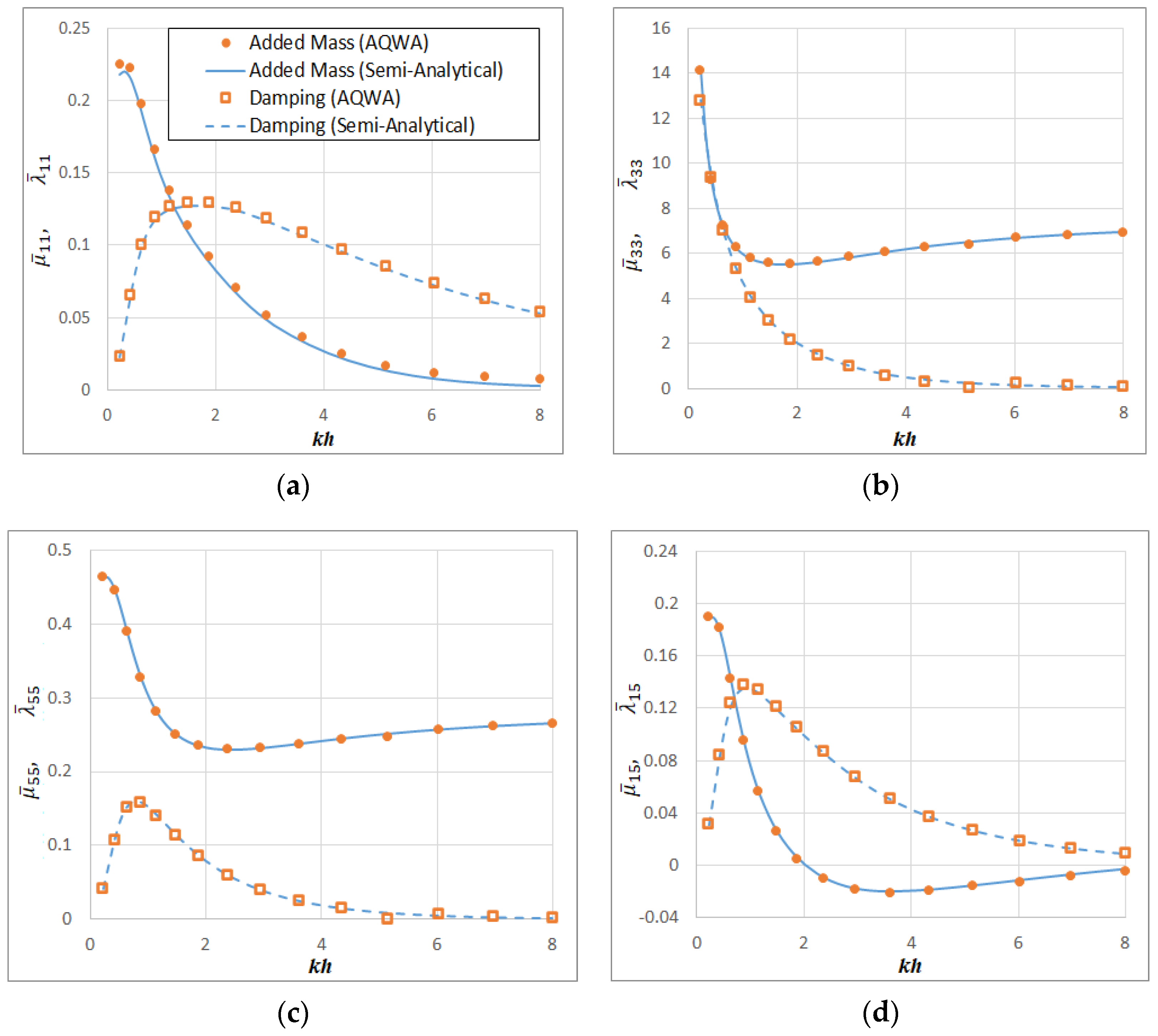
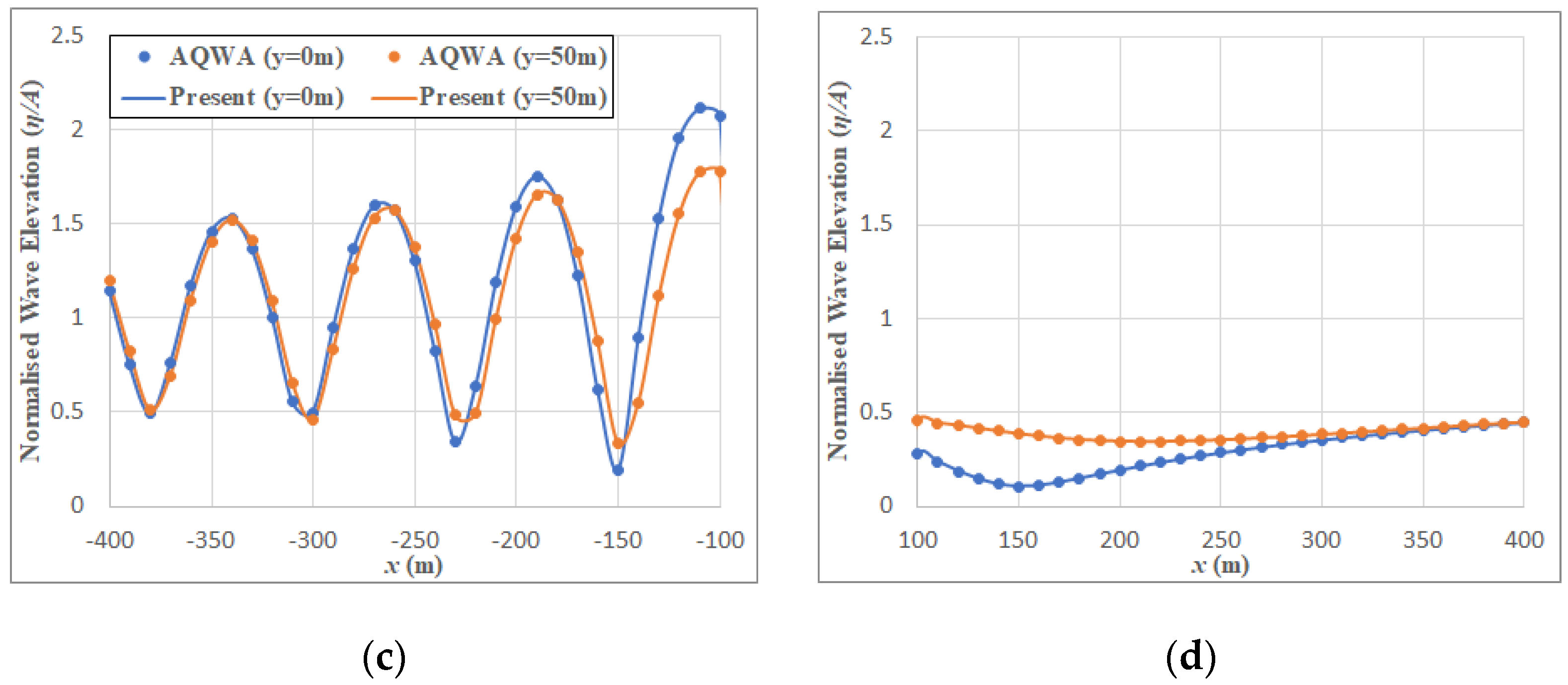
8. Verification of Semi-Analytical Approach and Computer Code
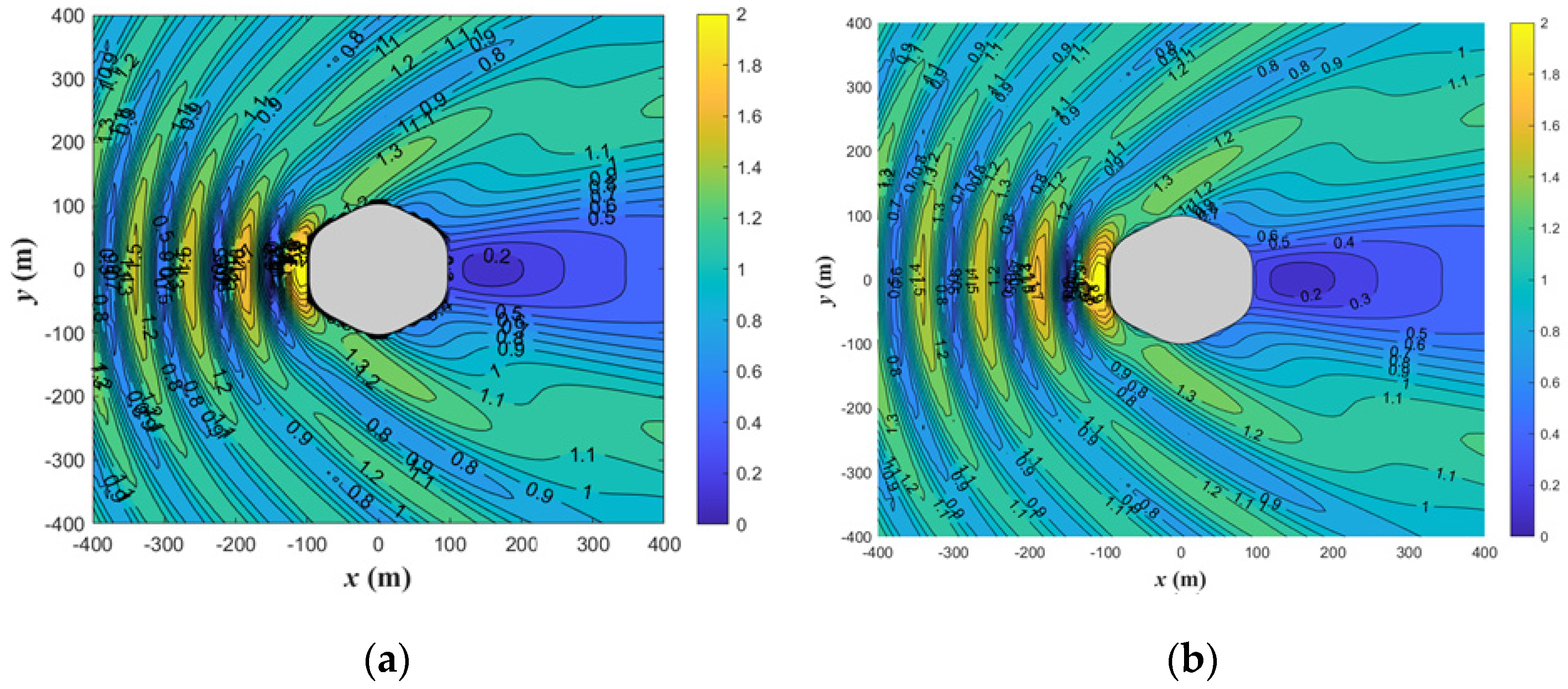
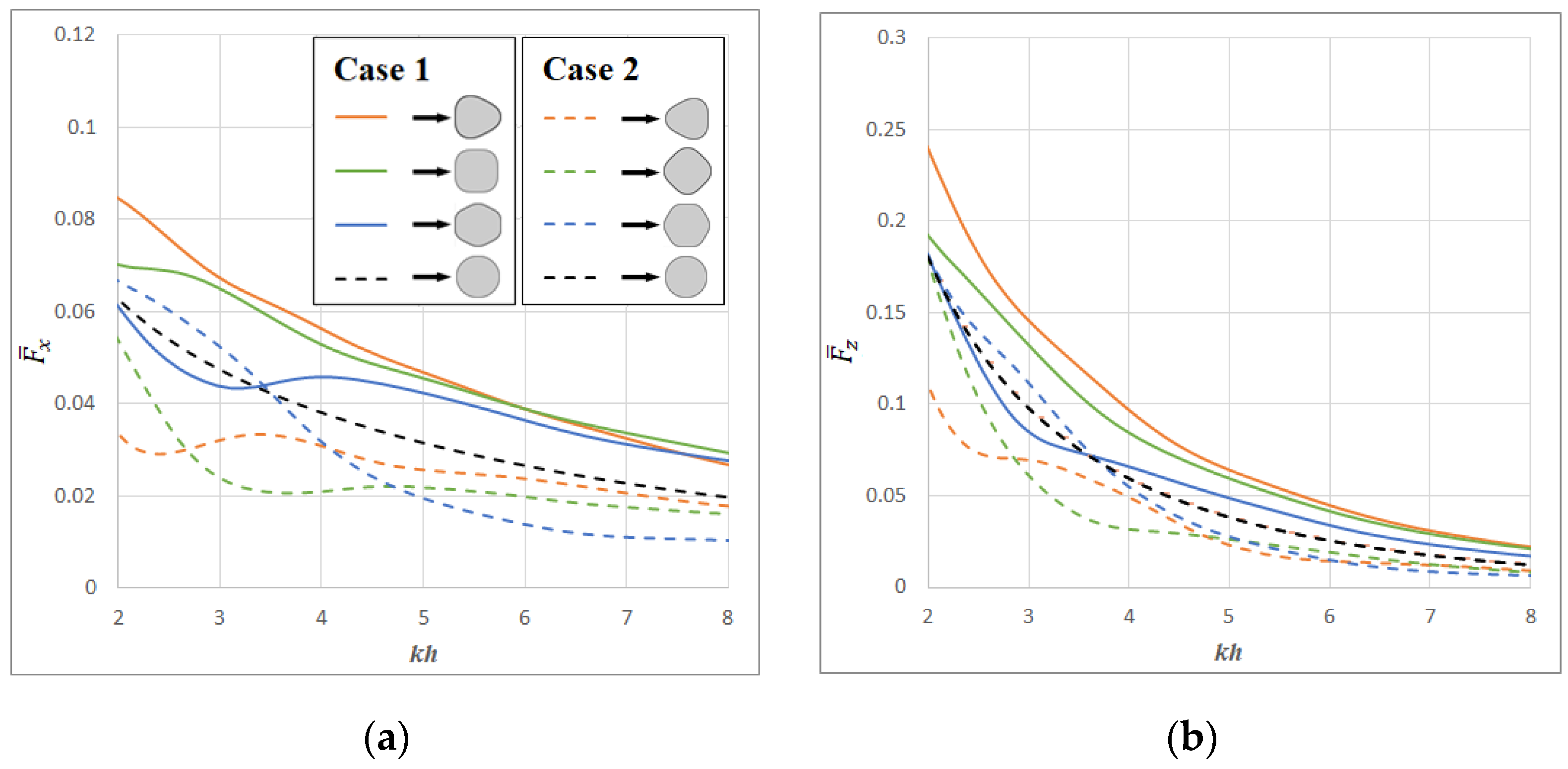
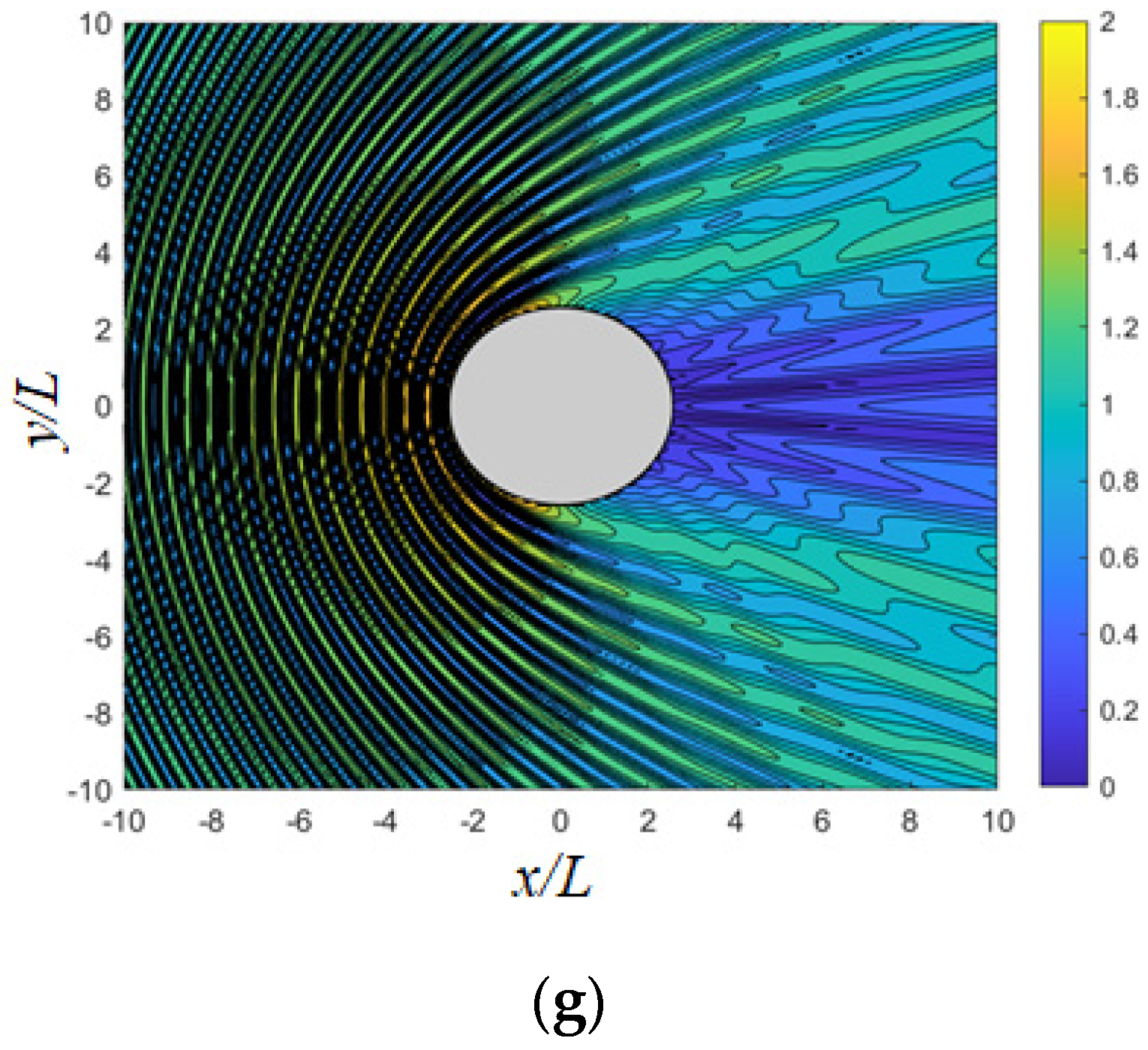
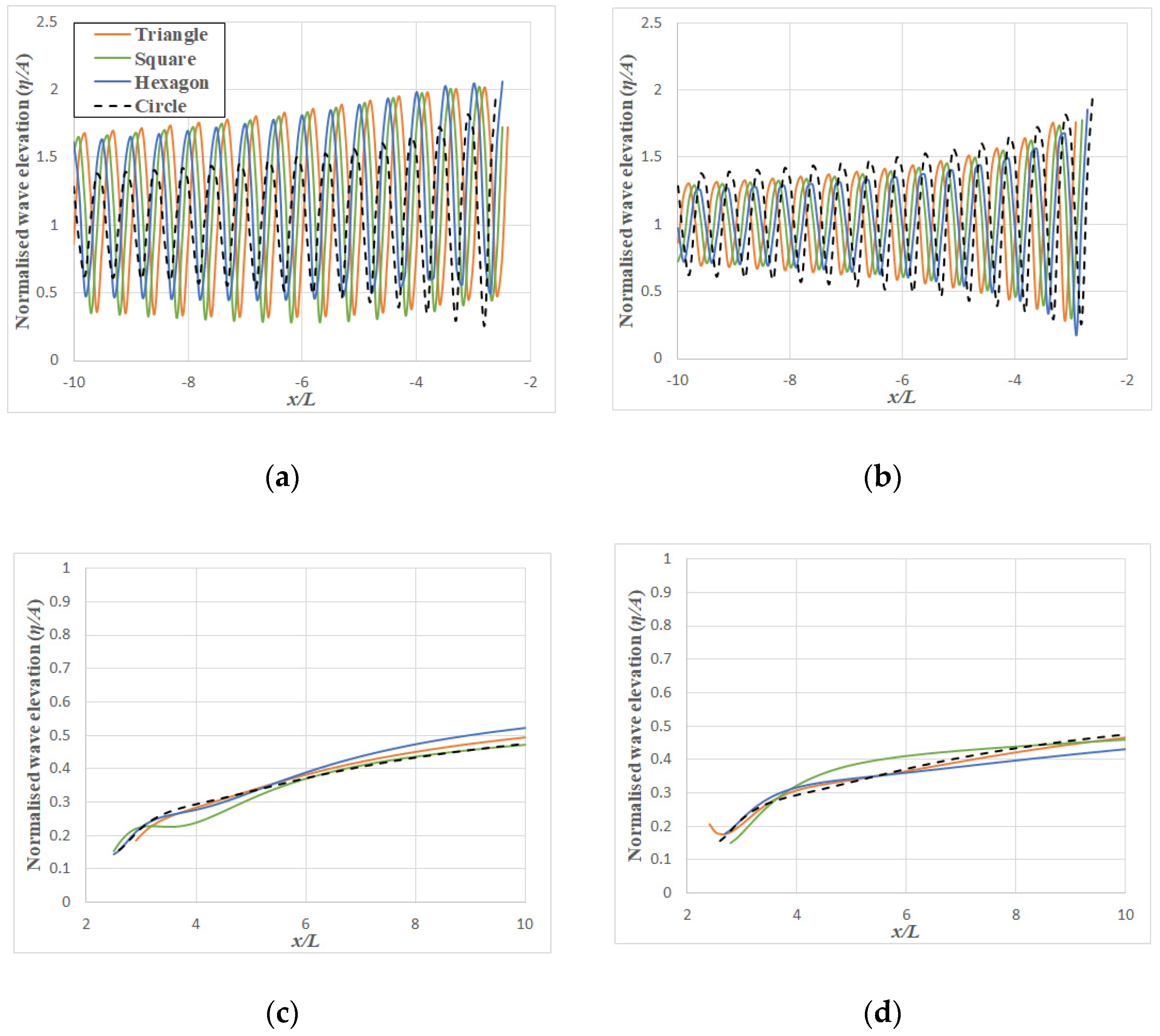
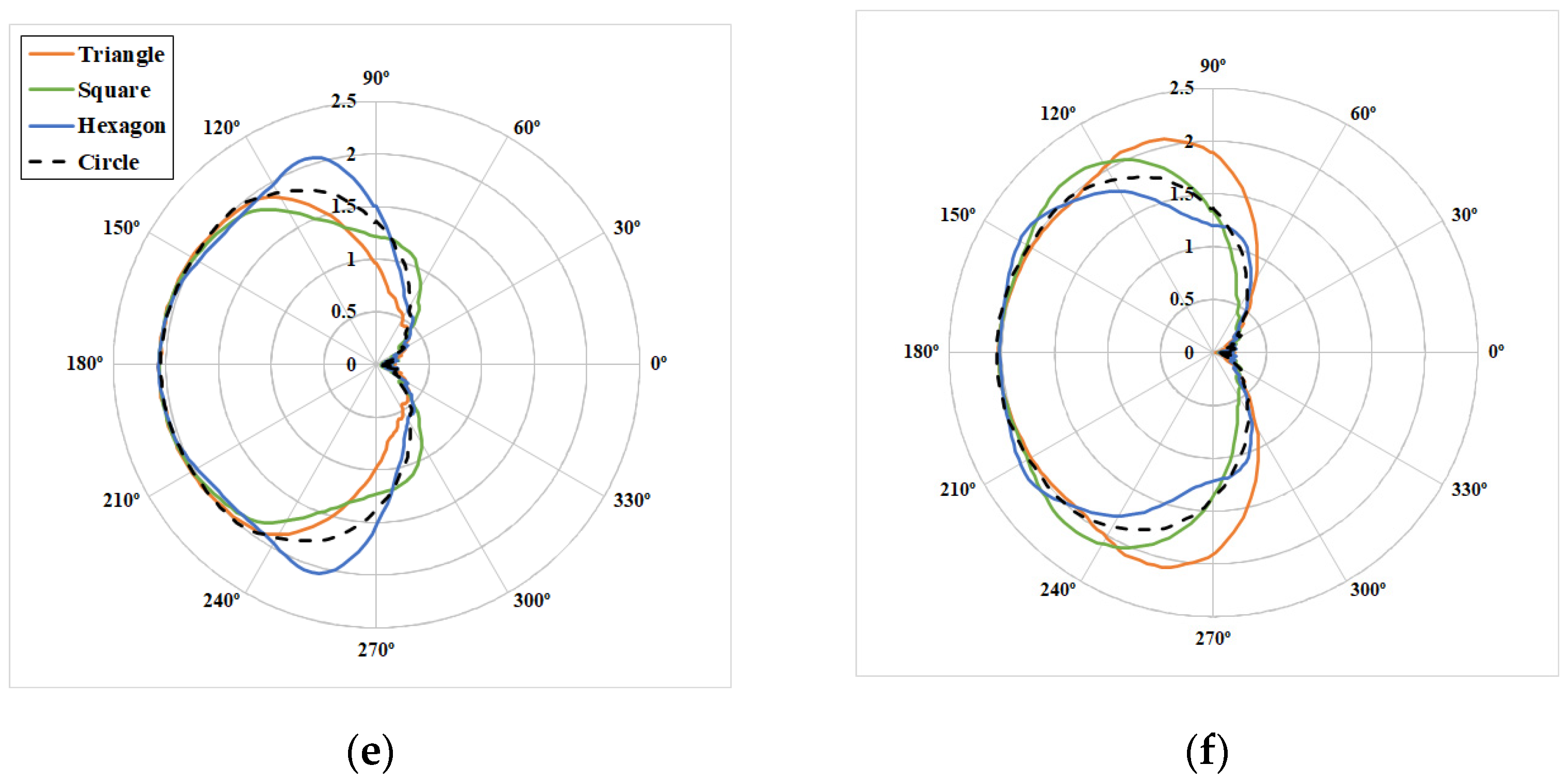
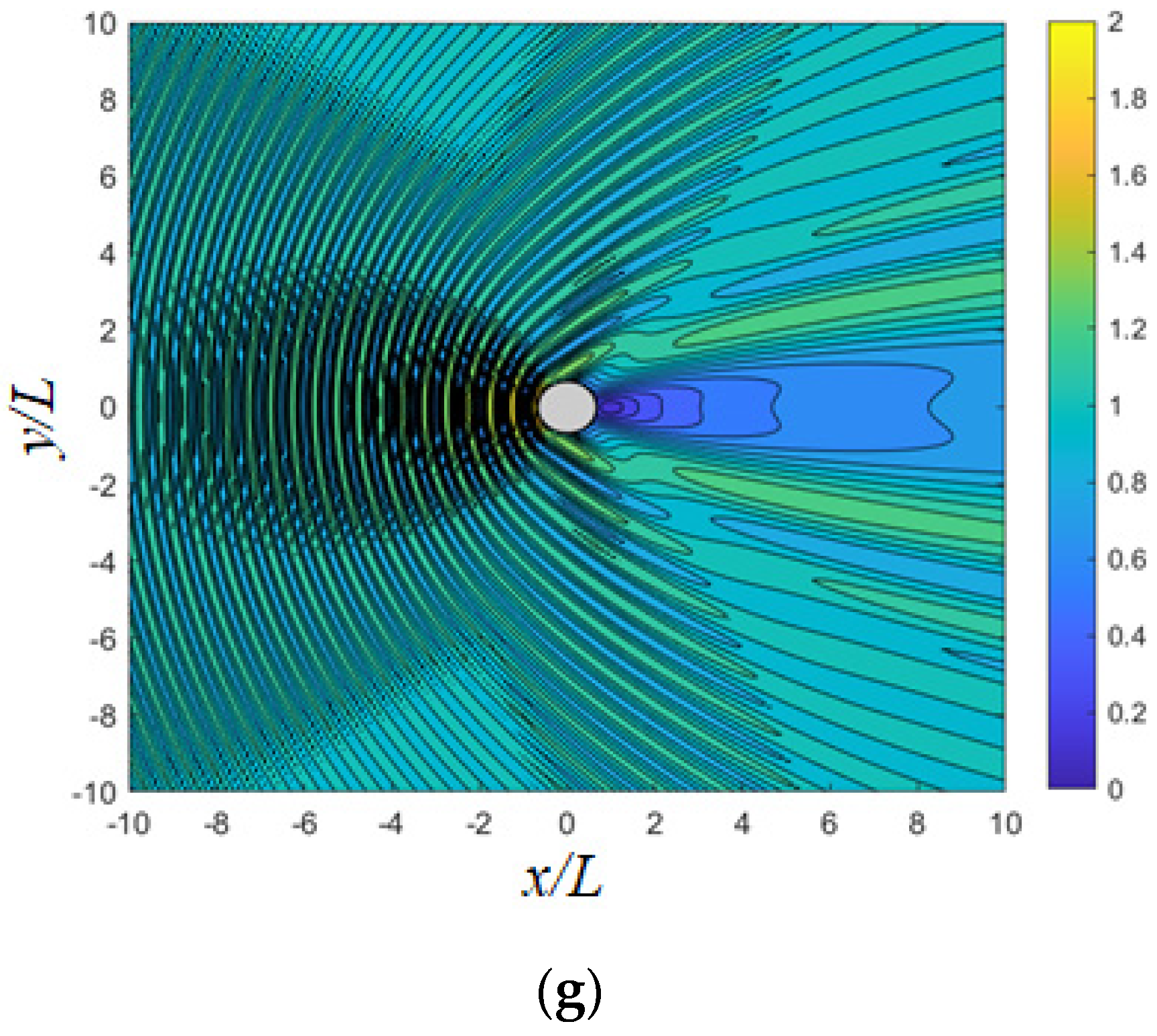
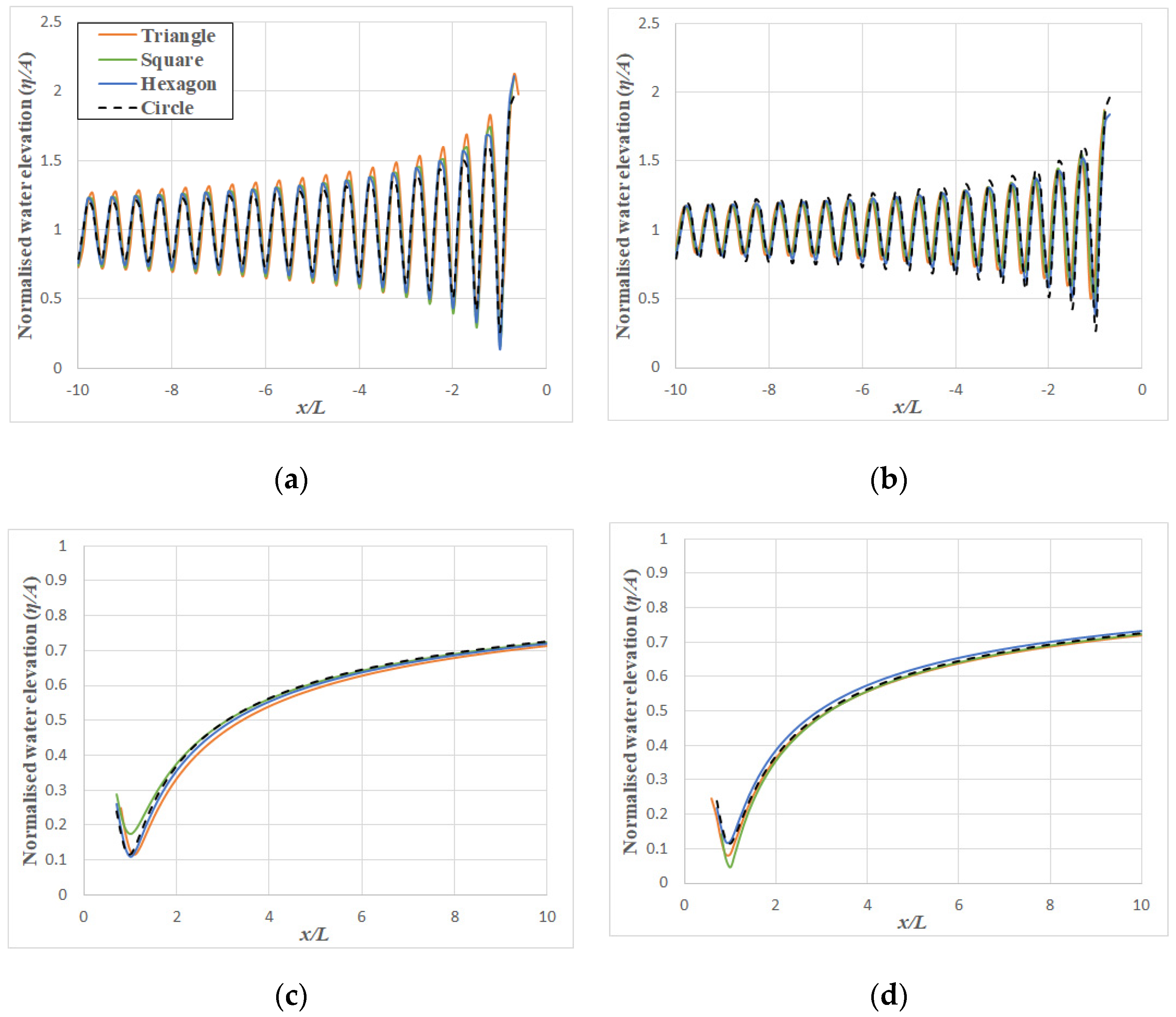
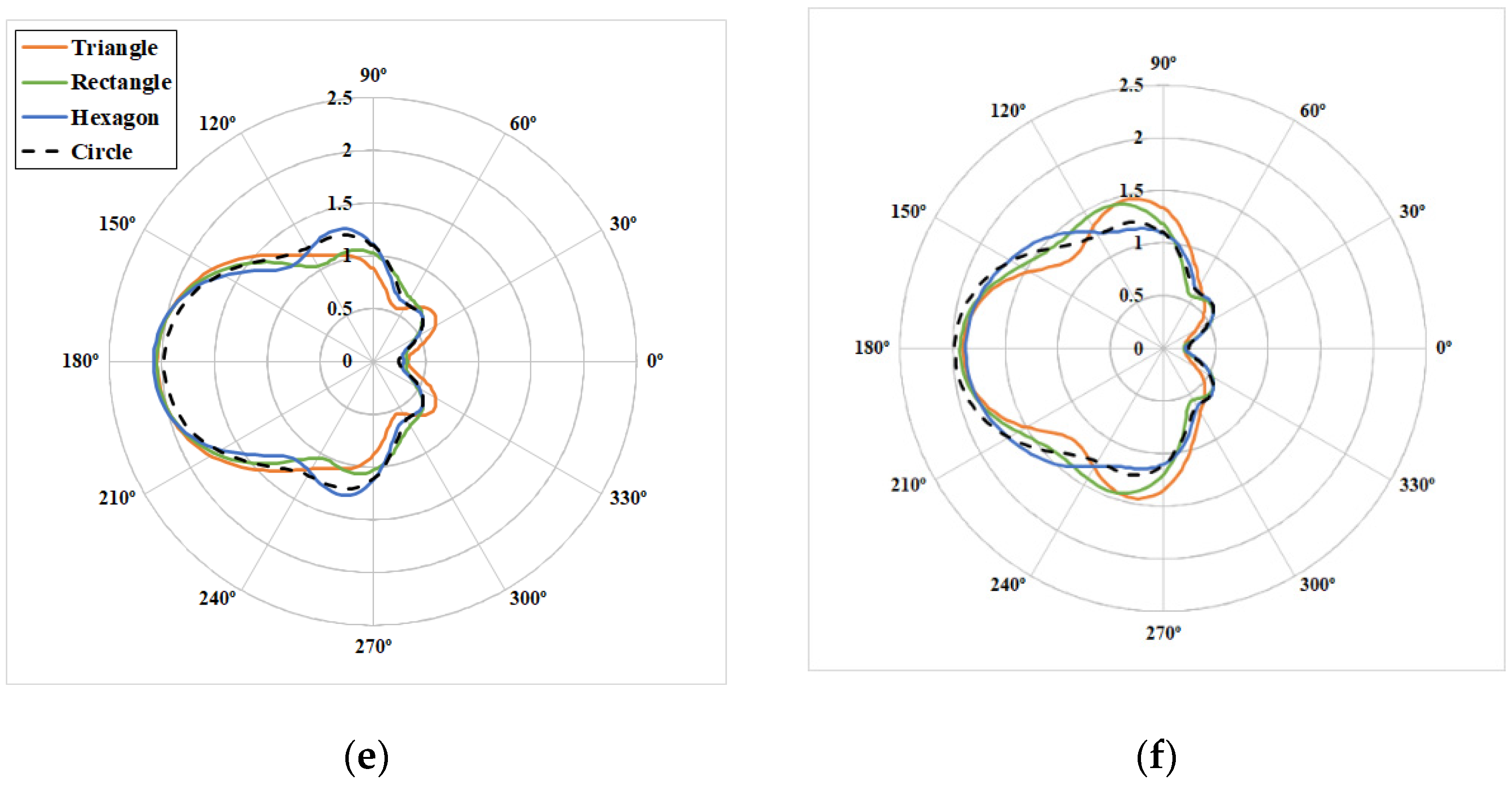
9. Hydrodynamic Results of Polygonal Platforms
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Wang, C.M.; Wang, B.T. Large Floating Structures; Springer: Singapore, 2015; Volume 3. [Google Scholar]
- Dai, J.; Wang, C.M.; Utsunomiya, T.; Duan, W.H. Review of recent research and developments on floating breakwaters. Ocean Eng. 2018, 158, 132–151. [Google Scholar] [CrossRef]
- VisitSeoul. Sebitseom. Available online: https://english.visitseoul.net/nature/Sebitseom-en_/24646 (accessed on 25 July 2021).
- Broom, D. Denmark Approves Artificial Island to Site 10 GW Offshore Win Hub. Available online: https://energypost.eu/denmark-approves-artificial-island-to-site-10gw-offshore-wind-hub/ (accessed on 25 July 2021).
- Fishfarmexpert. FjordMAX Promises more Fish and Smaller Footprint. Available online: https://www.fishfarmingexpert.com/article/fjordmax-promises-more-fish-and-smaller-footprint/ (accessed on 25 July 2021).
- Revkin, A. Floating Cities Could Ease the World’s Housing Crunch, the UN Says. Available online: https://www.nationalgeographic.com/environment/article/floating-cities-could-ease-global-housing-crunch-says-un (accessed on 25 July 2021).
- Bai, K.J.; Yeung, R.W. Numerical solutions of free-surface flow problems. In Proceedings of the 10th Symposium Naval Hydrodynamics, Cambridge, MA, USA, 24–28 June 1974; pp. 609–641. [Google Scholar]
- Mei, C.C. Numerical methods in water-wave diffraction and radiation. Annu. Rev. Fluid Mech. 1978, 10, 393–416. [Google Scholar] [CrossRef]
- Garrison, C.J. Hydrodynamics of large objects in the sea, Part II: Motion of free-floating bodies. J. Hydronaut. 1975, 9, 58–63. [Google Scholar] [CrossRef]
- Belibassakis, K. A boundary element method for the hydrodynamic analysis of floating bodies in variable bathymetry regions. Eng. Anal. Bound. Elem. 2008, 32, 796–810. [Google Scholar] [CrossRef]
- Bhatta, D.; Rahman, M. On scattering and radiation problem for a cylinder in water of finite depth. Int. J. Eng. Sci. 2003, 41, 931–967. [Google Scholar] [CrossRef]
- Yeung, R.W. Added mass and damping of a vertical cylinder in finite-depth waters. Appl. Ocean Res. 1981, 3, 119–133. [Google Scholar] [CrossRef]
- Chen, H.S.; Mei, C.C. Scattering and Radiation of Gravity Waves by an Elliptical Cylinder, Report Number 140; Massachusetts Institute of Technology: Cambridge, MA, USA, 1971. [Google Scholar]
- Williams, A.; Darwiche, M. Wave radiation by truncated elliptical cylinder. J. Waterw. Port Coast. Ocean Eng. 1990, 116, 101–119. [Google Scholar] [CrossRef]
- Liu, J.; Guo, A.; Fang, Q.; Li, H.; Hu, H.; Liu, P. Investigation of linear wave action around a truncated cylinder with non-circular cross section. J. Mar. Sci. Technol. 2018, 23, 866–876. [Google Scholar] [CrossRef]
- Yu, H.; Zheng, S.; Zhang, Y.; Iglesias, G. Wave radiation from a truncated cylinder of arbitrary cross section. Ocean Eng. 2019, 173, 519–530. [Google Scholar] [CrossRef]
- Mansour, A.M.; Williams, A.N.; Wang, K. The diffraction of linear waves by a uniform vertical cylinder with cosine-type radial perturbations. Ocean Eng. 2002, 29, 239–259. [Google Scholar] [CrossRef]
- Liu, J.; Guo, A.; Li, H. Analytical solution for the linear wave diffraction by a uniform vertical cylinder with an arbitrary smooth cross-section. Ocean Eng. 2016, 126, 163–175. [Google Scholar] [CrossRef]
- Lee, C.H. WAMIT Theory Manual; Department of Ocean Engineering, Massachusetts Institute of Technology: Boston, MA, USA, 1995. [Google Scholar]
- Mavrako, S.; Katsaounis, G.; Nielsen, K.; Lemonis, G. Numerical performance investigation of an array of heaving wave power converters in front of a vertical breakwater. In Proceedings of the Fourteenth International Offshore and Polar Engineering Conference, Toulon, France, 23–28 May 2004. [Google Scholar]
- Konispoliatis, D.N.; Mavrakos, S.A. Theoretical performance investigation of a vertical cylindrical oscillating water column device in front of a vertical breakwater. J. Ocean Eng. Mar. Energy 2020, 6, 1–13. [Google Scholar] [CrossRef]




| Platform shapes |  triangle |  square |  pentagon |  hexagon |  octagon |
| 0.1 | 0.06 | 0.04 | 0.03 | 0.02 | |
| 3 | 4 | 5 | 6 | 8 | |
| T (s) | AQWA | Fourier Expansion [15] | Semi-Analytical Approach 1 | Semi-Analytical Approach 2 |
|---|---|---|---|---|
| 5 | (Δ = 2.6 m) | (18, 5, 6, 12) | (18, 5, NA, NA) | (18, 5, 6, 12) |
| 8 min 18 s | 26 s | 48 s | 16 s | |
| 10 | (Δ = 10 m) | (10, 10, 6, 12) | (10, 10, NA, NA) | (10, 10, 6, 12) |
| 24 s | 30 s | 23 s | 19 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.C.; Wang, C.M. Hydrodynamic Behaviour of Floating Polygonal Platforms under Wave Action. J. Mar. Sci. Eng. 2021, 9, 923. https://doi.org/10.3390/jmse9090923
Park JC, Wang CM. Hydrodynamic Behaviour of Floating Polygonal Platforms under Wave Action. Journal of Marine Science and Engineering. 2021; 9(9):923. https://doi.org/10.3390/jmse9090923
Chicago/Turabian StylePark, Jeong Cheol, and Chien Ming Wang. 2021. "Hydrodynamic Behaviour of Floating Polygonal Platforms under Wave Action" Journal of Marine Science and Engineering 9, no. 9: 923. https://doi.org/10.3390/jmse9090923
APA StylePark, J. C., & Wang, C. M. (2021). Hydrodynamic Behaviour of Floating Polygonal Platforms under Wave Action. Journal of Marine Science and Engineering, 9(9), 923. https://doi.org/10.3390/jmse9090923







