A Comparative Study of Model Predictive Control and Optimal Causal Control for Heaving Point Absorbers
Abstract
:1. Introduction
2. Glossary
| Variable | Description | Units |
| g | Acceleration due to gravity | m/s2 |
| Density of sea water | kg/m3 | |
| Mass of the buoy | kg | |
| Infinite Added Mass | kg | |
| Displacement of the buoy in heave | m | |
| Velocity of the buoy in heave | m/s | |
| Acceleration of the buoy in heave | m/s2 | |
| Radiation damping force | N | |
| PTO Force | N | |
| Hydrostatic spring stiffness | N | |
| Drag force related to viscous effects | N | |
| Wave excitation force | N | |
| Buoyancy stiffness coefficient | N/m | |
| Water plane area of the buoy | m2 | |
| Viscous damping coefficient | Ns/m | |
| Drag coefficient | - | |
| A matrix of state space model of the radiation damping sub-system | ||
| B matrix of state space model of the radiation damping sub-system | ||
| C matrix of state space model of the radiation damping sub-system | ||
| D matrix of state space model of the radiation damping sub-system | ||
| State vector comprising of all states used to model the radiation damping sub-system in state space form | ||
| Vector comprising of the derivatives of all states used to model the radiation damping sub-system in state space form | ||
| Number of states used to model the radiation damping sub-system. This is equal to the length of the state vector | ||
| Row vector of zeros with length | ||
| A matrix of WEC state space model | ||
| B matrix of WEC state space model | ||
| C matrix of WEC state space model | ||
| D matrix of WEC state space model | ||
| Prediction horizon | s | |
| H | Wave height of a monochromatic wave | m |
| T | Wave period of a monochromatic wave | s |
| Significant wave height of a polychromatic wave | m | |
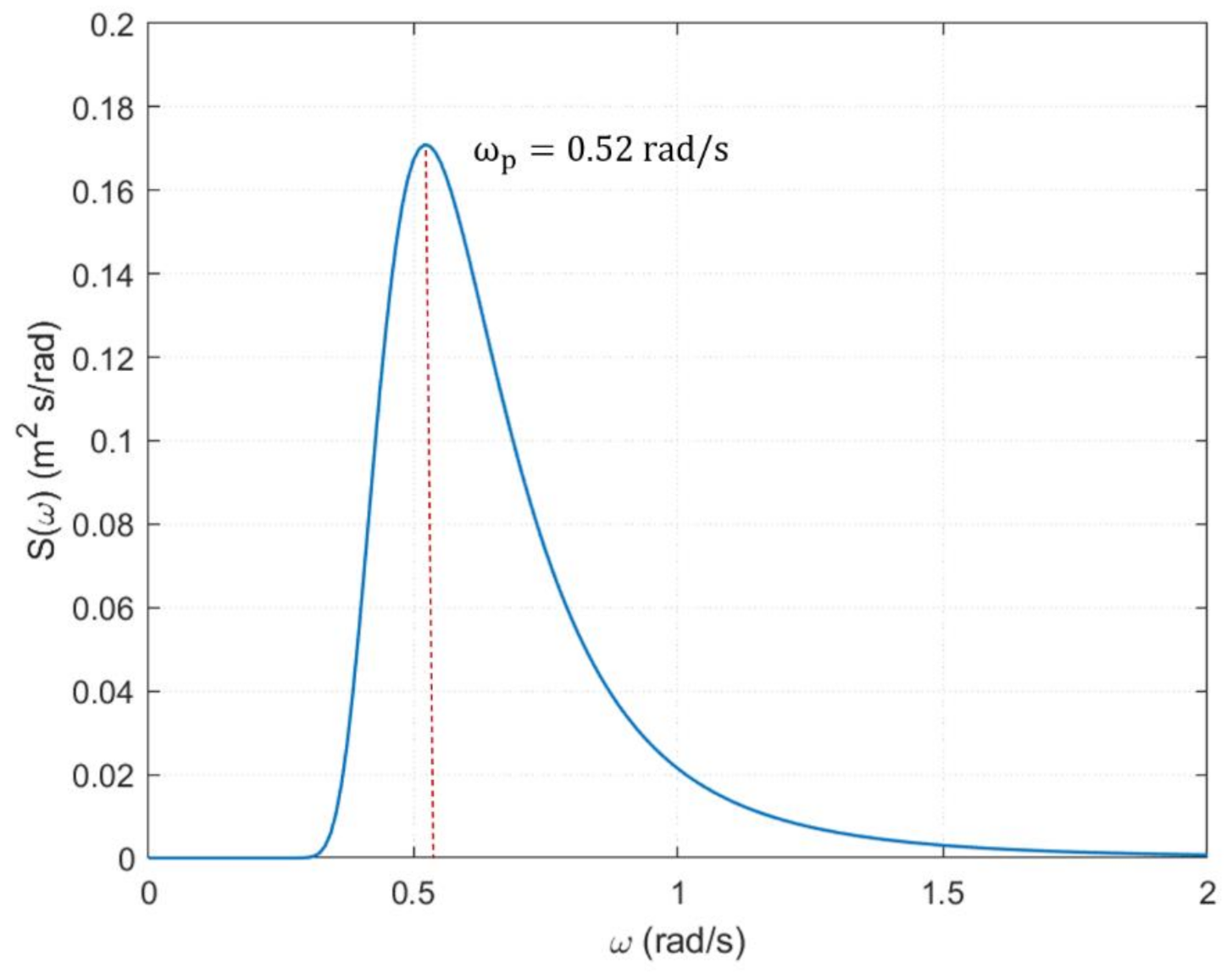
| Peak period of a polychromatic wave | s | |
| Wavelength | m | |
| Wavenumber | ||
| Average absorbed power | W | |
| Buoy heave velocity | m/s | |
| Radiation impulse-response function | Ns/m | |
| Excitation impulse-response function | N/m | |
| Time instant | s | |
| Control input at time instant t | N | |
| Wave excitation force at time instant t | N | |
| State vector at time instant t comprising of all states used to model the device dynamics | ||
| Derivative of the state vector at time instant t that is used to model the device dynamics |
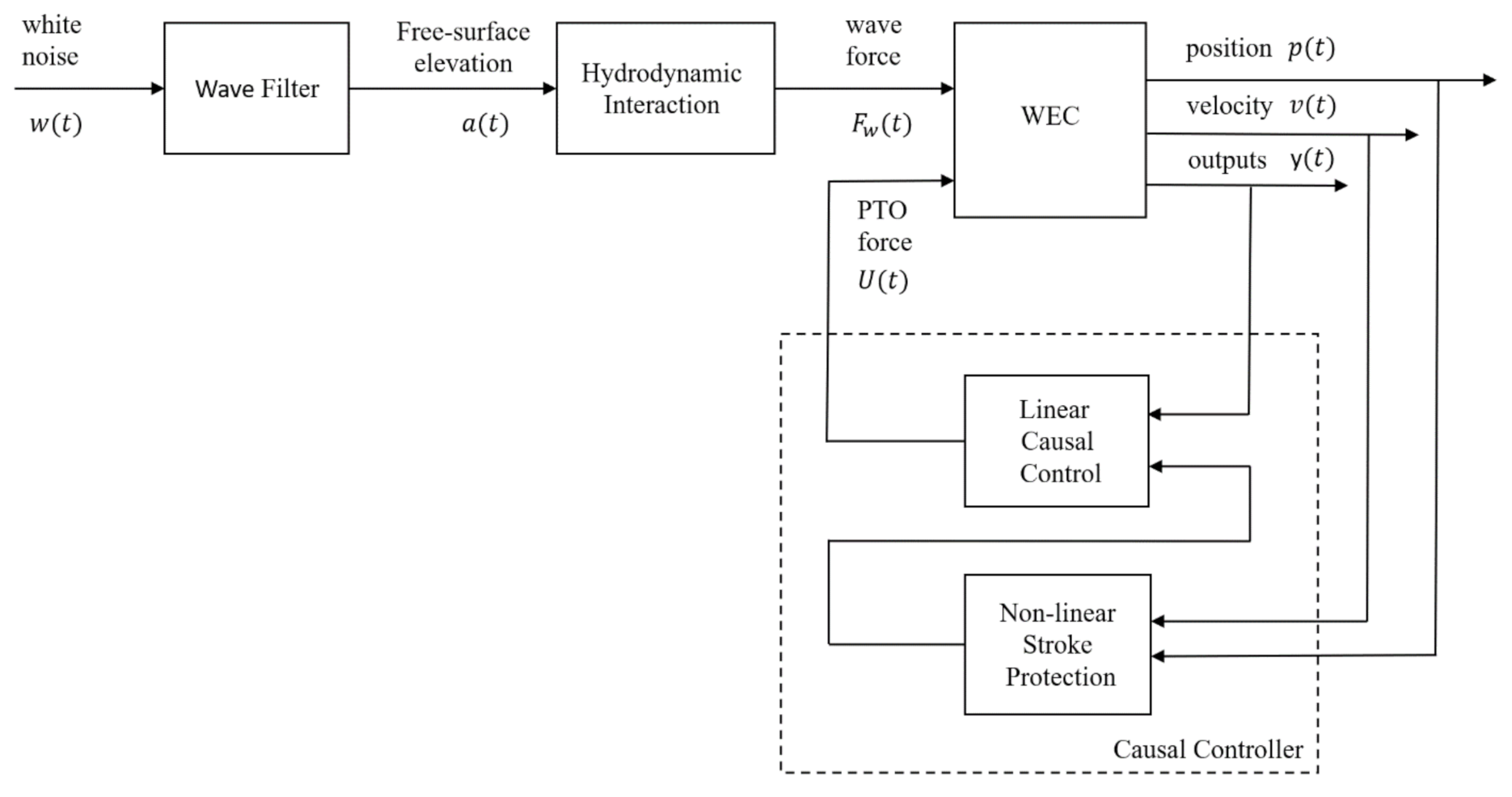
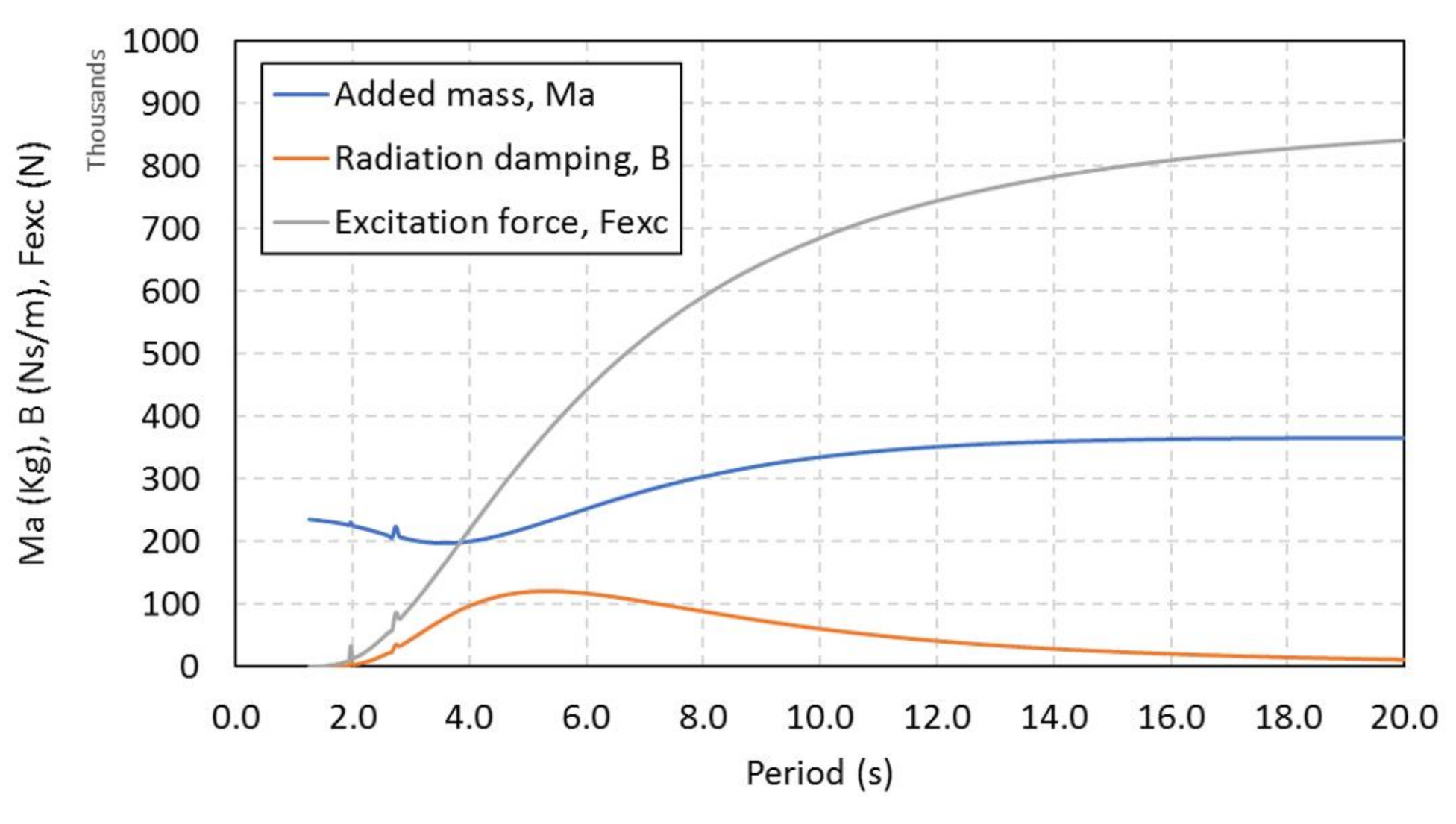
3. The Device Model
4. Control Methods
4.1. Model Predictive Control (MPC)
4.2. Causal Feedback Control
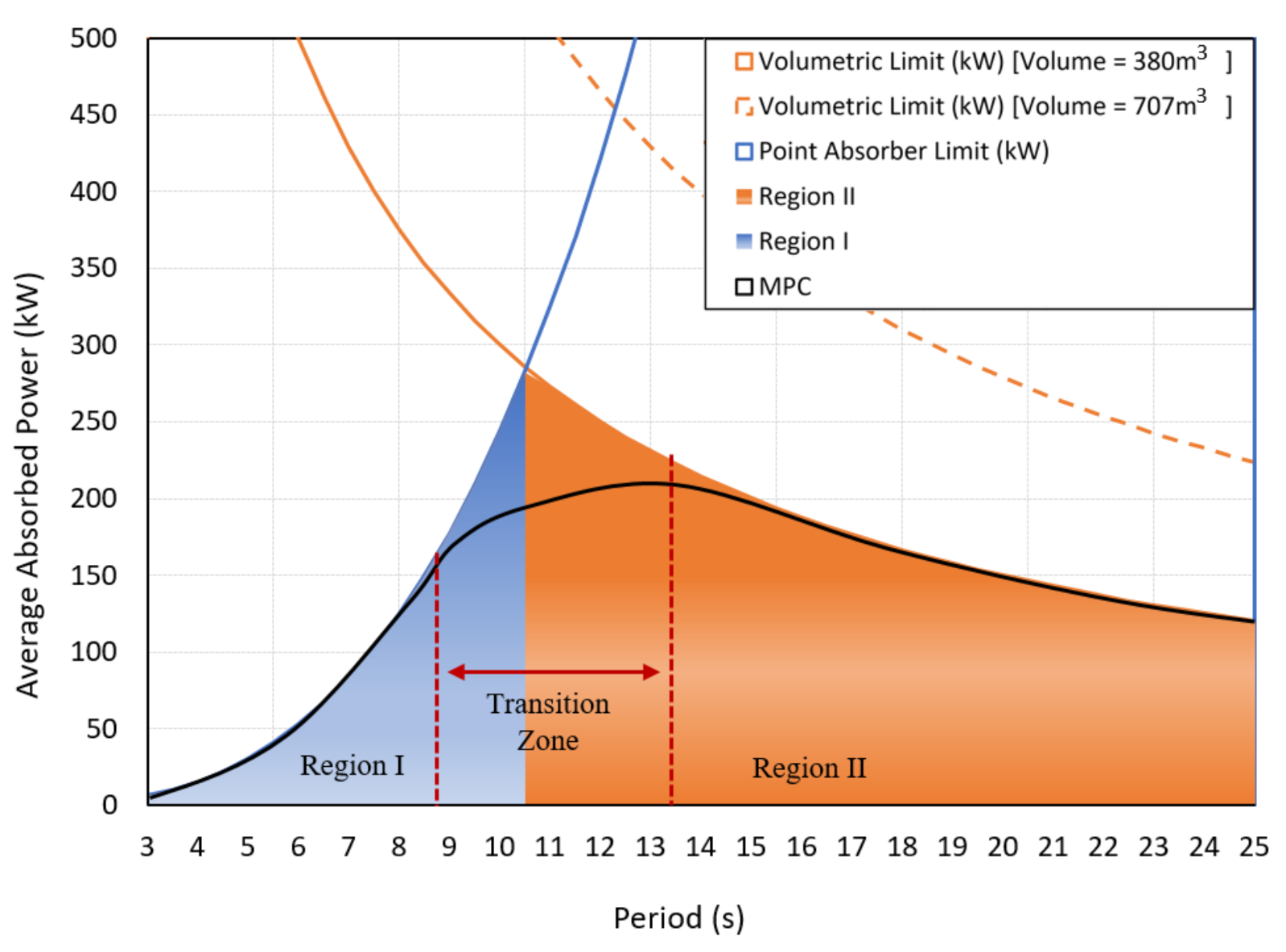
5. Theoretical Limits on the Average Absorbed Power
5.1. Point Absorber Limit
5.2. Volumetric Limit
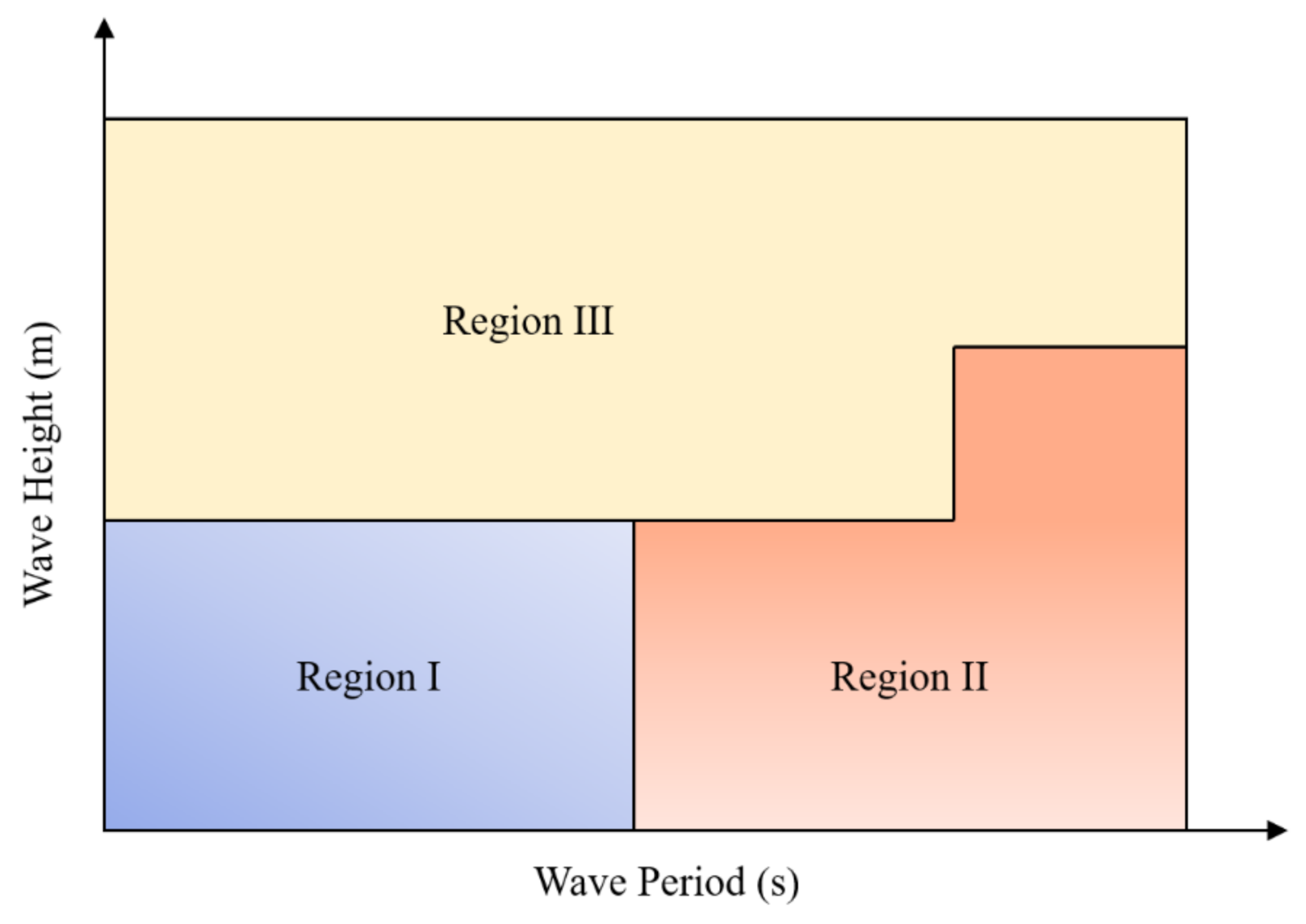
5.3. Controller Design Trade-Off Space
6. Results
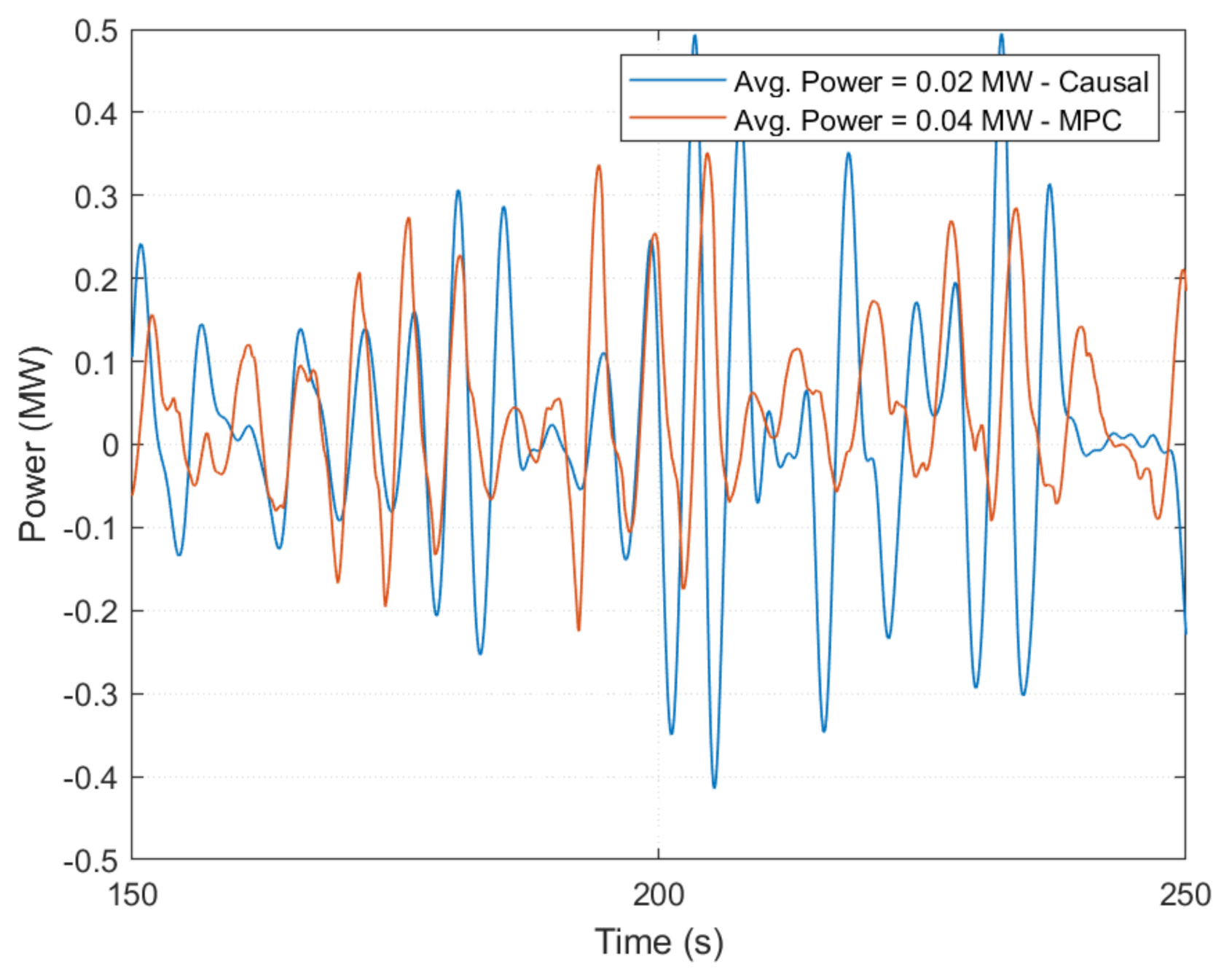
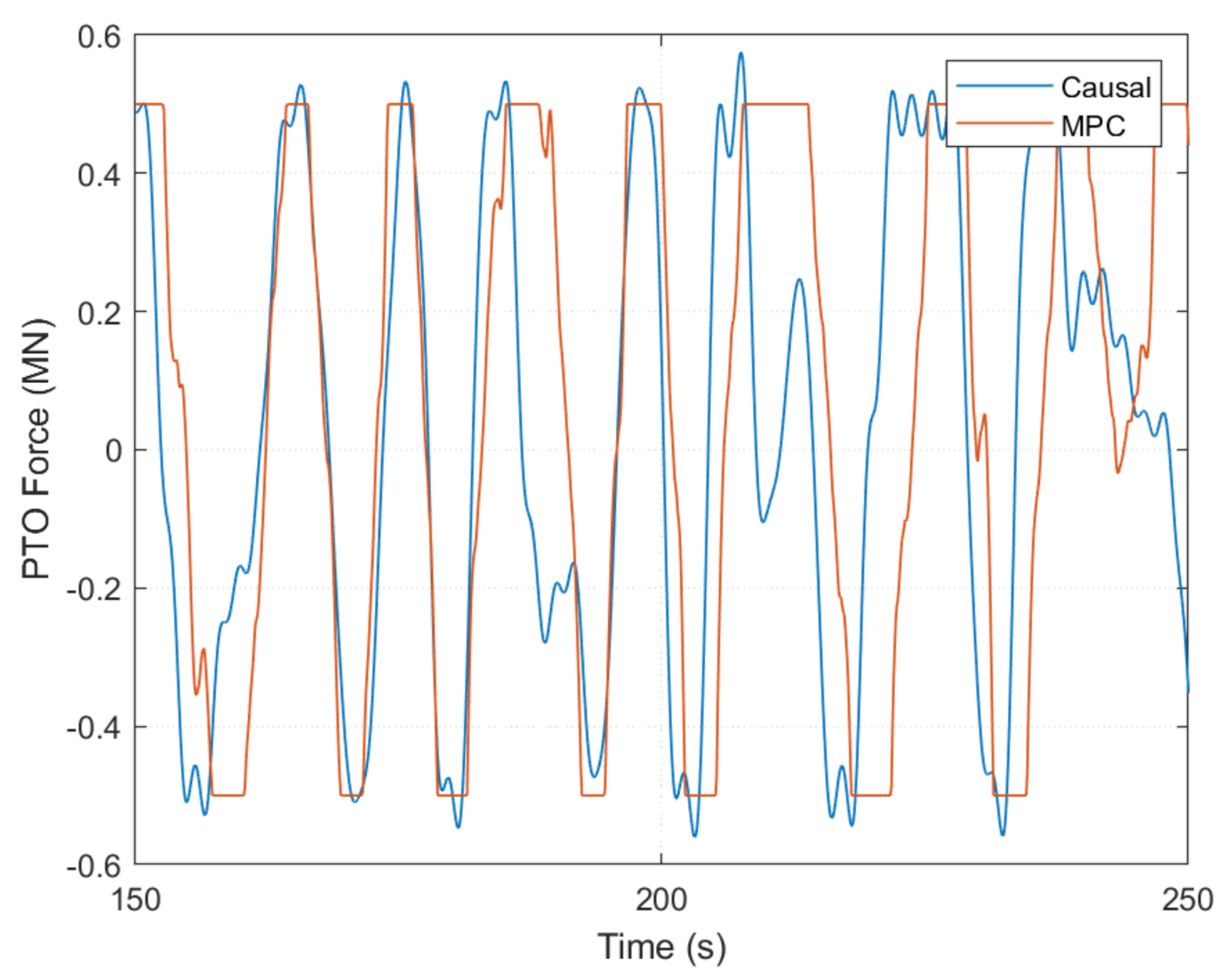
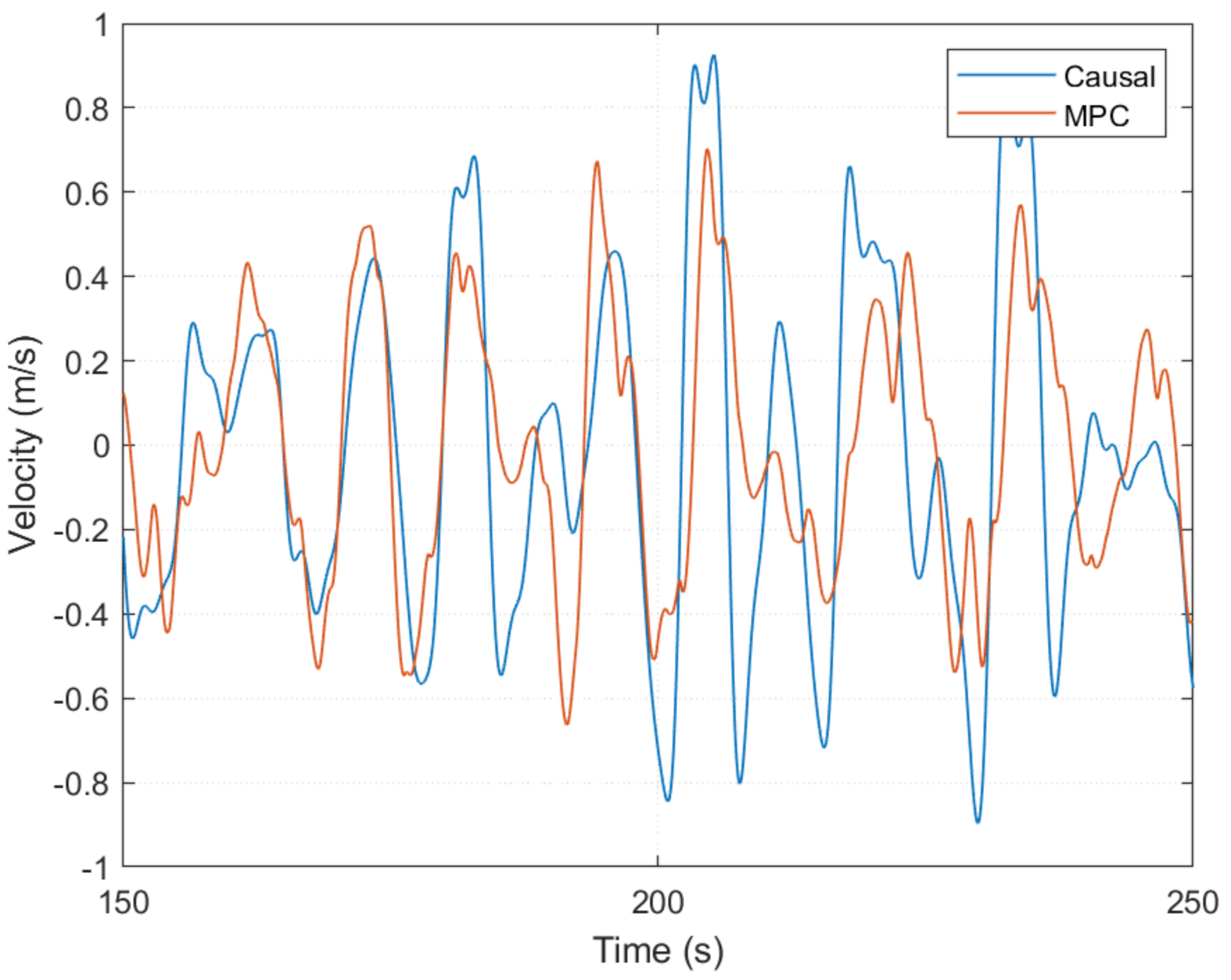
6.1. Benchmarking Performance of Causal Control Design Methods
6.2. Controller Performance with Unconstrained PTO Force
6.3. Comparison of Annual Average Energy Capture for Reference Site
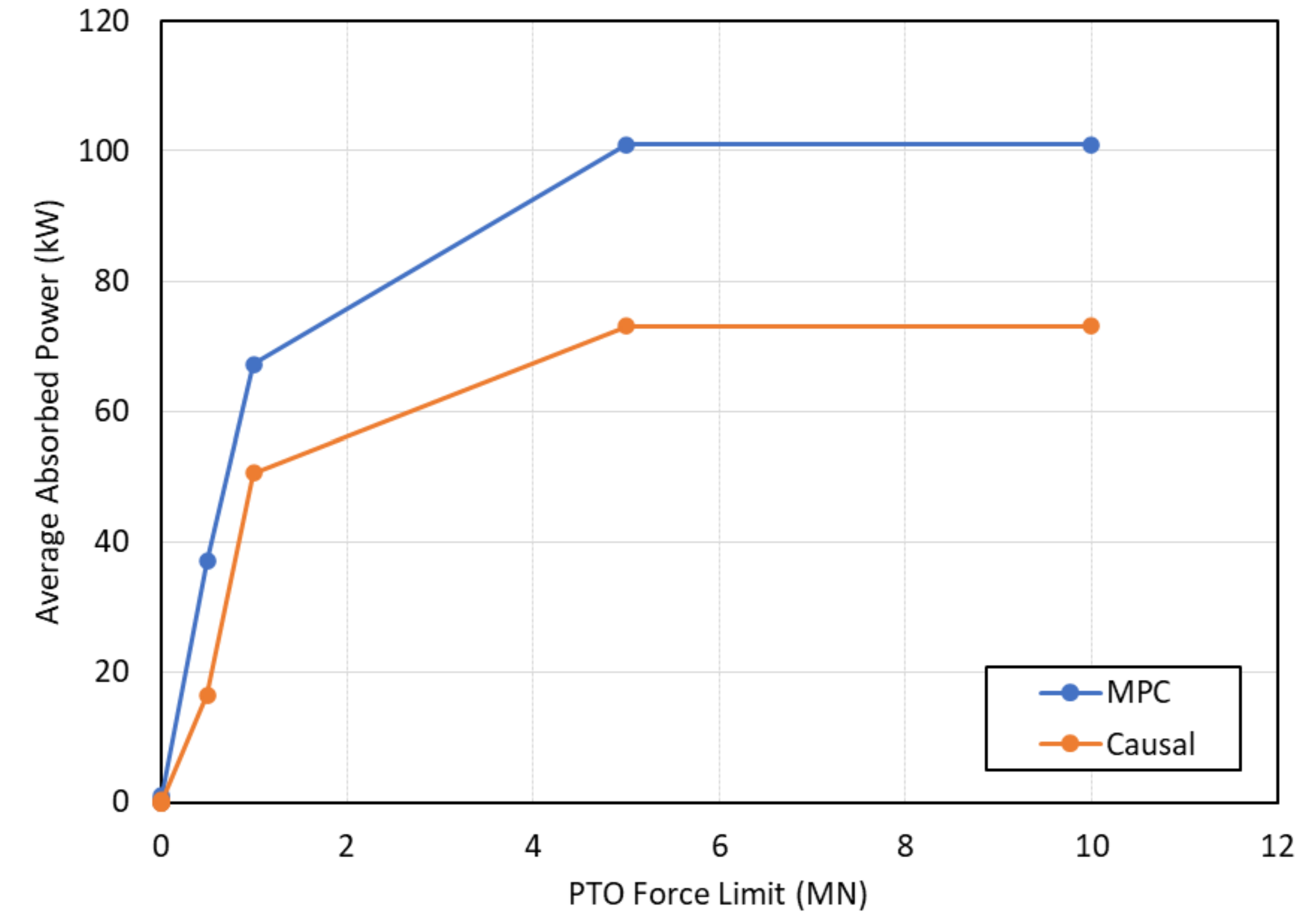
6.4. Controller Performance with Constrained PTO Force
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Nebel, P. Maximizing the Efficiency of Wave-Energy Plant Using Complex-Conjugate Control. J. Syst. Control Eng. 1992, 206, 225–236. [Google Scholar] [CrossRef]
- Budal, K.; Falnes, J. Interacting Point Absorbers with Controlled Motion. In Power from Sea Waves; Count, B., Ed.; Academic: London, UK, 1980; pp. 381–399. [Google Scholar]
- Evans, D.V. A theory for wave-power absorption by oscillating bodies. J. Fluid Mech. 1976, 77, 1–25. [Google Scholar] [CrossRef]
- Falnes, J.; Kurniawan, A. Ocean. Waves and Oscillating Systems: Linear Interactions Including Wave Energy Extraction; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Coe, R.; Bacelli, G.; Nevarez, V.; Cho, H.; Wilches-Bernal, F. A Comparative Study on Wave Prediction for WECs. SANDIA REPORT SAND2018-8602; Sandia National Lab.(SNL-NM): Albuquerque, NM, USA, 2018. [Google Scholar]
- Scruggs, J.; Lattanzio, S.; Taflanidis, A.; Cassidy, I. Optimal causal control of a wave energy converter in a random sea. Appl. Ocean Res. 2013, 42, 1–15. [Google Scholar] [CrossRef]
- Scruggs, J. Causal control design for wave energy converters with finite stroke. IFAC-PapersOnLine 2017, 50, 15678–15685. [Google Scholar] [CrossRef]
- Nie, R.; Scruggs, J.; Chertok, A.; Clabby, D.; Previsic, M.; Karthikeyan, A. Optimal causal control of wave energy converters in stochastic waves—Accommodating nonlinear dynamic and loss models. Int. J. Mar. Energy 2016, 15, 41–55. [Google Scholar] [CrossRef] [Green Version]
- Lao, Y.; Scruggs, J.; Karthikeyan, A.; Previsic, M. Discrete-time causal control of WECs with finite stroke in stochastic waves. In Proceedings of the 13th European Wave and Tidal Energy Conference, Napoli, Italy, 1–6 September 2019. [Google Scholar]
- Blondel, E.; Bonnefoy, F.; Ferrant, P. Deterministic non-linear wave prediction using probe data. Ocean Eng. 2010, 37, 913–926. [Google Scholar] [CrossRef]
- Lyzenga, D.; Nwogu, O.; Trizna, D.; Hathaway, K. Ocean wave field measurements using X-band Doppler radars at low grazing angles. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Lyzenga, D.R.; Walker, D.T. A Simple Model for Marine Radar Images of the Ocean Surface. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2389–2392. [Google Scholar] [CrossRef]
- Gieske, P. Model Predictive Control of a Wave Energy Converter: Archimedes Wave Swing. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2007. [Google Scholar]
- Karthikeyan, A.; Previsic, M.; Scruggs, J.; Chertok, A. Non-linear Model Predictive Control of Wave Energy Converters with Realistic Power Take-off Configurations and Loss Model. In Proceedings of the 2019 IEEE Conference on Control Technology and Applications (CCTA), Hong Kong, China, 19–21 August 2019. [Google Scholar]
- Eriksson, C. Model Predictive Control of CorPower Ocean Wave Energy Converter. Ph.D. Thesis, KTH, Stockholm, Sweden, 2016. [Google Scholar]
- Cretel, J.; Lewis, A.; Lightbody, G.; Thomas, G. An application of model predictive control to a wave energy point absorber. In Proceedings of the IFAC Conference on Control Methodologies and Technology for Energy Efficiency, Vilamoura, Portugal, 29–31 March 2010. [Google Scholar]
- Nathan, T.; Yeoung, R. Nonlinear model predicitve control applied to a generic ocean-wave energy extractor. J. Offshore Mech. Arct. Eng. 2014, 135, 41901. [Google Scholar]
- Richter, M.; Magana, M.E.; Sawodny, O.; Brekken, T.K.A. Nonlinear Model Predictive Control of a Point Absorber Wave Energy Converter. IEEE Trans. Sustain. Energy 2013, 4, 118–126. [Google Scholar] [CrossRef]
- Faedo, N.; Olaya, S.; Ringwood, J.V. Optimal control, MPC and MPC-like algorithms for wave energy systems: An overview. IFAC J. Syst. Control 2017, 1, 37–56. [Google Scholar] [CrossRef] [Green Version]
- WAMIT. Available online: https://www.wamit.com/ (accessed on 20 June 2020).
- Coleman, T.F.; Li, Y. A Reflective Newton Method for Minimizing a Quadratic Function Subject to Bounds on Some of the Variables. SIAM J. Optim. 1996, 6, 1040–1058. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Wright, M.H. Practical Optimization; Academic Press: London, UK, 1981. [Google Scholar]
- Lao, Y.; Scruggs, J.T. A Modified Technique for Spectral Factorization of Infinite-Dimensional Systems Using Subspace Techniques. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019. [Google Scholar]
- Budal, K.; Falnes, J. A Resonant Point Absorber of Ocean Waves. Nature 1975, 256, 478–479. [Google Scholar]
- Hals, J.; Falnes, J.; Moan, T. Constrained Optimal Control of a Heaving Buoy Wave-Energy Converter. J. Offshore Mech. Arct. Eng. 2010, 133, 011401. [Google Scholar] [CrossRef] [Green Version]
- Laboratories, S.N. MASK3 for Advanced WEC Dynamics and Controls [Data Set]. Available online: https://dx.doi.org/10.15473/1581762 (accessed on 20 May 2020).
- WAFO-Group. WAFO—A Matlab Toolbox for Analysis of Random Waves and Loads—A Tutorial; Center for Mathematical Sciences, Lund University: Lund, Sweden, 2000. [Google Scholar]

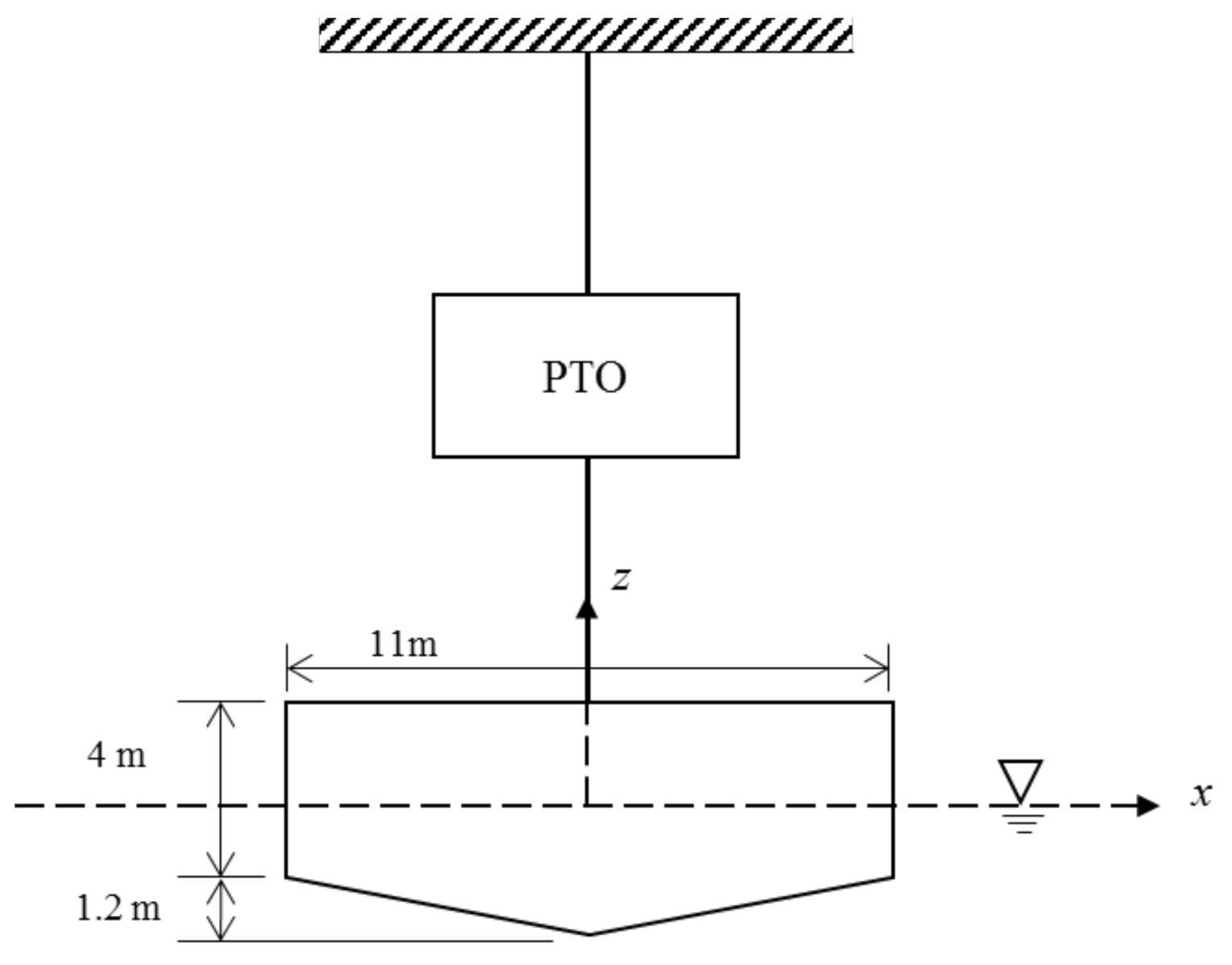

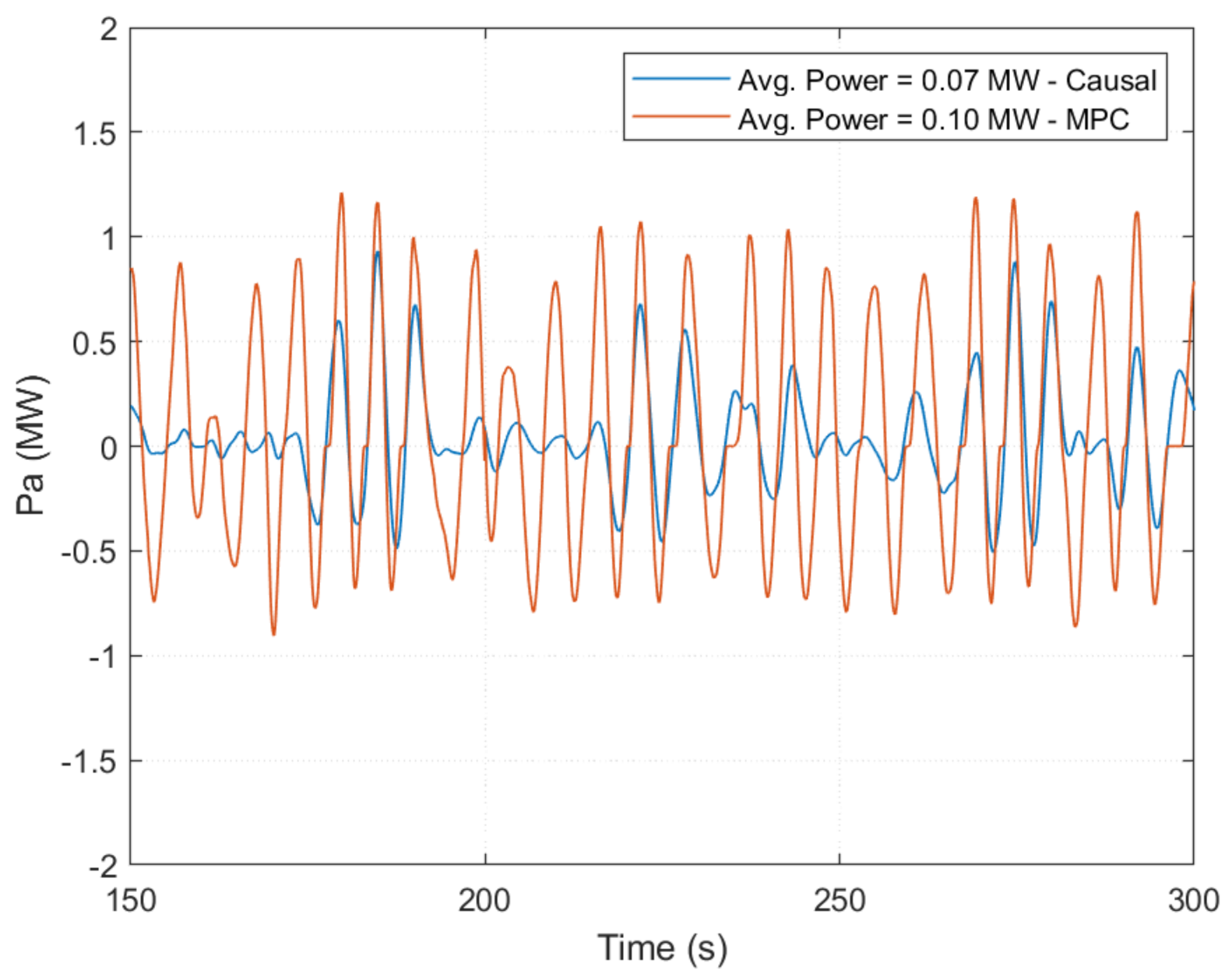
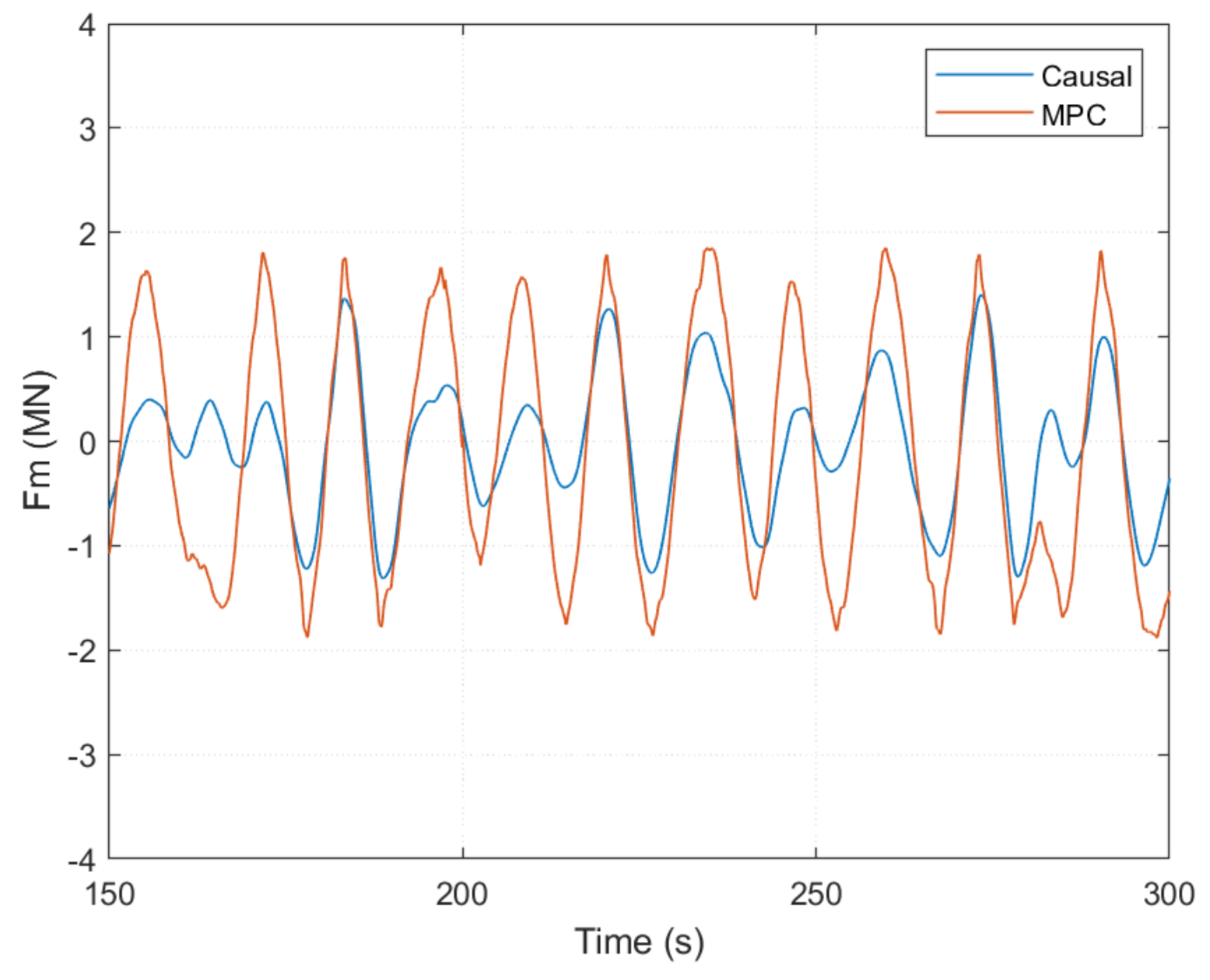
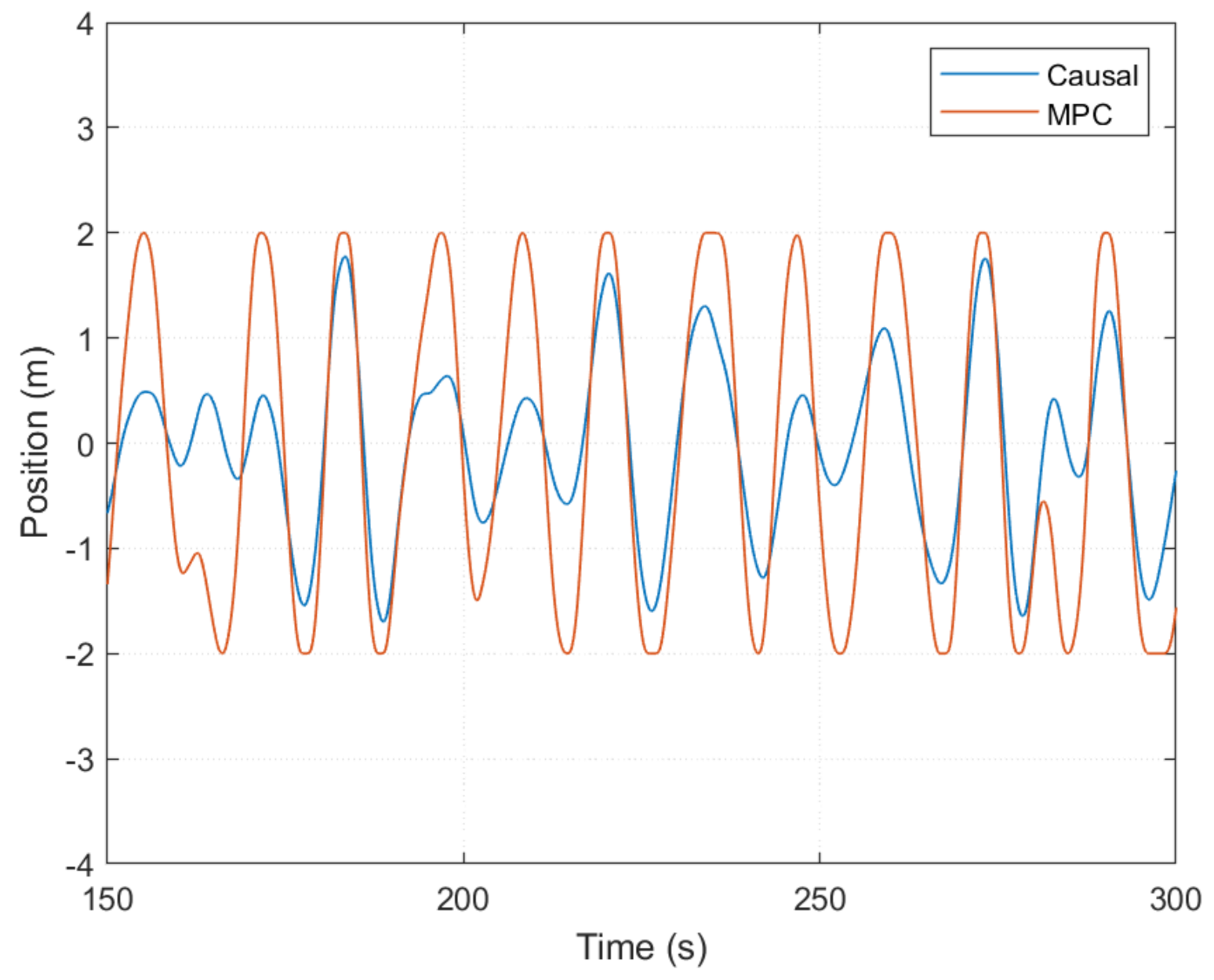
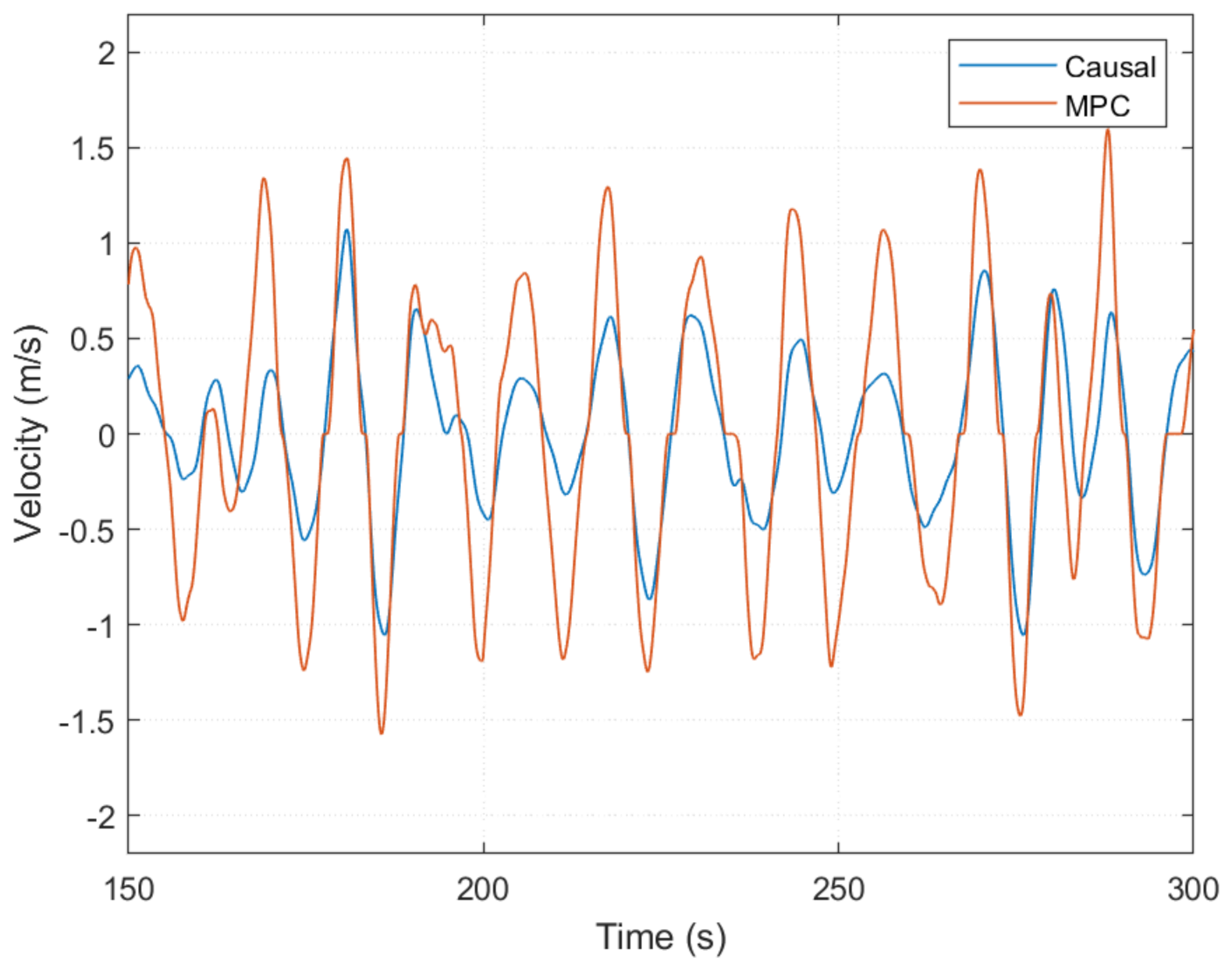

| Quantity | Value | Units |
|---|---|---|
| Buoy diameter | 11 | m |
| Buoy cylinder height | 4 | m |
| Reaction diameter | 11 | m |
| Buoy conical height | 1.2 | m |
| Motion limits | ±2 | m |
| Buoy mass | 228,080 | kg |
| Water Plane Area (S) | 95 | m2 |
| Coefficient of Drag (Cd) | 0.5 |
| % of Total Occurrence | Heaving Buoy (Swept Volume = 380 m3) | SANDIA WaveBot (Swept Volume = 4303 m3) |
|---|---|---|
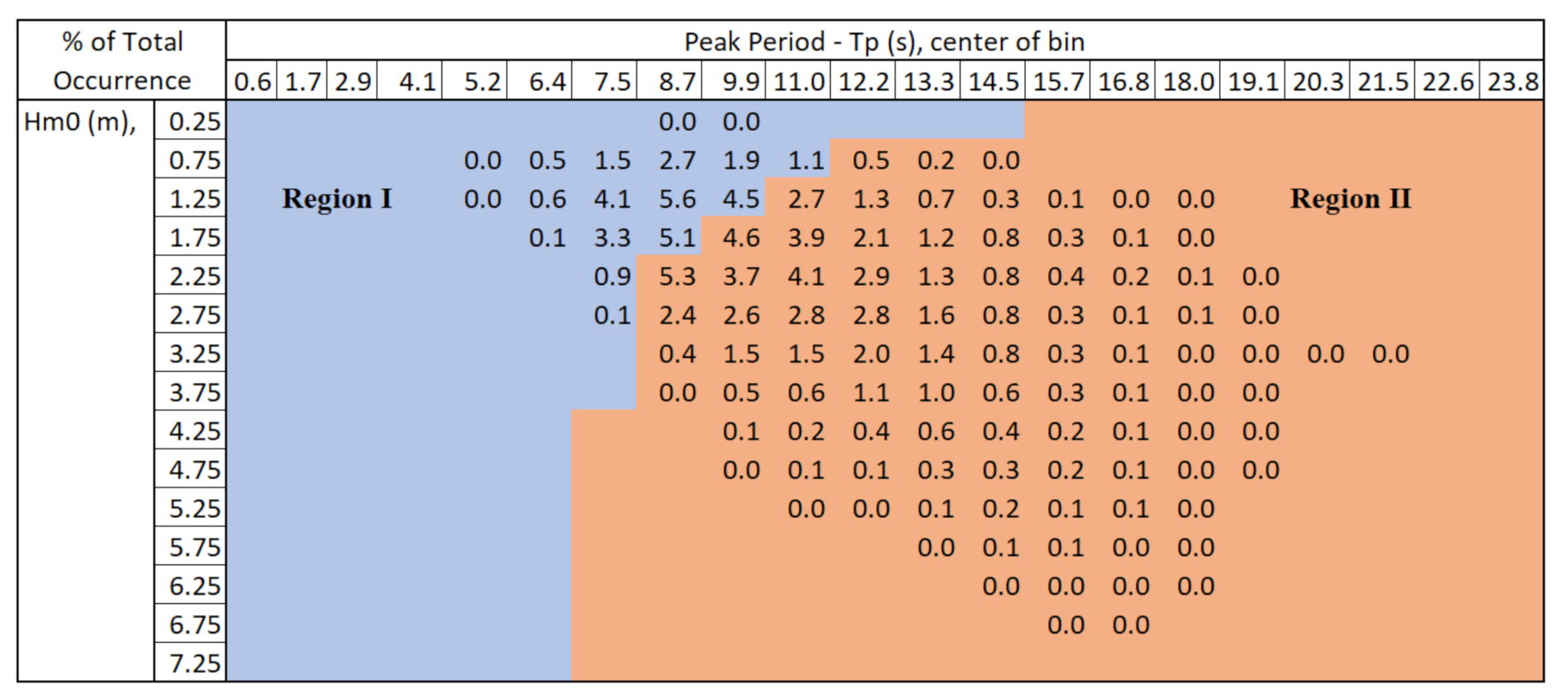
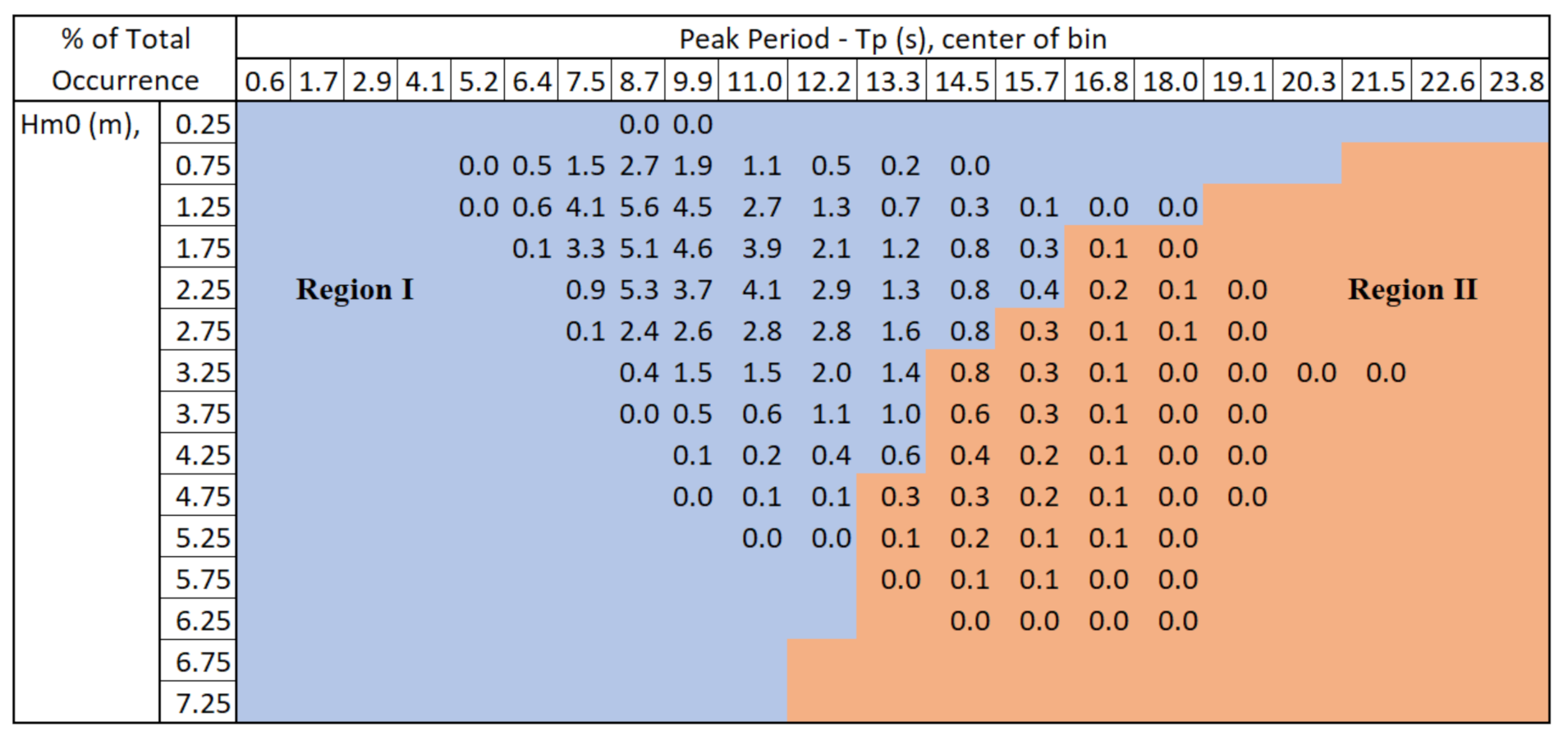
| Region I | 32% | 94% |
| Region II | 68% | 6% |
| MPC | Causal Control | ||
|---|---|---|---|
| Rated Power (kW) | 473 | 375 | |
| Average Power (kW) | 142 | 113 | |
| Capacity Factor | 30% | 30% | |
| % Annual Energy Captured | Region I | 19% | 18% |
| Region II | 81% | 82% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Previsic, M.; Karthikeyan, A.; Scruggs, J. A Comparative Study of Model Predictive Control and Optimal Causal Control for Heaving Point Absorbers. J. Mar. Sci. Eng. 2021, 9, 805. https://doi.org/10.3390/jmse9080805
Previsic M, Karthikeyan A, Scruggs J. A Comparative Study of Model Predictive Control and Optimal Causal Control for Heaving Point Absorbers. Journal of Marine Science and Engineering. 2021; 9(8):805. https://doi.org/10.3390/jmse9080805
Chicago/Turabian StylePrevisic, Mirko, Anantha Karthikeyan, and Jeff Scruggs. 2021. "A Comparative Study of Model Predictive Control and Optimal Causal Control for Heaving Point Absorbers" Journal of Marine Science and Engineering 9, no. 8: 805. https://doi.org/10.3390/jmse9080805
APA StylePrevisic, M., Karthikeyan, A., & Scruggs, J. (2021). A Comparative Study of Model Predictive Control and Optimal Causal Control for Heaving Point Absorbers. Journal of Marine Science and Engineering, 9(8), 805. https://doi.org/10.3390/jmse9080805






