Improving Significant Wave Height Forecasts Using a Joint Empirical Mode Decomposition–Long Short-Term Memory Network
Abstract
:1. Introduction
2. Data and Methodology
2.1. Buoy Data and Data Preprocessing
2.2. The Long Short-Term Memory Network
2.3. Empirical Mode Decomposition
- For signal, identify all the maxima and minima.
- Through a cubic spline interpolation, fit upper and lower envelopes of signal . The mean of the two envelopes is the average envelope curve :
- To obtain an IMF candidate, subtract m from :
- If does not satisfy the two IMF conditions, then is set as the original signal and the prior step is repeated k times. Here, can be estimated as follows:where and represent the signal after shifting k − 1 and k times, respectively. is the average envelope of .
- However, if satisfies the two IMF conditions, then define as . The standard deviation is defined as follows:
- To obtain a new signal , subtract from :
- Repeat steps 1–6 until cannot be further decomposed into IMFs. The residual of the original signal is given by The original signal can finally be presented as a collection of n components and a residual :
2.4. Performance Indicators
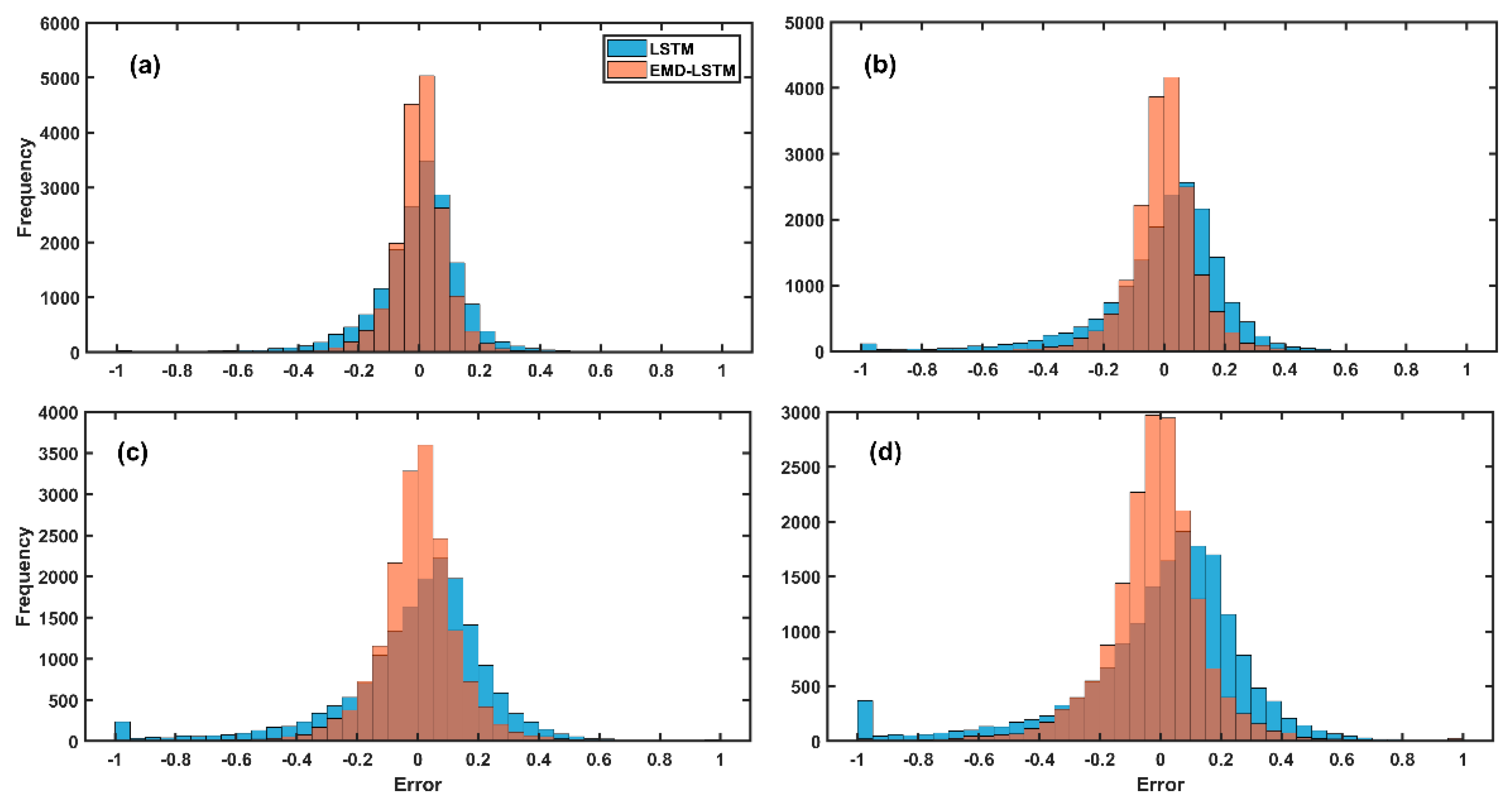
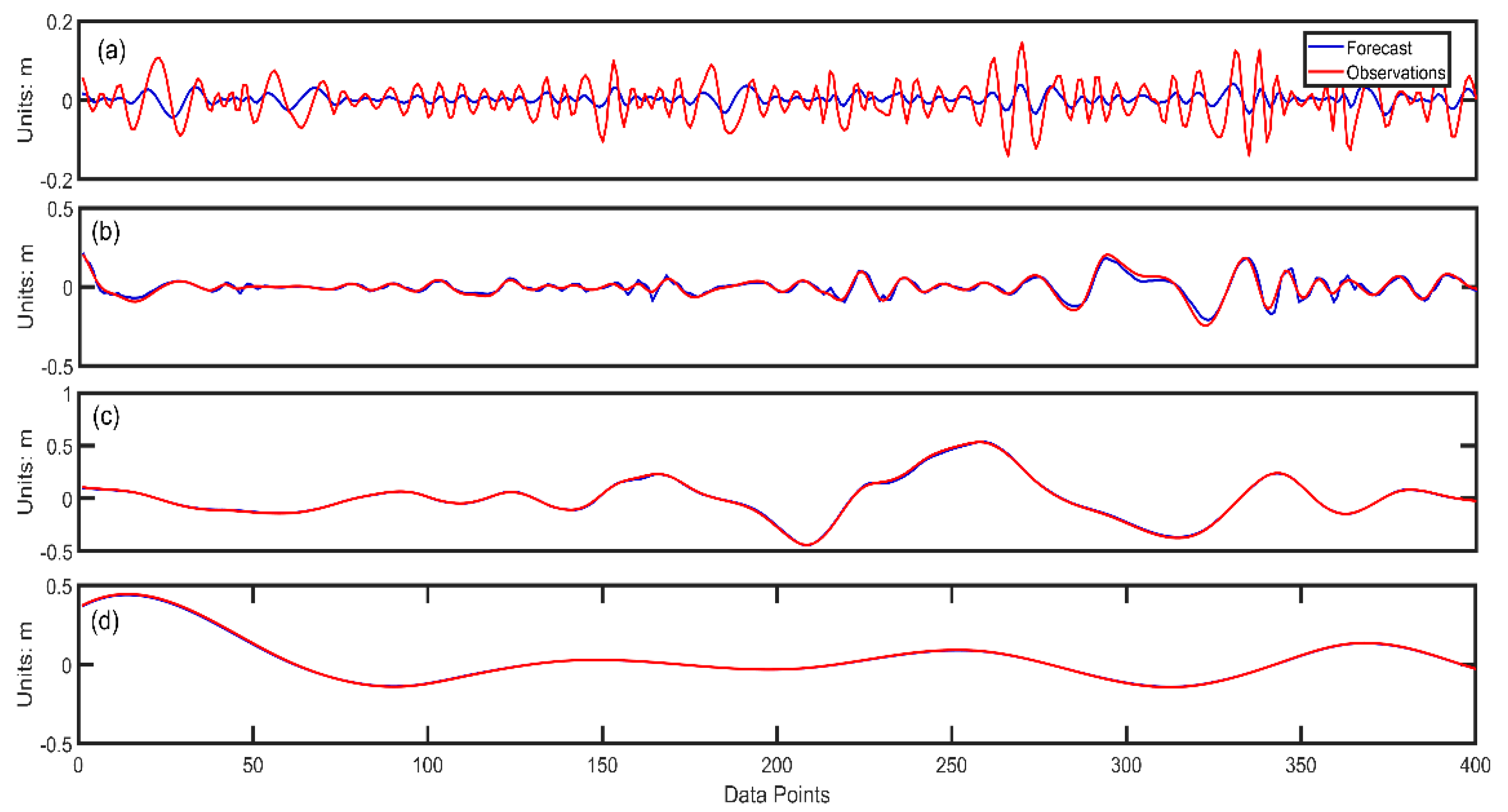
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dinwoodie, I.; Catterson, V.M.; McMillan, D. Wave height forecasting to improve off-shore access and maintenance scheduling. In Proceedings of the Power and Energy Society General Meeting (PES), Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]
- Taylor, J.W.; Jeon, J. Probabilistic Forecasting of Wave Height for Offshore Wind Turbine Maintenance. Eur. J. Oper. Res. 2018, 267, 877–890. [Google Scholar] [CrossRef]
- Guillou, N.; Lavidas, G. Wave Energy Resource Assessment for Exploitation—A review. J. Mar. Sci. Eng. 2020, 8, 705. [Google Scholar] [CrossRef]
- Chen, C.; Shiotani, S. Numerical ship navigation based on weather and ocean simulation. Ocean Eng. 2013, 69, 44–53. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Sasa, K. Statistical analysis of waves’ effects on ship navigation using high-resolution numerical wave simulation and shipboard measurements. Ocean Eng. 2021, 229, 108757. [Google Scholar] [CrossRef]
- Fazeres-Ferradosa, T.; Taveira-Pinto, F.; Vanem, E.; Reis, M.T.; Neves, L.D. Asymmetric copula-based distribution models for met-ocean data in offshore wind engineering applications. Wind Eng. 2018, 42, 304–334. [Google Scholar] [CrossRef] [Green Version]
- Fazeres-Ferradosa, T.; Welzel, M.; Schendel, A.; Baelus, L.; Santos, P.R.; Pinto, F.T. Extended characterization of damage in rubble mound scour protections. Coast. Eng. 2020, 148, 103671. [Google Scholar] [CrossRef]
- Tolman, H.L. User Manual and System Documentation of WAVEWATCH III TM Version 3.14. NOAA/NWS/NCEP/MMAB. Technical Note, May 2009; U.S. Department of Commerce, National Oceanic and Atmospheric Administration National Weather Service, National Centers for Environmental Prediction: College Park, MD, USA, 2019; p. 187.
- Booij, N.; Ris, R.C. A third-generation wave model for coastal regions 1. Model description and validation. J. Geophys. Res. Atmos. 1999, 104, 7649–7666. [Google Scholar] [CrossRef] [Green Version]
- Vanem, E.; Fazeres-Ferradosa, T.; Rosa-Santos, P.; Taveira-Pinto, F. Statistical description and modeling of extreme ocean wave conditions. Marit. Eng. 2019, 172, 124–132. [Google Scholar] [CrossRef]
- Jäger, W.S.; Nagler, T.; Czado, C.; McCall, R.T. A Statistical Simulation Method for Joint Time Series of Non-Stationary Hourly Wave Parameters. Coast. Eng. 2019, 146, 14–31. [Google Scholar] [CrossRef] [Green Version]
- Deo, M.C.; Naidu, C.S. Real Time Forecasting Using Neural Networks. Ocean Eng. 1998, 26, 191–203. [Google Scholar] [CrossRef]
- Mandal, S.; Prabaharan, N. Ocean wave forecasting using recurrent neural networks. Ocean Eng. 2006, 33, 1401–1410. [Google Scholar] [CrossRef]
- Zubier, K.M. Using an Artificial Neural Network for Wave Height Forecasting in the Red Sea. Indian J. Geo Mar. Sci. 2020, 49, 184–191. [Google Scholar]
- Ali, M.; Prasad, R. Significant wave height forecasting via an extreme learning machine model integrated with improved complete ensemble empirical mode decomposition. Renew. Sustain. Energy Rev. 2019, 104, 281–295. [Google Scholar] [CrossRef]
- Gao, S.; Huang, J.; Li, Y.; Liu, G.; Bi, F.; Bai, Z. A forecasting model for wave heights based on a long short-term memory neural network. Acta Oceanol. Sin. 2021, 40, 62–69. [Google Scholar] [CrossRef]
- Fan, S.; Xiao, N.; Dong, S. A novel model to predict significant wave height based on long short-term memory network. Ocean Eng. 2020, 205, 107298. [Google Scholar] [CrossRef]
- Zhang, B. Foreign exchange rates forecasting with an EMD-LSTM neural networks model. J. Phys. Conf. Ser. 2018, 1053, 012005. [Google Scholar] [CrossRef]
- Xuan, Y.; Yu, Y.; Wu, K. Prediction of Short-term Stock Prices Based on EMD-LSTM-CSI Neural Network Method. In Proceedings of the 2020 5th IEEE International Conference on Big Data Analytics (ICBDA), Xiamen, China, 8–11 May 2020; pp. 135–139. [Google Scholar]
- Yang, Y.; Yang, Y.; Xiao, J. A Hybrid Prediction Method for Stock Price Using LSTM and Ensemble EMD. Complexity 2002, 2020, 6431712. [Google Scholar]
- Zheng, H.; Yuan, J. Short-Term Load Forecasting Using EMD-LSTM Neural Networks with a Xgboost Algorithm for Feature Importance Evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Wen, D. Empirical mode decomposition based long short-term memory neural network forecasting model for the short-term metro passenger flow. PLoS ONE 2019, 15, e0231199. [Google Scholar] [CrossRef]
- Dai, S.; Chen, Q. Time series prediction based on EMD-LSTM model. J. Shenzhen Univ. Sci. Eng. 2020, 37, 265–270. [Google Scholar] [CrossRef]
- Liu, D.; Jiang, W.; Mu, L.; Wang, S. Streamflow Prediction Using Deep Learning Neural Network: Case Study of Yangtze River. IEEE Access 2020, 8, 90069–90086. [Google Scholar] [CrossRef]
- Guo, Y.; Cao, X. El Niño Index Prediction Using Deep Learning with Ensemble Empirical Mode Decomposition. Symmetry 2020, 12, 893. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, S. Wind Speed Forecasting Method Using EEMD and the Combination Forecasting Method Based on GPR and LSTM. Sustainability 2018, 10, 3693. [Google Scholar] [CrossRef] [Green Version]
- Tang, G.; Du, H. An EMD-PSO-LSSVM hybrid model for significant wave height prediction. Ocean Sci. Discuss. 2021. [Google Scholar] [CrossRef]
- Raj, N.; Brown, J. An EEMD-BiLSTM Algorithm Integrated with Boruta Random Forest Optimiser for Significant Wave Height Forecasting along Coastal Areas of Queensland, Australia. Remote Sens. 2021, 13, 1456. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Computation 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. R. Soc. Lond. Proc. Ser. A 1998, 454, 903–998. [Google Scholar] [CrossRef]
- Bethel, B.J.; Dong, C.; Zhou, S.; Cao, Y. Bidirectional Modeling of Surface Winds and Significant Wave Heights in the Caribbean Sea. J. Mar. Sci. Eng. 2021, 9, 547. [Google Scholar] [CrossRef]
- Ibarra-Berastegi, G.; Sáenz, J.; Esnaola, G.; Ezcurra, A.; Ulazia, A.; Rojo, N.; Gallastegui, G. Wave Energy Forecasting at Three Coastal Buoys in the Bay of Biscay. IEEE J. Ocean. Eng. 2016, 41, 923–929. [Google Scholar] [CrossRef]
- Mérigaud, A.; Ramos, V. Ocean forecasting for wave energy production. J. Mar. Res. 2017, 75, 459–505. [Google Scholar] [CrossRef] [Green Version]
- Ni, C. Data-driven models for short-term ocean wave power forecasting. IET Renew. Power Gener. 2021, 1–9. [Google Scholar] [CrossRef]
- Wang, T.; Yang, Z. A Sensitivity Analysis of the Wind Forcing Effect on the Accuracy of Large-Wave Hindcasting. J. Mar. Sci. Eng. 2018, 6, 139. [Google Scholar] [CrossRef] [Green Version]
- Kuznetsova, A.; Baydakov, G. Wind Waves Modeling Under Hurricane Wind Conditions. J. Phys. Conf. Ser. 2019, 1163, 012054. [Google Scholar] [CrossRef]
- Ding, Y.; Ding, T. Simulation and Prediction of Storm Surges and Waves Using a Fully Integrated Process Model and a Parametric Cyclonic Wind Model. J. Geophys. Res. Ocean. 2020, 25, e2019JC015793. [Google Scholar] [CrossRef]
- Kohno, N.; Dube, S.K. Recent Progress in Storm Surge Forecasting. Trop. Cyclone Res. Rev. 2018, 7, 128–139. [Google Scholar]
- Yang, K.; Paramygin, V.A. A Rapid Forecasting and Mapping System of Storm Surge and Coastal Flooding. Weather Forecast. 2020, 35, 1663–1681. [Google Scholar] [CrossRef] [Green Version]
- Bozorgzadeh, L.; Bakhtiari, M. Forecasting of Wind-Wave Height by Using Adaptive NeuroFuzzy Inference System and Decision Tree. J. Soft Comput. Civ. Eng. 2019, 3, 22–36. [Google Scholar]
- Chen, S.; Wang, Y. Improving Coastal Ocean Wave Height Forecasting during Typhoons by using Local Meteorological and Neighboring Wave Data in Support Vector Regression Models. J. Mar. Sci. Eng. 2020, 8, 149. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.; Stefanakos, C. Multi-Step-Ahead Forecasting of Wave Conditions Based on a Physics-Based Machine Learning (PBML) Model for Marine Operations. J. Mar. Sci. Eng. 2020, 8, 992. [Google Scholar] [CrossRef]
- Wang, H.; Yang, J. Estimation of Significant Wave Heights from ASCAT Scatterometer Data via Deep Learning Network. Remote Sens. 2021, 13, 195. [Google Scholar] [CrossRef]
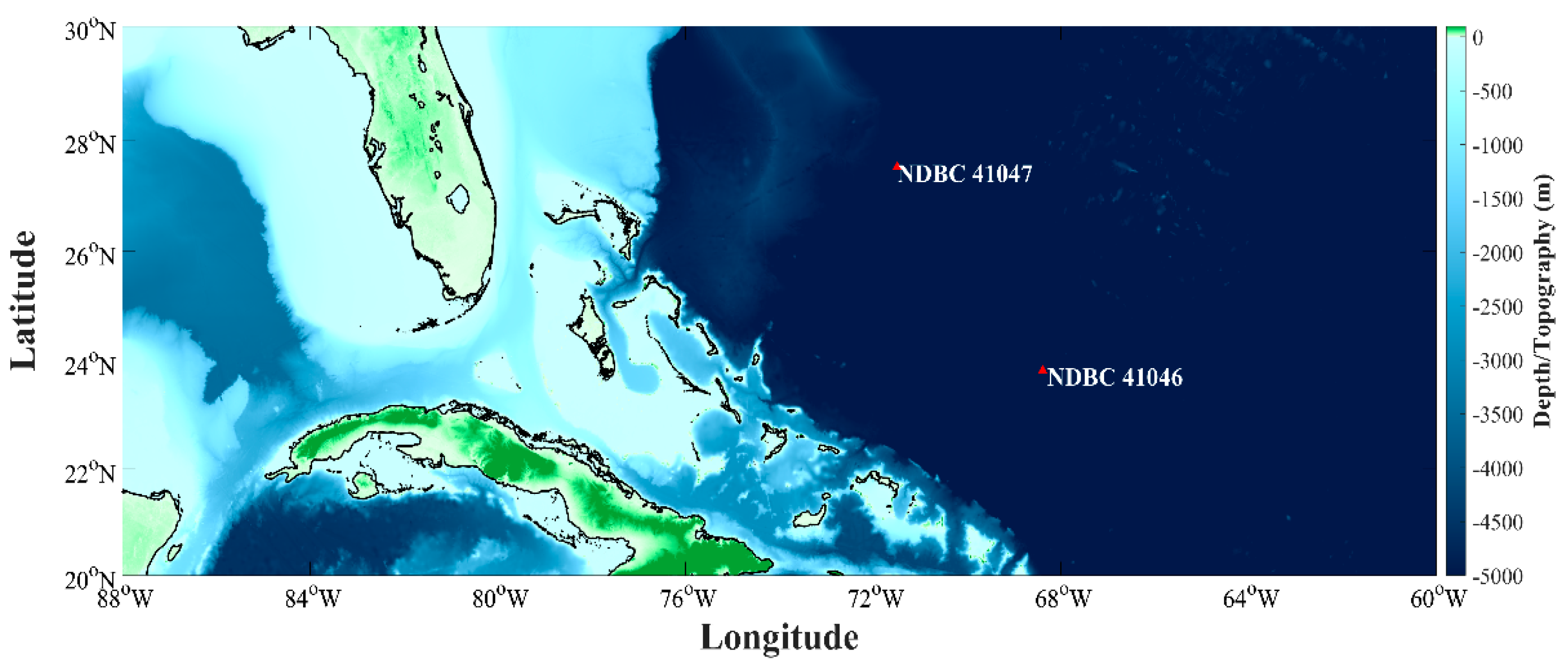
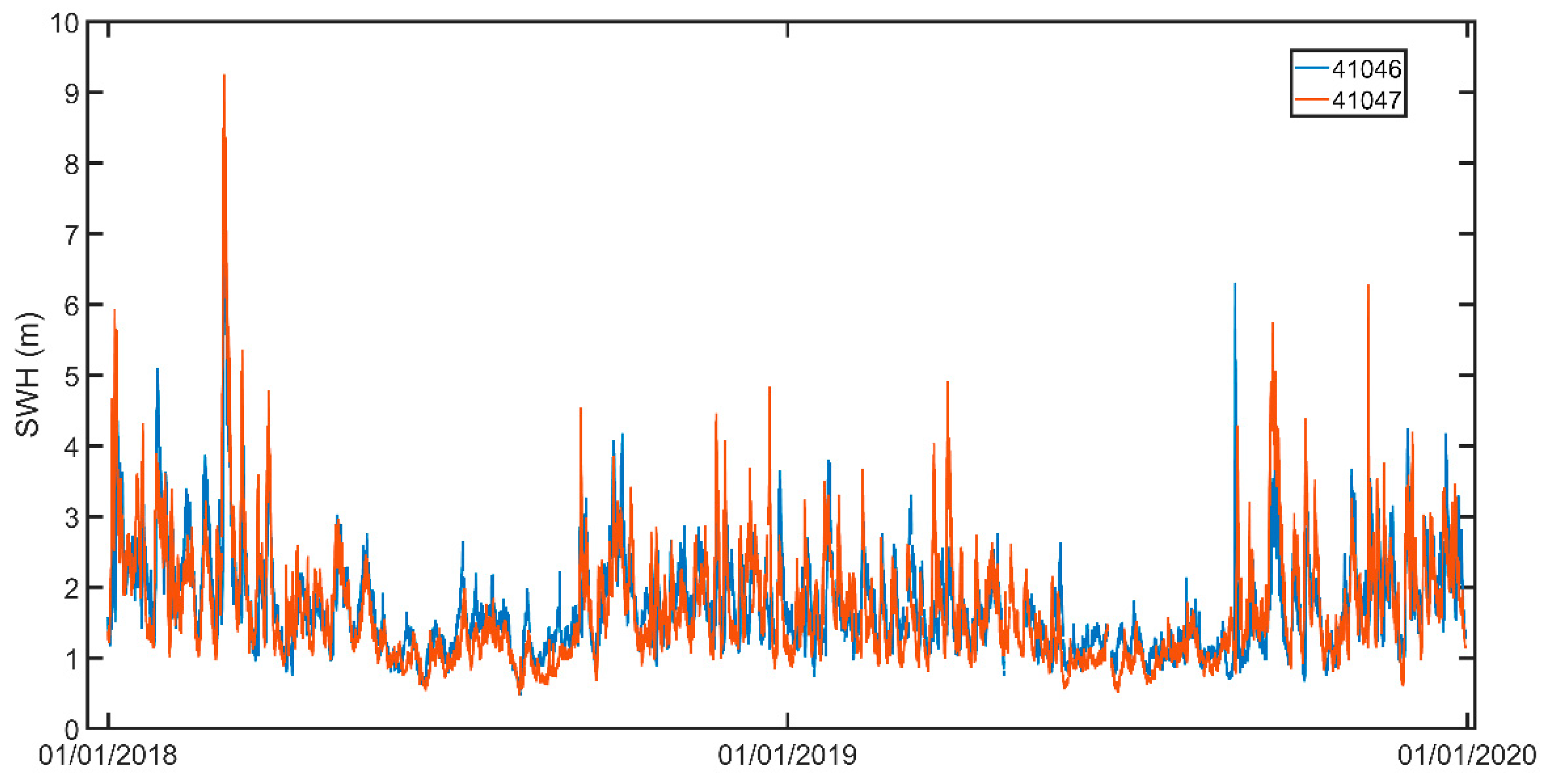
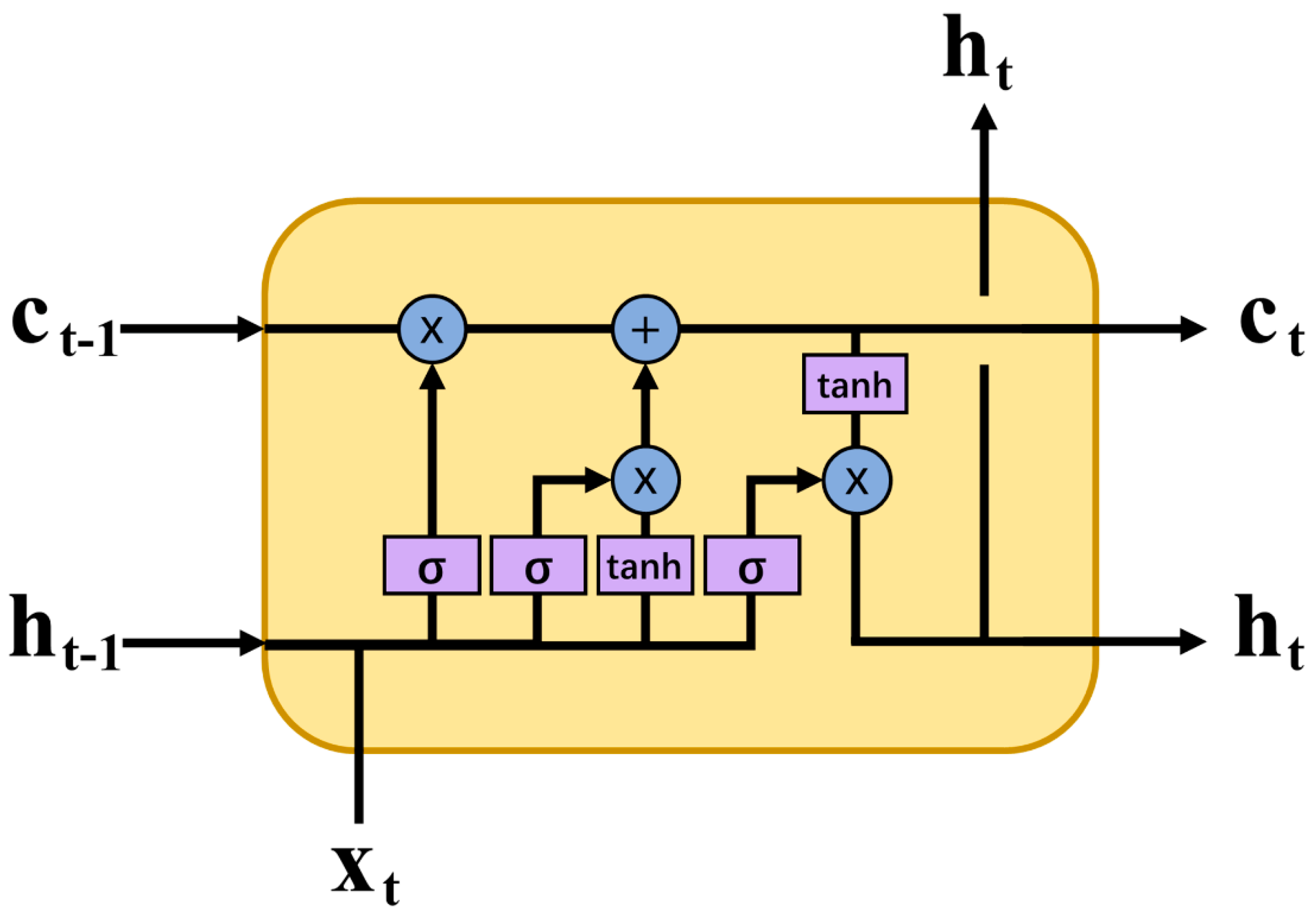


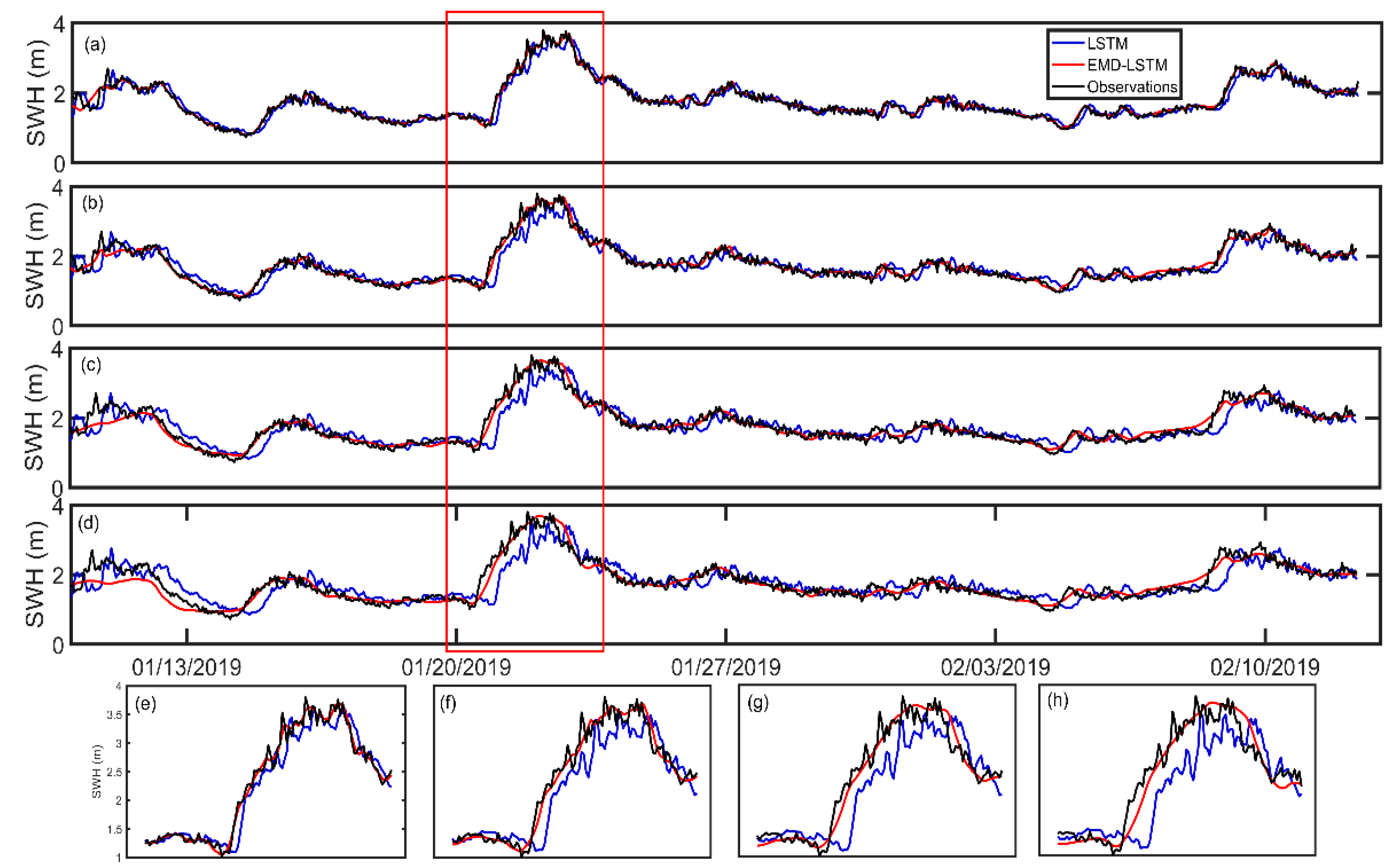

| Buoy ID | Latitude (°N) | Longitude (°W) | Water Depth (m) | No. of Observations before Interpolation | No. of Observations after Interpolation |
|---|---|---|---|---|---|
| 41046 | 23.822 | 68.384 | 5549 | 17,420 | 17,520 |
| 41047 | 27.514 | 71.494 | 5321 | 17,402 | 17,520 |
| LSTM | EMD-LSTM | Degree of Improvement | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Forecast Hours | RMSE (m) | MAPE (%) | R | RMSE (m) | MAPE (%) | R | RMSE (%) | MAPE (%) | R (%) | |
| 41046 | 3 | 0.15 | 6.4 | 0.97 | 0.11 | 1.41 | 0.985 | 30.1 | 77.8 | 1.5 |
| 6 | 0.22 | 9.2 | 0.92 | 0.12 | 6.68 | 0.979 | 44.6 | 27.4 | 6.4 | |
| 9 | 0.28 | 11.1 | 0.88 | 0.16 | 10.20 | 0.960 | 42.4 | 7.8 | 9.1 | |
| 12 | 0.33 | 13.2 | 0.84 | 0.19 | 12.01 | 0.950 | 41.1 | 9.2 | 13.1 | |
| 24 | 0.45 | 19.0 | 0.67 | 0.26 | 11.41 | 0.900 | 41.8 | 39.9 | 34.3 | |
| 48 | 0.58 | 31.1 | 0.41 | 0.38 | 18.90 | 0.790 | 33.7 | 39.2 | 92.7 | |
| 72 | 0.60 | 33.7 | 0.32 | 0.44 | 18.70 | 0.690 | 26.1 | 44.5 | 115.6 | |
| 41047 | 3 | 0.19 | 7.2 | 0.97 | 0.10 | 3.96 | 0.991 | 46.8 | 44.9 | 2.1 |
| 6 | 0.28 | 11.3 | 0.93 | 0.14 | 5.51 | 0.982 | 50.2 | 51.2 | 5.6 | |
| 9 | 0.35 | 13.1 | 0.88 | 0.18 | 7.38 | 0.971 | 49.2 | 43.7 | 10.3 | |
| 12 | 0.40 | 15.0 | 0.83 | 0.21 | 8.42 | 0.957 | 47.0 | 43.9 | 15.3 | |
| 24 | 0.55 | 22.0 | 0.67 | 0.28 | 11.76 | 0.922 | 48.2 | 46.5 | 37.6 | |
| 48 | 0.67 | 33.4 | 0.43 | 0.47 | 20.35 | 0.769 | 29.9 | 39.1 | 78.9 | |
| 72 | 0.71 | 38.8 | 0.34 | 0.48 | 21 | 0.757 | 32.2 | 45.9 | 122.6 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Bethel, B.J.; Sun, W.; Zhao, Y.; Xie, W.; Dong, C. Improving Significant Wave Height Forecasts Using a Joint Empirical Mode Decomposition–Long Short-Term Memory Network. J. Mar. Sci. Eng. 2021, 9, 744. https://doi.org/10.3390/jmse9070744
Zhou S, Bethel BJ, Sun W, Zhao Y, Xie W, Dong C. Improving Significant Wave Height Forecasts Using a Joint Empirical Mode Decomposition–Long Short-Term Memory Network. Journal of Marine Science and Engineering. 2021; 9(7):744. https://doi.org/10.3390/jmse9070744
Chicago/Turabian StyleZhou, Shuyi, Brandon J. Bethel, Wenjin Sun, Yang Zhao, Wenhong Xie, and Changming Dong. 2021. "Improving Significant Wave Height Forecasts Using a Joint Empirical Mode Decomposition–Long Short-Term Memory Network" Journal of Marine Science and Engineering 9, no. 7: 744. https://doi.org/10.3390/jmse9070744
APA StyleZhou, S., Bethel, B. J., Sun, W., Zhao, Y., Xie, W., & Dong, C. (2021). Improving Significant Wave Height Forecasts Using a Joint Empirical Mode Decomposition–Long Short-Term Memory Network. Journal of Marine Science and Engineering, 9(7), 744. https://doi.org/10.3390/jmse9070744







