Vertical Profile Diving and Floating Motion Control of the Underwater Glider Based on Fuzzy Adaptive LADRC Algorithm
Abstract
:1. Introduction
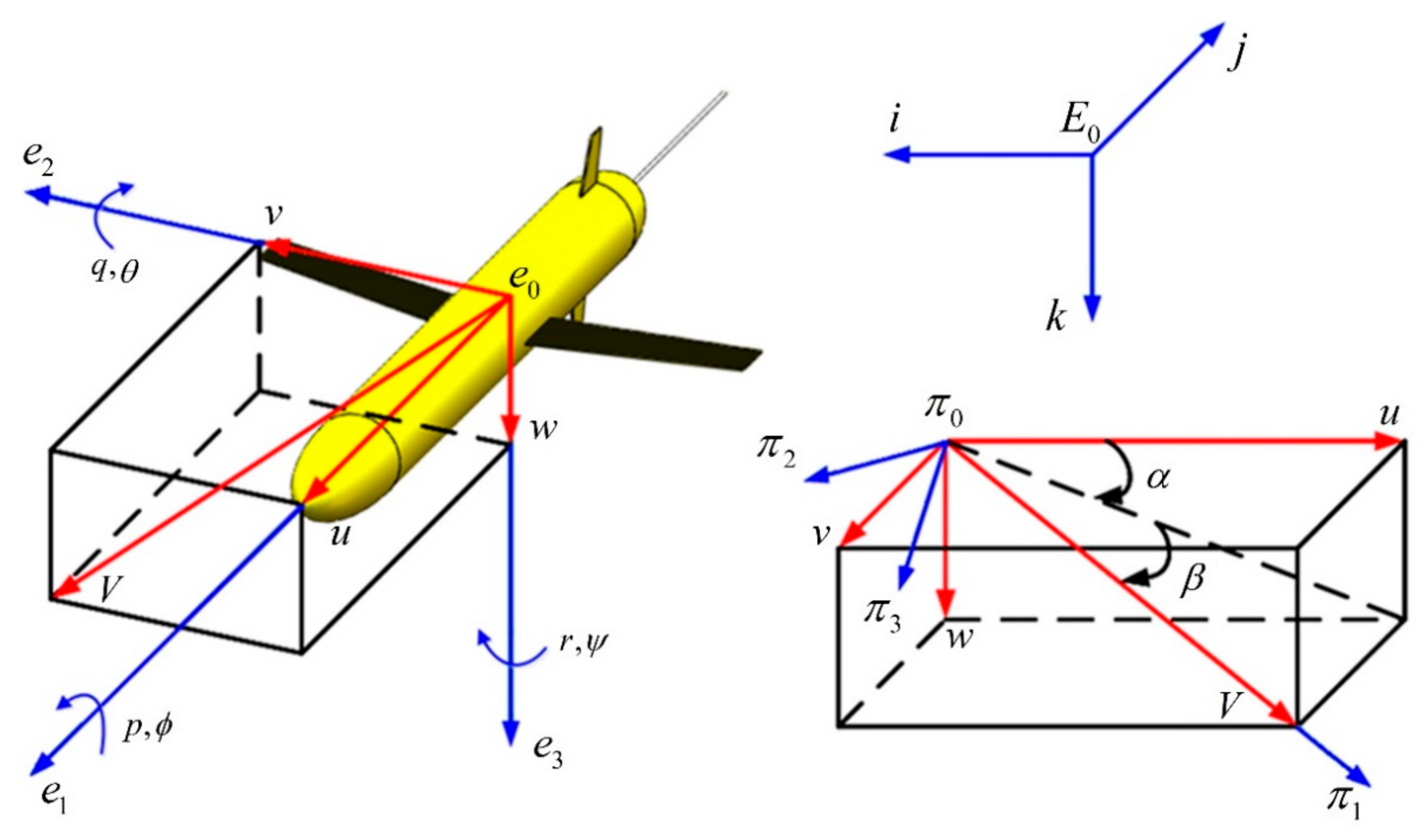
2. Dynamic Model of the Underwater Glider
3. Design of the Fuzzy Adaptive LADRC Controller
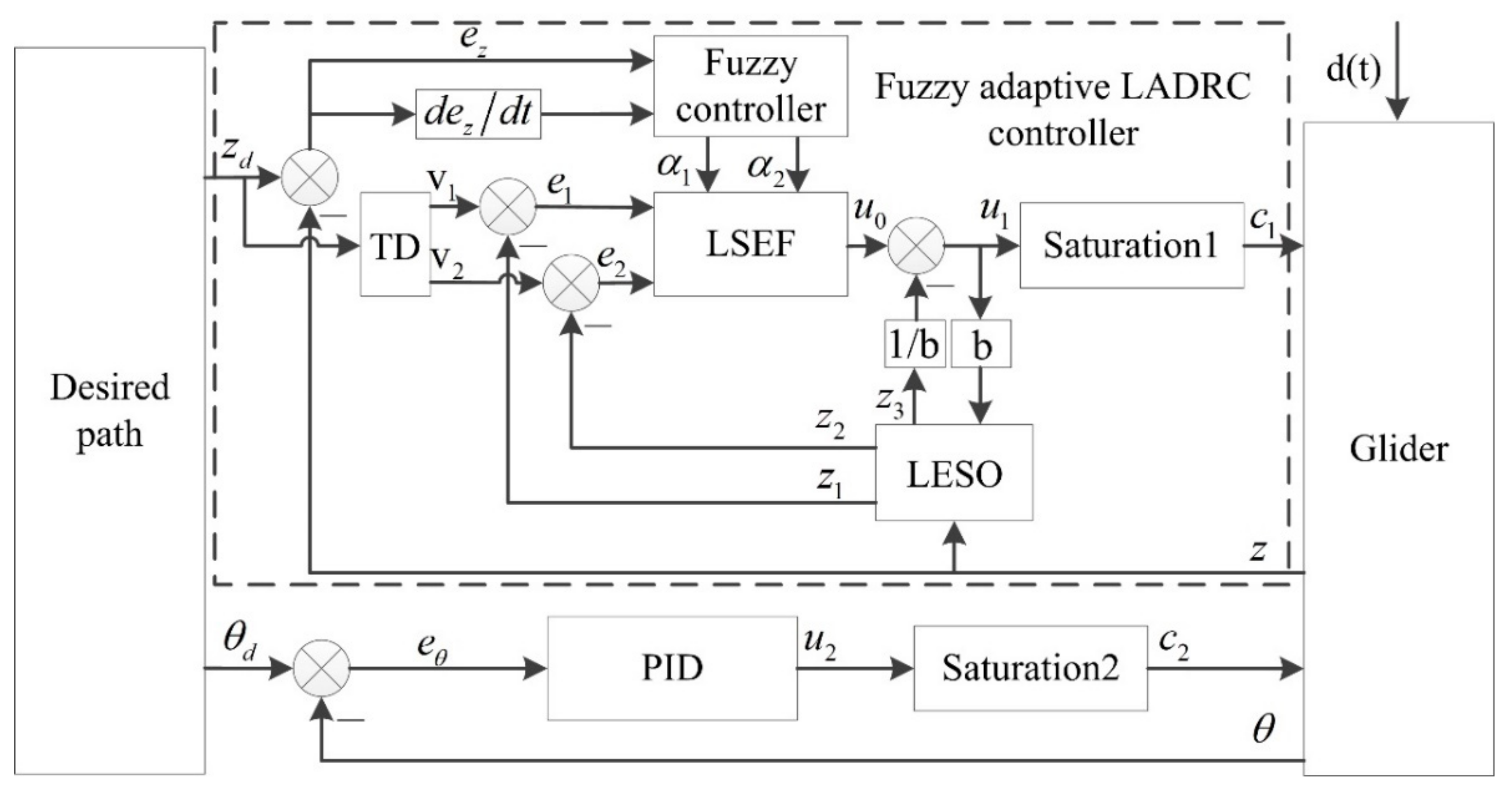
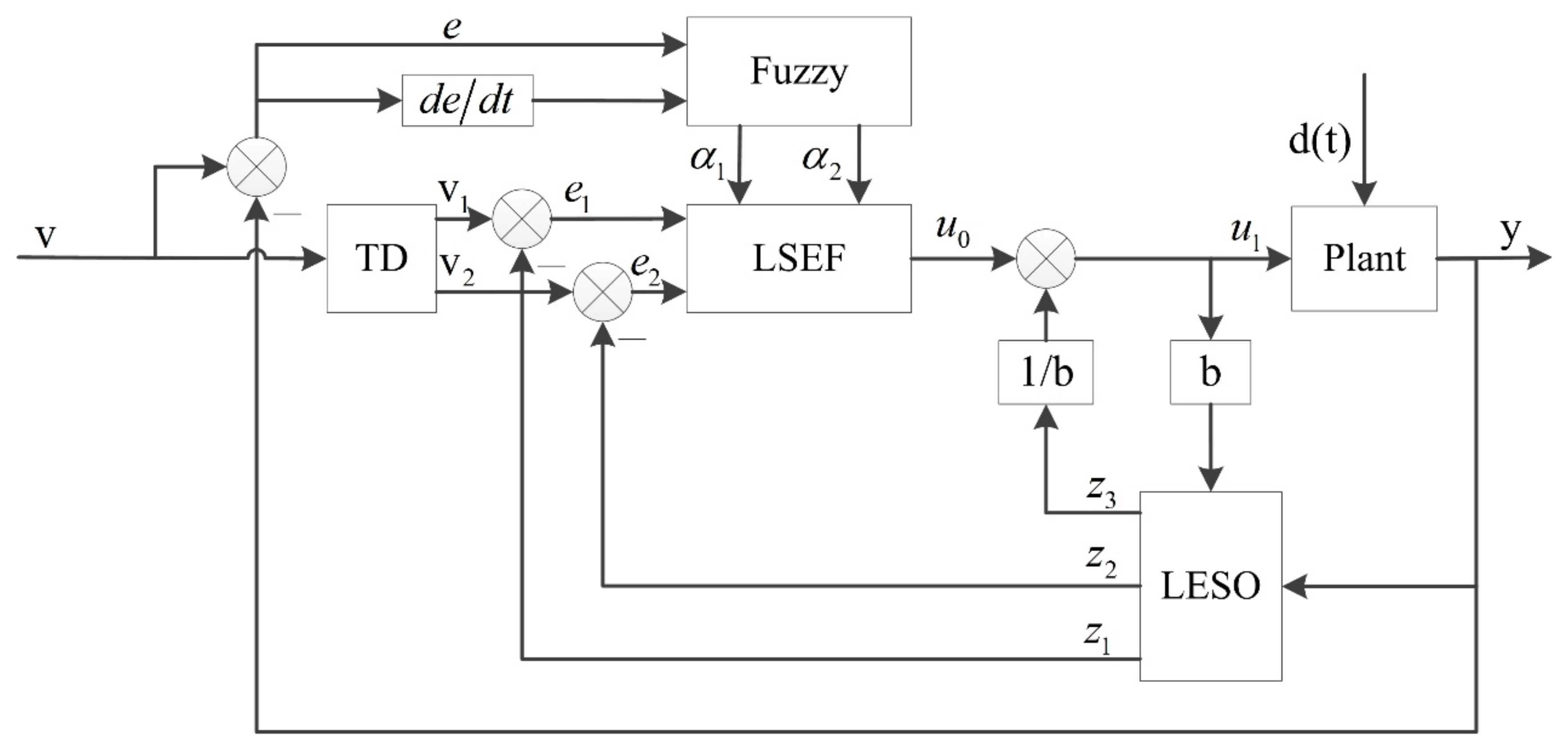
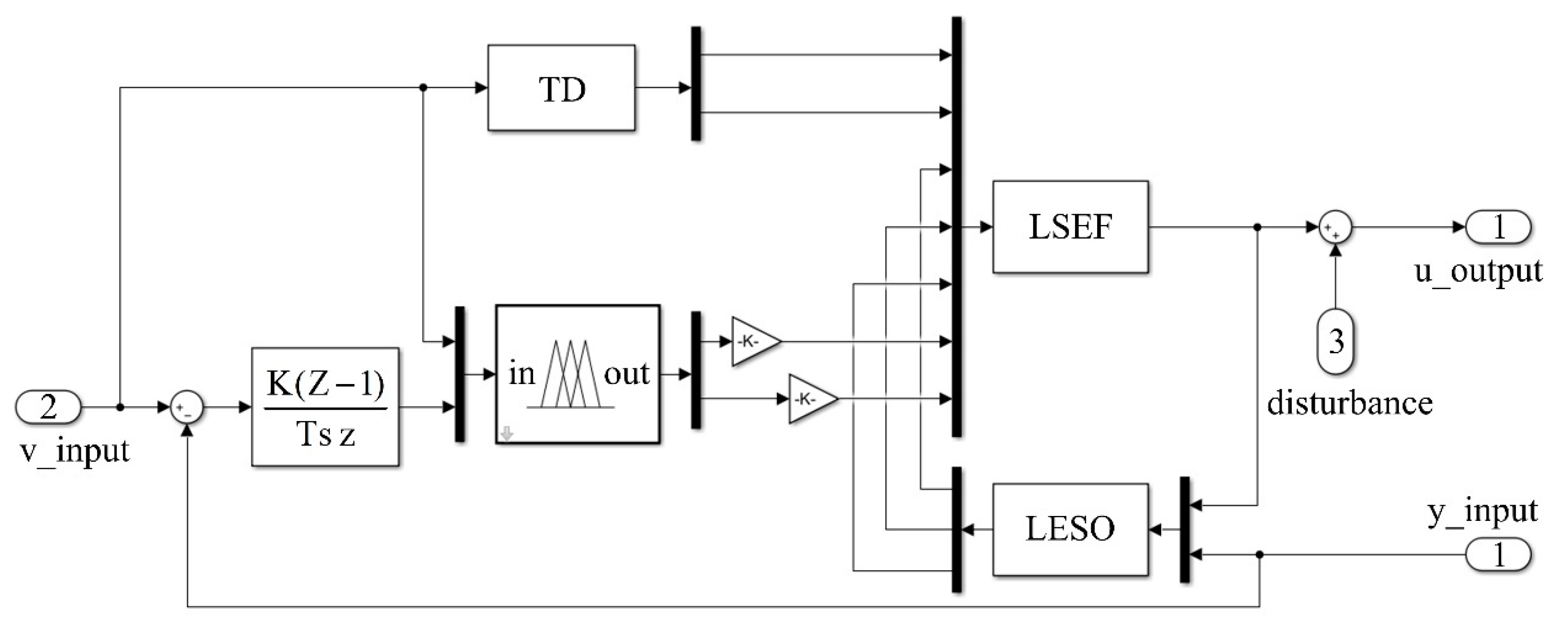
3.1. Fuzzy Adaptive LADRC Control Block Diagram
3.2. Fuzzy Adaptive LADRC Controller
- Construction of the control structure;
- Estimating the value of and set other LADRC parameters;
- Finding out the variation laws of e, ec and , according to the engineering practice, where ec is the differential value of the diving depth error e of the underwater glider;
- Design the fuzzy membership function and establish the fuzzy law.
3.2.1. LADRC Controller
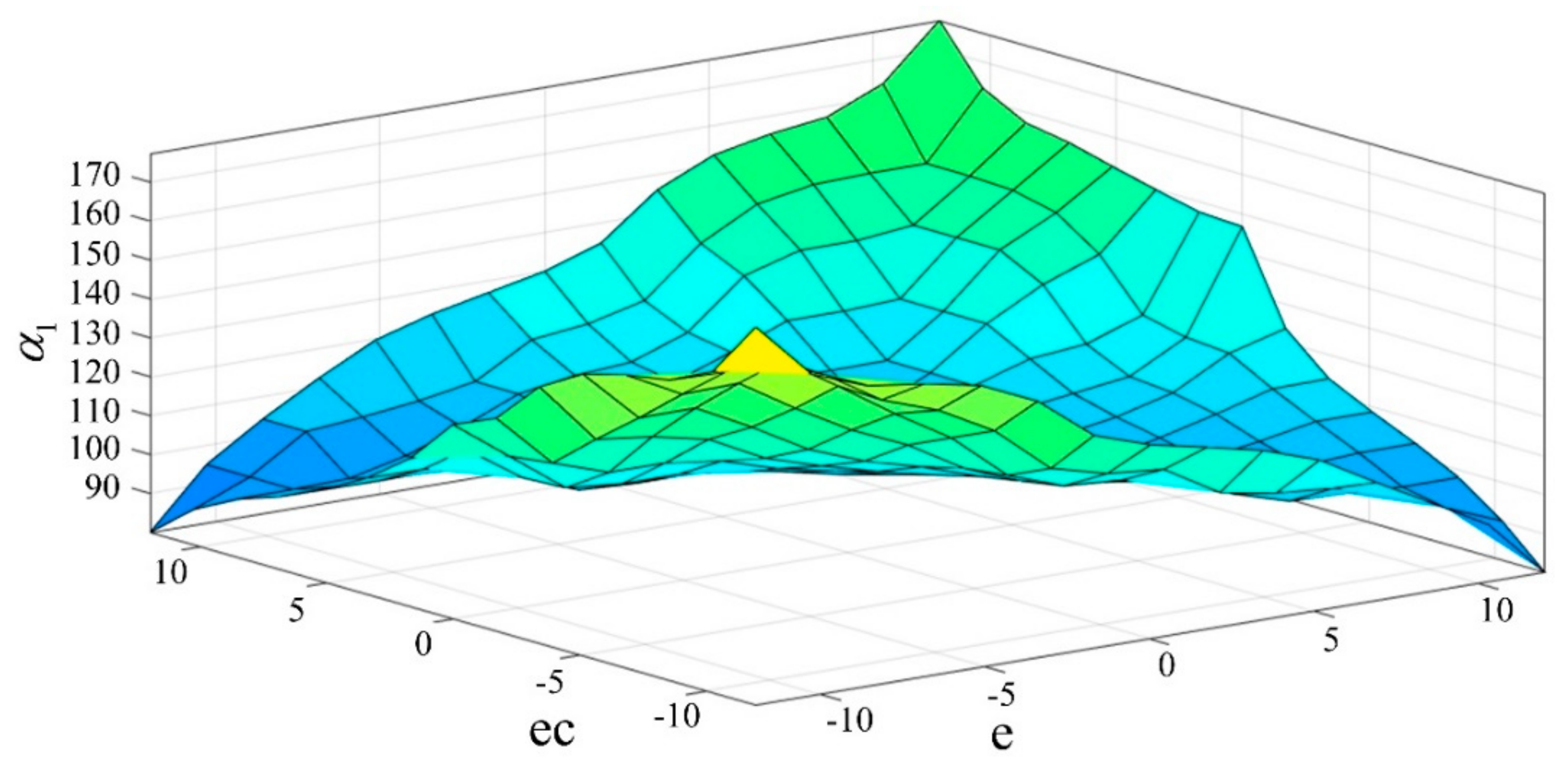
3.2.2. Design of Fuzzy Controller
- When the deviation |e| is large, the system is in the rising stage, and in order to improve the system response speed, it should take a larger . Meanwhile, |e| of the instantaneously large may lead to the differential oversaturation and make the control effect beyond the permitted range, so take a smaller ;
- When the control system is in normal operation, |e| and |ec| are medium, and in order to make the depth with a small overshoot, should be taken smaller. At this time, the value of the impact on the system is larger, should take a smaller value;
- When |e| is small, should be increased appropriately so that the system has good steady-state performance. In order to prevent the system from oscillation near the set value, while taking into account the performance of the system against interference, the value must be properly selected, as is mainly based on |ec| to regulate; when |ec| larger, choose a smaller , and vice versa to take a larger .
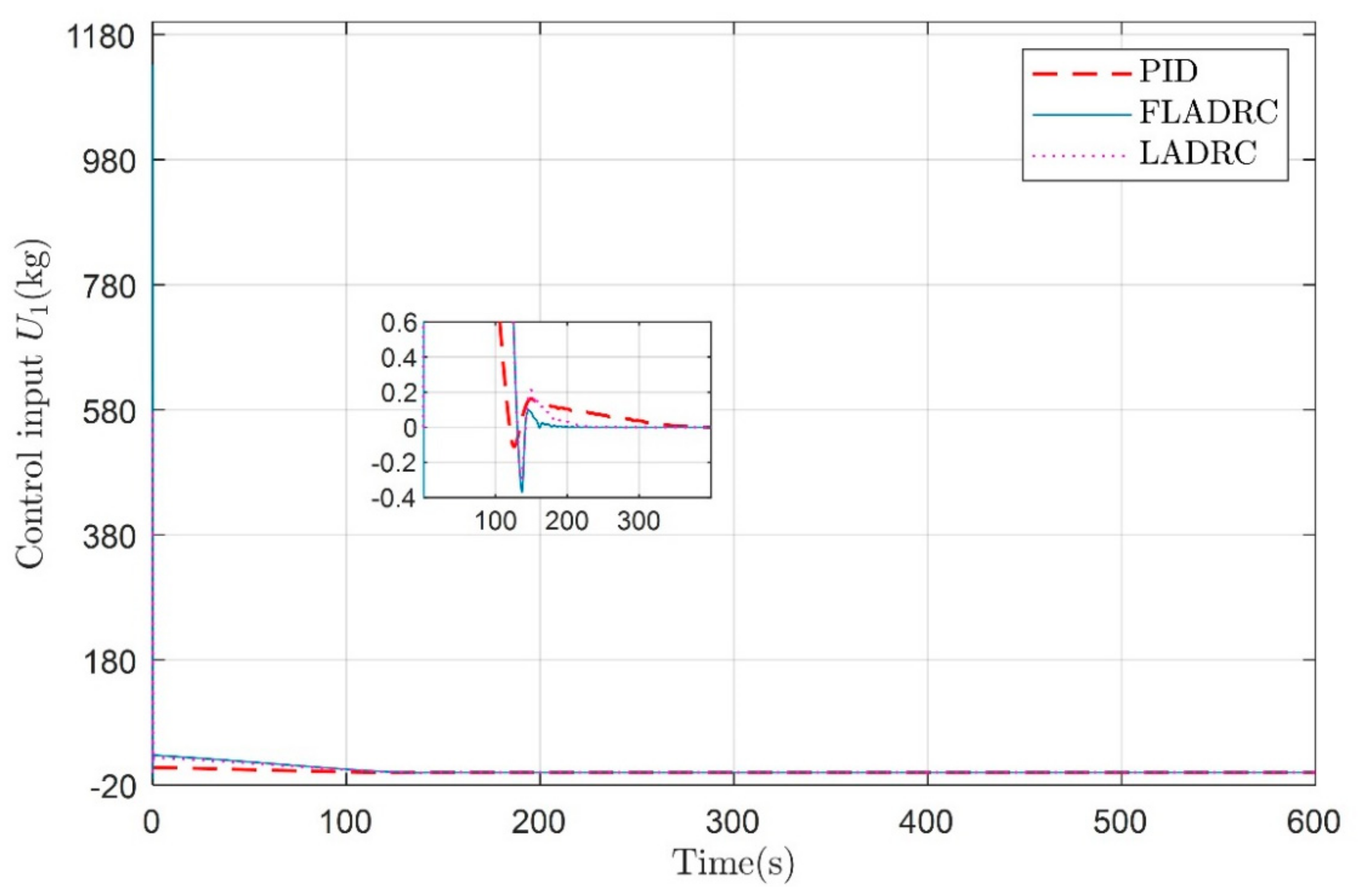
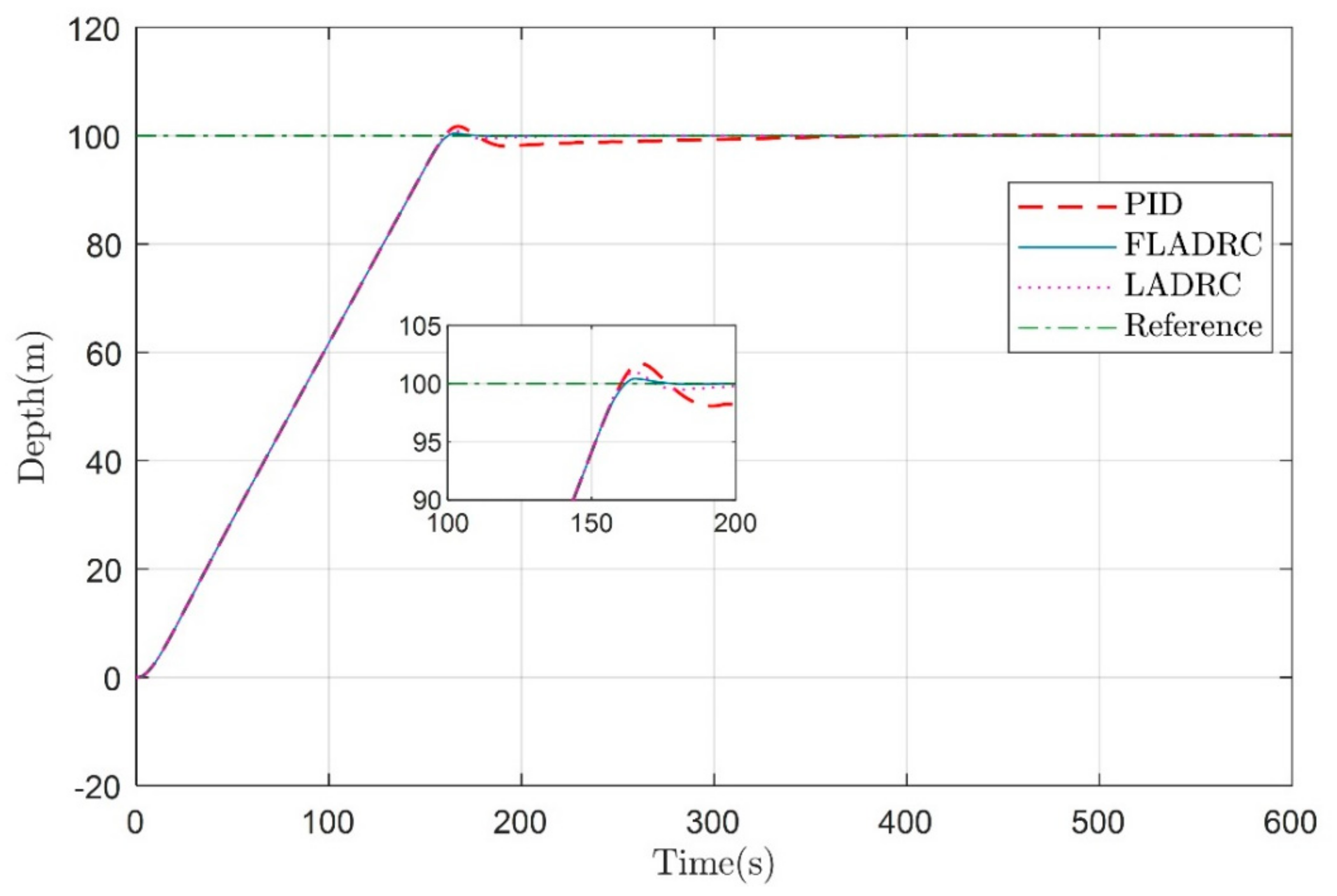
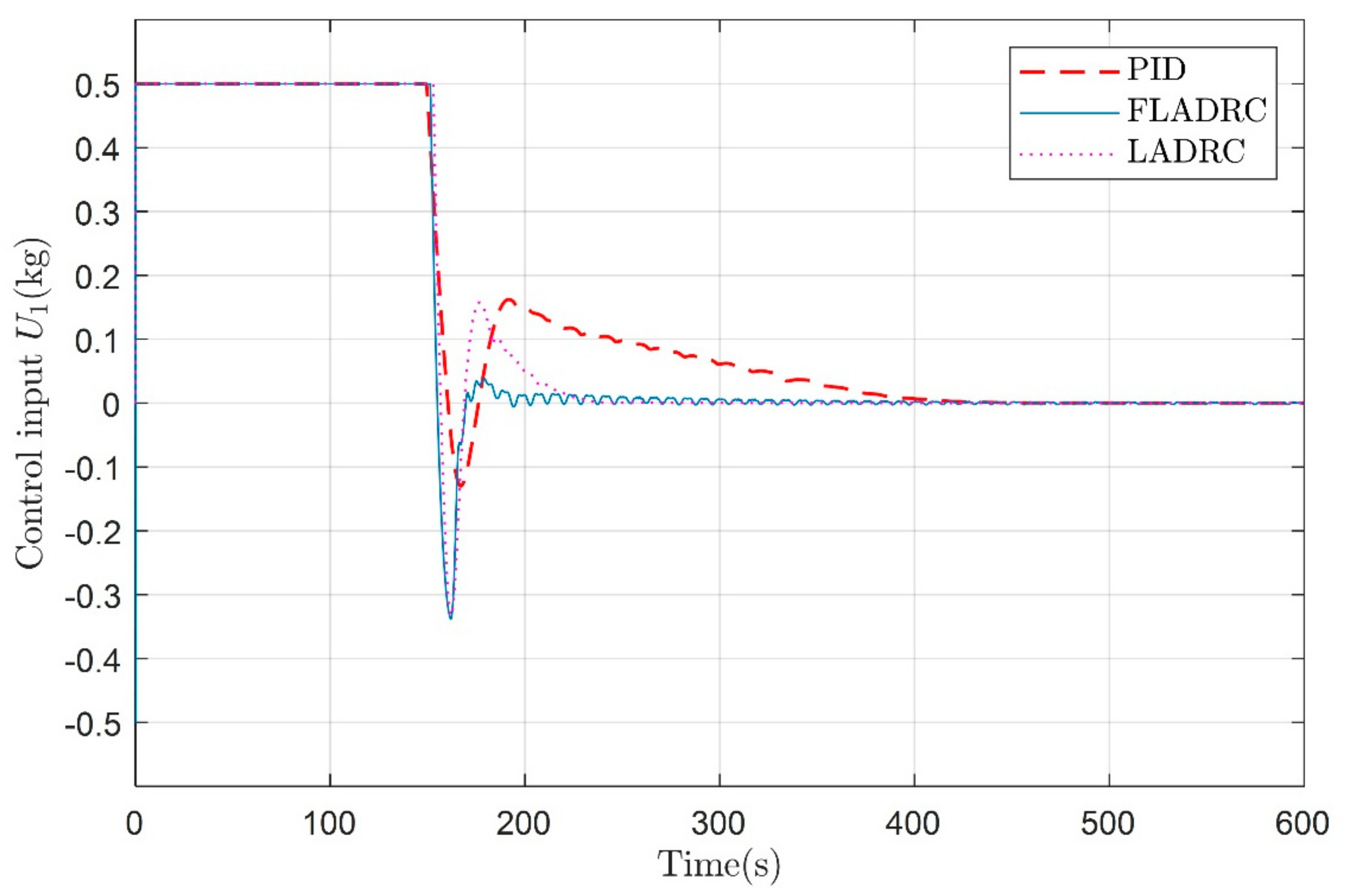
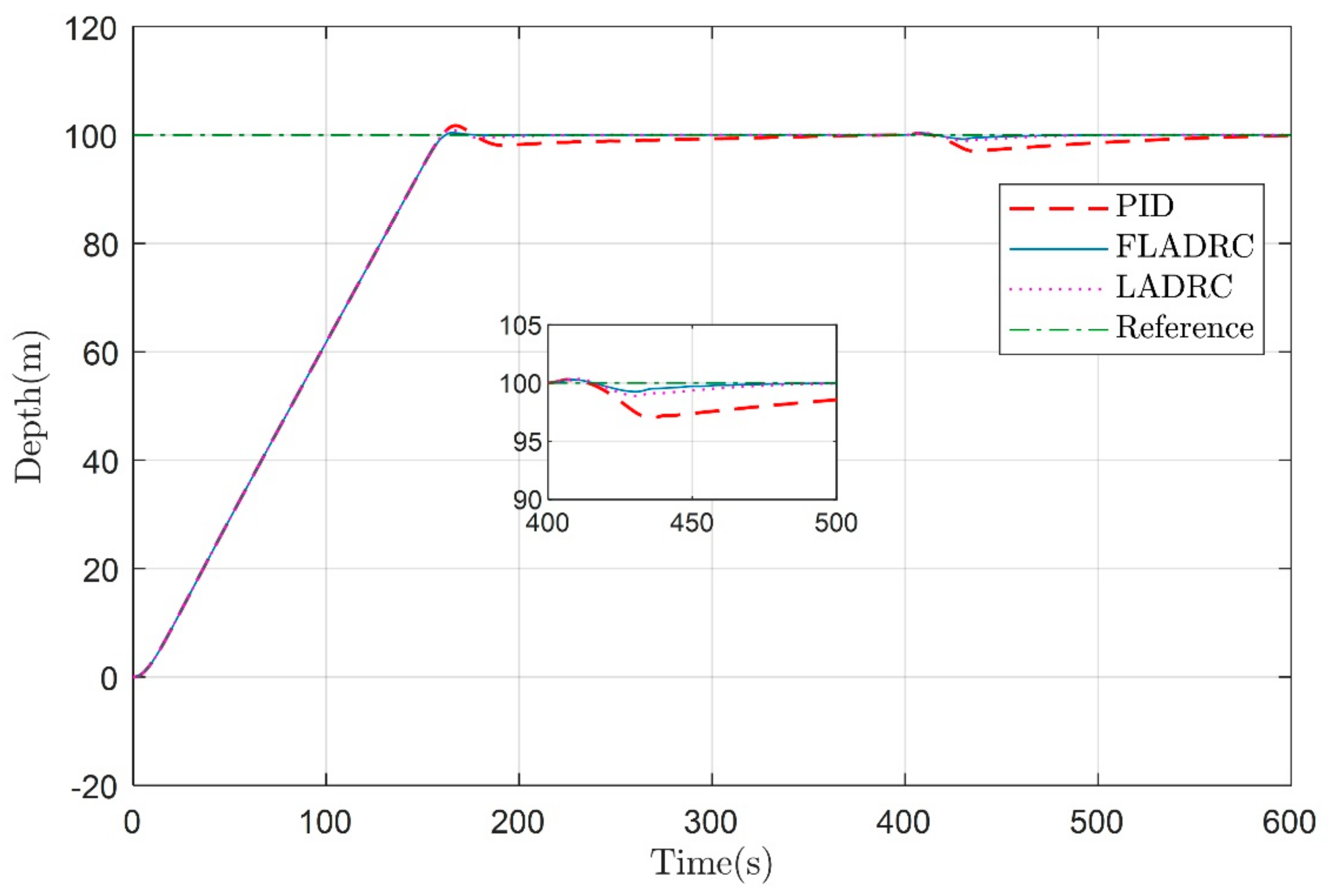
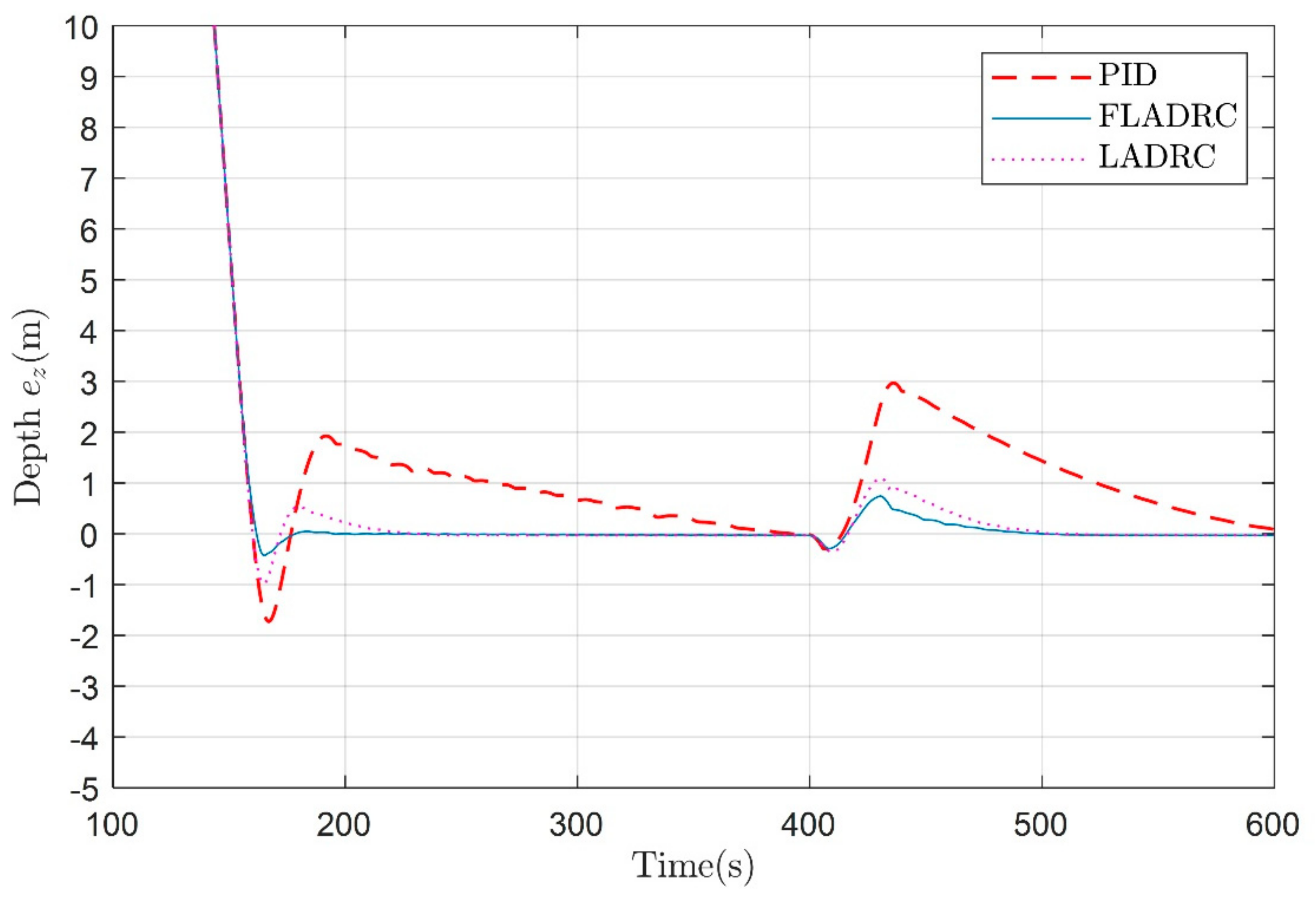
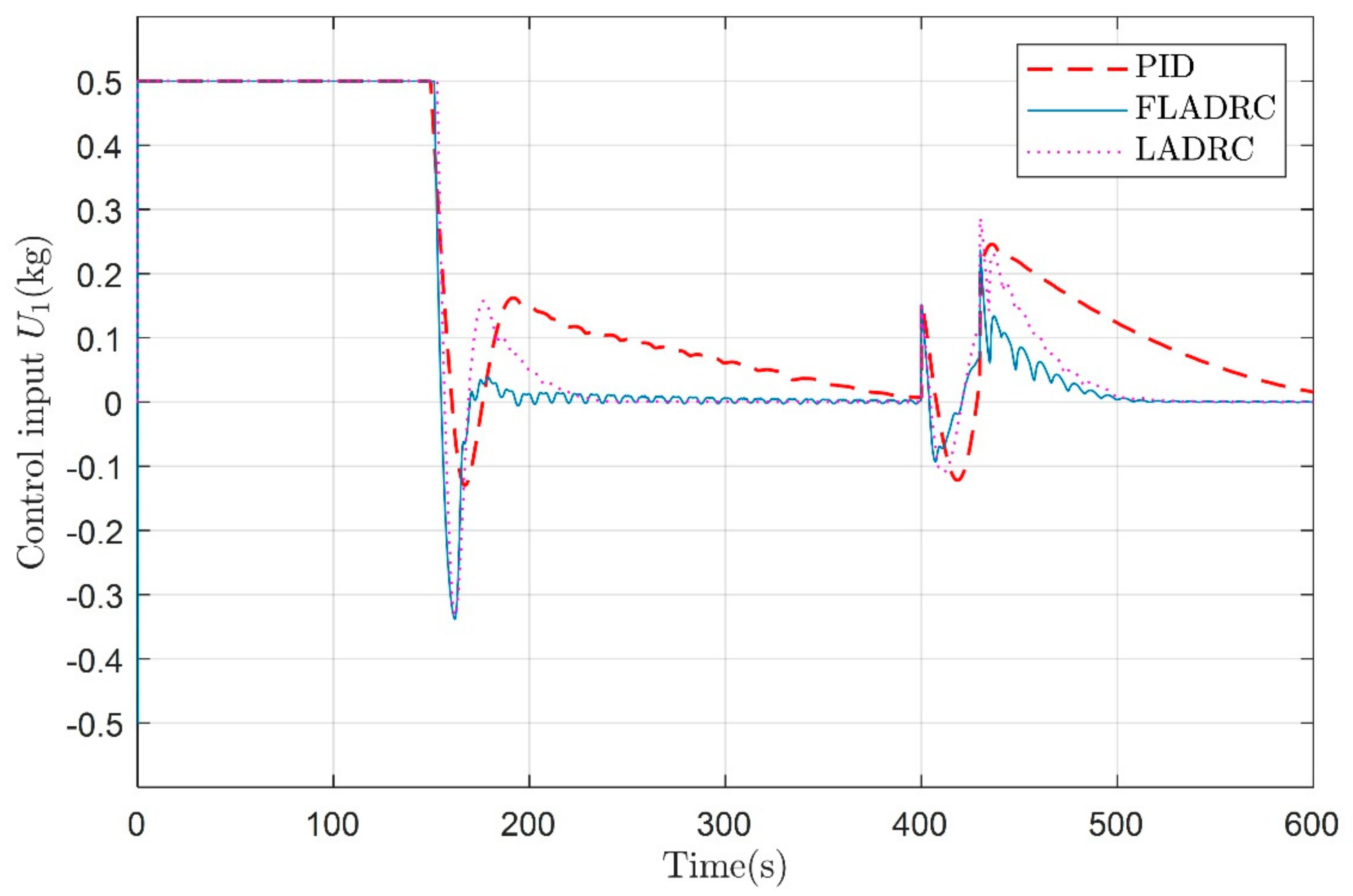
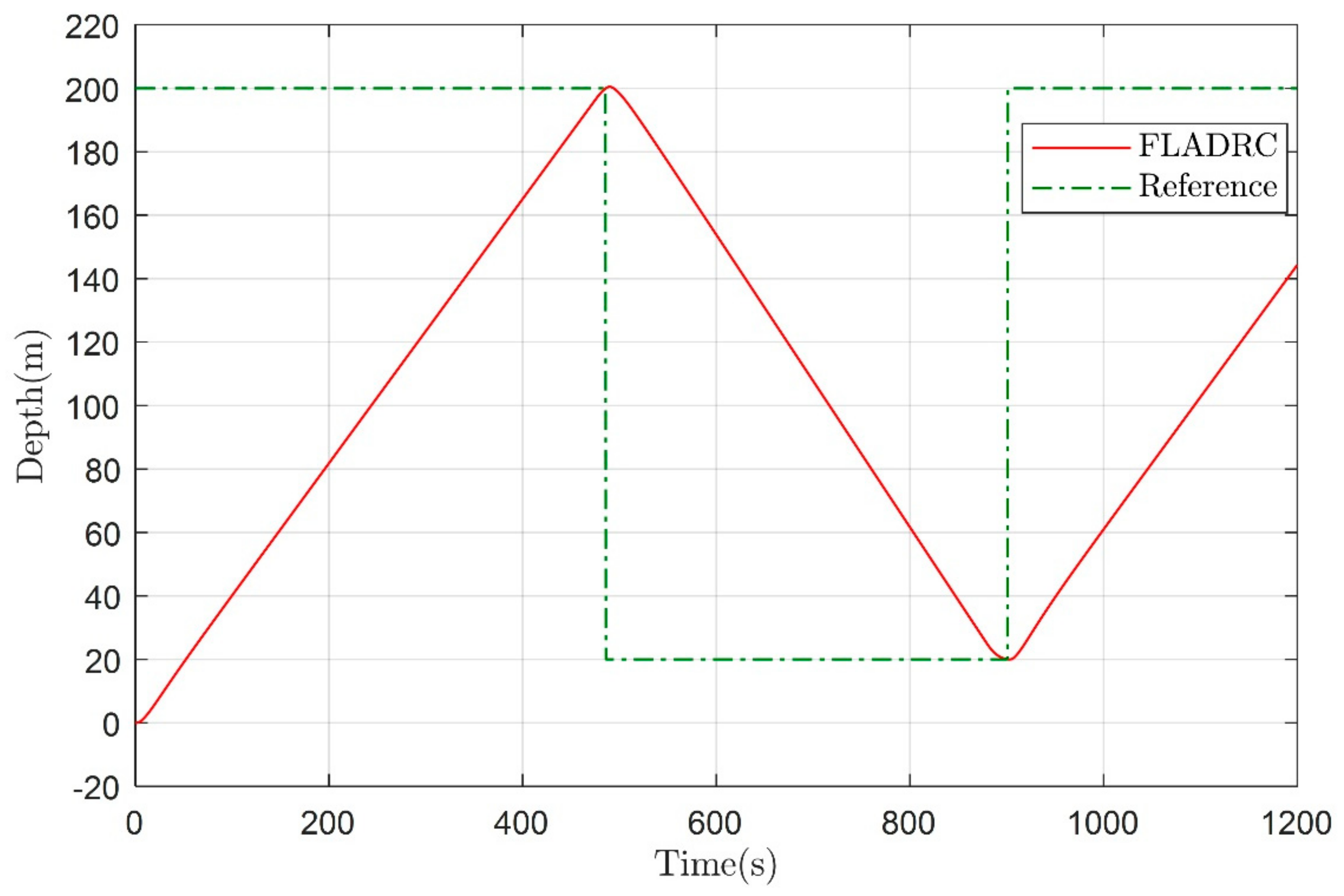
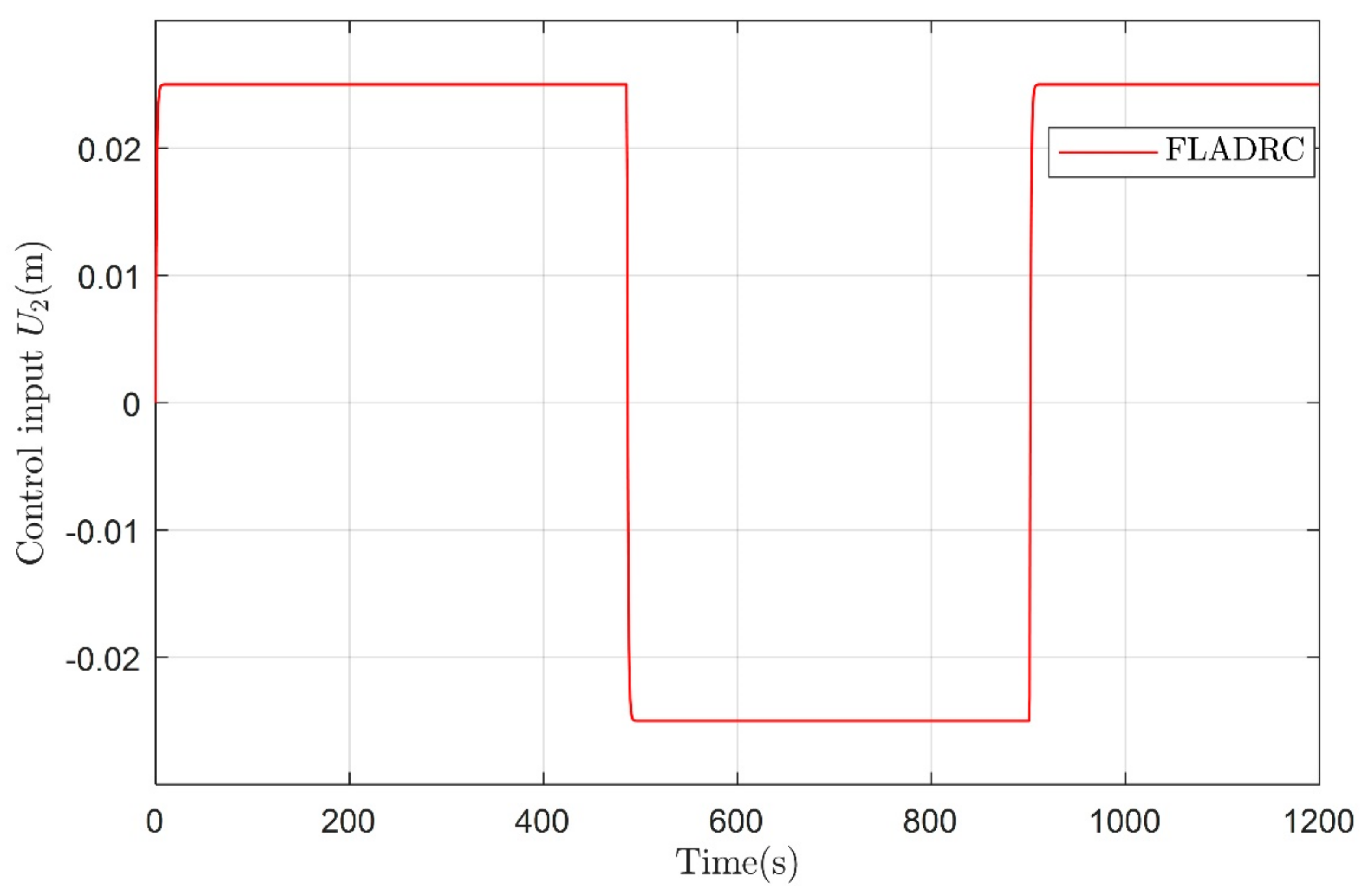
4. Simulation and Results Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Abbreviations and Variable | Definition |
|---|---|
| PID | Proportion integral differential |
| ADRC | Active disturbance rejection control |
| LADRC | Linear active disturbance rejection control |
| FLADRC | Fuzzy adaptive linear active disturbance rejection control |
| TD | Tracking differentiator |
| LSEF | Linear state error feedback |
| LESO | Linear extended state observer |
| LQR | Linear quadratic regulator |
| DSMC | Dynamic sliding mode control |
| Position of the origin of the body coordinate system | |
| Cross-roll angle | |
| Pitch angle | |
| Yaw angle | |
| Linear velocity in the body coordinate system | |
| , , | Angular velocity in the body coordinate system |
| Attack angle | |
| β | Sideslip angle |
| , , | Added mass |
| , , | Added moment of inertia |
| , | Hydrodynamic coefficients |
| Mass of the adjustable net buoyancy | |
| Mass of the movable block | |
| Mass of the underwater glider shell | |
| Offset of the movable block | |
| Rotation angle of the movable block | |
| The position of the variable ballast mass on the -axis of the body coordinate system | |
| Position of the movable block in the body coordinate system | |
| Mass of pump oil to adjust the net buoyancy | |
| Position of the moving mass |
References
- Yu, C.; Liu, C.; Lian, L.; Xiang, X.; Zeng, Z. ELOS-based path following control for underactuated surface vehicles with actuator dynamics. Ocean Eng. 2019, 187, 106139. [Google Scholar] [CrossRef]
- Jawhar, I.; Mohamed, N.; Al-Jaroodi, J.; Zhang, S. An Architecture for Using Autonomous Underwater Vehicles in Wireless Sensor Networks for Underwater Pipeline Monitoring. IEEE Trans. Ind. Inform. 2019, 15, 1329–1340. [Google Scholar] [CrossRef]
- Cho, H.; Jeong, S.-K.; Ji, D.-H.; Tran, N.-H.; Vu, M.T.; Choi, H.-S. Study on Control System of Integrated Unmanned Surface Vehicle and Underwater Vehicle. Sensors 2020, 20, 2633. [Google Scholar] [CrossRef] [PubMed]
- Davis, R.E.; Eriksen, C.C.; Jones, C.P. Autonomous buoyancy-driven underwater gliders. In Technology and Applications of Autonomous Underwater Vehicles; Taylor and Francis: London, UK, 2002; pp. 37–58. [Google Scholar]
- Tian, X.; Zhang, H.; Zhang, L.; Wang, Y.; Yang, Y. Research on positive buoyancy underwater glider and its sailing efficiency. Appl. Ocean Res. 2021, 110, 102592. [Google Scholar] [CrossRef]
- Edwards, D.; Arnold, N.; Heinzen, S.; Strem, C.; Young, T. Flying emplacement of an underwater glider. In Proceedings of the OCEANS 2017-Anchorage, Anchorage, AK, USA, 18–21 September 2017; pp. 1–6. [Google Scholar]
- Imlach, J.; Mahr, R. Modification of a military grade glider for coastal scientific applications. In Proceedings of the 2012 Oceans, Hampton Roads, VA, USA, 14–19 October 2012; pp. 1–6. [Google Scholar]
- Castelao, R.; Glenn, S.; Schofield, O.; Chant, R.; Wilkin, J.; Kohut, J. Seasonal evolution of hydrographic fields in the central middle atlantic bight from glider observations. Geophys. Res. Lett. 2008, 35, 183–199. [Google Scholar] [CrossRef]
- Daniel, L.R.; Sylvia, T.C. On sampling the ocean using underwater gliders. J. Geophys. Res. Ocean. 2011, 116, C08010. [Google Scholar]
- Webb, D.; Simonetti, P.; Jones, C. SLOCUM: An underwater glider propelled by environmental energy. IEEE J. Ocean. Eng. 2001, 26, 447–452. [Google Scholar] [CrossRef]
- Sherman, J.; Davis, R.; Owens, W.; Valdes, J. The autonomous underwater glider “spray”. IEEE J. Ocean. Eng. 2001, 26, 437–446. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, M.; Asakawa, K.; Hyakudome, T.; Kishima, S.; Matsuoka, H.; Minami, T. Hydrodynamic Coefficients and Motion Simulations of Underwater Glider for Virtual Mooring. IEEE J. Ocean. Eng. 2013, 38, 581–597. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Zhang, A.; Jin, W.; Chen, Q.; Tian, Y.; Liu, C. Development and Experiments of the Sea-Wing Underwater Glider. China Ocean Eng. 2011, 25, 721–736. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Wang, Y.; Wu, Z.; Wang, S. Motion analysis and trials of the deep sea hybrid underwater glider Petrel-II. China Ocean. Eng. 2017, 31, 55–62. [Google Scholar] [CrossRef]
- Leonard, N.E.; Graver, J.G. Model-based feedback control of autonomous underwater gliders. Ocean. Eng. 2001, 26, 633–645. [Google Scholar] [CrossRef] [Green Version]
- Fan, S. Dynamics Modeling, Motion Analysis and Controller Design of Underwater Gliders under the Influence of Ocean Currents; Zhejiang University: Hangzhou, China, 2013. [Google Scholar]
- Huang, Z.; Zheng, H.; Wang, S.; Ma, J.; Liu, Y. A self-searching optimal ADRC for the pitch angle control of an underwater thermal glider in the vertical plane motion. Ocean Eng. 2018, 159, 98–111. [Google Scholar] [CrossRef]
- Zhou, H.; Wei, Z.; Zeng, Z.; Yu, C.; Yao, B.; Lian, L. Adaptive robust sliding mode control of autonomous underwater glider with input constraints for persistent virtual mooring. Appl. Ocean Res. 2020, 95, 102027. [Google Scholar] [CrossRef]
- Vu, M.T.; Le, T.-H.; Thanh, H.L.N.N.; Huynh, T.-T.; Van, M.; Hoang, Q.-D.; Do, T.D. Robust Position Control of an Over-actuated Underwater Vehicle under Model Uncertainties and Ocean Current Effects Using Dynamic Sliding Mode Surface and Optimal Allocation Control. Sensors 2021, 21, 747. [Google Scholar] [CrossRef]
- Xiang, X.; Yu, C.; Lapierre, L.; Zhang, J.; Zhang, Q. Survey on Fuzzy-Logic-Based Guidance and Control of Marine Surface Vehicles and Underwater Vehicles. Int. J. Fuzzy Syst. 2018, 20, 572–586. [Google Scholar] [CrossRef]
- Cao, J.; Cao, J.; Zeng, Z.; Lian, L. Nonlinear multiple-input-multiple-output adaptive backstepping control of underwater glider systems. Int. J. Adv. Robot. Syst. 2016, 13, 1729881416669484. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Oliveira, P.; Soares, C.G. L1 adaptive backstepping control for path-following of underactuated marine surface ships. Eur. J. Control 2021, 58, 357–372. [Google Scholar] [CrossRef]
- Isa, K.; Arshad, M. Neural network control of buoyancy-driven autonomous underwater glider. In Recent Advances in Robotics and Automation; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sands, T. Development of Deterministic Artificial Intelligence for Unmanned Underwater Vehicles (UUV). J. Mar. Sci. Eng. 2020, 8, 578. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, J.; Zhang, A.; Zhang, F. Spiraling motion of underwater gliders: Modeling, analysis, and experimental results. Ocean Eng. 2013, 60, 1–13. [Google Scholar] [CrossRef]
- Vu, M.T.; Van, M.; Bui, D.H.P.; Do, Q.T.; Huynh, T.-T.; Lee, S.-D.; Choi, H.-S. Study on Dynamic Behavior of Unmanned Surface Vehicle-Linked Unmanned Underwater Vehicle System for Underwater Exploration. Sensors 2020, 20, 1329. [Google Scholar] [CrossRef] [Green Version]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z.; Hu, S.; Jiang, F. A novel motion control design approach based on active disturbance rejection. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; pp. 1547–1552. [Google Scholar]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, Colorado, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Wang, Y.; Zhang, W.; Dong, H.; Yu, L. A LADRC based fuzzy PID approach to contour error control of networked motion control system with time arying delays. Asian J. Control 2019, 22, 1973–1985. [Google Scholar] [CrossRef]
- Li, H.; Liu, X.; Li, J. The research of fuzzy immune linear active disturbance rejection control strategy for three-motor synchronous system. Control Eng. Appl. Inform. 2015, 14, 50–58. [Google Scholar]






| α1 | ec | NB | NM | NS | ZO | PS | PM | PB |
|---|---|---|---|---|---|---|---|---|
| e | ||||||||
| NB | PB | PB | PM | PM | PS | ZO | ZO | |
| NM | PB | PB | PM | PS | PS | ZO | PS | |
| NS | PM | PM | PM | PS | ZO | PS | PS | |
| ZO | PM | PM | PS | ZO | PS | PM | PM | |
| PS | PS | PS | ZO | PS | PS | PM | PM | |
| PM | PS | ZO | PS | PM | PM | PM | PB | |
| PB | ZO | ZO | PM | PM | PM | PB | PB | |
| α2 | ec | NB | NM | NS | ZO | PS | PM | PB |
|---|---|---|---|---|---|---|---|---|
| e | ||||||||
| NB | PS | PS | PB | PB | PB | PM | PS | |
| NM | PS | PS | PB | PM | PM | PS | ZO | |
| NS | ZO | PS | PM | PM | PS | PS | ZO | |
| ZO | ZO | PS | PS | PS | PS | PS | ZO | |
| PS | ZO | PS | PS | ZO | PS | PS | ZO | |
| PM | PS | PM | PS | PS | PS | PM | PS | |
| PB | PB | PM | PM | PM | PS | PS | PB | |
| Parameters | Value |
|---|---|
| Shell static mass | = 54.28 kg |
| Moving mass block | = 11 kg |
| Buoyancy adjustment mass | −0.5 kg ≤ ≤ 0.5 kg |
| Overall drainage mass | = 65.28 kg |
| Additional mass factor | = diag [1.48, 49.58, 65.92] |
| Additional inertia term | = diag [0.53, 7.88, 10.18] |
| Resistance factor | = 386.29, = 7.19 |
| Lift force factor | = −0.36, = 440.99 |
| Lateral force coefficient | = −115.65 |
| Transverse rocking moment coefficient | = −58.27, = −19.83 |
| Pitch moment coefficient | = 0.28, = −205.64, = −65.84 |
| Depth Controller | Parameter | Value |
|---|---|---|
| TD | r | 6000 |
| h | 0.01 | |
| LSEF | 0.25 (initial) | |
| 0.75 (initial) | ||
| b | 0.5 | |
| LESO | 160 | |
| 1820 | ||
| 0.069 |
| Controller | Maximum Overshoot | FLADRC Relatively Reduction |
|---|---|---|
| PID | 1.73 m | 75.1% |
| LADRC | 0.99 m | 56.6% |
| FLADRC | 0.43 m | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yu, C.; Li, M.; Yao, B.; Lian, L. Vertical Profile Diving and Floating Motion Control of the Underwater Glider Based on Fuzzy Adaptive LADRC Algorithm. J. Mar. Sci. Eng. 2021, 9, 698. https://doi.org/10.3390/jmse9070698
Wang Z, Yu C, Li M, Yao B, Lian L. Vertical Profile Diving and Floating Motion Control of the Underwater Glider Based on Fuzzy Adaptive LADRC Algorithm. Journal of Marine Science and Engineering. 2021; 9(7):698. https://doi.org/10.3390/jmse9070698
Chicago/Turabian StyleWang, Zhiguang, Caoyang Yu, Mingjie Li, Baoheng Yao, and Lian Lian. 2021. "Vertical Profile Diving and Floating Motion Control of the Underwater Glider Based on Fuzzy Adaptive LADRC Algorithm" Journal of Marine Science and Engineering 9, no. 7: 698. https://doi.org/10.3390/jmse9070698
APA StyleWang, Z., Yu, C., Li, M., Yao, B., & Lian, L. (2021). Vertical Profile Diving and Floating Motion Control of the Underwater Glider Based on Fuzzy Adaptive LADRC Algorithm. Journal of Marine Science and Engineering, 9(7), 698. https://doi.org/10.3390/jmse9070698








