Step Approximation for Water Wave Scattering by Multiple Thin Barriers over Undulated Bottoms

Abstract

This paper investigates the scattering of oblique water waves by multiple thin barriers over undulation bottoms using the eigenfunction matching method (EMM). In the solution procedures of the EMM, the bottom topographies are sliced into shelves separated by steps. On each step, surface-piercing or/and bottom-standing barriers can be presented or not. For each shelf, the solution is composed of eigenfunctions with unknown coefficients representing the wave amplitudes. Then applying the conservations of mass and momentum, a system of linear equations is resulted and can be solved by a sparse-matrix solver. If no barriers are presented on the steps, the proposed EMM formulation degenerates to the water wave scattering over undulating bottoms. The effects on the barrier lengths, barrier positions and oblique wave incidences by different undulated bottoms are studied. In addition, the EMM is also applied to solve the Bragg reflections of normal and oblique water waves by periodic barrier over sinusoidal bottoms. The accuracy of the solution is demonstrated by comparing it with the results in the literature.

1. Introduction

The interaction of surface water waves with an undulation bottom topography is a fundamental interest in understanding wave diffraction along the coastal region. When water waves are generated in deep to a shallow area in natural environments, they experience bathymetric variations, underwater obstacles, nonlinear wave interactions and others. These are some of the main natural causes that lead to coastal hazards, which seriously affect coastline and human activities. Several previous studies [1,2,3,4] have focused on the water wave scattering by bathymetric variations and underwater obstacles.

Breakwaters are conventional structures that often rest on the bottom foundation or pierced on the free surface. They are specially designed to reduce the directed affectation of water waves from the open sea approach to the nearshore area. In addition, they are usually built to satisfy the requirements of maritime economic activities. As traditional breakwaters may require higher construction costs due to larger amount of material and complex installation, thin barriers could be alternative solutions. Thin barriers may create natural habitats and/or fishing farms for ecology conservation, such as oil exploration stations, offshore accommodations and oceanographic research centers. Engineers also use assembled floating thin barriers to constructing artificial islands on the sea to provide hospitable environments on the surface of the water. Thin barriers are also intended to protect the shoreline from the direct impacts of coastal erosion and storm surge. In the literature, several authors have studied the problems of water wave interaction by thin barriers. The issue of water wave scattering by a single surface-piercing or bottom-standing barrier over uniform bottom topography has been examined by Losada et al. [5,6,7] and Abul-Azm [8]. Porter and Evans [9] used the Chebychev polynomials to formulate a complementary approximation and obtained highly accurate results to improve the convergence of the solutions. Additionally, Das et al. [10] and Roy et al. [11] studied the water wave scattering by multiple barriers. Furthermore, Wang et al. [12] considered the combined effects of multiple barriers and a single step bottom.

Numerical solutions are important for solving water wave problems as analytic solutions are rare. Therefore, Berkhoff [13] derived the mild-slope equation (MSE) to solve water wave scattering problems. The MSE has also been employed by Kirby [4], Belibassakis et al. [14,15,16] and Toledo et al. [17], to examine the problems of wave scattering by rippled bottom, nonlinear waves and wave-current interactions, respectively. Even though MSE has been modified and improved several times, it still has some special requirements on the spatial derivatives of the eigenfunctions and needs to be improved. In addition, the MSE has seldom been applied for problems of water wave scattering by thin barriers.

Alternately, Takano [18] developed the eigenfunction matching method (EMM) for solving water wave scattering by an elevated sill and a fixed surface obstacle. Mei and Black [19] applied the EMM for solving surface waves normally incident on a rectangular obstacle in a channel of finite depth. Sequentially, Kirby and his co-authors [20,21] used the EMM to study the problems of oblique wave scattering by trenches. Newman [22,23] employed the EMM to transform the integral equation into an infinite set of algebraic equations in terms of the eigenfunctions describing the evanescent modes. The EMM has also been extended to water wave scattering by rectangular submerged bar [24] and surface-piercing breakwaters [25]. For waves propagating over an arbitrary bottom topography, Devillard et al. [26], O’Hare and Davies [27] and Tsai et al. [28,29,30] decomposed the bottom profiles into a sequence of flat shelves separated by multiples steps and used the EMM to solved the resultant problem. The accuracy of the EMM solutions was shown by Tsai et al. [31] to be comparable with that of the MSE solutions.

In the present study, we consider the applications of EMM for solving problems of water wave scattering by multiple barriers over undulation bottom profiles. These barriers can be either surface-piercing or bottom-standing. By applying the conservations of mass and momentum to the eigen solutions on shelves, the problems can be converted into a system of linear equations with unknown coefficients representing the wave amplitudes on the shelves. The sparse-matrix solver SuperLU [32] is adopted to solve the resulted system. The present EMM formulation is the extension of the existing EMM for solving problems of water wave scattering solely by undulation bottom profiles [20,27,31] or by barriers [33]. The proposed EMM model is validated by comparisons with analytical solutions in the literatures of Losada et al. [5], Porter and Evans [9], Wang et al. [12], Porter and Porter [34], and Davies and Heathershaw [1] for some degenerated cases.

This paper is organized as follows: the wave problem is mathematically modeled, and the EMM solution is developed in Section 2, and the EMM model is validated in Section 3. Discussions on Bragg reflections by multiple periodic thin barriers over sinusoidal rippled bottom are provided in Section 4. Finally, Section 5 presented the conclusions of the whole study.

2. Materials and Methods

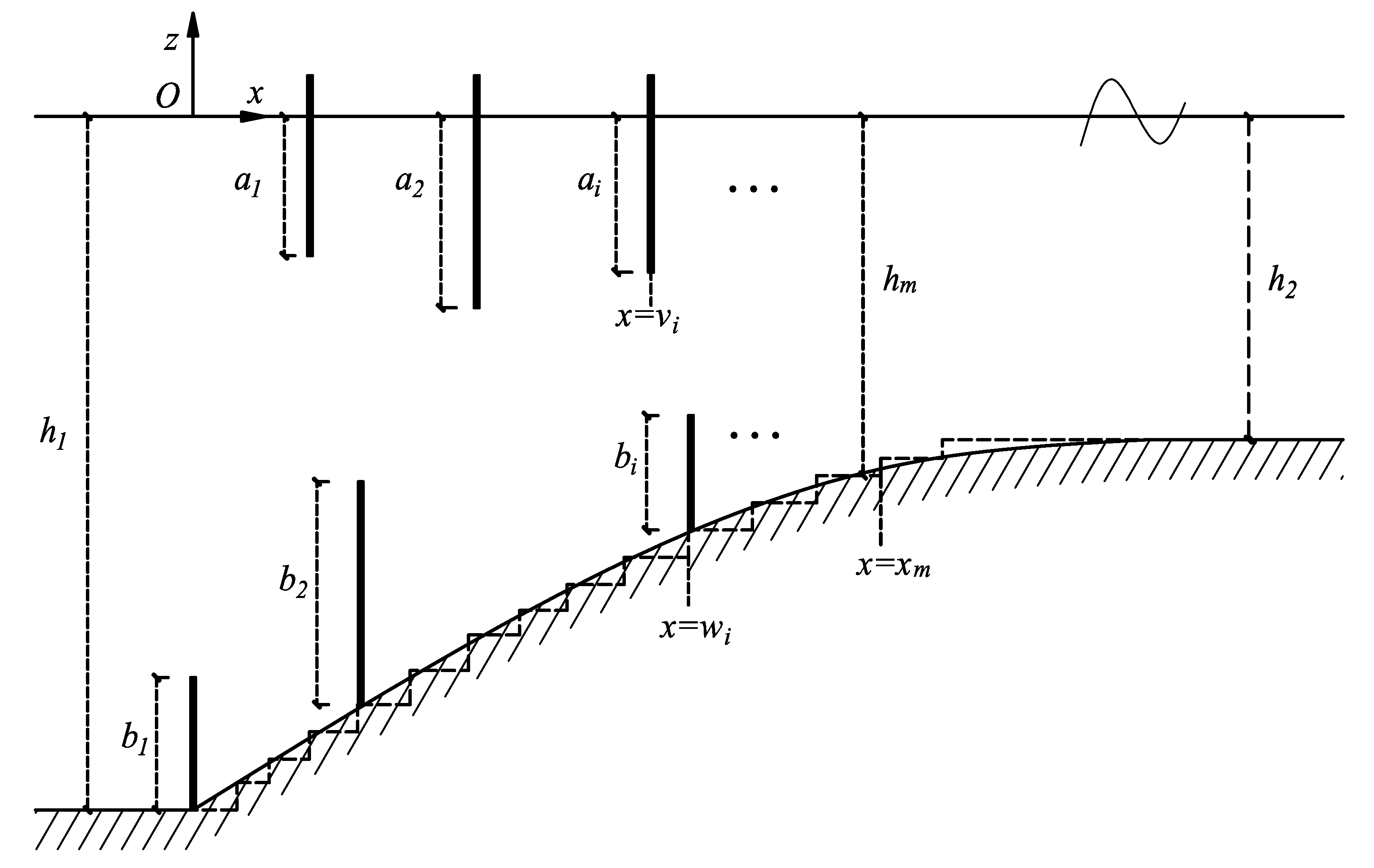
2.1. The Mathematical Model

In this section, surface water wave scattering problems by thin impermeable barriers of submerged and bottom-standing configurations are formulated for waves over undulation bottom topography. Considering a train of monochromatic surface waves with incidence angle $\gamma$, amplitude $\overline{a}$, angular frequency $\sigma$ and wavelength $\lambda$ propagate towards thin impermeable barriers over an undulating bottom. Figure 1 illustrates a schematic representation of the wave scattering problem induced by multiple thin barriers over the undulation bottom. In this figure, a Cartesian coordinate system is taken in which $z$-axis is chosen vertically upwards, and the $x$-plane is taken as the rest position of the free surface. The wave amplitude is assumed to be small enough that the linear wave theory is applicable. The wave motion is supposed to be time-harmonic by $e^{-i\sigma t}$, where $\sigma$ is defined by $2\pi /T$ with $T$ being the wave period, $t$ is the time and $i$ is the unit of complex numbers. To facilitate the approximate bottom topography process, thin barriers and sea bottom could be discretized into a series of $M$ shelves in the interval of $x_{m-1}\le x\le x_m$ for $m=1,2,\dots ,M$ with a water depth $h_m$. Furthermore, $x_0=-\infty$ and $x_M=\infty$ are assumed. The $i$-th surface-piercing barrier is placed at a location $x=v_i$ with the submerged length being equal to $a_i$. In addition, the $i$-th bottom-standing barrier is placed at a location $x=w_i$ with length $b_i$. In the following of this article, $a=a_i$, $v=v_i$, $b=b_i$ or $w=w_i$ if there is only one surface-piercing or bottom-standing barrier.

Considering the solution on the $m$-th shelf in the interval $x_{m-1}\le x\le x_m$ for $m=1,2,\dots ,M$, the velocity of the fluid is defined by:

$$u_m=\nabla {\varphi }_m,$$

(1)

where $\nabla =(\partial /\partial x,\partial /\partial y,\partial /\partial z)$ denotes the three-dimensional del operator with respect to the three-dimensional Cartesian co-ordinate $\left(x,y,z\right)$ and ${\varphi }_m$ is the velocity potential. As maintained by the linear wave theory, the velocity potential is governed by the Laplace equation:

$${\nabla }^2{\varphi }_m=0,$$

(2)

which subjected to the kinematic and dynamic free-surface boundary conditions, respectively as:

$$-i\sigma {\eta }_m-\frac{\partial {\varphi }_m}{\partial z}=0$$

(3)

and

$$-i\sigma {\varphi }_m+g{\eta }_m=0 \mathrm{on} z=0,$$

(4)

where ${\eta }_m$ is surface elevation. Equations (3) and (4) can be combined to obtain:

$$\frac{\partial {\varphi }_m}{\partial z}-\frac{{\sigma }^2}{g}{\varphi }_m=0 \mathrm{on} z=0.$$

(5)

Furthermore, the condition for bottom boundary can be written as:

$$\frac{\partial {\varphi }_m}{\partial z}=0 \mathrm{on} z=-h_m.$$

(6)

The diffraction of water waves at a step-type bottom is considered by Miles [35]. As described in Figure 2, between two shelves, the velocity potentials ${\varphi }_m$ and ${\varphi }_{m+1}$ require connection conditions:

$${\varphi }_m={\varphi }_{m+1} \mathrm{for} x\in L_g,$$

(7)

$$\frac{\partial {\varphi }_m}{\partial x}=\frac{\partial {\varphi }_{m+1}}{\partial x} \mathrm{for} x\in L_g,$$

(8)

and

$$\frac{\partial {\varphi }_m}{\partial x}=\frac{\partial {\varphi }_{m+1}}{\partial x}=0 \mathrm{for} x\in L_b,$$

(9)

where $L_g$ and $L_b$ are the vertical intervals of the gap and barrier, respectively. Additionally, the condition for the vertical wall is described by:

$$\frac{\partial \varphi }{\partial x}=0 \mathrm{for} x\in L_w$$

(10)

In Equation (10), $\varphi$ stands for either ${\varphi }_m$ or ${\varphi }_{m+1}$ depending on the waterside of the barrier and $L_w$ is the vertical intervals of the wall.

In order to make the solution unique, the following far-field conditions are required:

$$\eta =\overline{a}\left(e^{i{\widehat{k}}_{1.0}x}+K_R{e}^{i{\theta }_R}{e}^{-i{\widehat{k}}_{1.0}x}\right)e^{i{k}_{y}y} \mathrm{as} x\to -\infty$$

(11)

and

$$\eta =\overline{a}{K}_T{e}^{i{\theta }_T}{e}^{i{\widehat{k}}_{M.0}x}{e}^{i{k}_{y}y} \mathrm{as} x\to \infty ,$$

(12)

where $K_R$, $K_T$, ${\theta }_R$ and ${\theta }_T$ are real numbers, the reflection and transmission coefficients are defined by $K_R{e}^{i{\theta }_R}$ and $K_T{e}^{i{\theta }_T}$, respectively.

In Equation (11) and Equation (12), ${\widehat{k}}_{M,0}$, $k_y$ and ${\widehat{k}}_{1.0}$ are positive real wavenumbers expressed by:

$${\widehat{k}}_{m,n}=\sqrt{k_{m,n}^2-k_y^2}$$

(13)

and

$$k_y=k_{1,0}\sin \gamma ,$$

(14)

where $k_{1,0}=2\pi /\lambda >0$ and $k_{M,0}>0$ are the progressive wavenumbers obtained from the dispersion relation:

$$\frac{{\sigma }^2}{g}=k_{m,0}\tanh k_{m,0}{h}_m.$$

(15)

In Equation (13), the indices vary as $m=1,2,\dots ,M$ and $n=0,1,\dots$. Additionally, the evanescent wavenumbers $k_{m,n}$ in Equation (13) with $n=1,2,3,\dots$ are defined by:

$$k_{m,n}=i{\kappa }_{m,n},$$

(16)

where ${\kappa }_{m,n}$ is the $n$-th smallest positive root of the dispersion relation:

$$\frac{{\sigma }^2}{g}=-{\kappa }_{m,n}\tan {\kappa }_{m,n}{h}_m.$$

(17)

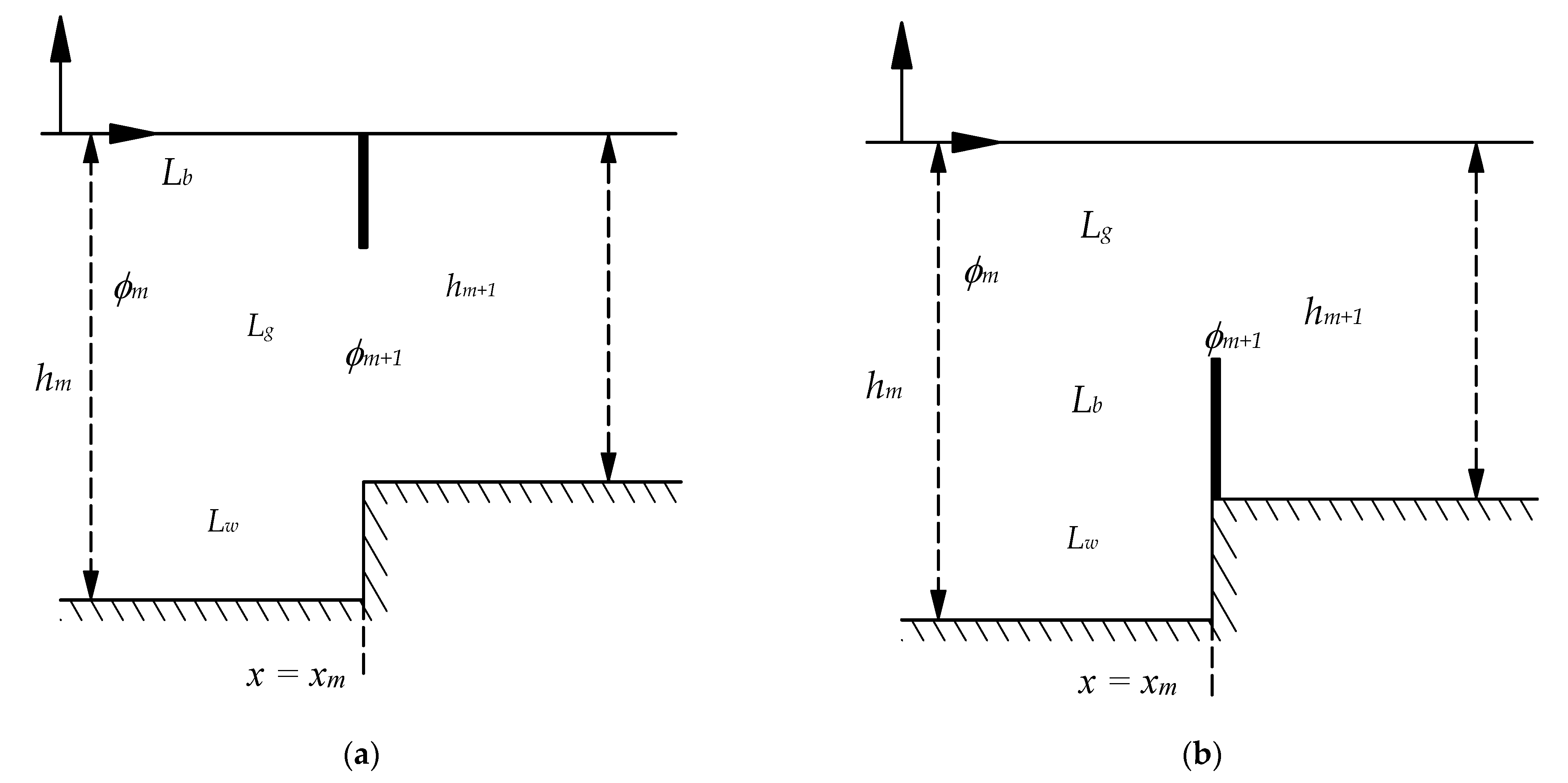
2.2. Eigenfuction Matching Method (EMM)

Constructed on the linear theory, the complete solution of the velocity potential for the $m$-th shelf can be defined by:

$${\varphi }_m\left(x,y,z\right)={\displaystyle \sum _{n=0}^N\left(A_{m,n}{\xi }_{m,n}^{\left(1\right)}\left(x\right)+B_{m,n}{\xi }_{m,n}^{\left(2\right)}\left(x\right)\right){\zeta }_{m,n}\left(z\right)}{e}^{i{k}_{y}y}$$

(18)

for $m=1,2,3,\dots ,M$, where $A_{m,n}$ and $B_{m,n}$ are unknown coefficients to be determined. In Equation (18), $N$ is the number of evanescent modes. To build up a complete solution by the method of the separation of variables, the eigenfunctions from Equation (18) can be defined by:

$${\zeta }_{m,n}\left(z\right)=\cosh k_{m,n}\left(h_m+z\right),$$

(19)

$${\xi }_{m,n}^{\left(1\right)}\left(x\right)=e^{i{\widehat{k}}_{m,n}\left(x-{\overline{x}}_{m-1}\right)},$$

(20)

and

$${\xi }_{m,n}^{\left(2\right)}\left(x\right)=e^{-i{\widehat{k}}_{m,n}\left(x-{\overline{x}}_m\right)}$$

(21)

with

$$\left\{\begin{array}{l}{\overline{x}}_m=x_m\\ {\overline{x}}_0={\overline{x}}_M=0\end{array}\right. \mathrm{for} m=1,2,\dots ,M-1.$$

(22)

It can be noticed that the solutions defined by Equations (13)–(22) satisfy Equations (2), (5) and (6) analytically and the unknown coefficients $A_{m,n}$ and $B_{m,n}$ can be found by using Equations (7)–(12).

The conservation of mass in Equations (8)–(10) can be formulated in the EMM as:

$$〈\frac{\partial {\varphi }_m}{\partial x}|{\zeta }_{m,l}^{\mathrm{larger}}〉=〈\frac{\partial {\varphi }_{m+1}}{\partial x}|{\zeta }_{m,l}^{\mathrm{larger}}〉 \mathrm{for} l=0,1,\dots ,N,$$

(23)

where the inner product of two depth eigenfunctions is defined by:

$$〈G_1|G_2〉={\displaystyle {\int }_{-\lambda }^0{G}_1\left(z\right)G_2\left(x\right)dz}$$

(24)

where $G_1$ and $G_2$ are the depth eigenfunction of ${\zeta }_{m,n}$ with arbitrary $m$ and $n$, $\lambda$ denotes the water depth of the depth eigenfunction $G_1$. In Equation (23), the depth eigenfunction ${\zeta }_{m,l}^{\mathrm{larger}}$ is defined by:

$${\zeta }_{m,l}^{\mathrm{larger}}=\left\{\begin{array}{l}{\zeta }_{m,l} \mathrm{for} h_m>h_{m+1}\\ {\zeta }_{m+1,l} \mathrm{for} h_{m+1}>h_m.\end{array}\right.$$

(25)

The conservation of momentum in Equation (7) as well as the barrier condition (9) can be expressed as:

$$〈{\zeta }_{m,l}^{\mathrm{smaller}}|{\varphi }_m〉=〈{\zeta }_{m,l}^{\mathrm{smaller}}|{\varphi }_{m+1}〉+〈{\zeta }_{m,l}^{\mathrm{smaller}}|F〉 \mathrm{for} l=0,1,\dots ,N,$$

(26)

where

$$F_m\left(z\right)=\left\{\begin{array}{l}0 \mathrm{for} x\in L_g\\ \frac{\partial {\varphi }_m}{\partial x}+{\varphi }_m\left(x_m\right)-{\varphi }_{m+1}\left(x_m\right) \mathrm{for} x\in L_b\end{array}\right.$$

(27)

and

$${\zeta }_{m,l}^{\mathrm{smaller}}=\left\{\begin{array}{l}{\zeta }_{m,l} \mathrm{for} h_m<h_{m+1}\\ {\zeta }_{m+1,l} \mathrm{for} h_{m+1}<h_m.\end{array}\right.$$

(28)

Based on the far-field conditions (11), (12) and the dynamic free-surface boundary condition (4), the far-field solutions of the velocity potential can be expressed as:

$${\varphi }_1=-\frac{i\overline{a}g}{\sigma }\frac{\cosh k_{1,0}\left(h_1+z\right)}{\cosh k_{1,0}{h}_1}\left(e^{i{\widehat{k}}_{1,0}x}+K_R{e}^{i{\theta }_R}{e}^{-i{\widehat{k}}_{1,0}x}\right)e^{i{k}_{y}y} \mathrm{as} x\to -\infty$$

(29)

and

$${\varphi }_M=-\frac{i\overline{a}g}{\sigma }\frac{\cosh k_{M,0}\left(h_M+z\right)}{\cosh k_{M,0}{h}_M}\left(K_T{e}^{i{\theta }_T}{e}^{i{\widehat{k}}_{M,0}x}\right)e^{i{k}_{y}y} \mathrm{as} x\to \infty .$$

(30)

Combine Equation (29) and Equation (30) into Equation (18), we can obtain the following equations:

$$B_{1,0}{e}^{i{\widehat{k}}_{m,n}\overline{x}}=-\frac{i\overline{a}{K}_R{e}^{i{\theta }_R}g}{\sigma }\frac{1}{\cosh k_{1,0}{h}_1},$$

(31)

$$A_{M,0}{e}^{-i{\widehat{k}}_{M,0}{\overline{x}}_{M-1}}=-\frac{i\overline{a}{K}_T{e}^{i{\theta }_T}g}{\sigma }\frac{1}{\cosh k_{M,0}{h}_M},$$

(32)

$$A_{1,0}=-\frac{i\overline{a}g}{\sigma }\frac{1}{\cosh k_{1,0}{h}_1},$$

(33)

$$A_{1,n}=0 \mathrm{for} n=1,2,\dots ,N,$$

(34)

and

$$B_{M,n}=0 \mathrm{for} n=0,1,\dots ,N.$$

(35)

By using Equation (18), Equations (23) and (26) can be rewritten as:

$$\begin{array}{l}{\displaystyle \sum _{n=0}^N\left(i{\widehat{k}}_{m,n}{A}_{m,n}{\xi }_{m,n}^{\left(1\right)}\left(x_m\right)-i{\widehat{k}}_{m,n}{B}_{m,n}{\xi }_{m,n}^{\left(2\right)}\left(x_m\right)\right)〈\left.{\zeta }_{m,n}\right|{\zeta }_{m,l}^{\mathrm{larger}}〉}\\ ={\displaystyle \sum _{n=0}^N\left(i{\widehat{k}}_{m+1,n}{A}_{m+1,n}{\xi }_{m+1,n}^{\left(1\right)}\left(x_m\right)-i{\widehat{k}}_{m+1,n}{B}_{m+1,n}{\xi }_{m,n}^{\left(2\right)}\left(x_m\right)\right)〈\left.{\zeta }_{m+1,n}\right|{\zeta }_{m,l}^{\mathrm{larger}}〉}\end{array}$$

(36)

and

$$\begin{array}{l}{\displaystyle \sum _{n=0}^N\left(A_{m,n}{\xi }_{m,n}^{\left(1\right)}\left(x_m\right)+B_{m,n}{\xi }_{m,n}^{\left(2\right)}\left(x_m\right)\right)〈\left.{\zeta }_{m,l}^{\mathrm{smaller}}\right|{\zeta }_{m,n}〉}\\ ={\displaystyle \sum _{n=0}^N\left(A_{m+1,n}{\xi }_{m,n}^{\left(1\right)}\left(x_m\right)+B_{m+1,n}{\xi }_{m,n}^{\left(2\right)}\left(x_m\right)\right)〈\left.{\zeta }_{m,l}^{\mathrm{smaller}}\right|{\zeta }_{m+1,n}〉}+〈{\zeta }_{m,l}^{\mathrm{smaller}}|F_m〉,\end{array}$$

(37)

for $l=0,1,\dots ,N$ and $m=1,2,\dots ,M-1$. Afterward, the EMM solution procedure can begin with Equations (33)–(37), which compose $2M(N+1)$ linear equations and can be used to solve the $2M(N+1)$ unknown $A_{m,n}$ and $B_{m,n}$. Then, Equations (31) and (32) can be used to solve the reflection and transmission coefficients $K_R{e}^{i{\theta }_R}$ and $K_T{e}^{i{\theta }_T}$. These complete the EMM solution procedures. In our study, the SuperLU library is used to solve the sparse matrix of the resulting linear Equation (21). It is noticeable that if $L_b=0$ or equivalently $F_m=0$, the proposed formulation reduces to the EMM formulation for cases of undulation bottom without barriers [20,27,31] and barriers on flat bottom [33].

3. Results

In order to validate the accuracy of EMM model, comparisons between the results by the proposed EMM and from the literature are made for cases of water wave scattering by barriers or undulated bottoms. The problem of convergence has been carefully taken into consideration by examining certain test cases.

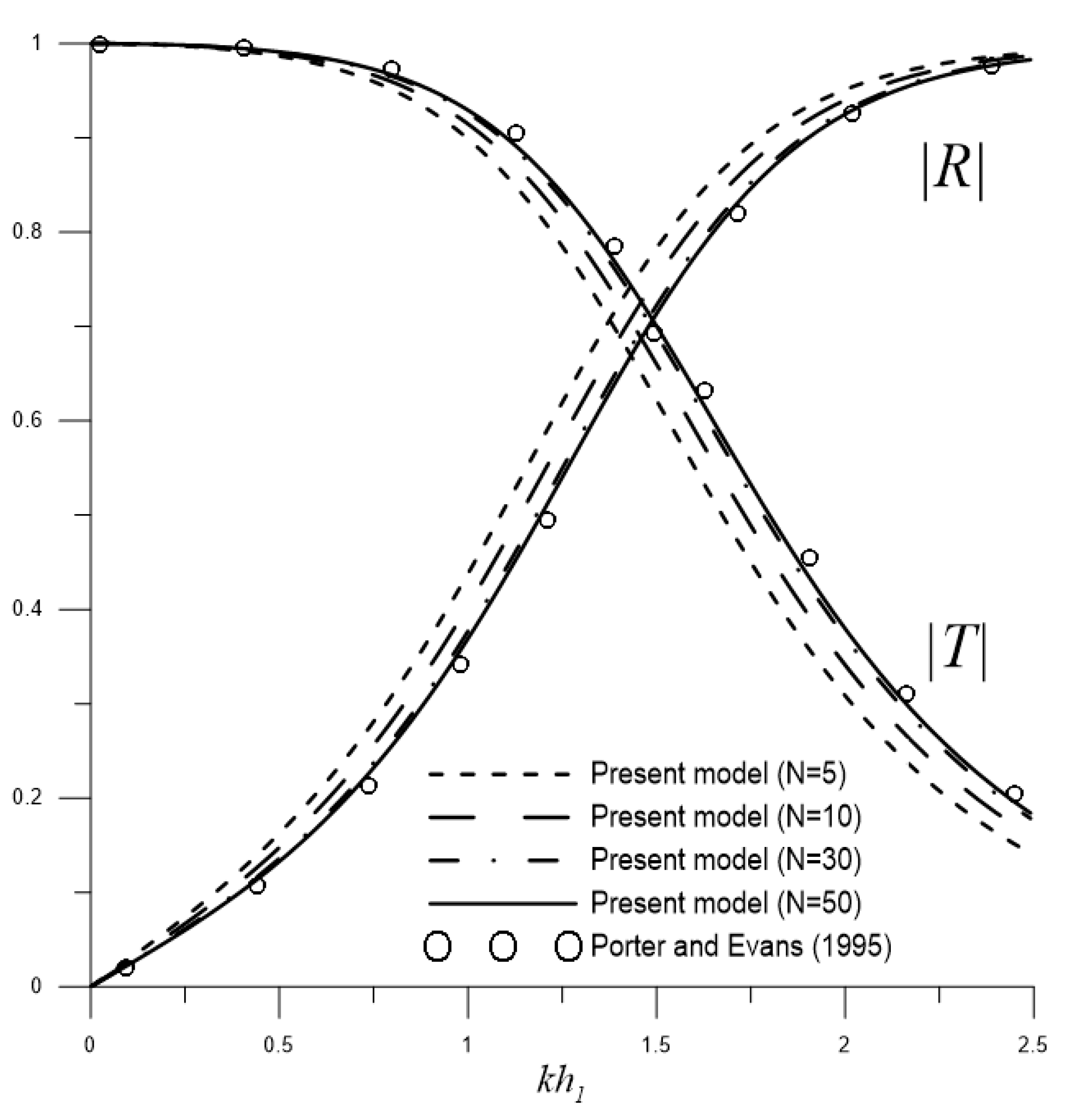
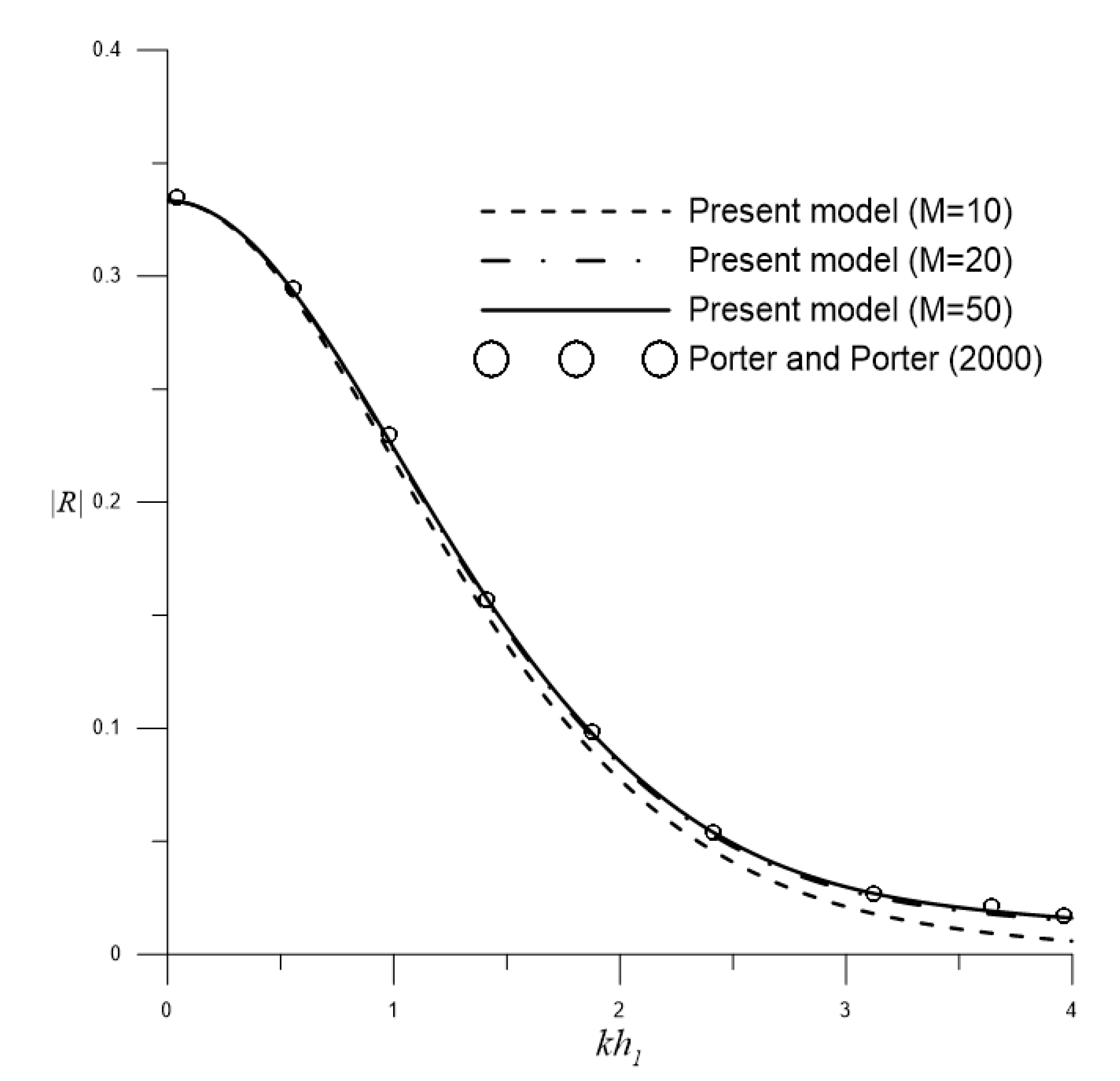
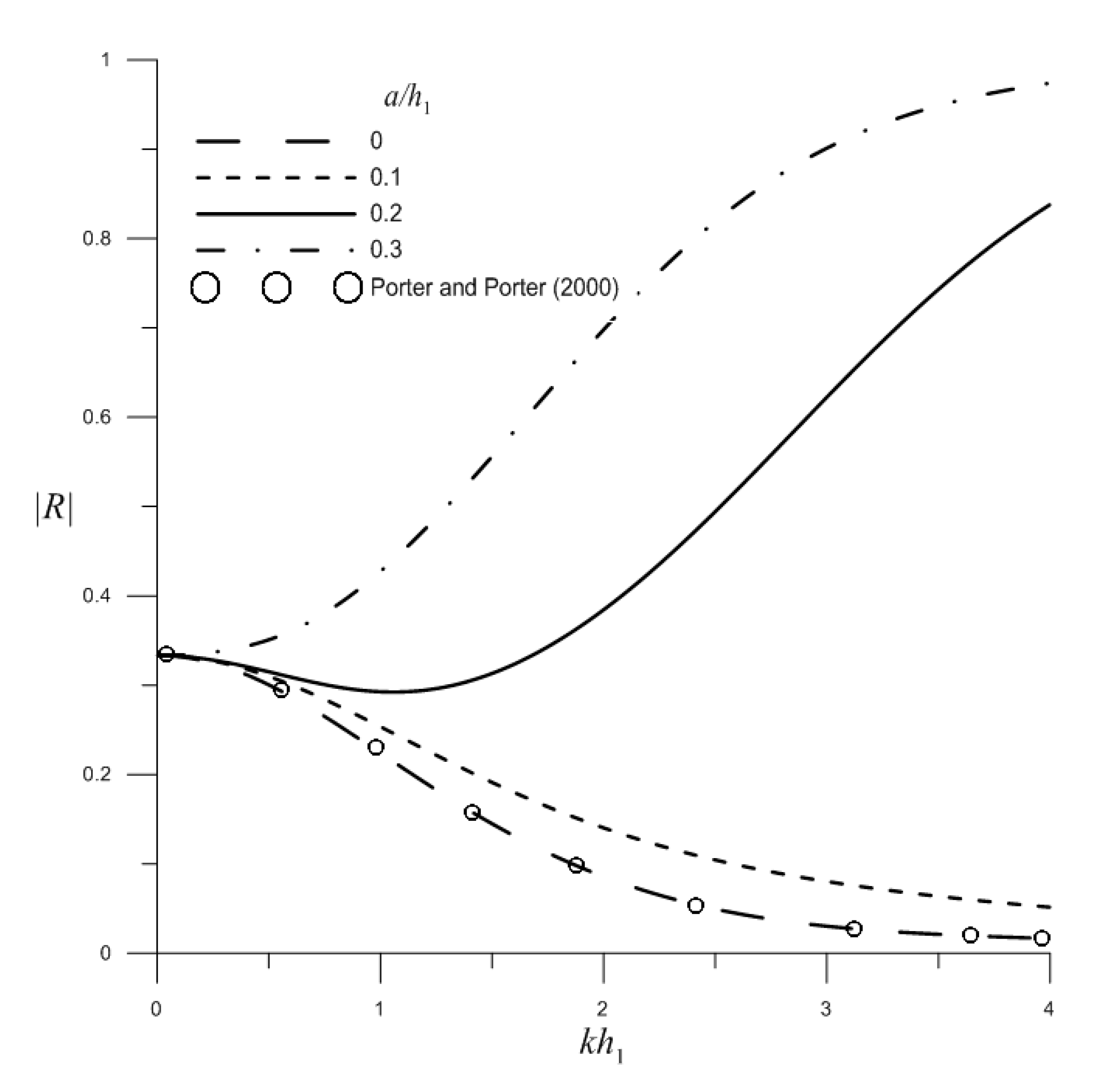
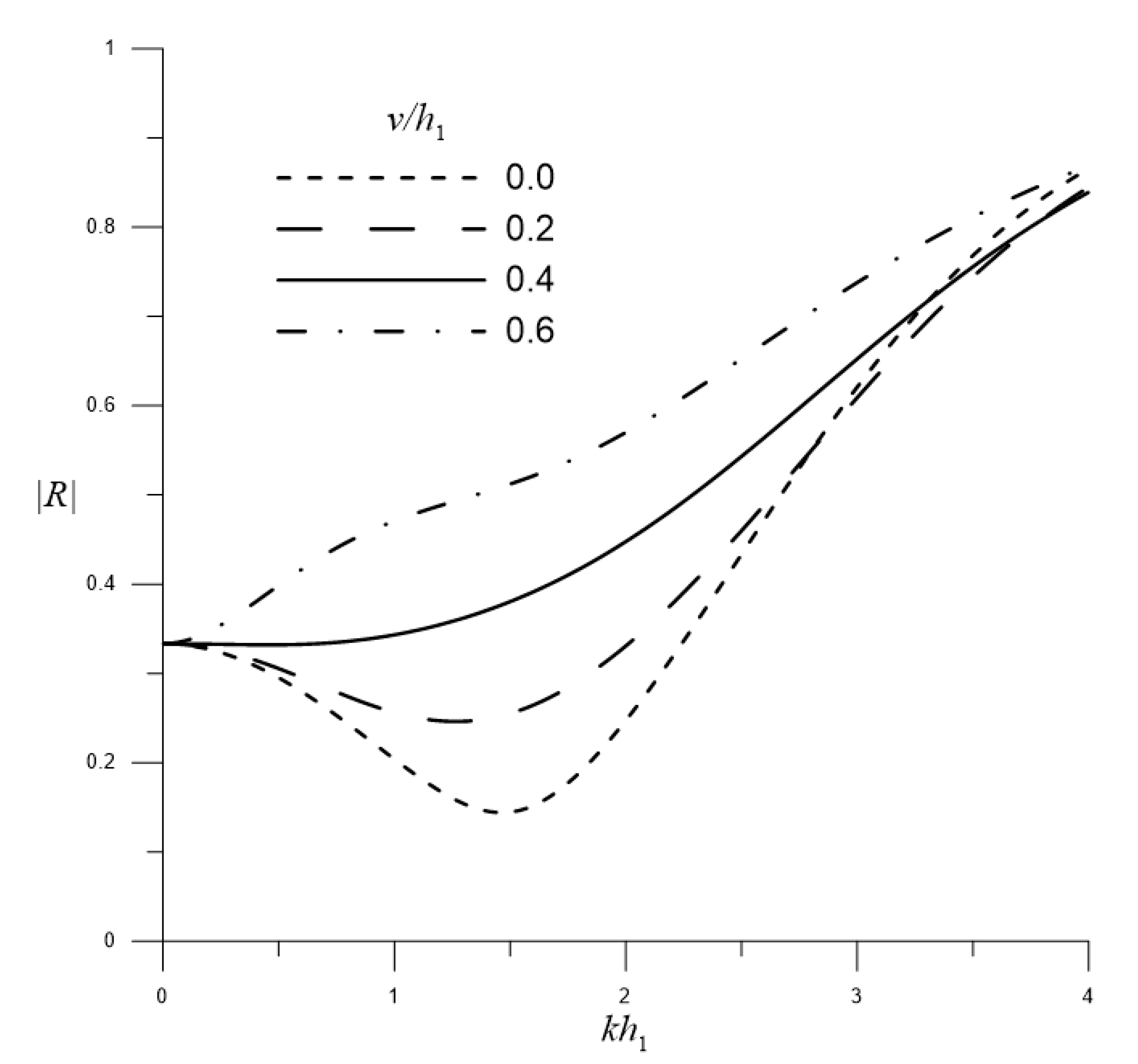
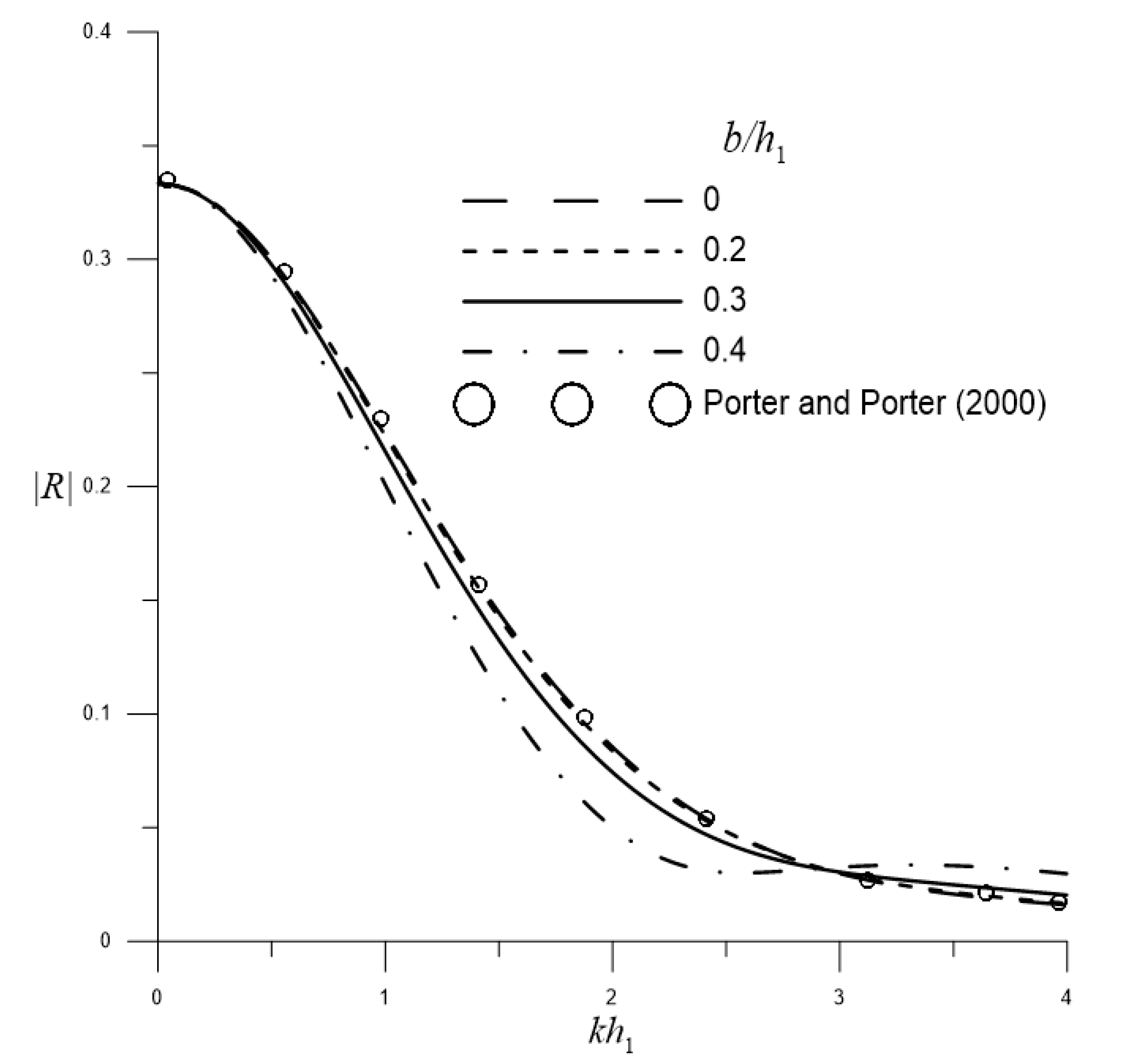
3.1. Water Wave Scattering by a Single Barrier over Flat-Bottom Topography

First of all, let us consider the water waves scattering by a single surface-piercing thin barrier over a uniform bottom where $h_1=h_2=1.0m$ with the submerged length of barrier from the free surface being equal to $a/h_1=0.5$. In order to study the convergences on the number of evanescent modes $N$, the reflection $\left|R\right|$ and transmission $\left|T\right|$ coefficients are plotted against the dimensionless wavenumber $kh$ in Figure 3. In the figure, it can be noted that the convergence is achieved for evanescent modes increase up to $N=50$. Furthermore, the results are in good agreement with those in Porter and Evans [9] for the whole frequency range.

After considering the water wave scattering over a single surface-piercing barrier, the EMM is also implemented to simulates the case of scattered waves over a single bottom-standing thin barrier by uniform bottom. We assume a single barrier standing from the bottom with length $b/h_1=0.3$, where the water depth is $h_1=h_2=1.0 m$ as exhibited in Figure 4, where curves of $\left|R\right|$ and $\left|T\right|$ are plotted against dimensionless wavenumber $k{h}_1$. The figure shows that convergence can be found for $N=50$ and good agreements with those in Losada et al. [5] are clear.

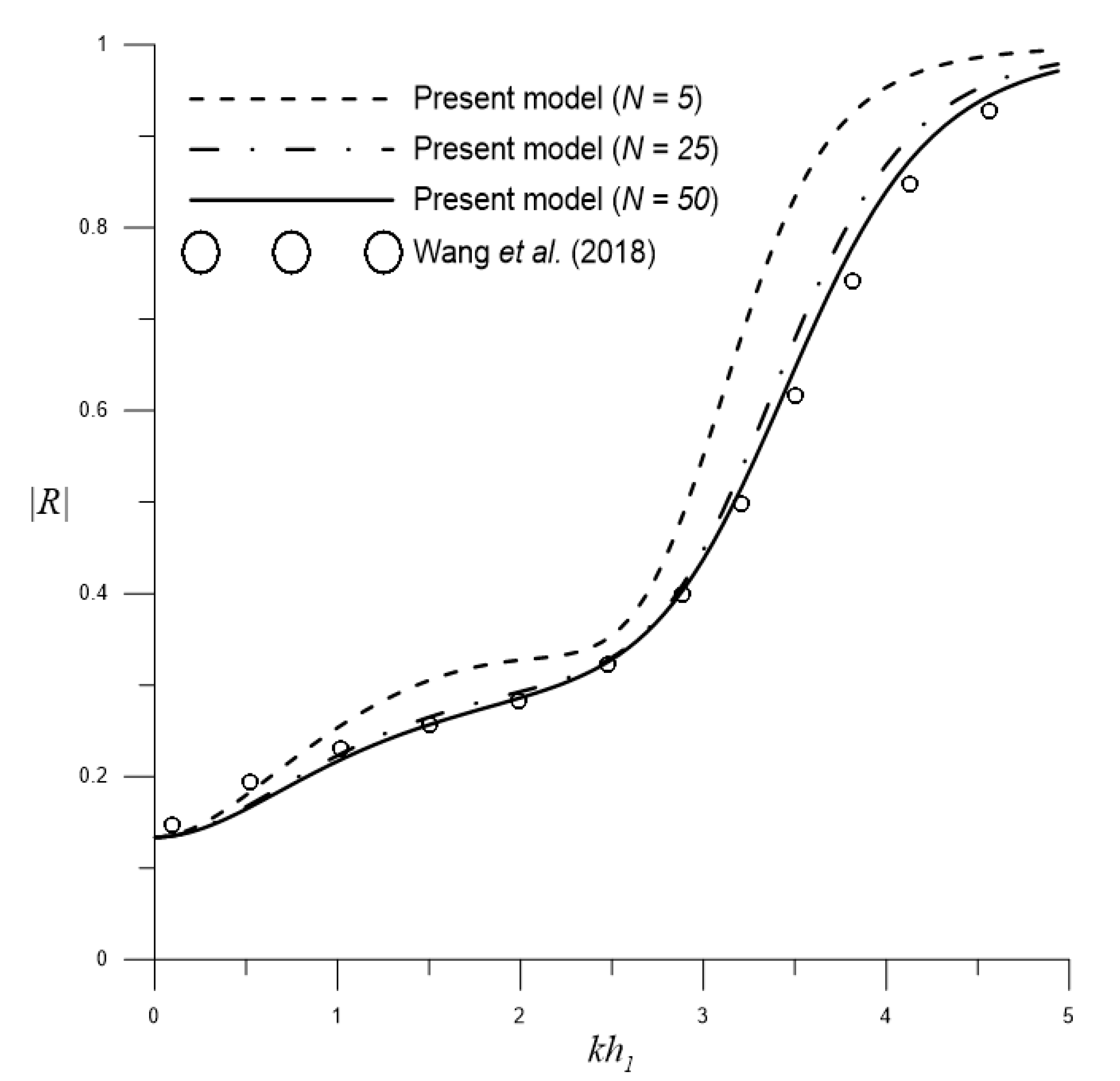
3.2. Water Wave Scattering by Barriers over Step-Type Bottom Topography

Then, we validate the proposed EMM by considering the scattering of oblique water waves by parallel thin barriers and a step bottom. Following Wang et al. [12], the two parallel surface-piercing barriers are of an equal submerged length $a/h_1=0.25$ and the step separates the deeper and shallower waters with depths being $h_1=1.0m$ and $h_2=0.25 m$, respectively. Additionally, the oblique incidence angle $\gamma$ is set to $30°$.

Figure 5 illustrates the relationship between the reflection $\left|R\right|$ and dimensionless wavenumber $k{h}_1$. Notably, numerical results of the present model with a number of modes $N=50$ are in good agreement with those from literature [12]. Based on the results of the above examples, we will adopt $N=50$ in the following of this study. Overall, this example demonstrates the proposed EMM can be applied for solving water wave scattering by multiple barriers over a step bottom.

3.3. Water Wave Scattering over Undulated Slope Bottom

Then we applied the proposed method for solving water wave scattering over the undulated bottom. Following Porter and Porter [34], we consider the bottom defined by

$$h(x)=\left\{\begin{array}{lll}1& & x\le 0\\ \frac{1}{4}& +\frac{3}{4}\left(1-\alpha {\left(\frac{4x}{3}\right)}^2+\left(\alpha -1\right)\left(\frac{4x}{3}\right)\right)& 0\le x\le \frac{3}{4}\\ \frac{1}{4}& & \frac{1}{4}\le x,\end{array}\right.$$

(38)

where $\alpha$ is parameter which defines the shape of the bottom. Figure 6 illustrates the reflection coefficients against dimensionless wavenumber $k{h}_1$ for the undulation bottom topography where $h_1=1m$ is the upstream water depth. In the figure, it can be observed that the curves of $\left|R\right|$ converge to the results computed by Porter and Porter [34] when step numbers increase to $M=50$.

3.4. Water Wave Scattering over the Sinusoidal Rippled Bottom

Davies et al. [1,2] studied the Bragg reflection by the sinusoidal rippled bottoms, which provides the groundwork for considering Bragg refletions as one of the main impact factors to water scattering. Combining the proposed step approximation with these studies, the EMM is applied to calculate the resonant reflection coefficients by sinusoidal rippled bottom, which is defined by:

$$h(x)=\left\{\begin{array}{ll}{h}_1-\frac{\sin Kx}{20}& , 0\le x\le \frac{2\pi \beta }{K}\\ h_1& , \mathrm{Otherwise} \end{array}\right.$$

(39)

where $h_1=0.156 m$ is the water depth away from the ripples, $K=2\pi$ is the wavenumber of ripples and $\beta$ is the number of sinusoidal ripples. When the case of two ripples ($\beta =2$) are considered, Figure 7 depicts the reflection coefficients against $2k/K$. In the figure, it is significant that the Bragg resonance happens when $2k/K~1$. In the figure, it can be observed that the curves of $\left|R\right|$ converge well with Davies and Heathershaw [1] as the step numbers increase to $M=100$.

These two examples validate the application of the EMM for solving problems of water wave scattering over undulated bottoms. Therefore, in this study, we will adopt $M=50$ and $M=50\beta$ for the undulated slope (38) and sinusoidal rippled (39) bottoms, respectively.

4. Discussion

In this section, the proposed EMM is applied to study the combined effects of multiple barriers and undulation bottom profiles for water wave scattering. We focus our attention on the undulated slope and sinusoidal rippled bottoms in the following.

4.1. Combined Effects of Thin Barriers and Undulated Slope Bottom

4.1.1. A Surface-Piercing Barrier

In this examination, the bottom profile is defined by Equation (38) as depicts in Figure 1. Additionally, a surface-piercing barrier is located at $x=v$ with $v/h_1=0.3$. Four values of barrier length $a/h_1$ equal to 0, 0.1, 0.2 and 0.3 are considered. As illustrates in Figure 8, with the first three values of $a/h_1$, with long waves which wavenumber $k{h}_1$ increases from 0 to 2, the reflection coefficient $\left|R\right|$ firstly drops down before grow up with the increasing of the dimensionless wavenumber $k{h}_1$. Different from the above three values, with $a/h_1=0.3$, $\left|R\right|$ stably increases when water waves become shorter. Basically, the results indicate that the reflection is stronger when the barrier length becomes larger, especially for short waves.

Then, we consider a surface-piercing barrier with length defined by $a/h_1=0.2$. Four values of barrier location $v/h_1$ equal to 0, 0.2, 0.4 and 0.6 are considered. Figure 9 illustrates the variation of $\left|R\right|$ against dimensionless wavenumber $k{h}_1$. From the figure, it can be observed that the reflection becomes stronger when the barrier moves to the right of the undulated slope bottom, especially for medium waves, i.e., $k{h}_1~1.5$.

4.1.2. A Bottom-Standing Barrier

Then, another case of a bottom-standing barrier is considered. The barrier length is located at $x=w$ with $w/h_1=0.1$. Four values of barrier length $b/h_1$ equal to 0, 0.2, 0.3 and 0.4 are considered. As demonstrates in Figure 10, the values of $\left|R\right|$ are plotted against dimensionless wavenumber $k{h}_1$. From the figure, It can be seen that the effects of barrier length are not significant when the barrier is located on the very left of the undulated slope bottom. Additionally, for the short wave limit $k{h}_1\to \infty$, total transmissions occur for all cases.

The problem of barrier location is also considered. We assume that the barrier length equal to $b/h_1=0.3$. The barrier moves to the right of the undulated slope bottom with four barrier locations $w/h_1$ being equal to 0, 0.3, 0.4 and 0.5, respectively. Figure 11 illustrates the variation of $\left|R\right|$ against dimensionless wavenumber $k{h}_1$. From the figure, it can be observed that the reflection becomes stronger when the barrier moves to the right of the undulated slope bottom for almost all wavelengths.

4.1.3. Combined Effects of Surfacing-Piecing and Bottom-Standing Barriers

Sequentially, the combined effects of surface-piecing and bottom-standing barriers over the undulated slope bottom, defined by Equation (38), are studied. The surface-piercing and bottom-standing barrier are located at $x=v$ and $x=w$, respectively. Typically, we adopt $v/h_1=0.4$ and $w/h_1=0.1$. Additionally, their barrier lengths are set to be equal, as depicted in Figure 12. Basically, the results indicate that the reflection is stronger when the barrier length becomes larger, especially for short waves. In the short wave limit $k{h}_1\to \infty$, total reflections occur when there are barriers ($a/h_1=b/h_1>0$).

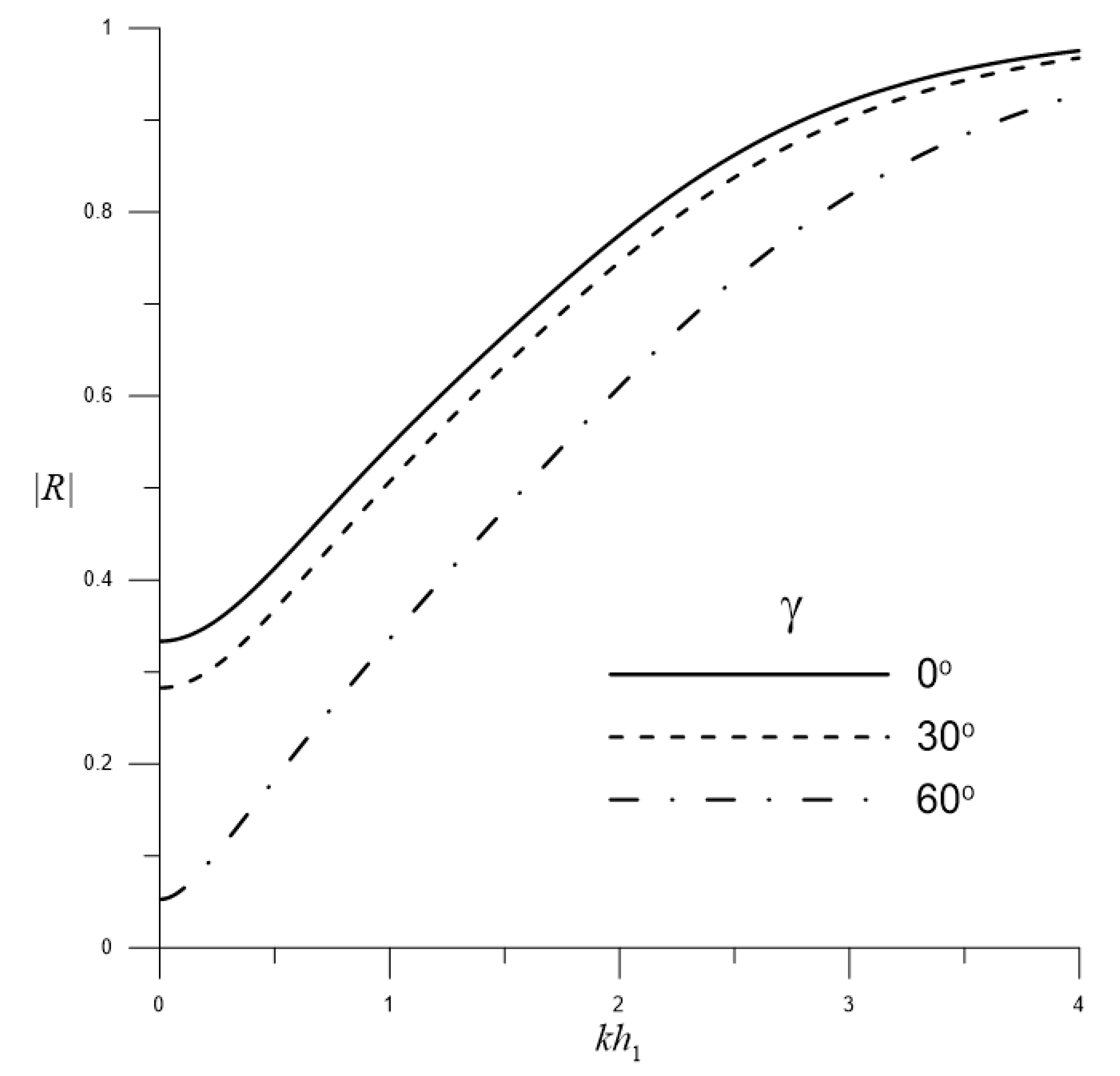
4.1.4. Effect of Oblique Water Waves

In general, water waves could approach to coastal line from either normal incident or oblique incidence. To enlarge the working efficiency of structures, the main target of this section is focusing on the mutation of approach oblique incidences. The parameters of multiple barriers are typically chosen as $a/h_1=0.2$, $v/h_1=0.4$, $b/h_1=0.3$ and $w/h_1=0.1$ with a variety of approaches oblique water wave incidence $\gamma$. As depicted in Figure 13, reflection coefficients are drawn against dimensionless wavenumber $k{h}_1$ under the effect of incidences $\gamma =0°,30°$ and $60°$, respectively. The resulting reflection coefficients are basically not significant with respect to the changes of the incident angles in this specific case. Further studies are still required.

4.2. Combined Effects of Thin Barriers and Sinusoidal Rippled Bottom

Then, the EMM is applied to solve water wave scattering problems by multiple barriers over the sinusoidal rippled bottom to study the Bragg resonance. The sinusoidal rippled bottom is set according to Equation (39) with the parameter defined therein if not otherwise mentioned.

4.2.1. A Single Surface-Piecing or Bottom-Standing Barrier

Let’s begin with the water wave scattering by a surface-piercing or bottom-standing barrier over the prescribed sinusoidal rippled bottom. The surface-piercing or bottom-standing barrier is located at $x=v$ and $x=w$, respectively. Firstly, a surface-piercing barrier is set at location $v/h_1=0.4$ with four values of barrier length $a/h_1$ equal to 0, 0.2, 0.3 and 0.4. Figure 14a illustrates the variation of $\left|R\right|$ against $2k/K$, which indicates that the effect of the surface-piercing barrier is to strengthen the reflection, especially for shorter waves by larger barriers.

Secondly, a bottom-standing barrier is set at location $w/h_1=0.1$ with four values of barrier length $b/h_1$ equal to 0, 0.4, 0.5 and 0.6. Figure 14b shows the variation of $\left|R\right|$ against $2k/K$. In the figure, it is clear that the larger bottom-standing barrier gives a stronger reflection for all wavelengths.

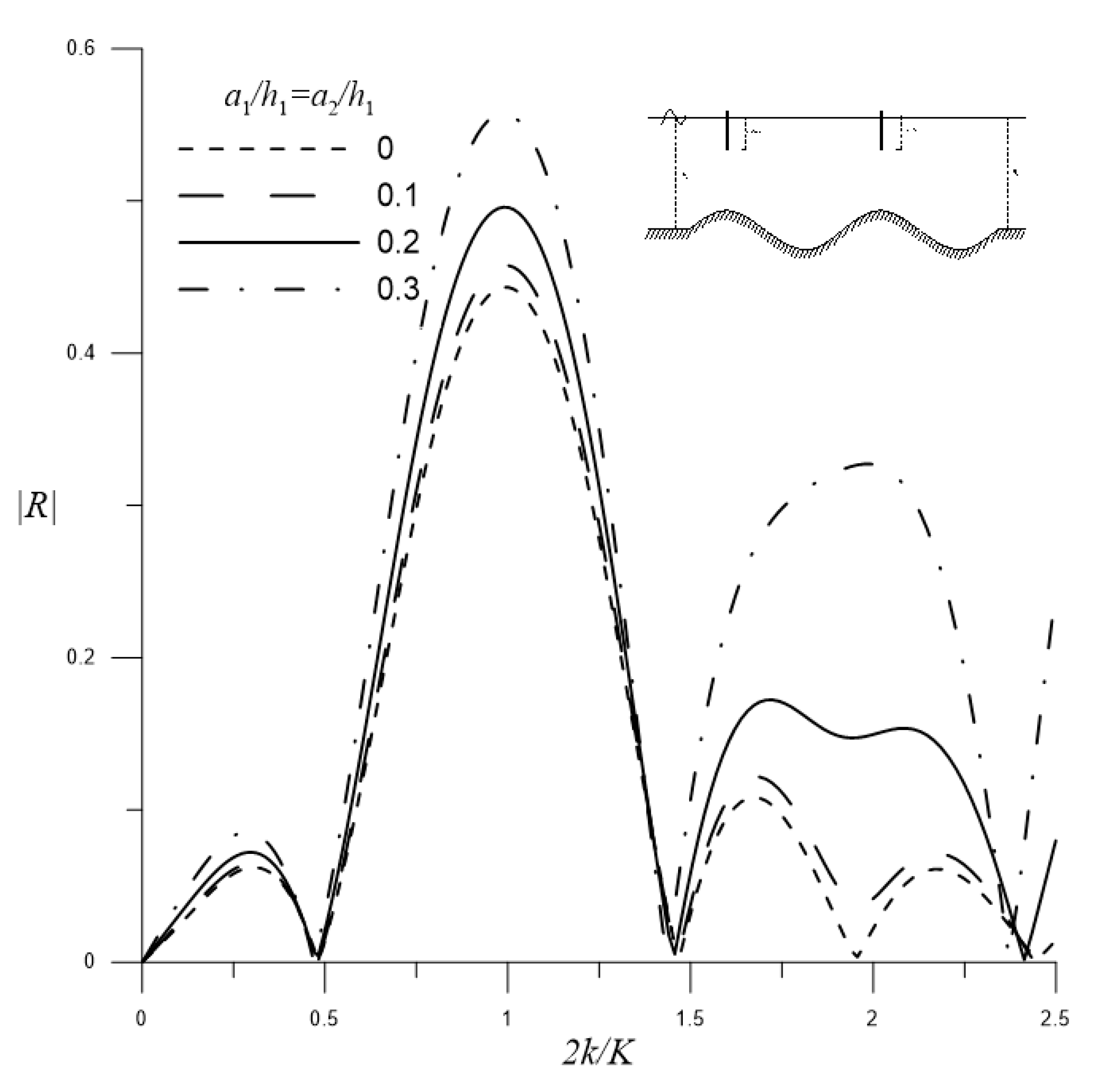
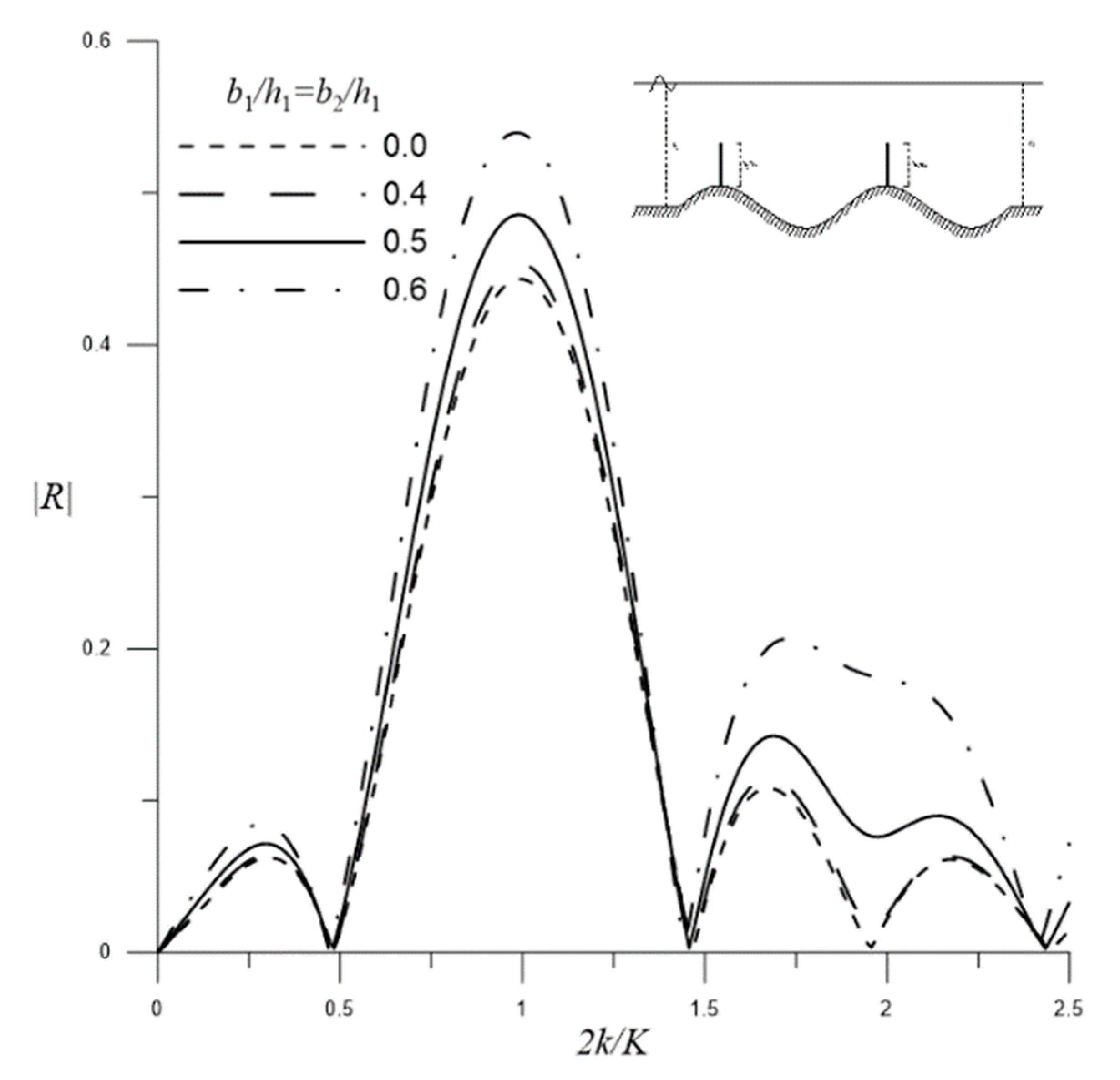
4.2.2. Enhanced Bragg Resonance by Dual Periodic Barriers and Sinusoidal Rippled Bottom

Sequentially, we consider the enhanced Bragg resonance by dual barriers and sinusoidal rippled bottom. At first, we consider the dual periodic surface-piercing barriers located at $x=v_1$ and $x=v_2$ with $v_1/h_1=\pi /2K$ and $v_2/h_1=5\pi /2K$, respectively. The lengths of the barriers are equal as $a_1/h_1=a_2/h_1$ and set to four values of 0, 0.1, 0.2 and 0.3. Figure 15 depicts the variation of $\left|R\right|$ against $2k/K$. In the figure, it is significant that the main effect of dual periodic barriers is to enhance both the primary ($2k/K\sim 1$) and secondary ($2k/K\sim 2$) Bragg resonances, especially for larger barriers. Here, the enhancement of the secondary Bragg resonances is especially observable for the case of $a_1/h_1=a_2/h_1=0.3$.

Secondly, we study the effect of dual periodic bottom-standing barriers located exactly the same as the previous case. The lengths of the barriers are also equal as $b_1/h_1=b_2/h_1$ and set to four values of 0, 0.4, 0.5 and 0.6. Figure 16 shows the variation of $\left|R\right|$ against $2k/K$, in which the enhanced primary and secondary Bragg resonances are also significant, especially for larger barriers.

From these two cases, it is clear that the effects of both the dual periodic surface-piercing and bottom-standing barriers are to enhance the Bragg resonances since they are located with the same frequency as the sinusoidal rippled bottom. The enhancement is significant, especially for the second Bragg resonance for cases of larger barrier lengths. Additionally, the enhanced Bragg resonances are obvious compared to the cases of single barriers in the previous subsection.

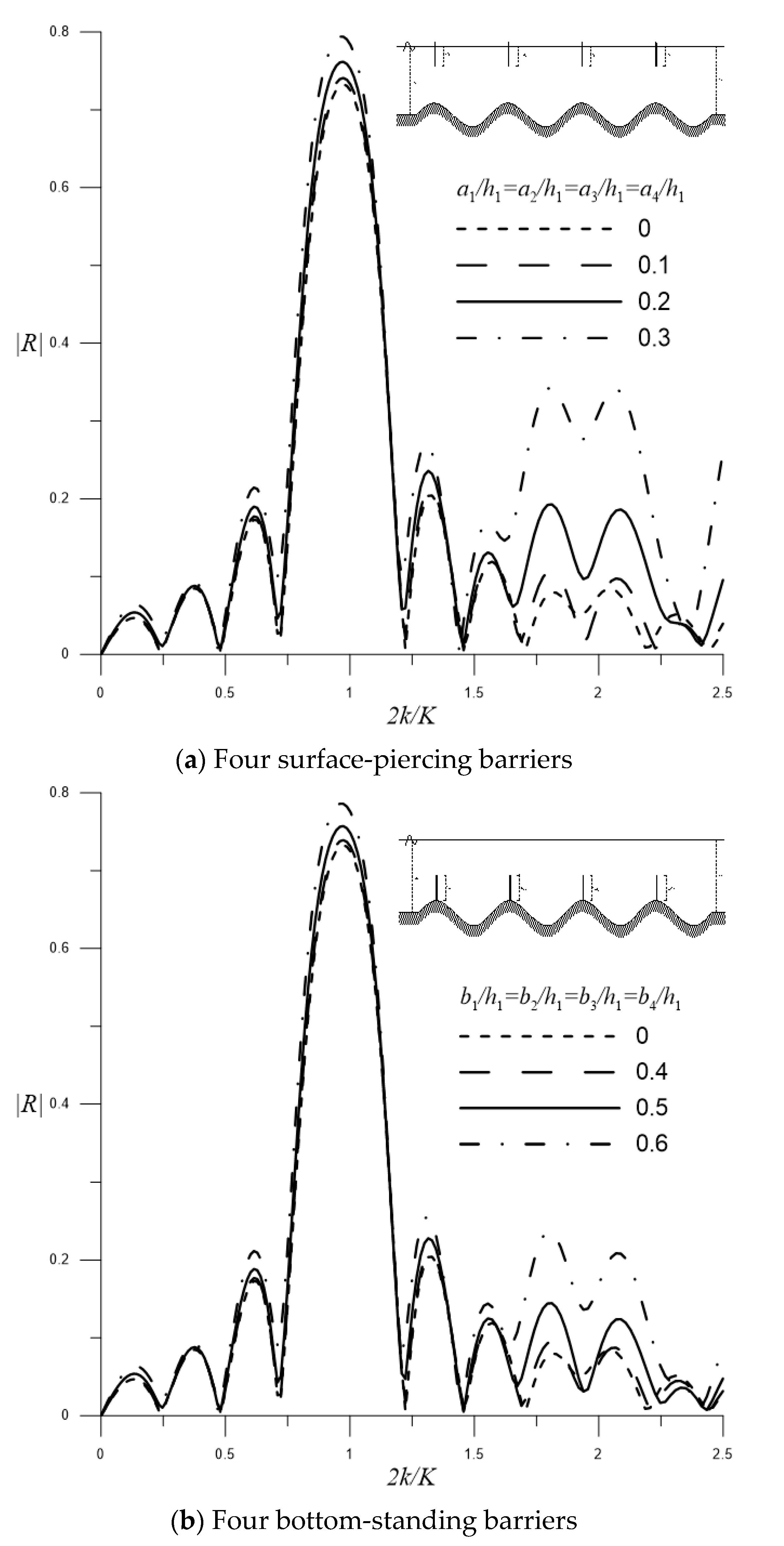
4.2.3. Enhanced Bragg Resonance by Four Periodic Barriers and Sinusoidal Rippled Bottom

In order to demonstrate the enhancements of the Bragg resonance, we consider the problems of water wave scattering by four periodic barries over sinusoidal rippled bottom with the number of ripples $\beta =4$. Both the four periodic barries and the sinusoidal rippled bottom are set to be of the same frequency $K$. In other words, the four periodic surface-piercing barriers are located at $x=v_1$, $x=v_2$, $x=v_3$ and $x=v_4$ with $v_1/h_1=\pi /2K$, $v_2/h_1=5\pi /2K$, $v_3/h_1=9\pi /2K$ and $v_4/h_1=13\pi /2K$, respectively. In addition, the four bottom-standing barriers are located exactly the same. Figure 17 depicts the variation of $\left|R\right|$ against $2k/K$, where the enhanced primary and secondary Bragg resonances are still significant for both the cases of surfacing-piecing and bottom-standing barriers over the sinusoidal rippled bottom. The enhancements are more considerable, especially for the issues of larger barriers.

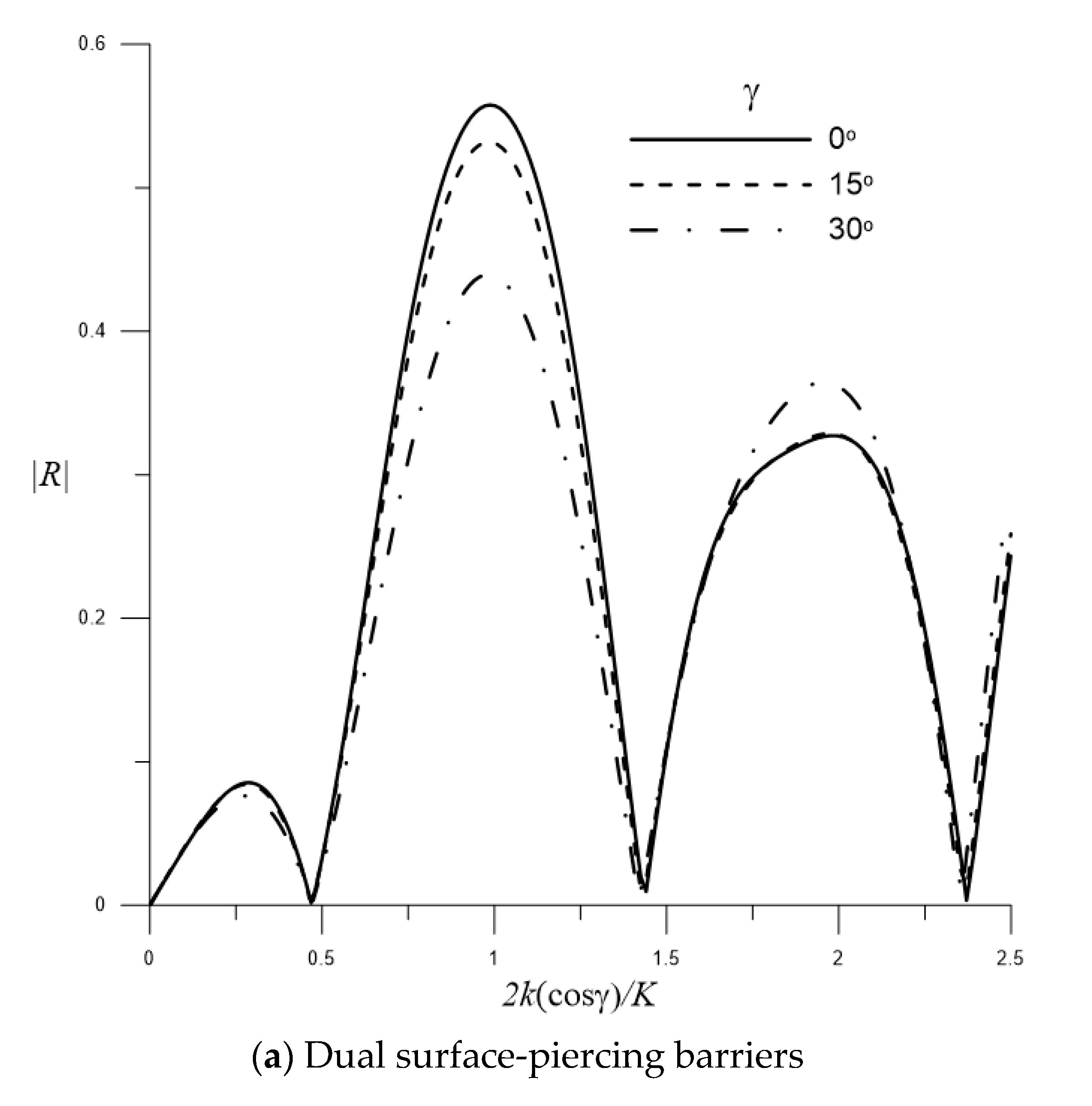
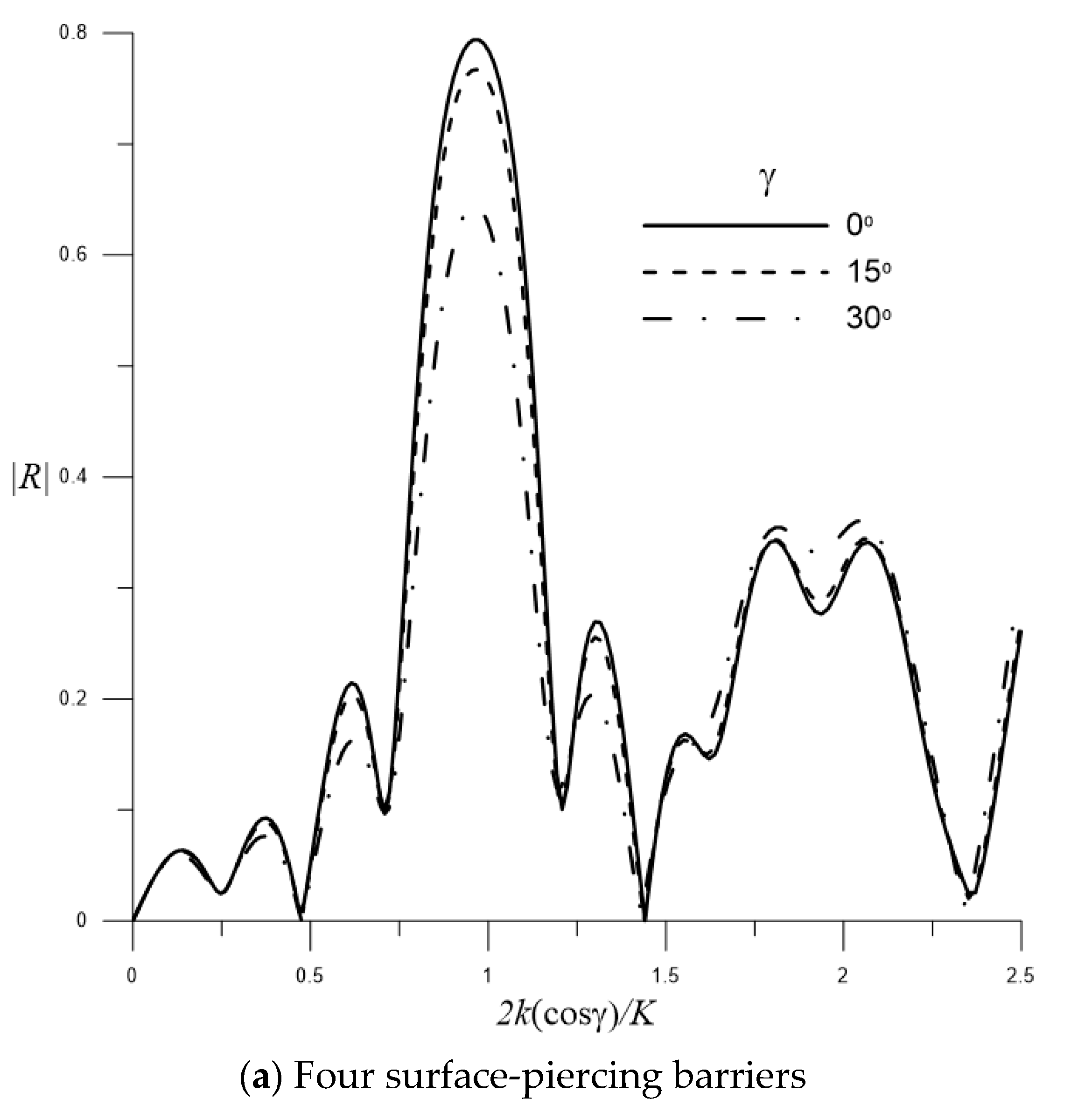
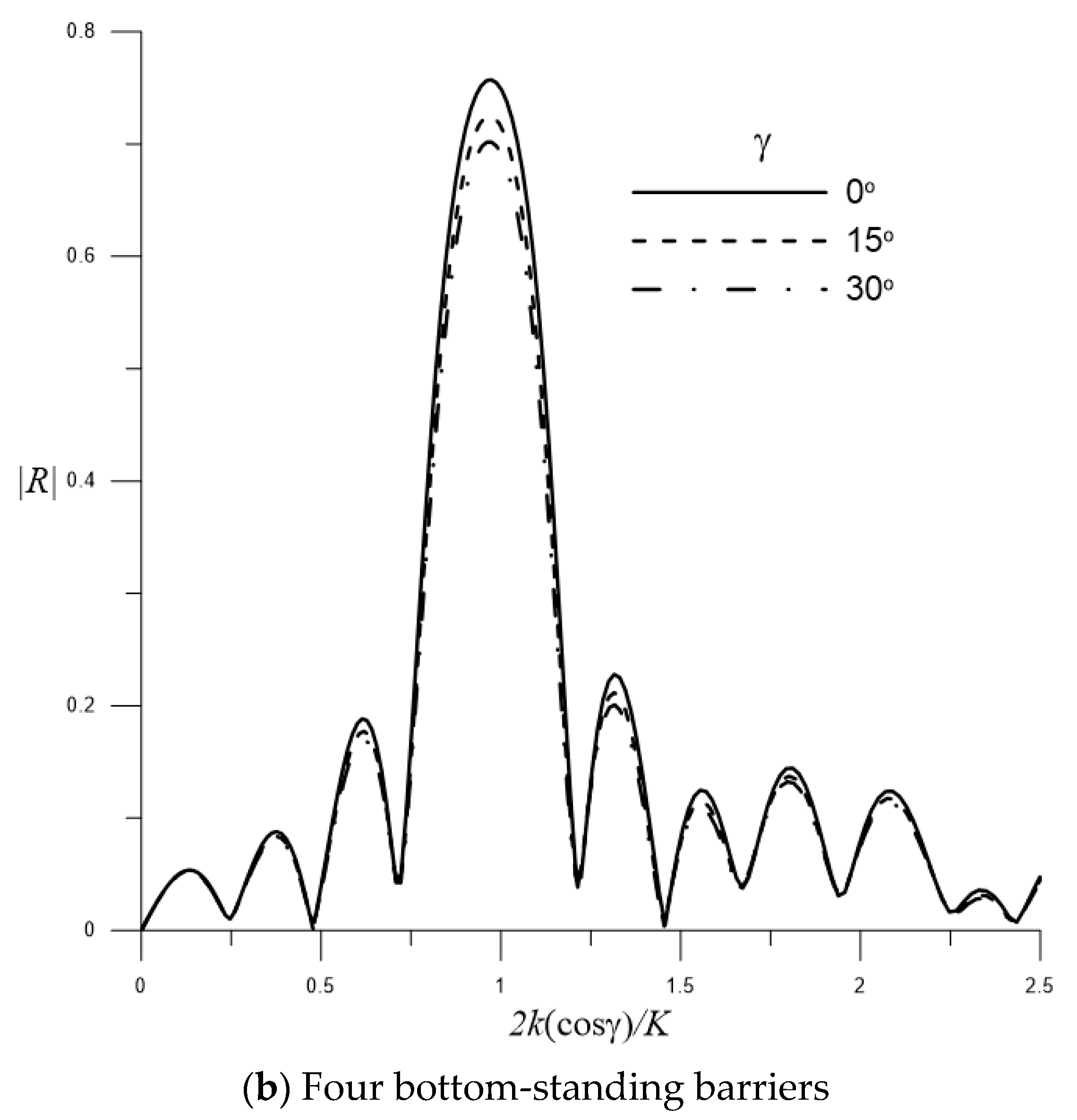
4.2.4. Enhanced Bragg Resonance by Multiple Barriers and Sinusoidal Rippled Bottom under Effects of Oblique Water Waves

In order to study the effects of oblique incidences, the dual thin barrier cases with $a_1/h_1=a_2/h_1=0.3$ and $b_1/h_1=b_2/h_1=0.5$ (in Figure 16) are extended by considering different incident angles. As demonstrated in Figure 18a, $\left|R\right|$ are plotted against $2k(\cos \gamma )/K$ for the surface-piercing case, where the enhanced primary ($2k(\cos \gamma )/K=1$) and secondary Bragg resonances ($2k(\cos \gamma )/K=2$) are still significant for the oblique water wave scattering by dual surfacing-piecing barriers over the sinusoidal rippled bottom. Additionally, the numerical results indicated that the cases with larger incident angles result in less intensive primary Bragg resonances. Then the effects of oblique water waves on the dual bottom-standing barrier over the sinusoidal rippled bottom are studied as depicted in in Figure 18b. In the figure, the Bragg’s law can also be found to be significant and the cases with larger incident angles give less intensive primary Bragg resonances.

Then the effects of oblique water waves are also studied for the cases of four barriers with $a_1/h_1=a_2/h_1=a_3/h_1=a_4/h_1=0.3$ and $b_1/h_1=b_2/h_1=b_3/h_1=b_4/h_1=0.5$ (in Figure 17). Figure 19 illustrates the variation of $\left|R\right|$ against $2k(\cos \gamma )/K$ with values of incident angles $\gamma$ equal to $0°$, $15°$ and $30°$. It is clear from Figure 19 that the enhanced primary ($2k(\cos \gamma )/K=1$) is still significant for the oblique water wave scattering by four surfacing-piecing or bottom-standing barriers over the sinusoidal rippled bottom. Similarly, the numerical results indicated that the cases with larger incident angles result in less intensive Bragg resonances.

5. Conclusions

In this paper, we proposed the EMM formulation to solve the scattering of oblique water waves by multiple thin barriers over undulation bottoms. The bottom topographies were sliced into shelves separated by steps in the solution procedures. Additionally, the solutions were composed of eigenfunctions and solved by the conservations of mass and momentum. The sparse-matrix solver, SuperLU, solved the resulted system of linear equations. The proposed EMM formulation can be reduced to the traditional EMM formulation for cases of undulation bottom without barriers and barriers on a flat bottom. Sequentially, the EMM was validated by the problems of water wave scattering by a single surface-piecing or bottom-standing barrier, dual barriers over a step, undulated slope and sinusoidal rippled bottoms. Then, the effects of barriers on the undulated slope bottom were discussed. Finally, the EMM was applied for studying the impact of barriers on the Bragg resonance by the sinusoidal rippled bottoms. It was found that the effects of the periodic barriers are to enhance the Bragg resonances since they are located with the same frequency as the sinusoidal rippled bottom. The enhanced Bragg resonances are obvious as compared with the cases of single barries over the sinusoidal rippled bottom. Additionally, the Bragg’s law of oblique waves is validated for the prescribed enhanced resonances of periodic barriers and sinusoidal rippled bottoms. Numerical results indicated that the cases with larger incident angles result in less intensive Bragg resonances.