Use of Genetic Programming for the Estimation of CODLAG Propulsion System Parameters
Abstract
1. Introduction
Literature Review
- does the correlation exist, and how strong is the correlation between the parameters of CODLAG propulsion system dataset [9], and
- is it possible to obtain the symbolic expressions using GP algorithm for fuel flow estimation, ship speed estimation, starboard and port propeller torque, and total torque-with and without decay state coefficients.
2. Materials and Methods
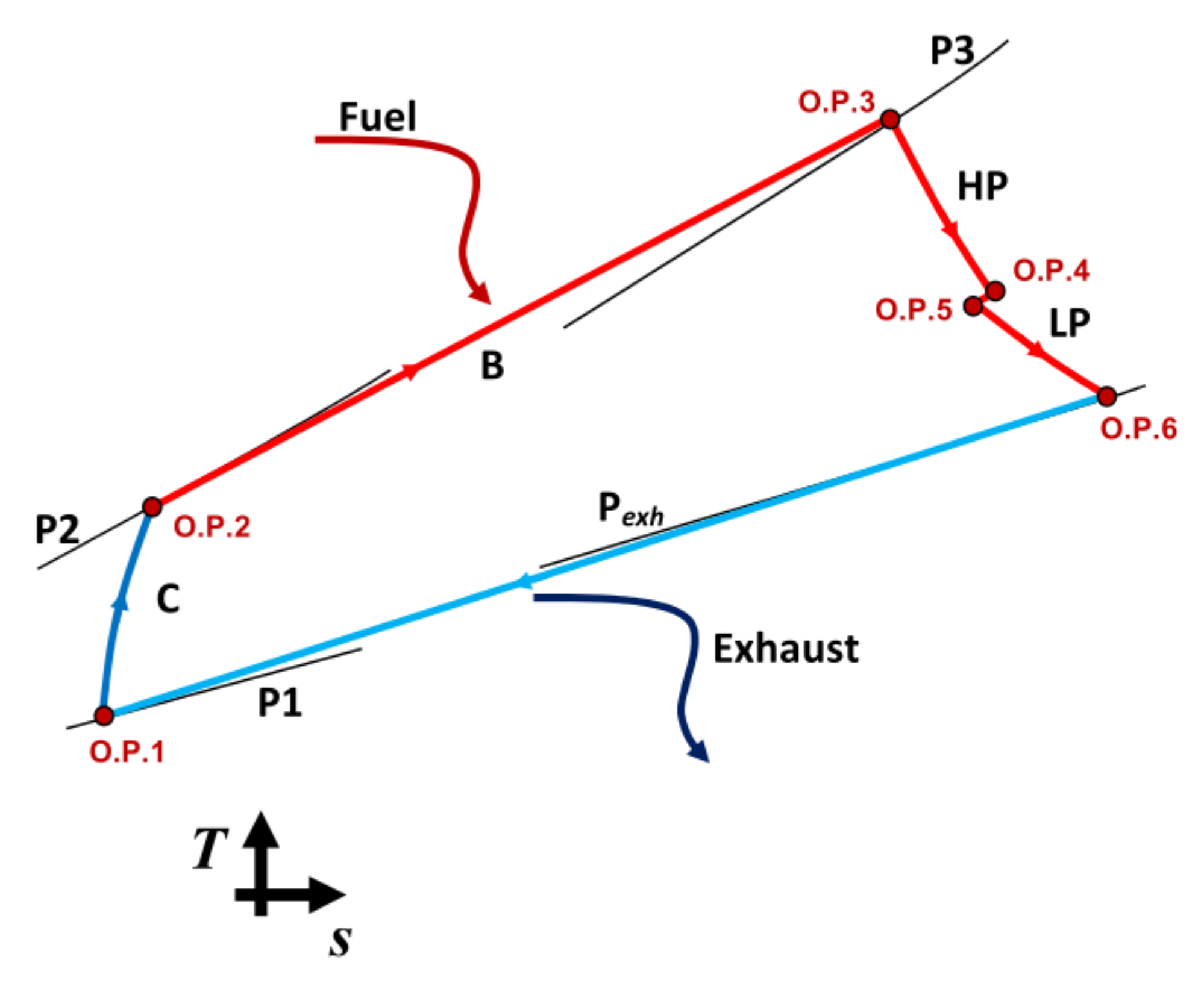
2.1. Dataset Description
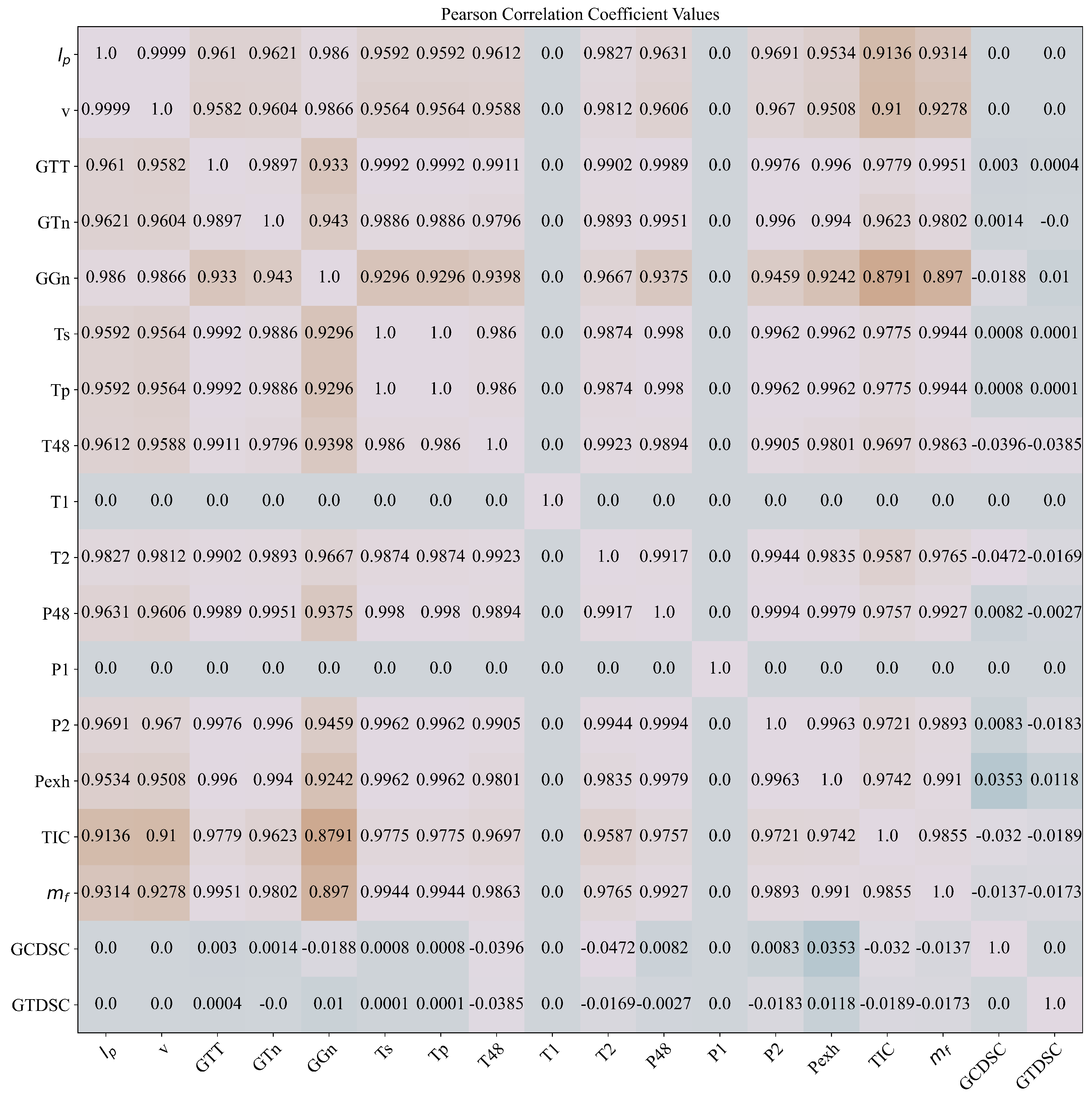
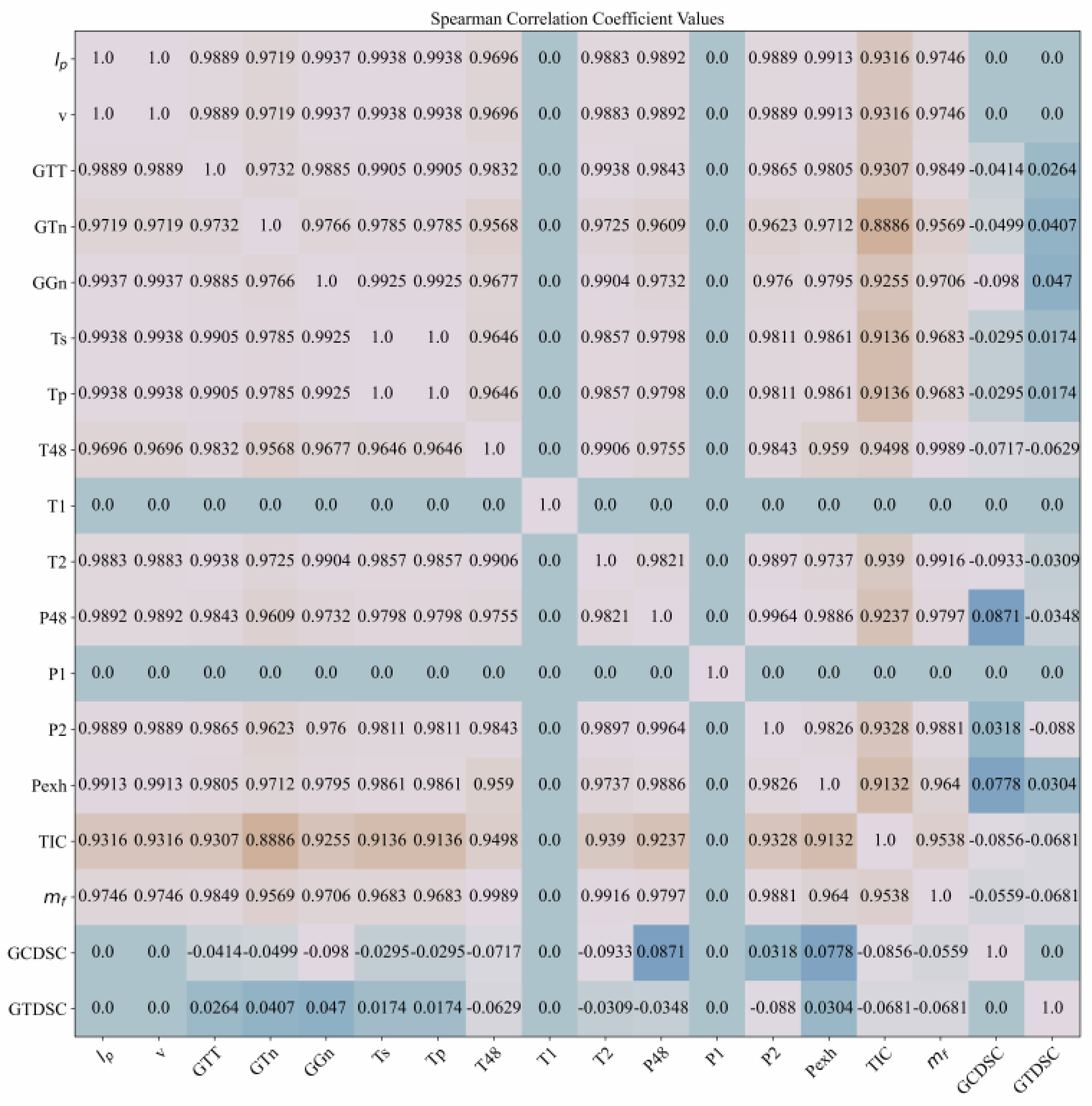
2.2. Correlation Analysis
- -the linear correlation between x and y are positive i.e., higher absolute levels of one variable are associated with lower levels of the other,
- -indicates the absence of any association between x and y, and
- -the linear correlation between x and y is negative i.e., higher absolute levels of one variable are associated with lower levels of the other.
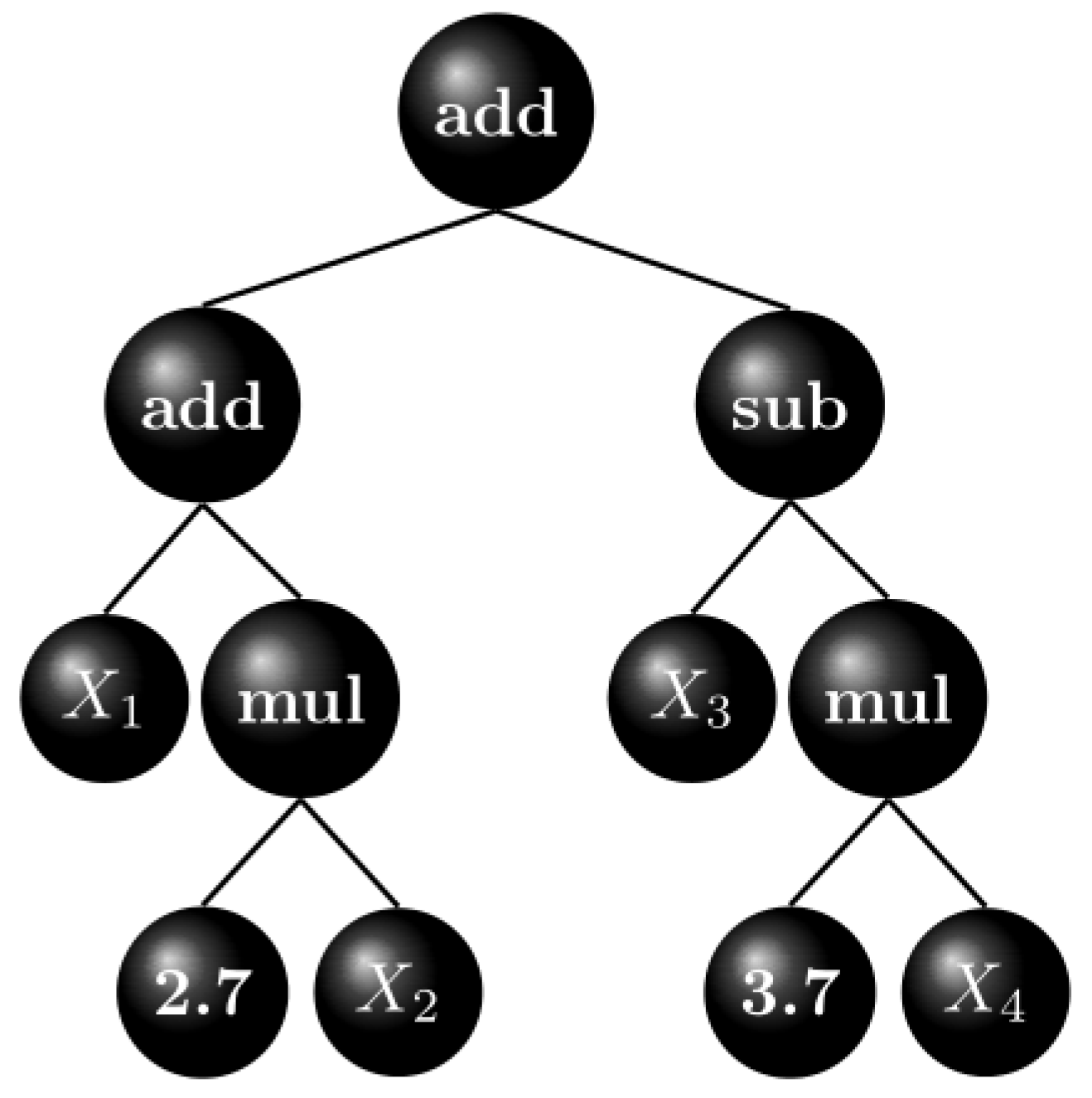
2.3. Genetic Programming
2.4. Evaluation Metrics
3. Results and Discussion
3.1. Results
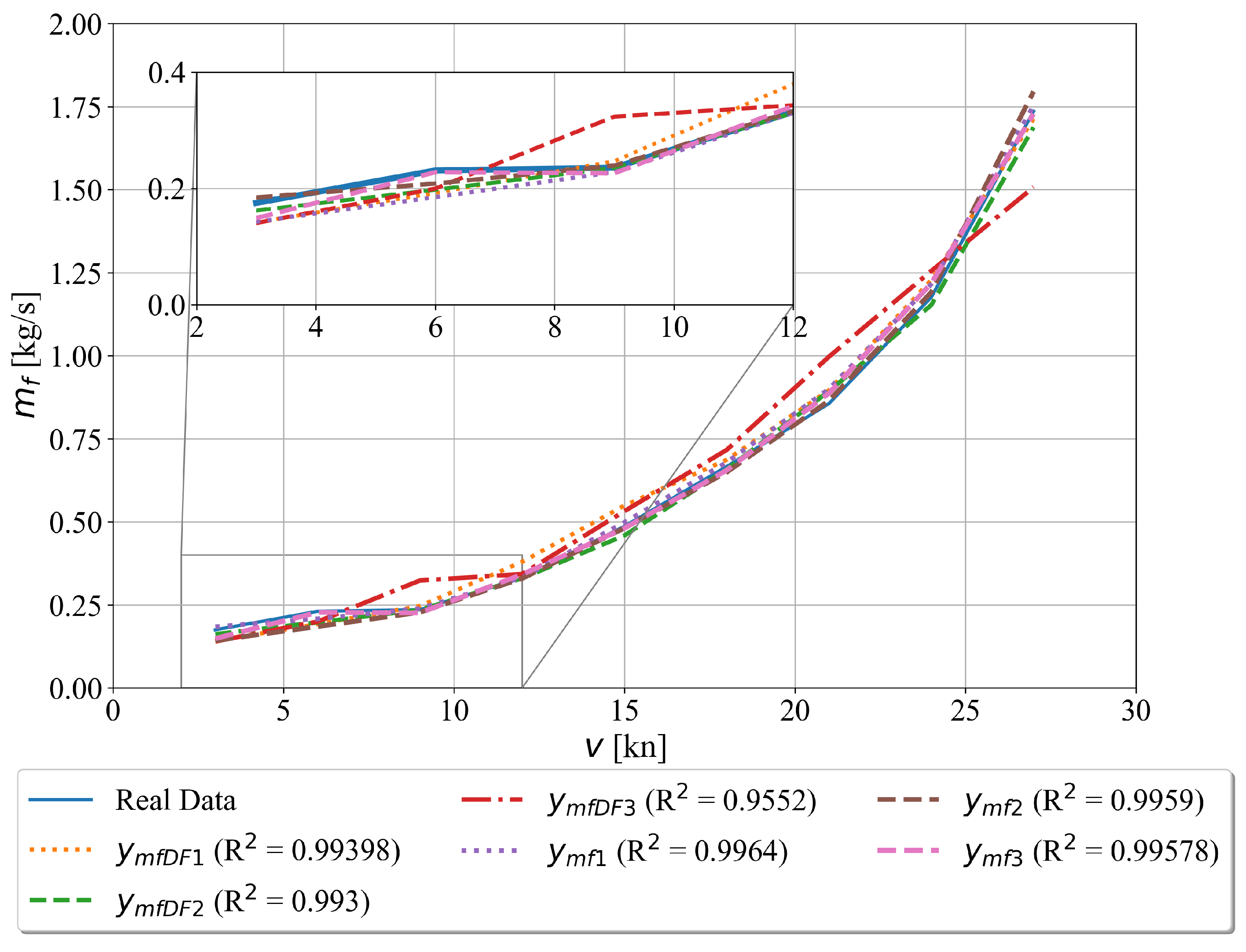
3.1.1. The Symbolic Expressions for Fuel Flow Estimation with and without Decay State Coefficients
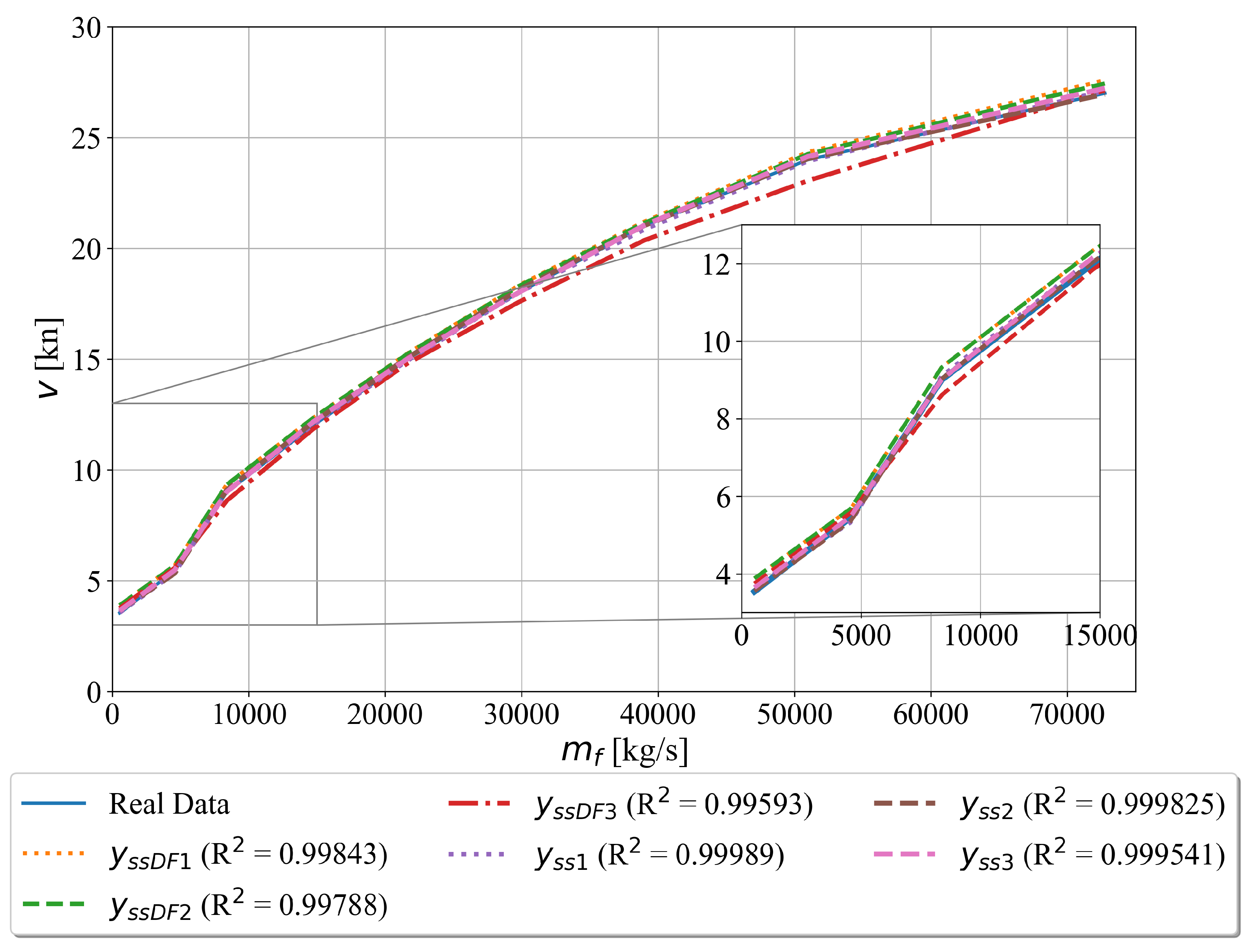
3.1.2. The Symbolic Expressions for Ship Speed Estimation with and without Decay State Coefficients
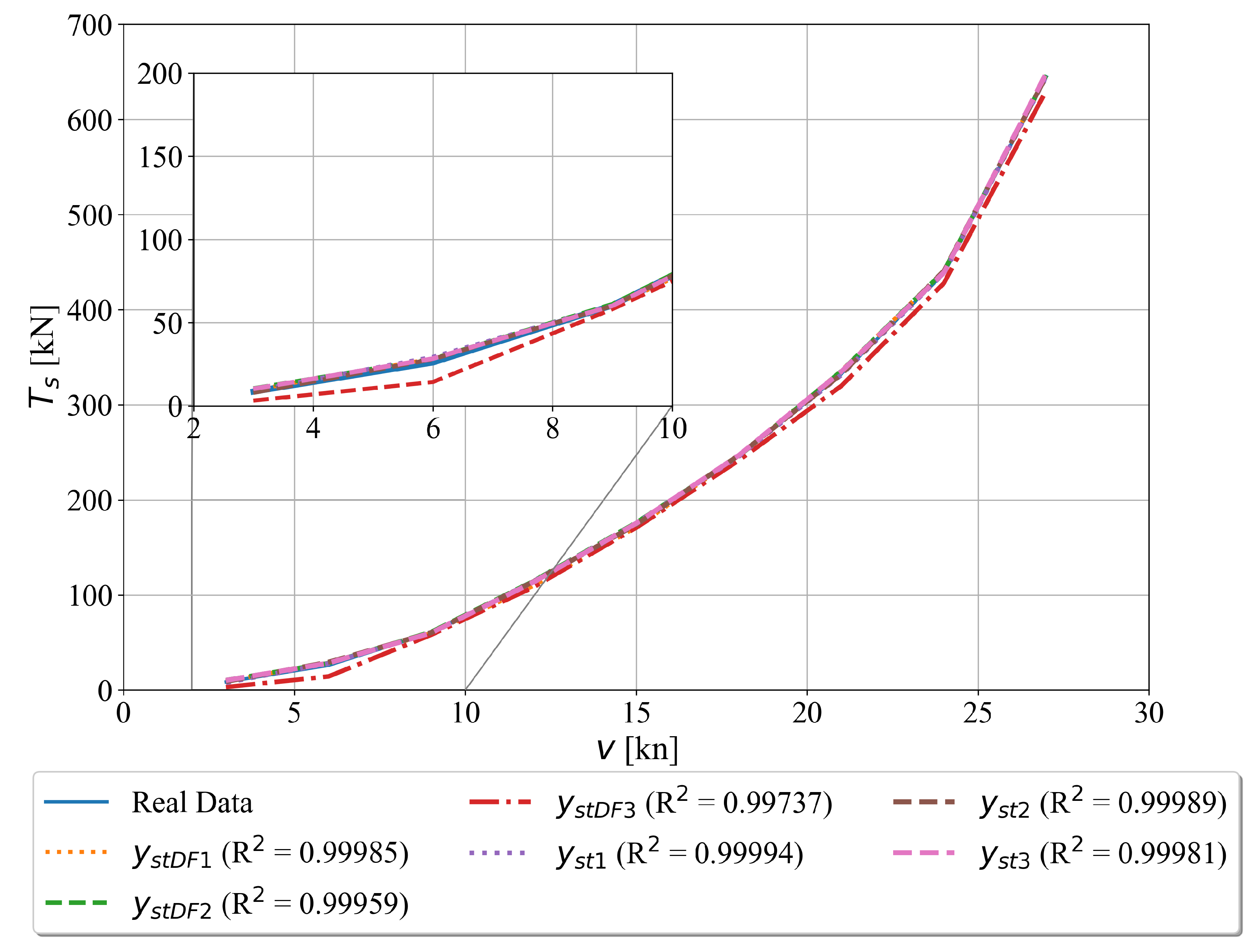
3.1.3. The Symbolic Expressions for Starboard Propeller Torque Estimation with and without Decay State Coefficients
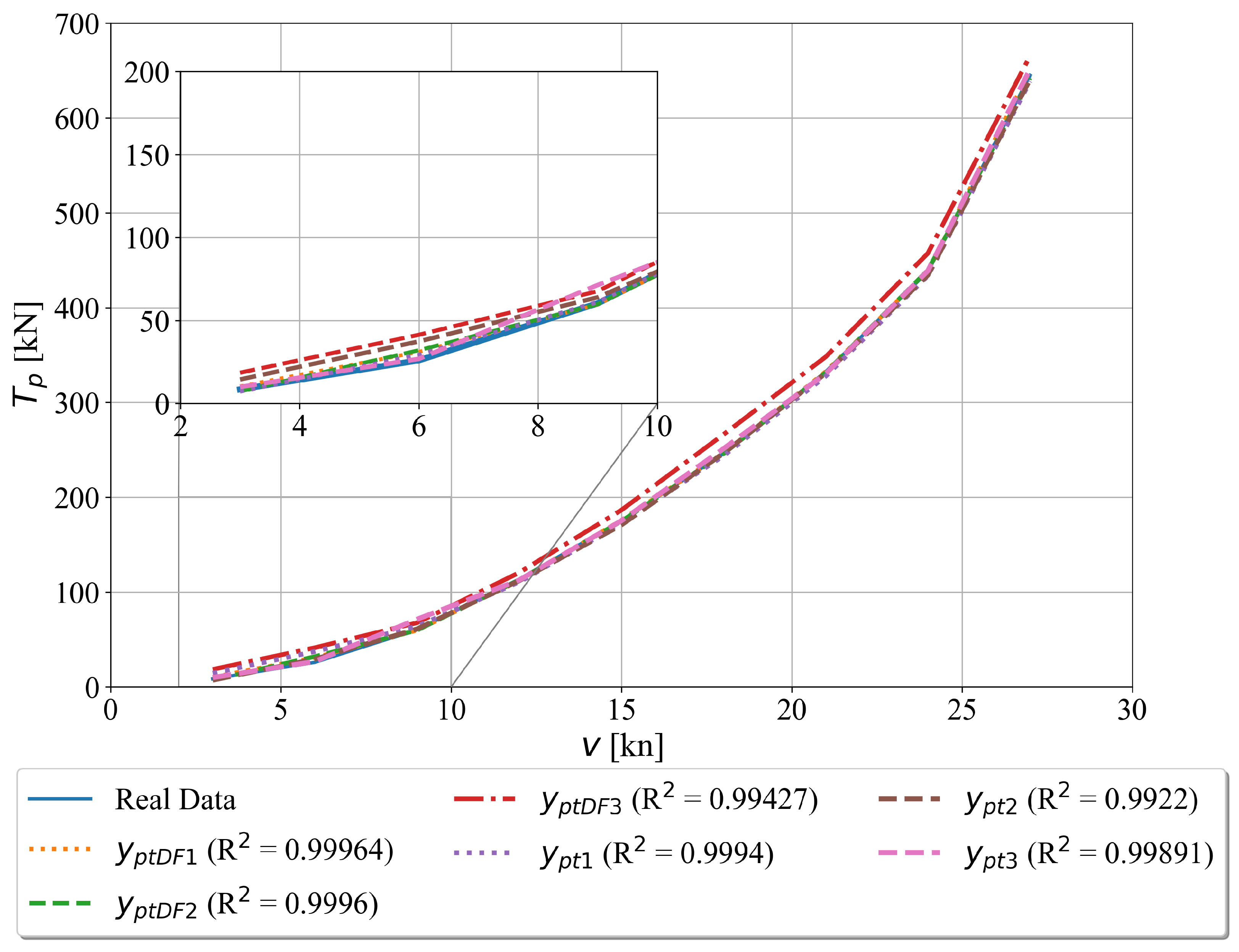
3.1.4. The Symbolic Expressions for Port Propeller Torque Estimation with and without Decay State Coefficients
3.1.5. The Symbolic Expressions for Total Propeller Torque Estimation with and without Decay State Coefficients
3.2. Discussion
4. Conclusions
- the Pearson’s and Spearman’s correlation analysis showed that from a total of 18 variables in the dataset 14 of them (without decay state coefficient, T1, and P1) have positive correlation values. The turbo compressor decay state coefficient and turbine decay state coefficient do not correlate with ship speed, have positive Pearsons correlation with starboard and port propeller torque, have positive and negative Spearman’s correlation with starboard and port propeller torque, and negative correlation with fuel flow. The T1 and P1 represent ambient temperature and pressure so they are constant values throughout the entire dataset. Hence there are not any correlation values with other parameters in the dataset.
- the GP algorithm can be used to obtain symbolic expressions for estimation of fuel flow, ship speed, starboard propeller torque, port propeller torque, and total propeller torque with and without decay state coefficients for the observed CODLAG propulsion system,
- the symbolic expressions for estimation of fuel flow, ship speed, starboard propeller, port propeller and total propeller torque with decay state coefficients generally have slightly lower and slightly higher values when compared to those symbolic expressions obtained without decay state coefficients. However, those symbolic expressions with decay state coefficients are more valuable from the CBM perspective which mean that they could be used to estimate or potentially predict possible degradation system states and schedule the system maintenance,
- the symbolic expressions for estimation of starboard propeller, port propeller, and total propeller torque with and without decay state coefficients showed slightly lower estimation performance for lower ship speeds.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Coefficients in Symbolic Expressions
Appendix A.1. Coefficients in Symbolic Expressions for Starboard Propeller Torque Estimation with Decay State Coefficients
Appendix A.2. Coefficients in Symbolic Expression for Starboard Propeller Torque Estimation without Decay State
Appendix A.3. Coefficients in Symbolic Expressions for Port Propeller Torque Estimation with Decay State Coefficients
Appendix A.4. Coefficients in Symbolic Expressions for Port Propeller Torque Estimation without Decay State Coefficients
Appendix A.5. Coefficients in Symbolic Expressions for Total Propeller Torque Estimation with Decay State Coefficients
Appendix A.6. Coefficients in Symbolic Expressions for Total Propeller Torque Estimation without Decay State Coefficients
References
- Fernández, I.A.; Gómez, M.R.; Gómez, J.R.; Insua, Á.B. Review of propulsion systems on LNG carriers. Renew. Sustain. Energy Rev. 2017, 67, 1395–1411. [Google Scholar] [CrossRef]
- Mrzljak, V.; Poljak, I.; Medica-Viola, V. Dual fuel consumption and efficiency of marine steam generators for the propulsion of LNG carrier. Appl. Therm. Eng. 2017, 119, 331–346. [Google Scholar] [CrossRef]
- Armellini, A.; Daniotti, S.; Pinamonti, P. Gas Turbines for power generation on board of cruise ships: a possible solution to meet the new IMO regulations? Energy Procedia 2015, 81, 540–547. [Google Scholar] [CrossRef]
- Kothamasu, R.; Huang, S.H. Adaptive Mamdani fuzzy model for condition-based maintenance. Fuzzy Sets Syst. 2007, 158, 2715–2733. [Google Scholar] [CrossRef]
- Widodo, A.; Yang, B.S. Support vector machine in machine condition monitoring and fault diagnosis. Mech. Syst. Signal Process. 2007, 21, 2560–2574. [Google Scholar] [CrossRef]
- Altosole, M.; Dubbioso, G.; Figari, M.; Viviani, M.; Michetti, S.; Millerani Trapani, A. Simulation of the dynamic behaviour of a CODLAG propulsion plant. In Proceedings of the WARSHIP 2010 Conference: Advanced Technologies in Naval Design and Construction, Beijing, China, 23–25 November 2010; pp. 9–10. [Google Scholar]
- Altosole, M.; Campora, U.; Martelli, M.; Figari, M. Performance Decay Analysis of a Marine Gas Turbine Propulsion System. J. Ship Res. 2014, 58, 117–129. [Google Scholar] [CrossRef]
- Martelli, M.; Figari, M. Real-Time model-based design for CODLAG propulsion control strategies. Ocean. Eng. 2017, 141, 265–276. [Google Scholar] [CrossRef]
- Coraddu, A.; Oneto, L.; Ghio, A.; Savio, S.; Anguita, D.; Figari, M. Machine Learning Approaches for Improving Condition?Based Maintenance of Naval Propulsion Plants. J. Eng. Marit. Environ. 2014, 230, 136–153. [Google Scholar] [CrossRef]
- Lorencin, I.; Anđelić, N.; Mrzljak, V.; Car, Z. Multilayer perceptron approach to condition-based maintenance of marine CODLAG propulsion system components. Pomorstvo 2019, 33, 181–190. [Google Scholar] [CrossRef]
- Baressi Šegota, S.; Lorencin, I.; Musulin, J.; Štifanić, D.; Car, Z. Frigate Speed Estimation Using CODLAG Propulsion System Parameters and Multilayer Perceptron. NAŠE MORE Znan. Časopis More Pomor. 2020, 67, 117–125. [Google Scholar] [CrossRef]
- Anđelić, N.; Baressi Šegota, S.; Lorencin, I.; Car, Z. Estimation of gas turbine shaft torque and fuel flow of a CODLAG propulsion system using genetic programming algorithm. Pomorstvo 2020, 34, 323–337. [Google Scholar] [CrossRef]
- Cheliotis, M.; Lazakis, I.; Theotokatos, G. Machine learning and data-driven fault detection for ship systems operations. Ocean. Eng. 2020, 216, 107968. [Google Scholar] [CrossRef]
- Uyanık, T.; Karatuğ, Ç.; Arslanoğlu, Y. Machine learning approach to ship fuel consumption: A case of container vessel. Transp. Res. Part Transp. Environ. 2020, 84, 102389. [Google Scholar] [CrossRef]
- Berghout, T.; Mouss, L.H.; Bentrcia, T.; Elbouchikhi, E.; Benbouzid, M. A deep supervised learning approach for condition-based maintenance of naval propulsion systems. Ocean. Eng. 2021, 221, 108525. [Google Scholar] [CrossRef]
- Tsaganos, G.; Nikitakos, N.; Dalaklis, D.; Ölcer, A.; Papachristos, D. Machine learning algorithms in shipping: improving engine fault detection and diagnosis via ensemble methods. WMU J. Marit. Aff. 2020, 19, 1–22. [Google Scholar] [CrossRef]
- Bachmayer, R.; Kampmann, P.; Pleteit, H.; Busse, M.; Kirchner, F. Intelligent Propulsion. In AI Technology for Underwater Robots; Springer: Berlin/Heidelberg, Germany, 2020; pp. 71–82. [Google Scholar]
- Turing, A.M. Computing machinery and intelligence. In Parsing the Turing Test; Springer: Berlin/Heidelberg, Germany, 2009; pp. 23–65. [Google Scholar]
- Forsyth, R. BEAGLE—A Darwinian approach to pattern recognition. Kybernetes 1981, 10, 159–166. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic programming for economic modeling. Stat. Comput. 1994, 4, 187–197. [Google Scholar]
- Loginov, A.; Heywood, M.; Wilson, G. Stock selection heuristics for performing frequent intraday trading with genetic programming. Genet. Program. Evolvable Mach. 2021, 22, 35–72. [Google Scholar] [CrossRef]
- Anđelić, N.; Baressi Šegota, S.; Lorencin, I.; Jurilj, Z.; Šušteršič, T.; Blagojević, A.; Protić, A.; Ćabov, T.; Filipović, N.; Car, Z. Estimation of covid-19 epidemiology curve of the united states using genetic programming algorithm. Int. J. Environ. Res. Public Health 2021, 18, 959. [Google Scholar] [CrossRef]
- Salgotra, R.; Gandomi, M.; Gandomi, A.H. Time series analysis and forecast of the COVID-19 pandemic in India using genetic programming. Chaos Solitons Fractals 2020, 138, 109945. [Google Scholar] [CrossRef] [PubMed]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Schirinzi, A.; Cazzolla, A.P.; Lovero, R.; Lo Muzio, L.; Testa, N.F.; Ciavarella, D.; Palmieri, G.; Pozzessere, P.; Procacci, V.; Di Serio, F.; et al. New insights in laboratory testing for COVID-19 patients: looking for the role and predictive value of Human epididymis secretory protein 4 (HE4) and the innate immunity of the oral cavity and respiratory tract. Microorganisms 2020, 8, 1718. [Google Scholar] [CrossRef] [PubMed]
- Lupton, R. 11. Least Squares Fitting for Linear Models. In Statistics in Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2020; pp. 81–97. [Google Scholar]
- Car, Z.; Baressi Šegota, S.; Anđelić, N.; Lorencin, I.; Mrzljak, V. Modeling the spread of COVID-19 infection using a multilayer perceptron. Comput. Math. Methods Med. 2020, 2020, 5714714. [Google Scholar] [CrossRef]
- Liu, Y.; Mu, Y.; Chen, K.; Li, Y.; Guo, J. Daily activity feature selection in smart homes based on pearson correlation coefficient. Neural Process. Lett. 2020, 51, 1–17. [Google Scholar] [CrossRef]
- Sedgwick, P. Spearman’s rank correlation coefficient. BMJ 2014, 349, g7327. [Google Scholar] [CrossRef]
- Li, C.; Yang, H.; Bao, B.; Guo, H.; Jiang, Y.; Zhang, J. Spearman Correlation Coefficient Abnormal Behavior Monitoring Technology Based on RNN in 5G Network for Smart City. In Proceedings of the 2020 International Wireless Communications and Mobile Computing (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 1440–1442. [Google Scholar]
- Okpala, B. A Measure of the Impact of Employee Motivation on Multicultural Team Performance Using the Spearman Rank Correlation Coefficient. SSRN 3702059 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Poli, R.; Langdon, W.B.; McPhee, N.F.; Koza, J.R. A Field Guide to Genetic Programming; Lulu. com, Lulupress: Morrisville, NC, USA, 2008. [Google Scholar]
- Strušnik, D.; Avsec, J. Artificial neural networking and fuzzy logic exergy controlling model of combined heat and power system in thermal power plant. Energy 2015, 80, 318–330. [Google Scholar] [CrossRef]
- Fang, Y.; Li, J. A review of tournament selection in genetic programming. In International Symposium on Intelligence Computation and Applications; Springer: Berlin/Heidelberg, Germany, 2010; pp. 181–192. [Google Scholar]
- Poli, R.; McPhee, N.F. Parsimony pressure made easy. In Proceedings of the 10th Annual Conference on Genetic and Evolutionary Computation, Atlanta, Georgia, 12–16 July 2008; pp. 1267–1274. [Google Scholar]
- Agrež, M.; Avsec, J.; Strušnik, D. Entropy and exergy analysis of steam passing through an inlet steam turbine control valve assembly using artificial neural networks. Int. J. Heat Mass Transf. 2020, 156, 119897. [Google Scholar] [CrossRef]



| Physical Variable | Range | Unit |
|---|---|---|
| Lever position () | 1.138–9.3 | - |
| Ship speed (v) | 3–27 | kn |
| Gas turbine shaft torque (GTT) | 253.547–72,784.872 | kNm |
| GT rate of revolutions (GTn) | 1307.675–3560.741 | rpm |
| Gas generator rate of revolutions (GGn) | 6589.002–9797.103 | rpm |
| Starboard propeller torque (Ts) | 5.304–645.249 | kN |
| Port propeller torque (Tp) | 5.304–645.249 | kN |
| High pressure turbine exit temperature (T48) | 442.364–1115.797 | C |
| Turbo compressor inlet air temperature (T1) | 288 | C |
| Turbo compressor outlet air temperature (T2) | 540.442–789.094 | C |
| HP turbine exit pressure (P48) | 1.093–4.56 | bar |
| Turbo compressor inlet air pressure (P1) | 0.998 | bar |
| Turbo compressor outlet air pressure (P2) | 5.828–23.14 | bar |
| GT exhaust gas pressure () | 1.019–1.052 | bar |
| Turbine injection control (TIC) | 0–92.556 | % |
| Fuel flow () | 0.068–1.832 | kg/s |
| Turbo compressor decay state coefficient | 0.95–1 | - |
| Turbine decay state coefficient | 0.975–1 | - |
| Physical Variable | Representation of Variables in GP | ||||
|---|---|---|---|---|---|
| Fuel Flow Analysis | Ship Speed Analysis | Starboard Propeller Torque Analysis | Port Propeller Torque Analysis | Total Propeller Torque Analysis | |
| Lever position () | |||||
| Ship speed (v) | y | ||||
| Gas turbine shaft torque (GTT) | |||||
| GT rate of revolutions (GTn) | |||||
| Gas generator rate of revolutions (GGn) | |||||
| Starboard propeller torque (Ts) | y | - | - | ||
| Port propeller torque (Tp) | - | y | - | ||
| High pressure turbine exit temperature (T48) | |||||
| turbo compressor inlet air temperature (T1) | |||||
| turbo compressor outlet air pressure (P2) | |||||
| HP turbine exit pressure (P48) | |||||
| Turbo compressor inlet air pressure (P1) | |||||
| Turbo compressor outlet air pressure (P2) | |||||
| GT exhaust gas pressure () | |||||
| Turbine injection control (TIC) | |||||
| Fuel flow () | y | ||||
| Turbo compressor decay state coefficient | |||||
| Trubine decay state coefficient | |||||
| Total Propeller Torque (Ts+Tp) | - | - | - | - | y |
| GP Parameter | Lower Bound | Upper Bound |
|---|---|---|
| Population size | 500 | 1000 |
| Number of generations | 100 | 500 |
| Tournament selection size | 50 | 100 |
| Tree depth | (3–7) | (6–12) |
| Crossover coefficient | 0.9 | 1 |
| Subtree mutation coefficient | 0.01 | 0.1 |
| Hoist mutation coefficient | 0.01 | 0.1 |
| Point mutation coefficient | 0.01 | 0.1 |
| Stopping criteria value | 0.001 | |
| Maximum number of samples | 0.9 | 1.0 |
| Constant range | −0.1 | 0.1 |
| Parsimony coefficient | 0.01 |
| GP Parameters - Population, Generations, Selection Size, Tree Depth, Crossover Coef., Subtree Mutation Coef., Hoist Mutation Coef., Point Mutation Coef., Stopping Criteria, Samples, Constant Range, Parsimony Coef. | Symbolic Expression | ||
|---|---|---|---|
| [930, 243, 81, (3, 11), 0.91, 0.021, 0.015, 0.041, 0.0002, 0.95, (−0.043, 0.021), 0.0003] | |||
| [742, 103, 92, (4, 11), 0.9, 0.026, 0.035, 0.02, 0.0002, 0.91, (−0.071, 0.02), 0.0038] | |||
| [927, 346, 80, (6, 9), 0.9, 0.032, 0.039, 0.019, 0.0002, 0.92, (−0.063, 0.056), 0.0008] |
| GP Parameters - Population, Generations, Selection Size, Tree Depth, Crossover Coef., Subtree Mutation Coef., Hoist Mutation Coef., Point Mutation Coef., Stopping Criteria, Samples, Constant Range, Parsimony Coef. | Symbolic Expression | ||
|---|---|---|---|
| [962, 289, 52, (6, 8), 0.91, 0.017, 0.035, 0.03, 0.000524, 0.99, (−0.073, 0.0014), 0.0029] | 0.9964 | 0.02276 | |
| [1000, 141, 83, (5, 9), 0.9, 0.022, 0.012, 0.032, 0.000986, 0.98, (−0.049, 0.0943), 0.0013] | 0.99591 | 0.02341 | |
| [582, 365, 85, (4, 7), 0.9, 0.022, 0.027, 0.018, 0.00046, 0.91, (−0.0103, 0.0905), 0.0003] | 0.99578 | 0.023027 |
| GP Parameters - Population, Generations, Selection Size, Tree Depth, Crossover Coef., Subtree Mutation Coef., Hoist Mutation Coef., Point Mutation Coef., Stopping Criteria, Samples, Constant Range, Parsimony Coef. | Symbolic Expression | ||
|---|---|---|---|
| [548, 311, 87, (3, 8), 0.91, 0.017, 0.017, 0.018, 0.000926, 0.92, (−0.015, 0.044), 0.0013] | 0.99843 | 0.2858 | |
| [784, 458, 77, (4, 7), 0.9, 0.015, 0.015, 0.06, , 0.9, (−0.0083, 0.082), 0.0063] | 0.99788 | 0.32584 | |
| [585, 286, 69, (3, 12), 0.9, 0.024, 0.025, 0.023, 0.000191, 0.92, (−0.00084, 0.018), 0.0053] | 0.99593 | 0.41067 |
| GP Parameters - Population, Generations, Selection Size, Tree Depth, Crossover Coef., Subtree Mutation Coef., Hoist Mutation Coef., Point Mutation Coef., Stopping Criteria, Samples, Constant Range, Parsimony Coef. | Symbolic Expression | ||
|---|---|---|---|
| [732, 352, 86, (6, 10), 0.92, 0.012, 0.013, 0.023, 0.000231, 0.9, (−0.073, 0.031), 0.003] | 0.9998925 | 0.06729 | |
| [945, 479, 70, (6, 7), 0.91, 0.016, 0.016, 0.014, , 0.98, (−0.085, 0.0049), 0.0097] | 0.999825 | 0.08665 | |
| [690, 152, 82, (6, 12), 0.9, 0.047, 0.01, 0.018, , 0.94, (−0.023, 0.058), 0.0078] | 0.999541 | 0.11797 |
| GP Parameters - Population, Generations, Selection Size, Tree Depth, Crossover Coef., Subtree Mutation Coef., Hoist Mutation Coef., Point Mutation Coef., Stopping Criteria, Samples, Constant Range, Parsimony Coef. | Symbolic Expression | ||
|---|---|---|---|
| [996, 399, 69, (3, 10), 0.92, 0.013, 0.035, 0.018, , 0.94, (−0.078, 0.077), 0.0061] | 0.99985 | 1.98477 | |
| [821, 418, 92, (4, 10), 0.909, 0.044, 0.018, 0.011, , 0.98, (−0.002, 0.07), 0.0022] | 0.99959 | 3.16776 | |
| [598, 398, 63, (4, 11), 0.9, 0.033, 0.018, 0.032, , 0.96, (−0.0055, 0.014), 0.0016] | 0.99737 | 7.9579 |
| GP Parameters - Population, Generations, Selection Size, Tree Depth, Crossover Coef., Subtree Mutation Coef., Hoist Mutation Coef., Point Mutation Coef., Stopping Criteria, Samples, Constant Range, Parsimony Coef. | Symbolic Expression | ||
|---|---|---|---|
| [554, 233, 81, (5, 11), 0.9, 0.052, 0.025, 0.017, , 0.95, (−0.087, 0.028), 0.0031] | 0.99994 | 1.0697 | |
| [792, 144, 63, (5, 8), 0.92, 0.039, 0.013, 0.025, , 0.92, (−0.07, 0.01), 0.0069] | 0.99989 | 1.3387 | |
| [824, 297, 57, (6, 7), 0.91, 0.014, 0.032, 0.031, , 0.92, (−0.08, 0.039), 0.0039] | 0.99981 | 1.8535 |
| GP Parameters - Population, Generations, Selection Size, Tree Depth, Crossover Coef., Subtree Mutation Coef., Hoist Mutation Coef., Point Mutation Coef., Stopping Criteria, Samples, Constant Range, Parsimony Coef. | Symbolic Expression | ||
|---|---|---|---|
| [788, 470, 94, (6, 8), 0.93, 0.016, 0.017, 0.032, , 0.93, (−0.072, 0.083), 0.0044] | 0.99964 | 1.9885 | |
| [979, 263, 77, (6, 8), 0.91, 0.047, 0.012, 0.022, , 0.91, (−0.062, 0.0027), 0.0043] | 0.9996 | 2.61963 | |
| [986, 394, 53, (3, 12), 0.91, 0.018, 0.051, 0.013, , 0.946, (−0.02, 0.016), 0.0095] | 0.99427 | 14.0996 |
| GP Parameters - Population, Generations, Selection Size, Tree Depth, Crossover Coef., Subtree Mutation Coef., Hoist Mutation Coef., Point Mutation Coef., Stopping Criteria, Samples, Constant Range, Parsimony Coef. | Symbolic Expression | ||
|---|---|---|---|
| [709, 445, 70, (5, 11), 0.9, 0.023, 0.029, 0.041, , 0.94, (−0.041, 0.01), 0.0031] | 0.9994 | 3.35254 | |
| [986, 294, 74, (4, 12), 0.91, 0.042, 0.012, 0.025, , 0.91, (−0.021, 0.081), 0.0061 ] | 0.99922 | 4.06154 | |
| [769, 415, 69, (3, 11), 0.93, 0.014, 0.011, 0.028, , 0.96, (−0.067, 0.035), 0.0046] | 0.99891 | 5.11714 |
| GP Parameters - Population, Generations, Selection Size, Tree Depth, Crossover Coef., Subtree Mutation Coef., Hoist Mutation Coef., Point Mutation Coef., Stopping Criteria, Samples, Constant Range, Parsimony Coef. | Symbolic Expression | ||
|---|---|---|---|
| [910, 285, 69, (5, 9), 0.91, 0.038, 0.016, 0.015, , 0.94, (−0.029, 0.09), 0.0096] | 0.99848 | 11.697387 | |
| [664, 116, 75, (3, 10), 0.9, 0.058, 0.015, 0.017, , 0.93, (−0.048, 0.015), 0.0096] | 0.991606 | 26.33334 | |
| [790, 112, 79, (3, 12), 0.91, 0.012, 0.031, 0.021, , 0.9, (−0.02, 0.054), 0.007] | 0.97971 | 49.89208 |
| GP Parameters - Population, Generations, Selection Size, Tree Depth, Crossover Coef., Subtree Mutation Coef., Hoist Mutation Coef., Point Mutation Coef., Stopping Criteria, Samples, Constant Range, Parsimony Coef. | Symbolic Expression | ||
|---|---|---|---|
| [682, 172, 56, (4, 7), 0.9, 0.018, 0.025, 0.029, , 0.93, (−0.012, 0.065), 0.0026] | 0.99808 | 9.2407 | |
| [798, 103, 77, (4, 11), 0.9, 0.01, 0.061, 0.021, , 0.92, (−0.039, 0.046), 0.0069] | 0.99806 | 13.25 | |
| [883, 209, 64, (6, 9), 0.93, 0.013, 0.023, 0.028, , 0.96, (−0.057, 0.057), 0.0099] | 0.9976 | 13.6284 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anđelić, N.; Baressi Šegota, S.; Lorencin, I.; Poljak, I.; Mrzljak, V.; Car, Z. Use of Genetic Programming for the Estimation of CODLAG Propulsion System Parameters. J. Mar. Sci. Eng. 2021, 9, 612. https://doi.org/10.3390/jmse9060612
Anđelić N, Baressi Šegota S, Lorencin I, Poljak I, Mrzljak V, Car Z. Use of Genetic Programming for the Estimation of CODLAG Propulsion System Parameters. Journal of Marine Science and Engineering. 2021; 9(6):612. https://doi.org/10.3390/jmse9060612
Chicago/Turabian StyleAnđelić, Nikola, Sandi Baressi Šegota, Ivan Lorencin, Igor Poljak, Vedran Mrzljak, and Zlatan Car. 2021. "Use of Genetic Programming for the Estimation of CODLAG Propulsion System Parameters" Journal of Marine Science and Engineering 9, no. 6: 612. https://doi.org/10.3390/jmse9060612
APA StyleAnđelić, N., Baressi Šegota, S., Lorencin, I., Poljak, I., Mrzljak, V., & Car, Z. (2021). Use of Genetic Programming for the Estimation of CODLAG Propulsion System Parameters. Journal of Marine Science and Engineering, 9(6), 612. https://doi.org/10.3390/jmse9060612











