Abstract
The surface crack, also known as the partly through-thickness crack, is a serious threat to the structural integrity of offshore metallic pipes. In this paper, we review the research progress in regard to surface crack growth in metallic pipes subjected to cyclic loads from the fracture mechanics perspective. The purpose is to provide state-of-the-art investigations, as well as indicate the remaining challenges. First, the available studies on surface cracked metallic pipes are overviewed from experimental, numerical, and analytical perspectives, respectively. Then, we analyse state-of-the-art research and discuss the insufficiencies of the available literature from different perspectives, such as surface cracks and pipe configurations, environmental influential parameters, the girth welding effect, and numerical and analytical evaluation methods. Building on these surveys and discussions, we identify various remaining challenges and possible further research topics that are anticipated to be of significant value both for academics and practitioners.
1. Introduction
The metallic pipeline is one of the primary devices for oil and natural gas production and transportation in the offshore industry. It has been widely applied owing to the advantages of cost-effectiveness, simplicity, ease of installation, and maintenance. Maintaining the structural integrity of offshore metallic pipelines is of great importance to guarantee operational safety. While as a matter of fact, offshore metallic pipelines are prone to the fatigue problem due to a variety of environmental and operational dynamic loads [1,2]. For instance, there are two typical layouts of offshore metallic pipes: the S-shape and the J-shape (as shown in Figure 1), where the critical areas, i.e., hang-off zone, touch-down zone, sag bend, and arch bend, seriously suffer from fatigue problems under dynamic loads induced by waves, wind, currents, 2nd order floater motions, and unstable internal pressure [3,4].
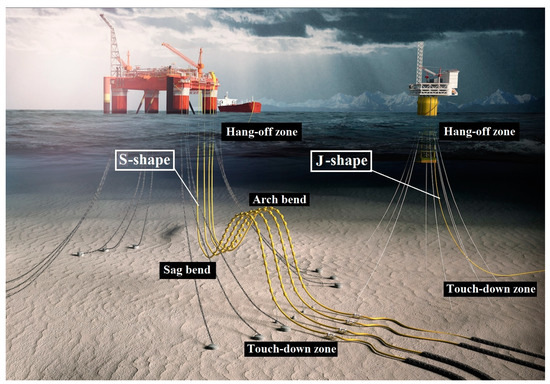
Figure 1.
Fatigue critical zones in two typical offshore metallic pipes: J-shape and S-shape.
Surface cracks, in most cases as a semi-elliptical shape [5,6] (see in Figure 2), frequently initiate and propagate in these critical areas. They may initiate from surface defects or corrosion pits on the base material or at weld toes [7], appearing on either the internal or the external surface. Under dynamic loads of combined tensile and bending loads (e.g., the hang-off zone), or high magnitude bending moments (e.g., the touch-down zone, sag bend, and arch bend), in combination with the internal pressure [8,9], surface cracks may continually propagate, and finally cause leakage or collapse. For instance, a report by the Petroleum Safety Authority Norway indicated that between 1975 and 2018, 140 out of around 930 total anomalies were due to cracks, accounting for around 15% [10].

Figure 2.
Circumferential semi-elliptical surface crack in metallic pipes, data from Ref. [12].
Particularly, besides the internal pressure, which is the principle load case for transportation pipelines, cyclic bending is a dominate load case on offshore pipes. In addition, the offshore metallic pipelines in practical situations are connected by standardised pipes through girth welding, which is the hotbed for crack initiation [7]. In a Det Norske Veritas (DNVGL) report, the data of 1719 fatigued metallic pipe specimens were collected, where 445 pipes failed due to circumferential surface crack growth, accounting for 25.89% [11].
Hence, surface crack growth is a huge threat to the structural integrity of metallic pipes, which has drawn wide attention from the offshore industry and academia. In our review effort, searching the SCOPUS and Google Scholar using “surface crack” or “part through crack” and “pipe” as well as their synonyms as key terms, plus by applying the forward and backward snowballing techniques [13], we selected the related topics regarding the issue of surface crack growth in metallic pipe structures. Figure 3 shows the research status on different surface cracked structures, where 60% of the research is on cracked plates. The research on pipe structures (including pressure vessels) accounts for 40%, which is the second biggest research hotspot.
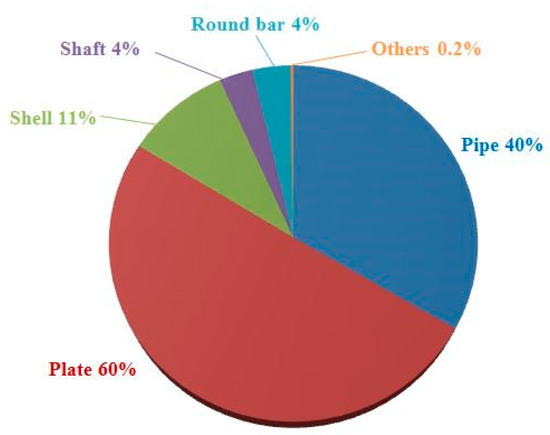
Figure 3.
Research status of surface crack growth in different structures.
In the past few decades, researchers have reviewed the surface crack problem from different perspectives. The surface crack growth and the Stress Intensity Factor (SIF) evaluation methods were reviewed by Newman and Raju [14] in 1979, Scott and Thorpe [15] in 1981, Parks [16] in 1990, and Pang [17] in 1990. These literature reviews majorly focused on surface crack growth and its analytical evaluation methods in plate structures, while issues such as longitudinal surface cracked pipes and surface cracks in fillet weld toes have been discussed in some reviews as well. In recent years, Brighenti and Carpinteri [18] reviewed the general problems of surface crack growth, where typical structural components with surface cracks were overviewed, and the part-through-crack shell was analysed as a case study. Along with the development of the three-dimensional finite element (FE) method, Branco, et al. [19] reviewed the re-meshing technique on simulating surface crack growth, as well as the research progress of such a technique applied on different situations from geometry and load case perspectives.
Among the literature in regard to the surface crack growth in pipes, experimental studies [12,20,21,22,23,24,25,26], as an indispensable and important component, have been conducted on surface cracked pipes for the purpose of understanding the mechanism of surface crack growth, calibrating and validating related numerical and analytical evaluation methods. The majority of the studies focused on numerical approaches, mostly by means of the FE method [12,27,28,29,30,31,32,33,34,35,36,37,38]. Analytical approaches [12,25,30], which are of significant value to guide practitioners in practical situations, are relatively insufficient. Through Table 1, we summarised the main research interests (e.g., load, crack orientation and dimension, pipe dimension, welding effect, and environmental effect) on the issue of surface crack growth in pipes. In general, research related to the first four issues has been widely conducted, while investigations regarding the welding effect and the environmental effect on surface crack growth in offshore metallic pipes are seriously lacking in the open documents.

Table 1.
A summary of the main research interests on the issue of surface cracked pipes.
To date, the literature review on surface crack growth in offshore metallic pipes is absent from the open documents. In light of the specificity of the offshore metallic pipes in terms of the load case, geometry, and influential parameters, such a literature review is in great demand for the sake of identifying the research gaps and providing possible further research topics. Given this, we reviewed the latest research by analysing state-of-the-art existing evaluation methods on the surface crack growth in pipe structures from the fracture mechanics perspective. Section 2 overviews the research progress from experimental, numerical, and analytical perspectives, respectively. Then, in Section 3, we analyse state-of-the-art research and discuss the insufficiencies of the available literature. In Section 4, we conclude with the remaining challenges, and finally possible further research topics are drawn in Section 5.
2. Overview of the Research on Surface Crack Growth in Metallic Pipes
Surface crack growth in metallic pipes has been investigated in the past decades. Generally, as shown in Figure 4, the scenarios of surface crack growth in metallic pipes include circumferential external (a) and internal (b) surface cracks, longitudinal external (c) and internal (d) surface cracks, and inclined surface cracks (e). In this section, the research progress of these scenarios is overviewed from experimental, numerical, and analytical perspectives.
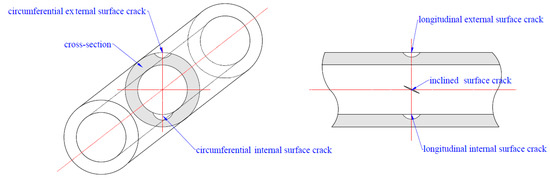
Figure 4.
Research status of surface crack growth in different structures.
2.1. Experimental Research
Experimental research is a reliable and important approach in terms of understanding mechanisms, and calibrating and validating relevant numerical and analytical methods. In the past decades, researchers have conducted a series of experimental studies on surface cracked metallic pipes subjected to cyclic loads, as listed in Table 2.

Table 2.
The available experimental studies on surface crack growth in metallic pipes.
2.1.1. Experimental Procedures and Methods
A rational experimental scheme of surface crack growth under cyclic loading is vital for data acquisition. Thus, it is important to follow the relevant fatigue test codes (e.g., ASTM E647 [39]). The manufacturing of semi-elliptical shaped notches is more complicated than making through-thickness notches. The recommended notch making methods can be referred to in ASTM E2899 [40] and ASTM 740 [41]. Micro electric-discharging machining (micro-EDM) is recommended for obtaining a user defined shape and size of a semi-elliptical notch, as well as for avoiding the heat effect. Other machining techniques such as conventional machining techniques (e.g., mill, grind) and laser cutting might be used effectively as well [39]. For the machined notch size design, fatigue test parameters should be identified based on both the standard requirement and the practical condition (e.g., critical size of surface crack in offshore metallic pipes [7], load amplitude, and load ratio of bending applied on the pipes). Among the experimental studies, the majority of machined notches were semi-elliptical shaped, except Ref. [23], which adopted a rectangular machined notch, and Ref. [25], which adopted the notch with a straight bottom, as shown in Figure 5. However, these notches soon propagated to a semi-elliptical shape and then continually grew in this shape until the end of the fatigue test.

Figure 5.
Notch type: (a) semi-elliptical notch; (b) rectangular notch [23], and (c) notch with a straight bottom [25].
Before the fatigue crack test, a pre-cracking procedure should be implemented in order to generate the fatigue crack from the manual notch. The pre-cracking procedure should follow the relevant standards, such as ASTM E647 [39], which regulate the pre-cracking steps, the load amplitude of each step, cyclic index, and the minimum propagation length of each step. After the pre-cracking procedure, the specimen is ready for the fatigue crack growth test.
Crack growth detection and measurement approaches are significant to acquire valid crack growth data. The beach mark (BM) technique, which might be the most reliable and efficient method of tracing surface crack growth, has been widely adopted, as indicated in Table 2. The BMs, which are usually obtained by changing the stress amplitude or load ratio, can be reserved permanently on the surface crack cross-section plain, as shown in Figure 6. In addition, the BMs are not influenced by the covering on metallic pipes (e.g., coating, composite repair), which widens its application scope. The electric potential drop (EPD), particularly the alternating current potential drop (ACPD), was adopted in Ref. [23,24] as well. This method is efficient, and while measurement errors still exist, it can be used as an alternative or a supplementary detection method.

Figure 6.
Photographs of surface crack growth in metallic pipes marked by the beach mark (BM) technique [12].
2.1.2. Crack Orientation and Load Cases
Most of the experimental studies on surface cracked pipes focused on the Mode-I crack growth, where surface cracks propagate perpendicular to the normal stress. Among those studies, the majority were conducted under cyclic bending loads. In these cases, a four-point bending set-up was adopted in order to generate a pure bending moment on the middle part of pipe specimens, as shown in Figure 7a. The longitudinal surface crack growth was subjected to cyclic loads, as is a common case for transportation pipelines, which have been studied as well. In addition to longitudinal normal stress, the circumferential tensile force induced by the cyclic internal pressure was the driving factor of the crack propagation, as shown in Figure 7b. Zhu, et al. [21] investigated the longitudinal surface crack growth subjected to cyclic internal pressure with the range of 0 to 294 MPa. The external surface cracked circular hollow sections subjected to tension [26], which usually exist in the hang-off zone, were investigated as well. The set-up of a pipe subjected to tension is shown in Figure 7c.
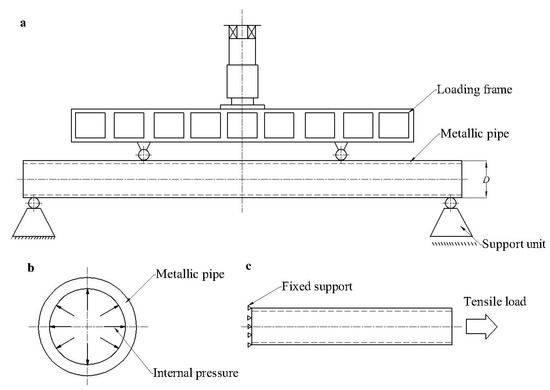
Figure 7.
Test set-up and load cases: (a) 4-point bending, (b) internal pressure, and (c) tension.
2.1.3. Load Ratio and the Paris Constants
A load ratio equal to 0.1 is commonly adopted for the fatigue tests. In the area along offshore pipes, such as the sag bend and arch bend, a load ratio equal to 0.5 is a more practical case [42]. The surface crack growth in metallic pipes under bending with a stress ratio of 0.1, 0.3, and 0.5 were investigated, indicating that for a given crack depth, the number of cycles required for initiation increased within the increase of the load ratio. This can be explained by the fact that the mechanism of initiation requires the development of slip planes in the material, which coincide with maximum shear stress, and become sites for crack initiation. The development of the slip bands depends on the magnitude of the stress range at the notch tip [23]. In addition, the load ratio can affect the crack growth rate as well because the load stress changes the range of the SIF . Load ratio has a minor influence on the Paris constants values as well, which can be obtained from crack growth assessment codes (e.g., BS 7910 [43], ASME Section XI [44]) or calibrated from fatigue crack growth tests [23,24]. Singh, et al. [23] also found that the Paris constants for predicting crack growth along the depth direction and along the length direction were the same. However, this was a contradiction with the experimental observation by Corn [45], who claimed that the Paris constant C of the deepest point and surface point were not equal due to the difference of plane stress and plain strain from the surface point to the deepest point of surface cracks.
2.2. Numerical Simulation of Predicting Surface Crack Growth in Metallic Pipes
Although experimental research offers reliable predictions of surface crack growth in metallic pipes, the relatively high cost hinders its application. The numerical simulation, as a cost-effective alternative, has been widely applied to evaluate the fracture mechanics parameters of surface cracks, such as the Stress Intensity Factor (SIF) and J-integral. At present, it is the most common adopted approach. In the two past decades, researchers have conducted a series of numerical investigations on surface cracked metallic pipes subjected to cyclic loads, as listed in Table 3. In this section, the numerical studies are overviewed from different perspectives.

Table 3.
Numerical simulations conducted on surface cracked metallic pipes.
2.2.1. FE modelling Strategy
To date, the majority of numerical simulations of surface cracks in metallic pipes have been conducted with the FE method (FEM), as shown in Table 3. The implementation and accuracy of the FEM are the major concerns, guaranteed by several aspects: modelling, element type choosing, meshing methods, the element size, and the solver algorithms. First, the contour numbers around the surface crack might affect the calculation results. At least two contours around the crack front are suggested in order to eliminate the errors [46]. Second, a spider web pattern of the meshing shape consisting of several concentric rings around the crack front is recommended, and the minimum angular discretisation of the elements should be [47]. Third, when using the displacement matching method to estimate SIFs, the orthogonal mesh (see in Figure 8a) around the crack front should be adopted, while if the energy based method is applied, the non-orthogonality mesh (see from Figure 8b–e) would not affect the results [48]. Fourth, the type of element commonly adopts the iso-parametric elements, with quadratic shape functions [49]. The iso-parametric elements can present curved shapes with a small number of elements owing to their distorted shapes. Fifth, the element size, especially for those around the surface crack tip, should be defined properly. For different model geometries, an investigation on the proper element size is necessary to guarantee the accuracy of SIFs evaluation and to save the computing time [50]. Last but not least, the interaction angle between the crack front and the free surface of the pipe should be carefully modelled in order to ensure the square singularity at the corner point [51]. More information on the FE modelling of three-dimensional cracks can be referred to in the review paper by Branco, et al. [19].
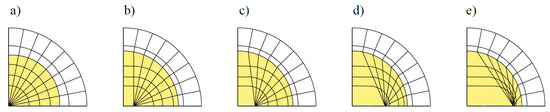
Figure 8.
Five degrees (a–e) of mesh non-orthogonality, from an orthogonal mesh to a distorted mesh [48].
2.2.2. Crack and Pipe Dimensions
As long as it is using proper modelling and analysis methods, the FEM is a reliable and accurate approach for modelling surface cracks in metallic pipes [12,38]. Table 3 lists the numerical studies of surface cracks in pipes. The FEM provides an efficient path to understand the mechanism of surface crack growth, such as the geometry effects (e.g., a/c, a/t and ) and load effects (e.g., internal pressure, bending, tension, and torsion) on SIF estimations. Most of the numerical studies focused on an aspect ratio (a/c) smaller than 1.0. The growth behaviour of shallow surface cracks () was studied, where it was concluded that shallow cracks grew more rapidly in the depth direction than in the surface direction; correspondingly, the largest SIF was at the deepest point of the surface crack, while for high aspect ratio surface cracks (), due to corrosion attacks, the maximum SIF might occur at different positions along the crack front. Deep surface crack growth () in pipes subjected to tension was studied [34], which indicated that the maximum and minimum SIF were always at the deepest point and the surface point, respectively. The effects of the ratio between the internal radius and the pipe thickness () were studied as well [36], which showed that the ratio was an independent coefficient to the a/c and a/t ratio of SIF evaluation on surface cracks in metallic pipes.
The initial crack dimensions can significantly affect the surface crack initiation and propagation. Singh, et al. [23] indicated that the surface crack initiation strongly depended on the crack depth. For a given stress range, the number of cycles required for crack initiation depended on the initial crack depth, owing to the fact that the SIF was less for a shallow crack than a deep crack. In the early stage, the surface crack growth strongly depended on the initial crack shape as well. Lin and Smith [53] investigated its influence by comparing the crack front of a V-notch and a U-notch, respectively, and demonstrated that the crack shape changed more rapidly for the V-notch than the U-notch due to its high stress concentration along the free boundary. Later on, with the semi-elliptical surface crack profile, Couroneau and Royer [54] ascertained that the surface crack growth could be divided into two stages: the first stage is affected by the initial crack shape and size, the exponent of Paris’ law, and the loading cases, while the second stage is no longer affected by the initial crack shape.
2.2.3. Crack Propagation Evaluation
Along with crack growth models such as Paris’ law [55], the propagation of surface cracks can be traced. This method is generally known as the adaptive re-meshing technique, which can be summarised into five main steps [19], indicated in Figure 9: Step 1: building a three-dimensional FE model; Step 2: dividing the crack front into a certain amount of nodes; Step 3: calculating the effective SIFs along the surface crack front; Step 4: choosing the adequate fatigue crack growth law and calculating the crack growth; and Step 5: defining a new crack front of a new FE model. These steps are then repeated until the crack propagates to a required crack length.
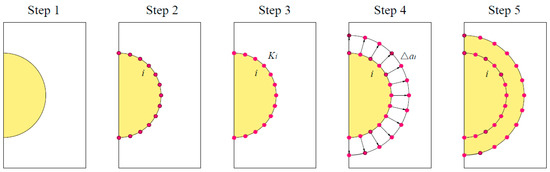
Figure 9.
Five steps of the adaptive re-meshing technique [19].
The surface point and the deepest point are the two most important points along the surface crack front. In general cases, only the crack growth along the depth and length directions need to be evaluated. The procedure of tracing the crack growth process along the depth direction and the length direction is shown in Figure 10. and are the crack growth rate along the depth direction and along the length direction, respectively; and are the range of stress intensity factors of the deepest point and the surface point, respectively; and C and m are two Paris constants. Afterwards, by assuming a small amount of cycles, the increments of the crack length and depth are calculated. Eventually, it is possible to trace the surface crack growth along the two directions.
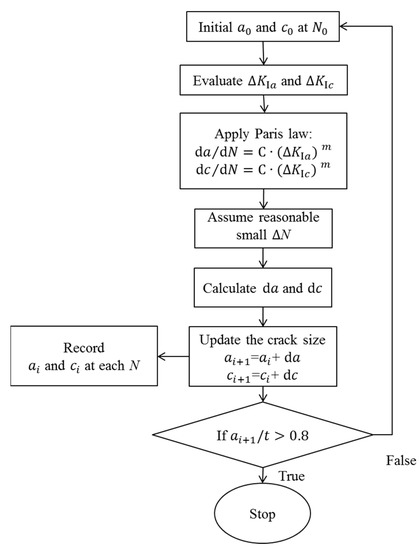
Figure 10.
The procedure of evaluating surface crack growth.
2.3. Analytical Methods of Predicting Surface Crack Growth in Metallic Pipes
Although numerical analysis is an accurate and cost-effective evaluation method, the following factor has restricted its application: the idealisation of numerical modelling is inherent with numerical approaches, and the reasonability of numerical approaches relies on a large extent on the user’s expertise. The analytical method is an efficient alternative, which provides a rapid and user-friendly assessment solution. To date, researchers have proposed a series of analytical methods to evaluate the surface crack growth in pipes under different situations.
2.3.1. The Foundation of Evaluating Surface Crack Growth
In general, the surface crack growth rate is evaluated by crack propagation criterion, such as Paris’ law [55] indicated in Figure 10, which is
where dA/dN is the crack growth rate and is the range of the SIF along the surface crack front. Equation (1) illustrates that evaluating the SIF of the crack front is the key for predicting the crack growth rate. The approach of estimating the SIF is [56]:
where is the Mode-I stress intensity factor, S is the nominal stress, F is the geometry correction factor, and A is the crack size including the crack depth and the crack length.
Evaluating the SIF along the surface crack front is the hinge of predicting the crack growth, as indicated in Equation (2), on which the proposed analytical methods for surface cracked pipes are based. In light of the pipe and crack dimensions and the load cases, the geometry correction factor F and the nominal stress S are modified, mainly through two approaches: the numerical analysis method [57,58] and the weight function method [59]. Table 4 lists the available analytical approaches for surface cracked steel pipes, including the approaches recommended by relevant crack growth evaluation codes (e.g., BS 7910, and API 579-1/ASME FFS-1) and the latest proposed methods.

Table 4.
Analytical methods of evaluating the Stress Intensity Factor (SIF) of surface cracks in metallic pipes.
2.3.2. The Numerical Analysis Method: Newman–Raju’s Method
The numerical analysis method modifies F and S by curving fitting and engineering judgment [63]. Easier in the 1970s, Newman and Raju [64] proposed an analytical method of evaluating the SIF of semi-elliptical surface cracks in plates subjected to tension, which is representative of the numerical analysis method. Later on, they expanded the load cases to combine tension and bending [58], which is recommended by BS 7910 [43] for estimating the SIF of circumferential external surface cracked pipes subjected to tension and bending, which is
where St and Sb represent tension stress and bending stress, respectively, and the boundary-correction factor F and bending correction function H are defined by curving fitting and engineering judgement [63,64]. Q is an approximation factor [65]. With further modifications by Dedhia and Harris [66] and Bergman [67], this method was adopted by BS 7910 [43] for circumferential internal surface cracks in pipes subjected to bending. The experimental results in Ref. [22] indicated that Newman–Raju’s method provided non-conservative prediction on the fatigue crack growth rate. Subsequently, Newman and Raju proposed the analytical method for circumferential surface cracked pipes subjected to tension and bending [61], where the geometry correction factor F is tabulated from a table index. Therefore, it is infeasible to continuously evaluate the SIF during the crack propagation.
Given that, recently, Li, et al. [12] proposed the analytical method to evaluate the SIF of circumferential surface cracks in metallic pipes subjected to bending on the basis of Newman–Raju’s method. The new bending correction factor and geometry correction factor are introduced by means of the deduction based on the bending stress gradient and a parametric study based on the FE analysis, respectively. The analytical method is able to predict the SIF of a surface crack within a wide range of crack and pipe dimensions. The SIF results were verified by the American Petroleum Institute’s (API’s) recommended analytical method and the crack growth results were validated by the experimental results, which indicated that it is an appropriate analytical method of evaluating the SIF of circumferential surface cracked pipes.
When evaluating the SIF of longitudinal surface cracks in pipes subjected to internal pressure, the pipe can be regarded as a curved plate. Thus, Newman and Raju [68] proposed an analytical method for evaluating the SIF of internal surface cracks in pipes subjected to internal pressure on the basis of Equation (1) by modifying the load case and the geometry factors. Then, they updated the equation to both longitudinal internal and external surface cracks [60], which is
where pR/t is the average hoop stress and F is the boundary-correction factor for either internal surface cracks or external surface cracks. Research indicated that this method is appropriate for evaluating the SIF of longitudinal surface cracks subjected to internal pressure [21].
2.3.3. The Weight Function Method
In the weight function, the nominal stress is expressed as the sum of the primary stresses and the secondary stresses, which are calculated by two equations containing a series of weight functions [69,70,71]. When needed, the corresponding weight function can be added into the equation. Anderson [62] modified the weight function methods with a comprehensive numerical study, including longitudinal surface cracks in pipes subjected to internal pressure and circumferential surface cracks in pipes subjected to bending, respectively, which are recommended by API 579-1/ASME FFS-1 [72] as
- (i)
- Longitudinal internal surface crack in pipe subjected to internal pressure:
- (ii)
- Longitudinal external surface crack in pipe subjected to internal pressure:
- (iii)
- Circumferential surface crack in pipe subjected to bending:
where the boundary correction factor is
where G0~G4 are determined by six order polynomials. p is the pressure and pc is the crack face pressure if the pressure is acting on the crack face. The values of A0 to A6 are referred to in the corresponding table sorted by the value of t/Ri, a/c, and a/t.
3. Discussion
On account of the overview in Section 2, in this section, state-of-the-art investigations are discussed from different perspectives.
3.1. Configurations of Surface Cracks and Pipes
In light of the overview, the majority of the studies focused on Mode-I surface crack growth issues, where the surface crack propagates perpendicular to the normal stress, such as longitudinal surface crack growth under internal pressure, and circumferential surface crack growth under bending or tension. Most of the experimental investigations were conducted under four-point bending. Internal pressure [21] and tension [26] were included in the available documents as well, and their experimental results can be used to validate the numerical and analytical methods. Compared to experimental studies, the numerical approach is more flexible in terms of realising the surface crack growth under different load conditions, such as combined loading cases [35,37]. Surface crack growth in a tubular structure under torsion was conducted [52], which had a referential value despite that the tubular was not an offshore metallic pipe. Since there might be possibilities that torsion exists on the metallic pipes, such analysis is necessary on offshore metallic pipes.
In practical situations, metallic pipes usually suffer from random loading cases. In other words, multiple loads with various frequencies, phases, and amplitudes could simultaneously or sequentially be applied on the metallic pipes. Under random loading, fatigue crack propagation is considerably influenced by a load sequence. However, the existing research on surface crack growth has mainly focused on a single load condition or combined loading cases with the same frequency simultaneously applied on the pipe structure. The research on fatigue crack growth under random loading has mainly been conducted on compact tension (CT) specimens [73,74], and related research on random loading on surface cracked pipes has not been included in the open documents yet.
As summarised in Table 3, the available studies have included a wide range of crack and pipe dimensions, determined by the a/c, a/t, and ratios. Most of the studies focused on thick-wall pipes, which are frequently applied in the offshore piping industry. The majority of studies focused on an aspect ratio smaller than 1.0 except Ref. [30], which studied longitudinal surface crack growth in sewer pipes. The study on circumferential surface cracks whose aspect ratio is larger than 1.0 is absent from the open documents. On account of the possibility of their existence on offshore metallic pipes owing to corrosion, such studies are necessary.
The Paris law is the most common method for crack growth evaluation. While the conflict of whether the Paris constants for surface crack growth along the depth direction and the length direction are the same still exists, such experimental and analytical analyses on general surface crack growths are necessary. Moreover, whether Paris’ constants for surface cracks in metallic pipes are influenced by the cylindrical geometry needs to be identified as well.
3.2. Environmental Influential Parameters
In this paper, we review the investigations on surface cracked metallic pipes from the fracture mechanism point of view. In practical situations, surface crack growth frequently combines with corrosion problems such as hydrogen corrosion, often known as the corrosion-cracking problem. In many cases, offshore metallic pipes are adopted in harsh marine environments, for example, sour or sweet seawater and low/high temperature. These environmental factors can significantly influence the fatigue crack growth rate, owing to the hydrogen enrichment at the crack tip in sour water [75] and sweet water [76].
Another considerable issue is the temperature influence. In general, those available studies were conducted at room temperature; meanwhile, in practical situations, offshore metallic pipes are often located in areas with extremely hot or cold situations. As it is well accepted that the temperature has an influence on the crack growth rate, it can be evaluated using the appropriate Paris constants. While more importantly, the variation of temperature acting on the hydrogen diffusion [77] will further influence the crack growth rate. By means of the investigations on small scale fatigue crack growth tests under an accelerated corrosion environment, the coupling effects of hydrogen corrosion and temperature on crack growth are understood [75,78]. Normally, when predicting the crack growth rate, these effects are taken into consideration as amplification factors. Based on these investigations on through-thickness cracks, it is possible to infer that these environmental parameters have similar effects on surface crack growth in offshore metallic pipes. To date, investigations of corrosion-cracking and temperature, as well as their coupling on surface cracked metallic pipes, are absent in open documents. However, the surface crack is more complicated than the through-thickness crack in terms of the semi-elliptical crack front. For instance, the corrosion effects on different points along the crack front might lead to different behaviours of cracks growing towards different directions.
3.3. Girth Welding Effect
The effects from girth welding on circumferential surface crack growth in offshore metallic pipes, i.e., welding residual stress, is an unavoidable topic, since offshore metallic pipes are connected by means of girth welding, while investigations of surface crack growth in girth welded metallic pipes are absent in open documents. By means of numerical simulations on the butt welded plate, researchers have indicated that the effect of welding residual stress on the SIF of surface cracks is either beneficial or detrimental, depending on the distribution of the residual stress [79]. In addition, owing to the distribution of the welding residual stress around the cracked zone, the SIF of each point along the surface crack front will be changed, which will result in the changing of the crack growth rate and the variation of the crack shape. What is more, in some cases, the surface crack might not grow as a semi-elliptical shape due to the influence of residual stress in the welding heat-effect zone [80].
However, such relevant investigations on surface crack growth in girth welded metallic pipes are lacking in open documents. Although Arora, et al. [24] tested surface crack growth in girth welding where the crack growth rate was estimated by using Paris’s constant of the welding material, the influence of residual stress on surface crack growth was not analysed. It might have a similar qualitative mechanism to surface cracks in other structures, while quantitative analysis is still in great demand to determine the girth welding residual stress effect on surface crack growth in girth welded offshore steel pipes.
3.4. Numerical Simulation
Section 2.2 summarised that the majority of the numerical analyses were conducted by means of the FEM. Although the adaptive re-meshing technique by FEM is a powerful tool, its time-consuming and complicated conformal modelling and re-meshing procedures hinder its application. In recent years, other numerical methods, such as the extended-FEM (XFEM) [81] and S-version FEM [82], have been developed as alternatives for handling three-dimensional surface crack modelling. In XFEM, the discontinuities are modelled by means of enrichment functions, which are obtained from the theoretical background of certain issues. It can significantly simplify the modelling of crack propagation problems [83]. The S-version FEM provides more flexibility for irregular regions of high gradients, which do not require special treatment to match the boundaries of the superimposed meshes.
The effectiveness and accuracy of these two methods has been validated in recent years, especially for handling the multiple surface cracks growth problem. A recent study of multiple surface cracks growth by XFEM [50] had a similar conclusion to the results indicated by FEM [84], which showed that each crack was growing independently until two adjacent cracks met, then the two cracks would combine into a single crack. The new crack depth equalled the previous larger cracks, and the sum of the two cracks’ lengths became the new crack length. A similar study was conducted for the S-version FEM as well [85]. Sharma, et al. [31] conducted a numerical evaluation on the SIF of a longitudinal surface crack in a pipe bend by means of XFEM, and the results were compared with other FEM results. The applications of XFEM or S-version FEM on offshore metallic pipes are still very limited in open documents.
Another approach to simplify the crack modelling and re-meshing using FEM is to apply the semi-elliptical crack modelling programme, such as the ANSYS workbench [86], FRANC3D [87]. These series of software provide automatic crack modelling and meshing functions, as well as ensuring the accuracy of SIF evaluation. In addition, the built-in loop program, similarly as indicated in Figure 10, can realise the automatic simulation of crack growth processes such as the smart crack growth function in the ANSYS workbench.
3.5. Analytical Evaluation
Generally, the available analytical methods have been developed based on the fundamental SIF evaluation method, e.g., Equation (2), by modifying the correction factors of load cases, crack profiles, and geometry, mainly through two approaches: the numerical analysis method, Newman and Raju’s law, and the weight function method. The advantages of the numerical analysis method are that it is convenient for usage, and the values of geometrical parameters can be consecutively input into the formula to trace the crack growth process. In addition, the prediction scope is not limited to the deepest point and the surface point, but any points along the crack front, which are determined by the eccentric angle . To date, these analytical methods have been proposed for Mode-I semi-elliptical crack growth, thus such analytical methods for mixed-mode surface crack growth and irregular shaped surface cracks are unavailable.
The advantage of the weight function method is that it has a wide range of adaptations by introducing weight functions, respectively, such that influential factors like welding effects and geometry factors could be considered [88]. However, the disadvantages of weight function methods are: first, the SIFs evaluation are restricted to the surface point and the deepest point, rather than along the whole crack front; second, since F is calculated by high order polynomials within which the coefficients are determined by discrete values tabulated in a table index, it is infeasible to continuously evaluate the SIF during the crack propagation, which means it is impracticable to trace the surface crack growth.
An accurate analytical result might not be achieved by hand calculations; therefore, a rational analytical approach can be developed based on extensive numerical studies. The analytical method of evaluating the SIF of surface cracks in metallic pipes has been developed in recent years with the assistance of FEM, such as Refs. [12,30,36]. Circumferential surface cracks in offshore metallic pipes are often induced by girth weld defects. Further on, the surface crack growth is affected by the welding residual stress. In recent years, surface crack growth in the weld zone of steel plates has been analytically investigated, together with the FE method [50,69], while such investigations on surface crack growth in girth weld steel pipes are still limited. In addition, the available analytical methods focus on the Mode-I surface crack growth and single crack growth, and analytical studies on subjects such as mixed-mode surface crack growth and multi-crack growth are needed in order to further facilitate the applications of the prediction methods.
4. Remaining Challenges
In this paper, the investigations of surface crack growth were overviewed from experimental investigations, numerical simulations, and analytical evaluation perspectives, respectively. Then, we analysed the state-of-the-art research and discussed the insufficiencies of the available literature. The remaining challenges regarding the available literature can be summarised as:
Surface crack initiation and growth adjacent to girth welds in metallic pipes is an unavoidable topic. The influential parameters such as hydrogen enrichment, temperature, and their coupling on surface crack growth in offshore metallic pipes have not been discussed yet.
The alternative simulation techniques such as XFEM and S-version FEM have been used to evaluate the SIF or the J-integral of the surface cracks in steel plates, although such investigations and their applications on multiple surface cracks growth and mixed-mode surface crack growth have not been conducted on offshore metallic pipes yet.
The majority of studies on surface crack growth in metallic pipes focused on Mode-I cracks, while mixed-mode surface crack growth has not been sufficiently studied, especially from the experimental and analytical points of view. In addition, research on random loading on surface cracked pipes, such as the influence of load sequence, has not been included in the open documents.
5. Possible Further Research Topics
In light of the remaining challenges, further studies are expected in order to facilitate the development of the evaluation methods on surface cracked metallic pipes, as well as to provide references for other surface cracked metallic structures. The possible further research topics can be concluded as:
Quantitative analysis on the influence of welding residual stress in terms of the direction and the distribution of the residual stress are in great demand. The FEM, which has been used for analysing the residual stress on butt weld surface cracks, is an appropriate method for such investigations. In addition, experimental measurement and investigation of the residual stress distribution for clarification and validation and analytical methods are demanded as well.
Further research on quantitatively analysing sour/sweet environments on surface crack growth is necessary. The environmental influence can be considered as an influential factor on surface crack growth, which will be introduced into the analytical method as an influential function. The experimental parametric study on small scale surface cracked specimens is a possible approach to achieve the influential factor.
Owing to the development of programmes such as the smart crack growth module of the ANSYS workbench and FRANC3D, the modelling procedures have been significantly simplified; the computational time has been dramatically reduced. The application on the surface crack growth in metallic pipes using these advanced approaches, as well as other numerical simulation methods such as XFEM and S-version, are expected in further research. In addition, since an accurate analytical result might not be achieved by hand calculations, more reliable analytical methods can be developed based on extensive numerical studies.
Author Contributions
Conceptualization, Z.L.; methodology, Z.L. and X.J.; formal analysis, Z.L.; investigation, Z.L.; resources, Z.L.; data curation, Z.L.; writing—original draft preparation, Z.L.; writing—review and editing, X.J.; supervision, X.J. and H.H.; project administration, X.J. and H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Department of Maritime and Transport Technology, Delft University of Technology, the Netherlands. The first author would like to acknowledge the China Scholarship Council for funding his research, grant number 201606950024.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | crack size |
| a | crack depth of surface cracks |
| a/c | aspect ratio |
| b | plate width |
| C | Paris’ law constant |
| c | half crack length of surface cracks |
| D | external diameter of pipes |
| d | internal diameter of pipes |
| crack growth rate | |
| surface crack growth along the depth direction | |
| surface crack growth along the length direction | |
| F | boundary correction factor |
| H | bending correction factor |
| m | Paris’ law constant |
| p | pressure |
| pc | crack face pressure |
| Q | an approximation factor |
| t | thickness of the pipe wall |
| R | load ratio |
| Ri | inner radius of pipes |
| Rt | outer radius of pipes |
| S | nominal stress |
| Sb | bending stress |
| St | tension stress |
| the range of stress intensity factors | |
| the range of the SIF of the deepest point | |
| the range of the SIF of the surface point | |
| Mode-I stress intensity factor | |
| the SIF of a node along the surface crack front | |
| the increment of the surface crack size | |
| the eccentric angle of the crack |
References
- DNVGL. Riser fatigue. In Offshore Standard, DNV-RP-F204; DNVGL: Høvik, Norway, 2010. [Google Scholar]
- Li, Z.; Jiang, X.; Hopman, H. Numerical analysis on the SIF of internal surface cracks in steel pipes reinforced with CRS subjected to bending. Ships Offshore Struct. 2019, 1–14. [Google Scholar] [CrossRef]
- DNVGL. Environmental conditions and environmental loads. In Recommended Practice, DNV-RP-C205; DNVGL: Høvik, Norway, 2014. [Google Scholar]
- DNVGL. Dynamic risers. In Offshore Standard, DNV-OS-F201; DNVGL: Høvik, Norway, 2010. [Google Scholar]
- Richard, H.A.; Sander, M. Fatigue Crack Growth; Springer: Berlin, Germany, 2016. [Google Scholar]
- Li, Z.; Jiang, X.; Hopman, H.; Zhu, L.; Liu, Z.; Tang, W. Experimental investigation on FRP-reinforced surface cracked steel plates subjected to cyclic tension. Mech. Adv. Mater. Struct. 2020, 1–15. [Google Scholar] [CrossRef]
- DNVGL. Assessment of flaws in pipeline and riser girth welds. In DNV Recommended Practice, DNV-RP-F108; DNVGL: Høvik, Norway, 2017. [Google Scholar]
- Martins, C.; Higashi, E.; Silva, R. A parametric analysis of steel catenary risers: Fatigue behavior near the top. In Proceedings of the Tenth International Offshore and Polar Engineering Conference, Seattle, WA, USA, 28 May–2 June 2000; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2000. [Google Scholar]
- Mansour, G. The impact of the second order vessel motion on the fatigue life of steel catenary risers. In Proceedings of the ASME 2004 23rd International Conference on Offshore Mechanics and Arctic Engineering, Vancouver, BC, Canada, 20–25 June 2004; American Society of Mechanical Engineers: New York, NY, USA, 2004; pp. 1177–1180. [Google Scholar]
- Norway, P.S.A. Riser Damage—Injuries and Incidents from the Petroleum Safety Authority Norway’s Codam Database; DNVGL: Høvik, Norway, 2018. [Google Scholar]
- Horn, A.M.; Lotsberg, I.; Orjaseater, O. The rationale for update of S-N curves for single sided girth welds forrisers and pipelines in DNV GL RP C-203 based on fatigue performance of more than 1700 full scale fatigue test results. In Proceedings of the ASME 2018 37th International, Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Li, Z.; Jiang, X.; Hopman, H.; Zhu, L.; Liu, Z. An investigation on the circumferential surface crack growth in steel pipes subjected to fatigue bending. Theor. Appl. Fract. Mech. 2020, 105, 102403. [Google Scholar] [CrossRef]
- Van Wee, B.; Banister, D. How to Write a Literature Review Paper? Transp. Rev. 2015, 36, 1–11. [Google Scholar] [CrossRef]
- Newman, J. A Review and Assessment of the Stress-Intensity Factors for Surface Cracks. In Part-Through Crack Fatigue Life Prediction; ASTM International: West Conshohocken, PA, USA, 2009; p. 16. [Google Scholar]
- Scott, P.M.; Thorpe, T.W. A Critical Review of Crack Tip Stress Intensity Factors for Semi-Elliptic Cracks. Fatigue Fract. Eng. Mater. Struct. 1981, 4, 291–309. [Google Scholar] [CrossRef]
- Parks, D. A Surface Crack Review: Elastic and Elastic-Plastic Behavior. In Surface-Crack Growth: Models, Experiments, and Structures; ASTM International: West Conshohocken, PA, USA, 2009; p. 9. [Google Scholar]
- Pang, H. A review of stress of intensity factors for semi-elliptical surface crack in a plate and fillet weld joint. Weld. Inst. Rpt. 1990, 426. (In Japanese). Available online: https://ci.nii.ac.jp/naid/10011466198/#cit (accessed on 2 April 2020).
- Brighenti, R.; Carpinteri, A. Surface cracks in fatigued structural components: A review. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 1209–1222. [Google Scholar] [CrossRef]
- Branco, R.; Antunes, F.; Branco, R. A review on 3D-FE adaptive remeshing techniques for crack growth modelling. Eng. Fract. Mech. 2015, 141, 170–195. [Google Scholar] [CrossRef]
- Shimakawa, T.; Takahashi, H.; Doi, H.; Watashi, K.; Asada, Y. Creep-fatigue crack propagation tests and the development of an analytical evaluation method for surface cracked pipe. Nucl. Eng. Des. 1993, 139, 283–292. [Google Scholar] [CrossRef]
- Zhu, L.; Tao, X.; Cengdian, L. Fatigue strength and crack propagation life of in-service high pressure tubular reactor under residual stress. Int. J. Press. Vessel. Pip. 1998, 75, 871–877. [Google Scholar] [CrossRef]
- Yoo, Y.S.; Ando, K. Circumferential inner fatigue crack growth and penetration behaviour in pipe subjected to a bending moment. Fatigue Fract. Eng. Mater. Struct. 2000, 23, 1–8. [Google Scholar] [CrossRef]
- Singh, P.; Vaze, K.; Bhasin, V.; Kushwaha, H.; Gandhi, P.; Murthy, D.R. Crack initiation and growth behaviour of circumferentially cracked pipes under cyclic and monotonic loading. Int. J. Press. Vessel. Pip. 2003, 80, 629–640. [Google Scholar] [CrossRef]
- Arora, P.; Singh, P.; Bhasin, V.; Vaze, K.K.; Ghosh, A.; Pukazhendhi, D.; Gandhi, P.; Raghava, G. Predictions for fatigue crack growth life of cracked pipes and pipe welds using RMS SIF approach and experimental validation. Int. J. Press. Vessel. Pip. 2011, 88, 384–394. [Google Scholar] [CrossRef]
- Sahu, V.K.; Ray, P.K.; Verma, B.B. Experimental fatigue crack growth analysis and modelling in part-through circumferentially pre-cracked pipes under pure bending load. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1154–1163. [Google Scholar] [CrossRef]
- Shlyannikov, V.; Yarullin, R.; Ishtyryakov, I. Effect of temperature on the growth of fatigue surface cracks in aluminum alloys. Theor. Appl. Fract. Mech. 2018, 96, 758–767. [Google Scholar] [CrossRef]
- Diamantoudis, A.; Labeas, G. Stress intensity factors of semi-elliptical surface cracks in pressure vessels by global-local finite element methodology. Eng. Fract. Mech. 2005, 72, 1299–1312. [Google Scholar] [CrossRef]
- Oh, C.S.; Song, T.K.; Kim, Y.; Kim, J.S.; Jin, T.E. Approximate J estimates for axial part-through surface-cracked pipes. Fatigue Fract. Eng. Mater. Struct. 2007, 30, 1127–1139. [Google Scholar] [CrossRef]
- Meshii, T.; Tanaka, T.; Lu, K. T-Stress solutions for a semi-elliptical axial surface crack in a cylinder subjected to mode-I non-uniform stress distributions. Eng. Fract. Mech. 2010, 77, 2467–2478. [Google Scholar] [CrossRef]
- Li, C.; Yang, S. Stress intensity factors for high aspect ratio semi-elliptical internal surface cracks in pipes. Int. J. Press. Vessel. Pip. 2012, 96, 13–23. [Google Scholar] [CrossRef]
- Sharma, K.; Singh, I.; Mishra, B.; Maurya, S. Numerical simulation of semi-elliptical axial crack in pipe bend using xfem. J. Solid Mech. 2014, 6, 208–228. [Google Scholar]
- Carpinteri, A.; Brighenti, R.; Vantadori, S. Circumferentially notched pipe with an external surface crack under complex loading. Int. J. Mech. Sci. 2003, 45, 1929–1947. [Google Scholar] [CrossRef]
- Ligoria, S.A.; Knight, G.M.S.; Murthy, D.S.R. Three-dimensional Finite Element Analysis of a Semi-Elliptical Circumferential Surface Crack in a Carbon Steel Pipe Subjected to a Bending Moment. J. Strain Anal. Eng. Des. 2005, 40, 525–533. [Google Scholar] [CrossRef]
- KouPang, K.; Burdekin, F. Stress intensity factors for a wide range of long-deep semi-elliptical surface cracks, partly through-wall cracks and fully through-wall cracks in tubular members. Eng. Fract. Mech. 2006, 73, 1693–1710. [Google Scholar] [CrossRef]
- Shahani, A.R.; Habibi, S.E. Stress intensity factors in a hollow cylinder containing a circumferential semi-elliptical crack subjected to combined loading. Int. J. Fatigue 2007, 29, 128–140. [Google Scholar] [CrossRef]
- Mechab, B.; Serier, B.; Bouiadjra, B.A.B.; Kaddouri, K.; Feaugas, X. Linear and non-linear analyses for semi-elliptical surface cracks in pipes under bending. Int. J. Press. Vessel. Pip. 2011, 88, 57–63. [Google Scholar] [CrossRef]
- Dao, N.H.; Sellami, H. Stress intensity factors and fatigue growth of a surface crack in a drill pipe during rotary drilling operation. Eng. Fract. Mech. 2012, 96, 626–640. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, X.; Liu, Z.; Hopman, H. Internal Surface Crack Growth in Offshore Rigid Pipes Reinforced With CFRP. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- ASTM. 647. Standard Test Method for Measurement of Fatigue Crack Growth Rates. In ASTM Annual Book of Standards; ASTM international: West Conshohocken, PA, USA, 2015; Volume 3. [Google Scholar]
- ASTM. 2899. Standard Test Method for Measurement of Initiation Toughness in Surface Cracks under Tension and Bending; ASTM international: West Conshohocken, USA, 2019; Volume 3. [Google Scholar]
- ASTM. 740-88: Standard Practice for Fracture Testing with Surface-Crack Tension Specimens. In ASTM Annual Book of Standards; ASTM international: West Conshohocken, PA, USA, 2016; Volume 3. [Google Scholar]
- Kim, S.; Kim, M.-H. Dynamic behaviors of conventional SCR and lazy-wave SCR for FPSOs in deepwater. Ocean Eng. 2015, 106, 396–414. [Google Scholar] [CrossRef]
- BSI. BS 7910: 2013+A1:2015; Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures; BSI Standards Limited: London, UK, 2015; ISBN 978-0-580-91721-9. [Google Scholar]
- Boiler, A.; Code, P.V. Section xi. Rules for Inservice Inspection of Nuclear Power Plant Components. In Companion Guide to the ASME Boiler and Pressure Vessel Code; Rao, K.R., Ed.; ASME Press: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Corn, D. A study of cracking techniques for obtaining partial thickness cracks of pre-selected depths and shapes. Eng. Fract. Mech. 1971, 3, 45–52. [Google Scholar] [CrossRef]
- Branco, R.; Antunes, F.; Branco, R. Extent of the Surface Region in Notched Middle Cracked Tension Specimens. Key Eng. Mater. 2013, 560, 107–127. [Google Scholar] [CrossRef]
- Guinea, G.; Planas, J.; Elices, M. KI evaluation by the displacement extrapolation technique. Eng. Fract. Mech. 2000, 66, 243–255. [Google Scholar] [CrossRef]
- Lin, X.; Smith, R. Finite element modelling of fatigue crack growth of surface cracked plates. Eng. Fract. Mech. 1999, 63, 503–522. [Google Scholar] [CrossRef]
- Sedmak, A.; Savovic, N.; Pavisic, M. Esis Recommendations for Use of Finite Element Method in Fracture Mechanics; ECF9: Varna, Bulgaria, 1992. [Google Scholar]
- Pang, J.H.; Tsang, K.S.; Hoh, H.J. 3D stress intensity factors for weld toe semi-elliptical surface cracks using XFEM. Mar. Struct. 2016, 48, 1–14. [Google Scholar] [CrossRef]
- Heyder, M.; Kolk, K.; Kuhn, G. Numerical and experimental investigations of the influence of corner singularities on 3D fatigue crack propagation. Eng. Fract. Mech. 2005, 72, 2095–2105. [Google Scholar] [CrossRef]
- Predan, J.; Močilnik, V.; Gubeljak, N. Stress intensity factors for circumferential semi-elliptical surface cracks in a hollow cylinder subjected to pure torsion. Eng. Fract. Mech. 2013, 105, 152–168. [Google Scholar] [CrossRef]
- Lin, X.; Smith, R.A. Direct simulation of fatigue crack growth for arbitrary-shaped defects in pressure vessels. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 1998, 213, 175–189. [Google Scholar] [CrossRef]
- Couroneau, N.; Royer, J. Simplified model for the fatigue growth analysis of surface cracks in round bars under mode I. Int. J. Fatigue 1998, 20, 711–718. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A Critical Analysis of Crack Propagation Laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Schijve, J. Fatigue of Structures and Materials; Springer Science & Business Media: Berlin, Germany, 2001. [Google Scholar]
- Newman, J.C., Jr.; Raju, I.S. Analysis of Surface Cracks in Finite Plates under Tension or Bending Loads; NASA-Langley: Hampton, VA, USA, 1979.
- Newman, J.C., Jr.; Raju, I.S. An empirical stress-intensity factor equation for the surface crack. Eng. Fract. Mech. 1981, 15, 185–192. [Google Scholar] [CrossRef]
- Petroski, H.; Achenbach, J. Computation of the weight function from a stress intensity factor. Eng. Fract. Mech. 1978, 10, 257–266. [Google Scholar] [CrossRef]
- Raju, I.S.; Newman, J.C., Jr. Stress-intensity factor influence coefficients for internal and external surface cracks in cylindrical vessels. J. Press. Vessel. 1982, 104, 37–49. [Google Scholar]
- Raju, I. Stress-intensity Factors for Circumferential Surface Cracks in Pipes and Rods under Tension and Bending Loads. In Fracture Mechanics: Seventeenth Volume; ASTM International: West Conshohocken, PA, USA, 2008; p. 789. [Google Scholar]
- Anderson, T.L. Development of stress intensity factor solutions for surface and embedded cracks in API579 (In Japanese). Welding Research Council Bulletin. 2002. Available online: https://ci.nii.ac.jp/naid/80015499214/ (accessed on 7 May 2020).
- Newman, J.C., Jr. Predicting Failure of Specimens with Either Surface Cracks or Corner Cracks at Holes; NASA-Langley: Hampton, VA, USA, 1976.
- Green, A.E.; Sneddon, I.N. The distribution of stress in the neighbourhood of a flat elliptical crack in an elastic solid. Math. Proc. Camb. Philos. Soc. 1950, 46, 159. [Google Scholar] [CrossRef]
- Russell, A. Application of Proof Testing to Assess k-Reactor Piping Integrity; Douglas United Nuclear, Inc.: Richland, WA, USA, 1970.
- Dedhia, D.; Harris, D. Improved influence functions for part-circumferential cracks in pipes. Circumferential Cracks Press. Vessel. Pip. 1983, 2, 35–48. [Google Scholar]
- Bergman, M. Stress Intensity Factors for Circumferential Surface Cracks in Pipes. Fatigue Fract. Eng. Mater. Struct. 1995, 18, 1155–1172. [Google Scholar] [CrossRef]
- Newman, J.C., Jr.; Raju, I.S. Stress-Intensity Factors for Internal Surface Cracks in Cylindrical Pressure Vessels. J. Press. Vessel. Technol. 1980, 102, 342–346. [Google Scholar] [CrossRef]
- Folias, E. On the effect of initial curvature on cracked flat sheets. Int. J. Fract. 1969, 5, 327–346. [Google Scholar] [CrossRef]
- Murakami, Y.; Keer, L.M. Stress Intensity Factors Handbook, Vol. 3. J. Appl. Mech. 1993, 60, 1063. [Google Scholar] [CrossRef]
- Green, D.; Knowles, J. The Treatment of Residual Stress in Fracture Assessment of Pressure Vessels. J. Press. Vessel. Technol. 1994, 116, 345–352. [Google Scholar] [CrossRef]
- API. API 579-1/ASME FFS-1: Fitness-for-Service; American Petroleum Institute: Houston, TX, USA, 2016. [Google Scholar]
- Lu, Z.; Liu, Y. Experimental investigation of random loading sequence effect on fatigue crack growth. Mater. Des. 2011, 32, 4773–4785. [Google Scholar] [CrossRef]
- Sumi, Y.; Inoue, T. Multi-scale modeling of fatigue crack propagation applied to random sequence of clustered loading. Mar. Struct. 2011, 24, 117–131. [Google Scholar] [CrossRef]
- Fassina, P.; Brunella, M.; Lazzari, L.; Re, G.; Vergani, L.; Sciuccati, A. Effect of hydrogen and low temperature on fatigue crack growth of pipeline steels. Eng. Fract. Mech. 2013, 103, 10–25. [Google Scholar] [CrossRef]
- Tognarelli, M.A.; Thodla, R.; Shademan, S. Fatigue Crack Growth Rate and Fracture Toughness of API5L X65 in Sweet Environments. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; American Society of Mechanical Engineers: New York, NY, USA, 2013; p. V003T003A006. [Google Scholar]
- Fassina, P.; Brunella, F.; Lazzari, L.; Re, G.; Vergani, L.; Sciuccati, A. Fatigue Behavior Of Pipeline Steel Under Hydrogen Environment And Low Temperature. Procedia Eng. 2011, 10, 3345–3352. [Google Scholar] [CrossRef]
- Qian, G.; Zhou, C.; Hong, Y. A model to predict S–N curves for surface and subsurface crack initiations in different environmental media. Int. J. Fatigue 2015, 71, 35–44. [Google Scholar] [CrossRef]
- Qiang, B.; Li, Y.; Yao, C.; Wang, X. Through-thickness welding residual stress and its effect on stress intensity factors for semi-elliptical surface cracks in a butt-welded steel plate. Eng. Fract. Mech. 2018, 193, 17–31. [Google Scholar] [CrossRef]
- Kikuchi, M.; Wada, Y.; Shimizu, Y.; Li, Y. Crack growth analysis in a weld-heat-affected zone using S-version FEM. Int. J. Press. Vessel. Pip. 2012, 90, 2–8. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Fish, J. The s-version of the finite element method. Comput. Struct. 1992, 43, 539–547. [Google Scholar] [CrossRef]
- Belytschko, T.; Gracie, R.; Ventura, G. A review of extended/generalized finite element methods for material modeling. Model. Simul. Mater. Sci. Eng. 2009, 17, 43001. [Google Scholar] [CrossRef]
- Kamaya, M. Growth evaluation of multiple interacting surface cracks. Part II: Growth evaluation of parallel cracks. Eng. Fract. Mech. 2008, 75, 1350–1366. [Google Scholar] [CrossRef]
- Akramin, M.R.M.; Shaari, M.; Ariffin, A.K.; Kikuchi, M.; Abdullah, S. Surface crack analysis under cyclic loads using probabilistic S-version finite element model. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 1851–1865. [Google Scholar] [CrossRef]
- ANSYS. Semi-Elliptical Crack. Defines a Semi-Elliptical Crack Based on an Internally Generated Mesh to Analyze Crack Fronts by Use of Geometric Parameters. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v191/wb_sim/ds_Crack_o_r.html (accessed on 7 May 2020).
- Fracture Analysis Consultants, Inc. Franc3d Abaqus Tutorial Version 7. Franc3D, Jan. 2017. Available online: http://www.franc3d.com/wp-content/uploads/2012/05/FRANC3D_V7_ABAQUS_Tutorial.pdf (accessed on 7 May 2020).
- Pachoud, A.J.; Manso, P.A.; Schleiss, A. Stress intensity factors for axial semi-elliptical surface cracks and embedded elliptical cracks at longitudinal butt welded joints of steel-lined pressure tunnels and shafts considering weld shape. Eng. Fract. Mech. 2017, 179, 93–119. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).