The Effect of Mass Ratio and Damping Coefficient on the Propulsion Performance of the Semi-Active Flapping Foil of the Wave Glider
Abstract
:1. Introduction
2. Problem Description and Methodology
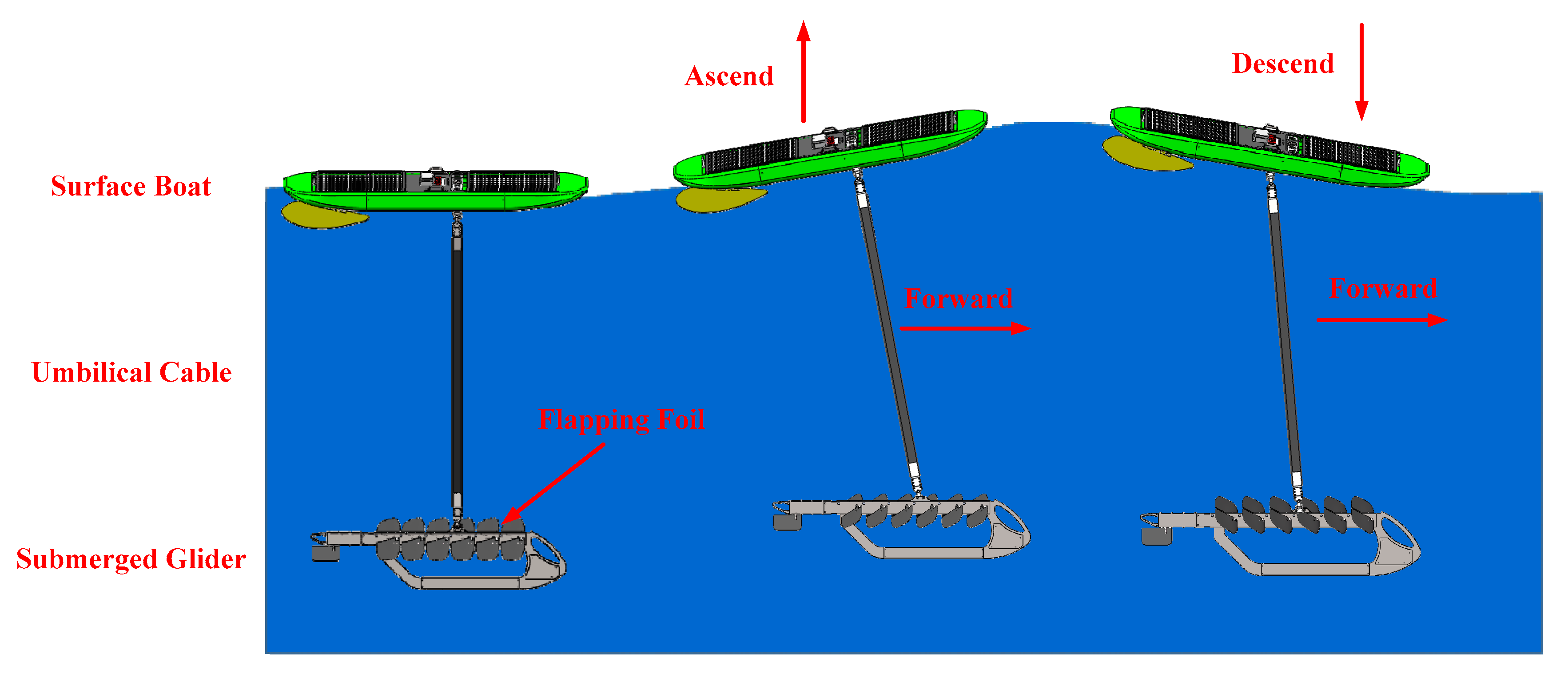
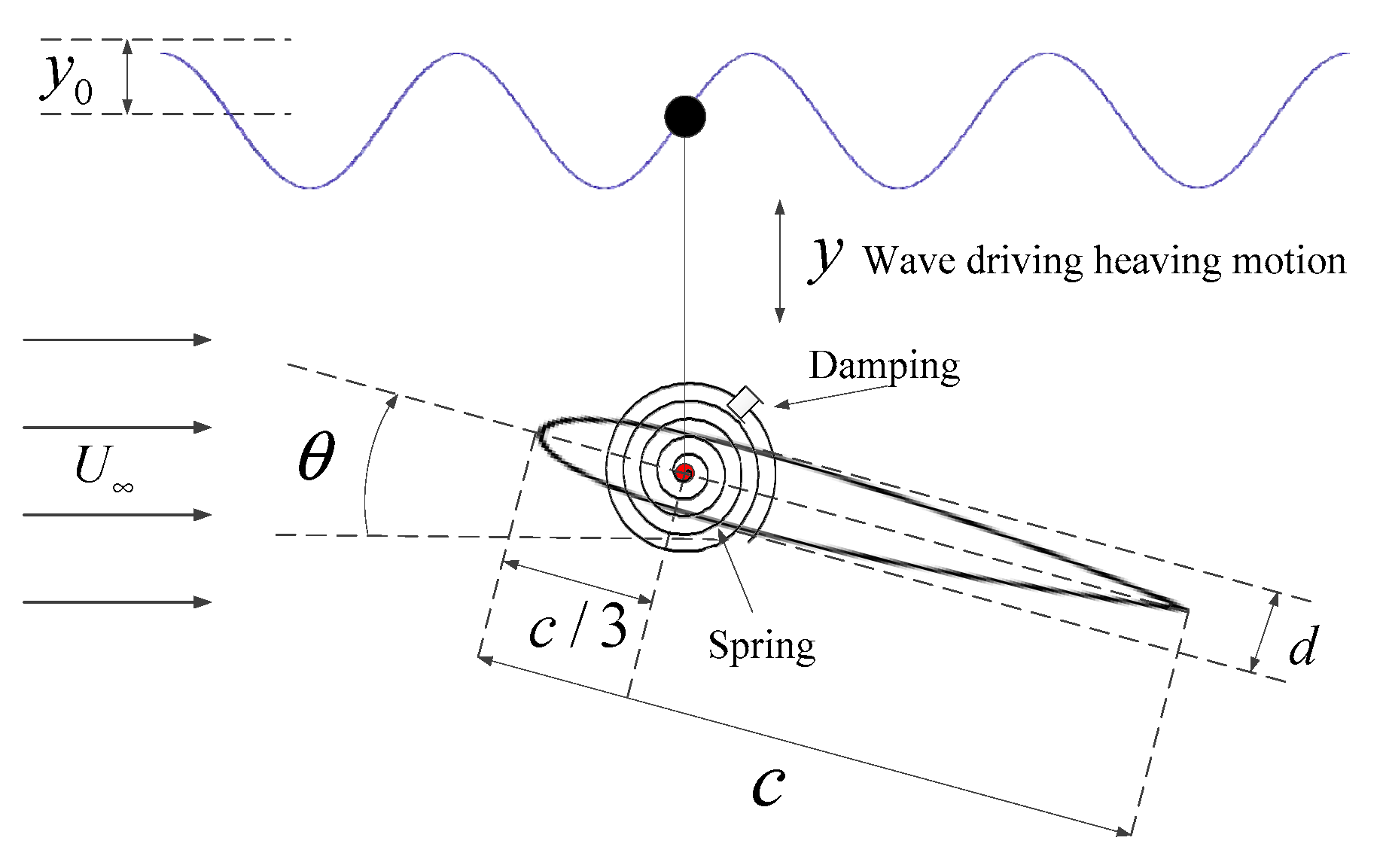
2.1. Problem Description
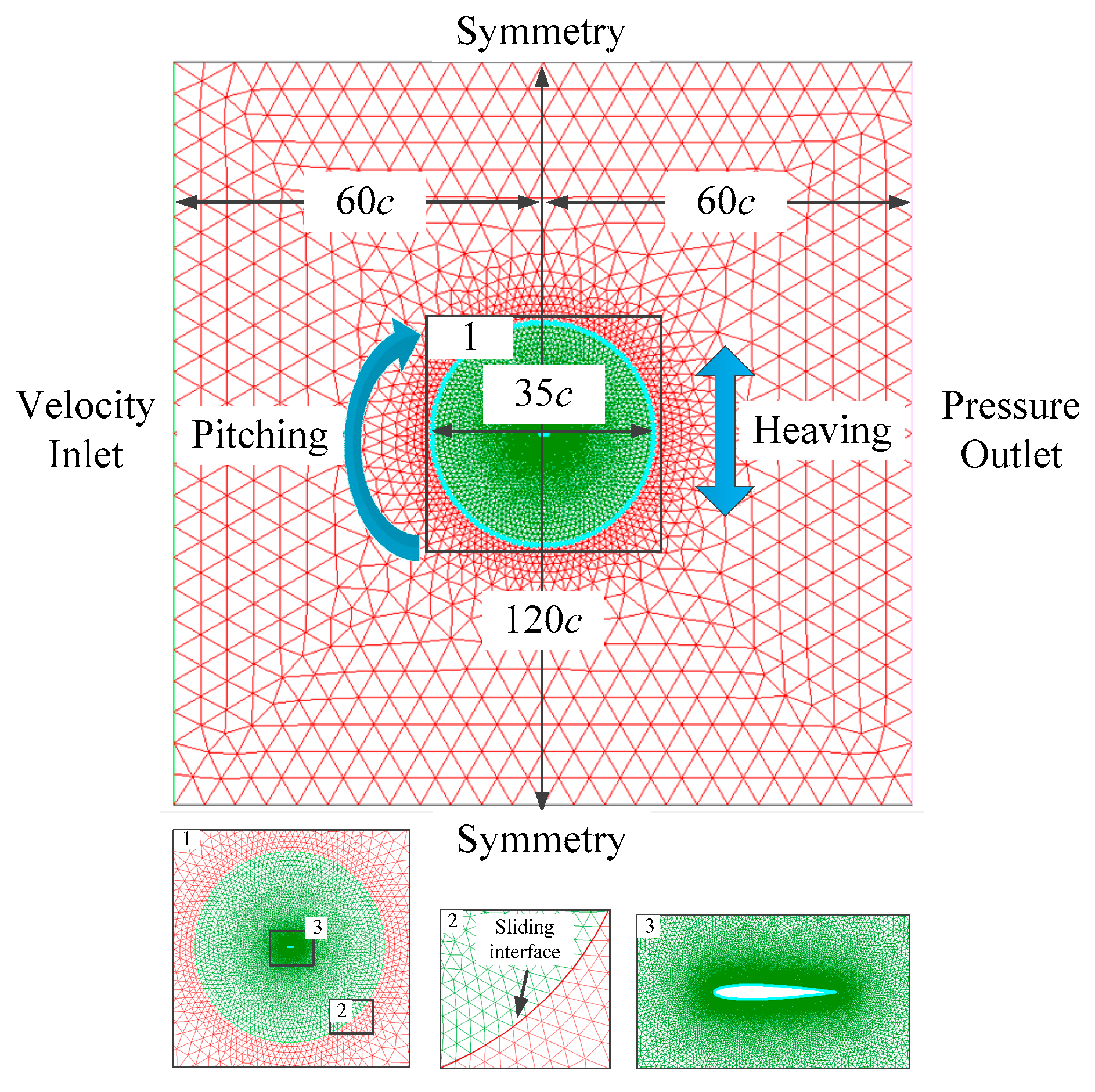
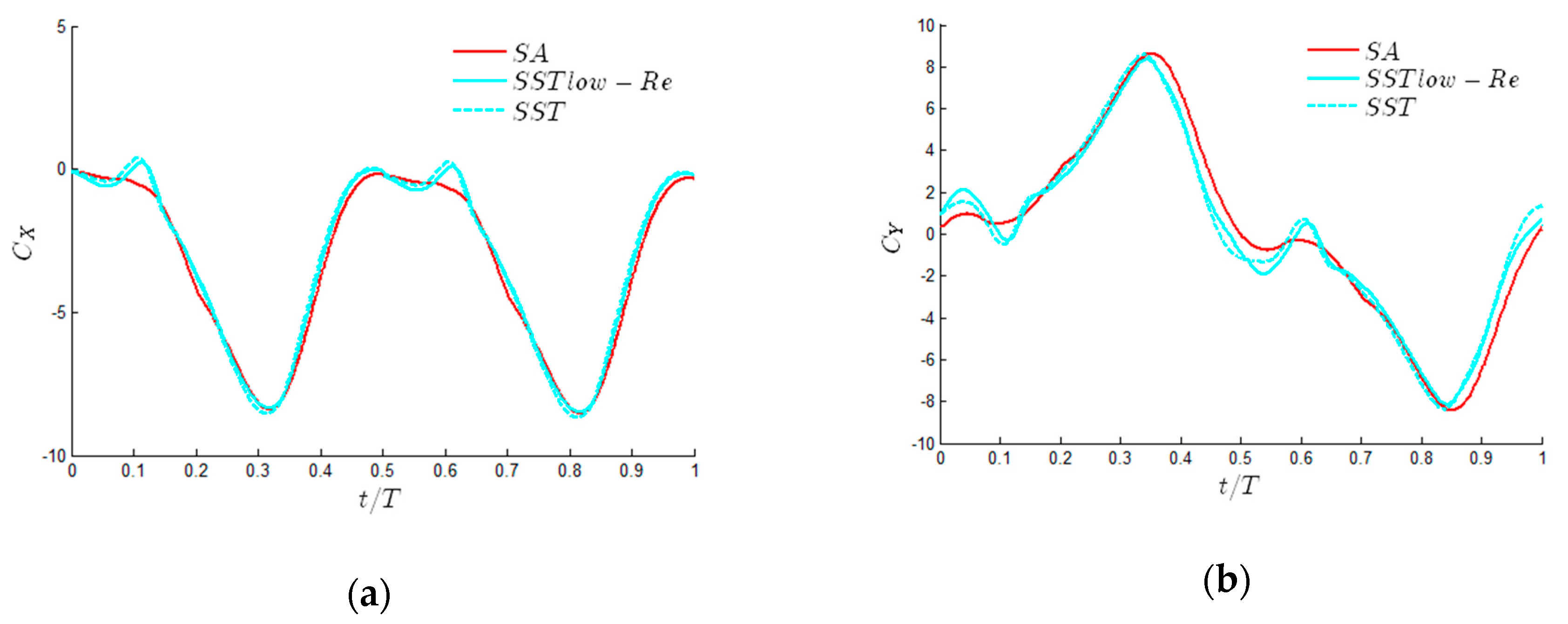
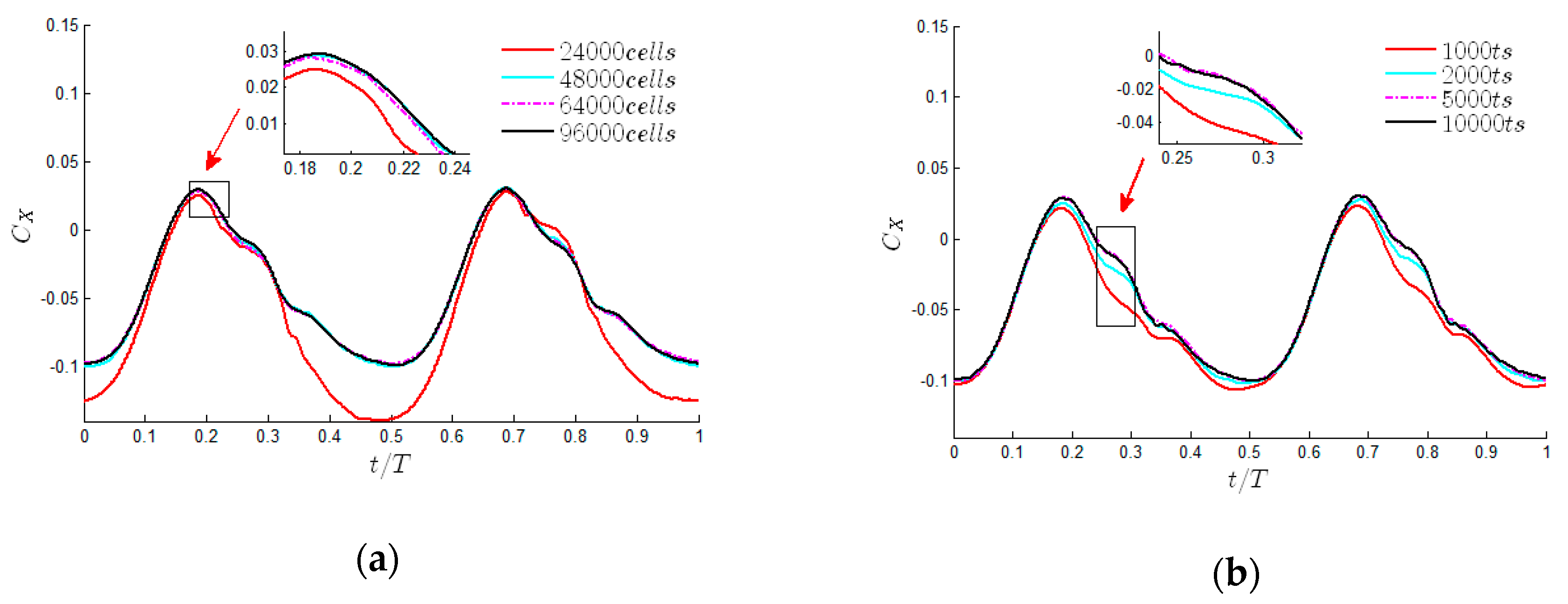
2.2. Numerical Methods and Validation
3. Results and Discussions
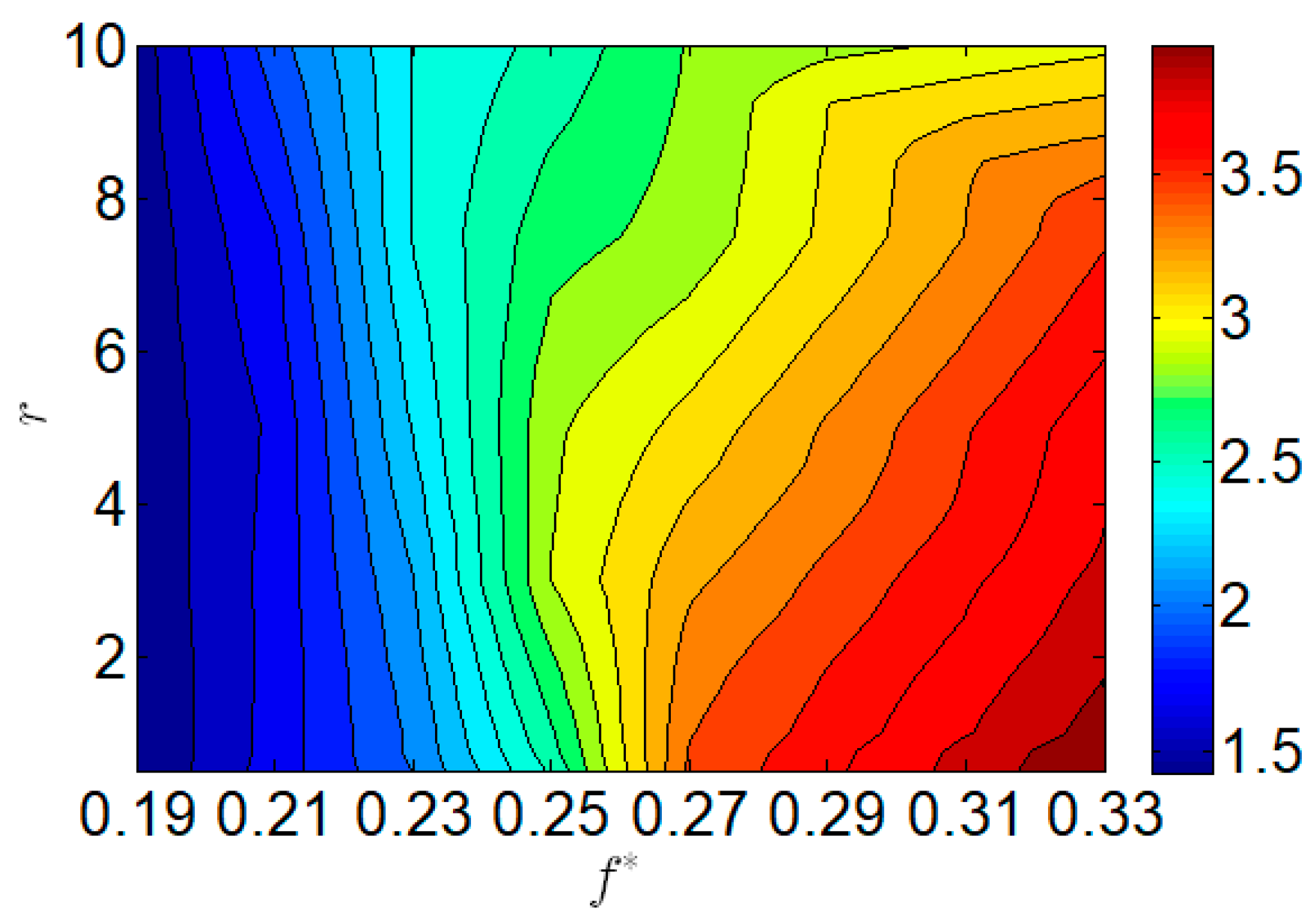
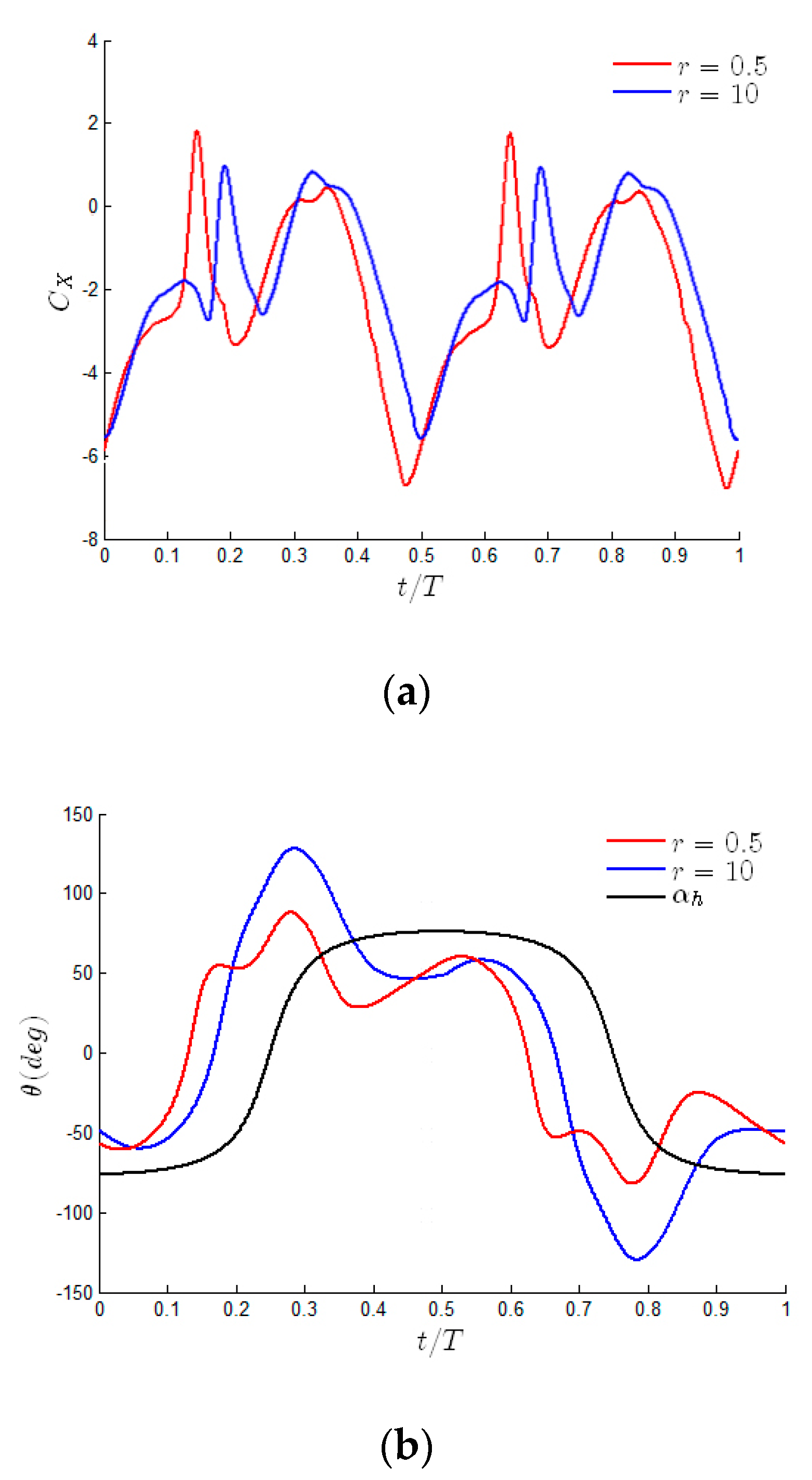
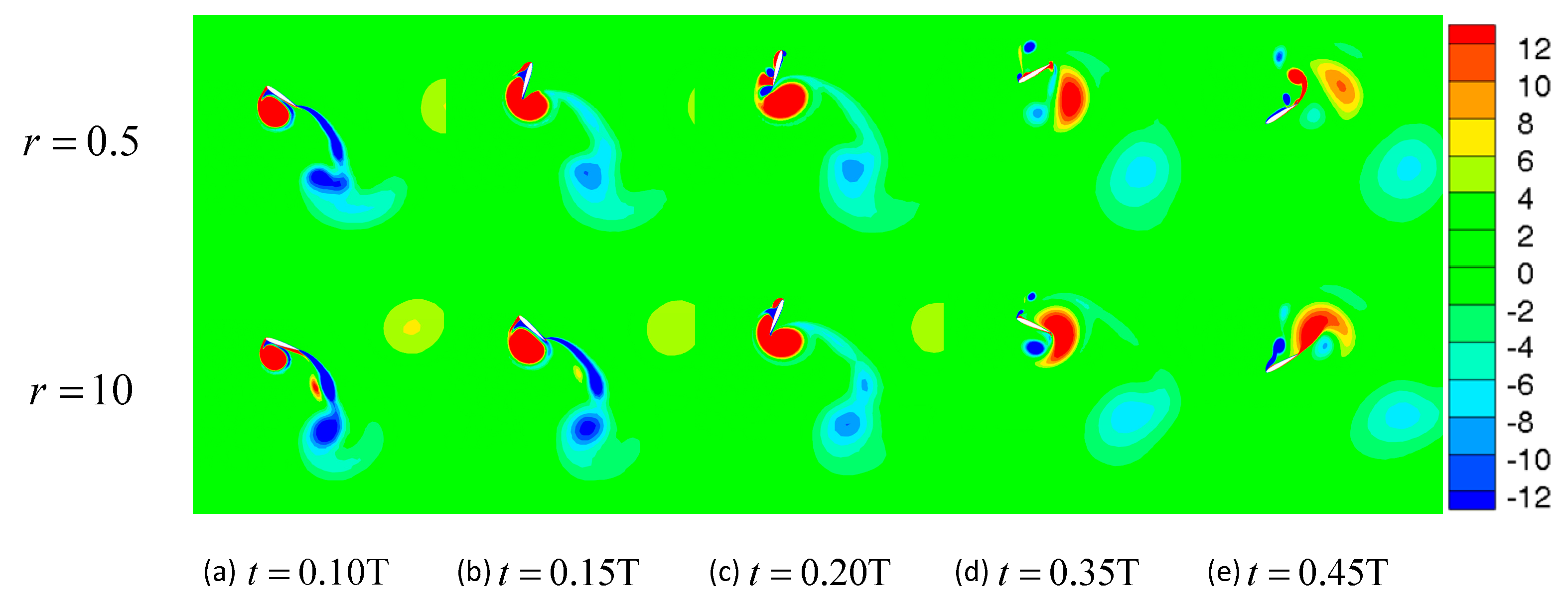
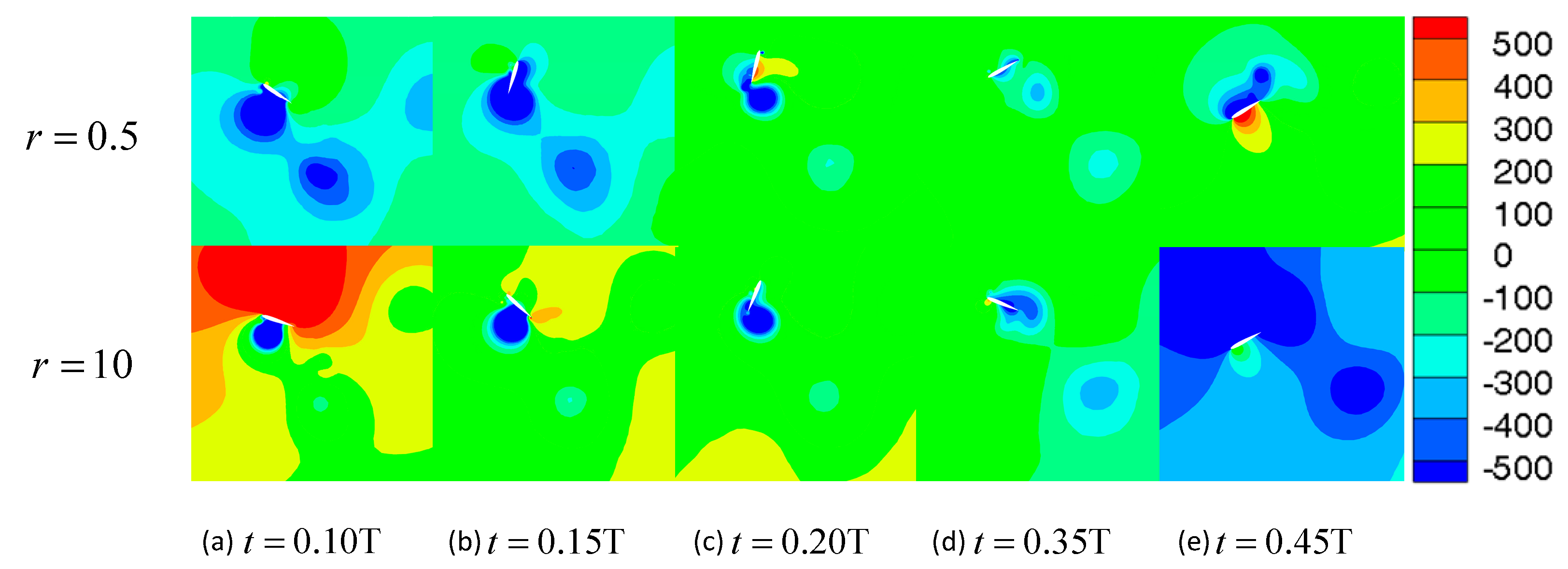
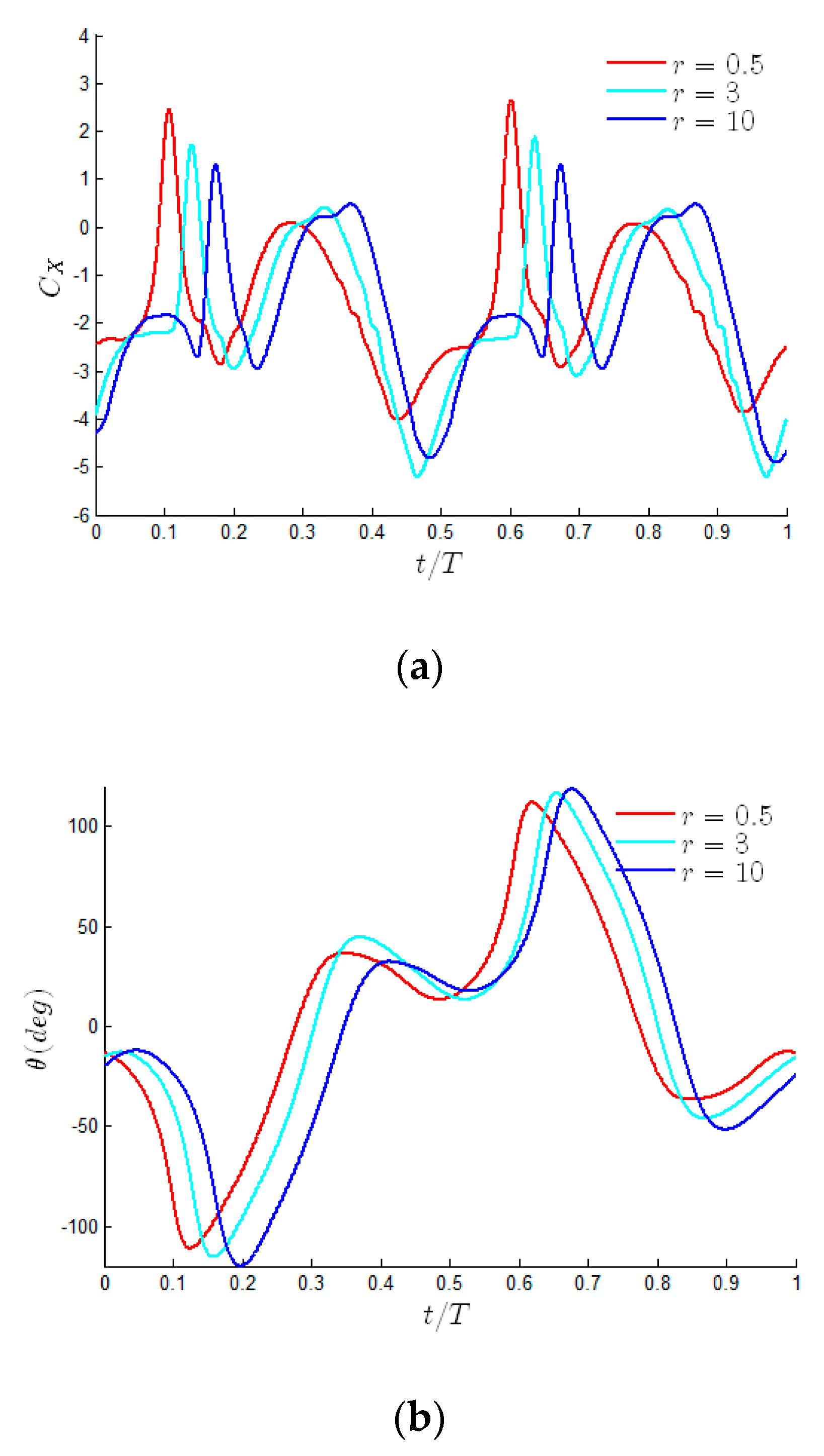
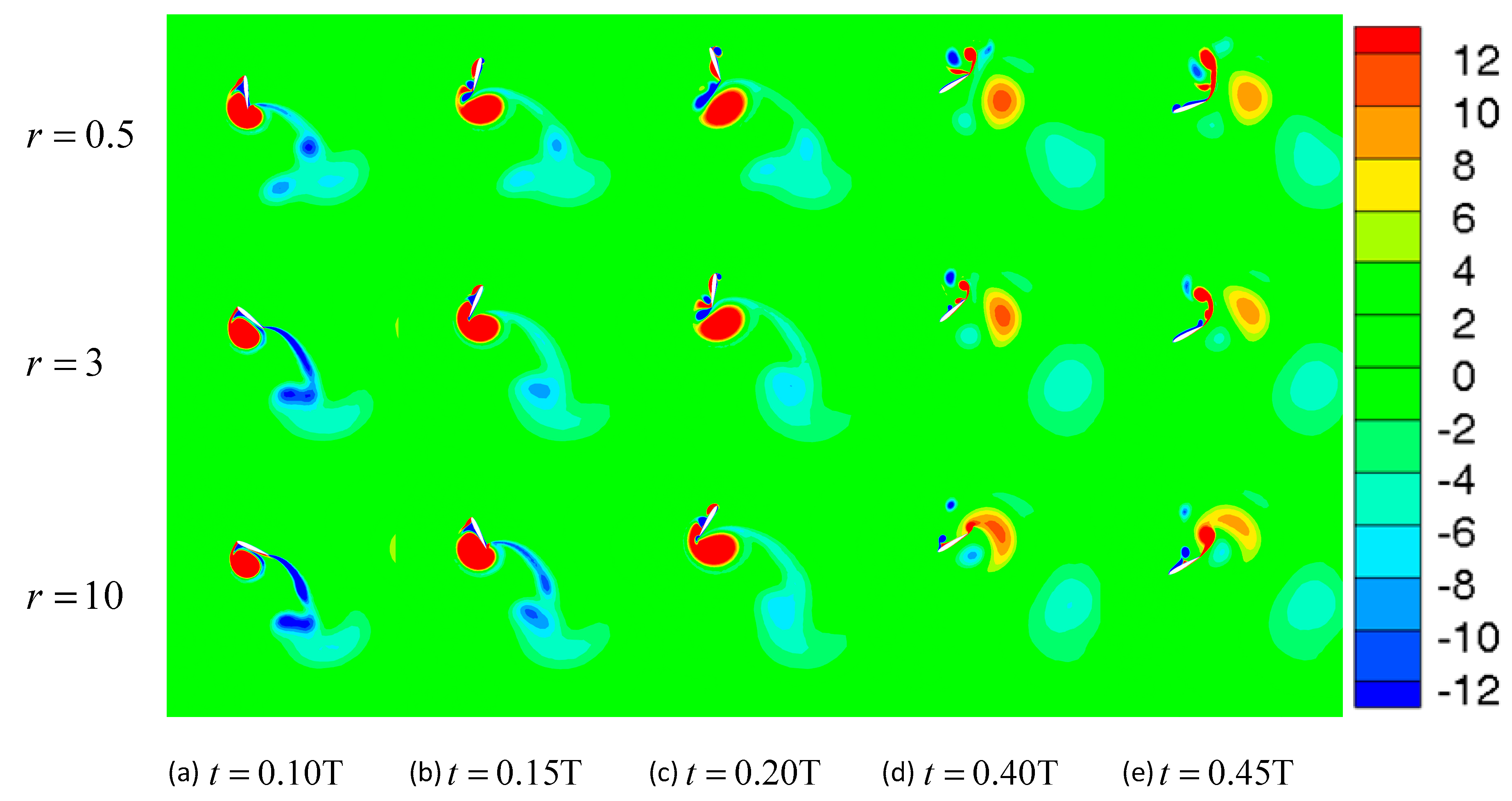
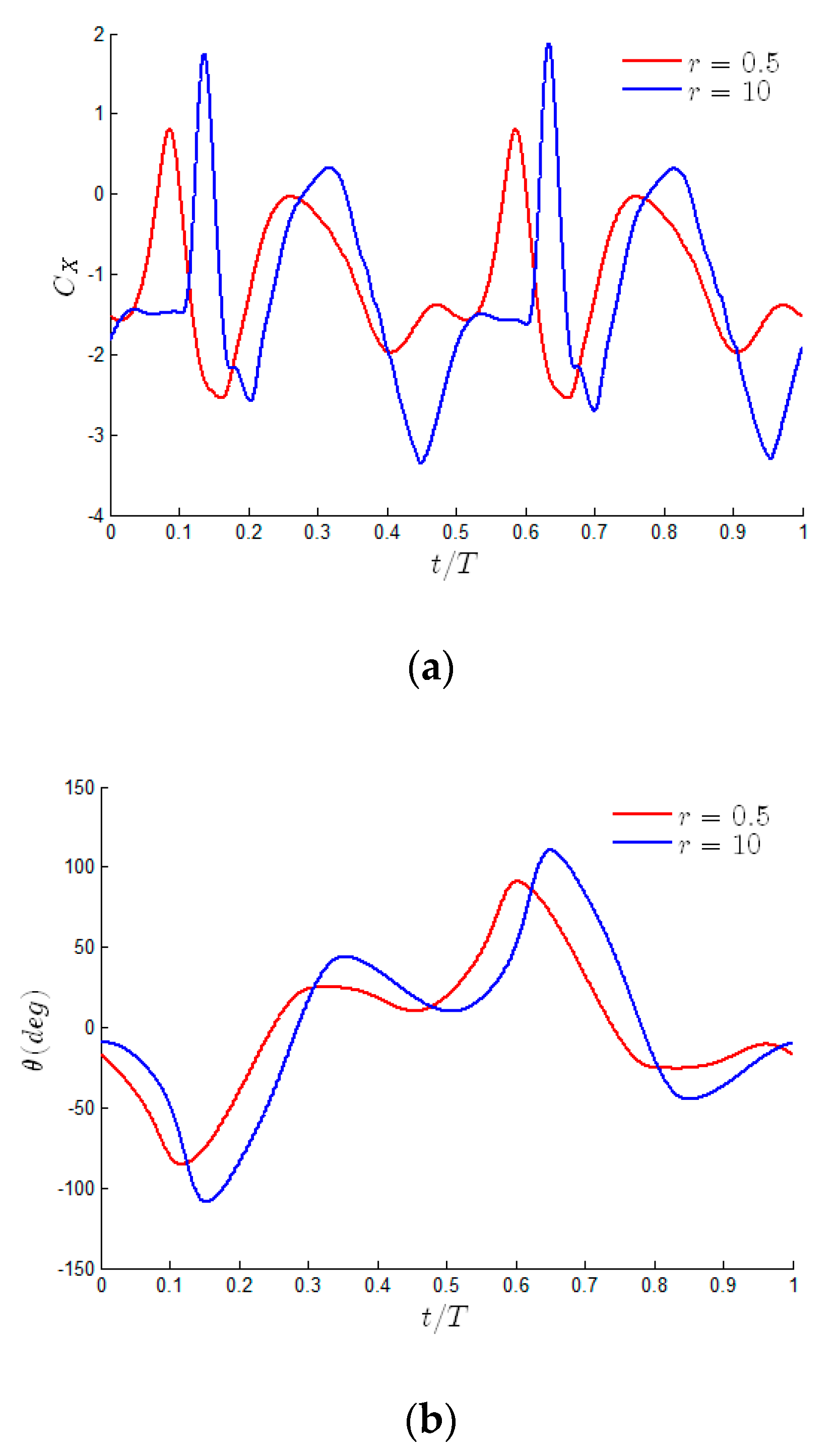
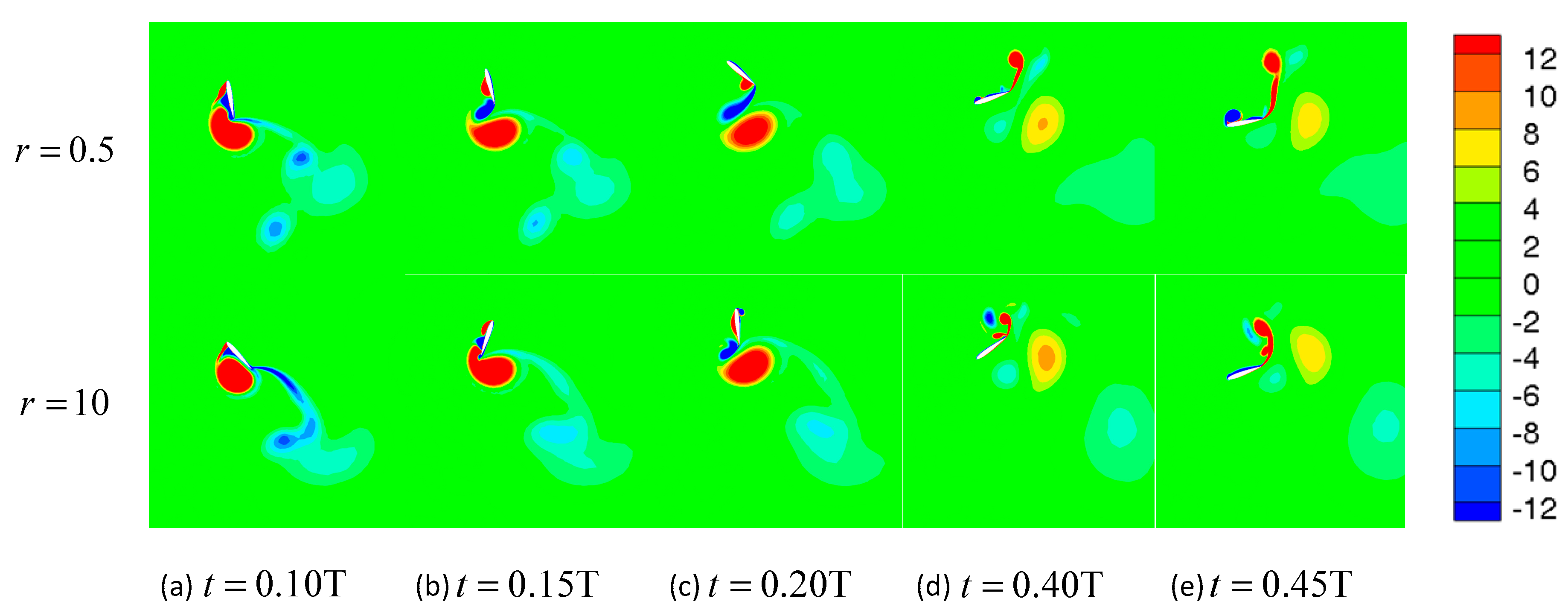
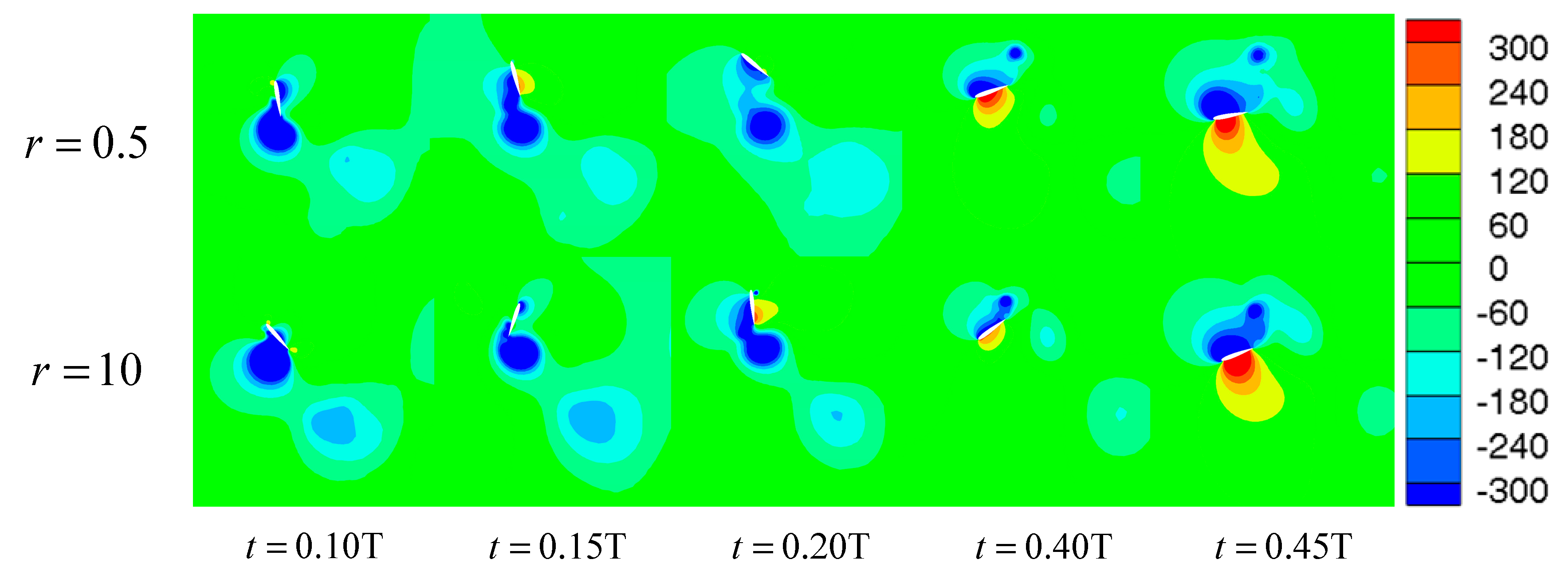
3.1. The Effect of the Mass Ratio
3.1.1. High Reduced Frequency
3.1.2. Critical Reduced Frequency
3.1.3. Low Reduced Frequency
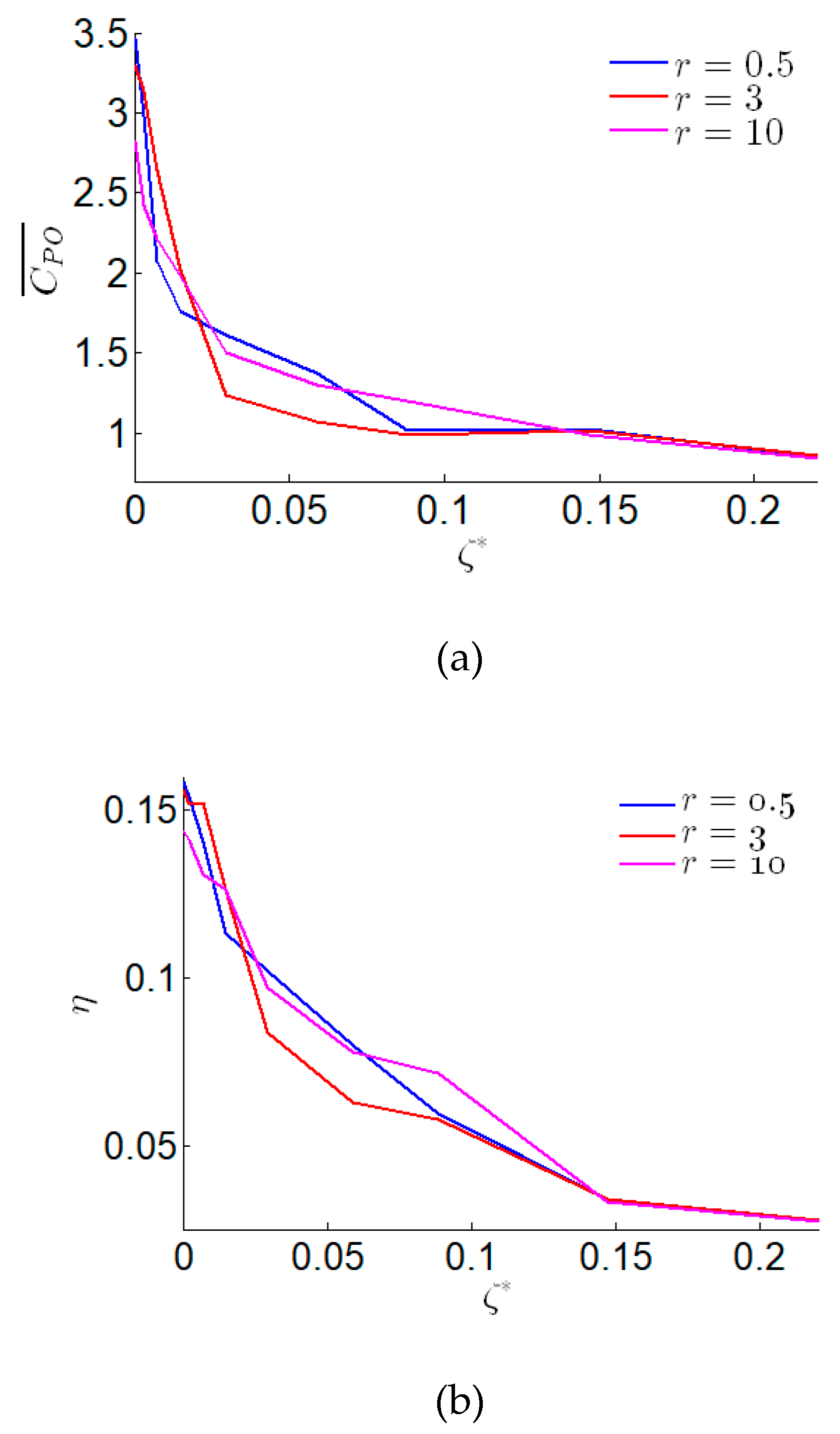
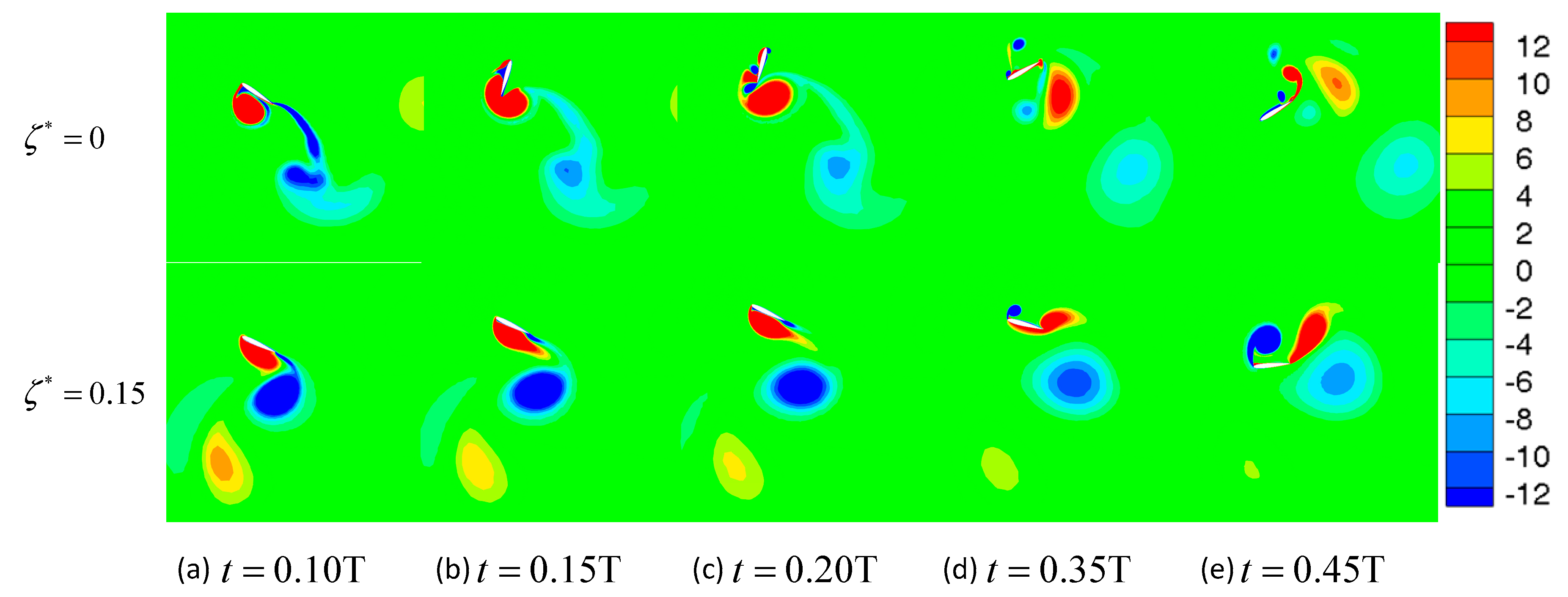
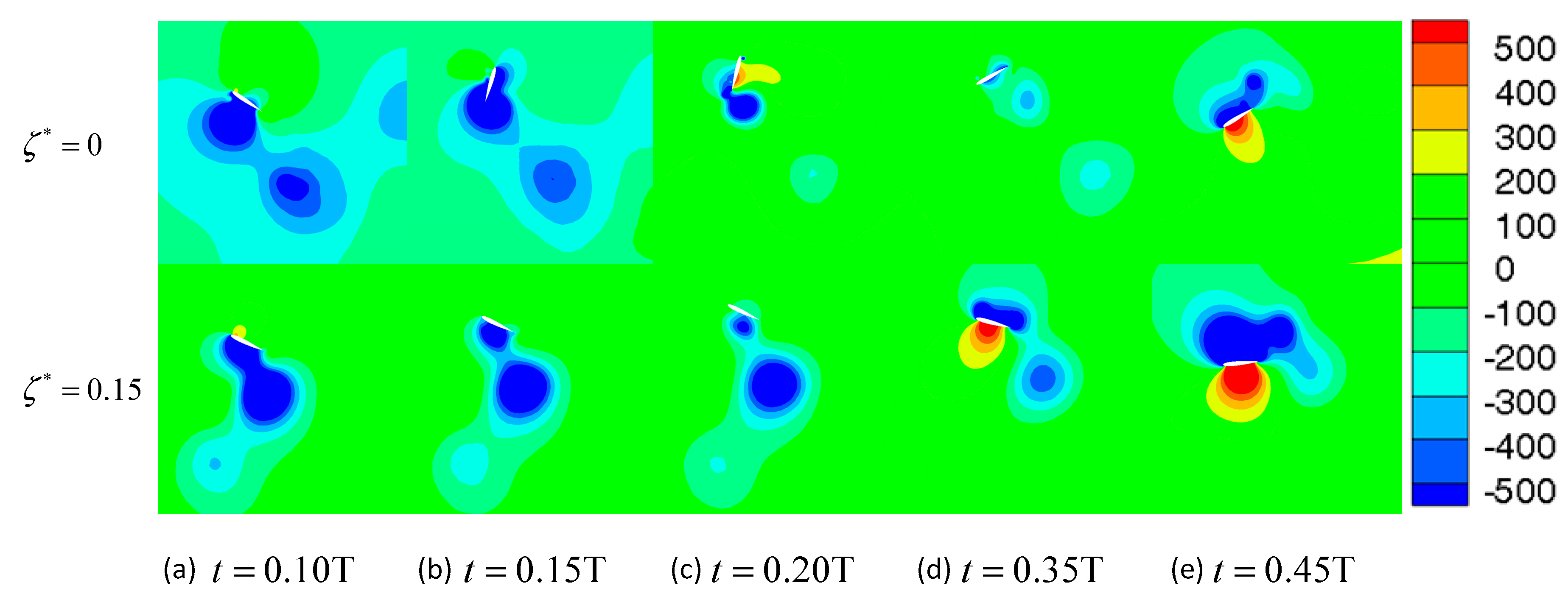
3.2. The Effect of the Damping Coefficient
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kraus, N.; Bingham, B. In Estimation of wave glider dynamics for precise positioning. In Proceedings of the Oceans 2011, Waikoloa, HI, USA, 19–22 September 2011; pp. 1–9. [Google Scholar]
- Hine, R.; Willcox, S.; Hine, G.; Richardson, T. In The Wave Glider: A Wave-Powered autonomous marine vehicle. In Proceedings of the Oceans 2009, Biloxi, MS, USA, 26–29 October 2009; pp. 1–6. [Google Scholar]
- Manley, J.; Willcox, S. In The Wave Glider: A persistent platform for ocean science. In Proceedings of the Oceans 2010, Sydney, Australia, 24–27 May 2010; pp. 1–5. [Google Scholar]
- Wiggins, S.; Manley, J.; Brager, E.; Woolhiser, B. Proceedings of the Monitoring Marine Mammal Acoustics Using Wave Glider, Oceans 2010, Seattle, WA, USA, 20–23 September 2010; pp. 1–4.
- German, C.R.; Jakuba, M.V.; Kinsey, J.C.; Partan, J.; Suman, S.; Belani, A.; Yoerger, D.R. In A long term vision for long-range ship-free deep ocean operations: Persistent presence through coordination of Autonomous Surface Vehicles and Autonomous Underwater Vehicles. In Proceedings of the 2012 IEEE/OES Autonomous Underwater Vehicles (AUV), Southampton, UK, 24–27 September 2012; pp. 1–7. [Google Scholar]
- Griffith, J. In Long Term Autonomous Ocean Remote Sensing Utilizing the Wave Glider. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 3–7 December 2012. [Google Scholar]
- Kraus, N.D. Wave Glider Dynamic Modeling, Parameter Identification and Simulation. Ph.D. Thesis, University of Hawaii, Honolulu, HI, USA, 2012. [Google Scholar]
- Ngo, P.; Al-Sabban, W.; Thomas, J.; Anderson, W.; Das, J.; Smith, R.N. In An analysis of regression models for predicting the speed of a wave glider autonomous surface vehicle. In Proceedings of the Australasian Conference on Robotics and Automation, Sydney, Australia, 2–4 December 2013. [Google Scholar]
- Wang, P.; Tian, X.; Lu, W.; Hu, Z.; Luo, Y. Dynamic modeling and simulations of the wave glider. Appl. Math. Model. 2019, 66, 77–96. [Google Scholar] [CrossRef]
- Tian, B.; Yu, J.; Zhang, A. In Lagrangian dynamic modeling of wave-driven unmanned surface vehicle in three dimensions based on the D-H approach. In Proceedings of the IEEE International Conference on Cyber Technology in Automation, Shenyang, China, 8–12 June 2015. [Google Scholar]
- Qi, Z.F.; Liu, W.X.; Jia, L.J.; Qin, Y.F.; Sun, X.J. Dynamic Modeling and Motion Simulation for Wave Glider. Appl. Mech. Mater. 2013, 397, 285–290. [Google Scholar] [CrossRef]
- Li, J.J.; Xuan, M.Z.; Zhan, F.Q.; Yu, F.Q.; Xiu, J.S. Hydrodynamic Analysis of Submarine of the Wave Glider. Adv. Mater. Res. 2014, 834, 1505–1511. [Google Scholar] [CrossRef]
- Liu, P.; Su, Y.M.; Liao, Y.L. Numerical and experimental studies on the propulsion performance of a Wave Glide propulsor. China Ocean Eng. 2016, 30, 393–406. [Google Scholar] [CrossRef]
- Bing, H.Z.; Xu, C.Y.; Chao, L.Y.; Jia, W.C. The Effect of Attack Angle on the Performance of Wave Glider Wings. Appl. Mech. Mater. 2015, 727, 587–591. [Google Scholar]
- Yang, F.; Shi, W.; Xu, Z.; Guo, B.; Wang, D. Numerical investigation of a wave glider in head seas. Ocean Eng. 2018, 164, 127–138. [Google Scholar] [CrossRef] [Green Version]
- Qi, Z.; Zou, B.; Lu, H.; Shi, J.; Li, G.; Qin, Y.; Zhai, J. Numerical Investigation of the Semi-Active Flapping Foil of the Wave Glider. J. Mar. Sci. Eng. 2019, 8, 13. [Google Scholar] [CrossRef] [Green Version]
- Triantafyllou, G.S.; Triantafyllou, M.S.; Grosenbaugh, M.A. Optimal Thrust Development in Oscillating Foils with Application to Fish Propulsion. J. Fluids Struct. 1993, 7, 205–224. [Google Scholar] [CrossRef]
- Murray, M.M.; Howle, L.E. Spring stiffness influence on an oscillating propulsor. J. Fluids Struct. 2003, 17, 915–926. [Google Scholar] [CrossRef]
- Pedro, G.; Suleman, A.; Djilali, N. A numerical study of the propulsive efficiency of a flapping hydrofoil. Int. J. Numer. Methods Fluids 2003, 42, 493–526. [Google Scholar] [CrossRef]
- Young, J.; Lai, J.C.S. Mechanisms Influencing the Efficiency of Oscillating Airfoil Propulsion. AIAA J. 2007, 45, 1695–1702. [Google Scholar] [CrossRef]
- Qi, Z.; Zhai, J.; Li, G.; Peng, J. Effects of non-sinusoidal pitching motion on the propulsion performance of an oscillating foil. PLoS ONE 2019, 14, e0218832. [Google Scholar] [CrossRef]
- Lin, X.; Wu, J.; Zhang, T. Performance investigation of a self-propelled foil with combined oscillating motion in stationary fluid. Ocean Eng. 2019, 175, 33–49. [Google Scholar] [CrossRef]
- Thaweewat, N.; Phoemsapthawee, S.; Juntasaro, V. Semi-active flapping foil for marine propulsion. Ocean Eng. 2018, 147, 556–564. [Google Scholar] [CrossRef]
- Wu, T.Y. Swimming of a Waving Plate. J. Fluid Mech. 1961, 10, 321–344. [Google Scholar] [CrossRef]
- Anderson, J.M.; Streitlien, K.; Barrett, D.S.; Triantafyllou, M.S. Oscillating foils of high propulsive efficiency. J. Fluid Mech. 1998, 360, 41–72. [Google Scholar] [CrossRef] [Green Version]
- Floc’H, F.; Phoemsapthawee, S.; Laurens, J.M.; Leroux, J.B. Porpoising foil as a propulsion system. Ocean Eng. 2012, 39, 53–61. [Google Scholar] [CrossRef]
- Jian, D.; Teng, L.; Pan, D.; Shao, X. Inertial effects of the semi-passive flapping foil on its energy extraction efficiency. Phys. Fluids 2015, 27, 174–191. [Google Scholar]
- Richards, A.J.; Oshkai, P. Effect of the stiffness, inertia and oscillation kinematics on the thrust generation and efficiency of an oscillating-foil propulsion system. J. Fluids Struct. 2015, 57, 357–374. [Google Scholar] [CrossRef]
- Zhu, J. The Effect of Damping Coefficient, Spring Coefficient, and Mass Ratio on the Power Extraction Performance of a Semiactive Flapping Wing. Int. J. Aerosp. Eng. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Kinsey, T.; Dumas, G.; Kinsey, T.; Dumas, G. Parametric Study of an Oscillating Airfoil in a Power-Extraction Regime. Aiaa J. 2008, 46, 1318–1330. [Google Scholar] [CrossRef]
- Jian, D.; Caulfield, C.P.; Shao, X. Effect of aspect ratio on the energy extraction efficiency of three-dimensional flapping foils. Phys. Fluids 2014, 26, 043102. [Google Scholar]




| Reference | Year | Influence Factor | Links |
|---|---|---|---|
| Nurray and Howle | 2003 | Spring stiffness | https://doi.org/10.1016/S0889-9746(03)00026-4 |
| Young and Lai | 2007 | Strouhal number | https://doi.org/10.2514/1.27628 |
| Teng et al | 2015 | Mass ratio | https://doi.org/10.1063/1.4921384 |
| Thaweewat et al | 2018 | Reduced frequency, spring stiffness | https://doi.org/10.1016/j.oceaneng.2017.11.008 |
| Qi et al. | 2019 | Spring stiffness, critical pitching amplitude | https://doi.org/10.3390/jmse8010013 |
| Turbulence Model | Mesh | Time-Step | Mean Error (%) | |
|---|---|---|---|---|
| Spalart-Allmaras | Medium-1 grid | 5000ts | −2.9692 | −1.8 |
| SST with low-Re corrections | Medium-1 grid | 5000ts | −3.0238 | --- |
| SST | Medium-1 grid | 5000ts | −2.9987 | −0.8 |
| Mesh | Time-Step | Mean Error (%) | ||
|---|---|---|---|---|
| Mesh Independence | Coarse grid | 5000 ts | −0.0636 | 40.39 |
| Medium-1 grid | −0.0456 | 0.66 | ||
| Medium-2 grid | −0.0455 | 0.44 | ||
| Fine Grid | −0.0453 | --- | ||
| Time-step Independence | Medium-1 grid | 1000 ts | −0.0542 | 18.34 |
| 2000 ts | −0.0485 | 5.89 | ||
| 5000 ts | −0.0456 | 0.43 | ||
| 10000 ts | −0.0458 | --- |
| Parameters | Range |
|---|---|
| Chord length, c | 0.17 m |
| Hydrofoil shape | 2D NACA0012 |
| Hydrofoil thickness, d | 0.02 m |
| Free stream velocity, | 0.25 m/s |
| Heaving amplitude, | 2c |
| Normalized spring constant, | 0.09 |
| Mass ratio, r | 0.5–10 |
| Reduced frequency, | 0.19–0.34 |
| Damping coefficient, | 0–0.22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Z.; Jiang, M.; Jia, L.; Zou, B.; Zhai, J. The Effect of Mass Ratio and Damping Coefficient on the Propulsion Performance of the Semi-Active Flapping Foil of the Wave Glider. J. Mar. Sci. Eng. 2020, 8, 303. https://doi.org/10.3390/jmse8050303
Qi Z, Jiang M, Jia L, Zou B, Zhai J. The Effect of Mass Ratio and Damping Coefficient on the Propulsion Performance of the Semi-Active Flapping Foil of the Wave Glider. Journal of Marine Science and Engineering. 2020; 8(5):303. https://doi.org/10.3390/jmse8050303
Chicago/Turabian StyleQi, Zhanfeng, Min Jiang, Lishuang Jia, Bo Zou, and Jingsheng Zhai. 2020. "The Effect of Mass Ratio and Damping Coefficient on the Propulsion Performance of the Semi-Active Flapping Foil of the Wave Glider" Journal of Marine Science and Engineering 8, no. 5: 303. https://doi.org/10.3390/jmse8050303
APA StyleQi, Z., Jiang, M., Jia, L., Zou, B., & Zhai, J. (2020). The Effect of Mass Ratio and Damping Coefficient on the Propulsion Performance of the Semi-Active Flapping Foil of the Wave Glider. Journal of Marine Science and Engineering, 8(5), 303. https://doi.org/10.3390/jmse8050303






