Robust Output Path-Following Control of Marine Surface Vessels with Finite-Time LOS Guidance

Abstract

This paper proposes a finite-time output feedback methodology for the path-following task of marine surface vessels. First, a horizontal path-following model is established with unknown sideslip angle, unmeasured system state and system uncertainties. A hierarchical control structure is adopted to deal with the cascade property. For kinematics system design, a finite-time sideslip angle observer is first proposed, and thus the sideslip angle estimation is compensated in a nonlinear line-of-sight (LOS) guidance strategy to acquire finite-time convergence. For the heading control design, an extended state observer is introduced for the unmeasured state and equivalent disturbance estimation, based on which an output feedback backstepping approach is proposed for the desired tracking of command course angle. The global stability of the cascade system is analyzed. Simulation results validate the effectiveness of the proposed methodology.

1. Introduction

With the rapid growth of marine sciences and the improvement of advanced motion control technique in recent years, investigations of unmanned marine surface vessels have received increasing interest in both military and civil applications. The dynamics of marine surface vessels is regarded as an underactuated system with nonholonomic constraints, so there is no gloss or time invariant controller that can stabilize the vehicle to the equilibrium point [1]. Meanwhile, when the vehicles sail with a high speed, external disturbances which contain wind, waves and currents make it difficult for maneuvering. Thus, the path-following task of the marine surface vessels is a challenge work due to its nonlinearity, strong coupling and underactuated properties, internal and external uncertainties, etc.

According to the cascade property, the hierarchical technique has been widely concerned for control system implementation of the marine vessels [2,3,4,5,6,7,8]. For a hierarchical control structure, the kinematics controller, which is also known as the guidance law, is first proposed for desired path-following performance, while the dynamics controller is then designed to enable the vehicle to track the command course angle of the guidance law. The line-of-sight (LOS) guidance law was originally proposed in [9] and quickly becomes widely used in the aspect of vehicle path-following control. In [10], the LOS guidance algorithm has also been extended to the aspect of obstacle avoidance.

In [11], the proportional LOS guidance algorithm is developed, and uniform semi-global exponential stability is acquired. In [12], adaptive LOS law is proposed to acquire asymptotical stable result. However, the above results assume that the sideslip angle can be measured. To increase the robustness of the kinematics system, the integral LOS guidance algorithm is proposed in [2,13], where the influence caused by the drift forces of the ocean is weakened. However, the error-based methods impede the further improvement of the path-following accuracy, and the conservatism of this method should be further discussed. Recently, the observer-based sideslip compensation methodologies have been widely explored, such as adaptive law-based observer [3,14], extended state observer (ESO) [15], etc. However, performance and stability of the guidance system still need to be improved and discussed. Recently, disturbance observer (DOB)-based control methodology has been widely investigated [16,17,18,19]. Although the first-order DOB is used in most existing research to estimate the uncertainties due to its intuitional structure and simple parameters tuning, the estimation performance of high order time-varying disturbance is largely limited due to its simple structure. In [17], a generalized NDOB is proposed to deal with the high order disturbances. It is shown that estimation performance for time-varying disturbances of generalized NDOB is much better than that of tradition DOB. Considering the time-varying property, the sideslip angle can be treated as the disturbance, then the system kinematics with unknown sideslip angle can be reconstructed into the system with disturbance. Thus, the DOB-based control technique can be adopted for guidance algorithm design.

Governed by the guidance algorithm, advanced motion control technique can be presented for the vessels to track the command course angle. In [6,7], the neural network is used to approximate the uncertainties; however, overdependence of the initial value makes these methods difficult to be used in practice. The backstepping technique has been used for controller design in [20,21]; however, the system states should be measurable. In [22,23,24], sliding mode control (SMC) is used for control design of vessels; however, the chattering phenomenon affects the system performance. Although the high order SMC [25,26] can suppress the chattering phenomenon of traditional SMC, the requirement of high order derivation of system states will lead to the problem of calculation explosion. In [27,28], the adaptive robust controller is designed to acquire desired performance with uncertainties. However, this approach brings more conservatism to the system. Among the existing motion control methodologies, active disturbance rejection control (ADRC), which was originally proposed in [29], has been widely investigated in practical applications [30,31,32,33]. The ESO, which is known as the most important part of ADRC, can estimate the unmeasured system states and total disturbance respectively to formulate the feedback controller [34,35,36]. Therefore, the ADRC technique is introduced to deal with the output feedback problem with uncertainties in many cases.

According to the descriptions above, robust output feedback path-following methodology is proposed in this paper for the vessels based on a finite-time LOS guidance algorithm. First, by considering the unknown time-varying sideslip angle, unmeasured system state and uncertainties, system model of path-following problem is presented, based on which hierarchical technique is adopted for control system implementation. Then, a finite-time generalized observer (FGO) is proposed to estimate and compensate the sideslip angle together with a nonlinear LOS guidance law to acquire finite-time convergence. Meanwhile, an ESO is proposed to formulate an output feedback backstepping controller to track the command course angle accurately. Finally, Lyapunov stability is analyzed for the overall system. The main contributions of this work are summarized as follows:

• The path-following problem is formulated with unknown time-varying sideslip angle, unmeasured system state and system uncertainties, thus, the observation technique is adopted to estimate all these unknown terms.
• A finite-time generalized observer is proposed for sideslip angle estimation, based on which a nonlinear LOS guidance law is proposed, and finite-time convergence of the cross-track error is hence obtained.
• An ESO is adopted for both unknown system state and total disturbance estimation, based on which an output feedback backstepping controller is proposed without angular velocity measurement.

The rest of this paper is organized as follows: the path-following problem is formulated and the hierarchical control structure is introduced in Section 2. In Section 3, an observer-based finite-time LOS guidance algorithm and an ESO-based output feedback backstepping controller are implemented for the desired performance. In Section 4, closed-loop Lyapunov stability is analyzed. Simulations are carried out in Section 5, followed by Conclusions in Section 6.

2. Preliminaries and System Description

2.1. Preliminaries

Definition 1.

The operator ${\mathrm{sign}}^{\varrho }(·)$ for the variable x is defined as

$${\mathrm{sign}}^{\varrho }\left(x\right)=x·{\left|x\right|}^{\varrho -1}$$

(1)

It is easy to verify the following equations hold

$$\frac{\mathrm{d}{\mathrm{sign}}^{\varrho }\left(x\right)}{\mathrm{d}t}=\varrho {\left|x\right|}^{\varrho -1}\dot{x},\frac{{\mathrm{d}\left|x\right|}^{\varrho }}{\mathrm{d}t}=\varrho {\mathrm{sign}}^{\varrho -1}\left(x\right)\dot{x}.$$

Lemma 1

([37]). Considering the system in following form

$$\dot{\mathit{x}}=\mathit{f}\left(\mathit{x}\right),\mathit{f}\left(\mathbf{0}\right)=\mathbf{0},$$

(2)

where $\mathit{x}=\left[\begin{array}{ccc}{x}_1& ···& x_n\end{array}\right]\in {\mathcal{R}}^n$ is a state vector, $\mathit{f}\left(\mathit{x}\right)=\left[\begin{array}{ccc}{f}_1\left(\mathit{x}\right)& ···& f_n\left(\mathit{x}\right)\end{array}\right]\in {\mathcal{R}}^n$ is a known continuous vector field. Assume that there exists a continuous positive definite Lyapunov function $V\left(\mathit{x}\right)$ which satisfies the following inequality:

$$\dot{V}\left(\mathit{x}\left(t\right)\right)+{\kappa }_1{V}^{\kappa }\left(\mathit{x}\left(t\right)\right)\le 0,\forall t>t_0,$$

(3)

where $\kappa >0$ and $0<\kappa <1$. Then the origin of the system is globally stable in finite-time $t_s$:

$$t_s\le t_0+\frac{1}{{\kappa }_1(1-\kappa )}{V}^{1-\kappa }\left({\mathit{x}}_{t_0}\right).$$

(4)

2.2. Kinematics of Path Following

The path-following task of marine vessel on the horizontal degree-of-freedom (DOF) is to make the vessel follow a time-independent path quickly and accurately. Therefore, the nominal vessel dynamics of 3 DOF is usually applied for the control system design in most previous works. The horizontal kinematics of the vessel is established as

$$\left\{\begin{array}{cc}\hfill \dot{x}& =ucos\psi -vsin\psi \hfill \\ \hfill \dot{y}& =usin\psi +vcos\psi \hfill \\ \hfill \dot{\psi }& =r,\hfill \end{array}\right.$$

(5)

where $\psi$ is the yaw angle, u, v and r represent the surge, sway and yaw velocities, respectively.

LOS guidance geometry of a surface vessel is shown in Figure 1. For the surface vessel located at $(x,y)$, the cross-track error $y_e$ is known as the orthogonal distance from the vehicle to the reference path, while $(x_p,y_p)$ is the orthogonal path point. The Serret–Frenet frame is rotated from the North-East-Down (NED) frame by using the rotation matrix $R\left({\gamma }_p\right)\in SO\left(2\right)$ as

$$\left[\begin{array}{c}0\\ y_e\end{array}\right]=R{\left({\gamma }_p\right)}^{\mathrm{T}}\left[\begin{array}{c}x-x_p\\ y-y_p\end{array}\right],$$

(6)

where ${\gamma }_p$ is the path-tangential angle and $R\left({\gamma }_p\right)$ is the attitude transition matrix defined as

$$R{\left({\gamma }_p\right)}^{\mathrm{T}}=\left[\begin{array}{cc}cos\left({\gamma }_p\right)& -sin\left({\gamma }_p\right)\\ sin\left({\gamma }_p\right)& cos\left({\gamma }_p\right)\end{array}\right].$$

Figure 1. LOS guidance geometry for curved path.

The first-order time derivative of $y_e$ can be obtained as

$$\begin{array}{c}\hfill {\dot{y}}_e=-(\dot{x}-{\dot{x}}_p)sin\left({\gamma }_p\right)+(\dot{y}-{\dot{y}}_p)cos\left({\gamma }_p\right)+[(x-x_p)cos\left({\gamma }_p\right)-(y-y_p)sin\left({\gamma }_p\right)]{\dot{\gamma }}_p.\end{array}$$

(7)

According to Equation (6) and the definition of ${\gamma }_p$, we have

$$\left\{\begin{array}{cc}& (x-x_p)cos\left({\gamma }_p\right)-(y-y_p)sin\left({\gamma }_p\right)=0,\hfill \\ \hfill & {\dot{x}}_{p}sin\left({\gamma }_p\right)-{\dot{y}}_{p}cos\left({\gamma }_p\right)=0,\hfill \end{array}\right.$$

then the time derivative of $y_e$ can be written as

$$\begin{array}{cc}\hfill {\dot{y}}_e=& -(ucos\left(\psi \right)-vsin\left(\psi \right))sin\left({\gamma }_p\right)+(usin\left(\psi \right)+vcos\left(\psi \right))cos\left({\gamma }_p\right)\hfill \\ \hfill =& Usin(\psi -{\gamma }_p+{\beta }_s),\hfill \end{array}$$

(8)

where amplitude $U=\sqrt{u^2+v^2}>0$ and phase ${\beta }_s=\mathrm{atan}2(v,u)$ are known as the linear speed and sideslip angle, respectively.

Equation (8) can be further expanded as

$${\dot{y}}_e=Usin(\psi -{\gamma }_p)cos\beta +Ucos(\psi -{\gamma }_p)sin{\beta }_s,$$

(9)

then the sideslip angle can be separated for the guidance design.

By using the approximations $cos{\beta }_s\approx 1$ and $sin{\beta }_s\approx {\beta }_s$, the final state equation of cross-track error is given as

$${\dot{y}}_e=Usin(\psi -{\gamma }_p)+Ucos(\psi -{\gamma }_p){\beta }_s.$$

(10)

2.3. Yaw Dynamics of Marine Surface Vessels

Assume that the surge speed is positive constant and neglecting the underactuated properties caused by the sway velocity, the yaw dynamics of the vessel is in the following form:

$$\left\{\begin{array}{cc}\hfill \dot{\psi }& =r\hfill \\ \hfill \dot{r}& =-\frac{d_{r1}}{m_{33}}r-{\Sigma }_{i=2}^3\frac{d_{ri}}{m_{33}}{\left|r\right|}^{i-1}·r+\frac{1}{m_{33}}{\tau }_r+\frac{1}{m_{33}}{\tau }_{wr},\hfill \end{array}\right.$$

(11)

where r is the yaw angle velocity, $m_{ii}$ are given by the inertia and added mass effects of the vessel, the parameters $d_{ri}>0$ are given by the hydrodynamic damping, ${\tau }_r$ and ${\tau }_{wr}$ denote the yaw moment and wave disturbance moment, respectively.

Without loss of generality, Equation (11) can be rewritten as

$$\left\{\begin{array}{cc}\hfill \dot{\psi }=& r\hfill \\ \hfill \dot{r}=& -(a_1+\Delta a_1)r-(a_2+\Delta a_2)\left|r\right|r-(a_3+\Delta a_3)r^3\hfill \\ & +(b_1+\Delta b_1){\tau }_r+d_w,\hfill \end{array}\right.$$

(12)

where $a_i$ and $\Delta a_i,i=1\sim 3$ denote the nominal and perturbation of the system parameters related to the moment of inertia and added inertia of the yaw dynamics, $b_1$ and $\Delta b_1$ are the nominal and perturbation of control parameter, ${\delta }_r$ is the rudder angle and $d_w$ represents the external disturbances caused by the stochastic ocean waves.

By combining the parameter perturbation and wave disturbance moment together as the total disturbances, Equation (12) can be rewritten as follows

$$\left\{\begin{array}{cc}\hfill \dot{\psi }=& r\hfill \\ \hfill \dot{r}=& -a_{1}r-a_2\left|r\right|r-a_3{r}^3+b_1{\delta }_r+f\left(t\right)\hfill \\ \hfill f\left(t\right)=& -\Delta a_{1}r-\Delta a_2\left|r\right|r-\Delta a_3{r}^3+\Delta b_3{\delta }_r+d_w,\hfill \end{array}\right.$$

(13)

where $f\left(t\right)$ is the total disturbance with both internal and external uncertainties.

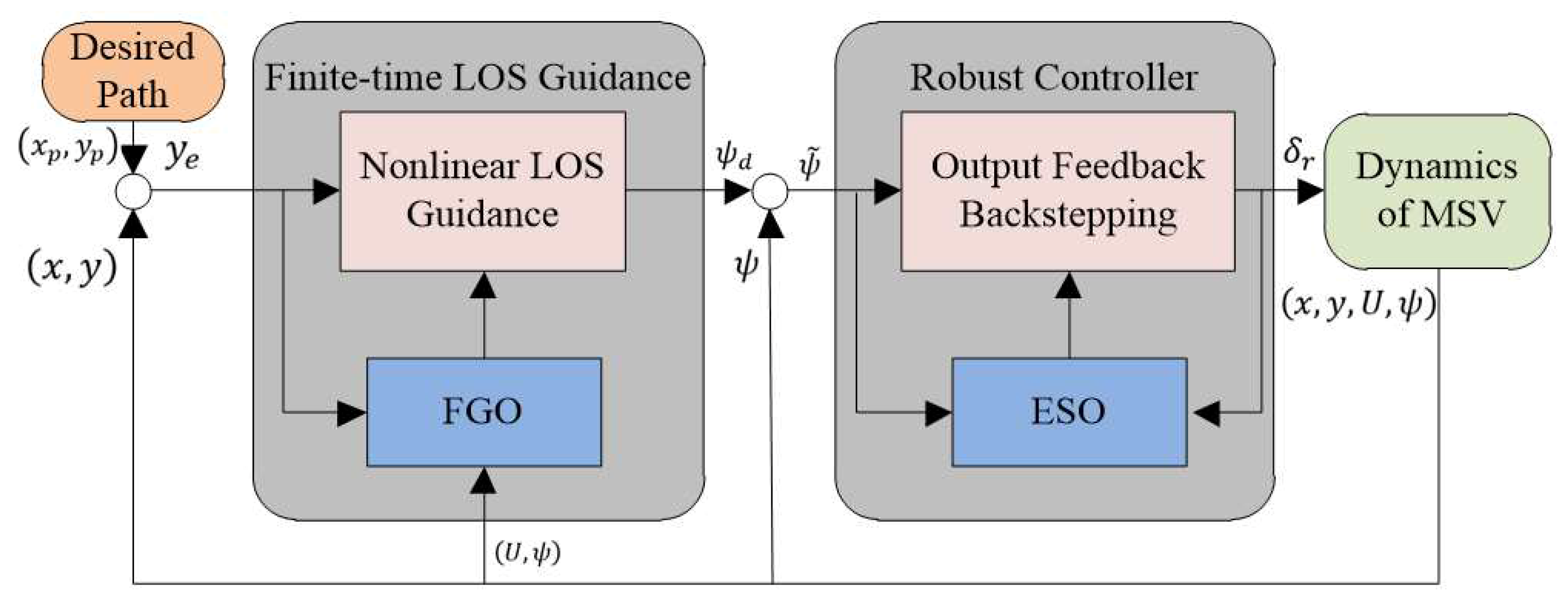
3. Control System Design

The control objective of this work is motivated in the following two aspects: first, the command course angle ${\psi }_{\mathrm{d}}$ is designed to stabilize the error system shown in Equation (8) based on the finite-time LOS guidance algorithm; Secondly, the ESO-based output feedback backstepping controller is presented to enable the yaw angle $\psi$ to track ${\psi }_{\mathrm{d}}$ of LOS guidance strategy quickly and accurately. The hierarchical control structure is shown in Figure 2.

Figure 2. The control structure.

3.1. FGO Based Finite-Time LOS Guidance

Notice that ${\gamma }_p$ and $y_e$ can be obtained according to the way points of the reference path, it is necessary to estimate the sideslip angle ${\beta }_s$ for the guidance law design.

By introducing the generalized disturbance term $\delta =Ucos(\psi -{\gamma }_p){\beta }_s$, Equation (10) can be reconstructed as

$${\dot{y}}_e=Usin(\psi -{\gamma }_p)+\delta .$$

(14)

Accordingly, the observer of $\delta$ can be designed as

$$\left\{\begin{array}{cc}\hfill \dot{z}=& Usin(\psi -{\gamma }_p)+\widehat{\delta }\hfill \\ \hfill \widehat{\delta }=& {\lambda }_1{\mathrm{sign}}^{{\varrho }_2}(y_e-z)+{\lambda }_2{\int }_0^t{\mathrm{sign}}^{{\varrho }_1}(y_e\left(\tau \right)-z\left(\tau \right))d\tau \hfill \\ \hfill {\widehat{\beta }}_s=& \frac{\widehat{\delta }}{Ucos(\psi -{\gamma }_p)}.\hfill \end{array}\right.$$

(15)

where ${\lambda }_1$ and ${\lambda }_2$ are positive constants, ${\varrho }_1$ is chosen as ${\varrho }_1\in (0.5,1)$.

With the estimation of ${\widehat{\beta }}_s$, the command course angle ${\psi }_{\mathrm{d}}$ is given as:

$${\psi }_{\mathrm{d}}={\gamma }_p+{tan}^{-1}\left(-\frac{{\mathrm{sign}}^{{\varrho }_2}\left(y_e\right)}{\Delta }\right)-{\widehat{\beta }}_s,$$

(16)

where ${\widehat{\beta }}_s$ is the sideslip angle to be estimated, $\Delta$ is the lookahead distance, ${\varrho }_2$ is chosen as ${\varrho }_2\in (\frac{1}{3},\frac{1}{2})$.

By substituting Equation (16) into the system kinematics, we can obtain

$${\dot{y}}_e=Usin\left({tan}^{-1}\left(-\frac{{\mathrm{sign}}^{{\varrho }_2}\left(y_e\right)}{\Delta }\right)+{\tilde{\beta }}_s\right).$$

(17)

By using the following transformation

$$\begin{array}{c}\hfill sin\left({tan}^{-1}\left(-\frac{{\mathrm{sign}}^{{\varrho }_2}\left(y_e\right)}{\Delta }\right)\right)=-\frac{{\mathrm{sign}}^{{\varrho }_2}\left(y_e\right)}{\sqrt{{\Delta }^2+{\left|y_e\right|}^{2{\varrho }_2}}},cos\left({tan}^{-1}\left(-\frac{{\mathrm{sign}}^{{\varrho }_2}\left(y_e\right)}{\Delta }\right)\right)=\frac{\Delta }{\sqrt{{\Delta }^2+{\left|y_e\right|}^{2{\varrho }_2}}},\end{array}$$

(18)

we have

$$\begin{array}{c}\hfill {\dot{y}}_e=-\frac{U}{\sqrt{{\Delta }^2+{\left|y_e\right|}^{2{\varrho }_2}}}{\mathrm{sign}}^{{\varrho }_2}\left(y_e\right)+\frac{U\Delta }{\sqrt{{\Delta }^2+{\left|y_e\right|}^{2{\varrho }_2}}}{\tilde{\beta }}_s.\end{array}$$

(19)

Theorem 1.

Considering the path-following kinematics of a nonlinear vessel in Equation (8), with the proposed FGO in Equation (15), the estimation error $\tilde{\delta }$ is globally uniformly asymptotic stable. By selecting suitable parameters, $\tilde{\delta }$ can converge to a sufficiently small region of 0 in finite-time.

Proof. 

For the proposed observer in Equation (15), by defining the following error variables:

$${ϵ}_1=y_e-z_1,{ϵ}_2=\delta -\widehat{\delta }+{\lambda }_1{\mathrm{sign}}^{{\varrho }_1}\left({ϵ}_1\right),$$

if follows:

$$\left\{\begin{array}{cc}\hfill {\dot{ϵ}}_1& ={ϵ}_2-{\lambda }_1{\mathrm{sign}}^{{\varrho }_1}\left({ϵ}_1\right)\hfill \\ \hfill {\dot{ϵ}}_2& =-{\lambda }_2{\mathrm{sign}}^{{\varrho }_1}\left({ϵ}_1\right)+\dot{\delta }.\hfill \end{array}\right.$$

(20)

For the proposed observer, Lyapunov function is selected as

$$V_1={\mathit{\theta }}^{\mathrm{T}}{P}_1\mathit{\theta },\mathit{\theta }={\left[\begin{array}{cc}{\mathrm{sign}}^{{\varrho }_1}\left({ϵ}_1\right)& {ϵ}_2\end{array}\right]}^{\mathrm{T}}.$$

(21)

Notice that $V_1$ satisfies

$${\lambda }_{min}\left(P_1\right){\parallel \mathit{\theta }\parallel }^2\le V_1\le {\lambda }_{max}\left(P_1\right){\parallel \mathit{\theta }\parallel }^2,$$

where operator ${\lambda }_{min}(·)$ and ${\lambda }_{max}(·)$ denote the minimum and maximum singular values of a matrix.

The dynamic equation of $\mathit{\theta }$ is give as

$$\dot{\mathit{\theta }}=A_0\mathit{\theta }+B_0\dot{\delta },$$

(22)

with

$$A_0=\left[\begin{array}{cc}-{\varrho }_1\mu {\lambda }_1& {\varrho }_1\mu \\ -{\lambda }_2& 0\end{array}\right],B_0=\left[\begin{array}{c}0\\ 1\end{array}\right],$$

where $\mu =|{ϵ}_1{|}^{({\varrho }_1-1)}>0$. For the proper defined ${\lambda }_1$ and ${\lambda }_2$, the matrix $A_0$ is a Hurwitz matrix. Thus, there exists a positive definite matrix $Q_0$ such that

$$A_0^{\mathrm{T}}{P}_0+P_0{A}_0=-Q_0.$$

(23)

Thus, the first-order time derivative of $V_1$ is

$${\dot{V}}_1\le -\left({\lambda }_{min}\left(Q_0\right)\parallel \mathit{\theta }\parallel -2\overline{\delta }\parallel B_0^{\mathrm{T}}{P}_0\parallel \right)\parallel \mathit{\theta }\parallel .$$

(24)

The matrix $A_0$ can also be expressed as

$$A_0=A_1{A}_2,A_1=-\left[\begin{array}{cc}{\varrho }_1\mu & 0\\ 0& 1\end{array}\right],A_2=\left[\begin{array}{cc}{\lambda }_1& -1\\ {\lambda }_2& 0\end{array}\right],$$

(25)

then it follows that

$${\lambda }_{min}(-A_0)={\lambda }_{min}\left(A_1{A}_2\right)\ge {\lambda }_{min}\left(A_1\right)·{\lambda }_{min}\left(A_2\right).$$

(26)

Since $A_1$ is a diagonal matrix and ${\varrho }_1\mu <\mu$, there exists

$${\lambda }_{min}\left(A_1\right)=\left\{\begin{array}{cc}& 1,|{ϵ}_1|<{\left(\frac{1}{{\varrho }_1}\right)}^{\frac{1}{{\varrho }_1-1}}\hfill \\ \hfill & {\varrho }_1\mu ,\left|{ϵ}_1\right|\ge {\left(\frac{1}{{\varrho }_1}\right)}^{\frac{1}{{\varrho }_1-1}}.\hfill \end{array}\right.$$

(27)

If $|{ϵ}_1|\ge {\left(\frac{1}{{\varrho }_1}\right)}^{\frac{1}{{\varrho }_1-1}}$ then $\parallel \mathit{\theta }\parallel \ge {\left(\frac{1}{{\varrho }_1}\right)}^{\frac{{\varrho }_1}{{\varrho }_1-1}}$, we have

$${\lambda }_{min}\left(Q_0\right)\ge 2{\varrho }_1\mu {\lambda }_{min}\left(A_2\right){\lambda }_{min}\left(P_0\right).$$

(28)

Substituting Equation (28) into Equation (24), it can be obtained

$$\begin{array}{cc}\hfill {\dot{V}}_1\le & -\left(2{\varrho }_1\mu {\lambda }_{min}\left(A_2\right){\lambda }_{min}\left(P_0\right)|{ϵ}_1{|}^{{\varrho }_1}-2\overline{\delta }\parallel B_0^{\mathrm{T}}{P}_0\parallel \right)\parallel \mathit{\theta }\parallel \hfill \\ \hfill \le & -\left(2{\varrho }_1|{ϵ}_1{|}^{\frac{2{\varrho }_1-1}{{\varrho }_1-1}}{\lambda }_{min}\left(A_2\right){\lambda }_{min}\left(P_0\right)-2\overline{\delta }\parallel B_0^{\mathrm{T}}{P}_0\parallel \right)\parallel \mathit{\theta }\parallel .\hfill \end{array}$$

(29)

With ${\varrho }_1\in (0.5,1)$, there exists a constant ${\nu }_1$ such that

$${\varrho }_1{\left(\frac{1}{{\varrho }_1}\right)}^{\frac{2{\varrho }_1-1}{{\varrho }_1-1}}\ge {\nu }_1.$$

(30)

Notice that ${\lambda }_1$ and ${\lambda }_2$ are adjusted to make sure ${\nu }_1{\lambda }_{min}\left(A_2\right){\lambda }_{min}\left(P_0\right)>\overline{\delta }\parallel B_0^{\mathrm{T}}{P}_0\parallel$, we can obtain that

$$\begin{array}{c}\hfill \dot{V}\le -{\Lambda }_1{V}_1^{\frac{1}{2}},{\Lambda }_1=\frac{{\rho }_1}{\sqrt{\left({\lambda }_{max}\left(P_0\right)\right)}},{\rho }_1=2{\nu }_1{\lambda }_{min}\left(A_2\right){\lambda }_{min}\left(P_0\right)-\overline{\delta }\parallel B_0^{\mathrm{T}}{P}_0\parallel .\end{array}$$

(31)

Thus, $\parallel \mathit{\theta }\parallel$ converges to the region $\parallel \mathit{\theta }\parallel \le {\left(\frac{1}{{\varrho }_1}\right)}^{\frac{{\varrho }_1}{{\varrho }_1-1}}$ in finite-time $t_1$, which is defined as

$$t_1\le \frac{2}{{\Lambda }_1}{V}_1^{\frac{1}{2}}\left(\mathit{\theta }\left(t\right)\right)\le \frac{2}{{\Lambda }_1}{V}_1^{\frac{1}{2}}\left(\mathit{\theta }\left(t_0\right)\right).$$

(32)

If $\parallel \mathit{\theta }\parallel <{\left(\frac{1}{{\varrho }_1}\right)}^{\frac{{\varrho }_1}{{\varrho }_1-1}}$ then $|{ϵ}_1|<{\left(\frac{1}{{\varrho }_1}\right)}^{\frac{1}{{\varrho }_1-1}}$, we have

$${\lambda }_{min}\left(Q_0\right)\ge 2{\lambda }_{min}\left(A_2\right){\lambda }_{min}\left(P_0\right).$$

(33)

Substituting Equation (33) into Equation (24), we have

$$\begin{array}{cc}\hfill {\dot{V}}_1\le & -\left(2{\lambda }_{min}\left(A_2\right){\lambda }_{min}\left(P_0\right)\parallel \mathit{\theta }\parallel -2\overline{\delta }\parallel B_0^{\mathrm{T}}{P}_0\parallel \right)\parallel \mathit{\theta }\parallel .\hfill \end{array}$$

(34)

If

$${\left(\frac{1}{{\varrho }_1}\right)}^{\frac{{\varrho }_1}{{\varrho }_1-1}}>\parallel \mathit{\theta }\parallel >\frac{\overline{\delta }\parallel B^{\mathrm{T}}{P}_0\parallel }{{\lambda }_{min}\left(A_2\right){\lambda }_{min}\left(P_0\right)}={\nu }_2$$

(35)

is satisfied, it follows that

$$\begin{array}{c}\hfill {\dot{V}}_1\le -{\Lambda }_2{V}_1^{\frac{1}{2}},{\Lambda }_2=\frac{{\rho }_2}{\sqrt{\left({\lambda }_{max}\left(P_0\right)\right)}},{\rho }_2>2{\lambda }_{min}\left(A_2\right){\lambda }_{min}\left(P_0\right){\nu }_2-2\overline{\delta }\parallel B_0^{\mathrm{T}}{P}_0\parallel =0.\end{array}$$

(36)

Then, we can obtain

$$t_2\le \frac{2}{{\Lambda }_2}{V}_1^{\frac{1}{2}}\left(\mathit{\theta }\left(t\right)\right)\le \frac{2}{{\Lambda }_2}{V}_1^{\frac{1}{2}}\left(\mathit{\theta }\left(t_1\right)\right).$$

(37)

Therefore, $\parallel \mathit{\theta }\parallel$ can converge to the region

$$\parallel \mathit{\theta }\parallel \le \frac{\overline{\delta }\parallel B_0^{\mathrm{T}}{P}_0\parallel }{{\lambda }_{min}\left(A_2\right){\lambda }_{min}\left(P_0\right)}$$

(38)

in finite-time $T_1=t_1+t_2$. According to Equation (31) and Equation (36), the estimation error is global uniform asymptotic stable.

Notice that if the suitable parameters are selected to make ${\lambda }_{min}\left(A_2\right){\lambda }_{min}\left(P_0\right)$ sufficiently large, the defined error variables $\mathit{\theta }$ can converge to a sufficiently small region of 0 in finite-time, which indicates that the estimation error of $\delta$ will converge to a sufficiently small region of 0 in finite-time.  □

Theorem 2.

Considering the kinematics of a nonlinear vessel in Equation (8). By using the proposed FGO in Equation (15) to estimate the unknown sideslip angle, and compensate in the nonlinear guidance strategy in Equation (16), the cross-track error of the vessel is globally uniformly ultimately bounded (UUB). By selecting the suitable parameters, $y_e$ can converge to a sufficiently small region of zero in finite-time for all $0<|y_e|\le \overline{y}$.

Proof. 

Define the Lyaponov function as

$$V_2=\frac{1}{2-2{\varrho }_2}{\left|y_e\right|}^{2-2{\varrho }_2},$$

(39)

by taking Equation (8) into account, the time derivative of $V_2$ is given as

$$\begin{array}{c}\hfill {\dot{V}}_2=-\frac{U}{\sqrt{{\Delta }^2+{\left|y_e\right|}^{2{\varrho }_2}}}|y_e{|}^{(1-{\varrho }_2)}+\frac{U\Delta }{\sqrt{{\Delta }^2+{\left|y_e\right|}^{2{\varrho }_2}}}·\frac{1}{U·cos(\varphi -{\gamma }_p)}|y_e{|}^{(1-2{\varrho }_2)}\left|\tilde{\delta }\right|,\end{array}$$

(40)

where $\tilde{\delta }=\delta -\widehat{\delta }$.

According to the definition of $\mathit{\theta }$, the estimation error $\tilde{\delta }$ can be expressed as

$$\tilde{\delta }=\left[\begin{array}{cc}-{\lambda }_1& 1\end{array}\right]·\mathit{\theta },$$

(41)

which means $|\tilde{\delta }|\le \sqrt{{\lambda }_1^2+1}\parallel \mathit{\theta }\parallel$.

According to the Young’s inequality, the second term of Equation (40) can be rewritten as

$$\begin{array}{cc}\hfill \frac{U\Delta }{\sqrt{{\Delta }^2+{|y_e|}^{2{\varrho }_2}}}·\frac{1}{U·cos(\psi -{\gamma }_p)}& |y_e{|}^{(1-2{\varrho }_2)}|\tilde{\delta }|\le \frac{U}{\sqrt{{\Delta }^2+{|y_e|}^{2{\varrho }_2}}}·\frac{(1-2{\varrho }_2){\epsilon }_1^{\frac{(1-{\varrho }_2)}{(1-2{\varrho }_2)}}}{1-{\varrho }_2}·{|y_e|}^{(1-{\varrho }_2)}\hfill \\ & +\underset{{\alpha }_0\left(y_e\right)}{\underbrace{\frac{\sqrt{{\lambda }_1^2+1}{\varrho }_{2}U}{(1-{\varrho }_2)\sqrt{{\Delta }^2+{|y_e|}^{2{\varrho }_2}}}{\left(\frac{\Delta }{{\epsilon }_1·U·cos(\psi -{\gamma }_p))}\right)}^{\frac{1-{\varrho }_2}{{\varrho }_2}}}}·{\parallel \mathit{\theta }\parallel }^{\frac{1-{\varrho }_2}{{\varrho }_2}}.\hfill \end{array}$$

(42)

The variable ${\epsilon }_1$ is chosen such that

$$\frac{(1-2{\varrho }_2)·{\epsilon }_1^{\frac{(1-{\varrho }_2)}{(1-2{\varrho }_2)}}}{1-{\varrho }_2}+{\alpha }_1<1,$$

where ${\alpha }_1$ is a positive constant.

By defining a new system state vector as

$$\mathsf{\Theta }=\left[\begin{array}{c}|y_e{|}^{1-{\varrho }_2}\\ \mathit{\theta }\end{array}\right],$$

and a new Lyapunov function can be defined as

$$V_3={\mathsf{\Theta }}^{\mathrm{T}}{P}_1\mathsf{\Theta },P_1=\left[\begin{array}{ccc}2-2{\varrho }_2& & 0_{1\times 2}\\ 0_{2\times 1}& & P_0\end{array}\right],$$

(43)

where 0 is the zero matrix.

If $t<T_1$, by taking Equation (24) into account, we have the time derivative of $V_3$ is given as

$$\begin{array}{cc}\hfill {\dot{V}}_3\le & -\frac{U}{\sqrt{{\Delta }^2+{|y_e|}^{2{\varrho }_2}}}|y_e{|}^{(1-{\varrho }_2)}+\frac{U\Delta }{\sqrt{{\Delta }^2+{|y_e|}^{2{\varrho }_2}}}·\frac{1}{U·cos(\psi -{\gamma }_p)}|y_e{|}^{(1-2{\varrho }_2)}|\tilde{\delta }|\hfill \\ & -{\lambda }_{min}\left(Q_0\right){\parallel \mathit{\theta }\parallel }^2+2\overline{\delta }\parallel B_0^{\mathrm{T}}{P}_0\parallel \parallel \mathit{\theta }\parallel \hfill \\ \hfill \le & -\frac{{\alpha }_{1}U}{\sqrt{{\Delta }^2+{|y_e|}^{2{\varrho }_2}}}|y_e{|}^{(1-{\varrho }_2)}+{\alpha }_0{\left(0\right)\parallel \mathit{\theta }\parallel }^{\frac{1-{\varrho }_2}{{\varrho }_2}}-{\lambda }_{min}\left(Q_0\right){\parallel \mathit{\theta }\parallel }^2+2\overline{\delta }\parallel B_0^{\mathrm{T}}{P}_0\parallel \parallel \mathit{\theta }\parallel \hfill \\ \hfill \le & -\frac{{\alpha }_{1}U}{\sqrt{{\Delta }^2+{|y_e|}^{2{\varrho }_2}}}|y_e{|}^{(1-{\varrho }_2)}-{\alpha }_2{\parallel \mathit{\theta }\parallel }^2+{\alpha }_3,\hfill \end{array}$$

(44)

where ${\epsilon }_2$ and ${\epsilon }_3$ are chosen such that

$$\frac{1-{\varrho }_2}{2{\varrho }_2}{\epsilon }_2^{\frac{2{\varrho }_2}{1-{\varrho }_2}}+{\epsilon }_3+{\alpha }_2>{\lambda }_{min}\left(Q_0\right),$$

and

$${\alpha }_3=\frac{2{\varrho }_2}{3{\varrho }_2-1}{\left(\frac{{\alpha }_0\left(0\right)}{{\epsilon }_2}\right)}^{\frac{2{\varrho }_2}{3{\varrho }_2-1}}+\frac{(\overline{\delta }\parallel B_0^{\mathrm{T}}{P}_0{\parallel )}^2}{{\epsilon }_3}.$$

If $t<T_1$, the closed-loop system is globally UUB.

If $t\ge T_1$, notice from Equation (38) that the estimation error of observer is already bounded as $\parallel \mathit{\theta }\parallel \le {\nu }_2$, thus we have

$$\begin{array}{cc}\hfill {\dot{V}}_2\le & -\frac{{\alpha }_{1}U}{\sqrt{{\Delta }^2+{|y_e|}^{2{\varrho }_2}}}{|y_e|}^{(1-{\varrho }_2)}+{\alpha }_0\left(\overline{y}\right){\nu }_2^{\frac{2{\varrho }_2-1}{{\varrho }_2}}\hfill \\ \hfill \le & -{\Lambda }_3{V}_2^{\frac{1}{2}}+{\alpha }_0\left(\overline{y}\right){\nu }_2^{\frac{2{\varrho }_2-1}{{\varrho }_2}},{\Lambda }_3=\frac{{\alpha }_{1}U}{\sqrt{(2-2{\varrho }_2)({\Delta }^2+|\overline{y}{|}^{2{\varrho }_2})}}.\hfill \end{array}$$

(45)

Therefore, the cross-track error is globally uniformly bounded after the convergence of the sideslip angle observer, with final upper bound as $({\alpha }_0\left(\overline{y}\right)/{\alpha }_1){\nu }_2^{\frac{2{\varrho }_2-1}{{\varrho }_2(1-{\varrho }_2)}}$. And the cross-track error can converge to the ultimate bound in finite-time $T_2$ as

$$T_2=\frac{2}{{\Lambda }_3}{V}_2^{\frac{1}{2}}\left(y_e\left(T_1\right)\right)+T_1.$$

(46)

Notice that if the suitable parameters are selected such that estimation error can converge to a sufficiently small region of zero, the cross-track error can also converge in finite-time.  □

3.2. Output Feedback Controller Based on ADRC

In this section, the ESO is first introduced to estimate the angular velocity along with the total disturbance for controller design. By introducing the notation: $x_1=\psi ,x_2=r,x_3=f\left(t\right)$, we have:

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_1& =x_2,\hfill \\ \hfill {\dot{x}}_2& =F\left(x_2\right)+Hu+x_3,\hfill \\ \hfill {\dot{x}}_3& =h\left(t\right).\hfill \end{array}\right.$$

(47)

where $F\left(x_2\right)=-a_1{x}_2-a_2|x_2|x_2-a_3{x}_2^3$, $H=b_1$, $u={\delta }_r$.

It is assumed that the first-order time derivative of equivalent disturbance is bounded

$$\parallel h\left(t\right)\parallel \le \overline{h}.$$

(48)

With the definition of $\mathit{X}={\left[\begin{array}{ccc}{x}_1& x_2& x_3\end{array}\right]}^{\mathrm{T}}$, Equation (47) can be rewritten into the following form

$$\dot{\mathit{X}}=A\mathit{X}+\Psi \left(\mathit{X}\right)+U+D,$$

(49)

where

$$\begin{array}{cc}\hfill A& =\left[\begin{array}{ccccc}0& & 1& & 0\\ 0& & 0& & 1\\ 0& & 0& & 0\end{array}\right],\Psi \left(\mathit{X}\right)=\left[\begin{array}{c}0\\ -F\left(x_2\right)\\ 0\end{array}\right],\hfill \\ \hfill U& =\left[\begin{array}{c}0\\ Hu\\ 0\end{array}\right],D=\left[\begin{array}{c}0\\ 0\\ h\left(t\right)\end{array}\right].\hfill \end{array}$$

The specific ESO is designed as

$$\dot{\widehat{\mathit{X}}}=A_0\widehat{\mathit{X}}+\Psi \left(\widehat{\mathit{X}}\right)+U+L(x_1-{\widehat{x}}_1),$$

(50)

where the observer gain matrix L is defined as

$$L={\left[\begin{array}{ccc}3{\omega }_0& 3{\omega }_0^2& {\omega }_0^3\end{array}\right]}^{\mathrm{T}},$$

where ${\omega }_0$ is the cut-off frequency to be selected.

Define the estimation error vector of system state as $\tilde{\mathit{X}}={\left[\begin{array}{ccc}(x_1-{\widehat{x}}_1)& (x_2-{\widehat{x}}_2)/{\omega }_0& (x_3-{\widehat{x}}_3)/{\omega }_0^2\end{array}\right]}^{\mathrm{T}}$, the estimation error dynamics can be obtained as

$$\dot{\tilde{\mathit{X}}}={\omega }_0\overline{A}\tilde{\mathit{X}}+\frac{\Psi \left(\mathit{X}\right)-\Psi \left(\widehat{\mathit{X}}\right)}{{\omega }_0}+\frac{D}{{\omega }_0^2},$$

(51)

where

$$\overline{A}=\left[\begin{array}{ccccc}3·I_2& & I_2& & 0_{2\times 2}\\ 3·I_2& & 0_{2\times 2}& & I_2\\ I_2& & 0_{2\times 2}& & 0_{2\times 2}\end{array}\right].$$

Assumption A1.

With the measurable system states ${\mathit{x}}_1$, the nonlinear function $\Psi (·)$ is continuously differentiable and satisfies local Lipschitz condition with Lipschitz constant σ such that

$$\parallel \Psi \left(\mathit{X}\right)-\Psi \left(\widehat{\mathit{X}}\right)\parallel \le \sigma \parallel x_2-{\widehat{x}}_2\parallel \le \sigma \parallel \tilde{\mathit{X}}\parallel .$$

(52)

With the estimation of angular velocity and equivalent disturbances, the backstepping technique is adopted for the controller design. By introducing the following auxiliary variables

$$\left\{\begin{array}{cc}\hfill e_1& =x_1-{\psi }_{\mathrm{d}}\hfill \\ \hfill e_2& =x_2-{\dot{\psi }}_{\mathrm{d}}+k_1{e}_1.\hfill \end{array}\right.$$

(53)

the backstepping controller is designed as

$$\begin{array}{cc}\hfill u& =H^{-1}\left({\ddot{\psi }}_{\mathrm{d}}-(1-k_1^2)e_1-(k_1+k_2){\widehat{e}}_2-F\left({\widehat{x}}_2\right)-{\widehat{x}}_3\right),\hfill \end{array}$$

(54)

where ${\widehat{e}}_2={\widehat{x}}_2-{\dot{\psi }}_{\mathrm{d}}+k_1{e}_1$.

Theorem 3.

Considering the yaw dynamics in Equation (12), with the proposed ESO in Equation (50) and output feedback backstepping controller in Equation (54), the error of yaw angle $\tilde{\psi }$ is semi-globally UUB.

Proof. 

We first analyze the convergence of the ESO. By defining the Lyaponov function

$$V_4={\tilde{\mathit{X}}}^{\mathrm{T}}{P}_2\tilde{\mathit{X}}$$

where the matrix $P_2$ satisfies ${\overline{A}}^{\mathrm{T}}{P}_2+P_2\overline{A}=-I$, thus, the time derivative of $V_4$ can be obtained as

$${\dot{V}}_4\le -{\omega }_0{\parallel \tilde{\mathit{X}}\parallel }^2+{\lambda }_{max}\left(P_2\right)\frac{\Psi \left(\mathit{X}\right)-\Psi \left(\widehat{\mathit{X}}\right)}{{\omega }_0}+{\lambda }_{max}\left(P_2\right)\frac{D}{{\omega }_0^2}$$

(55)

Considering the assumptions in Equations (48) and (52), we can obtain

$${\dot{V}}_4\le -\left({\omega }_0-\frac{{\lambda }_{min}\left(P_2\right)\sigma }{{\omega }_0}\right)\parallel \tilde{\mathit{X}}{\parallel }^2+\frac{{\lambda }_{max}\left(P_2\right)\overline{h}}{{\omega }_0^2}\parallel \tilde{\mathit{X}}\parallel .$$

(56)

For the heading dynamics, a new Lyapunov function is defined as

$$V_5=\frac{1}{2}\left(e_1^2+e_2^2\right)+V_4.$$

The time derivative of $V_5$ is given as

$$\begin{array}{cc}\hfill {\dot{V}}_5\le & -k_1|e_1{|}^2-k_2|e_2{|}^2+(\sigma +k_1+k_2+1)|e_2|\parallel \tilde{\mathit{X}}\parallel -\left({\omega }_0-\frac{{\lambda }_{min}\left(P_2\right)\sigma }{{\omega }_0}\right)\parallel \tilde{\mathit{X}}{\parallel }^2+\frac{{\lambda }_{max}\left(P_2\right)\overline{h}}{{\omega }_0^2}\parallel \tilde{\mathit{X}}\parallel \hfill \\ \hfill \le & -k_1|e_1{|}^2-\frac{k_2}{2}|e_2{|}^2+\underset{{\alpha }_4}{\underbrace{\frac{1}{2{\omega }_0}{\left(\frac{{\lambda }_{max}\left(P_2\right)\overline{h}}{{\omega }_0^2}\right)}^2}}-\underset{k_3}{\underbrace{\left(\frac{{\omega }_0}{2}-\frac{{\lambda }_{min}\left(P_2\right)\sigma }{{\omega }_0}-\frac{{(\sigma +k_1+k_2+1)}^2}{2k_2}\right)}}{\parallel \tilde{\mathit{X}}\parallel }^2.\hfill \end{array}$$

(57)

We can conclude that the heading dynamics of the marine vessel is semi-globally UUB.  □

4. Stability Analysis

In above sections, stability conclusions are obtained based on the kinematics and heading dynamics, respectively. To analyze the closed-loop stability, the error of heading control system is considered by rewriting Equation (10) as follows

$${\dot{y}}_e=Usin({\psi }_d-{\gamma }_p+{\beta }_s)+2Usin\left(\frac{\tilde{\psi }}{2}\right)cos\left({\gamma }_p-{\beta }_s-\frac{\psi +{\psi }_{\mathrm{d}}}{2}\right).$$

(58)

where $\tilde{\psi }=\psi -{\psi }_{\mathrm{d}}=e_1$. According to Equation (58), we can see how the heading error dynamics acts on the horizontal kinematics to prevent it becoming equal to the desired state.

Theorem 4.

Considering the system model of the marine surface vessel described in Equations (8) and (13), with the proposed FGO and nonlinear guidance law in Equations (15) and (16), and the ESO-based output feedback backstepping controller in Equations (50) and (54), the system states of the close-loop system are semi-globally UUB.

Proof. 

Define the final Lyapunov function as

$$V=V_3+V_5.$$

(59)

By differentiating V with respect to time, and taking the dynamics of ${\dot{y}}_e$ with attitude tracking error into account, one yields

$$\begin{array}{cc}\hfill \dot{V}\le & -\frac{{\alpha }_{1}U}{\sqrt{{\Delta }^2+{|y_e|}^{2{\varrho }_2}}}|y_e{|}^{(1-{\varrho }_2)}-{\alpha }_2{\parallel \mathit{\theta }\parallel }^2+{\alpha }_3+{|y_e|}^{1-2{\varrho }_2}·2Usin\left(\frac{e_1}{2}\right)cos\left({\gamma }_p-{\beta }_s-\frac{\psi +{\psi }_{\mathrm{d}}}{2}\right)\hfill \\ & -k_1|e_1{|}^2-\frac{k_2}{2}|e_2{|}^2-k_3{\parallel \tilde{\mathit{X}}\parallel }^2+{\alpha }_4.\hfill \end{array}$$

(60)

Notice that

$$\begin{array}{c}\hfill \left|sin\left(\frac{e_1}{2}\right)\right|\le \left|\frac{e_1}{2}\right|,cos\left({\gamma }_p-{\beta }_s-\frac{\psi +{\psi }_{\mathrm{d}}}{2}\right)\le 1.\end{array}$$

Then we have

$$\begin{array}{cc}\hfill \dot{V}\le & -\frac{{\alpha }_{1}U}{\sqrt{{\Delta }^2+{|y_e|}^{2{\varrho }_2}}}|y_e{|}^{(1-{\varrho }_2)}-{\alpha }_2{\parallel \mathit{\theta }\parallel }^2+{\alpha }_3+U|y_e{|}^{1-2{\varrho }_2}|e_1|-k_1|e_1{|}^2-\frac{k_2}{2}|e_2{|}^2-k_3{\parallel \tilde{\mathit{X}}\parallel }^2+{\alpha }_4\hfill \\ \hfill \le & -\left(\frac{{\alpha }_{1}U}{\sqrt{{\Delta }^2+{|\overline{y}|}^{2{\varrho }_2}}}-\frac{1-2{\varrho }_2}{1-{\varrho }_2}{\epsilon }_4^{\frac{1-{\varrho }_2}{1-2{\varrho }_2}}\right)|y_e{|}^{(1-{\varrho }_2)}-{\alpha }_2{\parallel \mathit{\theta }\parallel }^2-\left(k_1-\frac{1-{\varrho }_2}{2{\varrho }_2}{\epsilon }_5^{\frac{2{\varrho }_2}{1-{\varrho }_2}}\right)|e_1{|}^2-\frac{k_2}{2}{|e_2|}^2\hfill \\ & -k_3{\parallel \tilde{\mathit{X}}\parallel }^2+\alpha .\hfill \end{array}$$

(61)

where

$$\alpha ={\alpha }_3+{\alpha }_4+\frac{2{\varrho }_2}{3{\varrho }_2-1}{\left(\frac{{\varrho }_2}{{\epsilon }_5(1-{\varrho }_2)}{\left(\frac{U}{{\epsilon }_4}\right)}^{\frac{1-{\varrho }_2}{{\varrho }_2}}\right)}^{\frac{2{\varrho }_2}{3{\varrho }_2-1}}.$$

By selecting the suitable parameters, the closed-loop system is semi-globally UUB.  □

5. Numerical Simulations

In this section, simulations are carried out on a supply vessel [38] to validate the effectiveness of the proposed methodology. The parameters are as follows: $a_1=8.524\times {10}^{-2},a_2=2.173\times {10}^{-2},a_3=1.126\times {10}^{-2},b_1=3.369\times {10}^{-10}$.

The parameters of the proposed methodology are chosen as ${\lambda }_1=10.0$, ${\lambda }_2=40.0$, ${\varrho }_1=0.8$, ${\varrho }_2=0.45$, ${\omega }_0$ = 30.0 rad/s, $k_1=2.5$, $k_2=5.0$. The length of the ship is 76.2 m and the lookahead distance is selected as 5 times of its length. The surge speed in the simulation is chosen as $u=9\mathrm{m}/\mathrm{s}$. The initial position and yaw angle are selected as (500 m, 320 m, 1.3 rad), and the initial cross-track error is about 230 m. To obtain the wave disturbance in the simulation, the Pierson–Moskowitz spectrum is chosen to acquire the standard wave energy spectrum [38], and the significant wave height is chosen as $H_{1/3}$ = 3.8 m.

The performance of the proposed approach is compared with adaptive LOS guidance and integral LOS guidance in Figure 3, while the cross-track error is illustrated in Figure 4. It can be seen that all these three methods can enable the vessel to follow the reference path with large initial error. However, settling time of the proposed method is less than the adaptive LOS and integral LOS algorithm. The specified performance in transient-state is shown in Table 1. Meanwhile, compared to the proposed methodology, the integral LOS algorithm bring the system with obvious overshot. And also, the output oscillation of the proposed method is less than the other two methods. Thus, the transient-state performance of the proposed methodology is better than that of the other two methods. According to the enlarged view in Figure 3, the path follow error of the proposed method is less than that of the other two methods. The accuracy indexes are shown in Table 2.

Figure 3. Path control performance comparisons of proposed method, ALOS and ILOS-based method.

Figure 4. Cross-track error comparisons of proposed method, ALOS and ILOS-based method.

Table 1. Comparisons of path-following performance in transient state.

	Settling Time	Overshot
Proposed method	113 s	0.0089%
Adaptive LOS	162 s	1.3521%
Integral LOS	259 s	31.6269%

Table 2. Comparisons of path-following performance in steady-state.

	Maximum Error	RMSE
Proposed method	0.1564 m	0.0275 m
Adaptive LOS	3.1063 m	1.5261 m
Integral LOS	4.5996 m	1.7025 m

The sideslip angle estimation effect of the proposed FGO is shown in Figure 5. With the drift force and wave disturbance, the sideslip angle varies from −5°∼5°, with period of about 16 s. It can be seen that with the proposed FGO, the time-varying sideslip angle can be estimated accurately without time-delay.

Figure 5. The sideslip angle estimation of the FGO.

Figure 6, Figure 7 and Figure 8 show the performance of the proposed ADRC control system. Figure 6 shows that the control torque can enable the heading dynamics track the command angle of $\psi$ from the guidance law quickly and accurately. The state r estimation effect of ESO is expressed in Figure 7, while the disturbance estimation effect of ESO is shown in Figure 8. The proposed ESO can estimate the disturbance as well as unknown system state accurately.

Figure 6. Control performance of $\psi$.

Figure 7. r estimation effect of the proposed ESO.

Figure 8. Disturbance estimation effect of the proposed ESO.

The control system performance with different design parameters is also analyzed in the simulations. The FGO and ESO play a very important role in the control system, we first analyze the performance of proposed LOS guidance algorithm with different gains of FGO. Three sets of gains for FGO are selected as follows: (1) low gains ${\lambda }_1=2$, ${\lambda }_2=4$, (2) medium gains ${\lambda }_1=10$, ${\lambda }_2=40$, (3) high gains ${\lambda }_1=20$, ${\lambda }_2=160$. The control performance of these three set of parameters are compared in Figure 9. From Figure 9, we can see that the cross-track error with low FGO gains is higher than that with medium FGO gains, which indicates that higher gains will increase the control accuracy under steady-state. However, it is also shown that the high gains will bring the system will vibration with sudden changes of environment, such as external disturbances or path curvature. For the autopilot of the vessel dynamics, the disturbance and state estimation effect will largely determine the tracking performance of the command course angle. Three sets of bandwidth parameters for ESO are chosen as follows: (1) low bandwidth ${\omega }_0=15.0$ rad/s, (2) medium bandwidth ${\omega }_0$ = 30.0 rad/s, (3) high bandwidth ${\omega }_0$ = 40.0 rad/s. The disturbance estimation error is compared in Figure 10. It can be seen that the estimation accuracy is mainly determined by the bandwidth of the ESO. Higher bandwidth will decrease the disturbance estimation error. However, the bandwidth is a trade-off between the robustness and performance of the closed-loop system, which is limited by the system uncertainties and measurement noise. In this simulation case, if the bandwidth ${\omega }_0$ is higher than 40.0 rad/s, the closed-loop system will be instable. According to the analysis above, empirical parameters should be selected to balance the control performance between the steady and transient state under the robustness condition.

Figure 9. Cross-track error comparisons with different FGO gains.

Figure 10. Disturbance estimation comparisons with different ESO bandwidth.

6. Conclusions

This paper proposes a robust output feedback methodology for path-following task of marine surface vessels. We first establish the kinematics and dynamics of path-following problem with unknown sideslip angle, unmeasured system state and system uncertainties, the hierarchical control technique is adopted for control system implementation. A finite-time observer is proposed for sideslip angle estimation, based on which a finite-time nonlinear LOS guidance algorithm is proposed for the horizontal kinematics design. It is demonstrated that with the proposed guidance law, the cross-track error can converge in finite-time. For the output feedback control of the yaw dynamics, an ESO is introduced to estimate both unknown system state and total disturbance, and thus compensated in a backstepping controller. Global stability analysis is carried out based on Lyapunov theory. Numerical simulations validate that the proposed LOS guidance law acquires a faster convergence rate. The proposed ESO can estimate the total disturbance as well as unknown system state, which enables the autopilot to track the desired command course angle quickly and accurately.

The approach proposed in this paper can be used to deal with the path-following of the marine surface vessels. However, this work does not contain the path planning algorithm of the vessels. In future works, the multi-objectives path planner will be investigated along with the motion controller. And also, this paper only considers the vessel model in horizontal DOF, the 6 DOF model will be considered in future design. Moreover, the experimental setup will be implemented to validate the effectiveness of the corresponding methodologies.