FiniteAmplitude Power Budget Equations for Acoustic Fish Abundance Estimation
Abstract
1. Introduction
1.1. Conventional Acoustic Fish Abundance Estimation
1.2. Finite-Amplitude Effects in Fisheries Acoustics
1.3. Objectives and Outline
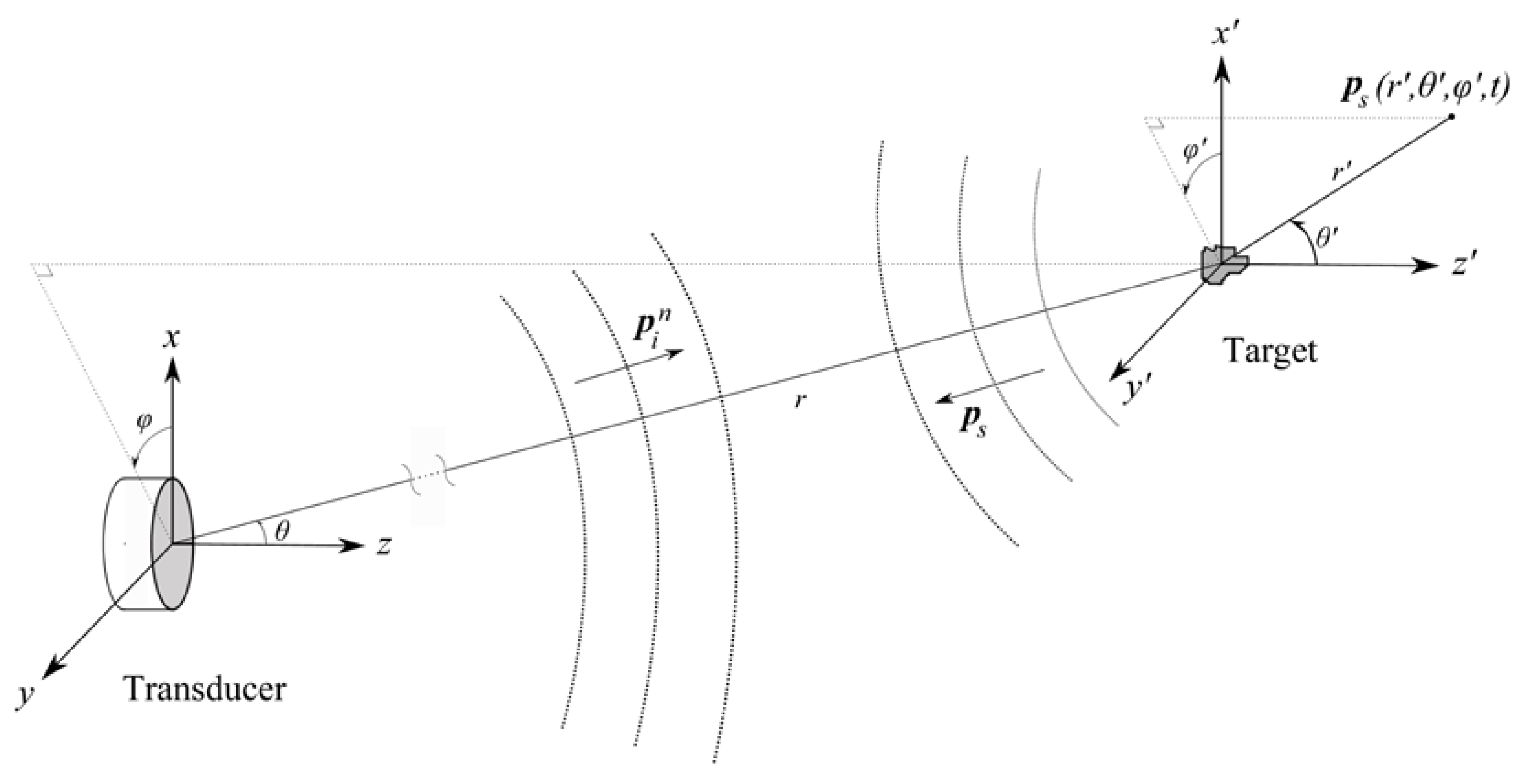
2. Single-Target Backscattering of Finite-Amplitude Incident Sound
2.1. Acoustic Backscattering from a Single Target in the Farfield
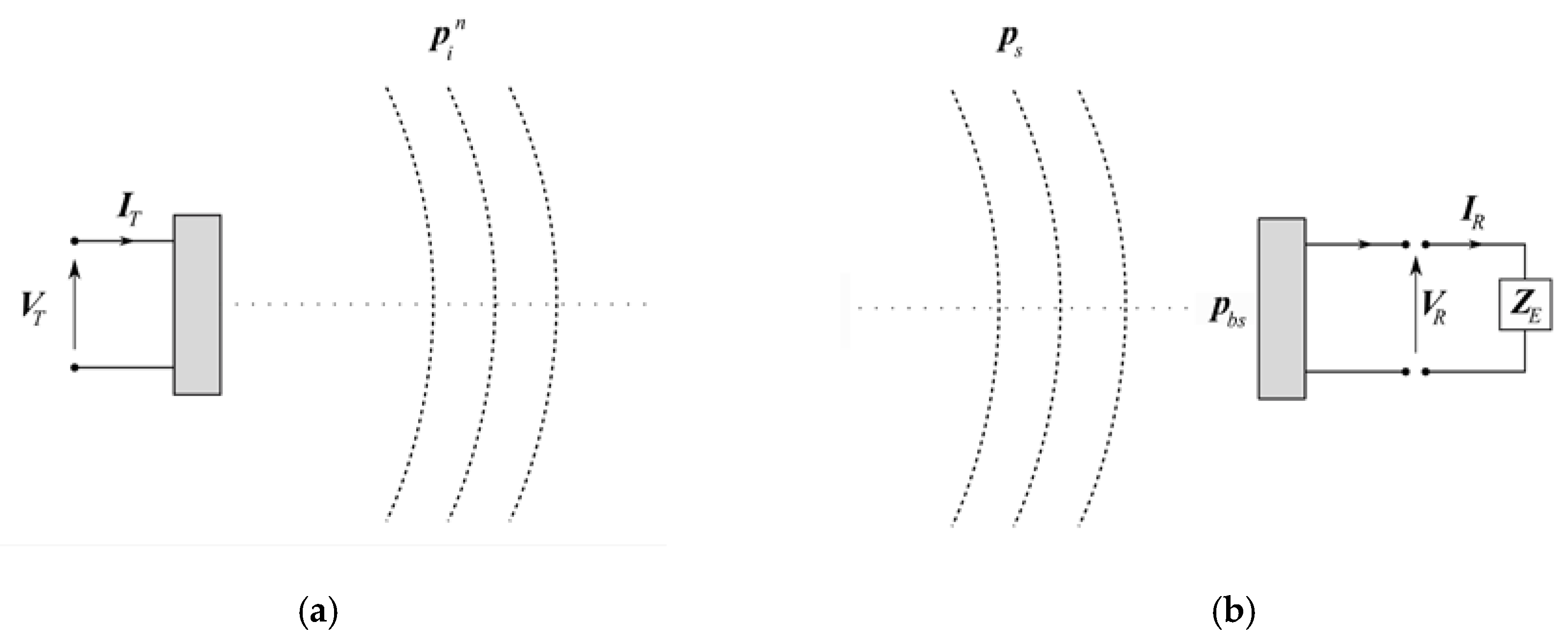
2.2. Electroacoustic Transmit—Receive Transfer Functions for Single-Target Backscattering
2.3. Electroacoustic Power Budget Equation for Single-Target Backscattering
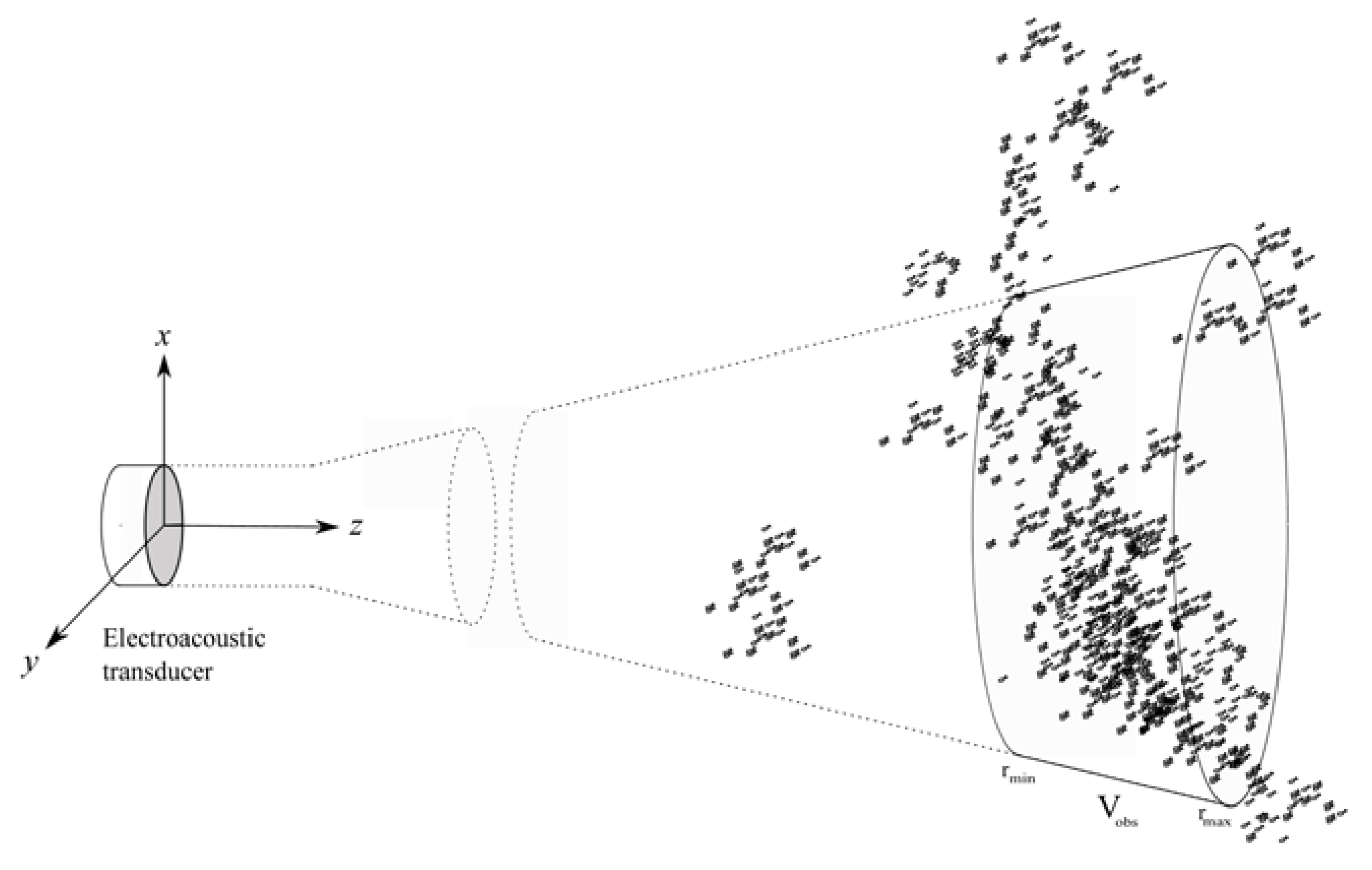
3. Volume Backscattering of Finite-Amplitude Incident Sound
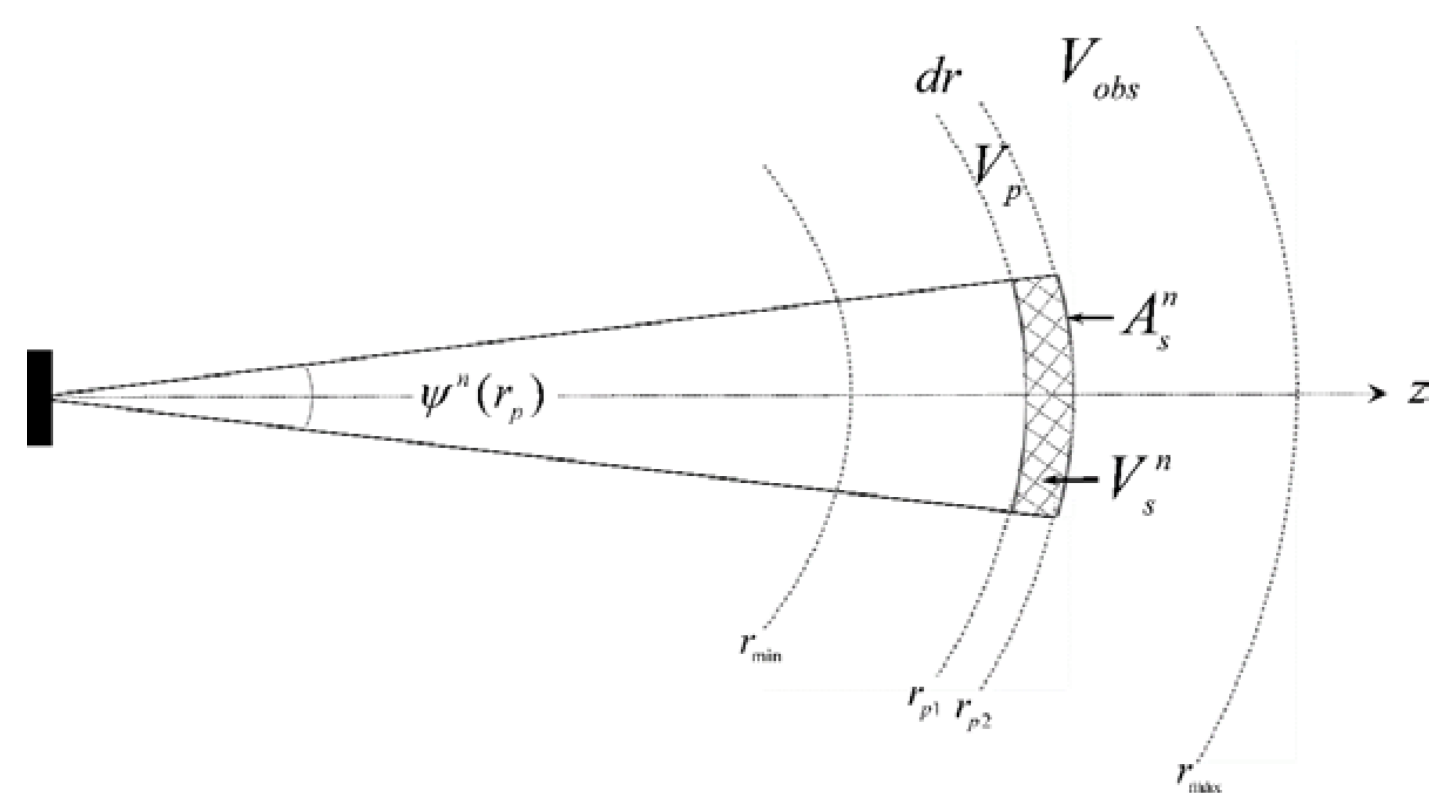
3.1. Electroacoustic Power Budget Equation for Volume Backscattering
3.2. Volume Backscattering Coefficient
4. Discussion
4.1. Consistency with Prior Literature
4.1.1. Small-Amplitude Signals (Linear Sound Propagation)
4.1.2. Finite-Amplitude Signals (Nonlinear Sound Propagation)
4.2. Summary of Assumptions Underlying the Analysis
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Interpretation in Terms of Power “Flow”
Appendix A.1. Single-Target Backscattering
Appendix A.2. Volume Backscattering
Appendix B. Transducer Gain,
Appendix C. Effective Receiving Area
Appendix D. Symbols and Nomenclature
| Symbol | Nomenclature | Unit |
|---|---|---|
| Ambient density of the fluid medium | kg/m3 | |
| Small-amplitude sound velocity of the fluid medium | m/s | |
| Sound pressure acoustic attenuation coefficient of the fluid medium | Np/m | |
| Sound pressure acoustic attenuation coefficient of the fluid medium | dB/m | |
| Frequency of the monochromatic wave = fundamental frequency of the finite-amplitude wavefield | Hz | |
| Angular frequency of the monochromatic wave | rad/s | |
| Acoustic wavenumber in the fluid medium | rad/m | |
| Acoustic wavelength in the fluid medium | m | |
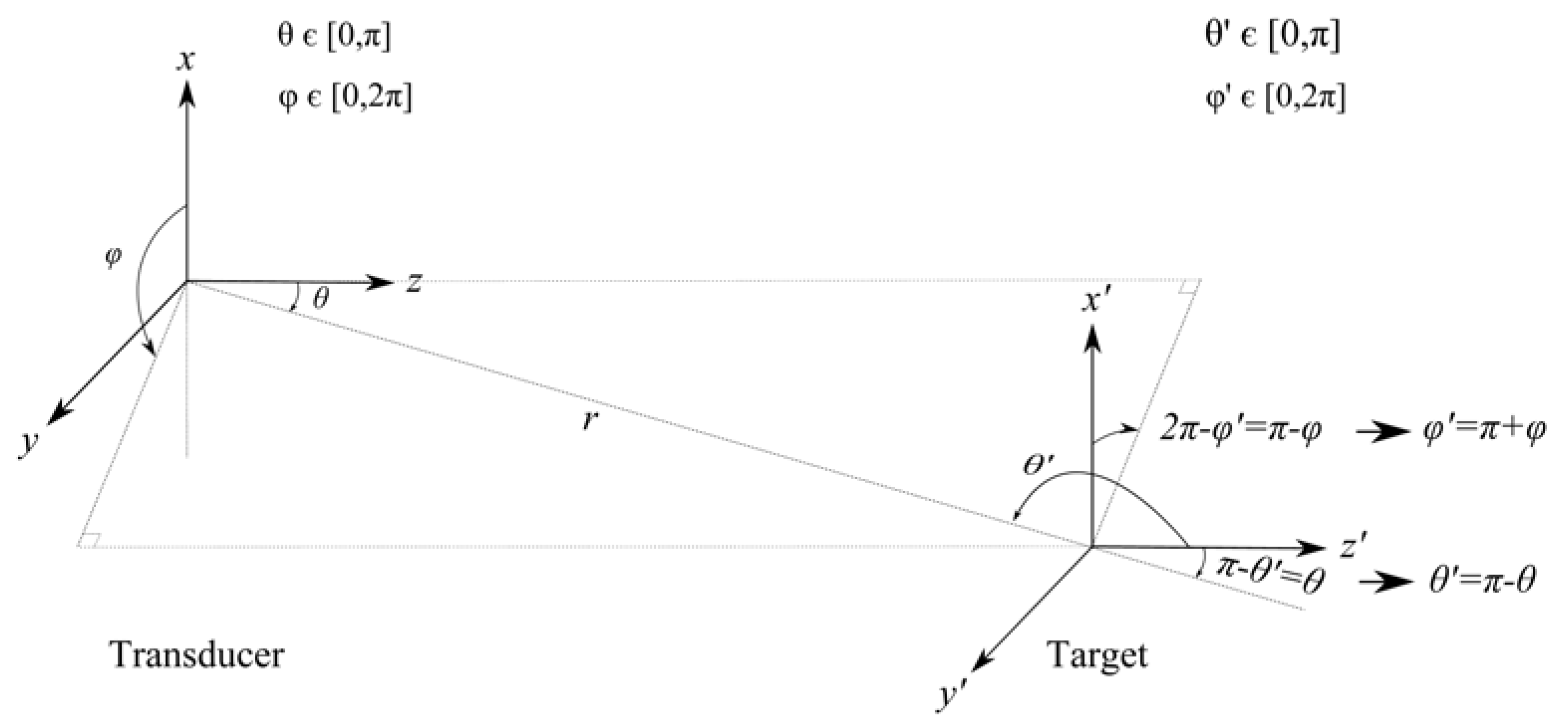
| Position vector expressed in the spherical coordinate system of the echo sounder | ||
| Position vector expressed in the spherical coordinate system of the target | ||
| Range from the center of the transducer front surface | m | |
| Axial reference range from the center of the transducer front surface (e.g., 1 m) | m | |
| Reference range from a single scattering target (e.g., 1 m) | m | |
| Incident pressure wave radiated by the transducer, for small-amplitude sound propagation in the fluid | Pa | |
| Incident pressure wave radiated by the transducer, for finite-amplitude sound propagation in the fluid, for the fundamental frequency of the wavefield | Pa | |
| Pressure wave scattered by a single target | Pa | |
| Amplitude of | Pa | |
| Amplitude of | Pa | |
| Amplitude of | Pa | |
| Amplitude of at axial reference range , extrapolated from the transducer’s far-field | Pa | |
| Free-field sound pressure in the fluid, backscattered from a single target, in the position of the center of the transducer front | Pa | |
| Sound pressure amplitude backscattered from a single target, at reference range from the target, extrapolated from the target’s far-field | Pa | |
| Amplitude constant for the incident scattered field | Pa-m | |
| Amplitude function for the scattered field | Pa-m | |
| Free-field intensity of the incident wave at the center position of a single target, for finite-amplitude sound propagation in the fluid, for the fundamental frequency of the wavefield | W/m2 | |
| Intensity of the wave scattered from a single target, in the far-field of the target | W/m2 | |
| Intensity of the wave scattered from a single target, at reference range from the target, extrapolated from the target’s far-field | W/m2 | |
| Intensity of the wave backscattered from a single target, at reference range from the target, extrapolated from the target’s far-field | W/m2 | |
| Axial finite-amplitude factor | − | |
| Far-field beam pattern of the incident sound pressure wave = far-field beam pattern of the transducer in transmit and receive operations, for small-amplitude sound propagation in the fluid | − | |
| Far-field beam pattern of the incident sound pressure wave = far-field beam pattern of the transducer in transmit operation, for finite-amplitude sound propagation in the fluid, for the fundamental frequency of the wavefield | − | |
| Beam pattern of the sound pressure wave scattered from a single target, in the far-field of the target | − | |
| Beam pattern finite-amplitude factor | − | |
| Axial directivity factor | − | |
| Directivity factor | − | |
| Axial transducer gain | − | |
| Transducer gain | − | |
| Equivalent two-way beam solid angle of the transducer, for small-amplitude sound propagation in the fluid | sr | |
| Equivalent two-way beam solid angle of the transducer, for finite-amplitude sound propagation in the fluid | sr | |
| Beam solid angle finite-amplitude factor | sr | |
| Backscattering cross section of a single target (e.g., calibration sphere, or fish) | m2 | |
| Expected value of the backscattering cross section of a single target (e.g., fish) | m2 | |
| Scattering function | − | |
| Backscattering function | − | |
| Volume backscattering coefficient | m−1 | |
| Target (fish) density in the volume | − | |
| Number of scattering objects of type j per unit volume | ||
| Number of scattering objects of type j in a unit volume | ||
| Backscattering cross section for a scattering object of type j | m2 | |
| Backscattering cross section over all scatterer types, in a unit volume | m2 | |
| Relative frequency response of | − | |
| Axial transmitting current response of the transducer | Pa/A | |
| Free-field open-circuit voltage receiving sensitivity of the transducer | V/Pa | |
| Free-field open-circuit voltage receiving sensitivity of the transducer, for normally incident pressure waves | V/Pa | |
| Input electric current amplitude delivered to the transducer during transmission | A | |
| Output voltage amplitude across the transducer’s electrical terminals at reception, under open-circuit conditions | V | |
| Voltage amplitude across the transducer’s electrical terminals at transmission | V | |
| Voltage amplitude across the transducer’s electrical terminals upon reception, for single-target backscattering | V | |
| Current amplitude at the transducer’s electrical terminals upon reception, for single-target backscattering | A | |
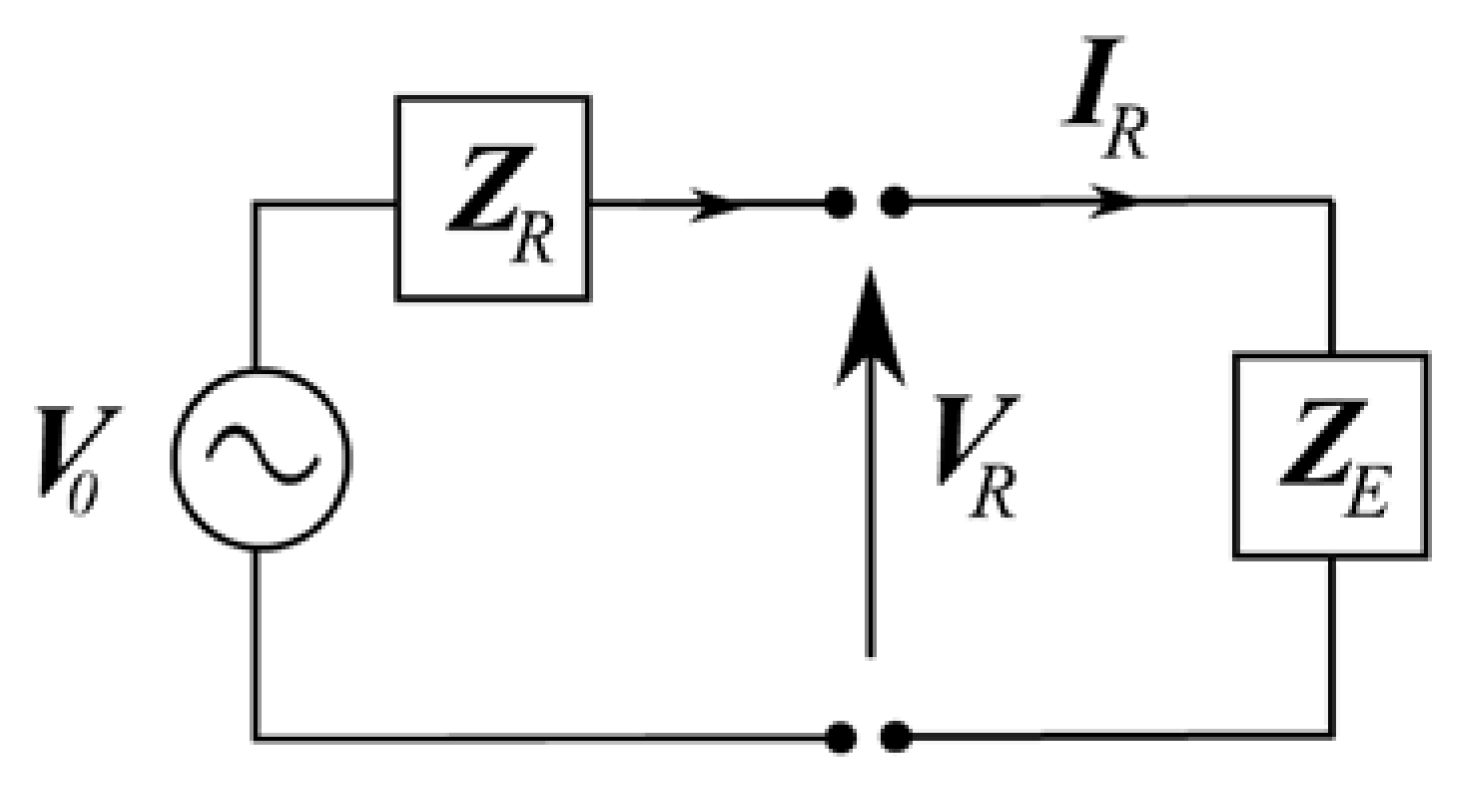
| Input electrical impedance of the transducer in transmit operation, with resistance and reactance | Ω | |
| Output (internal) electrical impedance of the transducer in receive operation, with resistance and reactance | Ω | |
| Input electrical impedance of the receiving electronics network, with resistance and reactance | Ω | |
| , , | Electrical termination factors | − |
| , | Electrical termination factors | Ω, Ω−1 |
| Average electrical power delivered to the transducer at transmission (“average transmit electrical power”), for single-target () or volume backscattering (field survey) () applications (depends on situation, cf. Equations (1)–(2)) | W | |
| Average electrical power delivered to the transducer at transmission (“average transmit electrical power”), for single-target backscattering operation (i.e., calibration sphere, individual fish) | W | |
| Average electrical power delivered to the transducer at transmission (“average transmit electrical power”), for volume scattering (field survey) operation | W | |
| Average electrical power delivered by the transducer to the receiving electronics (“average received electrical power”), for single-target backscattering operation (i.e., calibration sphere, individual fish), for finite-amplitude sound propagation in the fluid | W | |
| Average electrical power delivered by the transducer to the receiving electronics (“average received electrical power”), for volume backscattering (field survey) operation, for finite-amplitude sound propagation in the fluid | W | |
| reduces to for small-amplitude sound propagation in the fluid | W | |
| reduces to for small-amplitude sound propagation in the fluid | W | |
| Average acoustic power radiated by the transducer into the fluid, under small-amplitude and lossless sound propagation conditions in the fluid | W | |
| Transducer’s (one-way) electroacoustic conversion efficiency under conditions of small-amplitude and lossless sound propagation in the fluid | − | |
| Spherical–wave reciprocity parameter | m4·s/kg | |
| Transmit–receive transfer function factor | − | |
| Spherical shell observation volume | m3 | |
| Spherical shell sub-volume in (“ping volume"), determined by | m3 | |
| Sampled volume portion of | m3 | |
| , | Minimum and maximum range of | m |
| , | Minimum and maximum range of | m |
| , | Transit time to the minimum and maximum ranges of | s |
| Time duration of the transmitted voltage signals, determining the thickness of | s | |
| Mid-radius range of | m | |
| Thickness of | m |
References
- Dragesund, O.; Olsen, S. On the possibility of estimating year-class strength by measuring echo-abundance of 0-group fish. Fiskeridirektoratets Skrifter Serie Havundersøkelser 1965, 13, 48–75. [Google Scholar]
- Clay, C.S.; Medwin, H. Acoustical Oceanography: Principles and Applications; John Wiley & Sons: New York, NY, USA, 1977; pp. 180–182, 205, 220, 225–235, 395–404. [Google Scholar]
- Foote, K.G. Optimizing copper spheres for precision calibration of hydro acoustic equipment. J. Acoust. Soc. Am. 1982, 71, 742–747. [Google Scholar] [CrossRef]
- Dalen, J.; Nakken, O. On the Application of the Echo Integration Method; ICES Doc. CM 1983/B:19; International Council for the Exploration of the Sea: Copenhagen, Denmark, 1983. [Google Scholar]
- Nakken, O.; Ulltang, Ø. A Comparison of the Reliability of Acoustic Estimates for Fish Stock Abundance and Estimates Obtained by Other Assessment Methods in Northeast Atlantic; FAO Fish. Rep. No. 300; Food and Agriculture Organization of the United Nations: Rome, Italy, 1983; pp. 249–260. [Google Scholar]
- Foote, K.G.; Knudsen, H.P.; Vestnes, G.; MacLennan, D.N.; Simmonds, E.J. Calibration of Acoustic Instruments for Fish Density Estimation: A Practical Guide; ICES Coop. Res. Rep. No. 144; International Council for the Exploration of the Sea: Copenhagen, Denmark, 1987. [Google Scholar]
- MacLennan, D.N. Acoustical measurements of fish abundance. J. Acoust. Soc. Am. 1990, 87, 1–15. [Google Scholar] [CrossRef]
- MacLennan, D.N.; Simmonds, E.J. Fisheries Acoustics; Chapman & Hall: London, UK, 1992; pp. 68–69, 147–151. [Google Scholar]
- Medwin, H.; Clay, C.S. Fundamentals of Acoustical Oceanography; Academic Press: Boston, MA, USA, 1998; pp. 153–158, 350–361. [Google Scholar]
- MacLennan, D.N.; Fernandes, P.G.; Dalen, J. A consistent approach to definitions and symbols in fisheries acoustics. ICES J. Mar. Sci. 2002, 59, 365–369. [Google Scholar] [CrossRef]
- Simmonds, J.; MacLennan, D.N. Fisheries Acoustics. Theory and Practice, 2nd ed.; Blackwell Science Ltd.: Oxford, UK, 2005; pp. 32, 35–38, 47, 59–60, 110, 119–121, 187–191, 195–197. [Google Scholar]
- Korneliussen, R.J. The acoustic identification of Atlantic mackerel. ICES J. Mar. Sci. 2010, 67, 1749–1758. [Google Scholar] [CrossRef]
- Holliday, D.V. Extracting bio-physical information from the acoustic signature of marine organisms. In Oceanic Sound Scattering Prediction; Andersen, N.R., Zahuranec, B.J., Eds.; Plenum Press: New York, NY, USA, 1977; pp. 619–624. [Google Scholar]
- Korneliussen, R.J.; Diner, N.; Ona, E.; Berger, L.; Fernandes, P.G. Proposals for the collection of multifrequency acoustic data. ICES J. Mar. Sci. 2008, 65, 982–994, Published earlier as: Korneliussen, R.J.; Diner, N.; Ona, E.; Fernandes, P.G. Recommendations for the Collection of Multi-Frequency Acoustic Data; ICES Doc. CM 2004/R:36; International Council for the Exploration of the Sea: Copenhagen, Denmark, 2004. [Google Scholar] [CrossRef]
- Tichy, F.E.; Solli, H.; Klaveness, H. Nonlinear effects in a 200 kHz sound beam and consequences for target strength measurement. ICES J. Mar. Sci. 2003, 60, 571–574. [Google Scholar] [CrossRef]
- Baker, A.C.; Lunde, P. Nonlinear Propagation from Circular Echo-Sounder Transducers. Numerical Simulation Results; CMR Tech. Note CMR-TN01-A10010-Rev-01; Christian Michelsen Research AS: Bergen, Norway, 2011; De-classified revision of CMR Tech. Note CMR-TN01-F10010, 2001 (confidential). [Google Scholar]
- Baker, A.C.; Lunde, P. Nonlinear Effects in Sound Propagation from Echo-Sounders Used in Fish Abundance Estimation. Numerical Simulation Results; CMR Tech. Note CMR-TN02-A10008-Rev-01; Christian Michelsen Research AS: Bergen, Norway, 2011; De-classified revision of CMR Tech. Note CMR-TN02-F10008, 2002 (confidential). [Google Scholar]
- Nonlinear Effects: Recommendation for Fishery Research Investigations; Revised Version of Simrad News Bulletin; Simrad AS (now Kongsberg Maritime AS): Horten, Norway, 2002.
- Pedersen, A.; Vestrheim, M.; Lunde, P. Quantification of nonlinear sound propagation effects in fisheries research echosounders. In Proceedings of the Underwater Acoustic Measurements, Technologies & Results, Heraklion, Crete, 28 June–1 July 2005; Papadakis, J.S., Bjørnø, L., Eds.; Foundation for Research and Technology: Heraklion, Greece, 2005; Volume II, pp. 751–756. [Google Scholar]
- Pedersen, A. Effects of Nonlinear Sound Propagation in Fisheries Research. Ph.D. Thesis, University of Bergen, Dept. of Physics and Technology, Bergen, Norway, 2006. Available online: https://bora.uib.no/handle/1956/2158?mode=full&submit_simple=Show+full+item+record (accessed on 23 December 2019).
- Operator Manual: SIMRAD EK500 Fishery Research Echo Sunder. Scientific Echo Sounder: Base Version; Doc. No. P2170/Revision G; Simrad AS (now Kongsberg Maritime AS): Horten, Norway, 1997; Section 7: Theory of operation, pp. 165–169, and Appendix Calibration of the EK500, pp. 211–212.
- Lunde, P.; Pedersen, A.O.; Korneliussen, R.J.; Tichy, F.E.; Nes, H. Power-Budget and Echo-Integrator Equations for Fish Abundance Estimation; Fisken og Havet No. 10/2013; Institute of Marine Research: Bergen, Norway, 2013; Available online: http://www.imr.no/publikasjoner/andre_publikasjoner/fisken_og_havet/nb-no (accessed on 23 December 2019).
- Lunde, P.; Korneliussen, R.J. A Unifying Theory Explaining Different Power Budget Formulations Used in Modern Scientific Echosounders for Fish Abundance Estimation; Fisken og Havet No. 7/2014; Institute of Marine Research: Bergen, Norway, 2014; Available online: http://www.imr.no/publikasjoner/andre_publikasjoner/fisken_og_havet/nb-no. (accessed on 23 December 2019).
- Lunde, P.; Korneliussen, R.J. Power budget equations and calibration factors for fish abundance estimation using scientific echo sounders and sonar systems. J. Mar. Sci. Eng. 2016, 4, 43. [Google Scholar] [CrossRef]
- Korneliussen, R.J. Analysis and Presentation of Multifrequency Echograms. Ph.D. Thesis, University of Bergen, Department of Physics, Bergen, Norway, 2002. [Google Scholar]
- Demer, D.A.; Renfree, J.S. Variations in echosounder-transducer performance with water temperature. ICES J. Mar. Sci. 2008, 65, 1021–1035. [Google Scholar] [CrossRef]
- Ona, E.; Mazauric, V.; Andersen, L.N. Calibration methods for two scientific multibeam systems. ICES J. Mar. Sci. 2009, 66, 1326–1334. [Google Scholar] [CrossRef]
- Demer, D.A.; Berger, L.; Bernasconi, M.; Bethke, E.; Boswell, K.; Chu, D.; Domokos, R.; Dunford, A.; Fassler, S.; Gauthier, S.; et al. Calibration of Acoustic Instruments; ICES Coop. Res. Rep. No. 326; International Council for Exploration of the Sea: Copenhagen, Denmark, 2015; pp. 12–16, 62. [Google Scholar]
- Demer, D.A.; Andersen, L.N.; Bassett, C.; Berger, L.; Chu, D.; Condiotty, J.; Cutter, G.R.; Hutton, B.; Korneliussen, R.; Bouffant, N.L.; et al. Evaluation of a Wideband Echosounder for Fisheries and Marine Ecosystem Science; ICES Coop. Res. Rep. No. 336; International Council for Exploration of the Sea: Copenhagen, Denmark, 2017. [Google Scholar] [CrossRef]
- Korneliussen, R.J. (Ed.) Acoustic Target Classification; ICES Coop. Res. Rep. No. 344; International Council for Exploration of the Sea: Copenhagen, Denmark, 2018. [Google Scholar] [CrossRef]
- Caruthers, J.W. Fundamentals of Marine Acoustics; Elsevier Scientific Publ. Co.: Amsterdam, The Netherlands, 1977; pp. 113–116. [Google Scholar]
- Burdic, W.S. Underwater Acoustics System Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984; pp. 370–373. [Google Scholar]
- Lurton, X. An Introduction to Underwater Acoustics. Principles and Applications, 2nd ed.; Springer: Berlin, Germany, 2010; pp. 98–100, 205. [Google Scholar]
- Bjørnø, L. Applied Underwater Acoustics; Neighbors, T.H., Bradley, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 346–348. [Google Scholar]
- Hamilton, M.F. Sound beams. In Nonlinear Acoustics; Hamilton, M.F., Blackstock, D.T., Eds.; Academic Press: San Diego, CA, USA, 1998; Chapter 8. [Google Scholar]
- Lunde, P.; Pedersen, A.O. Sonar and power budget equations for backscattering of finite amplitude sound waves, with implications in fishery acoustics for abundance estimation of marine resources. In Proceedings of the Scandinavian Symposium on Physical Acoustics, Geilo, Norway, 29 January–1 February 2012; Kristiansen, U., Ed.; Norwegian Physical Society: Oslo, Norway, 2012. ISBN 978-82-8123-012-5. Available online: http://www.ntnu.edu/sspa/sspa2012 (accessed on 23 December 2019).
- Lunde, P. Equations describing finite-amplitude effects in acoustic fish abundance estimation. J. Acoust. Soc. Am. 2015, 138 Pt 2, 1949. [Google Scholar] [CrossRef]
- Zabolotskaya, E.A.; Khokhlov, R.V. Quasi-plane waves in the nonlinear acoustics of confined beams. Sov. Phys. Acoust. 1969, 15, 35–40. [Google Scholar]
- Kuznetsov, V.P. Equations of nonlinear acoustics. Sov. Phys. Acoust. 1971, 16, 467–470. [Google Scholar]
- Aanonsen, S.; Barkve, T.; Naze Tjøtta, J.; Tjøtta, S. Distortion and harmonic generation in the nearfield of a finite amplitude sound beam. J. Acoust. Soc. Am. 1984, 75, 749–768. [Google Scholar] [CrossRef]
- Hamilton, M.F.; Naze Tjøtta, J.; Tjøtta, S. Nonlinear effects in the farfield of a directive sound source. J. Acoust. Soc. Am. 1985, 78, 202–216. [Google Scholar] [CrossRef]
- Berntsen, J.; Naze Tjøtta, J.; Tjøtta, S. Interaction of sound waves. Part IV: Scattering of sound by sound. J. Acoust. Soc. Am. 1989, 86, 1968–1983. [Google Scholar] [CrossRef]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics, 4th ed.; John Wiley & Sons: New York, NY, USA, 2000; pp. 15, 181–184, 189. [Google Scholar]
- Foldy, L.L.; Primakoff, H. A general theory of passive linear electroacoustic transducers and the electroacoustic reciprocity theorem. I. J. Acoust. Soc. Am. 1945, 17, 109–120. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory: Analysis and Design, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 50, 66, 89–95. [Google Scholar]
- ANSI S1.20-1988 (R2003): Procedures for Calibration of Underwater Electroacoustic Transducers; American National Standards Institute: New York, NY, USA, 1988.
- Stanton, T.K. Multiple scattering with applications to fish-echo processing. J. Acoust. Soc. Am. 1983, 73, 1164–1169. [Google Scholar] [CrossRef]
- Foote, K.G. Correcting acoustic measurements of scatterer density for extinction. J. Acoust. Soc. Am. 1990, 88, 1543–1546. [Google Scholar] [CrossRef]
- Zhao, X.; Ona, E. Estimation and compensation models for the shadowing effect in dense fish aggregations. ICES J. Mar. Sci. 2003, 60, 155–163. [Google Scholar] [CrossRef]
- Foote, K.G. Linearity of fisheries acoustics, with addition theorems. J. Acoust. Soc. Am. 1983, 73, 1932–1940. [Google Scholar] [CrossRef]
- Foote, K.G. Rather-high-frequency sound scattering by swimbladdered fish. J. Acoust. Soc. Am. 1985, 78, 688–700. [Google Scholar] [CrossRef]
- Lunde, P.; Pedersen, A.O. Volume backscattering of finite-amplitude acoustic waves: Power flow, sampled volume, and scattering cross section. In Proceedings of the 38th Scandinavian Symposium on Physical Acoustics, Geilo, Norway, 1–4 February 2015; Norwegian Physical Society: Oslo, Norway, 2015. ISBN 978-82-8123-015-6. Available online: http://www.norskfysikk.no/nfs/faggrupper/akustikk2015/index.html (accessed on 3 January 2020).
| 1 | Note that except for [22,23,24], prior literature does not appear to distinguish between and (i.e., the received powers in calibration and survey operations, cf. Equations (1) and (2)), although these are obviously not equal. In practical implementations and operation, however, these are normally handled as two different quantities. For clarity, thus, different symbols and are used in Equations (1) and (2). |
| 2 | Other small-amplitude power budget equations for and than those given by Equations (1) and (2) [21] have been proposed [11,20,22,26,27,28]. The various expressions proposed are not necessarily equivalent nor consistent. The expressions given in [20] and [22,23,24] represent further developments of [21] to account for arbitrary electrical termination, and are otherwise consistent with [21], cf. [23,24]. The equations postulated by Simmonds and MacLennan [11] [their Equations (3.13) and (3.15)] may be shown [23,24] to differ from those given elsewhere [20,21,22,23,24,25,26,27,28], and power flow balance is not quite preserved (cf. Section 4.1.1). Demer and Renfree [26] used expressions for and that correspond to those of [21], where however the expression for is limited to the acoustic axis [23,24]. Ona et al. [27] postulated alternative expressions for and . A derivation of those expressions [27] was presented in [28]. The expression for proposed by [27,28] is however not consistent with those given in [20,21,22,23,24], and is not found to be valid [23,24]. These issues are all addressed and resolved elsewhere [23,24]. Small-amplitude power budget equations analogous or corresponding to and/or have been addressed in some textbooks, such as [2,9,31,32,33,34]. By Clay and Medwin [2] and Medwin and Clay [9] only “in water” expressions for and were discussed (i.e., in terms of sound pressures instead of electrical voltages), without accounting for the electroacoustic conversion of the transducer at transmission and reception. Apart from that, the expressions given by Clay and Medwin in [2,9] have been shown to be consistent with Equations (1) and (2) [22]. Similar “in-water” expressions for were given by Garuthers [31], Burdic [32], Lurton [33] and Bjørnø [34]. |
| 3 | At-sea target strength measurements conducted with the Simrad EK60/38 kHz echosounder system in seawater, using a Cu60 copper sphere reflector at a constant range 15.5 m below the transducer (the transducer being 8 m below the surface), and several transmit electrical power settings in the range 200–2000 W, have shown no sign of significant nonlinear loss. The deviations between target strength measurements at 200 W and 2000 W were less than 0.01 dB. (Pers. comm., R.J.; Korneliussen, Institute of Marine Research, Bergen, Norway, 2011.) Preliminary and tentative simulations using the Bergen Code solution of the KZK equation [16,17,19,20,35,36,37,38,39,40,41,42] indicate that—for 2000 W transmit electrical power—nonlinear loss in seawater at 38 kHz operating frequency is less than 0.08 and 0.25 dB, at 10 and 100 m ranges, respectively. (Pers. comm., Pedersen, A., Christian Michelsen Research AS, Bergen, Norway, 2011). |
| 4 | These directivity figures apply to a single frequency (the fundamental frequency). Most fish-finding sonars transmit about 10% bandwidth in each pulse. Lurton [33] have discussed the directivity of wideband signals and given expressions for a non-weighted linear array. It was demonstrated that the major lobe is not severely affected by the frequency bandwidth, while the sidelobes are decreased by an amplitude modulating term, and the beampattern throughs are smoothed (filled in) at a degree depending on frequency bandwidth. Although these results for a linear array are not directly applicable to circular echo sounder transducers, it may be expected that similar impacts of frequency bandwidth apply also to circular transducers, at least qualitatively. The figures given in the main text for the increased −3 dB beamwidth at the fundamental frequency, using “small” and “high” amplitude, and the corresponding flattening of the major lobe, are thus expected to be representative also for the directivity of a narrowband pulse transmitting e.g., 10% bandwidth. |
| 5 | This distinction is important to enable the use of the single-target expression, Equation (50), in the integration over a multitude of scattering objects contained in a volume of finite extent, to derive the volume backscattering coefficient, , given by Equation (56). The same assumption is implicitly underlying the conventional theory [21] for abundance estimation, Equations (1)–(3). |
| 6 | Today’s methods for fish abundance estimation and species identification are based on measurement of the signal power (“echo integration” [2,3,4,5,6,7,8,9,11,21,22,23,24,25,26,27,28,29]), for at-sea calibration as well as survey (field) operation. As part of this process the received voltage signal is squared, so that the inherent phase information about the individual scattering contributions to the received signal is not used. The conventional theoretical approach is based on the assumption of incoherent volume scattering, using sound intensity for the forward and scattered fields, with no phase information about the individual scattering contributions to the received signal. Alternative theoretical scattering approaches employ complex-valued expressions for the scattering function, accounting for phase and amplitude of the scattered field, relevant in studies of scattering from individual objects [cf. e.g., Bowman, Senior, and Uslenghi (eds.), “Electromagnetic and Acoustic Scattering by Simple Shapes”, North-Holland Publ. Co., Amsterdam, 1969]. Use of such approaches would be beyond the scope of the present article, which is intended to represent a generalization of the conventional operational expressions used in fisheries acoustics today to account for finite amplitude effects, based on the assumption of incoherent volume scattering. For this reason the definition of the scattering function used in [2], based on sound intensity, and not sound pressure, has been used here to describe single-target and volume scattering. This leads to a real-valued expression for the scattering function. |
| 7 | Foldy and Primakoff [44] considered a lossless fluid medium, using time dependence exp(iωt), as here, and the lossless version of Equation (40) was given, corresponding to α = 0 [cf. their Equation (50)]. By repeating their derivation with fluid absorption accounted for, using a complex wavenumber κ = k − iα in the fluid instead of the real wavenumber k = ω/c0 which was used by Foldy and Primakoff [44], Equation (40) results. |
| 8 | Excess attenuation from power extinction caused by volume scattering in (also referred to as the “shadow effect”) have been discussed e.g., by [9,11,48,49,50], and in references given therein. The shadow effect of caged fish at relevant fish densities, power levels, and four frequencies in the common operational frequency range used in fisheries acoustics, 38–120 kHz, was investigated by [50] (also reproduced and discussed in [11]), indicating errors in fish density (no. of fish per m2) of typically less than 10%. In a couple of cases errors in the range 14–16% were found, and in one case about 29%. In comparison with the figures given by Pedersen [20] (cf. Section 1.2), the impact of finite amplitude effects may thus be at the level of the shadow effect due to power extinction, or larger, depending on frequency, power setting, and calibration distance. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lunde, P. FiniteAmplitude Power Budget Equations for Acoustic Fish Abundance Estimation. J. Mar. Sci. Eng. 2020, 8, 98. https://doi.org/10.3390/jmse8020098
Lunde P. FiniteAmplitude Power Budget Equations for Acoustic Fish Abundance Estimation. Journal of Marine Science and Engineering. 2020; 8(2):98. https://doi.org/10.3390/jmse8020098
Chicago/Turabian StyleLunde, Per. 2020. "FiniteAmplitude Power Budget Equations for Acoustic Fish Abundance Estimation" Journal of Marine Science and Engineering 8, no. 2: 98. https://doi.org/10.3390/jmse8020098
APA StyleLunde, P. (2020). FiniteAmplitude Power Budget Equations for Acoustic Fish Abundance Estimation. Journal of Marine Science and Engineering, 8(2), 98. https://doi.org/10.3390/jmse8020098




