Multi-Degree of Freedom Propeller Force Models Based on a Neural Network and Regression
Abstract
1. Introduction
2. Methods
2.1. RANS CFD Setup & Specification of Unsteady Motion
2.2. Set-Up of the Neural Network for Unsteady Propeller Forces
2.2.1. Open Water Neural Network
2.2.2. Extension of Neural Network to Predict Unsteady Behind Condition Propeller Forces
2.3. Nonlinear Regression for Unsteady Propeller Forces
3. Training and Testing the Neural Network and Regression Model to Predict Unsteady Open Water Propeller Forces
3.1. Training the Neural Network and Nonlinear Regression Model
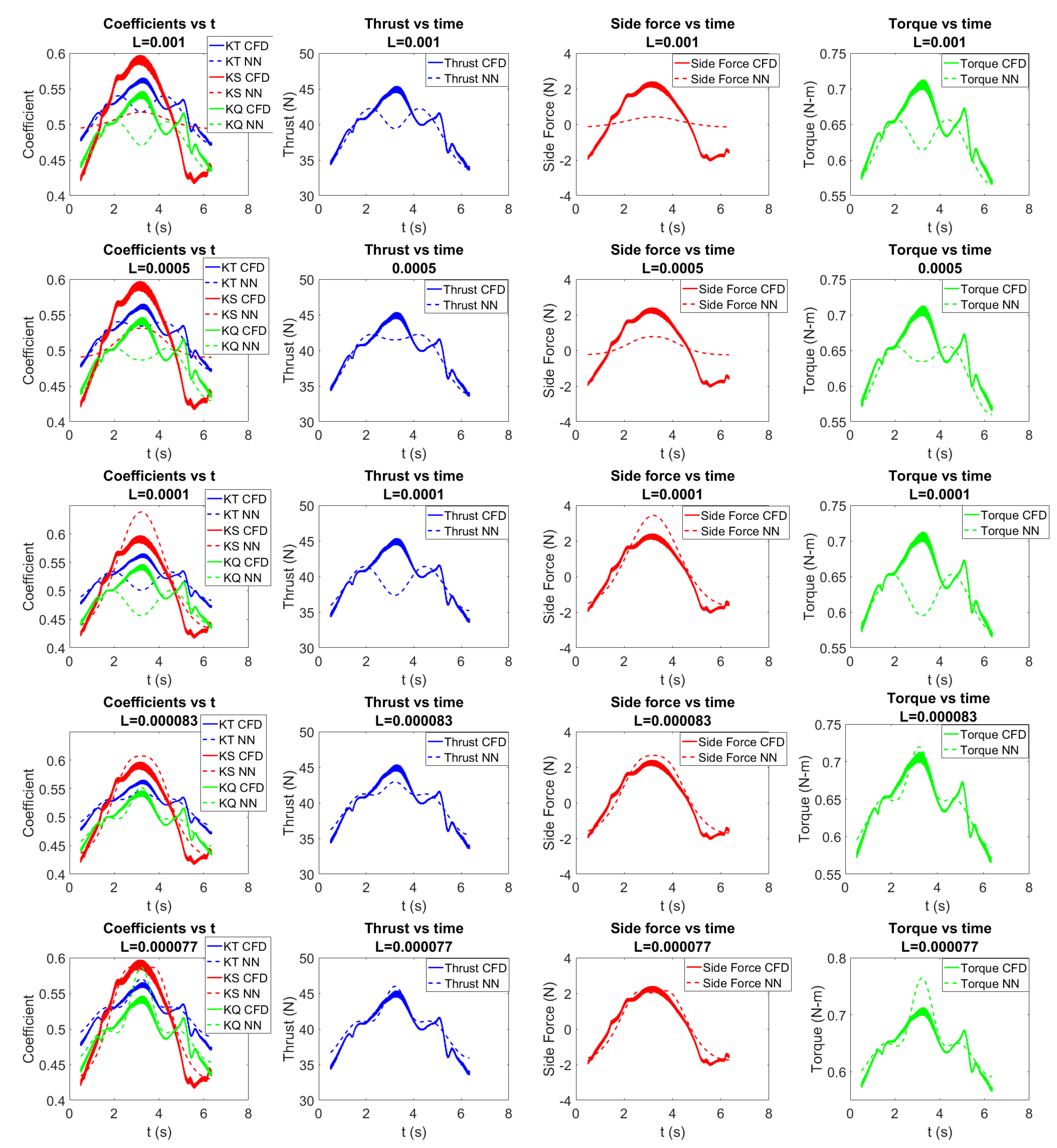
3.1.1. Training the Neural Network for Unsteady Open Water Propeller Forces
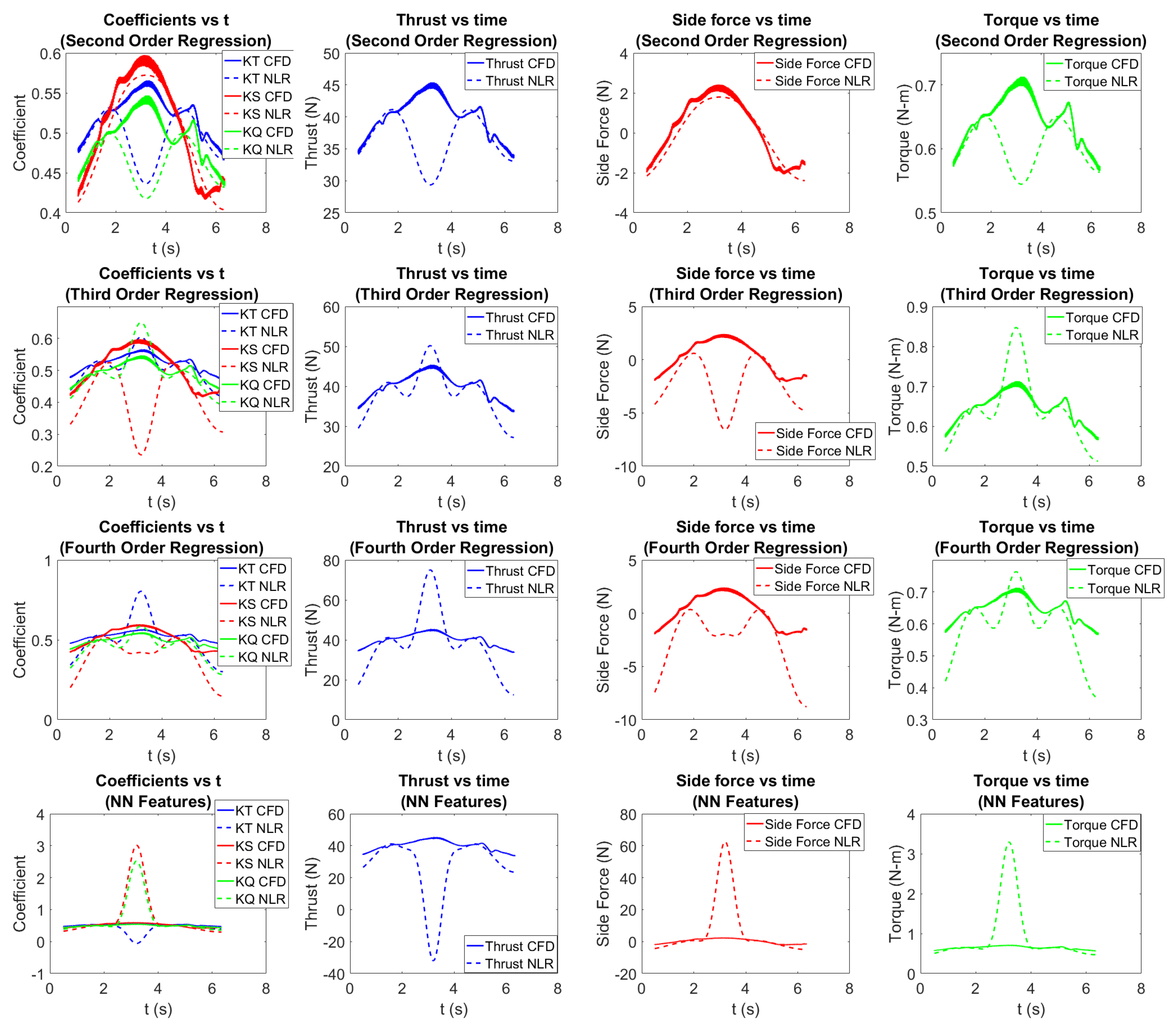
3.1.2. Training the Nonlinear Regression Model for Unsteady Open Water Propeller Forces
3.2. Testing the Models for Unsteady Open Water Propeller Force
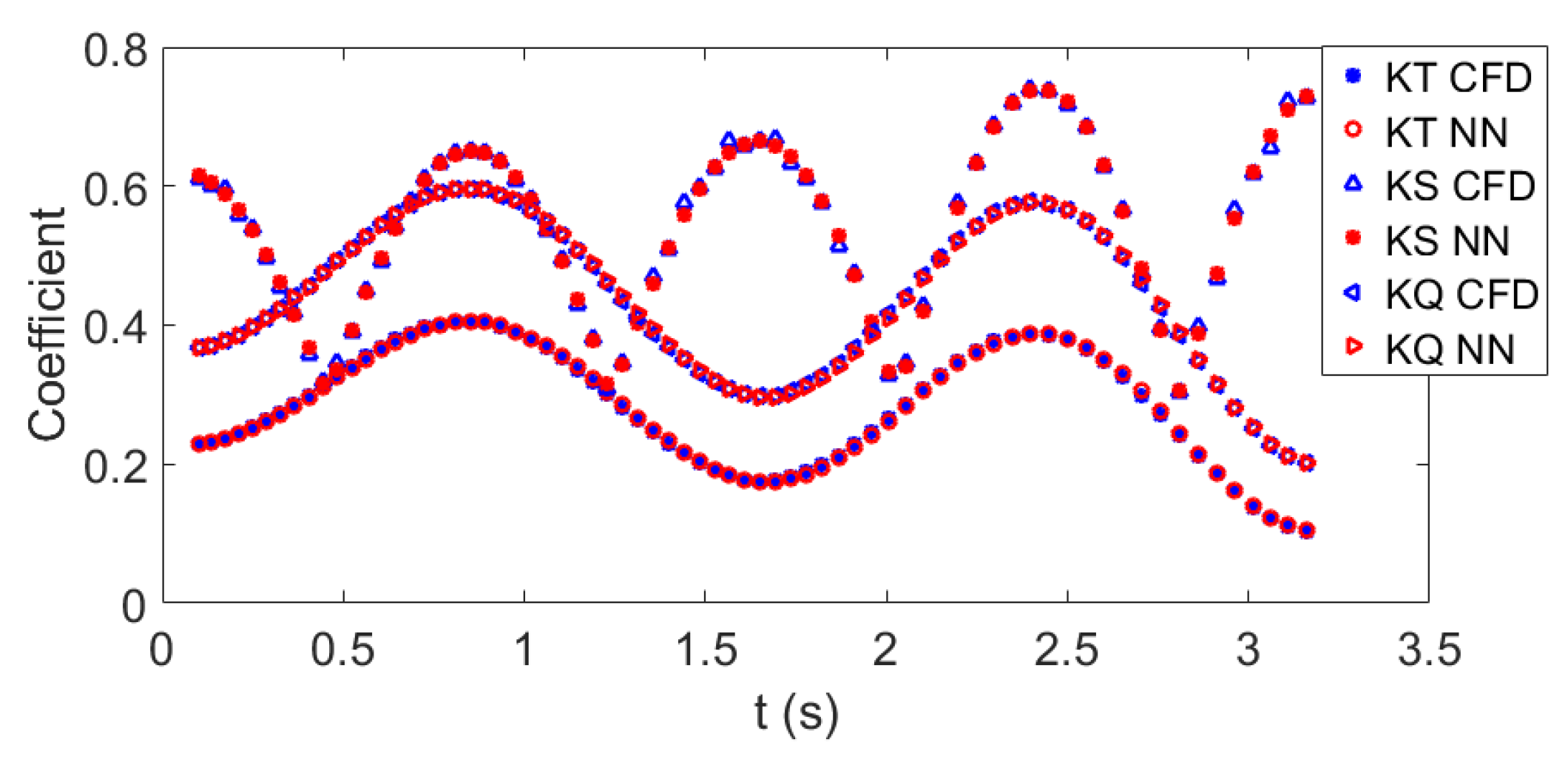
3.2.1. Testing the Neural Network for Unsteady Open Water Propeller Force
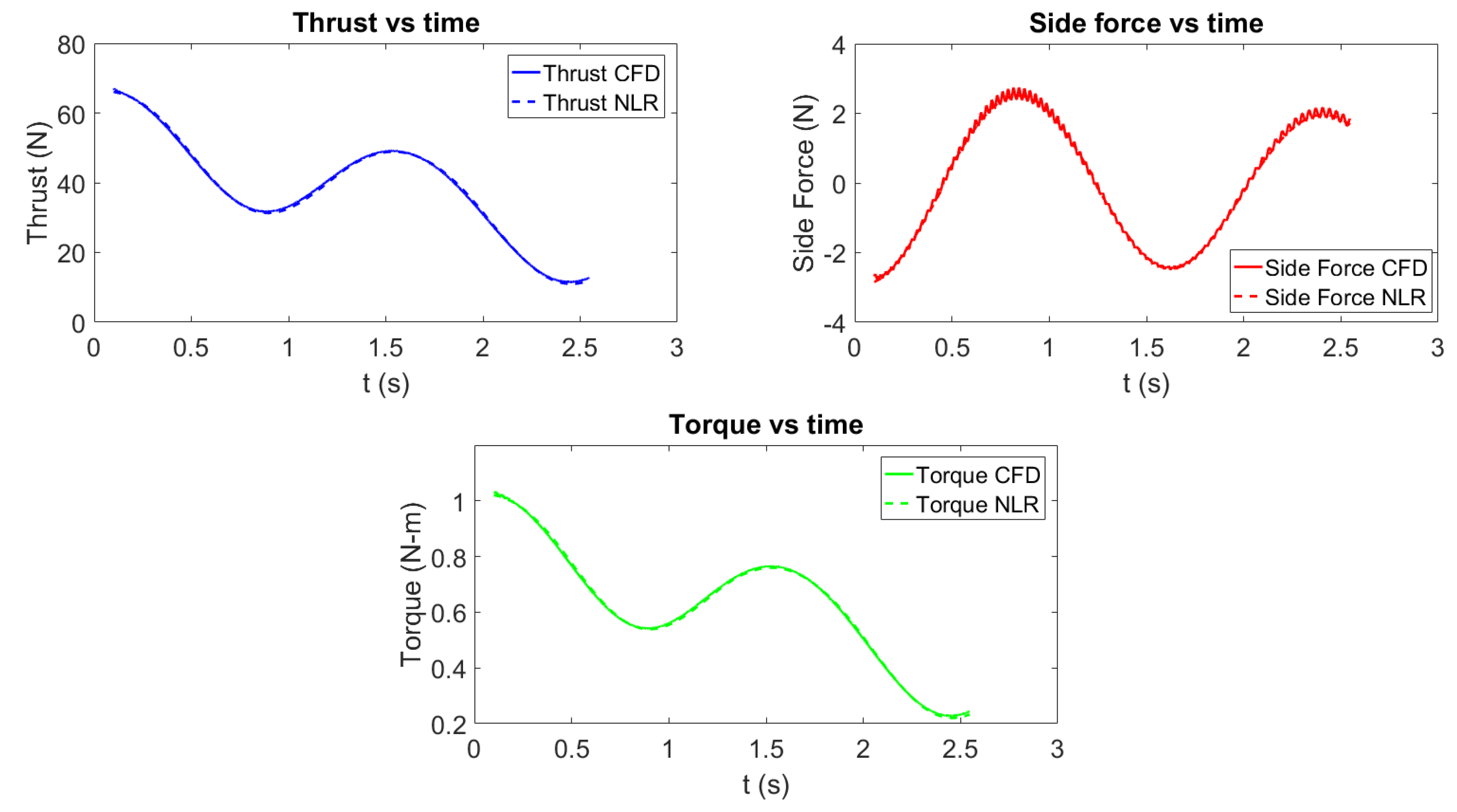
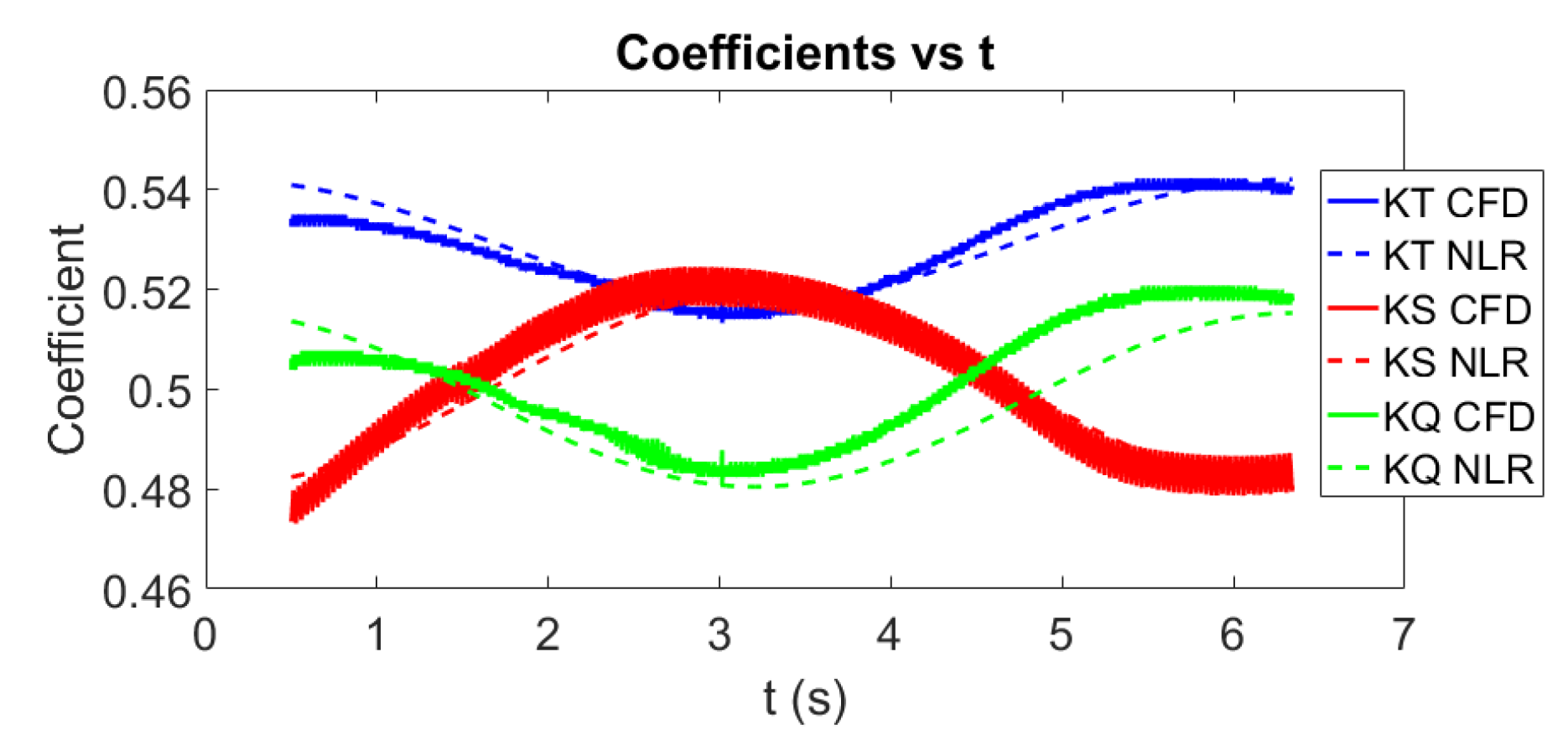
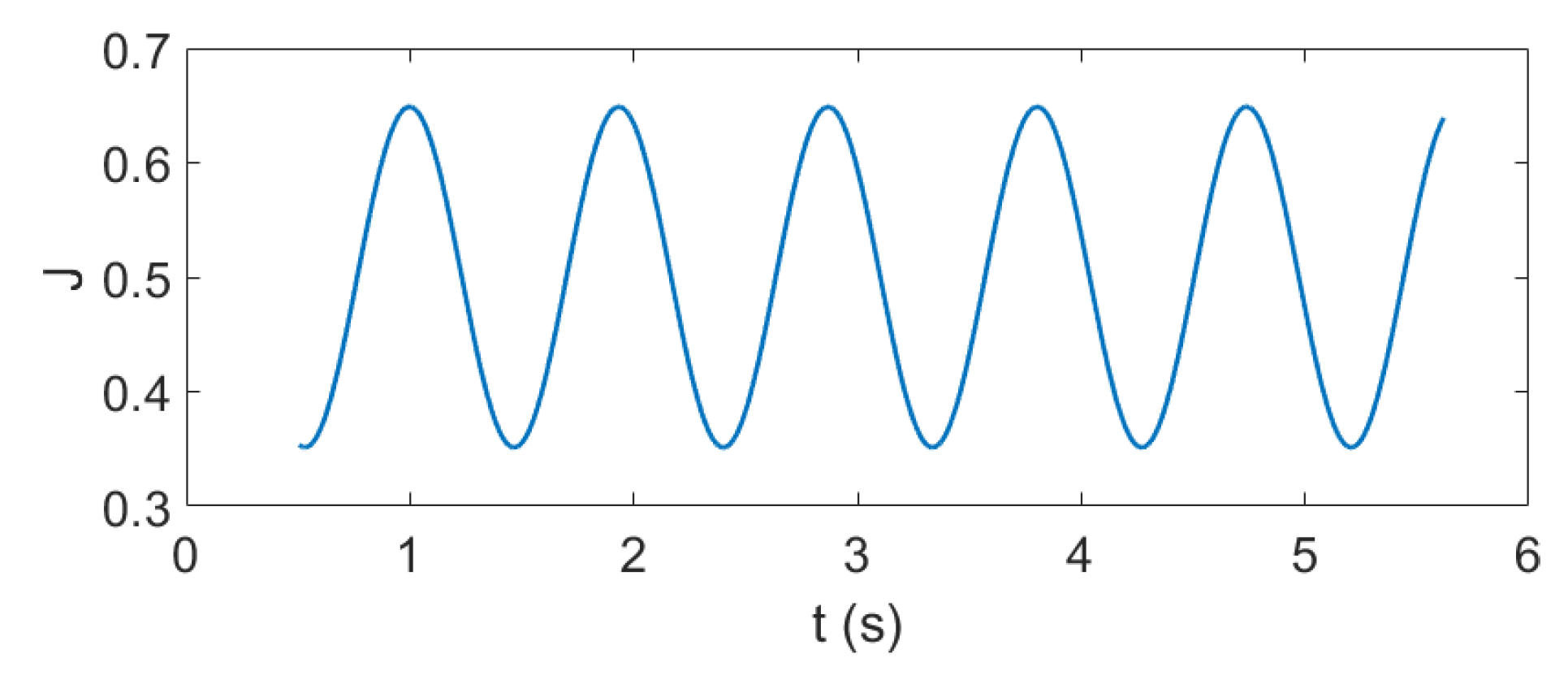
3.2.2. Testing the Nonlinear Regression for Unsteady Open Water Propeller Force
4. Training and Testing the Neural Network and Nonlinear Regression to Predict Unsteady Behind Condition Propeller Forces
4.1. Training the Models to Predict the Unsteady Behind Condition Propeller Force
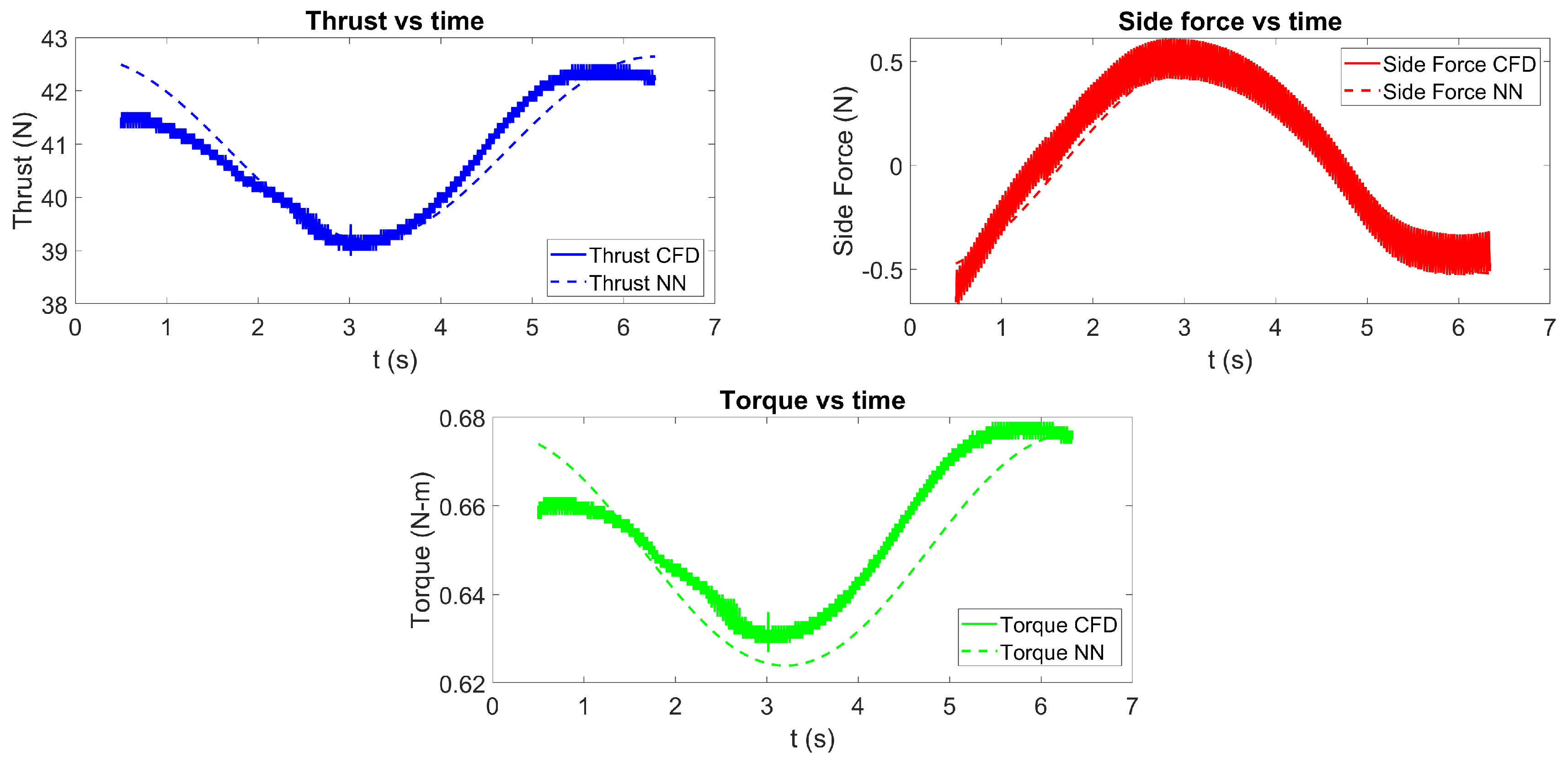
4.1.1. Training the Neural Network for the Unsteady Behind Condition Propeller Force
4.1.2. Training the Nonlinear Regression Model for the Unsteady Behind Condition Propeller Force
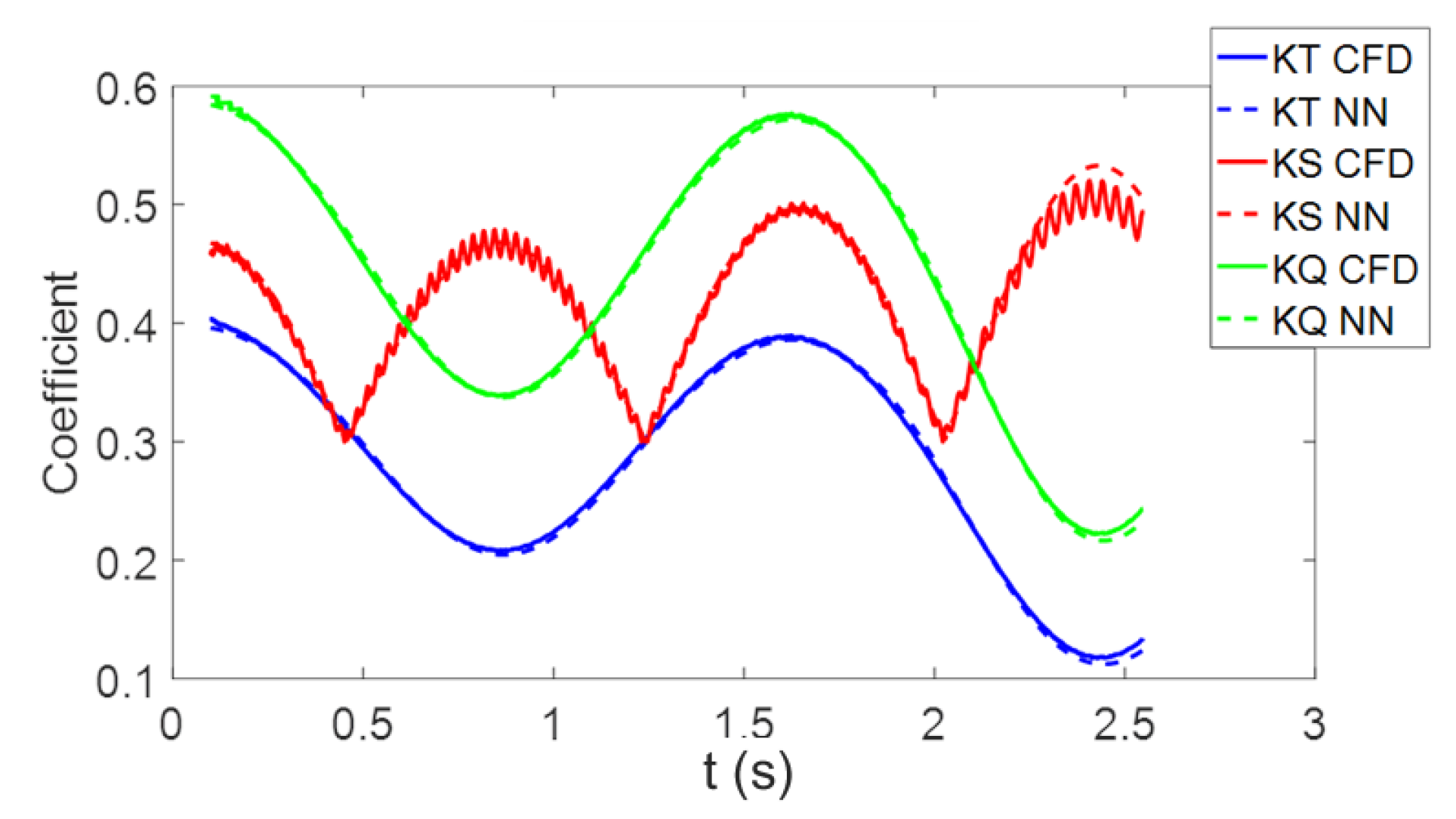
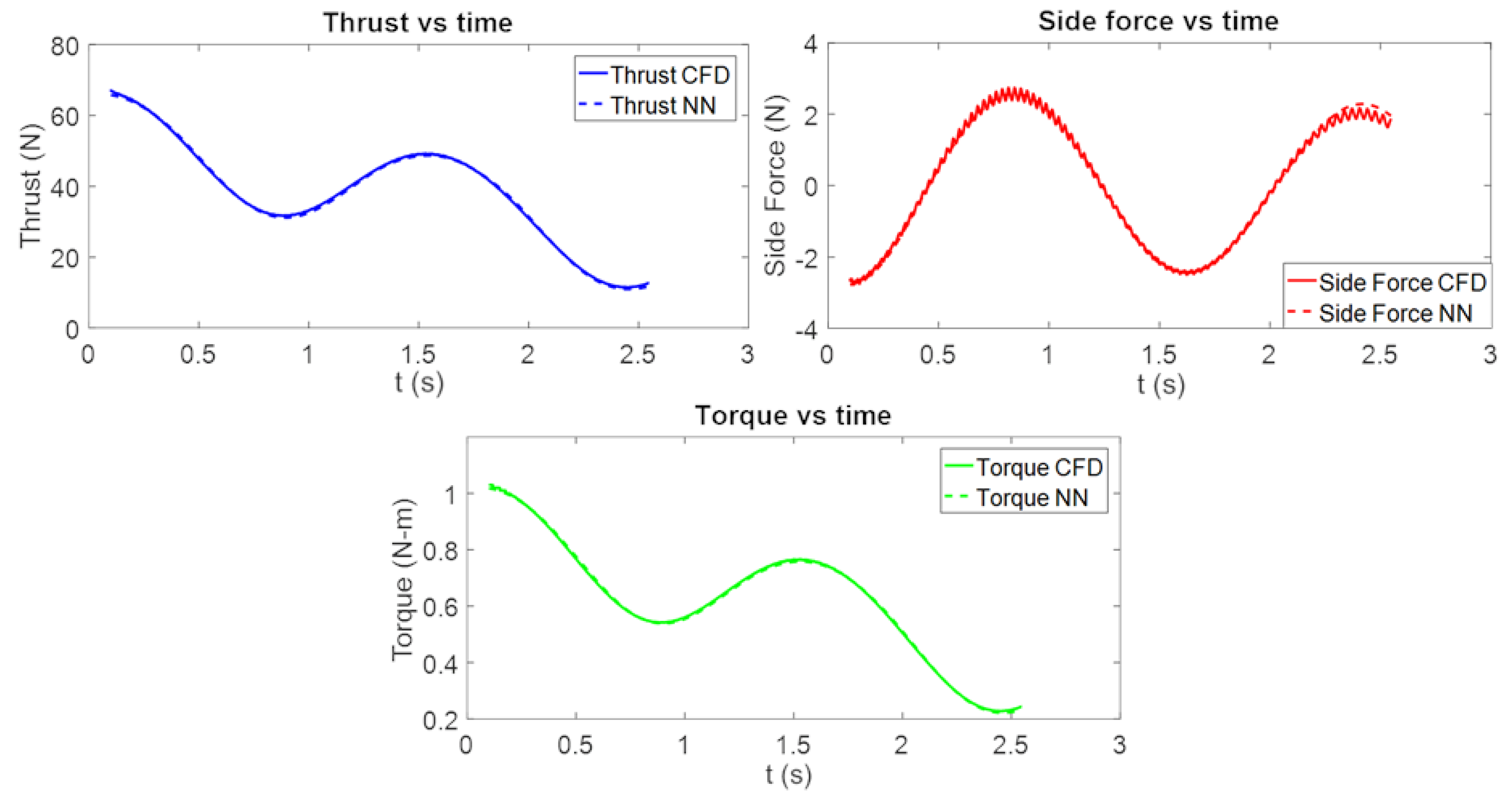
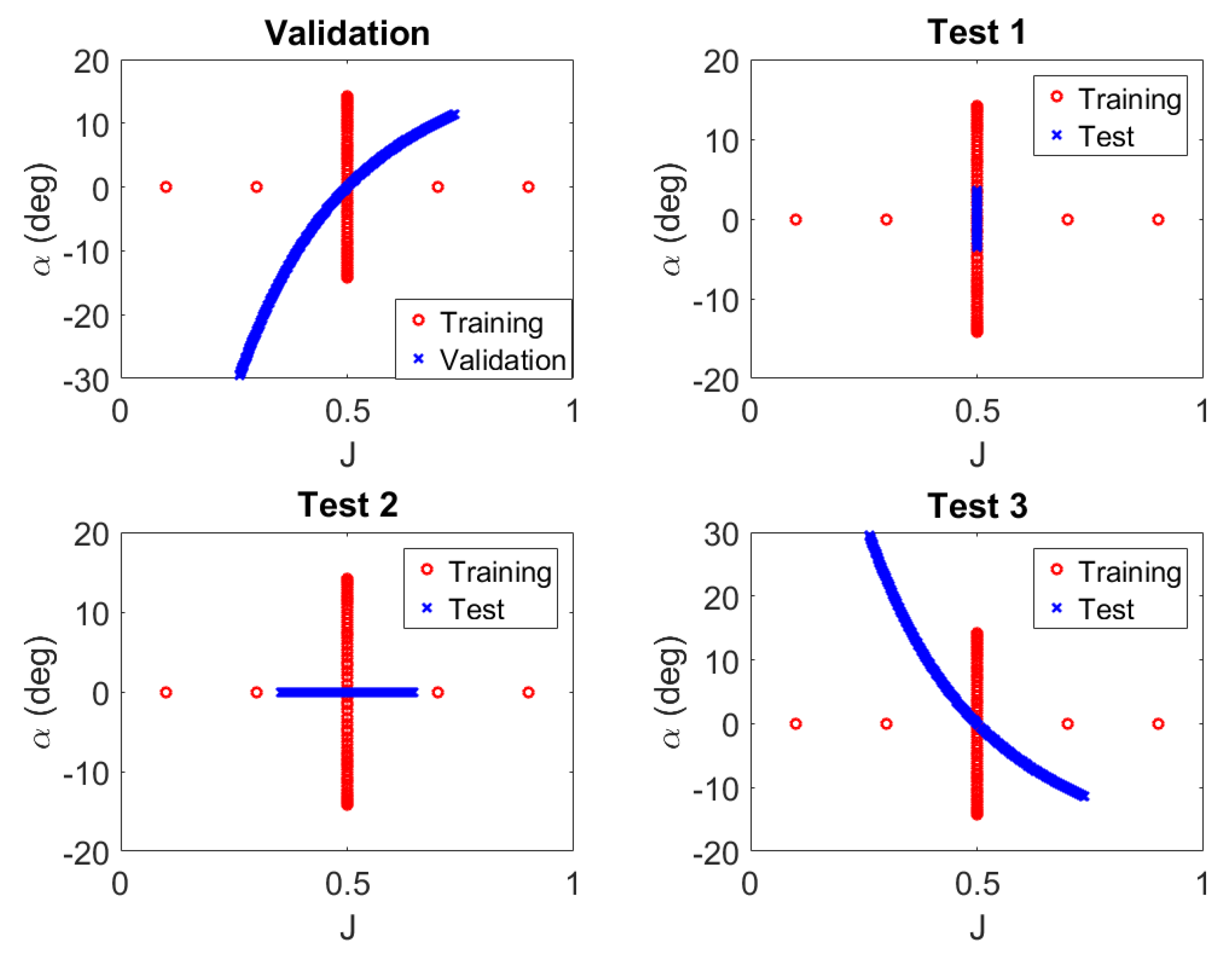
4.2. Testing the Neural Network for the Unsteady behind Condition Propeller Force
4.2.1. Behind Condition Test 1
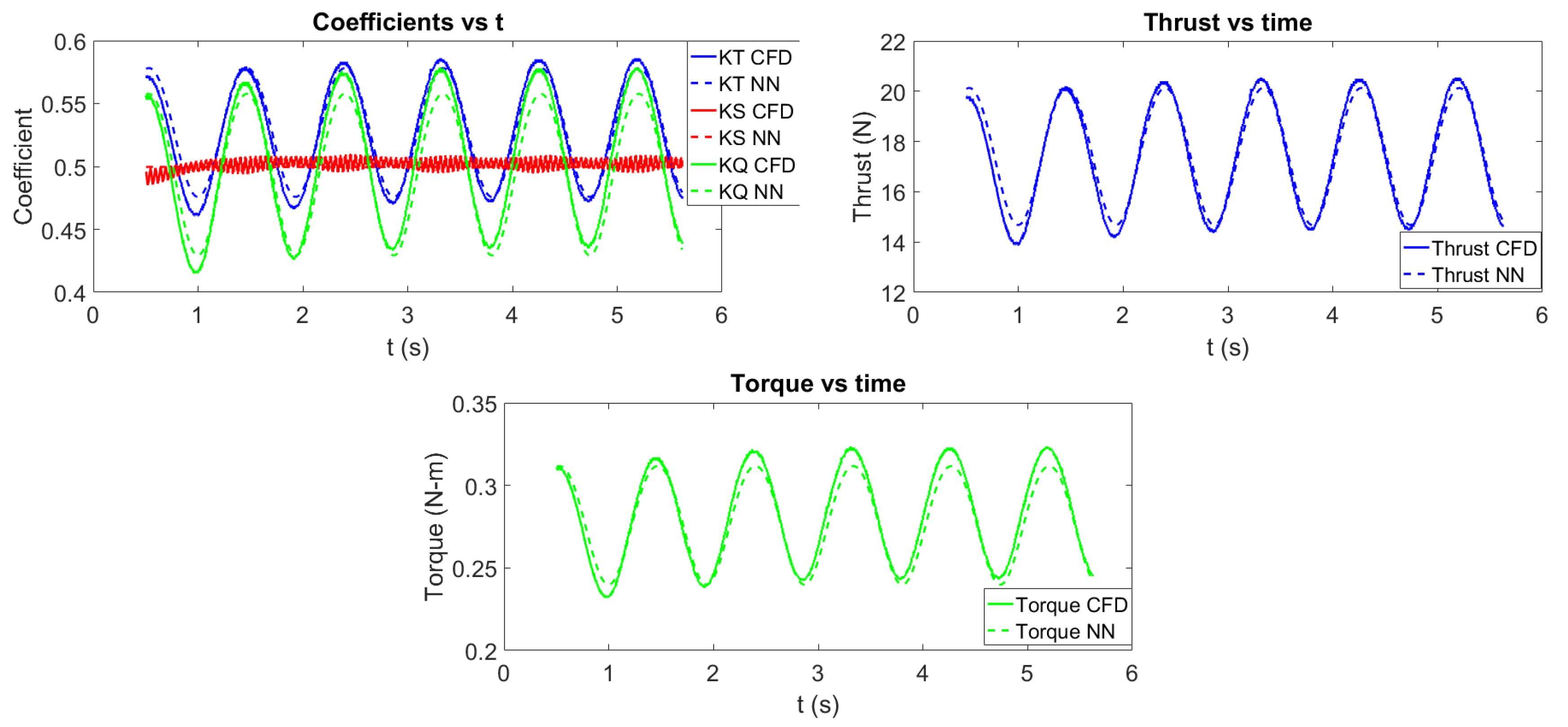
4.2.2. Behind Condition Test 2
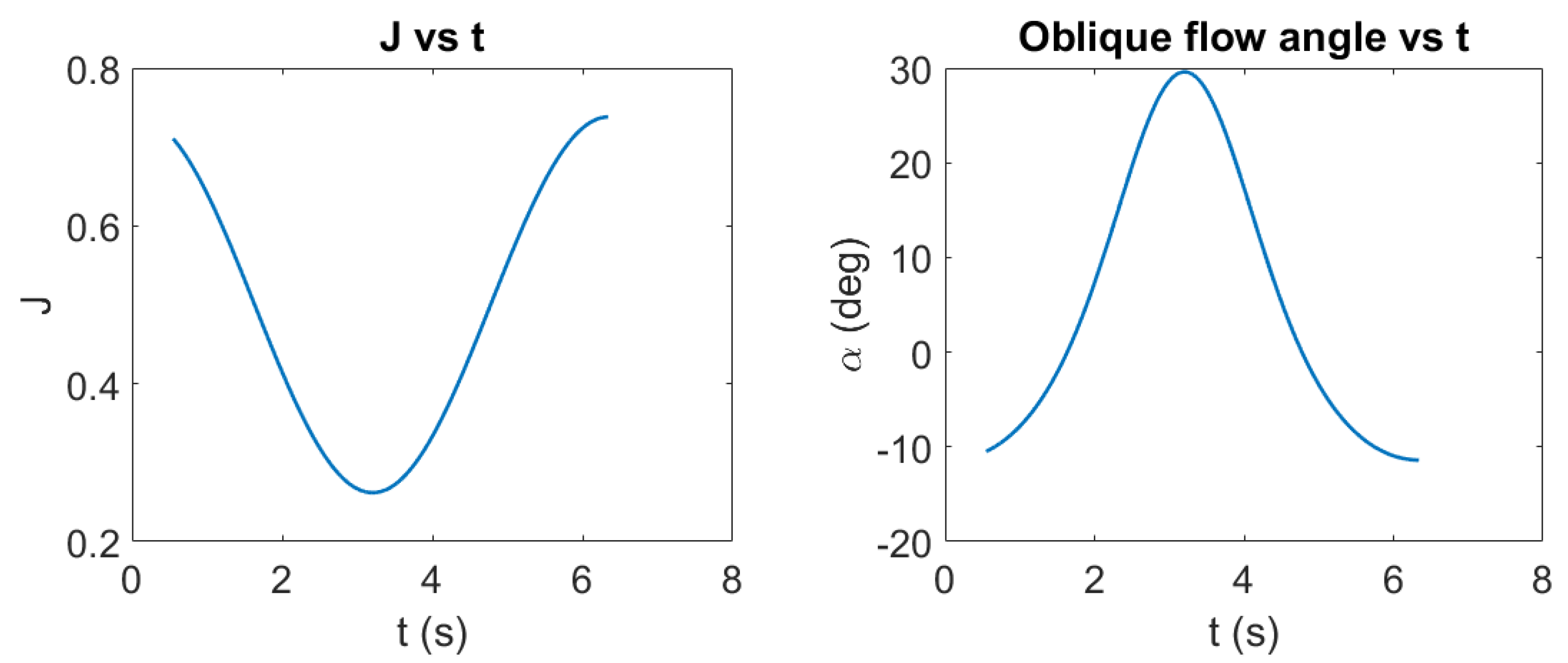
4.2.3. Behind Condition Test 3
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| DES | Detached Eddy Simulation |
| LES | Large Eddy Simulation |
| NLR | Nonlinear Regression |
| NN | Neural Network |
| RANS | Reynolds Averaged Navier–Stokes |
References
- Carrica, P.M.; Sadat-Hosseini, H.; Stern, F. CFD analysis of broaching for a model surface combatant with explicit simulation of moving rudders and rotating propellers. Comput. Fluids 2012, 53, 117–132. [Google Scholar] [CrossRef]
- Mizzi, K.; Demirel, Y.K.; Banks, C.; Turan, O.; Kaklis, P.; Atlar, M. Design optimisation of propeller boss cap fins for enhanced propeller performance. Appl. Ocean Res. 2017, 62, 210–222. [Google Scholar] [CrossRef]
- Wang, J.; Zou, L.; Wan, D. Numerical simulations of zigzag maneuver of free runnig ship in waves by RANS-Overset grid method. Ocean Eng. 2018, 162, 55–79. [Google Scholar] [CrossRef]
- Shen, Z.; Wan, D.; Carrica, P.M. Dynamic overset grids in OpenFOAM with application to KCS self-propulsion and maneuvering. Ocean Eng. 2015, 108, 287–306. [Google Scholar] [CrossRef]
- Ortolani, F.; Dubbioso, G.; Muscari, R.; Mauro, S.; Mascio, A.D. Experimental and Numerical Investigation of Propeller Loads in Off-Design Conditions. J. Mar. Sci. Eng. 2018, 6, 45. [Google Scholar] [CrossRef]
- Mousaviraad, S. CFD Prediction of Ship Response to Extreme Wind and/or Waves. Ph.D. Thesis, University of Iowa, Iowa City, IA, USA, 2010. [Google Scholar]
- Yao, J. On the Propeller Effect When Predicting Hydrodynamic Forces for Manoeuvring Using RANS Simulations of Captive Model Tests. Ph.D. Thesis, Technical University of Berlin, Berlin, Germany, 2015. [Google Scholar]
- Gaggero, S.; Dubbioso, G.; Villa, D.; Muscari, R.; Viviani, M. Propeller modeling approaches for off-design operative conditions. Ocean Eng. 2019, 178, 283–305. [Google Scholar] [CrossRef]
- Knight, B.; Maki, K. A Semi-Empirical Multi-Degree of Freedom Body Force Propeller Model. Ocean Eng. 2019, 178, 270–282. [Google Scholar] [CrossRef]
- White, P.F.; Knight, B.G.; Filip, G.P.; Maki, K.J. Numerical Simulations of the Duisburg Test Case Hull Maneuvering in Waves. In SNAME Maritime Convention; The Society of Naval Architects and Marine Engineers: Tacoma, WA, USA, 2019. [Google Scholar]
- Broglia, R.; Dubbioso, G.; Durante, D.; Mascio, A.D. Simulation of turning circle by CFD: Analysis of different propeller models and their effect on manoevring prediction. Appl. Ocean Res. 2013, 39, 1–10. [Google Scholar] [CrossRef]
- Phillips, A.; Turnock, S.; Furlong. Evaluation of manoeuvring coefficient of a self-propelled ship using blade element momentum propeller model coupled to a Reynolds averaged Navier–Stokes flow solver. Ocean Eng. 2009, 36, 1217–1225. [Google Scholar] [CrossRef]
- Winden, B. Powering Performance of a Self Propelled Ship in Waves. Ph.D. Thesis, University of Southampton, Southamptom, UK, 2014. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Singh, A.P.; Medida, S.; Duraisamy, K. Machine-Learning-Augmented Predictive Modeling of Turbulent Separated Flows over Airfoils. AIAA J. 2017, 55, 2215–2227. [Google Scholar] [CrossRef]
- Abramowski, T. Prediction of Propeller Forces During Ship Maneuvering. J. Theor. Appl. Mech. 2005, 43, 157–178. [Google Scholar]
- Knight, B.; Maki, K. Body Force Propeller Model for Unsteady Surge Motion. In Proceedings of the ASME 37th International Conference on Ocean Offshore and Arctic Engineering (OMAE), Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Knight, B.; Maki, K. A Data-Driven Multi-Degree of Freedom Body Force Propeller Model for Maneuvering. In Proceedings of the Sixth International Conference on Marine Propulsors (SMP 19), Rome, Italy, 26–30 May 2019. [Google Scholar]
- ITTC. ITTC-Recommended Procedures and Guidelines. 1978 ITTC Performance Prediction Method. International Towing Tank Conference, 2011, 7.5-02, 03-01.4. pp. 1–9. Available online: https://ittc.info/media/8372/index.pdf (accessed on 2 February 2020).
- Seber, G.A.F.; Wild, C.J. Nonlinear Regression; Wiley-Interscience: Hoboken, NJ, USA, 2003. [Google Scholar]












| Parameter | Train | Test |
|---|---|---|
| (m/s) | 1.68 | 1.68 |
| (m/s) | 0.00 | 0.00 |
| (rev/s) | 32.0 | 32.0 |
| 0.476 | 0.262 | |
| 0.500 | −0.476 | |
| 0.156 | 0.156 | |
| 0.020 | 0.020 | |
| 0.020 | 0.020 | |
| 0.005 | 0.005 |
| Parameter | Train | Validation | Test 1 | Test 2 | Test 3 |
|---|---|---|---|---|---|
| (m/s) | 1.68 | 1.68 | 1.68 | 1.10 | 1.68 |
| (m/s) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| (rev/s) | 32.00 | 32.00 | 32.00 | 20.95 | 32.00 |
| 0.00 | 0.48 | 0.00 | 0.31 | 0.48 | |
| 0.25 | 0.30 | 0.07 | 0.00 | −0.30 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| (rad/s) | 1.00 | 1.00 | 1.00 | 6.72 | 1.00 |
| Train L | L2 Error | L2 Error | L2 Error | Validation L |
|---|---|---|---|---|
| 1.0 | 2.8 | 5.3 | 1.0 | 1.0 |
| 5.0 | 1.2 | 4.7 | 2.4 | 1.5 |
| 1.0 | 2.4 | 2.6 | 3.4 | 1.1 |
| 8.3 | 9.6 | 1.9 | 8.8 | 2.58 |
| 7.7 | 8.3 | 1.6 | 1.7 | 3.0 |
| Regression Model | Train L | L2 Error | L2 Error | L2 Error | Validation L |
|---|---|---|---|---|---|
| Second Order | 9.3 | 5.0 | 1.8 | 5.1 | 2.7 |
| Third Order | 7.3 | 2.7 | 1.4 | 3.9 | 1.1 |
| Fourth Order | 7.0 | 9.9 | 1.4 | 6.4 | 1.6 |
| Neural Network Features | 6.9 | 2.0 | 7.3 | 5.9 | 4.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knight, B.; Maki, K. Multi-Degree of Freedom Propeller Force Models Based on a Neural Network and Regression. J. Mar. Sci. Eng. 2020, 8, 89. https://doi.org/10.3390/jmse8020089
Knight B, Maki K. Multi-Degree of Freedom Propeller Force Models Based on a Neural Network and Regression. Journal of Marine Science and Engineering. 2020; 8(2):89. https://doi.org/10.3390/jmse8020089
Chicago/Turabian StyleKnight, Bradford, and Kevin Maki. 2020. "Multi-Degree of Freedom Propeller Force Models Based on a Neural Network and Regression" Journal of Marine Science and Engineering 8, no. 2: 89. https://doi.org/10.3390/jmse8020089
APA StyleKnight, B., & Maki, K. (2020). Multi-Degree of Freedom Propeller Force Models Based on a Neural Network and Regression. Journal of Marine Science and Engineering, 8(2), 89. https://doi.org/10.3390/jmse8020089




