Development of An Integrated Numerical Model for Simulating Wave Interaction with Permeable Submerged Breakwaters Using Extended Navier–Stokes Equations
Abstract
1. Introduction
2. Governing Equations
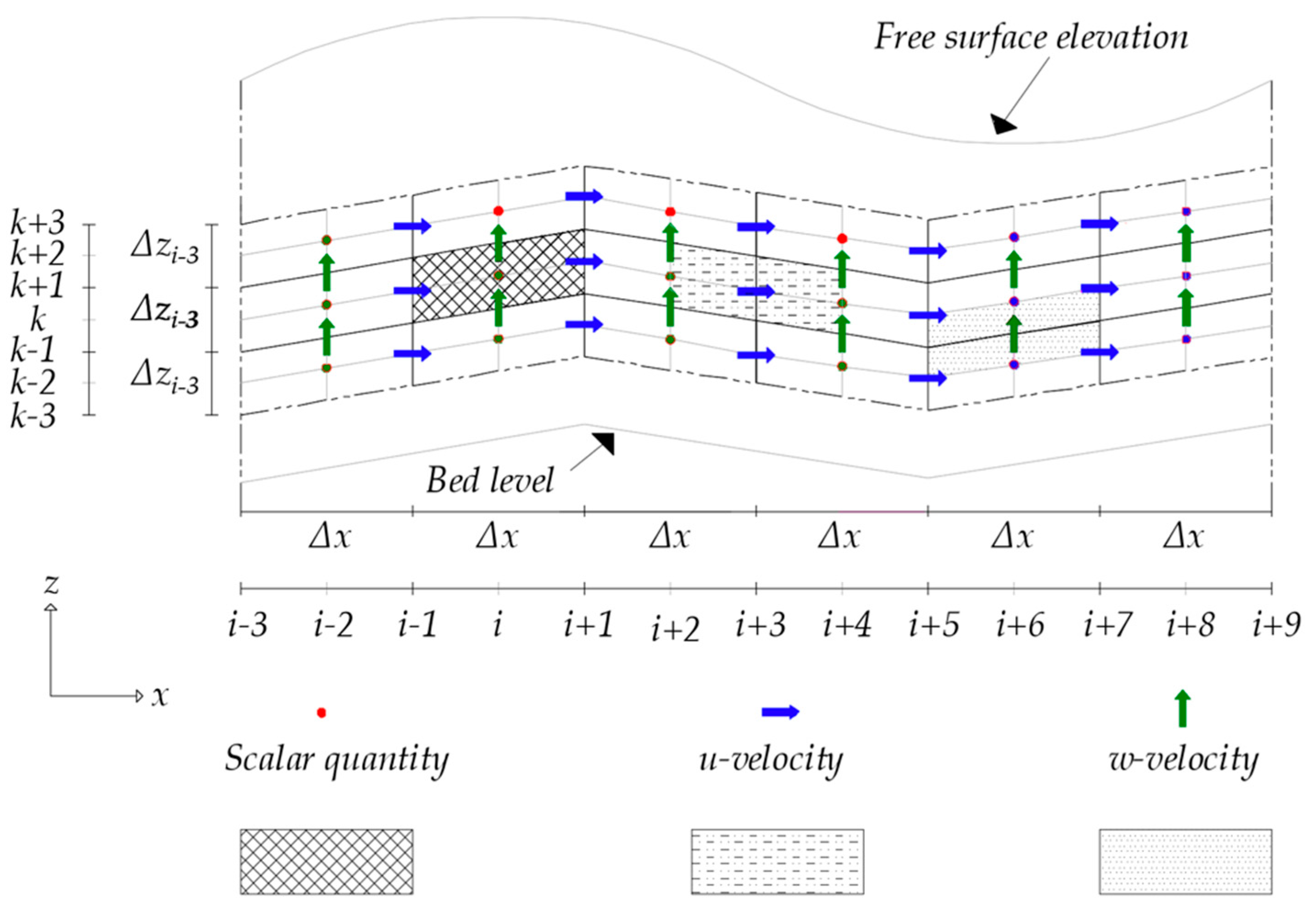
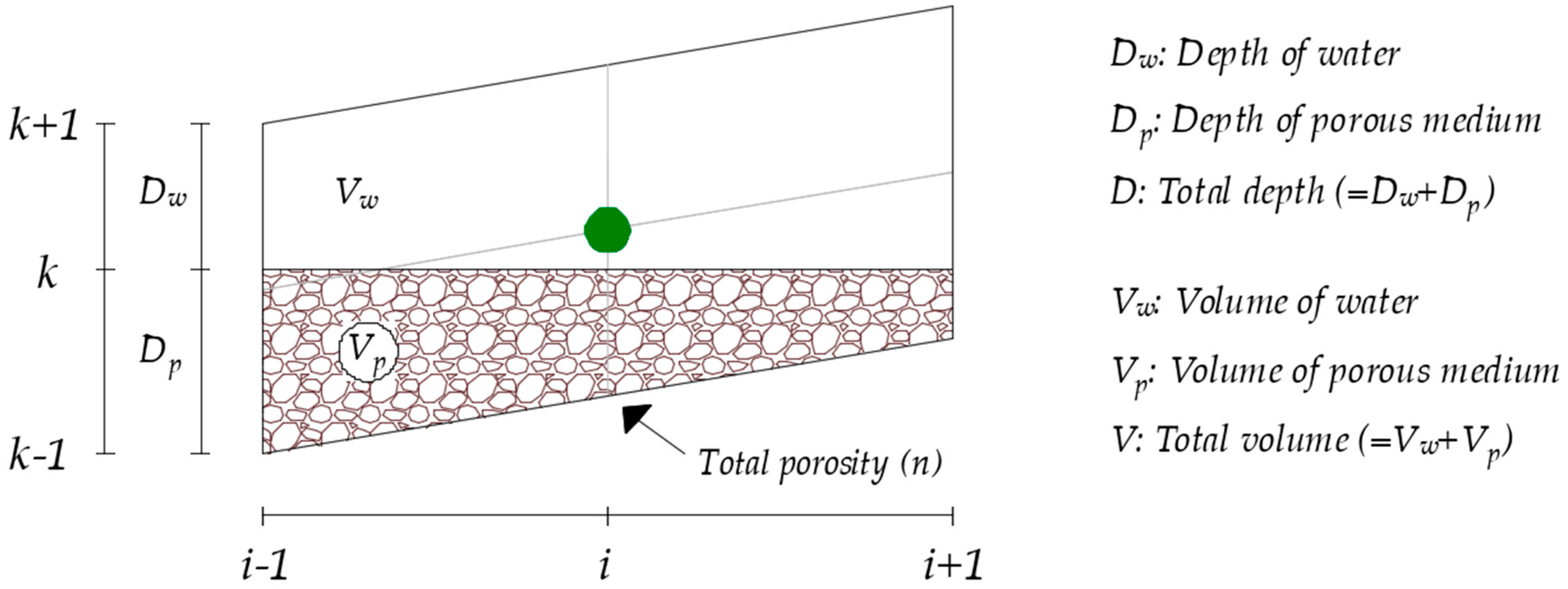
3. Discretization of the Computational Domain
4. Numerical Implementation
4.1. Pressure Equation at Free Surface Layer
4.2. Numerical Solution of the Pressure Poisson Equation (PPE)
4.3. Initial Boundary Conditions
5. Results and Discussions
5.1. Progressive Stokes Waves Propagation
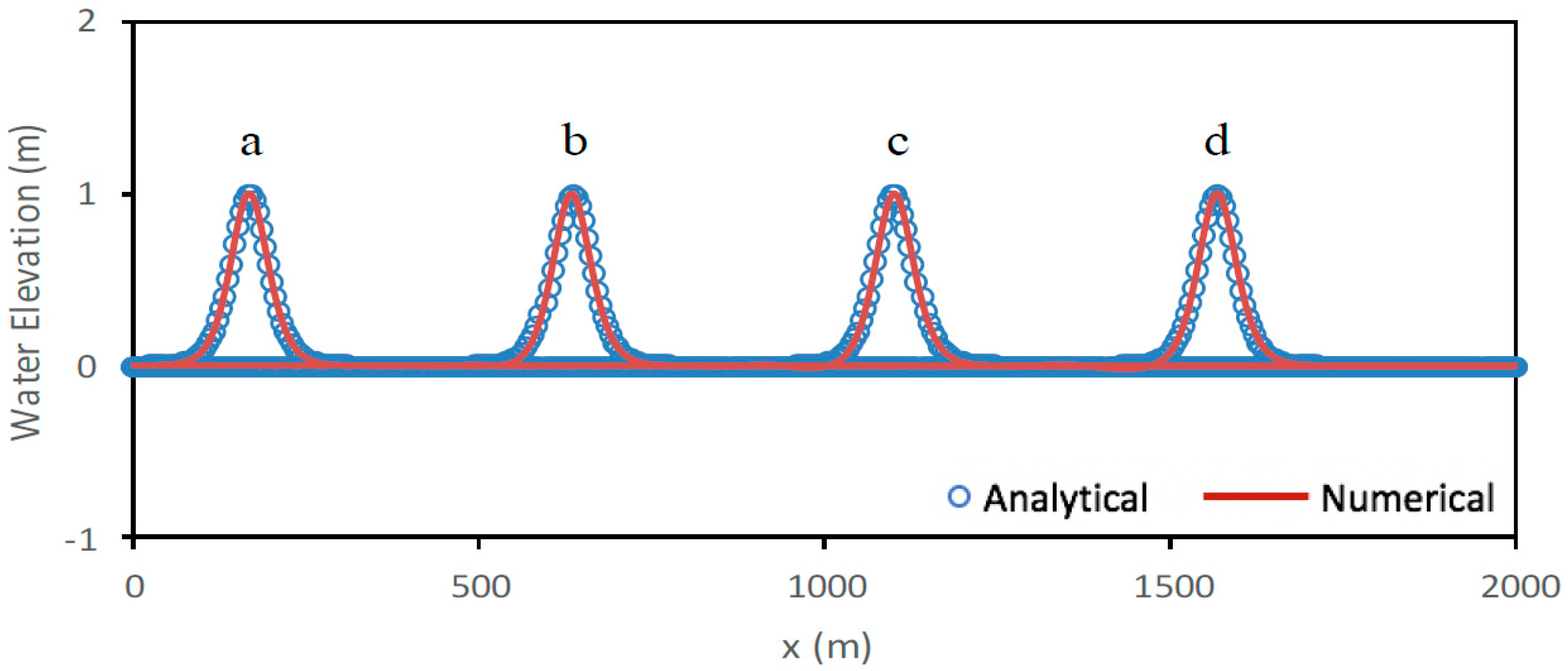
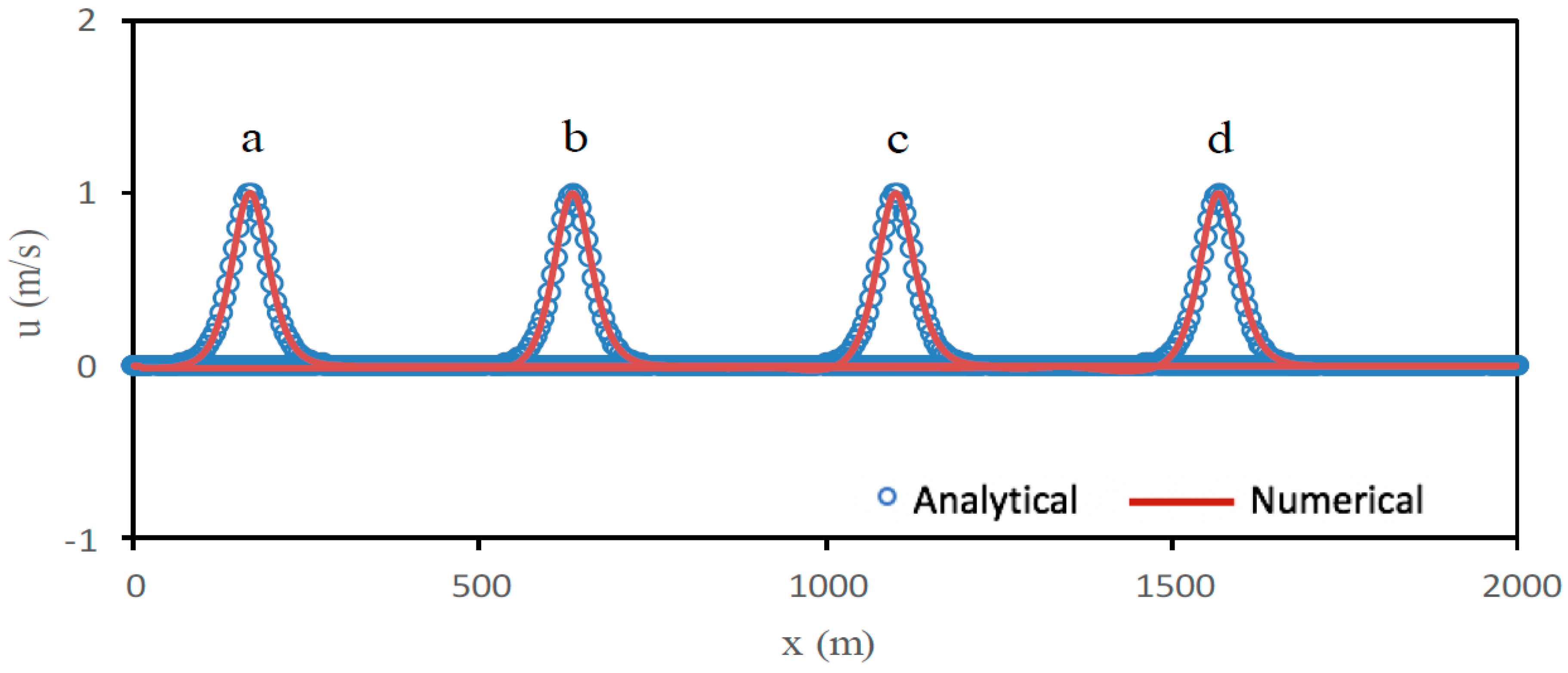
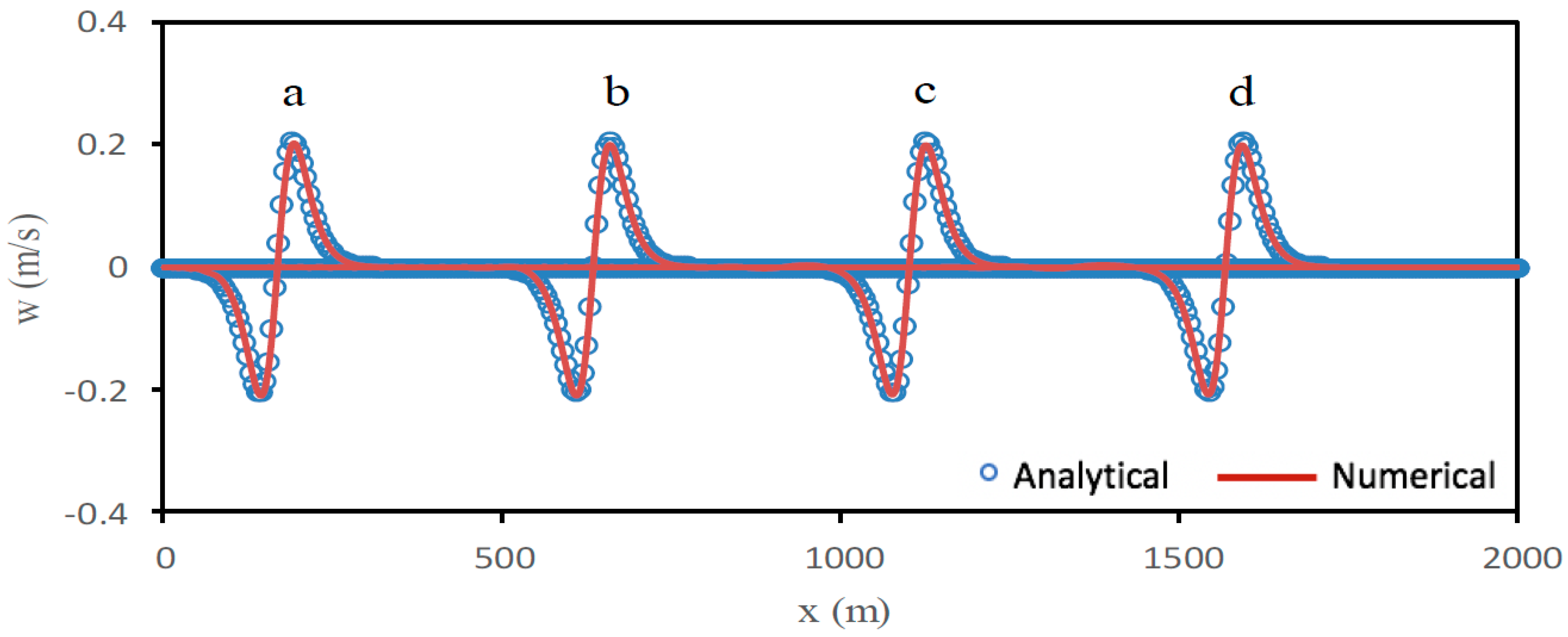
5.2. Solitary Wave Propagation
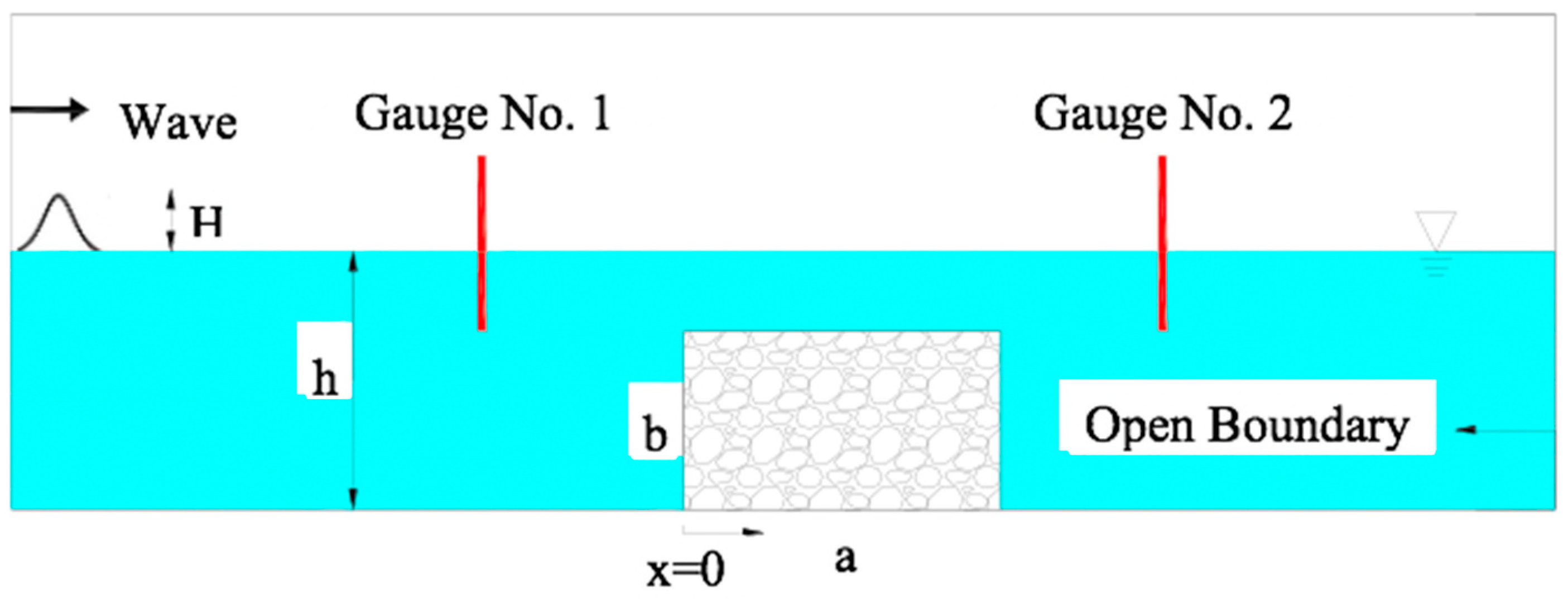
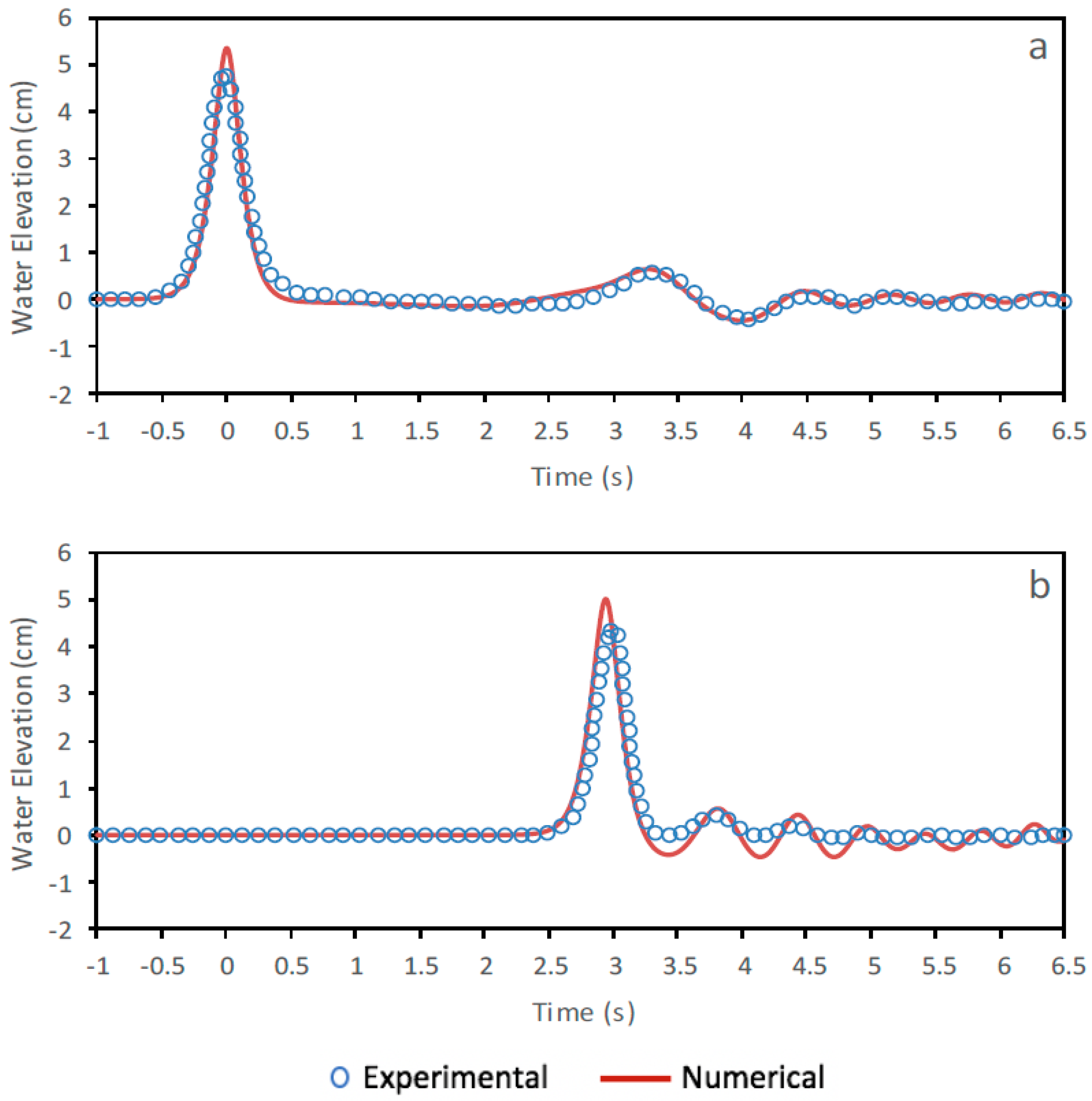
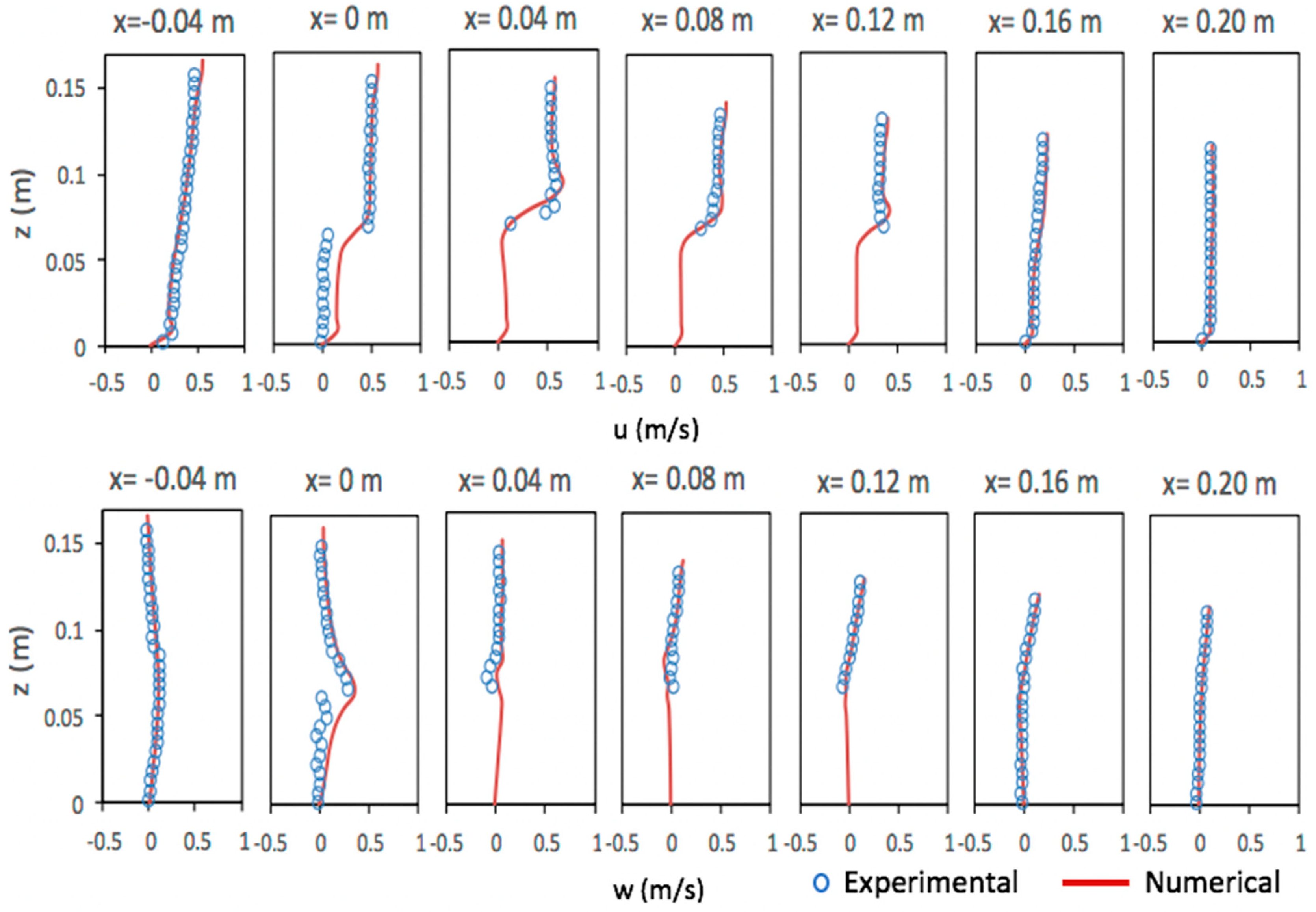
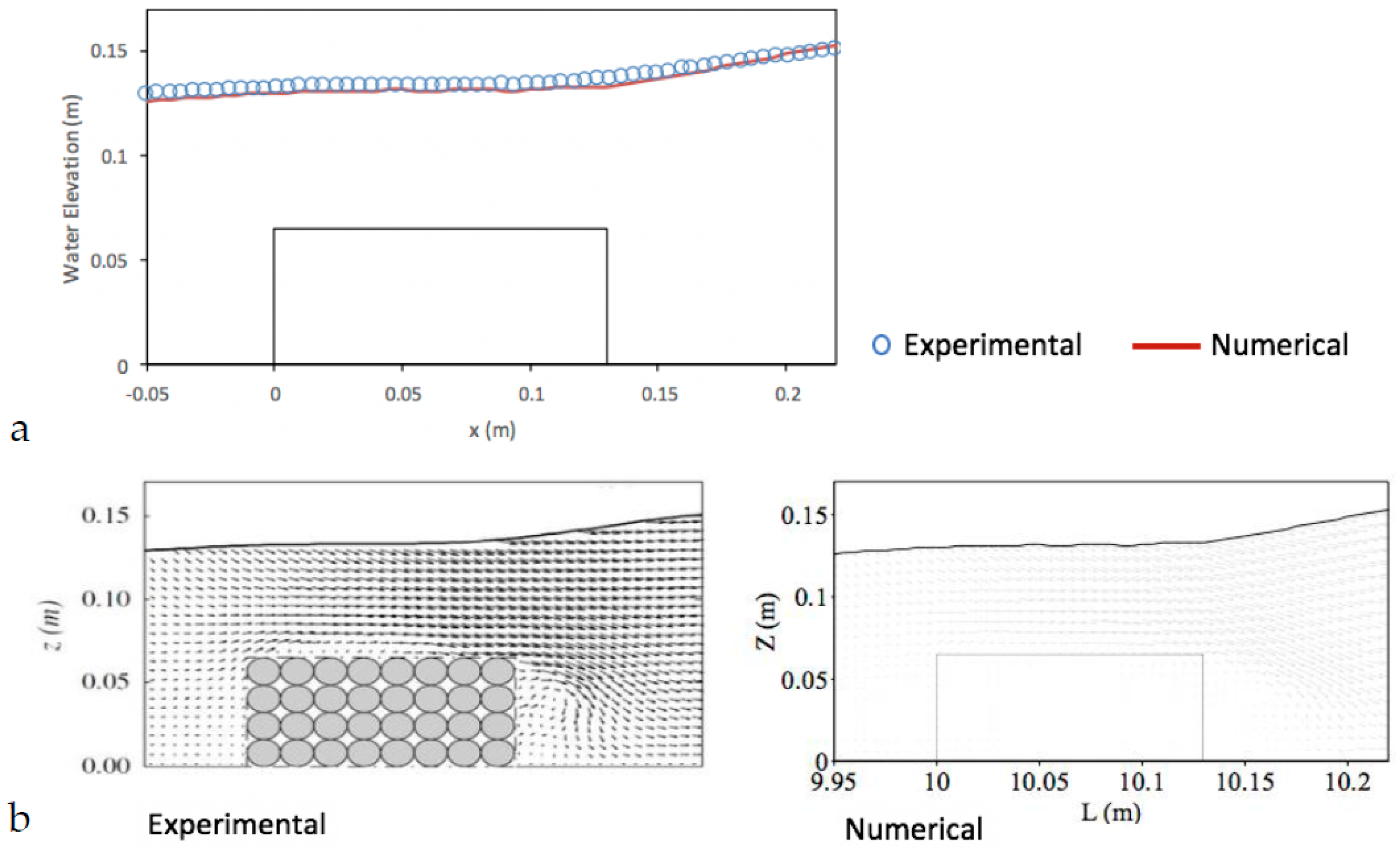
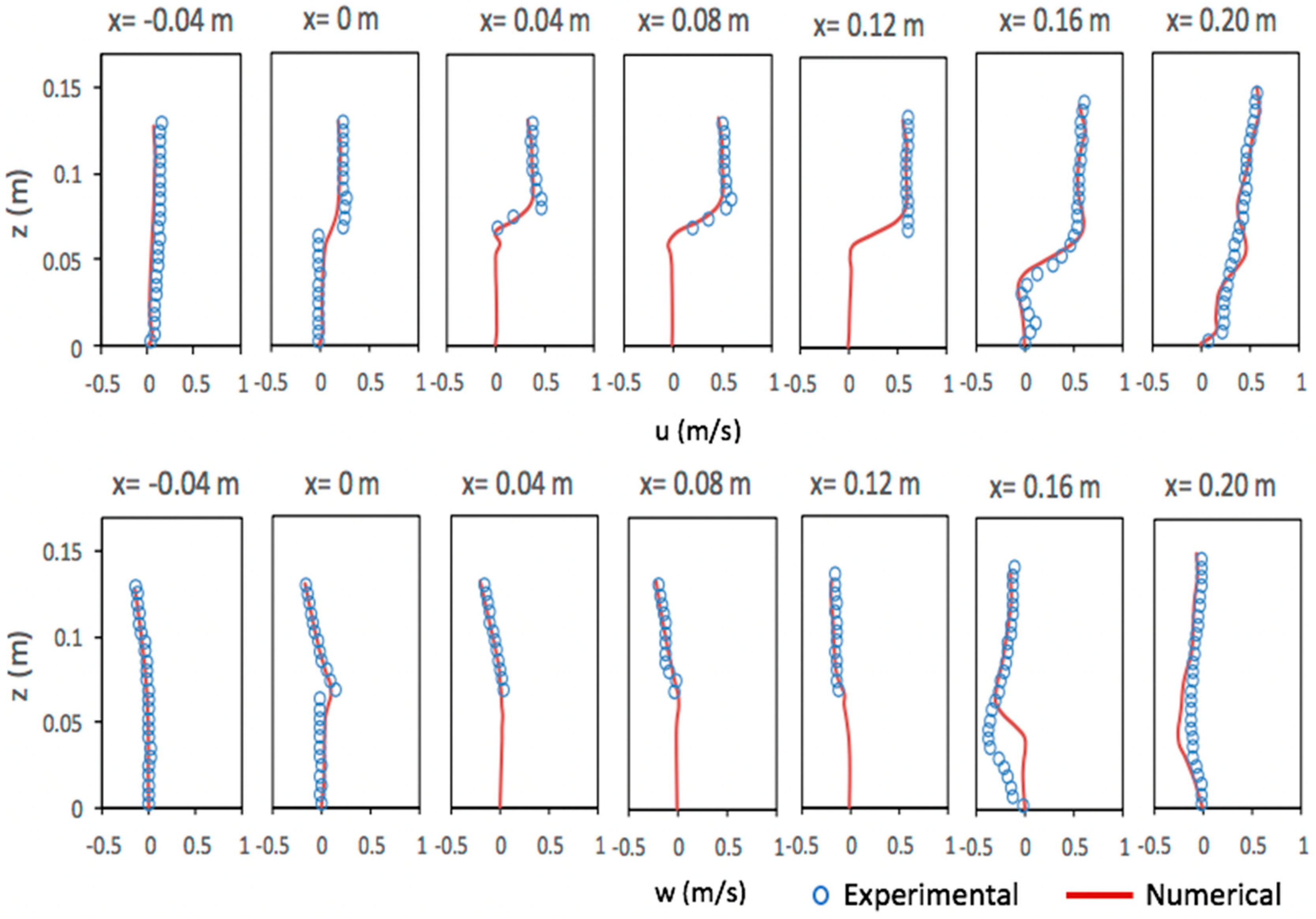
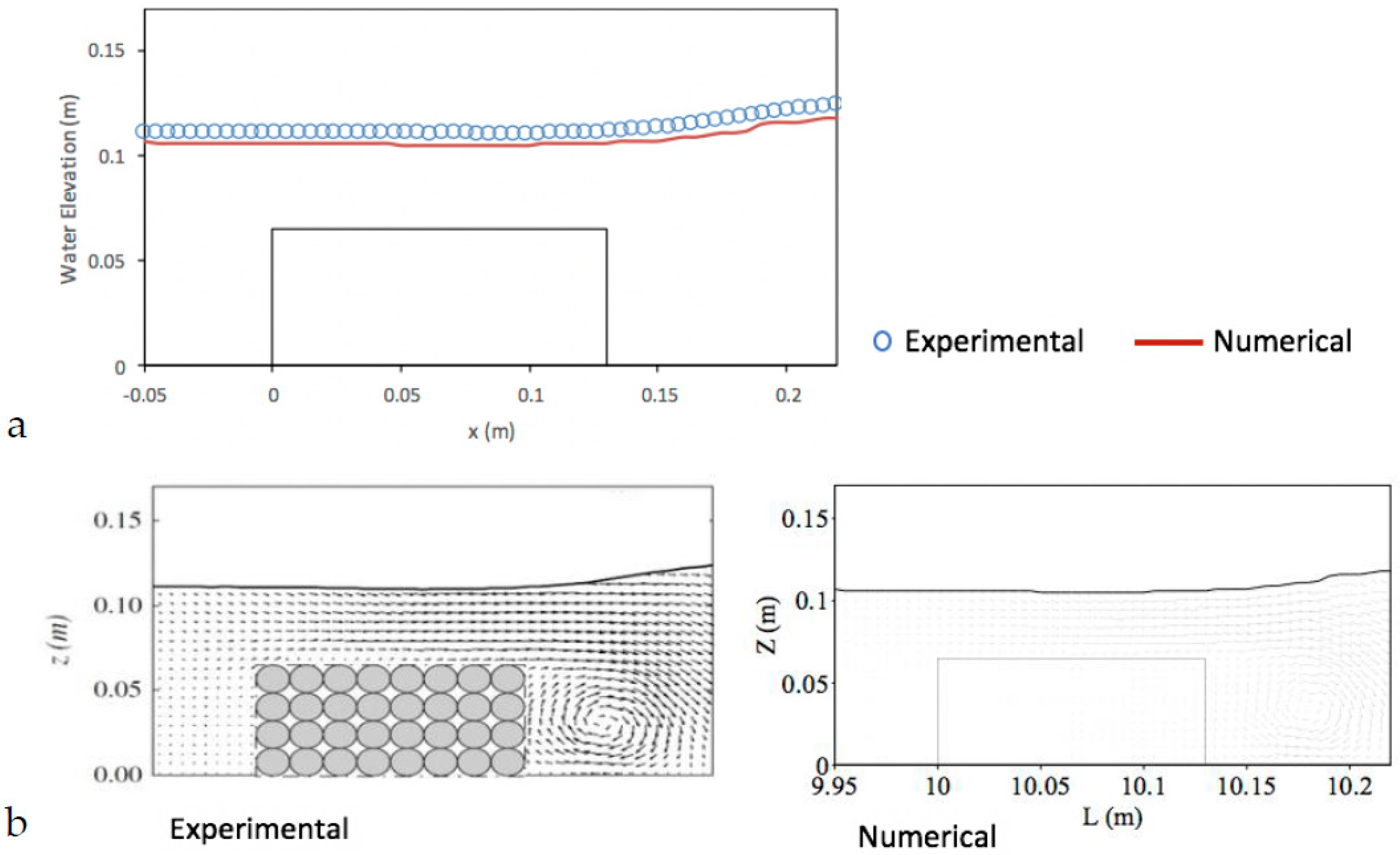
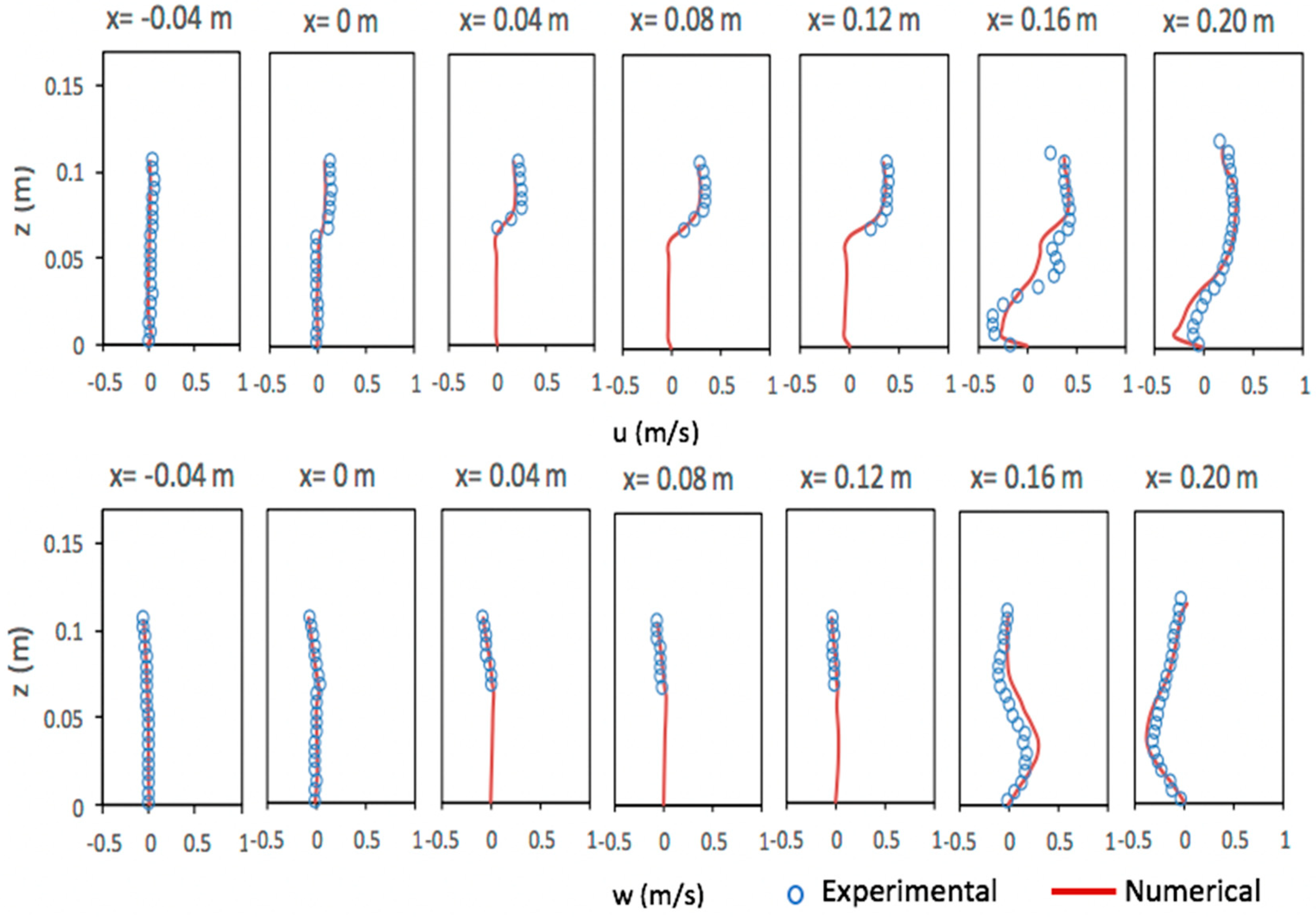
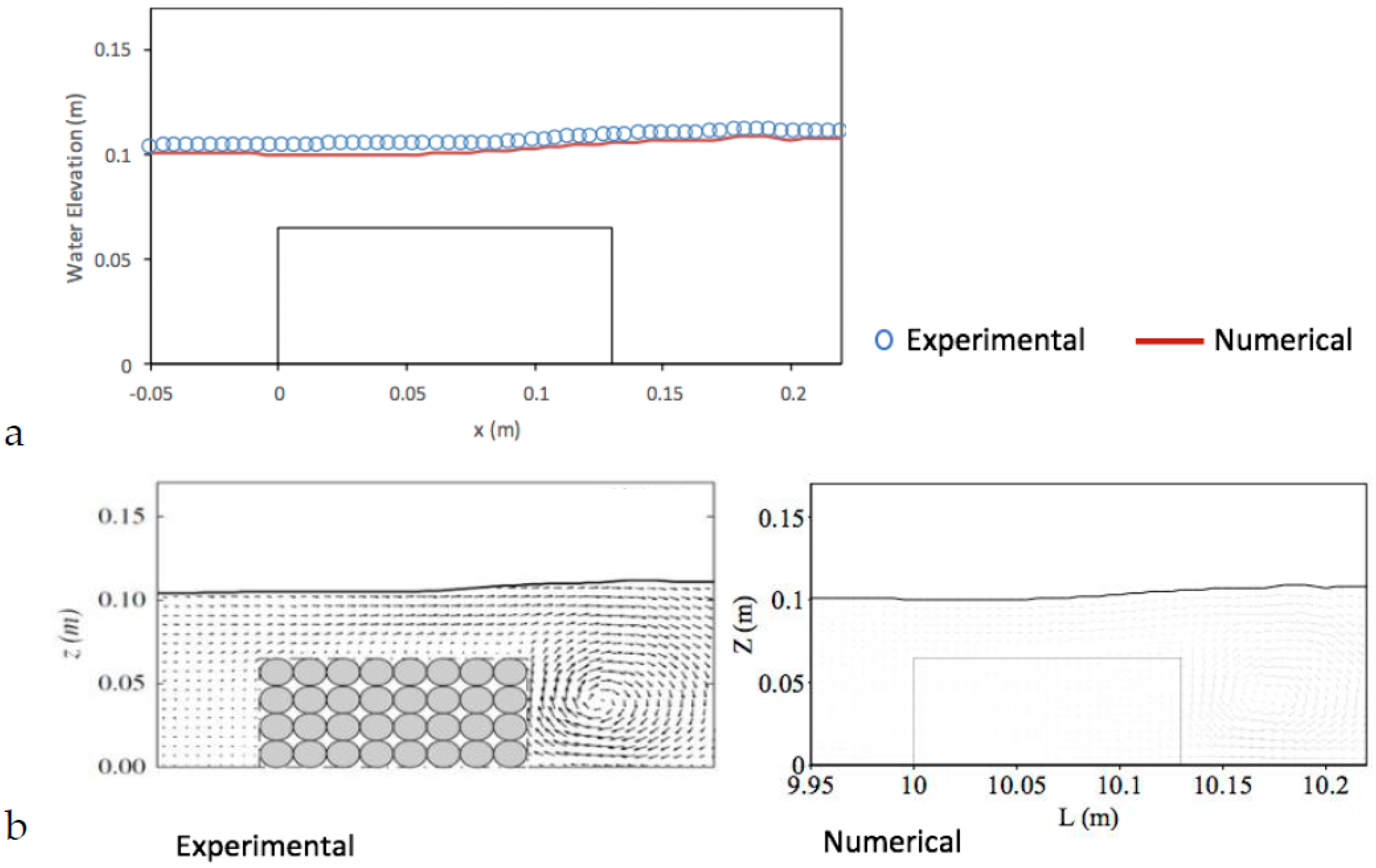
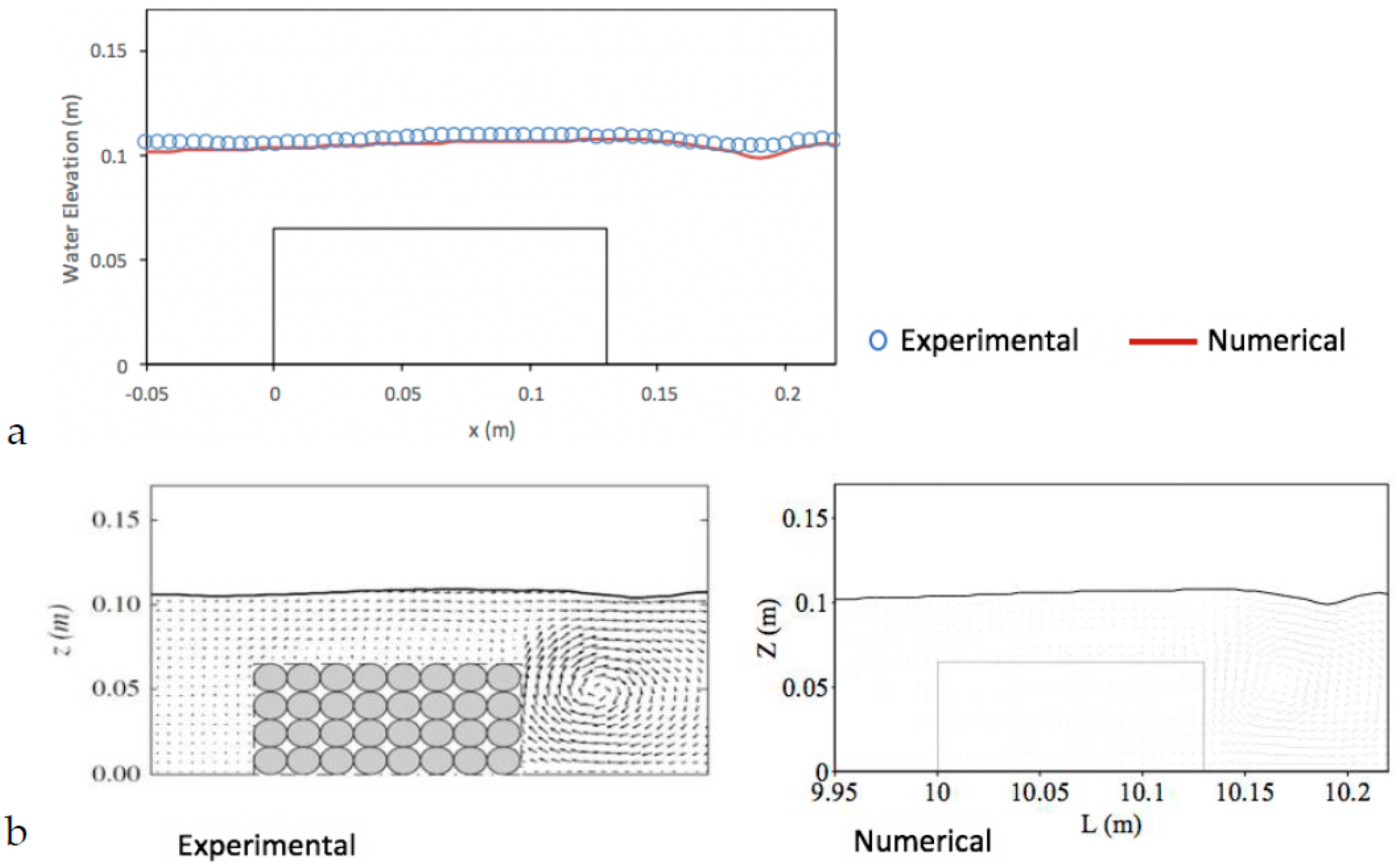
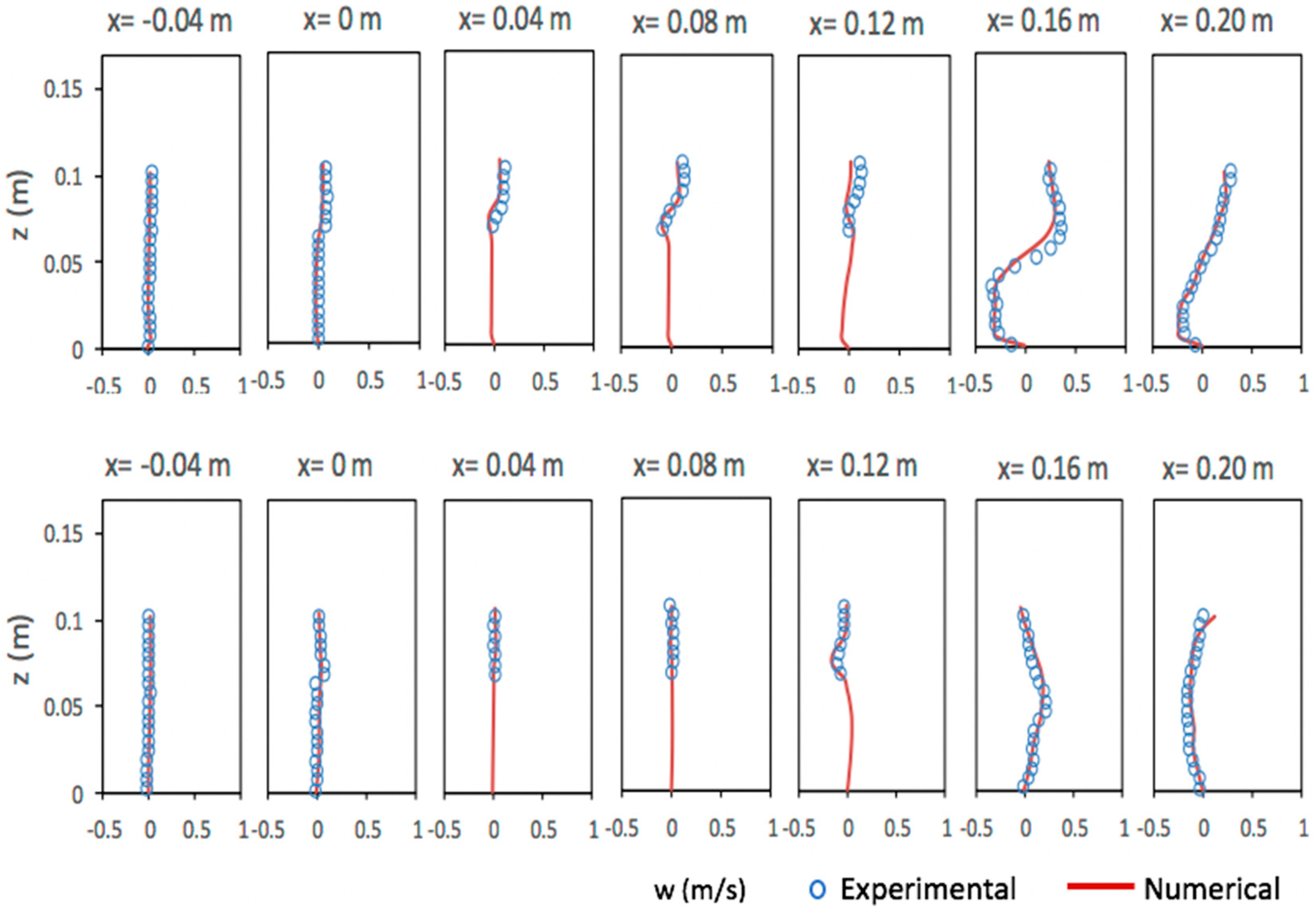
5.3. Solitary Wave Interaction with a Permeable Submerged Breakwater
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sollitt, C.K.; Cross, R.H. Wave transmission through permeable breakwaters. In Proceedings of the 13th International Conference on Coastal Engineering, Vancouver, BC, Canada, 10–14 July 1972; pp. 1827–1846. [Google Scholar]
- Rojanakamthorn, S.; Isobe, M.; Watanabe, A. A Mathematical Model of Wave Transformation over a Submerged Breakwater. Coast. Eng. Jpn. 1989, 32, 209–234. [Google Scholar] [CrossRef]
- Losada, I.; Silva, R.; Losada, M. Ángel 3-D non-breaking regular wave interaction with submerged breakwaters. Coast. Eng. 1996, 28, 229–248. [Google Scholar] [CrossRef]
- Méndez, F.J.; Losada, I.J.; Losada, M.A. Wave-Induced Mean Magnitudes in Permeable Submerged Breakwaters. J. Waterw. Port Coastal Ocean Eng. 2001, 127, 7–15. [Google Scholar] [CrossRef]
- Hsu, T.-W.; Chang, J.-Y.; Lan, Y.-J.; Lai, J.-W.; Ou, S.-H. A parabolic equation for wave propagation over porous structures. Coast. Eng. 2008, 55, 1148–1158. [Google Scholar] [CrossRef]
- Kobayashi, N.; Otta, A.K.; Roy, I. Wave Reflection and Run-Up on Rough Slopes. J. Waterw. Port Coastal Ocean Eng. 1987, 113, 282–298. [Google Scholar] [CrossRef]
- Kobayashi, N.; Wurjanto, A. Numerical model for waves on rough permeable slopes. J. Coast. Res. 1990, 7, 149–166. [Google Scholar]
- Wurjanto, A.; Kobayashi, N. Irregular Wave Reflection and Runup on Permeable Slopes. J. Waterw. Port Coastal Ocean Eng. 1993, 119, 537–557. [Google Scholar] [CrossRef]
- Van Gent, M. The modelling of wave action on and in coastal structures. Coast. Eng. 1994, 22, 311–339. [Google Scholar] [CrossRef]
- Cruz, E.C.; Isobe, M.; Watanabe, A. Boussinesq equations for wave transformation on porous beds. Coast. Eng. 1997, 30, 125–156. [Google Scholar] [CrossRef]
- Madsen, P.A.; Murray, R.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Coast. Eng. 1991, 15, 371–388. [Google Scholar] [CrossRef]
- Hsiao, S.-C.; Liu, P.L.-F.; Chen, Y. Nonlinear water waves propagating over a permeable bed. Proc. R. Soc. A Math. Phys. Eng. Sci. 2002, 458, 1291–1322. [Google Scholar] [CrossRef]
- Chen, Q. Fully Nonlinear Boussinesq-Type Equations for Waves and Currents over Porous Beds. J. Eng. Mech. 2006, 132, 220–230. [Google Scholar] [CrossRef]
- Hsiao, S.C.; Hu, K.C.; Hwung, H.H. Extended Boussinesq equations for water-wave propagation in porous media. J. Eng. Mech. 2009, 136, 625–640. [Google Scholar] [CrossRef]
- Sakakiyama, T.; Kajima, R. Numerical simulation of nonlinear wave interacting with permeable breakwaters. Coast. Eng. Proc. 1992, 1. [Google Scholar] [CrossRef]
- Van Gent, M.R.A. Wave Interaction with Permeable Coastal Structures. Ph.D. Thesis, Delft University of Technology, Stevinweg, The Netherlands, 1996; p. 27. [Google Scholar]
- Liu, P.L.-F.; Lin, P.; Chang, K.-A.; Sakakiyama, T. Numerical Modeling of Wave Interaction with Porous Structures. J. Waterw. Port Coastal Ocean Eng. 1999, 125, 322–330. [Google Scholar] [CrossRef]
- Hsu, T.-J.; Sakakiyama, T.; Liu, P.L.-F. A numerical model for wave motions and turbulence flows in front of a composite breakwater. Coast. Eng. 2002, 46, 25–50. [Google Scholar] [CrossRef]
- Huang, C.-J.; Chang, H.-H.; Hwung, H.-H. Structural permeability effects on the interaction of a solitary wave and a submerged breakwater. Coast. Eng. 2003, 49, 1–24. [Google Scholar] [CrossRef]
- Karunarathna, S.; Lin, P. Numerical simulation of wave damping over porous seabeds. Coast. Eng. 2006, 53, 845–855. [Google Scholar] [CrossRef]
- Del Jesus, M.; Lara, J.L.; Losada, I.J. Three-dimensional interaction of waves and porous coastal structures: Part I: Numerical model formulation. Coast. Eng. 2012, 64, 57–72. [Google Scholar] [CrossRef]
- Wu, Y.-T.; Hsiao, S.-C. Propagation of solitary waves over a submerged permeable breakwater. Coast. Eng. 2013, 81, 1–18. [Google Scholar] [CrossRef]
- Ma, G.; Shi, F.; Hsiao, S.-C.; Wu, Y.-T. Non-hydrostatic modeling of wave interactions with porous structures. Coast. Eng. 2014, 91, 84–98. [Google Scholar] [CrossRef]
- Bonovas, M.; Belibassakis, K.; Rusu, E. Multi-DOF WEC Performance in Variable Bathymetry Regions Using a Hybrid 3D BEM and Optimization. Energies 2019, 12, 2108. [Google Scholar] [CrossRef]
- Belibassakis, K.; Bonovas, M.; Rusu, E. A Novel Method for Estimating Wave Energy Converter Performance in Variable Bathymetry Regions and Applications. Energies 2018, 11, 2092. [Google Scholar] [CrossRef]
- Hejazi, K.; Soltanpour, M.; Sami, S. Numerical modeling of wave–mud interaction using projection method. Ocean Dyn. 2013, 63, 1093–1111. [Google Scholar] [CrossRef][Green Version]
- Chorin, A.J. Numerical solution of the Navier-Stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Temam, R. Sur l’approximation de la solution des équations de Navier-Stokes par la méthode des pas fractionnaires (II). Arch. Ration. Mech. Anal. 1969, 33, 377–385. [Google Scholar] [CrossRef]
- Yuan, H.; Wu, C.H. A two-dimensional vertical non-hydrostatic σ model with an implicit method for free-surface flows. Int. J. Numer. Methods Fluids 2004, 44, 811–835. [Google Scholar] [CrossRef]
- Yuan, H.; Wu, C.H. An implicit three-dimensional fully non-hydrostatic model for free-surface flows. Int. J. Numer. Methods Fluids 2004, 46, 709–733. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Company: Singapore, 1991; Volume 2. [Google Scholar]
- Le Méhauté, B. An Introduction to Hydrodynamics and Water Waves; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Lee, J.J.; Skjelbreia, J.E.; Raichlen, F. Measurement of velocities in solitary waves. J. Waterw. Port Coastal Ocean Div. 1982, 108, 200–218. [Google Scholar]
- Lin, P. Numerical Modeling of Water Waves; Informa UK Limited: Colchester, UK, 2014. [Google Scholar]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pourteimouri, P.; Hejazi, K. Development of An Integrated Numerical Model for Simulating Wave Interaction with Permeable Submerged Breakwaters Using Extended Navier–Stokes Equations. J. Mar. Sci. Eng. 2020, 8, 87. https://doi.org/10.3390/jmse8020087
Pourteimouri P, Hejazi K. Development of An Integrated Numerical Model for Simulating Wave Interaction with Permeable Submerged Breakwaters Using Extended Navier–Stokes Equations. Journal of Marine Science and Engineering. 2020; 8(2):87. https://doi.org/10.3390/jmse8020087
Chicago/Turabian StylePourteimouri, Paran, and Kourosh Hejazi. 2020. "Development of An Integrated Numerical Model for Simulating Wave Interaction with Permeable Submerged Breakwaters Using Extended Navier–Stokes Equations" Journal of Marine Science and Engineering 8, no. 2: 87. https://doi.org/10.3390/jmse8020087
APA StylePourteimouri, P., & Hejazi, K. (2020). Development of An Integrated Numerical Model for Simulating Wave Interaction with Permeable Submerged Breakwaters Using Extended Navier–Stokes Equations. Journal of Marine Science and Engineering, 8(2), 87. https://doi.org/10.3390/jmse8020087



