Downscaling Future Longshore Sediment Transport in South Eastern Australia
Abstract
1. Introduction
2. Methodological Review
2.1. Longshore Sediment Transport Models
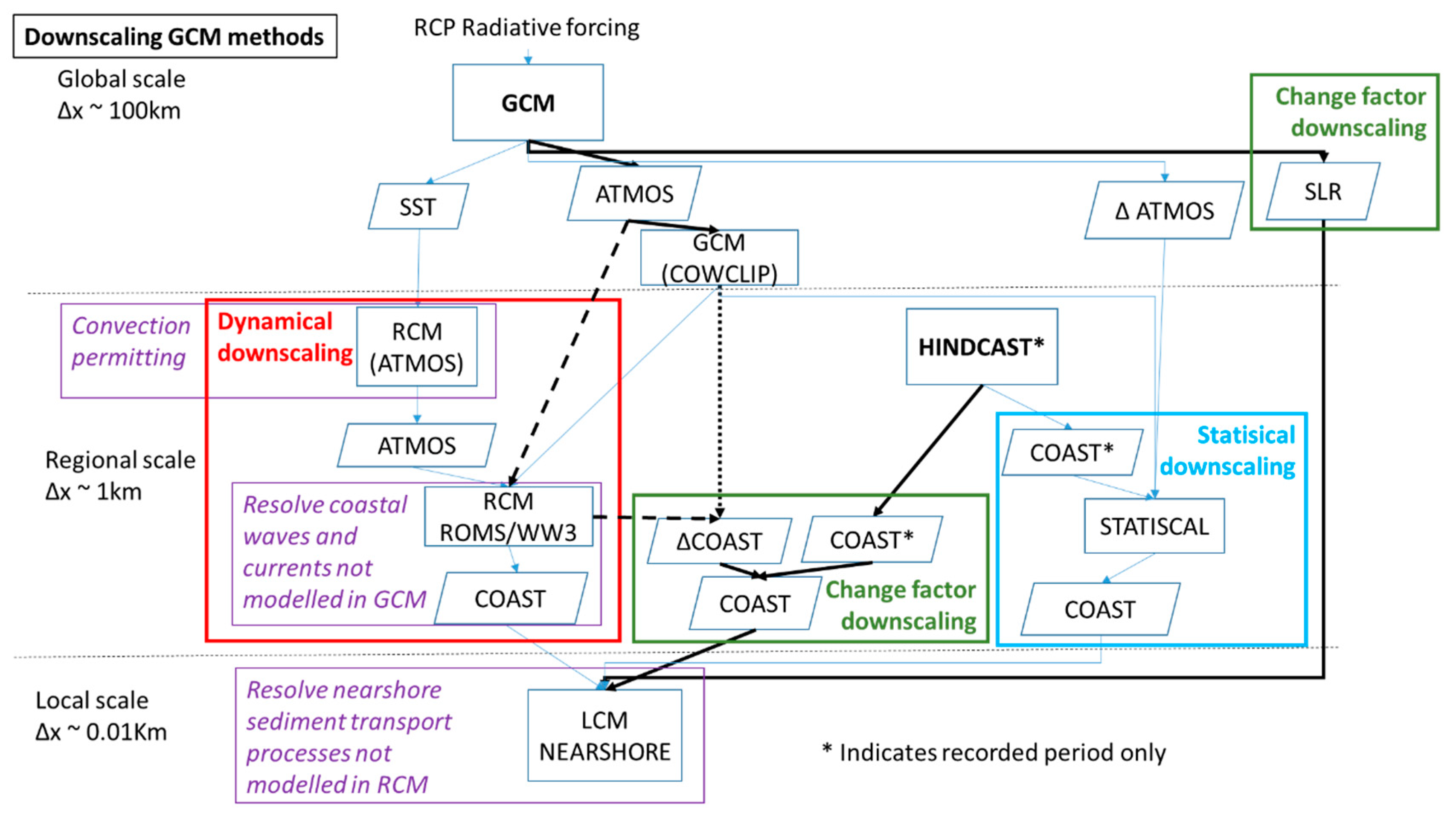
2.2. Downscaling
2.2.1. Dynamical Downscaling
2.2.2. Statistical Downscaling
2.2.3. Change Factor (CF) Downscaling
3. Datasets
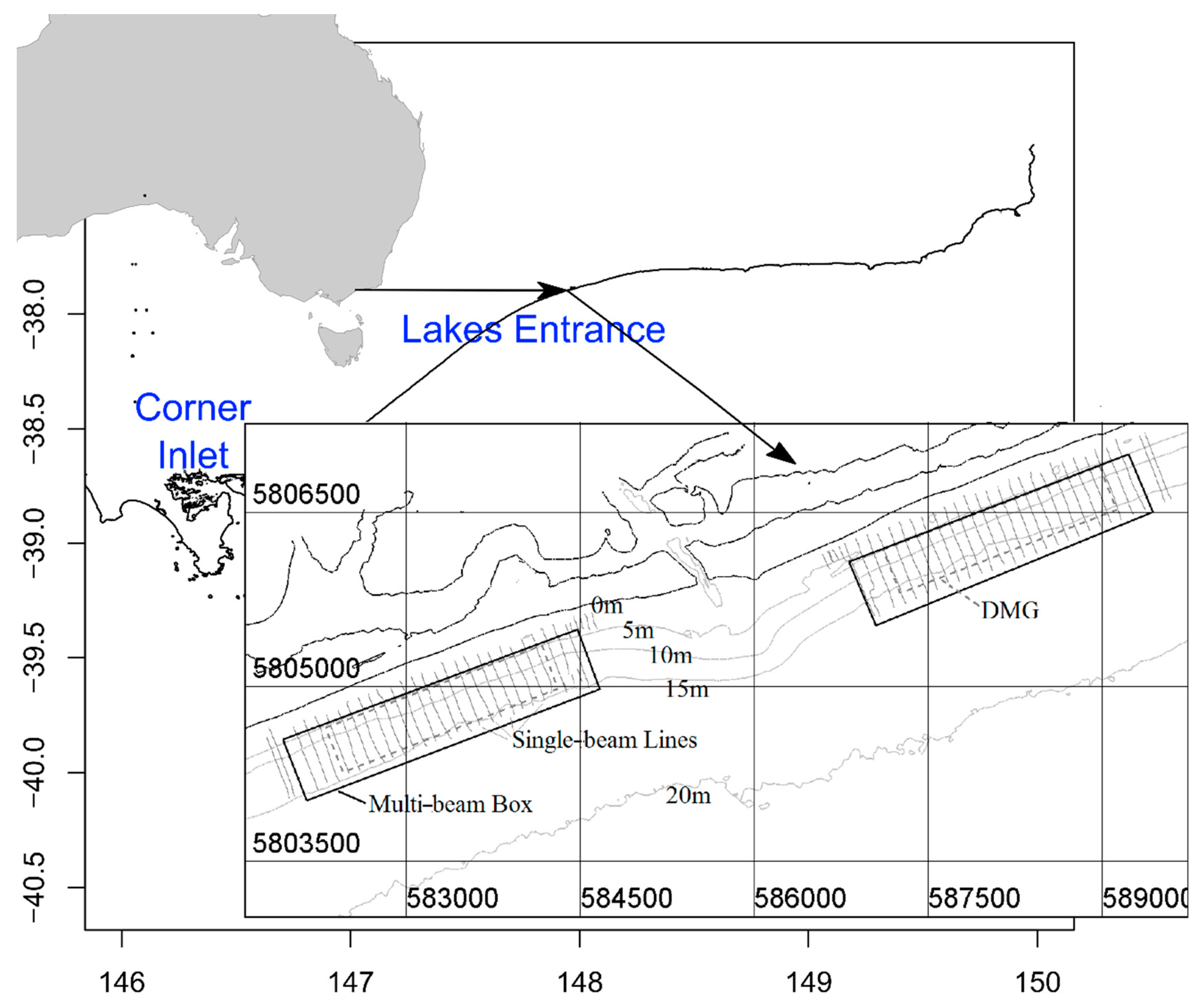
3.1. Wave and Hydrodynamic Measurements
3.2. Regional Wave and Hydrodynamic Model Forcing Data
3.3. Morphologic Measurements
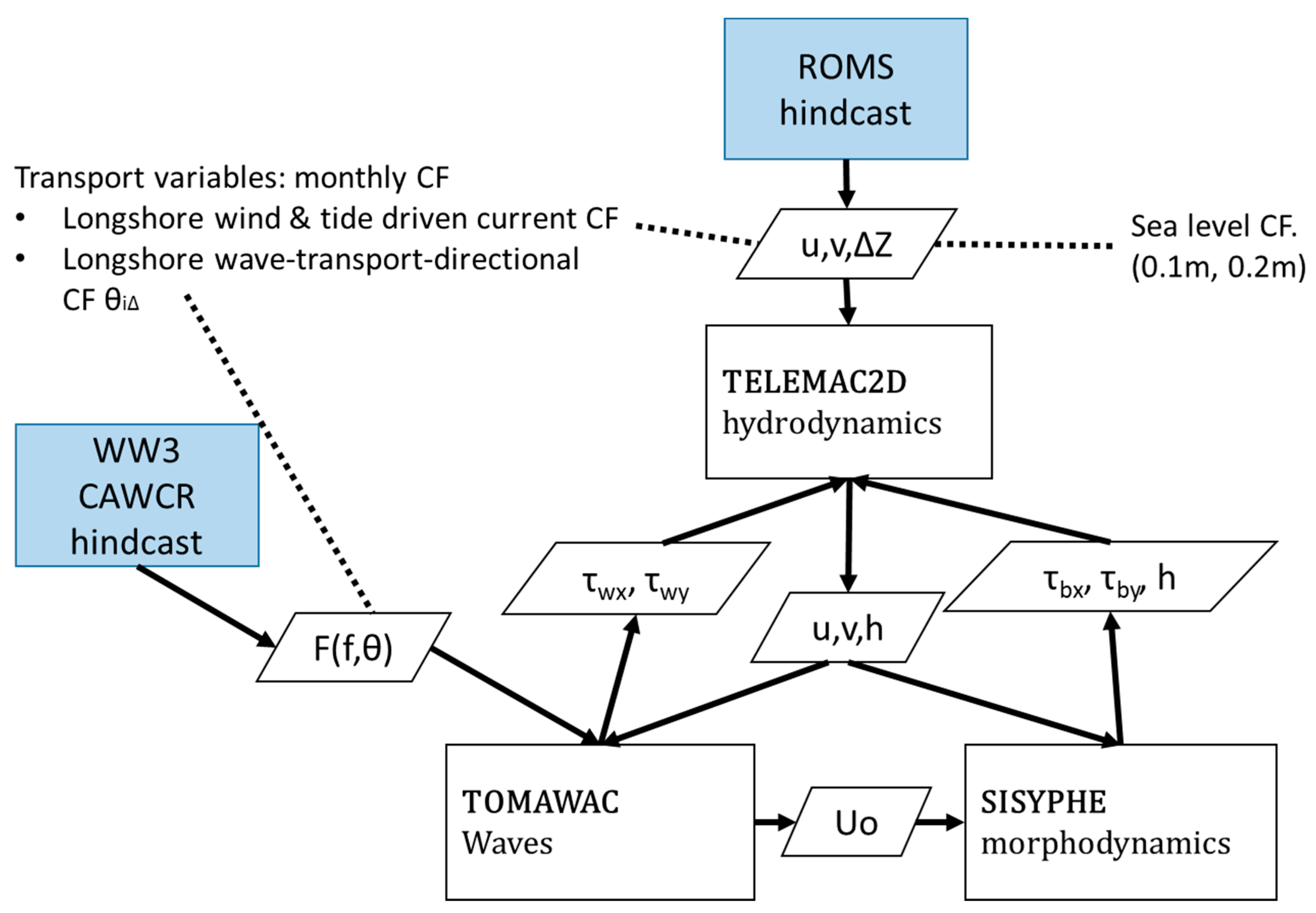
4. Methodology
4.1. Nearshore Numerical Local Climate Model
4.2. Change Factor Downscaling
4.3. Semi-Empirical NMB-LM Equation
5. Results
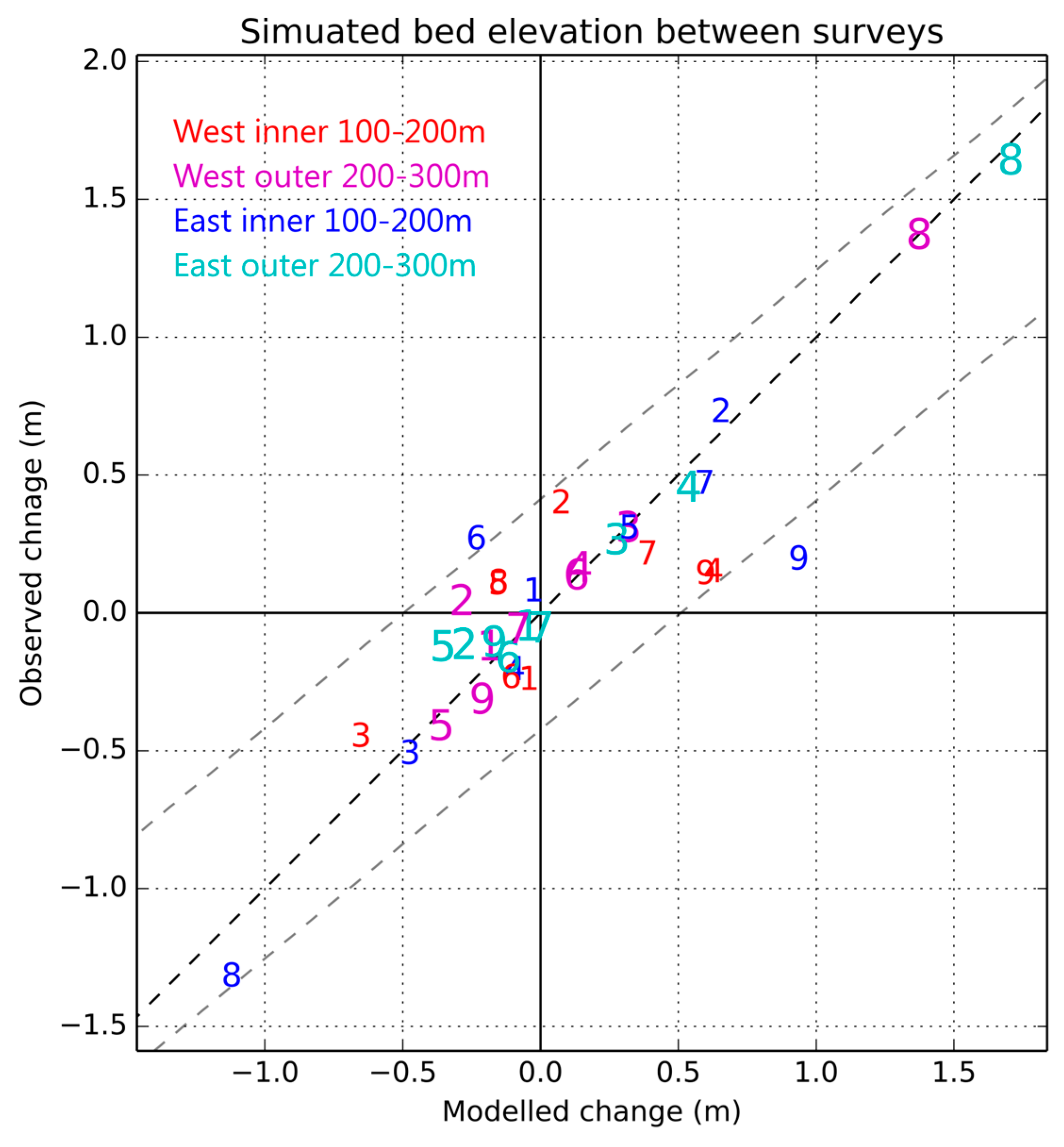
5.1. TELEMAC Sediment Transport Model Validation
5.2. Model Comparison
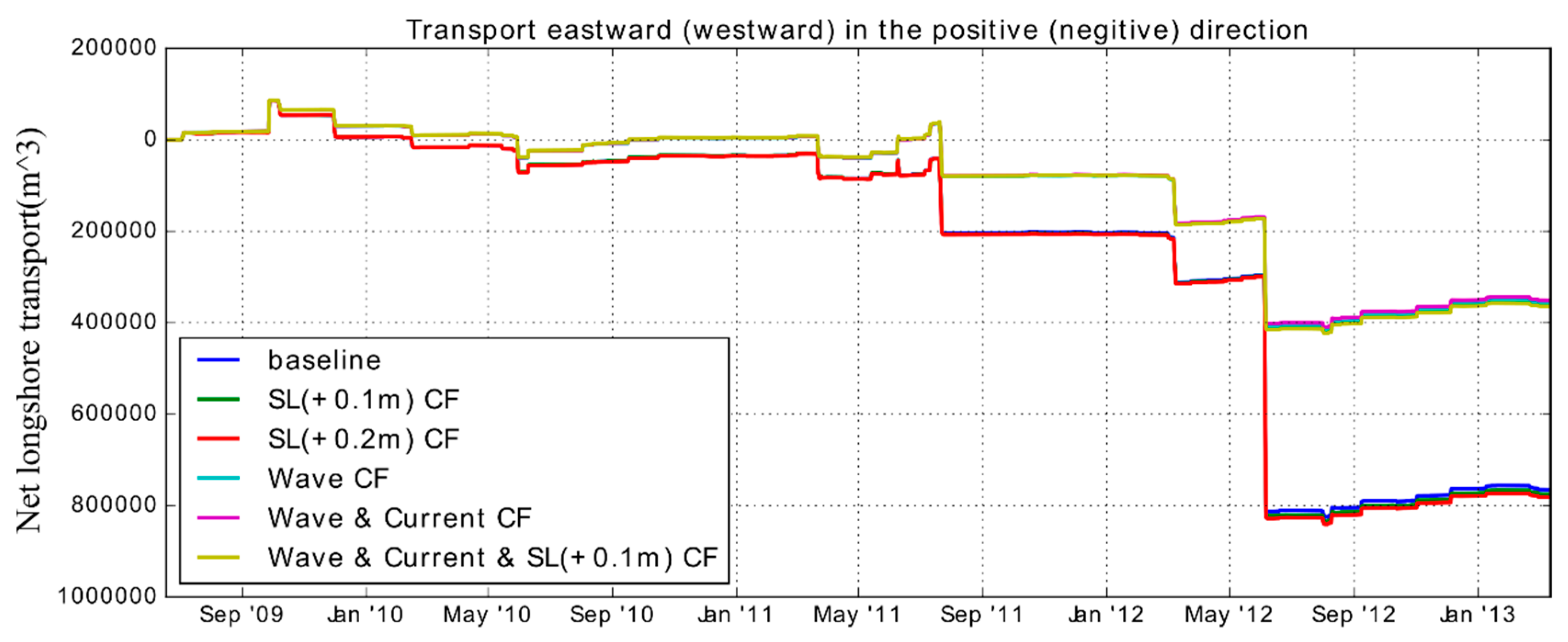
5.3. Downscaled Climate Change Analysis
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wong, P.; Lonsada, I.; Gattuso, J.; Hinkel, J.; Burkett, V.; Codignotto, J. Coastal Systems and Low-Lying Areas. In Climate Change 2014 Impacts, Adaptation and Vulnerability; Cambridge University Press: Cambridge, UK, 2014; pp. 361–410. ISBN 00472425. [Google Scholar]
- Bruun, P. Sea-level rise as a cause of shore erosion. J. Geol. 1962, 76–92. [Google Scholar]
- Aagaard, T.; Sørensen, P. Sea level rise and the sediment budget of an eroding barrier on the Danish North Sea coast. In Proceedings of the 12th International Coastal Symposium, Plymouth, UK, 8–12 April 2013; pp. 434–439. [Google Scholar]
- Houston, J.R.; Dean, R.G. Shoreline Change on the East Coast of Florida. J. Coast. Res. 2014, 30, 647–660. [Google Scholar]
- O’Grady, J.G.; McInnes, K.L.; Colberg, F.; Hemer, M.A.; Babanin, A.V.; O’Grady, J.G.; McInnes, K.L.; Colberg, F.; Hemer, M.A. Longshore Wind, Waves and Currents: Climate and Climate Projections at Ninety Mile Beach, South-eastern Australia. Int. J. Climatol. 2015, 35, 4079–4093. [Google Scholar] [CrossRef]
- Russell, K.; Rennie, J.; Sjerp, E. Gippsland State of the Coast Update; Water Technology: Melbourne, Australia, 2013. [Google Scholar]
- Hemer, M.A.; McInnes, K.L.; Ranasinghe, R. Climate and variability bias adjustment of climate model-derived winds for a southeast Australian dynamical wave model. Ocean Dyn. 2011, 62, 87–104. [Google Scholar] [CrossRef]
- Erikson, L.H.; Hegermiller, C.A.; Barnard, P.L.; Ruggiero, P.; van Ormondt, M. Projected wave conditions in the Eastern North Pacific under the influence of two CMIP5 climate scenarios. Ocean Model. 2015, 96, 171–185. [Google Scholar] [CrossRef]
- Mil-homens, J.; Ranasinghe, R.; De Vries, J.V.T.; Stive, M.J.F. Re-evaluation and improvement of three commonly used bulk longshore sediment transport formulas. Coast. Eng. 2013, 75, 29–39. [Google Scholar] [CrossRef]
- Tomasicchio, G.R.; Alessandro, F.D.; Barbaro, G.; Malara, G. General longshore transport model. Coast. Eng. 2013, 71, 28–36. [Google Scholar] [CrossRef]
- Bayram, A.; Larson, M.; Hanson, H. A new formula for the total longshore sediment transport rate. Coast. Eng. 2007, 54, 700–710. [Google Scholar] [CrossRef]
- Komar, P.D. The mechanics of sand transport on beaches. J. Geophys. Res. 1971, 76, 713. [Google Scholar] [CrossRef]
- Kamphuis, J.W.; Davies, M.H.; Nairn, R.B.; Sayao, O.J. Calculation of Littoral Sand Transport Rate. Coast. Eng. 1986, 10, 1–21. [Google Scholar] [CrossRef]
- van Rijn, L.C. A simple general expression for longshore transport of sand, gravel and shingle. Coast. Eng. 2014, 90, 23–39. [Google Scholar] [CrossRef]
- CERC. U.S. Army corps of Engineers shore protection manual-Volume I. Coast. Eng. Res. Cent. 1984, 1, 652. [Google Scholar]
- Van Rijn, L.C. Simple general formulae for sand transport in rivers, estuaries and coastal waters. Available online: www.leovanrijn-sediment.com (accessed on 11 November 2017).
- Roelvink, D.; Reniers, A. A Guide to Modelling Coastal Morphology; World Scientific: Singapore, 2011. [Google Scholar]
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation stresses in water waves; a physical discussion, with applications. Deep Sea Res. 1964, 11, 529–562. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. Longshore currents generated by obliquely incident sea waves: 1. J. Geophys. Res. 1970, 75, 6778. [Google Scholar] [CrossRef]
- van Rijn, L.C.; Walstra, D.-J.R.; van Ormondt, M. Unified View of Sediment Transport by Currents and Waves. IV: Application of Morphodynamic Model. J. Hydraul. Eng. 2007, 133, 776–793. [Google Scholar] [CrossRef]
- Vitousek, S.; Barnard, P.L.; Limber, P.; Erikson, L.; Cole, B. A model integrating longshore and cross-shore processes for predicting long-term shoreline response to climate change. J. Geophys. Res. Earth Surf. 2017, 122, 782–806. [Google Scholar] [CrossRef]
- Ashton, A.; Murray, A.B.; Arnault, O. Formation of coastline features by large-scale instabilities induced by high-angle waves. Nature 2001, 414, 296–300. [Google Scholar] [CrossRef] [PubMed]
- Szmytkiewicz, M.; Biegowski, J.; Kaczmarek, L.M.; Okroj, T.; Ostrowski, R.; Pruszak, Z.; Różyńsky, G.; Skaja, M. Coastline changes nearby harbour structures: Comparative analysis of one-line models versus field data. Coast. Eng. 2000, 40, 119–139. [Google Scholar] [CrossRef]
- GHD. Gippsland Lakes Ocean. Access Program. 2012 TSHD Maintenance Program. Final; Gippsland Ports: Bairnsdale, Australia, 2013. [Google Scholar]
- Samaras, A.G.; Gaeta, M.G.; Miquel, A.M.; Archetti, R. High-resolution wave and hydrodynamics modelling in coastal areas: Operational applications for coastal planning, decision support and assessment. Nat. Hazards Earth Syst. Sci. 2016, 16, 1499–1518. [Google Scholar] [CrossRef]
- Putzar, B.; Malcherek, A.M. Development of a long-term morphodynamic model for the German Bight. In Proceedings of the 19th Telemac-Mascaret User Conference, Oxford, UK, 18–19 October 2012; pp. 47–52. [Google Scholar]
- Chini, N.; Stansby, P. Broad-Scale Hydrodynamic Simulation, Wave Transformation and Sediment Pathways. In Broad Scale Coastal Simulation: New Techniques to Understand and Manage Shorelines in the Third Millennium; Nicholls, R.J., Dawson, R.J., Day, S.A., Eds.; Springer: Dordrecht, The Netherlands, 2015; pp. 103–124. ISBN 978-94-007-5258-0. [Google Scholar]
- Fowler, H.J.; Blenkinsop, S.; Tebaldi, C. Linking climate change modelling to impacts studies: Recent advances in downscaling techniques for hydrological modelling. Int. J. Climatol. 2007, 27, 1547–1578. [Google Scholar] [CrossRef]
- Ekström, M.; Grose, M.R.; Whetton, P.H. An appraisal of downscaling methods used in climate change research. Wiley Interdiscip. Rev. Clim. Chang. 2015, 6, 301–319. [Google Scholar] [CrossRef]
- Weisse, R.; von Storch, H. Past and future changes in wind, wave, and storm surge climates. In Marine Climate and Climate Change; Springer: Berlin/Heidelberg, Germany, 2010; pp. 165–203. [Google Scholar]
- Katzfey, J.J.; McGregor, J.; Nguyen, K.; Thatcher, M. Dynamical downscaling techniques: Impacts on regional climate change signals. In Proceedings of the 18th World IMACS Congress and MODSIM09 International Congress on Modelling and Simulation, Cairns, Australia, 13–17 July 2009; pp. 3942–3947. [Google Scholar]
- Kendon, E.J.; Ban, N.; Roberts, N.M.; Fowler, H.J.; Roberts, M.J.; Chan, S.C.; Evans, J.P.; Fosser, G.; Wilkinson, J.M. Do convection-permitting regional climate models improve projections of future precipitation change? Bull. Am. Meteorol. Soc. 2017, 98, 79–93. [Google Scholar] [CrossRef]
- Hemer, M.A.; McInnes, K.L.; Ranasinghe, R. Projections of climate change-driven variations in the offshore wave climate off south eastern Australia. Int. J. Climatol. 2013, 33, 1615–1632. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Voukouvalas, E.; Annunziato, A.; Giardino, A.; Feyen, L. Projections of extreme storm surge levels along Europe. Clim. Dyn. 2016, 47, 3171–3190. [Google Scholar] [CrossRef]
- Erikson, L.H.; Hemer, M.A.; Lionello, P.; Mendez, F.J.; Mori, N.; Semedo, A.; Wang, X.L.; Wolf, J. Projection of wave conditions in response to climate change: A community approach to global and regional wave downscaling. In The Coastal Sediments 2015; World Scientific: Singapore, 2015; p. 14. ISBN 9789814689977. [Google Scholar]
- Wandres, M.; Pattiaratchi, C.; Hemer, M.A. Projected changes of the southwest Australian wave climate under two atmospheric greenhouse gas concentration pathways. Ocean. Model. 2017, 117, 70–87. [Google Scholar] [CrossRef]
- Charles, E.; Idier, D.; Delecluse, P.; Déqué, M.; Le Cozannet, G.; Cozannet, G. Climate change impact on waves in the Bay of Biscay, France. Ocean. Dyn. 2012, 62, 831–848. [Google Scholar] [CrossRef]
- Howard, T.; Lowe, J.; Horsburgh, K. Interpreting century-scale changes in southern north sea storm surge climate derived from coupled model simulations. J. Clim. 2010, 23, 6234–6247. [Google Scholar] [CrossRef]
- Duong, T.M.; Ranasinghe, R.; Thatcher, M.; Mahanama, S.; Wang, Z.B.; Dissanayake, P.K.; Hemer, M.; Luijendijk, A.; Bamunawala, J.; Roelvink, D.; et al. Assessing climate change impacts on the stability of small tidal inlets: Part 1—Data poor environments. Mar. Geol. 2017, 390, 331–346. [Google Scholar] [CrossRef]
- Duong, T.M.; Ranasinghe, R.; Thatcher, M.; Mahanama, S.; Wang, Z.B.; Dissanayake, P.K.; Hemer, M.; Luijendijk, A.; Bamunawala, J.; Roelvink, D.; et al. Assessing climate change impacts on the stability of small tidal inlets: Part 2—Data rich environments. Mar. Geol. 2018, 395, 65–81. [Google Scholar] [CrossRef]
- Mortlock, T.R.; Goodwin, I.D.; McAneney, J.K.; Roche, K. The June 2016 Australian East Coast Low: Importance of wave direction for coastal erosion assessment. Water 2017, 9, 121. [Google Scholar] [CrossRef]
- Casas-Prat, M.; McInnes, K.L.; Hemer, M.A.; Sierra, J.P. Future wave-driven coastal sediment transport along the Catalan coast (NW Mediterranean). Reg. Environ. Chang. 2016, 16, 1739–1750. [Google Scholar] [CrossRef]
- Morim, J.; Hemer, M.; Cartwright, N.; Strauss, D.; Andutta, F. On the concordance of 21st century wind-wave climate projections. Glob. Planet. Change 2018, 167, 160–171. [Google Scholar] [CrossRef]
- Zhang, X.; Church, J.A.; Monselesan, D.; McInnes, K.L. Sea level projections for the Australian region in the 21st century. Geophys. Res. Lett. 2017, 44, 8481–8491. [Google Scholar] [CrossRef]
- Caires, S.; Swail, V.R.; Wang, X.L. Projection and analysis of extreme wave climate. J. Clim. 2006, 19, 5581–5605. [Google Scholar] [CrossRef]
- Von Storch, H.; Reichardt, H. A scenario of storm surge statistics for the german bight at the expected time of doubled atmospheric carbon dioxide concentration. J. Clim. 1997, 10, 2653–2662. [Google Scholar] [CrossRef]
- Antolínez, J.A.A.; Murray, A.B.; Méndez, F.J.; Moore, L.J.; Farley, G.; Wood, J. Downscaling Changing Coastlines in a Changing Climate: The Hybrid Approach. J. Geophys. Res. Earth Surf. 2018, 123, 229–251. [Google Scholar] [CrossRef]
- Anandhi, A.; Frei, A.; Pierson, D.C.; Schneiderman, E.M.; Zion, M.S.; Lounsbury, D.; Matonse, A.H. Examination of change factor methodologies for climate change impact assessment. Water Resour. Res. 2011, 47, 1–10. [Google Scholar] [CrossRef]
- Katzfey, J.J.; McInnes, K.L. GCM simulations of eastern Australian cutoff lows. J. Clim. 1996, 9, 2337–2355. [Google Scholar] [CrossRef]
- McInnes, K.L.; Hubbert, G.D. The impact of eastern Australian cut-off lows on coastal sea levels. Meteorol. Appl. 2001, 8, 229–243. [Google Scholar] [CrossRef]
- O’Grady, J.G. Nearshore Modelling of Longshore Sediment Transport in the Application to Climate Change Studies at Ninety Mile Beach, Australia. Ph.D. Thesis, Swinburne University of Technology, Melbourne, Australia, 2018. [Google Scholar]
- Durrant, T.; Greenslade, D.; Hemer, M.A.; Trenham, C. Global Wave Hindcast Focussed on the Central and South. Pacific; CAWCR: Aspendale, Australia, 2014. [Google Scholar]
- Colberg, F.; McInnes, K.L.; O’Grady, J.; Hoeke, R.K. Atmospheric Circulation Changes and their Impact on Extreme Sea Levels around Australia. Nat. Hazards Earth Syst. Sci. 2019, 19, 1067–1086. [Google Scholar] [CrossRef]
- Sinclair, M.J.; Quadros, N. Airborne Lidar Bathymetric Survey for Climate Change Airborne Lidar Bathymetric Survey for Climate Change; Springer: Berlin/Heidelberg, Germany, 2010; pp. 11–16. [Google Scholar]
- Wright, L.D.; Nielsen, P.; Short, A.D.; Coffey, F.C.; Green, M.O. Nearshore and Surfzone Morphodynamics of a Storm Wave Environment Eastern Bass Strait; Sydney Univ, Australian Coastal Studies Unit: Sydney, Australia, 1982. [Google Scholar]
- Hervouet, J.-M. Hydrodynamics of Free Surface Flows: Modelling With the Finite Element Method; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Villaret, C.; Hervouet, J.-M.M.; Kopmann, R.; Merkel, U.; Davies, A.G. Morphodynamic modeling using the Telemac finite-element system. Comput. Geosci. 2013, 53, 105–113. [Google Scholar] [CrossRef]
- Saint-Venant, B.D. Theory of unsteady water flow, with application to river floods and to propagation of tides in river channels. French Acad. Sci. 1871, 73, 237–240. [Google Scholar]
- Benoit, M.; Marcos, F.; Becq, F. Development of a third generation shallow-water wave model with unstructured spatial meshing. Coast. Eng. Proc. 1996, 465–478. [Google Scholar]
- Battjes, J.A.; Janssen, J.P.F.M. Energy Loss and Set-Up Due To Breaking of Random Waves. Coast. Eng. Proc. 1978, 569–587. [Google Scholar]
- Miche, A. Mouvements ondulatoires de la mer en profondeur croissante ou decroissante. Ann. des Ponts Chaussees 1944, 144, 369–406. [Google Scholar]
- Soulsby, R.L. Dynamics of Marine Sands; Thomas Telford: London, UK, 1997. [Google Scholar]
- Wright, L.D.; Nielsen, P.; Shi, N.C.; List, J.H. Morphodynamics of a bar-trough surf zone. Mar. Geol. 1986, 70, 251–285. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex algorithm for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.; Nunn, P.D.; et al. Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. In Sea Level Change; Cambridge University Press: Cambridge, UK, 2013; pp. 1137–1216. [Google Scholar]
- Kamphuis, J.W. Alongshore Sediment Transport Rate. J. Waterw. Port. Coastal Ocean. Eng. 1991, 117, 624–640. [Google Scholar] [CrossRef]
- Nielsen, P.; Callaghan, D.P. Shear stress and sediment transport calculations for sheet flow under waves. Coast. Eng. 2003, 47, 347–354. [Google Scholar] [CrossRef]
- Van Rijn, L.; Ribberink, J.S.; van der Werf, J.J.; Walstra, D.J.R. Coastal sediment dynamics: Recent advances and future research needs. J. Hydraul. Res. 2013, 51, 475–493. [Google Scholar] [CrossRef]
- Davies, A.G.; Villaret, C. Eulerian drift induced by progressive waves above rippled and very rough beds. J. Geophys. Res. 1999, 104, 1465–1488. [Google Scholar] [CrossRef]
- Nielsen, P. Dynamics and geometry of wave-generated ripples. J. Geophys. Res. Oceans 2006, 86, 6467–6472. [Google Scholar] [CrossRef]
- Smith, G.A.; Babanin, A.V.; Riedel, P.; Young, I.R.; Oliver, S.; Hubbert, G. Introduction of a new friction routine into the SWAN model that evaluates roughness due to bedform and sediment size changes. Coast. Eng. 2011, 58, 317–326. [Google Scholar] [CrossRef]
- Villaret, C.; Huybrechts, N.; Davies, A.G.; Way, O. Effect of bed roughness prediction on morphodynamic modelling: Application to the Dee estuary (UK) and to the Gironde estuary (France). In Proceedings of the 34th IAHR World Congress, Brisbane, Australia, 26 June–1 July 2011; pp. 1149–1156. [Google Scholar]
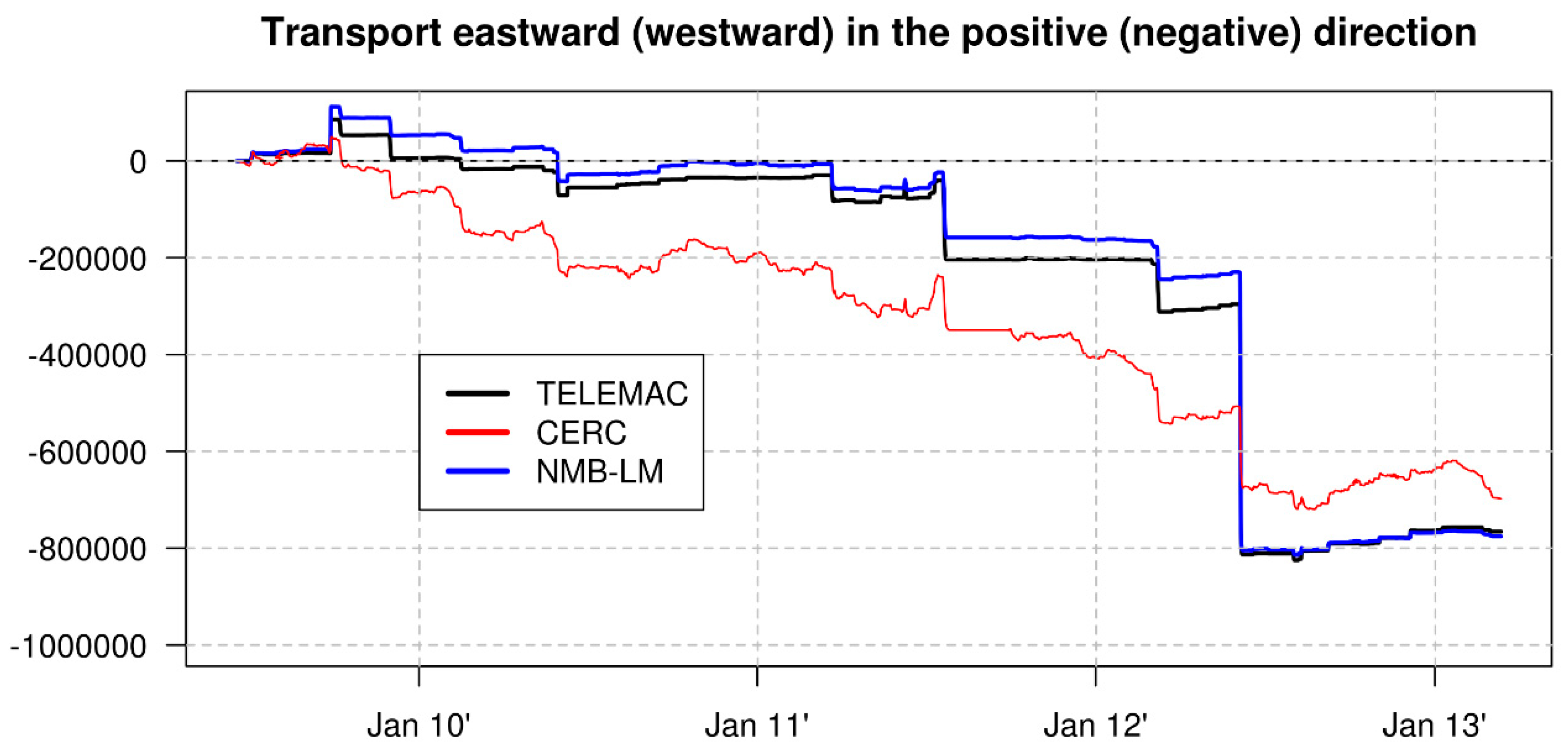
| Transport Per Year (m3 m−1 year−1) | TELEMAC | CERC | NMB-LM |
|---|---|---|---|
| ~3.7 year TELEMAC survey simulation period | −211,598 | −193,379 | −214,308 |
| ~30 year hindcast ROMs period | Not resolved. | −206,494 | −100,741 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
O’Grady, J.; Babanin, A.; McInnes, K. Downscaling Future Longshore Sediment Transport in South Eastern Australia. J. Mar. Sci. Eng. 2019, 7, 289. https://doi.org/10.3390/jmse7090289
O’Grady J, Babanin A, McInnes K. Downscaling Future Longshore Sediment Transport in South Eastern Australia. Journal of Marine Science and Engineering. 2019; 7(9):289. https://doi.org/10.3390/jmse7090289
Chicago/Turabian StyleO’Grady, Julian, Alexander Babanin, and Kathleen McInnes. 2019. "Downscaling Future Longshore Sediment Transport in South Eastern Australia" Journal of Marine Science and Engineering 7, no. 9: 289. https://doi.org/10.3390/jmse7090289
APA StyleO’Grady, J., Babanin, A., & McInnes, K. (2019). Downscaling Future Longshore Sediment Transport in South Eastern Australia. Journal of Marine Science and Engineering, 7(9), 289. https://doi.org/10.3390/jmse7090289






