1. Introduction
Model-scale physical testing is essential in the development of wave energy converters and especially for the advancement through the Technology Readiness Levels (TRLs) [
1]. Oscillating Water Column (OWC) devices are a major class of wave energy converters that have been the object of extensive research and development effort over many years, including the deployment of prototypes at sea [
2]. The OWC converter consists of a hollow (fixed or floating) structure, open to the sea below the water surface. Wave action alternately compresses and decompresses the air trapped above the inner water free-surface in the OWC chamber, converting wave energy into pneumatic energy. Different types of OWC devices can be distinguished on the basis of their working principle for harnessing the pneumatic energy. The most commonly-studied type of OWC device, which will be referred to as the conventional type in the rest of the paper, is equipped with a self-rectifying turbine located on top of the OWC chamber and connecting it with the atmosphere. The compression and decompression of the air in the OWC chamber forces air in and out of the chamber through the turbine, which is coupled to a generator. Self-rectifying turbines are able to harness both directions of air flow, but there efficiency is lower than a unidirectional turbine. Conventional OWC devices have been installed on the shoreline, standing near shore on the sea floor, incorporated into breakwaters or deployed offshore as floating structures. Other types of OWC devices use non-return valves to rectify the air flow across a unidirectional turbine. Various flow-rectifying OWC devices have been studied, such as Masuda’s navigation buoy [
2], the Kaimei [
3], the Leancon [
4], the vented OWC from Wave Swell Energy [
5] and the Tupperwave device [
6], all using different air flow rectification methods for rectifying the air flow.
In a full-scale conventional OWC device, the compressibility of the air in the OWC chamber acts as a brief storage of energy and introduces a phase shift between the air flow rate displaced by the water column and the flow rate across the turbine. This effect is called the spring-like effect and plays an important role in large-scale OWC devices [
7] and especially on the dynamic motion of the water column relative to the device structure. For accurate modelling of an OWC device, either numerically or physically, the spring-like effect of air needs to be taken into account.
Numerically, the modelling of air compressibility is easily achievable by using the linearised isentropic relationship between air density and pressure [
8]. Physically, modelling air compressibility in model-scale OWC devices can be demanding. Hydrodynamic similarity at model scale is commonly achieved using Froude scaling, which respects the geometrical similarity of the underwater part of the device by multiplying all geometrical dimensions by the Froude scaling factor
. Air compressibility in an air chamber is however not scalable with the Froude similarity law. It was recognized in [
9] that, to scale adequately air compressibility in an air chamber, the ratio between the air chamber volume of the model and full-scale device has to be equal to
and not to
as the Froude similarity would suggest. The required volume for the chamber is therefore a lot bigger than the volume suggested by Froude similarity. The solution to implement this method, without changing the geometry of the device on the water, is to connect the device chamber to an external reservoir of the required volume with a pipe, as was done in [
9,
10] on small bottom-fixed conventional OWC devices.
Implementing this method on a floating OWC devices is particularly difficult because the connection of a stationary air volume with the floating OWC may introduced elastic, damping and inertia forces associated with the motion and deformation of the flexible pipes. The difficulty of implementing this method increases with the scale of the tested device because the volume of the additional reservoirs increases with the square of the scaling factor. The method quickly becomes unpractical.
Moreover, this method introduces another dissimilarity between the full-scale device and the physical model: the relative volume change of the OWC chamber due to the elevation of the internal water column becomes much smaller in the physical model than in the full-scale device, thus omitting non-linearities due to significant volume changes in the full-scale device [
11].
Since the spring-like effect of the air in conventional OWC chambers is not fundamental to the working principle, it is often neglected in tank testing. Certain types of OWC devices do however rely on air compressibility to work, and the correct modelling of air compressibility at model scale is therefore important. This is the case for the Tupperwave device, which was physically tested at 1/24
th scale [
12]. The Tupperwave device is a floating OWC device, and more than three cubic meters of additional air reservoirs are connected to the floating device, making the testing particularly challenging.
The practical implementation difficulty of modelling air compressibility at model scale using additional fixed volume air reservoirs motivates the search for other approaches. In the present paper, a method for modelling air compressibility in OWC devices using deformable volume chambers is presented. The chamber deformation mimics the air compression or decompression by storing energy under the form of strain energy. A similar idea was already mentioned in [
13].
Section 2 of this paper mathematically demonstrates the possibility of modelling air compressibility happening in a large air chamber using a smaller chamber with slightly deformable walls.
Section 3 describes the effect of deformable air chambers observed during the model scale testing of the Tupperwave device.
Section 4 finally identifies practical applications to the new method and presents a new concept of OWC.
2. Deformable Volume Air Chamber
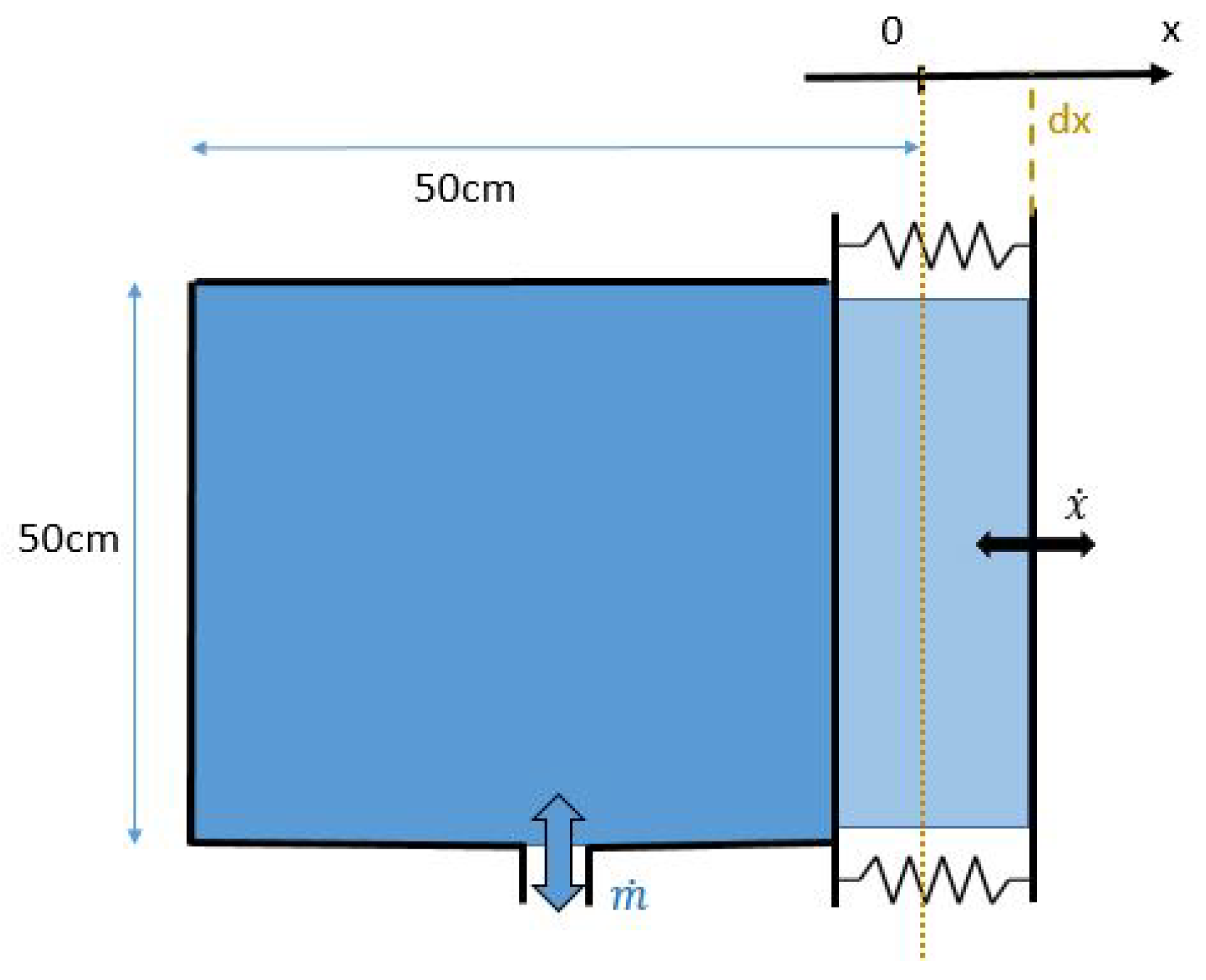
Consider the following open thermodynamic system: an air chamber containing a mass
m of air at the density
and at pressure
. The air mass flow rates
and
flow respectively in and out of the chamber. They are functions of the air excess pressure
. It is assumed that the transformations are slow enough for the thermodynamic state of air in the chamber to be uniform. The volume
of the chamber is elastically deformable, and the chamber walls have no inertia. Hence,
evolves linearly with the excess pressure such that:
where
is the initial volume of the chamber when the inner pressure equals atmospheric pressure and
C is the chamber deformation coefficient in
. We note that the excess pressure
can either be positive or negative. A dot over a variable indicates the variable’s derivative taken with respect to time.
It is assumed that in the pressure conditions considered, the volume variation of the chamber remains small compared to the initial volume:
and the air density variation remain small compared to atmospheric density:
Neglecting second order terms, the mass conservation equation in the system is:
Equation (
4) informs that the variation of mass in the chamber is the sum of two phenomena: air density variations (compressibility) and chamber volume variations.
The mass balance equation gives:
where
and
are the air mass flow rates flowing respectively in and out of the chamber.
If the system is considered adiabatic and the transformations slow enough to be reversible, the transformations become isentropic, and consequently, we may write:
where
is the air heat capacity ratio. Moreover, in the case where the excess pressure remains small compared to the atmospheric pressure, it is possible to linearise the isentropic relationship between density and pressure. Once linearised, Equation (
6) leads to:
and to:
Using Equations (
4), (
5), and (
8), the pressure variation in the deformable chamber can be written as:
Finally, using the derivative of Equation (
1) in Equation (
9), we can write:
We now consider a larger air chamber of fixed volume
, subjected to the same incoming and outcoming mass flow rates
and
.
is the air pressure in this chamber.
being a fixed volume, the mass variation of air in the chamber is only made possible by the compressibility of the air:
In a like manner as Equation (
9), the pressure variation in the fixed volume chamber is:
By analogy to Equations (
10) and (
12), it is clear that the pressures
in the elastically-deformable chamber and
in the fixed volume chamber will evolve in the same way if:
It is thus possible to mimic air compressibility effects happening in a large fixed volume chamber of volume
while using a smaller chamber of volume
, which is slightly elastically deformable with a deformation coefficient
C. It is however important to keep in mind that the conditions given by Equation (
2) and (
3) need to be respected. The possibility of using variable volume air chambers to model air compressibility effects in larger fixed volume chambers finds an application in model-scale testing of OWC devices. In the next section, the effect of air chamber volume variation is observed in a practical case.
3. Tank Testing of the Tupperwave Device
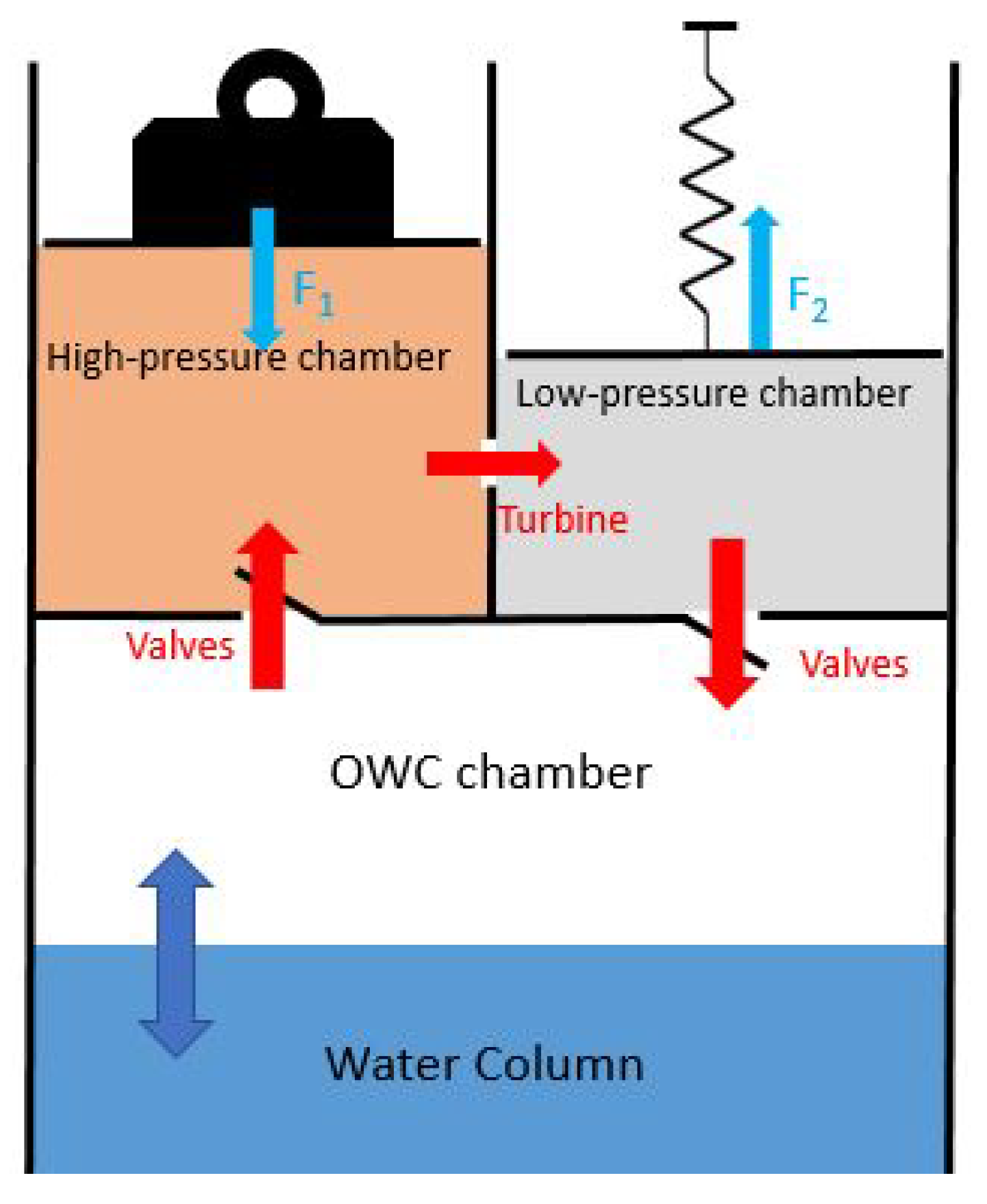
The Tupperwave concept is a flow-rectifying OWC working in closed-circuit, which uses non-return valves and two large fixed volume chambers acting as accumulators.
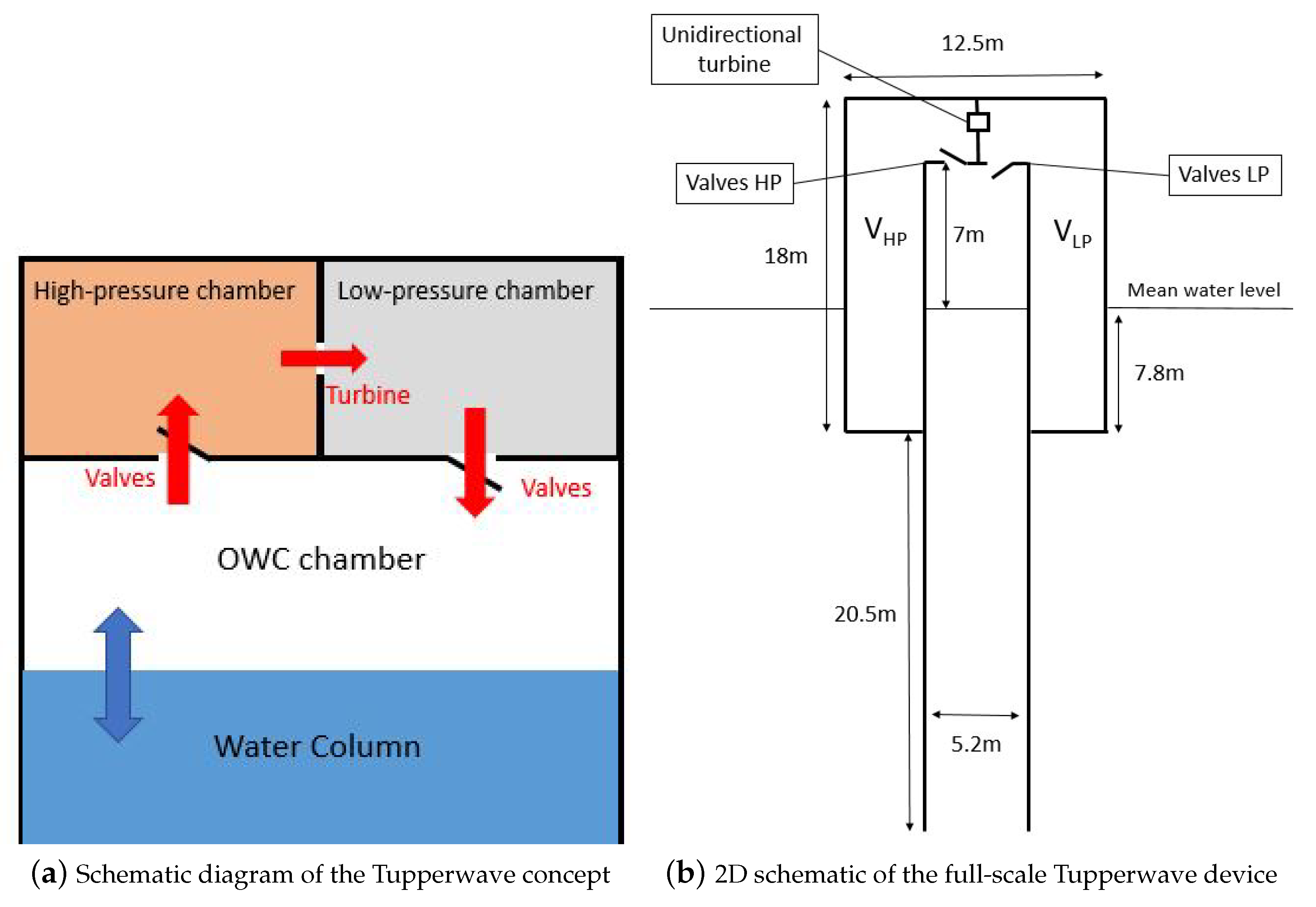
Figure 1a displays a schematic of the Tupperwave working principle: when the water column rises, air is compressed in the High-Pressure (HP) chamber, and when the water falls, the air is sucked from the Low-Pressure (LP) chamber. The continuous oscillatory motion of the water column creates a pressure differential between the HP and LP chambers, which creates a smooth unidirectional flow across the unidirectional turbine located in between. The Tupperwave working principle was studied in [
6] and applied to a floating spar buoy.
Figure 1b displays the geometry of the full-scale Tupperwave device. The volume of the HP and LP chambers has a constant value of
each, providing also buoyancy volume.
The Tupperwave working principle entirely relies on air compressibility in the HP and LP chambers. For this reason, it is essential to reproduce correctly air compressibility in the two chambers at model scale. The device was physically modelled and tested at
scale. The experiments took place at the Lir-National Ocean Test Facility (Lir-NOTF) of the MaREI centre in Cork, Ireland. The device was tested under regular and irregular sea states in the Deep Ocean Basin, which is 35 m long, 12 m wide, and 3 m deep. More details on the device fabrication and test setup can be found in [
12]. The exact Froude scaling ratio was
. To reproduce air compressibility, the volumes of the chambers on the model were scaled by
and were
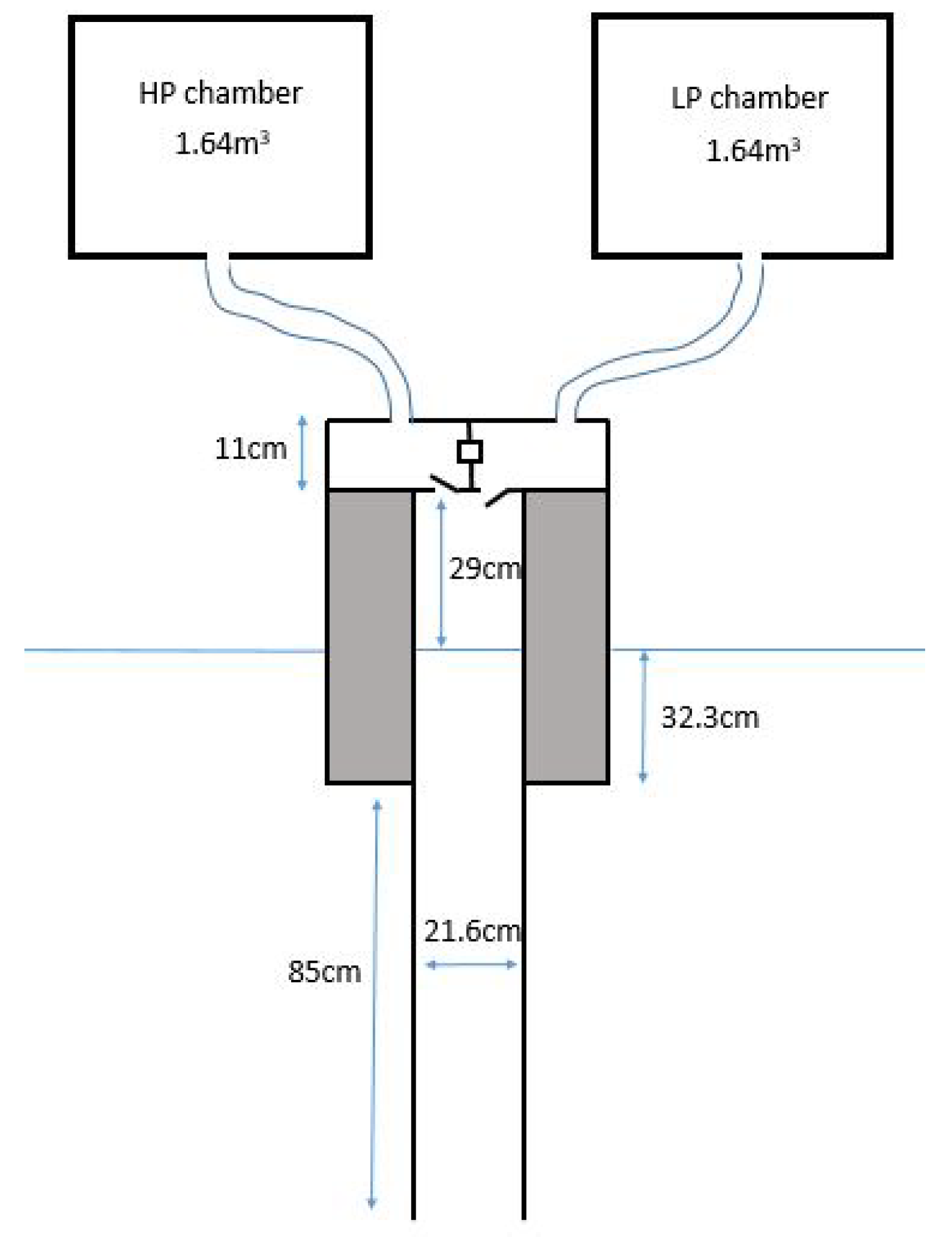
each. Unlike for the full scale, it is impossible to fit both chambers on the device as their volume largely exceeds the overall volume of the device. The alternative at small scale is to locate the main volume of the HP and LP chambers outside of the device and connect them to two smaller chambers on the device with flexible pipes. Large reservoirs were used for the HP and LP chambers and located on the pedestrian bridge above the tank.
Figure 2 displays the schematic of the device with the external reservoirs. The flexible pipes were chosen as lightweight and flexible as possible to reduce their influence on the floating device motion. Part of the pipes’ weight was supported by bungee ropes; see
Figure 3.
It is important to note that the modelling of the air compressibility effects in the OWC chamber was omitted during the experiment since it is not essential in the device working principle. In the case of conventional OWC devices, it is well-established that failure to model air compressibility effects results in an over-estimation of the device performance [
7,
14,
15]. In the case of the Tupperwave device, similar consequences are expected. However, modelling the air compressibility in the OWC chamber of the Tupperwave device would have increased the difficulty of the testing, as it would have required one more additional chamber on the bridge and one more flexible pipe linking the device to the chamber. Such a level of complexity to model the spring-like effect in the OWC chamber was not required at this stage of development.
A numerical model of the device was developed in [
6] and validated using the physical model results in [
16]. The numerical model did not take into account the presence of the flexible pipes (mass, inertia, elasticity, …), but provided good prediction of the physical model hydrodynamic behaviour. This showed that such effects due to the presence of the pipes were negligible.
The results of the initial version of the numerical model, assuming fixed volumes for the HP and LP chambers, did however not predict the pressure evolution in the chambers correctly. The reason for this was that the reservoirs used for the HP and LP chambers of the Tupperwave physical model did not have perfectly-rigid walls. During the tests, it was observed that the reservoir walls moved by a few millimetres proportional to the pressure building inside the chambers. The HP chamber was observed to inflate with the build-up of a positive excess pressure inside, and the LP chamber was observed to deflate due to the negative excess pressure inside. This required a correction in the numerical model to take into account the slight volumetric change of the HP and LP chambers. An elastic deformation of the chambers, a function of the excess pressure, was added to the numerical model such that:
where
is the initial volume of the chambers and
C is the chambers’ deformation coefficient assessed empirically. The value of
was calibrated using the experimental results and was obtained by an iterative process to minimise the error with the experimental results in the different tested irregular sea states.
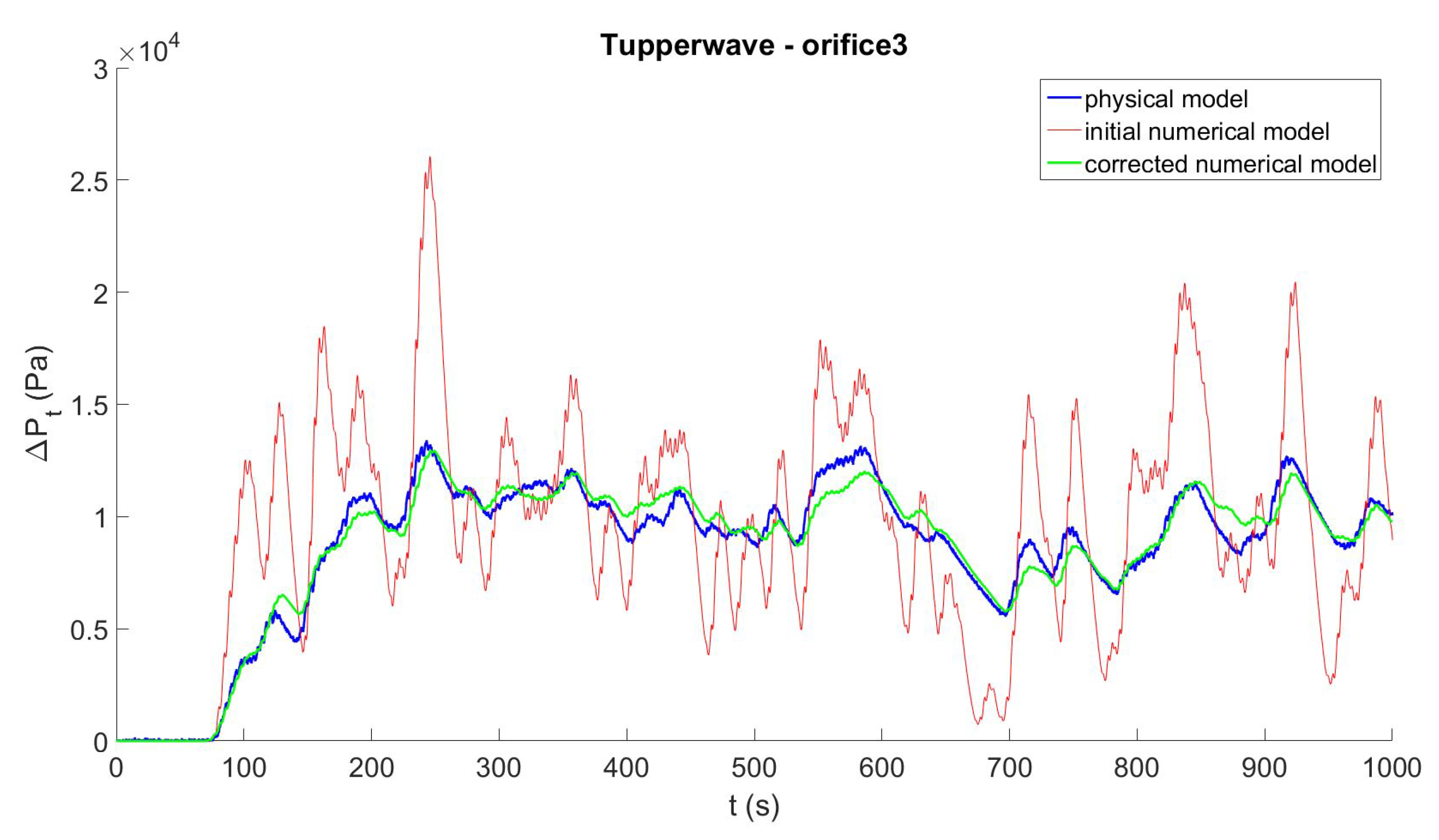
Figure 4 compares the time series of the pressure drop
across the orifice of the Tupperwave device in the irregular sea state {
m;
s} obtained by the physical model, the initial numerical model, and the corrected model. Results are given at full-scale equivalence to give the reader perspective. The pressures in the rigid-wall chambers from the initial numerical model varied quicker with the wave groups than in the chambers used in the physical tests. As a result of the chambers’ deformation, an extra smoothing effect of the pressure variations between the wave groups was observed in irregular waves. It is clearly shown in [
16] that the corrected numerical model, which accounts for the small volume variations of the HP and LP chambers, enhanced the fidelity with the physical model.
From an energy transfer perspective, the pneumatic energy stored in the HP and LP chamber was not only stored in the form of pressure, but also in the form of strain energy. This explains the lower pressure variations between wave groups. The strain energy stored by the elastic chamber deformation is recoverable. This is why the average value of the pressure drop across the orifice was not impacted.
According to Equation (
13), the
HP and LP deformable chambers of the physical model were actually behaving as if they were fixed volume chambers of volume:
and, therefore, modelling full-scale fixed volume HP and LP chambers of volume:
which is not what was intended in the first place, but explains the smoother evolution of the pressures in the chambers.
This experience constitutes the first (involuntary) physical implementation of the method suggested in Section
1 to model large fixed volume air chambers using smaller deformable air chamber. The device modelled was therefore not exactly the intended one, but the cause was understood and reproduced numerically.
In the next section, applications for deformable air chambers are identified, and the observations made in the present section are turned into opportunities.
5. Conclusions
In the present paper, a method to reproduce air compressibility effects occurring in a large fixed volume air chamber, using a smaller, but slightly elastically-deformable chamber, is presented and mathematically analysed. A formula to assess the chamber’s deformation coefficient was found.
The use of a deformable air chamber had its first application in the scaled physical modelling of OWC wave energy devices. It was implemented involuntarily during the testing of the Tupperwave device at a 1/24th scale. This provided a first experience of the method and revealed its potential.
The combination of the Tupperwave concept with the deformable air chamber also resulted in a novel closed-circuit OWC device concept called the Uilleann WEC concept. The deformable accumulator chambers of the Uilleann WEC can be smaller than the fixed volume accumulator chambers of the Tupperwave device. For that reason, the Uilleann WEC extends the application of the closed-circuit OWC system to onshore OWC structures and self-powered buoys.
In further works, the suggested method for modelling air compressibility will be put into practice and validated for model-scale testing. Specific applications of the Uilleann WEC concept will also be investigated, and its power performance and smoothing capacities will be studied.