Estimating Connectivity of Hard Clam (Mercenaria mercenaria) and Eastern Oyster (Crassostrea virginica) Larvae in Barnegat Bay
Abstract
1. Introduction
2. Methods
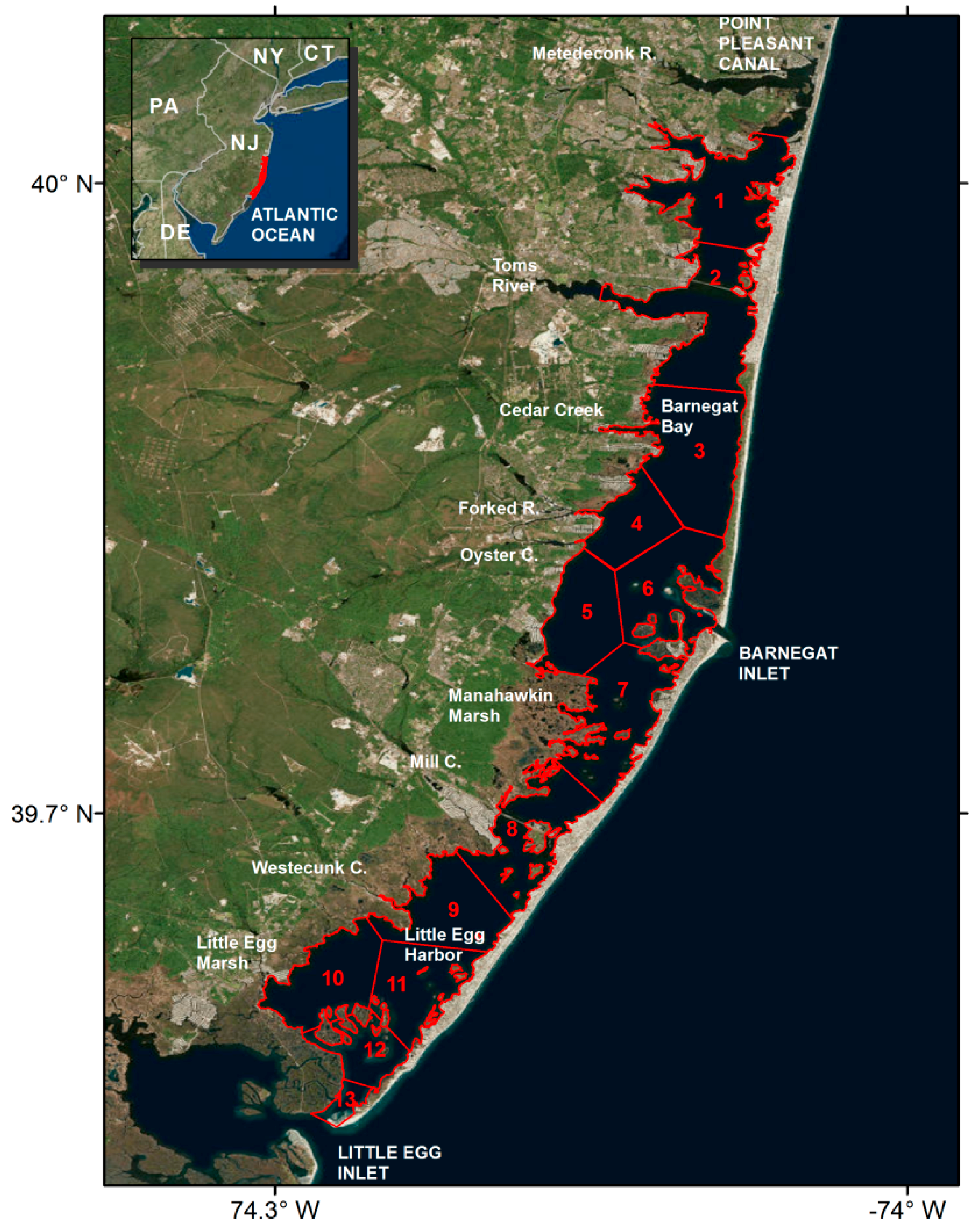
2.1. Barnegat Bay Little Egg Harbor (BBLEH)
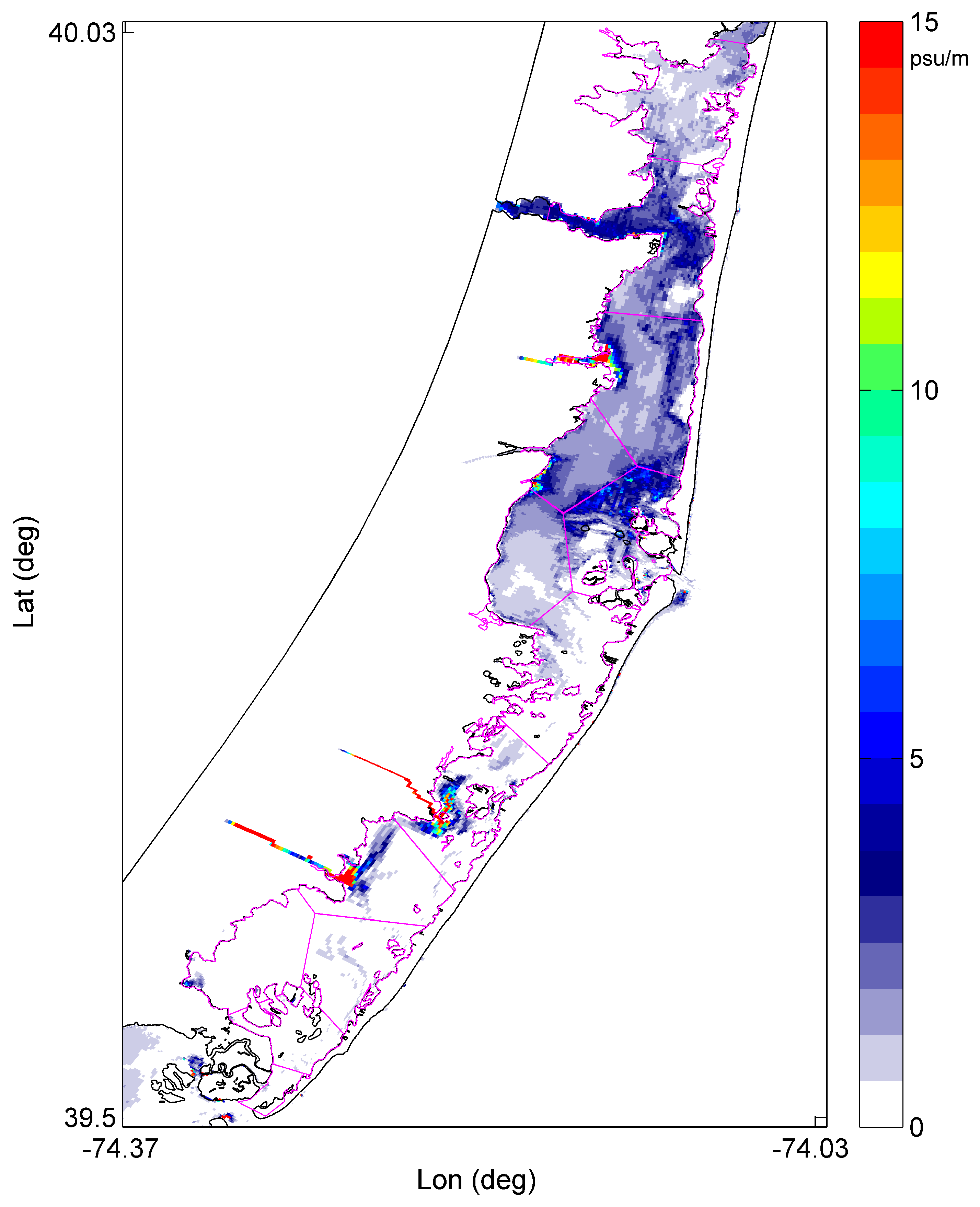
2.2. Modeling
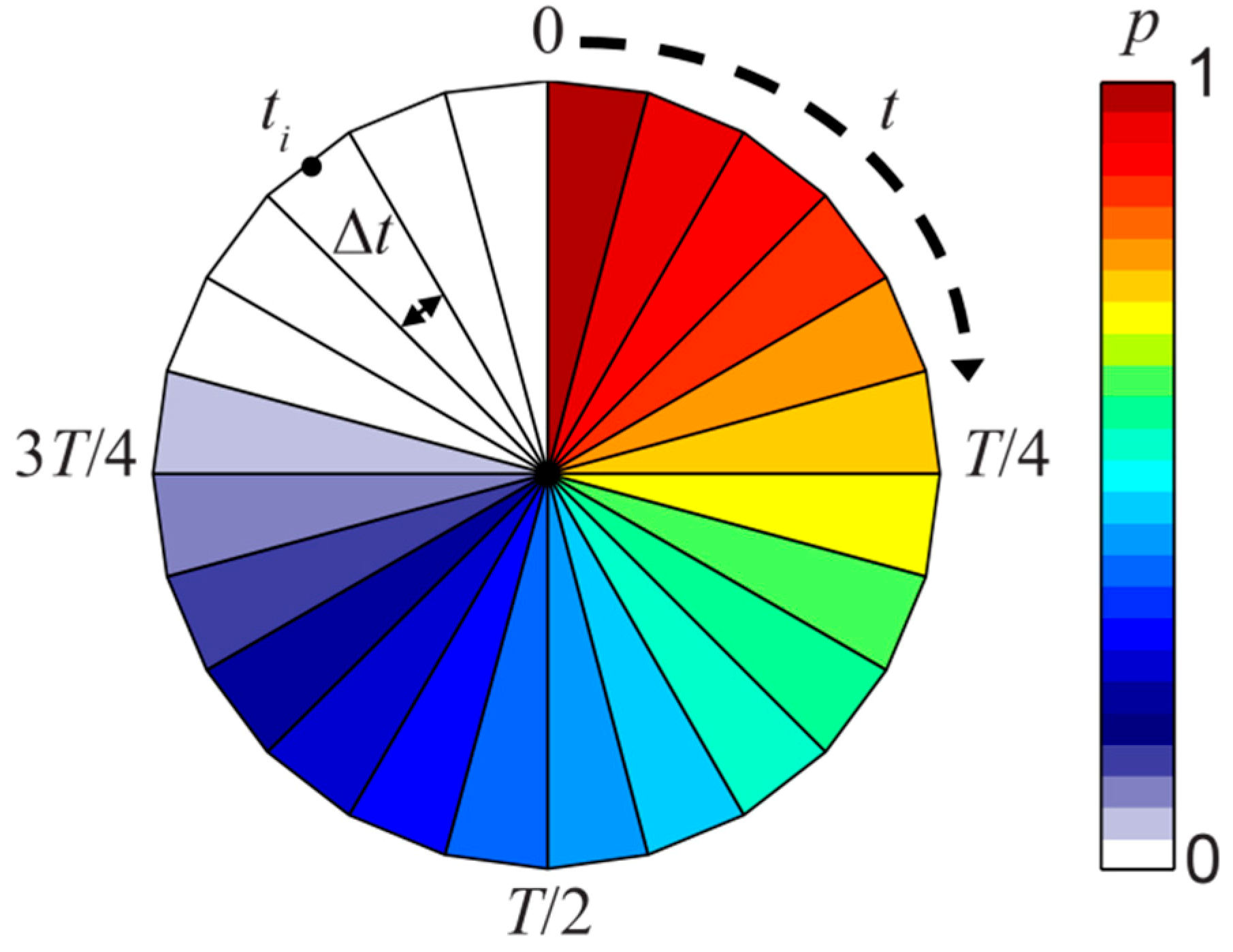
2.3. Retention Clock Matrix
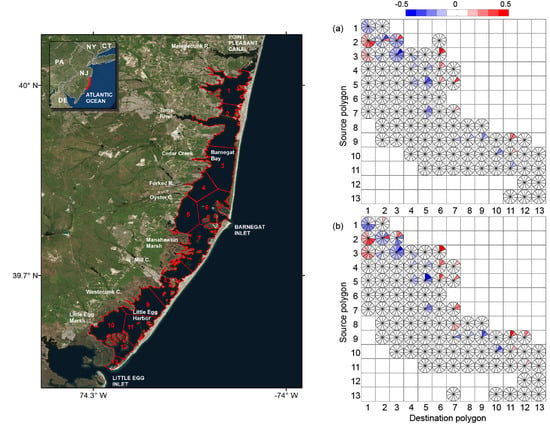
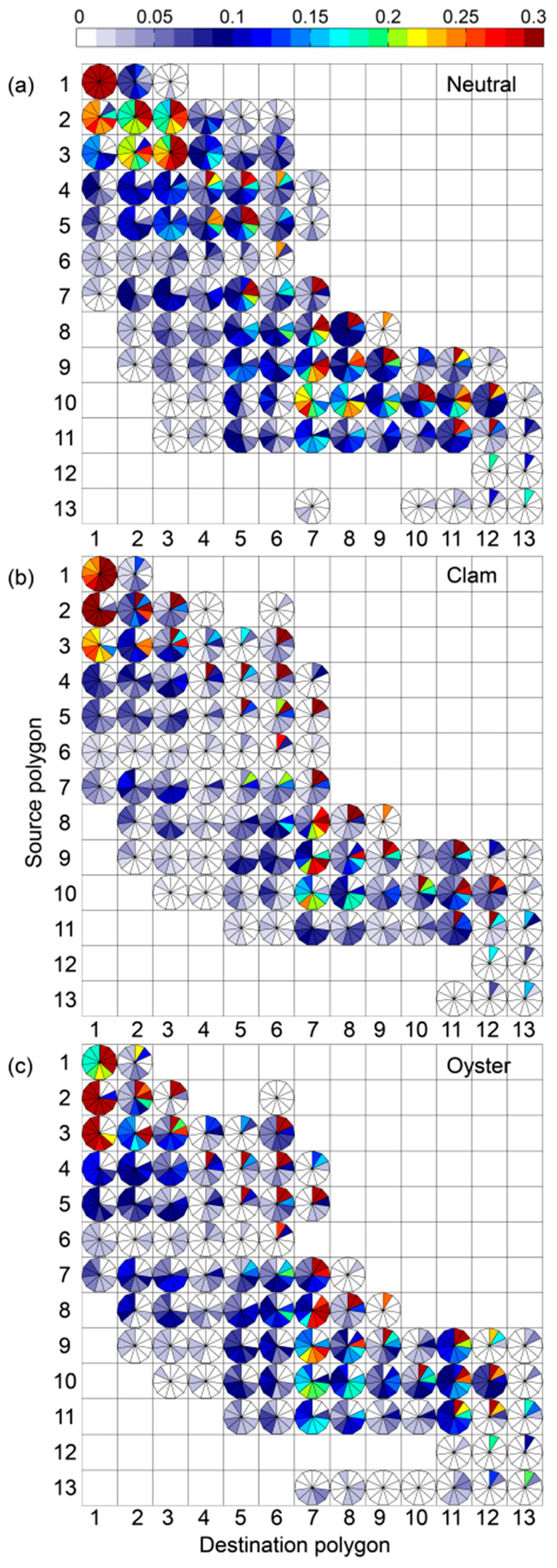
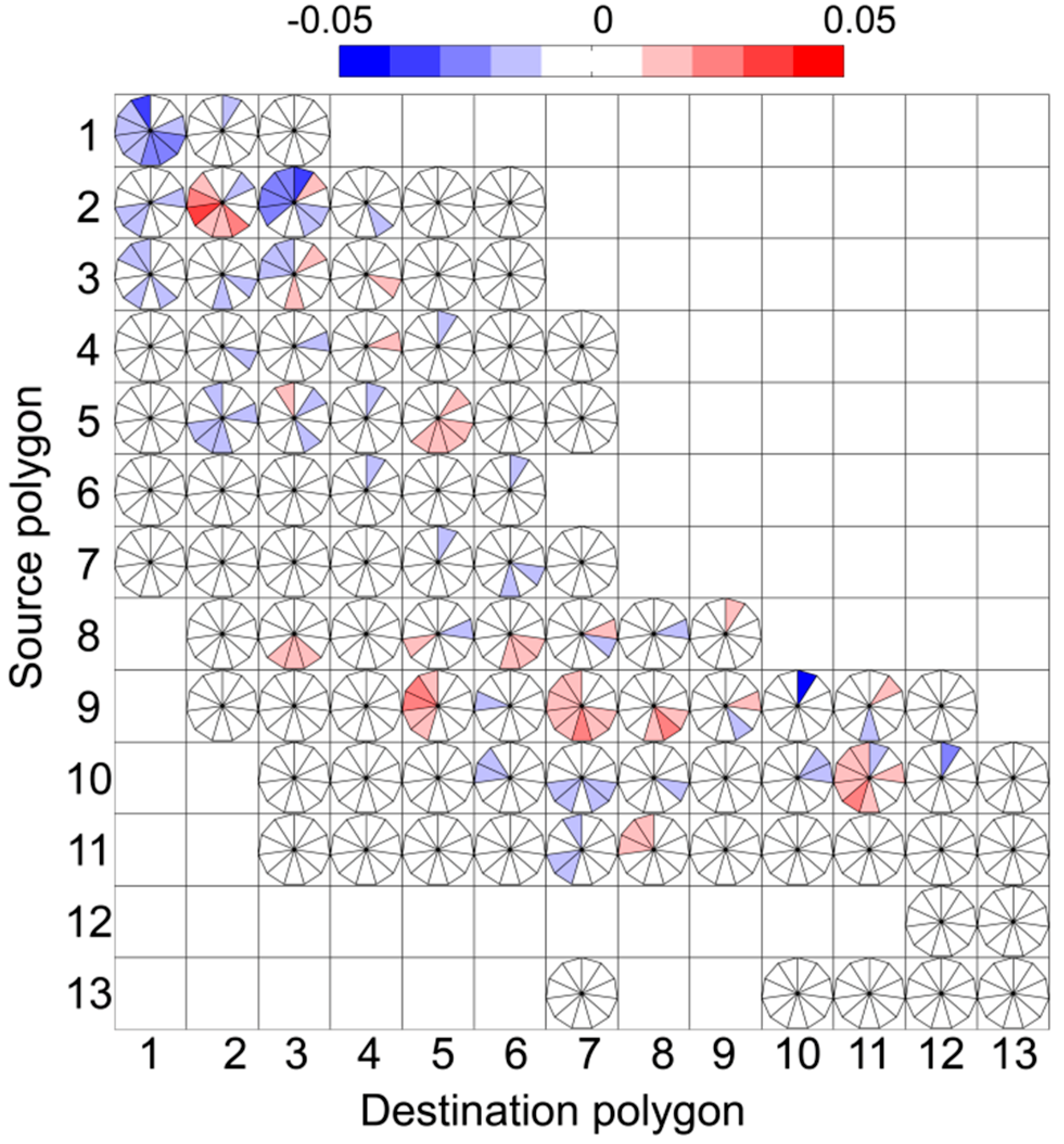
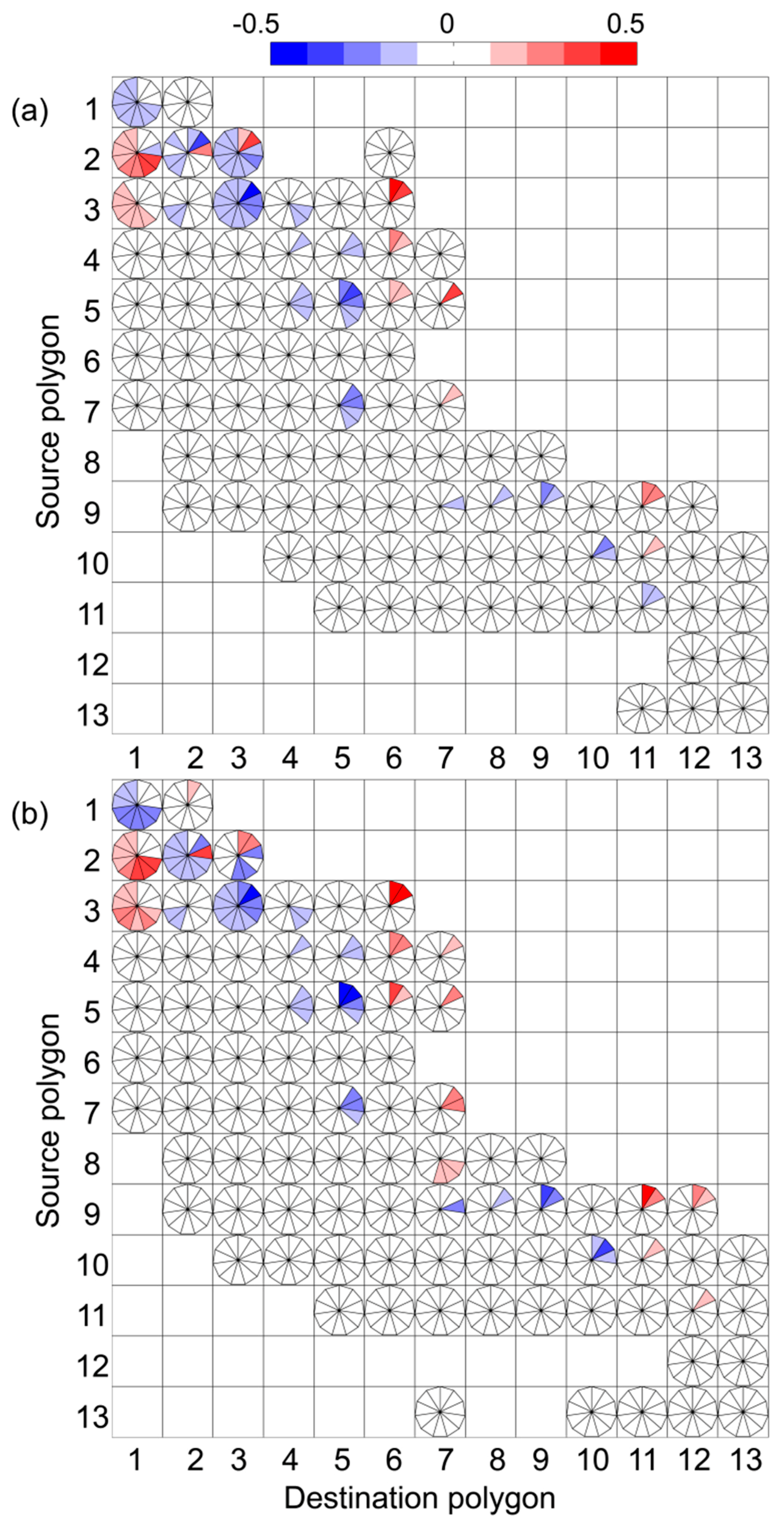
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kennedy, V.S.; Breitburg, D.L.; Christman, M.C.; Luckenbach, M.W.; Paynter, K.; Kramer, J.; Sellner, K.G.; Dew -Baxter, J.; Keller, C.; Mann, R. Lessons learned from efforts to restore oyster populations in Maryland and Virginia, 1990 to 2007. J. Shell. Res. 2011, 30, 719–731. [Google Scholar] [CrossRef]
- Kennedy, V.S. Biology of larvae and spat. In The Eastern Oyster Crassostrea virginica; Kennedy, V.S., Newell, I.E., Eble, E.F., Eds.; Maryland Sea Grant: College Park, MD, USA, 1996; pp. 371–421. [Google Scholar]
- Newell, R.I.E. Ecological Changes in Chesapeake Bay: Are they the result of the American oyster, Crassostrea virginica? In Understanding the Estuary: Advances in Chesapeake Bay Research; Lynch, M.P., Krome, E.C., Eds.; Chesapeake Research Consortium: Gloucester Point, VA, USA, 1988; pp. 536–546. [Google Scholar]
- Carmichael, R.H.; Walton, W.; Clark, H. Bivalve-enhanced nitrogen removal from coastal estuaries. Can. J. Aquat. Sci. 2012, 69, 1131–1149. [Google Scholar] [CrossRef]
- Scyphers, S.B.; Powers, S.P.; Heck, K.L., Jr.; Byron, D. Oyster Reefs as Natural Breakwaters Mitigate Shoreline Loss and Facilitate Fisheries. PLoS ONE 2011, 6, e22396. [Google Scholar] [CrossRef] [PubMed]
- Eversole, A.G. Reproduction in Mercenaria mercenaria. In Biology of the Hard Clam; Krauter, J.N., Castagna, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2001; Chapter 5; pp. 221–256. [Google Scholar]
- Gains, S.; Roughgarden, J. Larval settlement rate: A leading determinant of structure in an ecological community of the marine intertidal zone. Proc. Natl. Acad. Sci. USA 1985, 82, 3707–3711. [Google Scholar] [CrossRef]
- Puckett, B.J.; Eggleston, D.B.; Kerr, P.C.; Luettich, R.A., Jr. Larval dispersal and population connectivity among a network of marine reserves. Fish. Oceanogr. 2014, 23, 342–361. [Google Scholar] [CrossRef]
- Goodwin, J.D. Integrating Automated Imaging and a Novel Identification Technique to Estimate Mortality and Identify Factors That Influence the Vertical Distribution of Crassostrea virginica Larvae. Ph.D. Thesis, Digital Repository at the University of Maryland, College Park, MD, USA, 2015. [Google Scholar] [CrossRef]
- Steele, J.G. The ocean ‘landscape’. Landsc. Ecol. 1989, 3, 185–192. [Google Scholar] [CrossRef]
- Weins, J.A. Spatial scaling in ecology. Funct. Ecol. 1989, 3, 385–397. [Google Scholar] [CrossRef]
- Zhang, X.; Munroe, D.; Haidvogel, D.; Powell, E.N.P. Atlantic surfclam connectivity within the Middle Atlantic Bight: Mechanisms underlying variation in larval dispersal and settlement. Estuar. Coast. Shelf Sci. 2016, 173, 65–78. [Google Scholar] [CrossRef]
- Narvárez, D.A.; Klinck, J.M.; Powell, E.N.; Hofmann, E.E.; Wilkin, J.; Haidvogel, D.B. Circulation and behavior controls on dispersal of Eastern oyster (Crassostrea virginica) larvae in Delaware Bay. J. Mar. Res. 2012, 70, 411–440. [Google Scholar] [CrossRef]
- North, E.W.; Schlag, Z.; Hood, R.R.; Li, M.; Zhong, L.; Gross, T.; Kennedy, V.S. Vertical swimming behavior influences the dispersal of simulated oyster larvae in a coupled particle-tracking and hydrodynamic model of Chesapeake Bay. Mar. Ecol. Prog. Ser. 2008, 359, 99–115. [Google Scholar] [CrossRef]
- MacKenzie, C.L.; Tarnowski, M. Large shifts in commercial landings of estuarine and bay bivalve mollusks in northeastern United States after 1980 with assessment of causes. Mar. Fish. Rev. 2018, 8011, 1–28. [Google Scholar] [CrossRef]
- Bricelj, V.M.; Kraeuter, J.N.; Flimlin, G. Status and Tends of Hard Clam, Mercenaria Mercenara, Shellfish Populations in Barnegat Bay, NJ. Report to Barnegat Bay Partnership. 2012. Available online: http://bbp.ocean.edu/Reports/Barnegat%20Bay%20Hard%20Clam%20White%20Paper%20Final.pdf (accessed on 18 February 2019).
- Dacanay, K. Inventory of New Jersey’s Estuarine Shellfish Resources: Hard Clam Stock Assessment. Barnegat Bay (Survey Year 2012) with Post-Superstorm Sandy Investigation (2013) NJEDEP Marine Fish Admin. Bureau of Shellfish; NJDE: Trenton, NJ, USA, 2015; 54p. [Google Scholar]
- Carriker, M.R. Clam Biology. In Biology of the Hard Clam; Krauter, J.N., Castagna, M., Eds.; Elsevier Science: Amsterdam, The Netherlands, 2001; p. 772. [Google Scholar]
- Pineda, J.; Hare, M.; Sponaugle, S. Larval dispersal and dispersal in the coastal ocean and consequences for population connectivity. Oceanography 2007, 20, 22–39. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The Regional Ocean Modeling System (ROMS): A split-, free-surface, topography following coordinates ocean model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Defne, Z.; Ganju, N.K.; Aretxabaleta, A. Estimating time-dependent connectivity in marine systems. Geophys. Res. Lett. 2016, 43, 1–9. [Google Scholar] [CrossRef]
- Cowen, R.K.; Sponaugle, S. Larval dispersal and marine population connectivity. Ann. Rev. Mar. Sci. 2009, 1, 443–466. [Google Scholar] [CrossRef] [PubMed]
- Lough, R.G.; Aretxabaleta, A.L. Dispersal and retention of vertically migrating adult mysid and decapod shrimp in the tidal front on George’s Bank. Mar. Ecol. Prog. Ser. 2014, 514, 119–135. [Google Scholar] [CrossRef]
- Ford, S. History and present status of molluscan shellfisheries from Barnegat Bay to Delaware Bay. In The History, Present Condition and Future of the Molluscan Fisheries of North and Central America and Europe; MacKenzie, C.L., Jr., Burrell, V.G., Jr., Rosenfeild, A., Hobart, W.L., Eds.; Atlantic and Gulf Coasts; NOAA Technical Report; United States Department of Commerce, NOAA: Washington, DC, USA, 1997; Volume 1, 234p. [Google Scholar]
- Kennish, M.; Vouglitois, D.; Danila; Lutz, R.A. Shellfish. In Ecology of Barnegat Bay, NewJersey; Kennish, M.J., Lutz, R.A., Eds.; Springer: New York, NY, USA, 1984; pp. 171–200. [Google Scholar]
- Kauffman, G.J.; Cruz-Ortiz, C. Economic Value of the Barnegat Bay Watershed; Institute for Public Administration, University of Delaware: Newark, NJ, USA, 2012; 66p. [Google Scholar]
- Defne, Z.; Ganju, N.K. Quantifying the residence time and flushing characteristics of a shallow, back-barrier estuary: Application of hydrodynamic and particle tracking models. Estuaries Coasts 2015, 38, 1719–1734. [Google Scholar] [CrossRef]
- Warner, J.C.; Armstrong, B.; He, R.; Zambon, J.B. Development of a Coupled Ocean–Atmosphere–Wave–Sediment Dispersal (COAWST) Modeling System. Ocean Model. 2010, 35, 230–244. [Google Scholar] [CrossRef]
- USGS NWIS. National Water Information System, US Geological Survey. 2012. Available online: http://waterdata.usgs.gov/nwis (accessed on 8 December 2012).
- Mukai, A.Y.; Westerink, J.J.; Luettich, R.A., Jr.; Mark, D. East Coast 2001: A Tidal Constituent Database for the Western North Atlantic, Gulf of Mexico and Caribbean Sea; Technical Report, ERDC/CHL TR-02-24; US Army Engineer Research and Development Center, Coastal and Hydraulics Laboratory: Vicksburg, MS, USA, 2002.
- Wilkin, J.L.; Hunter, E.J. An assessment of the skill of real-time models of Mid-Atlantic Bight continental shelf circulation. J. Geophys. Res. Ocean. 2013, 118, 2919–2933. [Google Scholar] [CrossRef]
- NCEP NAM. NAM-12 North America, NOAA Operational Model Archive and Distribution System. 2012. Available online: http://nomads.ncep.noaa.gov/ (accessed on 8 December 2012).
- Schlag, Z.R.; North, E.W. Lagrangian Dispersal (LTRANS) v.2 Model User’s Guide; Technical Report of the University of Maryland Center for Environmental Science Horn Point Laboratory: Cambridge, MD, USA, 2012; 183p. [Google Scholar]
- North, E.W.; Hood, R.R.; Chao, S.Y.; Sanford, L.P. Using a random displacement model to simulate turbulent particle motion in a baroclinic frontal zone: A new implementation scheme and model performance tests. J. Mar. Syst. 2006, 60, 365–380. [Google Scholar] [CrossRef]
- Visser, A.W. Using random walk models to simulate the vertical distribution of particles in a turbulent water column. Mar. Ecol. Prog. Ser. 1997, 158, 275–281. [Google Scholar] [CrossRef]
- Hunter, J.; Craig, P.; Phillips, H. On the use of random walk models with spatially variable diffusivity. J. Comput. Phys. 1993, 106, 366–376. [Google Scholar] [CrossRef]
- Mann, R. Distribution of bivalve larvae at a frontal system in the James River, Virginia. Mar. Ecol. Prog. Ser. 1988, 50, 29–44. [Google Scholar] [CrossRef]
- Thiessen, A.H. Precipitation for large areas. Mon. Weather Rev. 1911, 39, 1082–1084. [Google Scholar]
- Chant, R.J. Tidal and subtidal motion in a shallow bar-built multiple inlet/bay system. J. Coast. Res. 2001, 32, 102–114. [Google Scholar]
- Dekshenieks, M.M.; Hofmann, E.E.; Klinck, J.M.; Powell, E.N. Modeling the vertical distribution of oyster larvae in response to environmental conditions. Mar. Ecol. Prog. Ser. 1996, 136, 971110. [Google Scholar] [CrossRef]
- Wood, L.; Hargis, W.J., Jr. Dispersal of Bivalve Larvae in a Tidal Estuary. Fourth European Marine Biology Symposium; Crisp, D.J., Ed.; Cambridge University Press: New York, NY, USA, 1971; pp. 29–44. [Google Scholar]
- Brown, C.A.; Jackson, G.A.; Brooks, D.A. Particle transport through a narrow tidal inlet due to tidal forcing and implications for larval transport. J. Geophys. Res. 2000, 105, 141–156. [Google Scholar] [CrossRef]
- Roegner, G.C. Transport of molluscan larvae through a shallow estuary. J. Plank. Res. 2000, 22, 1779–1800. [Google Scholar] [CrossRef]
- Carriker, M.R. Interrelation of functional morphology, behavior, and autecology in early stages of the bivalve Mercenaria mercenaria. J. Elisha Mitch. Sci. Soc. 1961, 77, 168–241. [Google Scholar]
- Chizmadia, P.A.; Kennish, M.J.; Ohori, V.L. Physical description of Barnegat Bay-Little Harbor estuary. In Ecology of Barnegat Bay, New Jersey; Kennish, M.J., Lutz, R.A., Eds.; Springer: New York, NY, USA, 1984; pp. 1–28. [Google Scholar]
- Andrews, J.D. Dispersal of bivalve larvae in James River, Virginia. J. Shell. Res. 1983, 3, 29–49. [Google Scholar]
- Fuchs, H.L.; Hunter, E.J.; Schmitt, E.L.; Guazzo, R.A. Active downward propulsion by oyster larvae in turbulence. J. Exp. Biol. 2013, 216, 1458–1469. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, H.L.; Gerbi, G.P.; Hunter, E.J.; Christman, A.J.; Diez, F.J. Hydrodynamic sensing and behavior by oyster larvae in turbulence and waves. J. Exp. Biol. 2015, 218, 1419–1432. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, J.D.; Helfrich, K.R.; Anderson, E.J.; Mullineaux, L.S. Isolating the hydrodynamic triggers of the dive response in eastern oyster larvae. Limnol. Oceanogr. 2015, 60, 1332–1343. [Google Scholar] [CrossRef]
- Warner, J.C.; Ganju, N.; Sherwood, C.R.; Kalra, T.; Aretxabaleta, A.; Olabarrieta, M. A Coupled Ocean Atmosphere Wave Sediment Transport Numerical Modeling System (COAWST): U.S. Geological Survey software; U.S. Geological Survey: Reston, VA, USA, 2019. [CrossRef]
| Clam | Oyster | |
|---|---|---|
| Salinity gradient threshold | 5 | 1.2 |
| Age swimming begins (days) | 1 | 1 |
| Age veliger (days) | 1–7 | 1–13 |
| Age pediveliger (days) | 8 | 14 |
| Swim speed veliger (mm s−1) | 1.30–0.49 | 0.50–3.00 |
| Swim speed pediveliger (mm s−1) | 0.49 | 3.00 |
| Polygon | Clam | Oyster |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 5 | 4 |
| 3 | 6 | 6 |
| 4 | 7 | 7 |
| 5 | 7 | 7 |
| 6 | 7 | 6 |
| 7 | 7 | 8 |
| 8 | 8 | 8 |
| 9 | 10 | 11 |
| 10 | 9 | 10 |
| 11 | 9 | 9 |
| 12 | 2 | 3 |
| 13 | 4 | 7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goodwin, J.D.; Munroe, D.M.; Defne, Z.; Ganju, N.K.; Vasslides, J. Estimating Connectivity of Hard Clam (Mercenaria mercenaria) and Eastern Oyster (Crassostrea virginica) Larvae in Barnegat Bay. J. Mar. Sci. Eng. 2019, 7, 167. https://doi.org/10.3390/jmse7060167
Goodwin JD, Munroe DM, Defne Z, Ganju NK, Vasslides J. Estimating Connectivity of Hard Clam (Mercenaria mercenaria) and Eastern Oyster (Crassostrea virginica) Larvae in Barnegat Bay. Journal of Marine Science and Engineering. 2019; 7(6):167. https://doi.org/10.3390/jmse7060167
Chicago/Turabian StyleGoodwin, Jacob D., Daphne M. Munroe, Zafer Defne, Neil K. Ganju, and James Vasslides. 2019. "Estimating Connectivity of Hard Clam (Mercenaria mercenaria) and Eastern Oyster (Crassostrea virginica) Larvae in Barnegat Bay" Journal of Marine Science and Engineering 7, no. 6: 167. https://doi.org/10.3390/jmse7060167
APA StyleGoodwin, J. D., Munroe, D. M., Defne, Z., Ganju, N. K., & Vasslides, J. (2019). Estimating Connectivity of Hard Clam (Mercenaria mercenaria) and Eastern Oyster (Crassostrea virginica) Larvae in Barnegat Bay. Journal of Marine Science and Engineering, 7(6), 167. https://doi.org/10.3390/jmse7060167