Assessment of Sea Level Rise at West Coast of Portugal Mainland and Its Projection for the 21st Century
Abstract
1. Introduction
2. Data and Methods
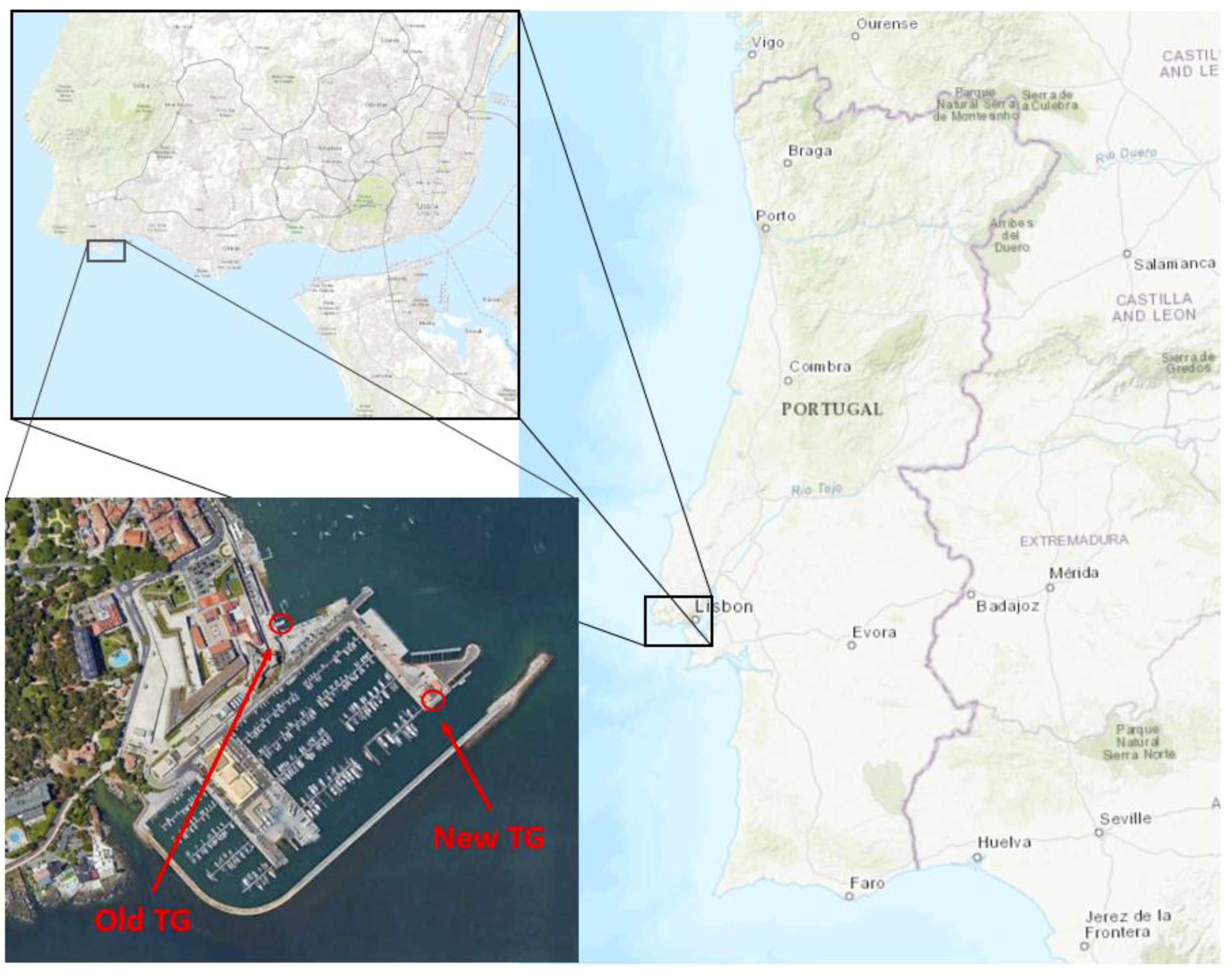
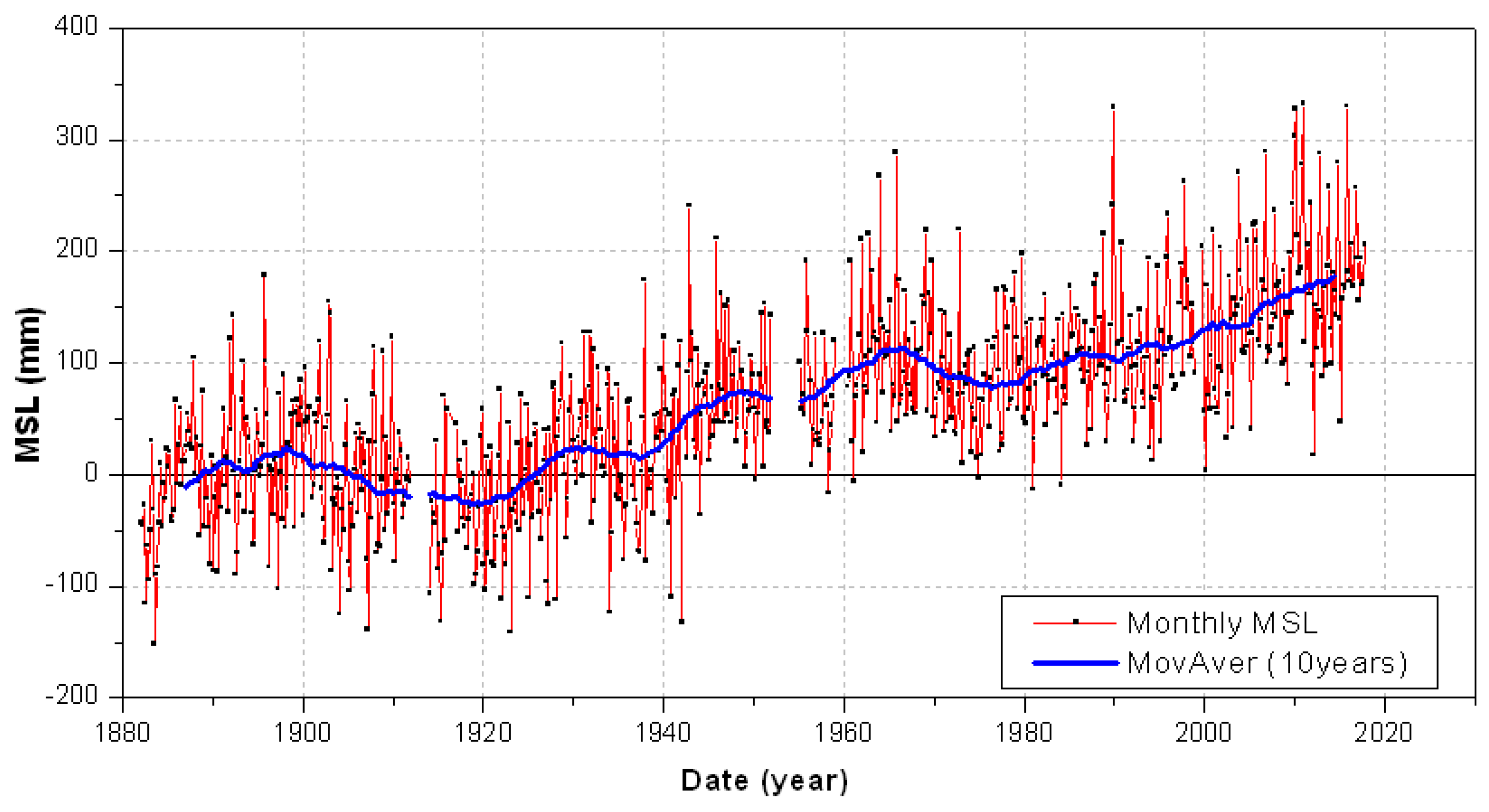
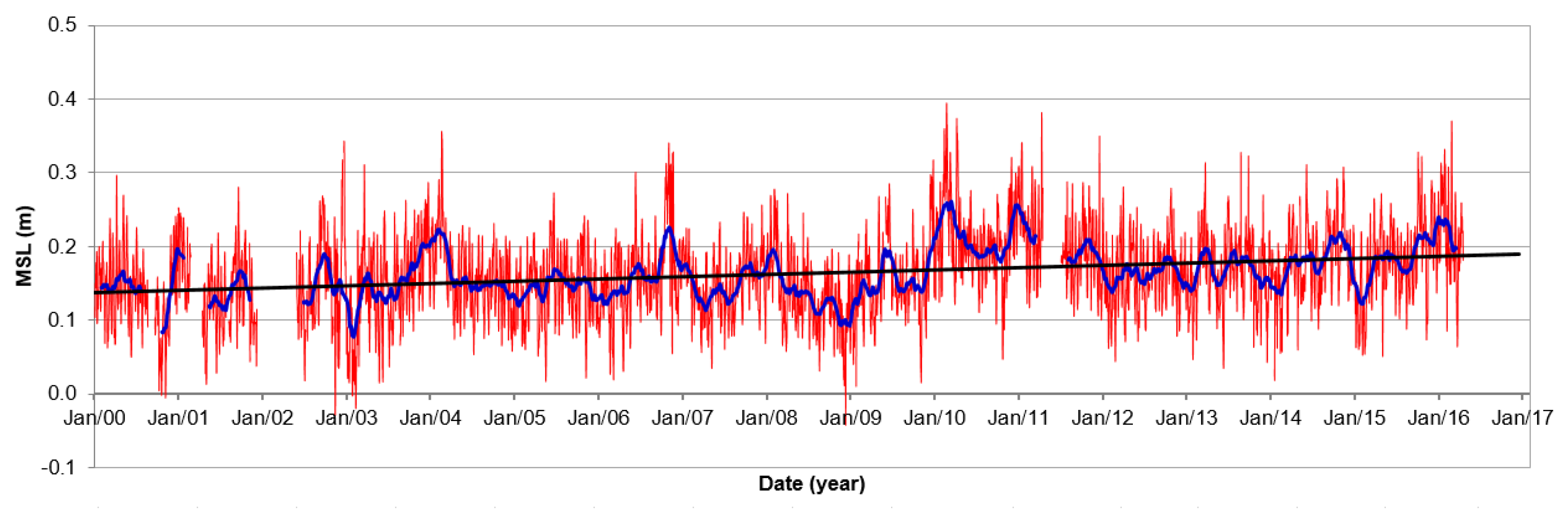
2.1. Sea Level Data
2.2. Methods of MSL Projection
2.2.1. Method One
2.2.2. Method Two
2.2.3. Method Three
3. Numerical Estimations
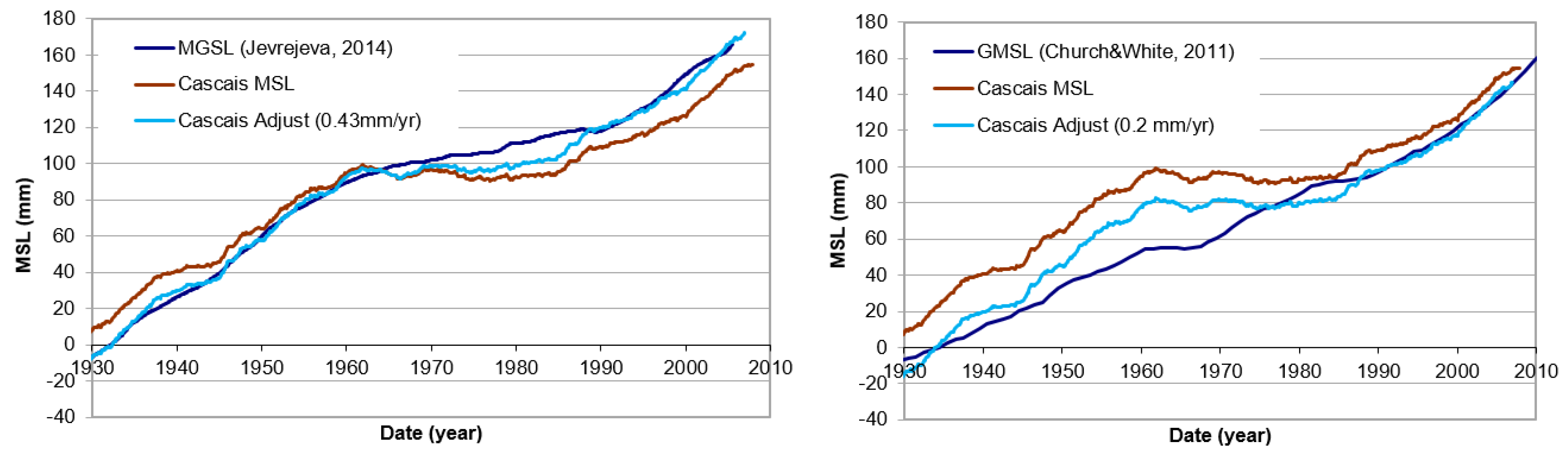
3.1. Uplift Rate
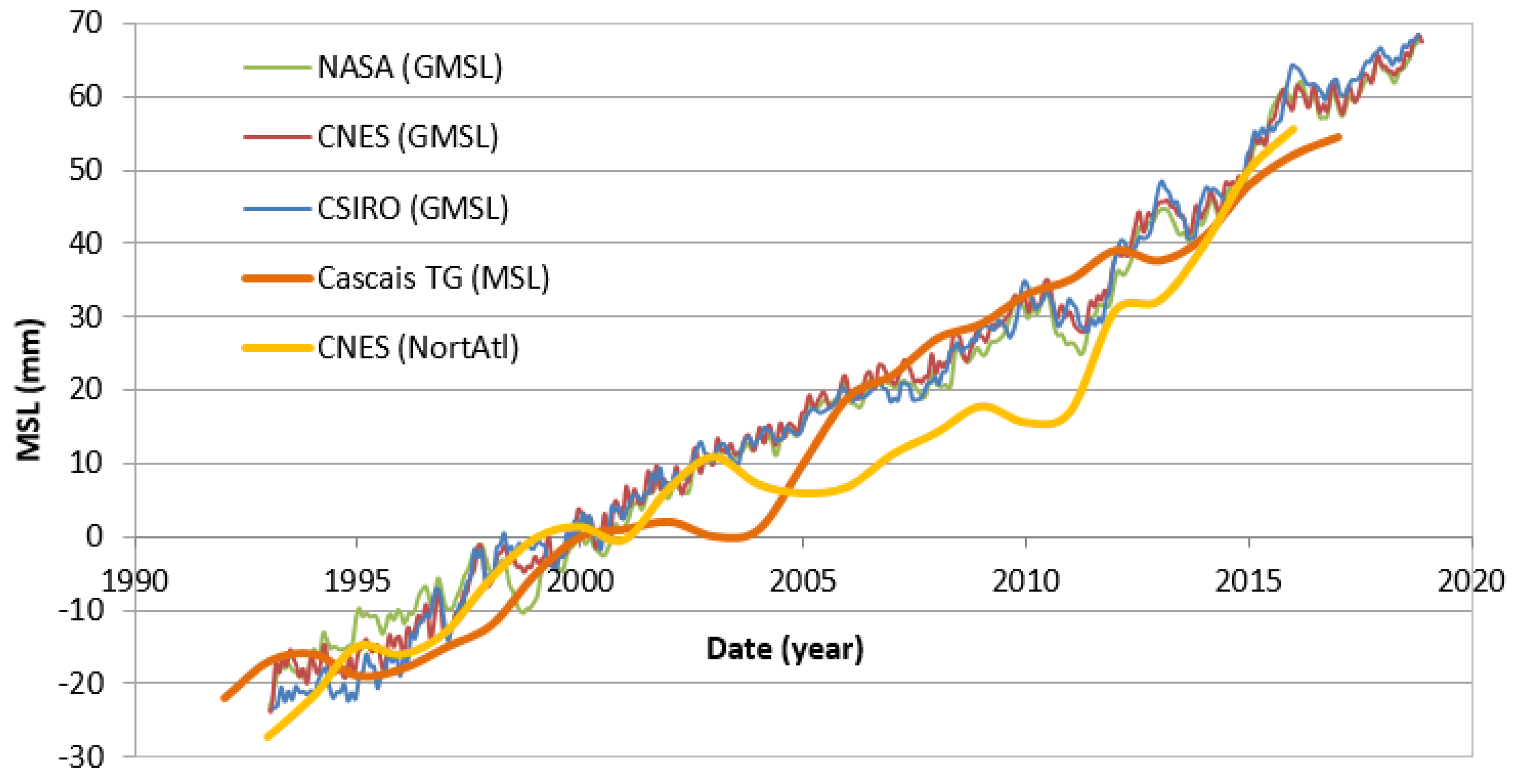
3.2. SLR Rates
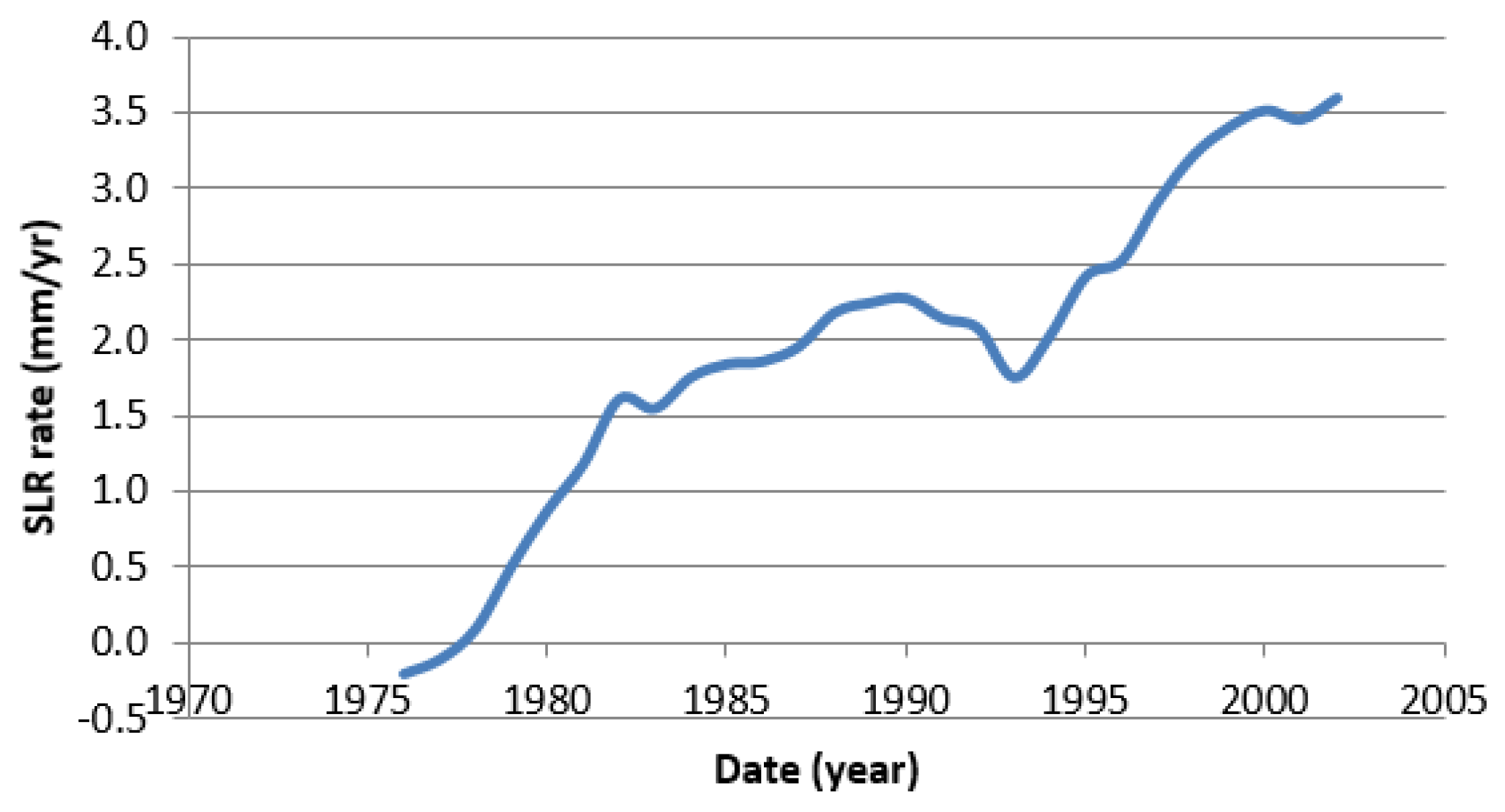
3.3. SLR Acceleration
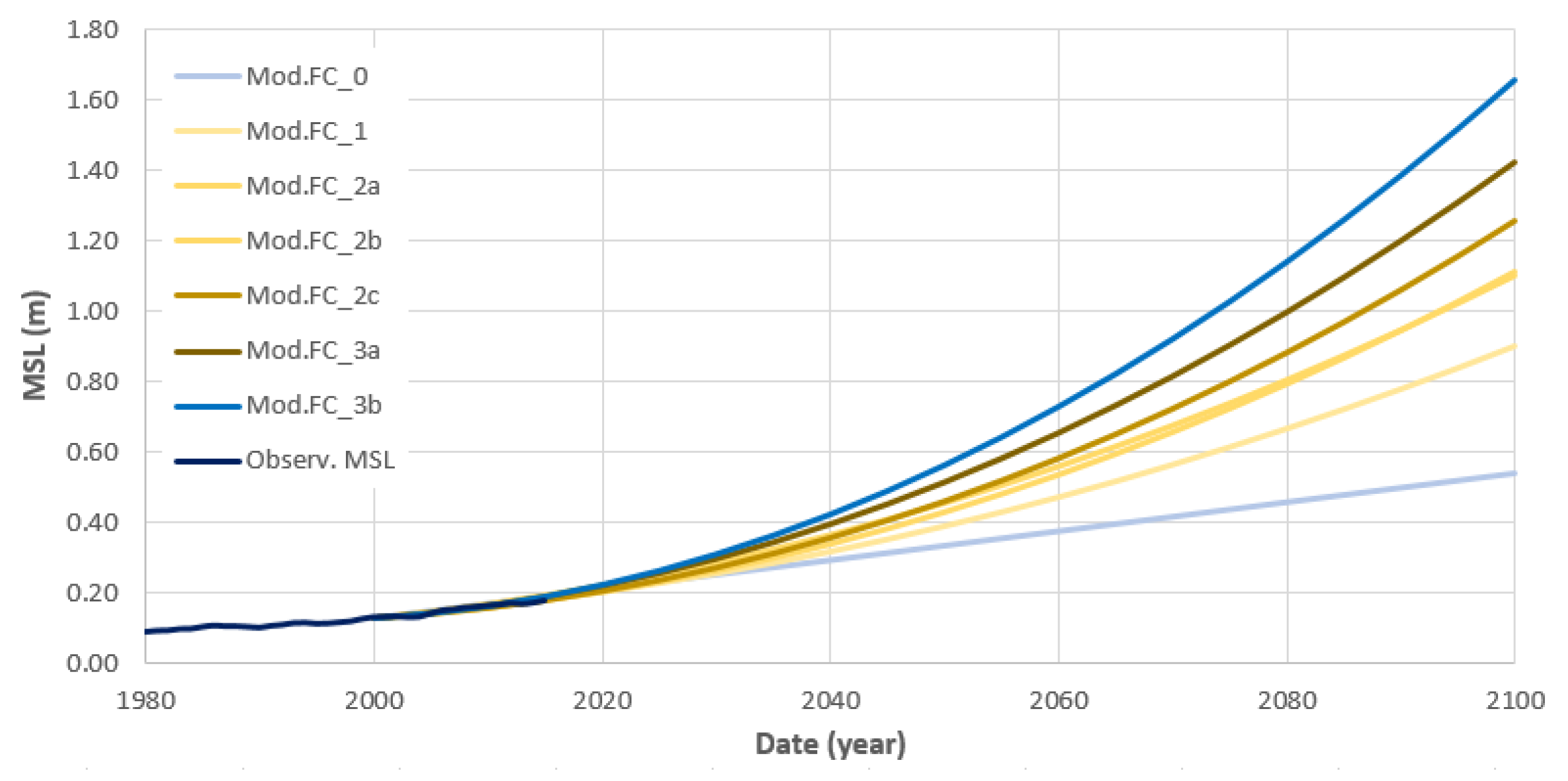
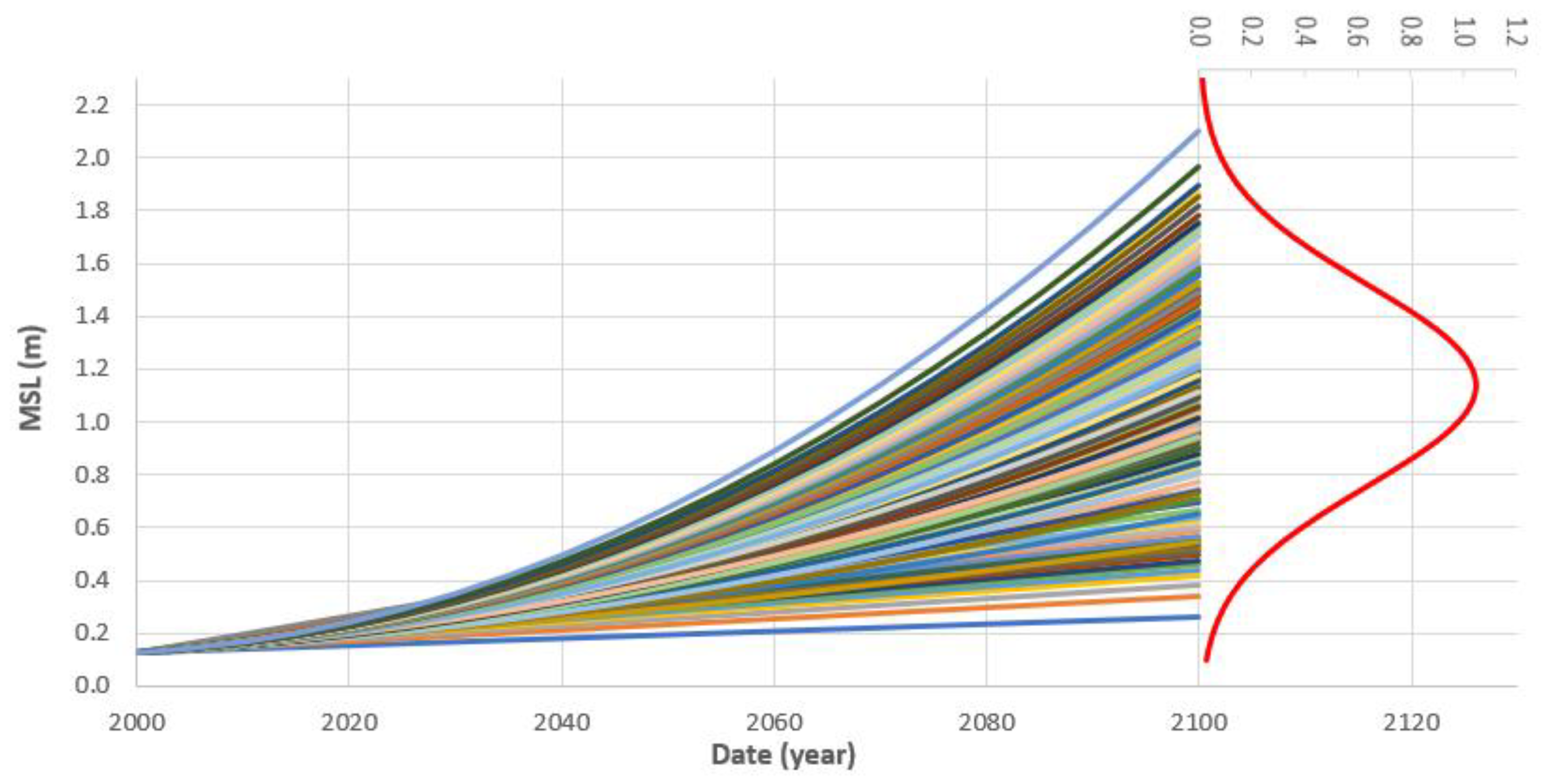
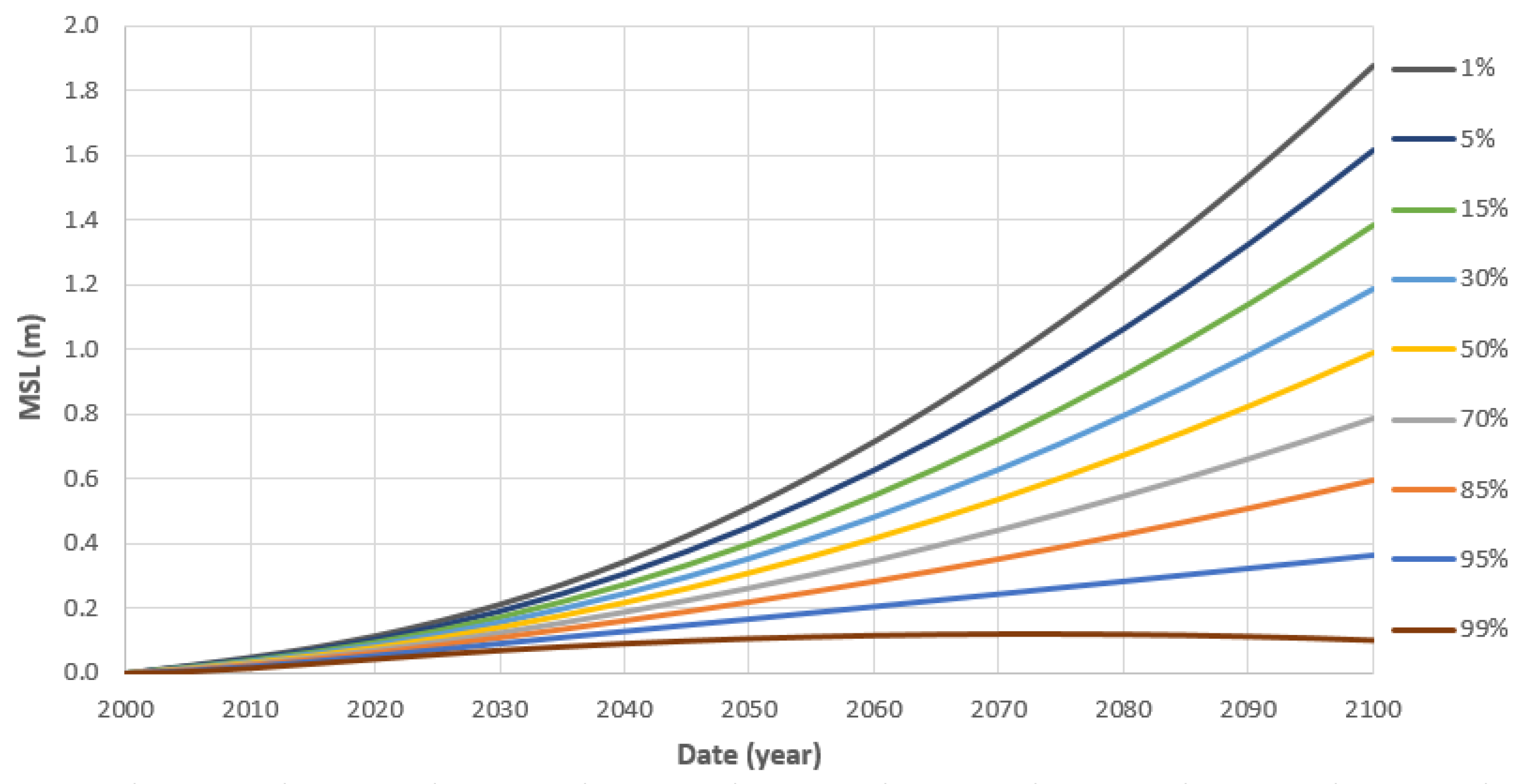
4. The Ensemble of Empirical SLR Projections for the 21st Century
4.1. Relative SLR Models for the West Coast of Portugal Mainland (WCPM)
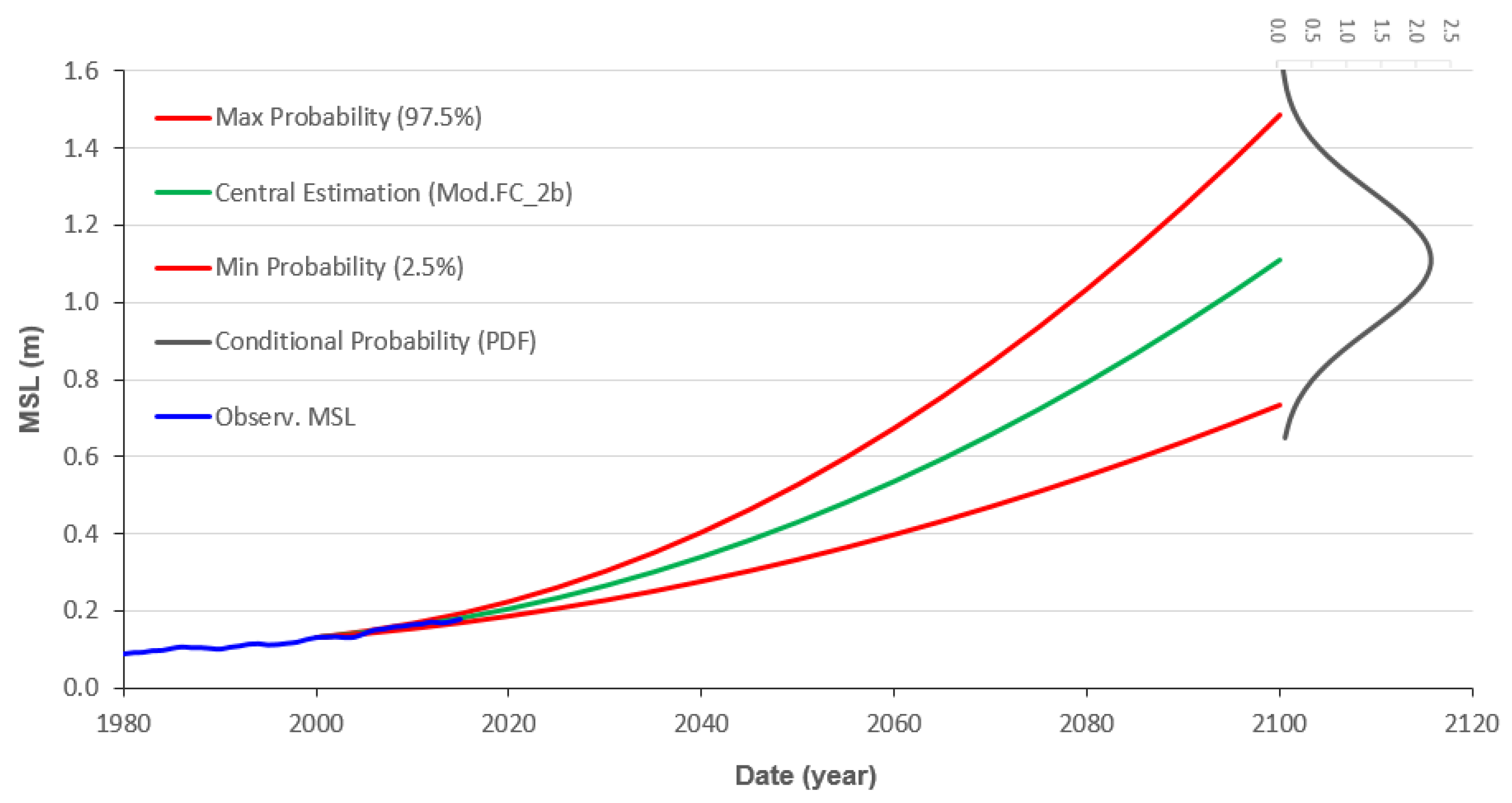
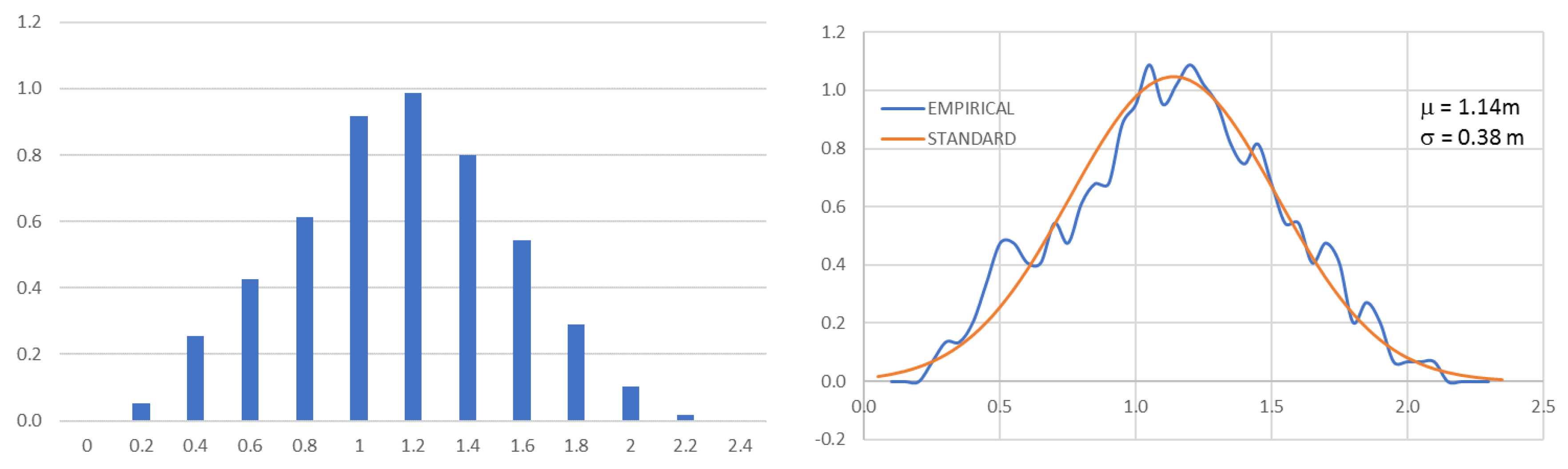
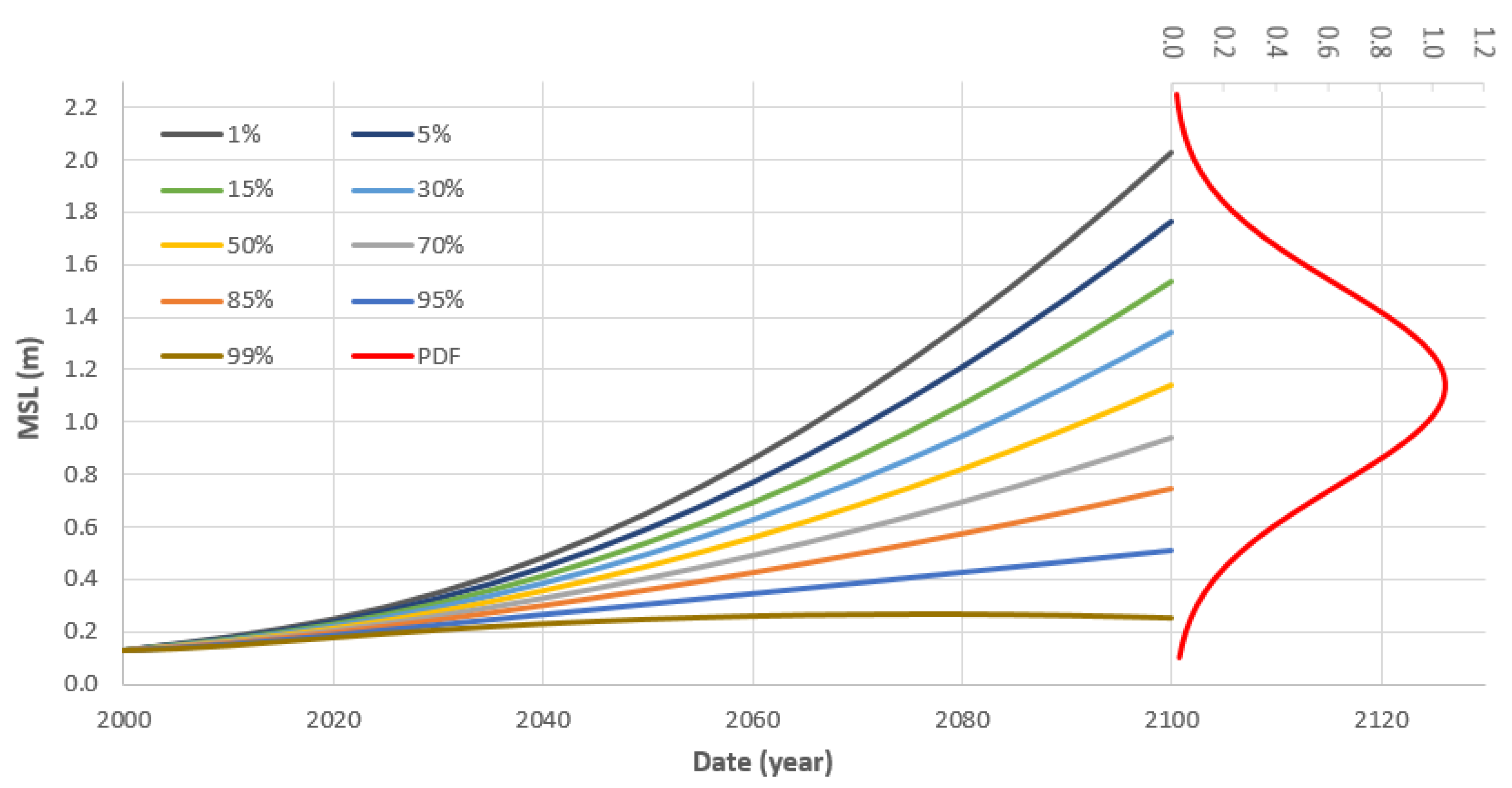
4.2. Probabilistic Ensemble of Empirical SLR Projections and Respective PDF
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; 1535p. [Google Scholar]
- Leuliette, E.W.; Nerem, R.S. Contributions of Greenland and Antarctica to global and regional sea level change. Oceanography 2016, 29, 154–159. [Google Scholar] [CrossRef]
- Antunes, C.; Taborda, R. Sea level at Cascais Tide Gauge: Data, Analysis and Results. J. Coast. Res. 2009, SI 56, 218–222. [Google Scholar]
- Antunes, C. Subida do Nível Médio do Mar em Cascais, revisão da taxa actual. In Actas das 4.as Jornadas de Engenharia Hidrográfica; Instituto Hidrográfico: Lisboa, Portugal, 2016; ISBN 978-989-705-097-8. [Google Scholar]
- Hansen, J.; Sato, M.; Hearty, P.; Ruedy, R.; Kelle, M.; Masson-Delmotte, V.; Russell, G.; Tselioudis, G.; Cao, J.; Rignot, E.; et al. Ice melt, sea level rise and superstorms: evidence from paleoclimate data, climate modeling, and modern observations that 2 °C global warming could be dangerous. Atmos. Chem. Phys. 2016, 16, 3761–3812. [Google Scholar] [CrossRef]
- Kopp, R.E.; DeConto, R.M.; Bader, D.A.; Hay, C.C.; Horton, R.M.; Kulp, S.; Oppenheimer, M.; Pollard, D.; Strauss, B.H. Evolving Understanding of Antarctic Ice-Sheet Physics and Ambiguity in Probabilistic Sea-Level Projections. Earth’s Future 2017, 5. [Google Scholar] [CrossRef]
- Scambos, T.A.; Bell, R.E.; Alley, R.B.; Anandakrishnan, S.; Bromwich, D.H.; Brunt, K.; Oppenheimer, M.; Pollard, D.; Strauss, B.H. How much, how fast?: A science review and outlook for research on the instability of Antarctica’s Thwaites Glacier in the 21st century. Glob. Planet. Chang. 2017, 153, 16–34. [Google Scholar] [CrossRef]
- Brown, T.P.; Caldeira, K. Greater future global warming inferred from Earth’s recent energy budget. Nature 2017, 552, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Jevrejeva, S.; Moore, J.C.; Grinsted, A.; Matthews, A.P.; Spada, G. Trends and acceleration in global and regional sea levels since 1807. Glob. Planet. Chang. 2014, 113, 11–22. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J. Sea-level rise from the late 19th to the early 21st Century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J. A 20th century acceleration in global sea-level rise. Geophys. Res. Lett. 2006, 33, L10602. [Google Scholar] [CrossRef]
- Beckley, B.D.; Callahan, P.S.; Hancock, D.W.; Mitchum, G.T.; Ray, R.D. On the “Cal-Mode” Correction to TOPEX Satellite Altimetry and Its Effect on the Global Mean Sea Level Time Series. J. Geophys. Res. Oceans 2017, 122, 8371–8384. [Google Scholar] [CrossRef]
- Nerem, R.S.; Beckley, B.D.; Fasullo, J.T.; Hamlington, B.D.; Masters, D.; Mitchum, G.T. Climate-change-driven accelerated sea-level rise detected in the altimeter era. Proc. Natl. Acad. Sci. USA 2018, 115, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Rhamstorf, S.; Foster, G.; Cazenave, A. Comparing climate projections to observations up to 2011. Environ. Res. Lett. 2012, 7, 044035. [Google Scholar] [CrossRef]
- Cabral, J. Neotectónica em Portugal Continental. Inst. Geol. Min. Mem. 1995, 31, 265. [Google Scholar]
- Figueiredo, P.M.; Cabral, J.; Rockwell, T.K. Recognition of Pleistocene marine terraces in the Southwest of Portugal (Iberian Peninsula): Evidences of regional Quaternary uplift. Ann. Geophys. 2013, 56. [Google Scholar] [CrossRef]
- Peltier, W.R.; Argus, F.F.; Drummond, R. Space geodesy constrains ice-age terminal deglaciation: The global ICE-6G_C (VM5a) model. Annu. Rev. Earth Planet. Sci. 2015, 32, 111–149. [Google Scholar] [CrossRef]
- Nerem, R.S.; Chambers, D.P.; Choe, C.; Mitchum, G.T. Estimating mean sea level change from the TOPEX and Jason altimeter missions. Mar. Geod. 2010, 33, 435–446. [Google Scholar] [CrossRef]
- Sweet, V.W.; Kopp, R.E.; Weaver, P.C.; Obeysekera, J.; Horton, M.H.; Thieler, E.R.; Zervas, C. Global and Regional Sea Level Rise Scenarios for the United States; NOAA Technical Report NOS CO-OPS 083; NOAA: Silver Spring, MD, USA, 2017; 77p.
- Seo, K.W.; Wilson, C.R.; Scambos, T.; Kim, B.M.; Waliser, D.E.; Tian, B.; Kim, B.-H.; Eom, J. Surface mass balance contributions to acceleration of Antarctic ice mass loss during 2003–2013. J. Geophys. Res. Solid Earth 2015, 120, 3617–3627. [Google Scholar] [CrossRef] [PubMed]
- Martín-Español, A.; Zammit-Mangion, A.; Clarke, P.J.; Flament, T.; Helm, V.; King, M.A.; Luthcke, S.B.; Petrie, E.; Rémy, F.; Schön, N.; et al. Spatial and temporal Antarctic Ice Sheet mass trends, glacio-isostatic adjustment, and surface processes from a joint inversion of satellite altimeter, gravity, and GPS data. J. Geophys. Res. Earth Surf. 2016, 121, 182–200. [Google Scholar] [CrossRef] [PubMed]
- Gardner, A.S.; Moholdt, G.; Scambos, T.; Fahnstock, M.; Ligtenberg, S.; van den Broeke, M.; Nilsson, J. Increase West Antarctic and unchanged East Antarctic ice discharge over the last 7 years. Cryosphere 2018, 12, 521–547. [Google Scholar] [CrossRef]
- DeConto, R.M.; Pollard, D. Contributions of Antarctica to past and future sea-level rise. Nature 2016, 531, 591–610. [Google Scholar] [CrossRef] [PubMed]
- Derksen, C.; Brown, R.; Mudryk, L.; Luojus, K.; Helfrich, S. Terrestrial Snow Cover. Arctic Report Card 2017. Available online: http://www.artic.noaa.gov/Report-Card (accessed on 5 March 2019).
- Jevrejeva, S.; Grinsted, A.; Moore, J.C. Upper limit for sea level projections by 2100. Environ. Res. Lett. 2014, 9, 104008. [Google Scholar] [CrossRef]
- Kopp, R.E.; Horton, R.M.; Little, C.M.; Mitrovica, J.X.; Oppenheimer, M.; Rasmussen, D.J.; Strauss, B.H.; Tebaldi, C. Probabilistic 21st and 22nd century sea-level projections at a global network of tide-gauge sites. Earth’s Future 2014, 2, 383–406. [Google Scholar] [CrossRef]
| Period | 1992–2004 | 2000–2016 | 2001–2016 | 2003–2016 | 2005–2016 |
|---|---|---|---|---|---|
| SLR rate | 2.2 | 3.0 | 3.2 | 3.4 | 4.1 |
| Standard Deviation | 0.07 | 0.09 | 0.10 | 0.11 | 0.14 |
| Series | 1993–2016 | SD | 2007–2016 | SD |
|---|---|---|---|---|
| NASA | 3.16 | 0.02 | 4.37 | 0.07 |
| CNES | 3.27 | 0.01 | 4.17 | 0.06 |
| CSIRO | 3.36 | 0.03 | 4.46 | 0.11 |
| Series & Period | Method | Model | Acceleration (mm/year2) | SD (mm/year2) |
|---|---|---|---|---|
| Cascais MSL (2007–2016) | Linear Regression | Mod.FC_0 | 0 | - |
| Cascais MSL (1980–2017) | 2nd order polynomial | Mod.FC_1 | 0.100 | 0.030 |
| Cascais MSL (1976–2016) | LR of SLR Velocity | Mod.FC_2a | 0.127 | 0.031 |
| Cascais MSL (1992–2016) | Finite Differences | Mod.FC_2b | 0.152 | 0.032 |
| NASA-NearCASC (1995–2017) | Finite Differences | Mod.FC_2c | 0.186 | 0.038 |
| CNES-North Atl. (1996–2017) | Finite Differences | Mod.FC_3a | 0.209 | 0.038 |
| NASA-WCPM (1995–2017) | Finite Differences | Mod.FC_3b | 0.263 | 0.038 |
| SLR Model | Initial Velocity (mm/year) | Acceleration (mm/year2) | MSL 2050 (m) | MSL 2100 (m) | Exceeding Probability |
|---|---|---|---|---|---|
| Mod.FC_0 | 4.10 | 0 | 0.34 | 0.54 | 94% |
| Mod.FC_1 | 2.72 | 0.100 | 0.39 | 0.90 | 72.9% |
| Mod.FC_2a | 3.35 | 0.127 | 0.46 | 1.10 | 53.7% |
| Mod.FC_2b | 2.20 | 0.152 | 0.43 | 1.11 | 52.7% |
| Mod.FC_2c | 1.98 | 0.186 | 0.46 | 1.26 | 37.5% |
| Mod.FC_3a | 2.49 | 0.209 | 0.52 | 1.43 | 22.4% |
| Mod.FC_3b | 2.08 | 0.263 | 0.56 | 1.65 | 8.8% |
| Confidence Level | Lower Limit (m) | Upper Limit (m) |
|---|---|---|
| 30% | 0.94 | 1.34 |
| 60% | 0.74 | 1.54 |
| 90% | 0.51 | 1.77 |
| 95% | 0.39 | 1.89 |
| 99% | 0.16 | 2.12 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antunes, C. Assessment of Sea Level Rise at West Coast of Portugal Mainland and Its Projection for the 21st Century. J. Mar. Sci. Eng. 2019, 7, 61. https://doi.org/10.3390/jmse7030061
Antunes C. Assessment of Sea Level Rise at West Coast of Portugal Mainland and Its Projection for the 21st Century. Journal of Marine Science and Engineering. 2019; 7(3):61. https://doi.org/10.3390/jmse7030061
Chicago/Turabian StyleAntunes, Carlos. 2019. "Assessment of Sea Level Rise at West Coast of Portugal Mainland and Its Projection for the 21st Century" Journal of Marine Science and Engineering 7, no. 3: 61. https://doi.org/10.3390/jmse7030061
APA StyleAntunes, C. (2019). Assessment of Sea Level Rise at West Coast of Portugal Mainland and Its Projection for the 21st Century. Journal of Marine Science and Engineering, 7(3), 61. https://doi.org/10.3390/jmse7030061





