Validation of Tidal Stream Turbine Wake Predictions and Analysis of Wake Recovery Mechanism
Abstract
1. Introduction
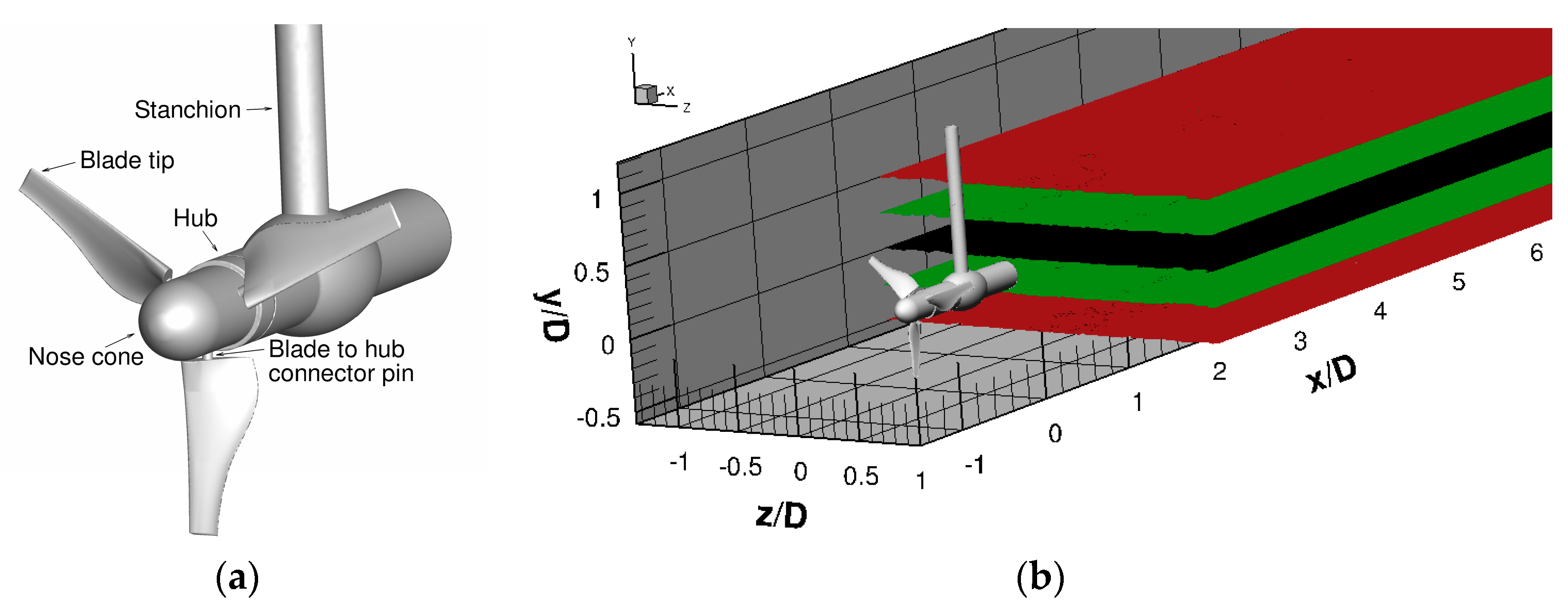
2. Tidal Stream Turbine Computational Model
2.1. Turbulence Modeling
2.2. Numerical Methods
3. Experimental Data
4. Simulation Setup
4.1. Simulation Conditions
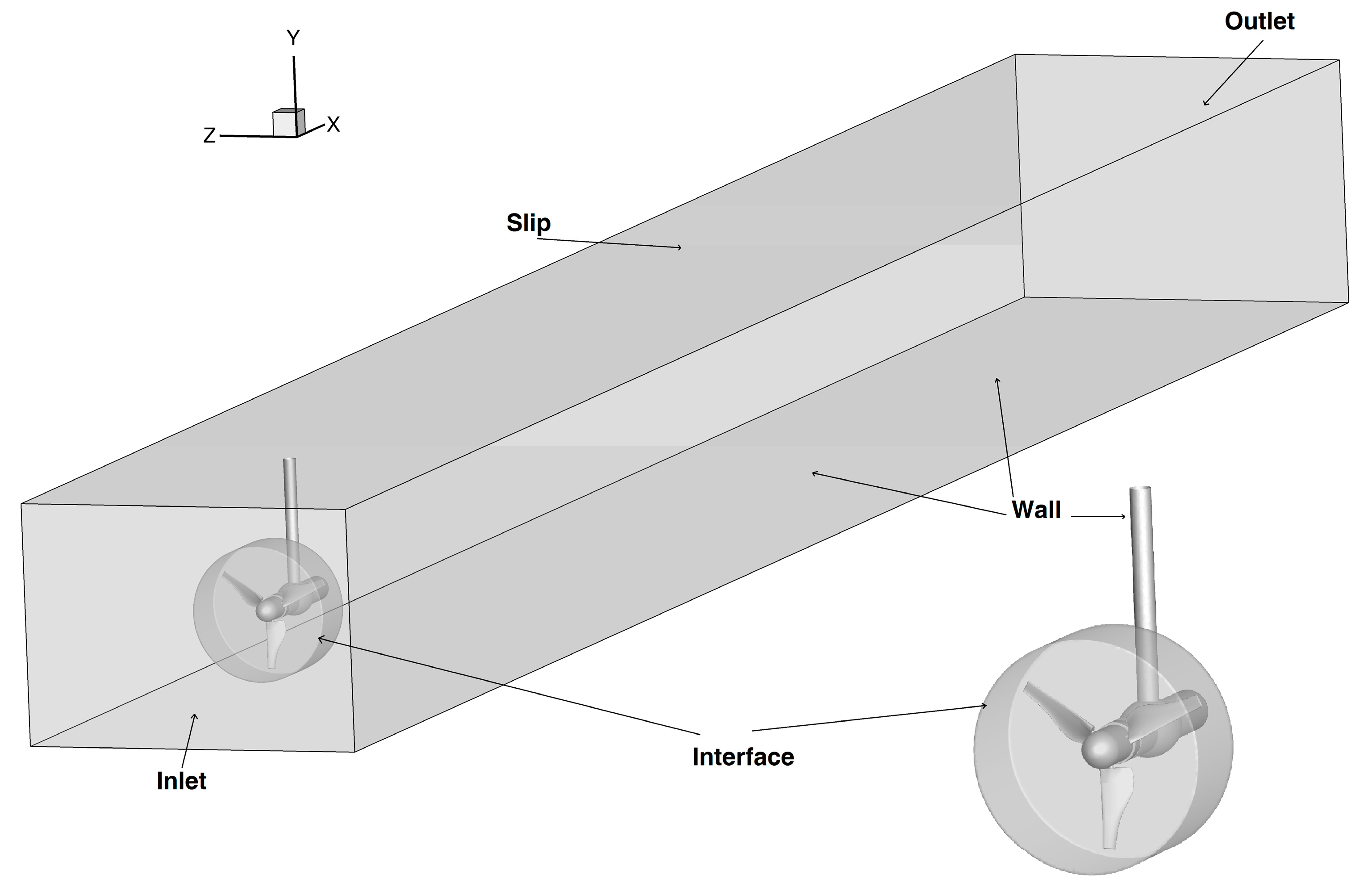
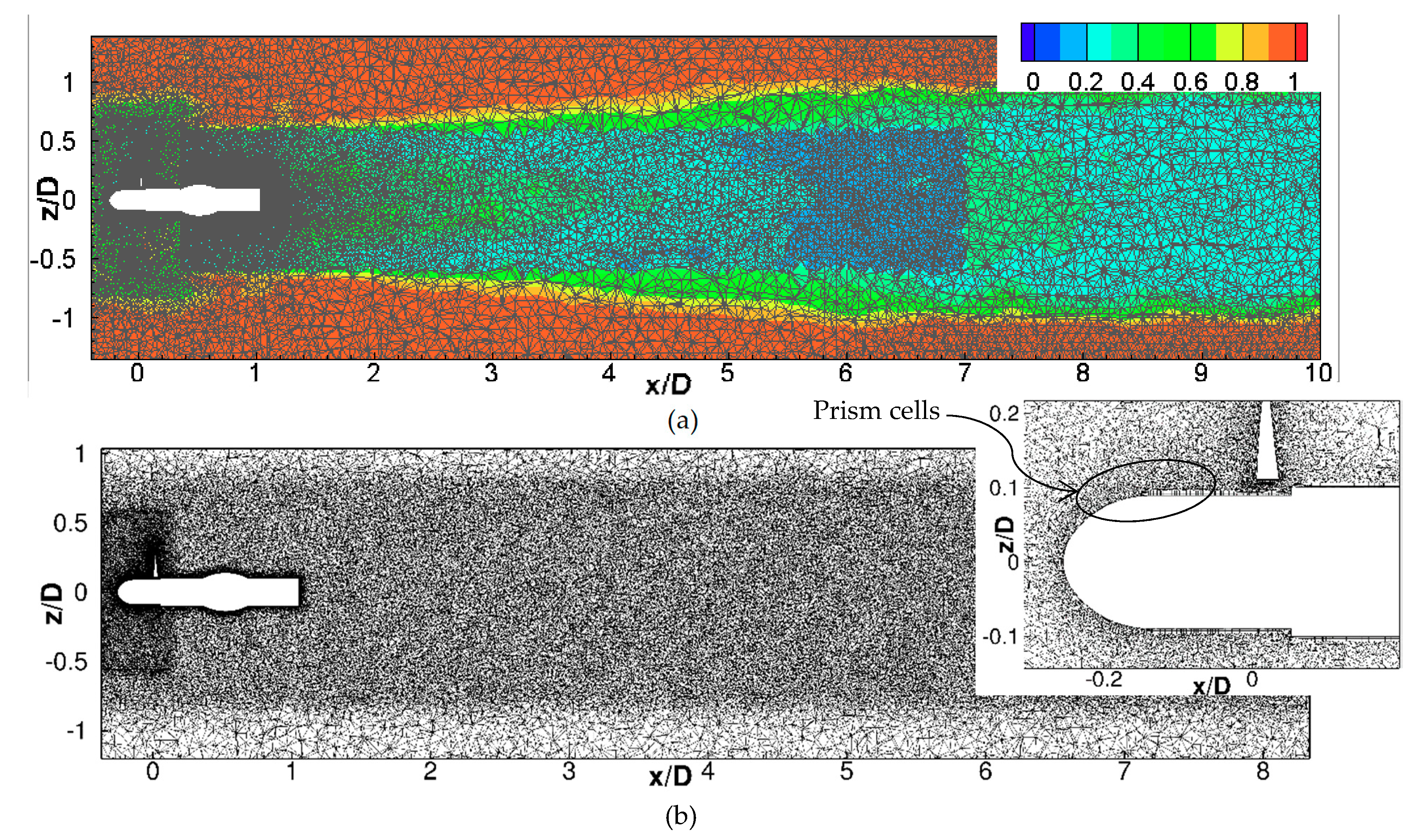
4.2. Domains and Grids
4.3. Boundary Conditions
4.4. Solution Parameters and High Performance Computing
5. Results and Discussions
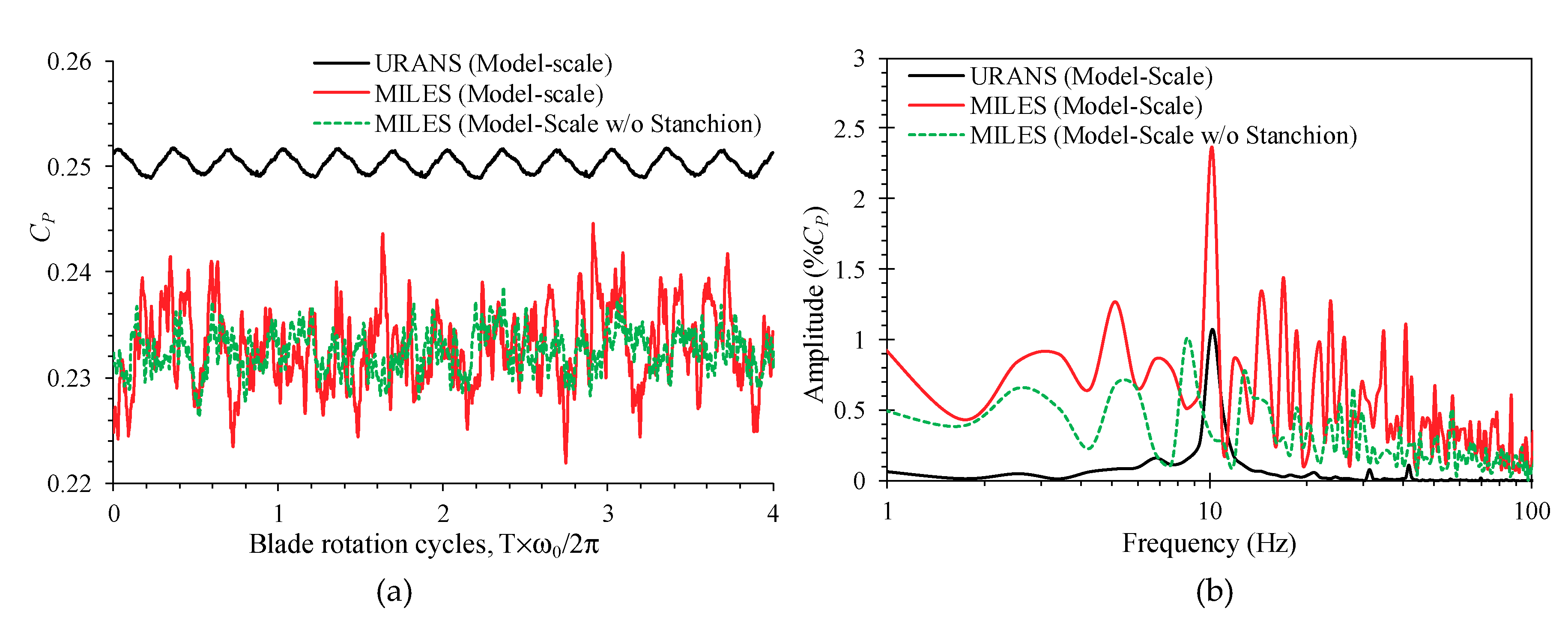
5.1. Thrust and Power Predictions
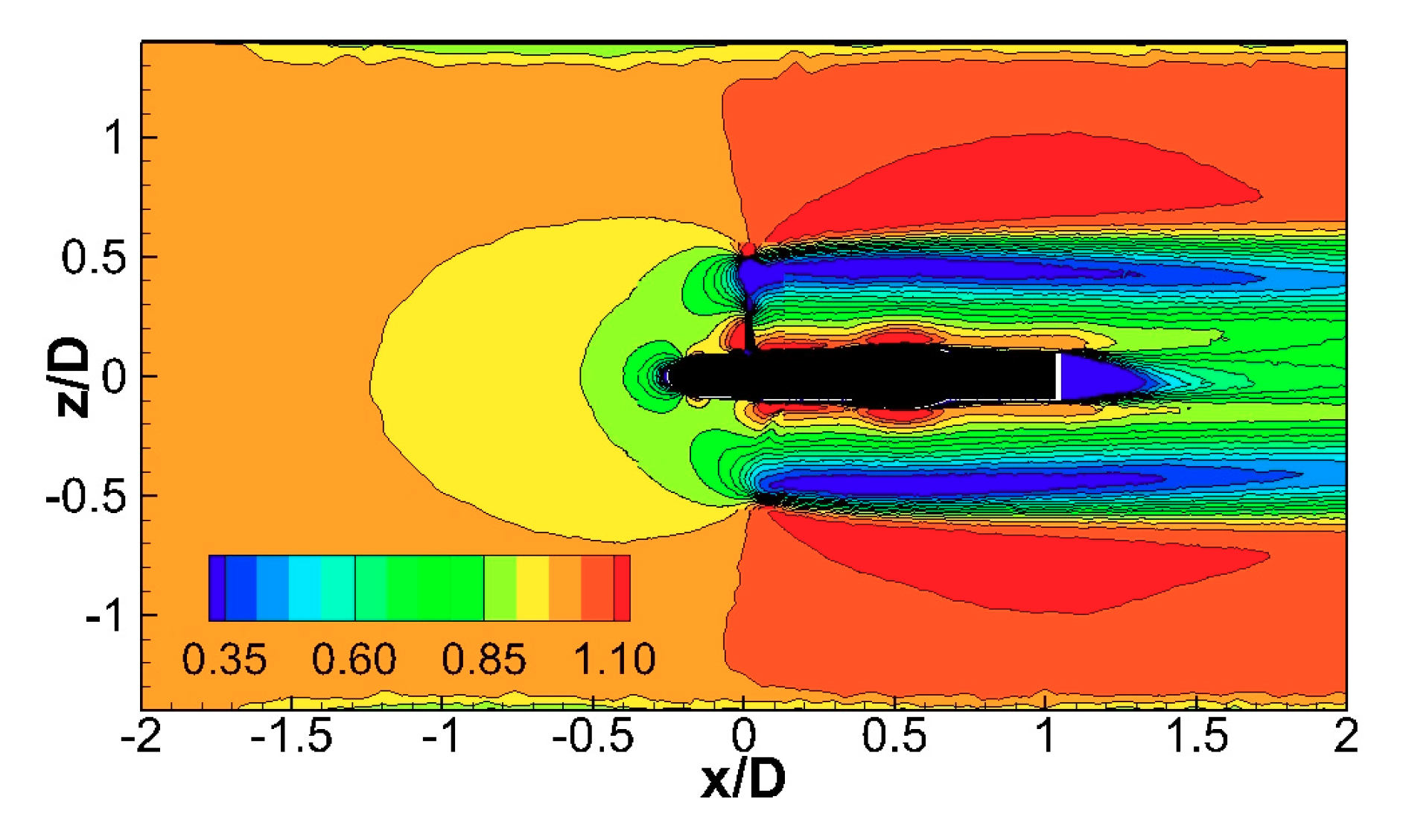
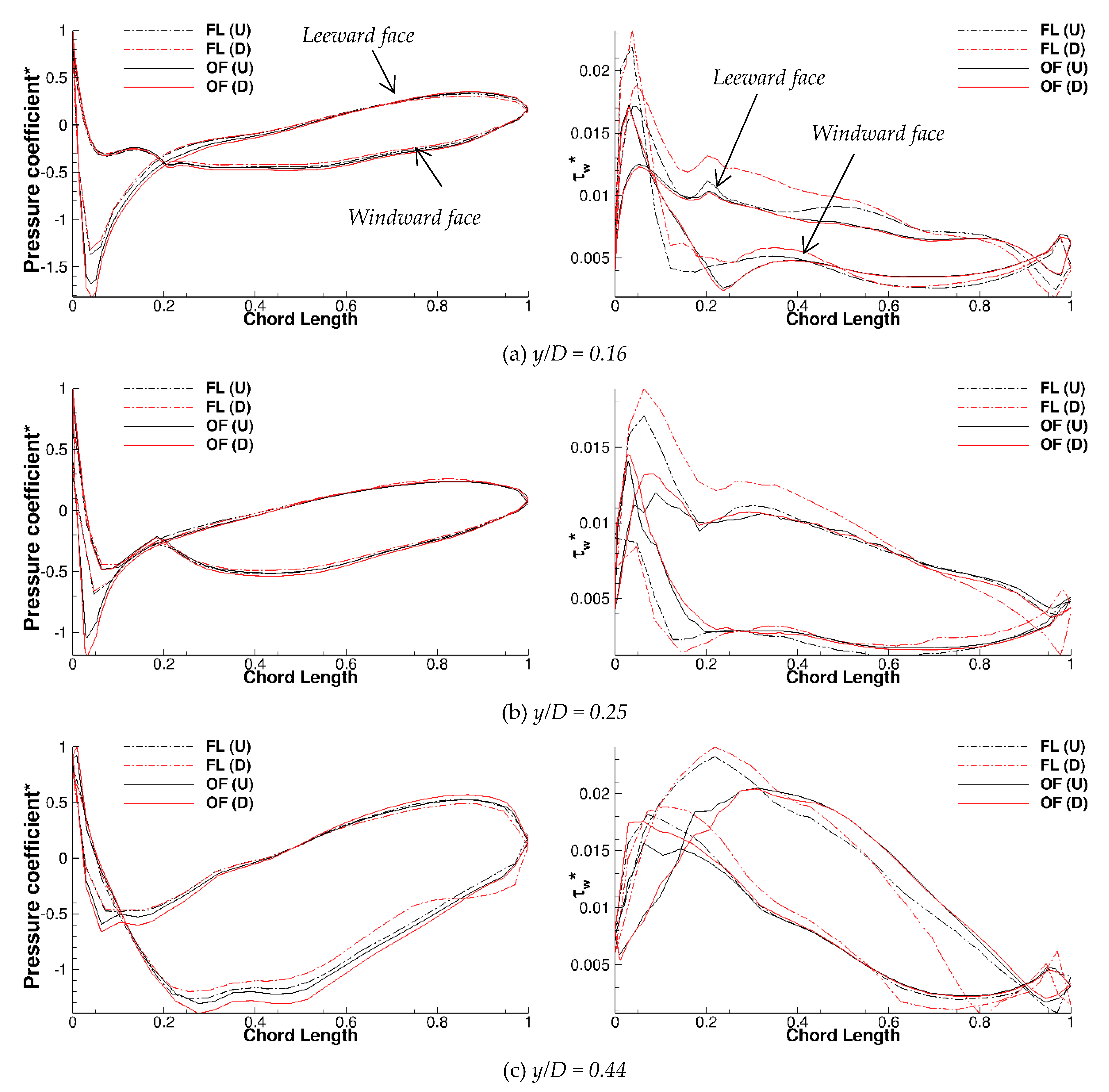
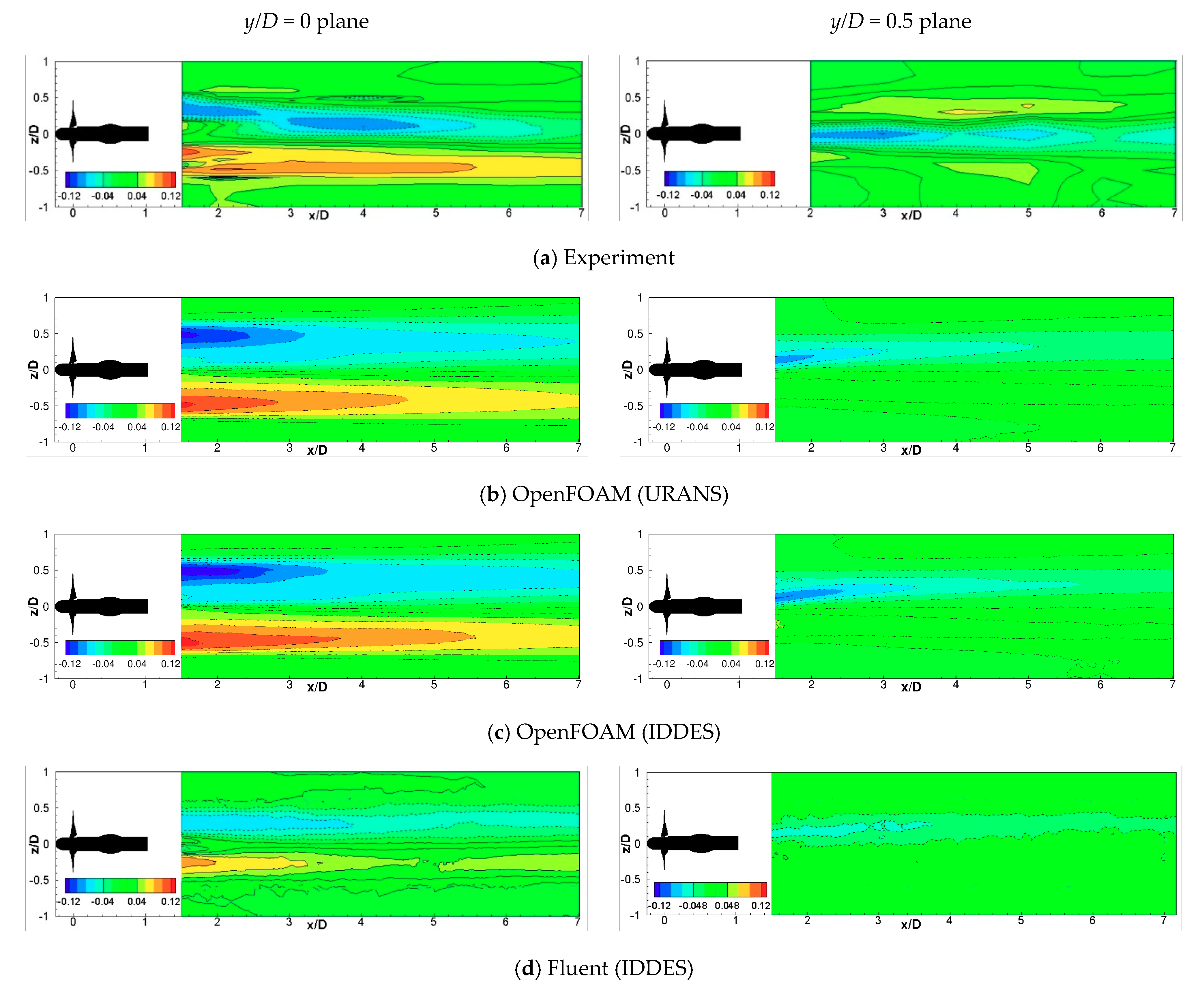
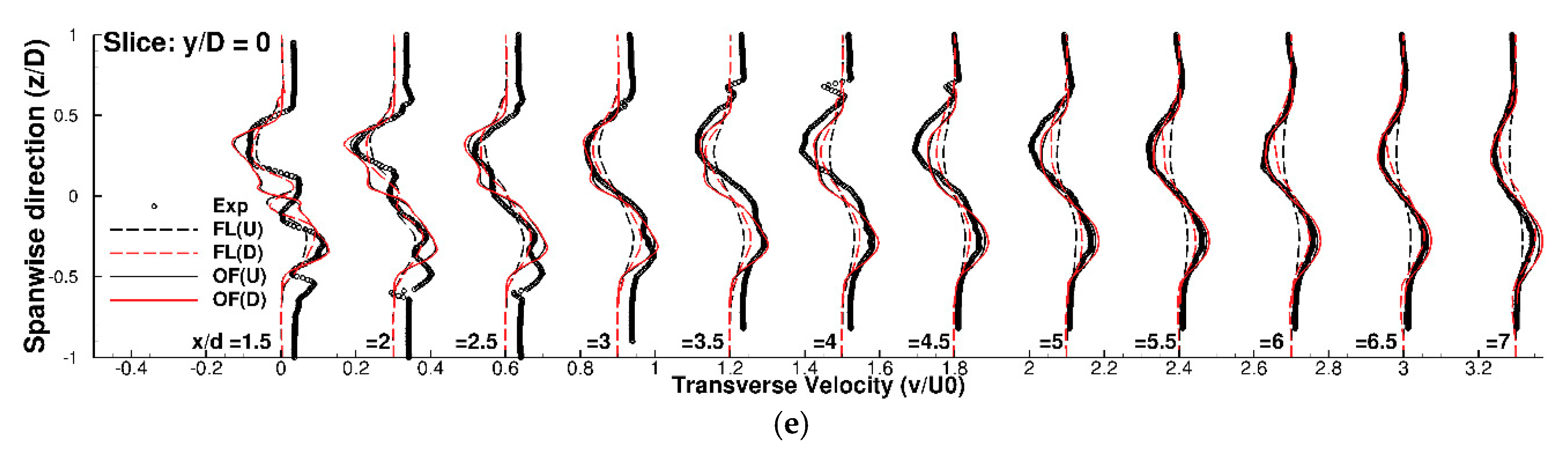
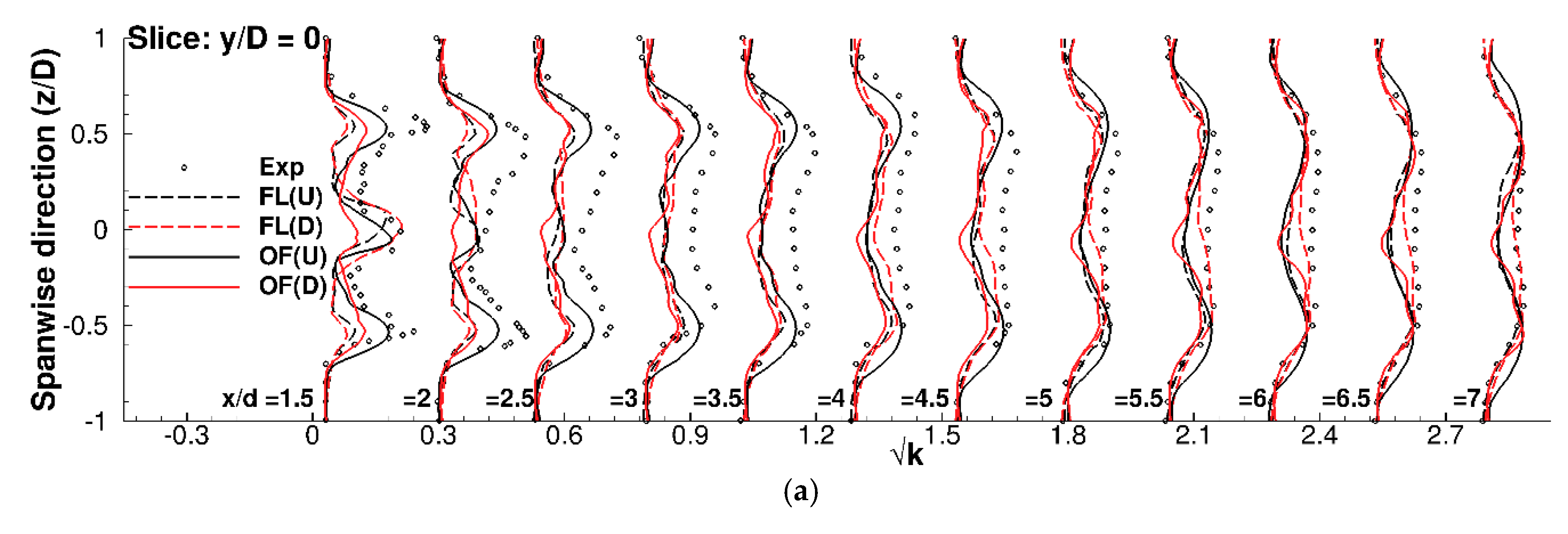
5.2. Mean and Turbulent Wake Validation
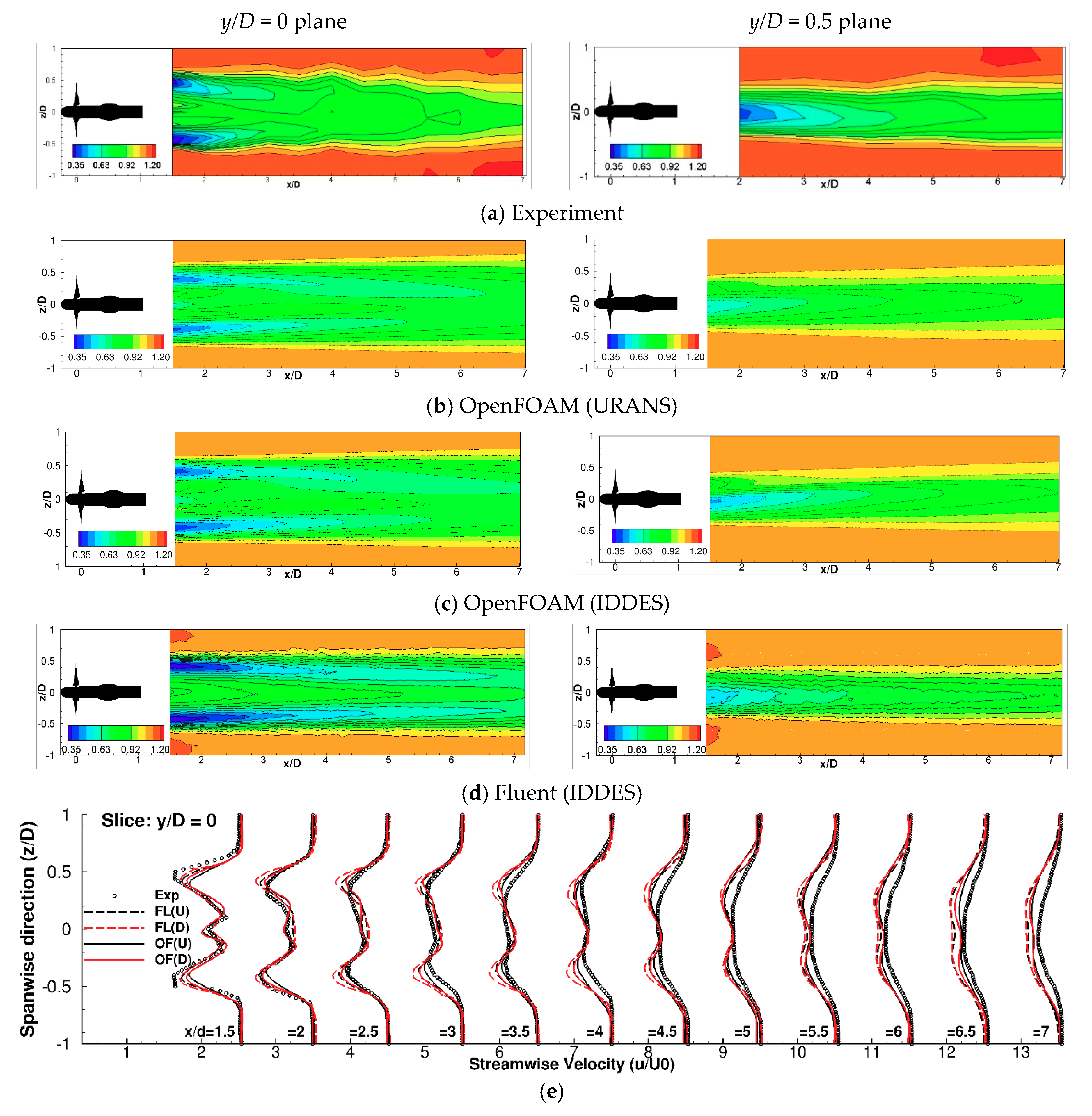
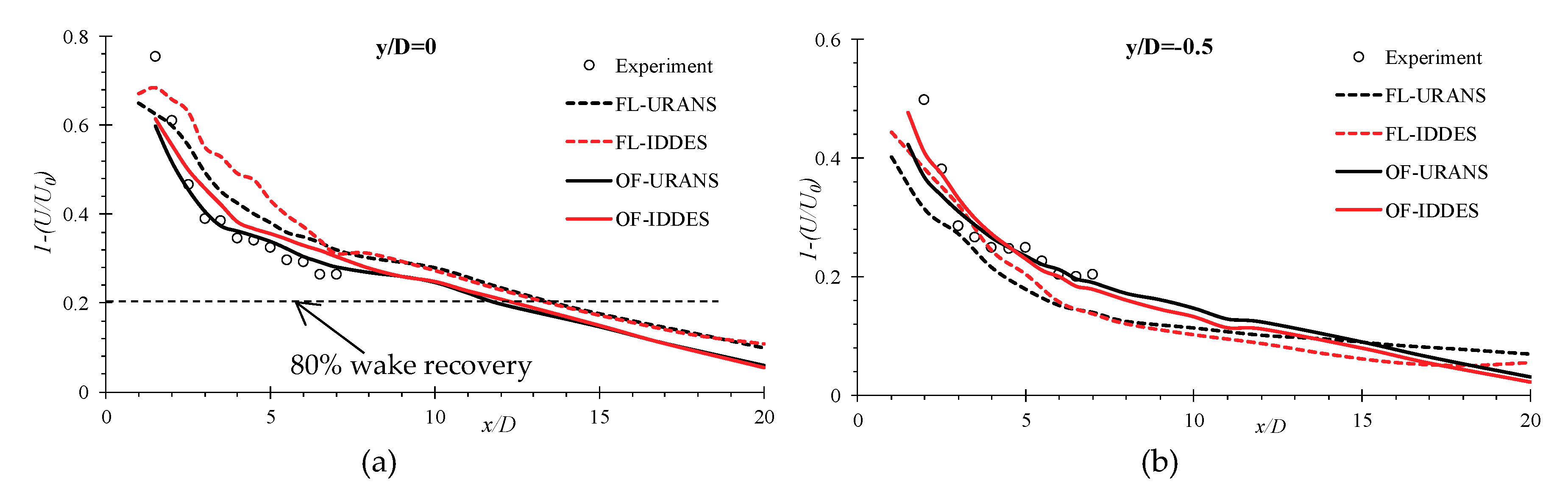
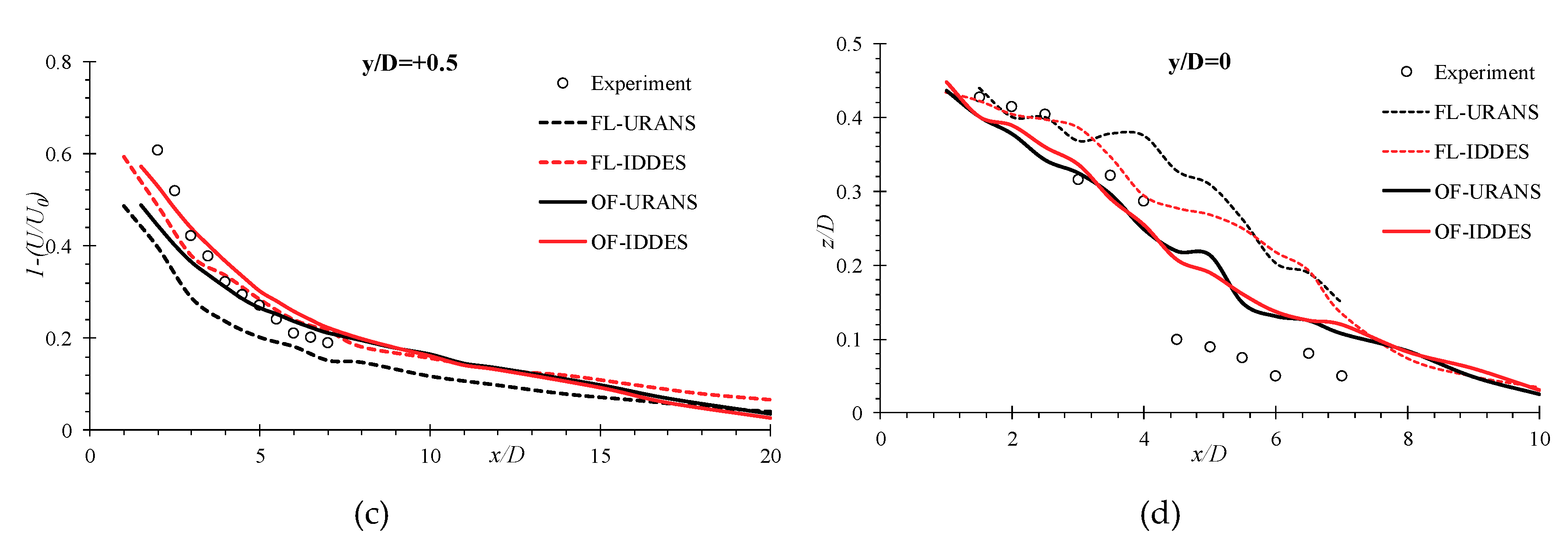
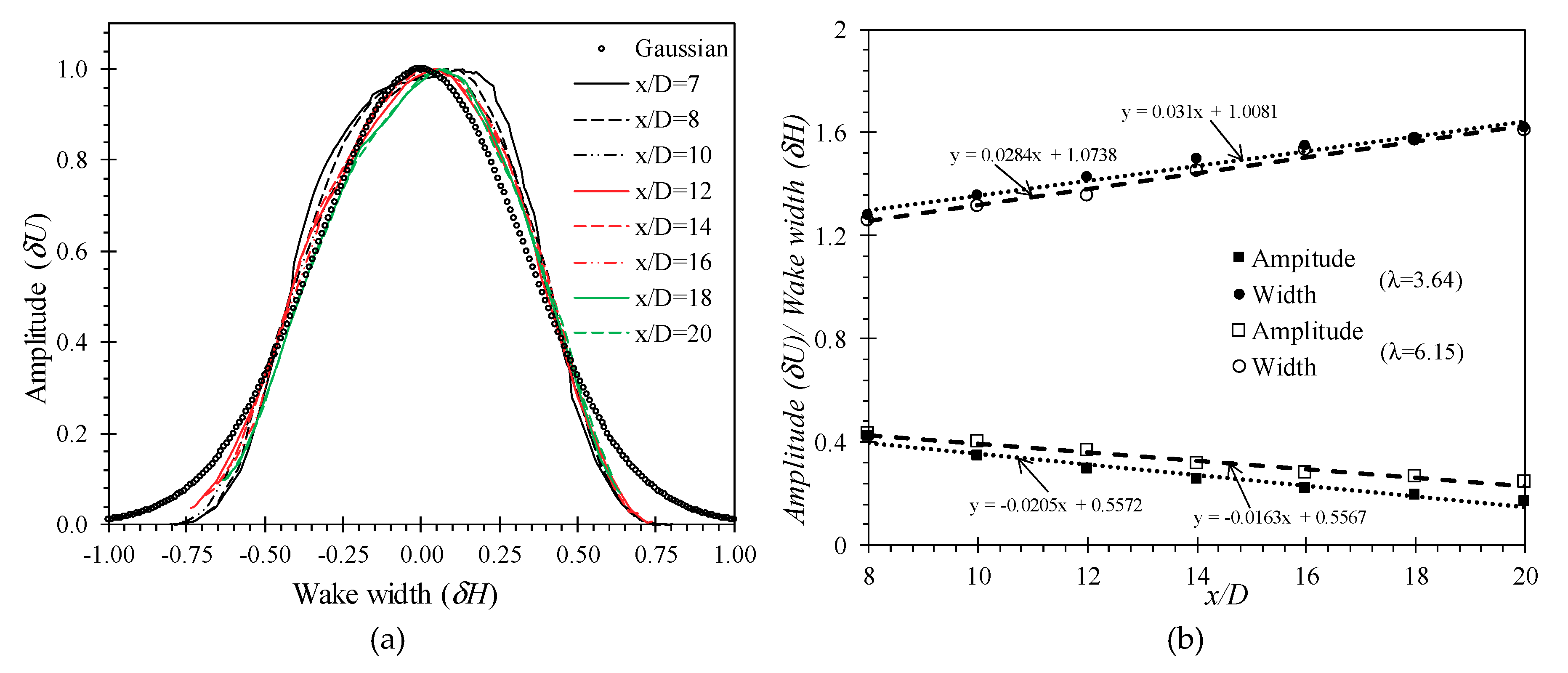
5.3. Far Wake Prediction
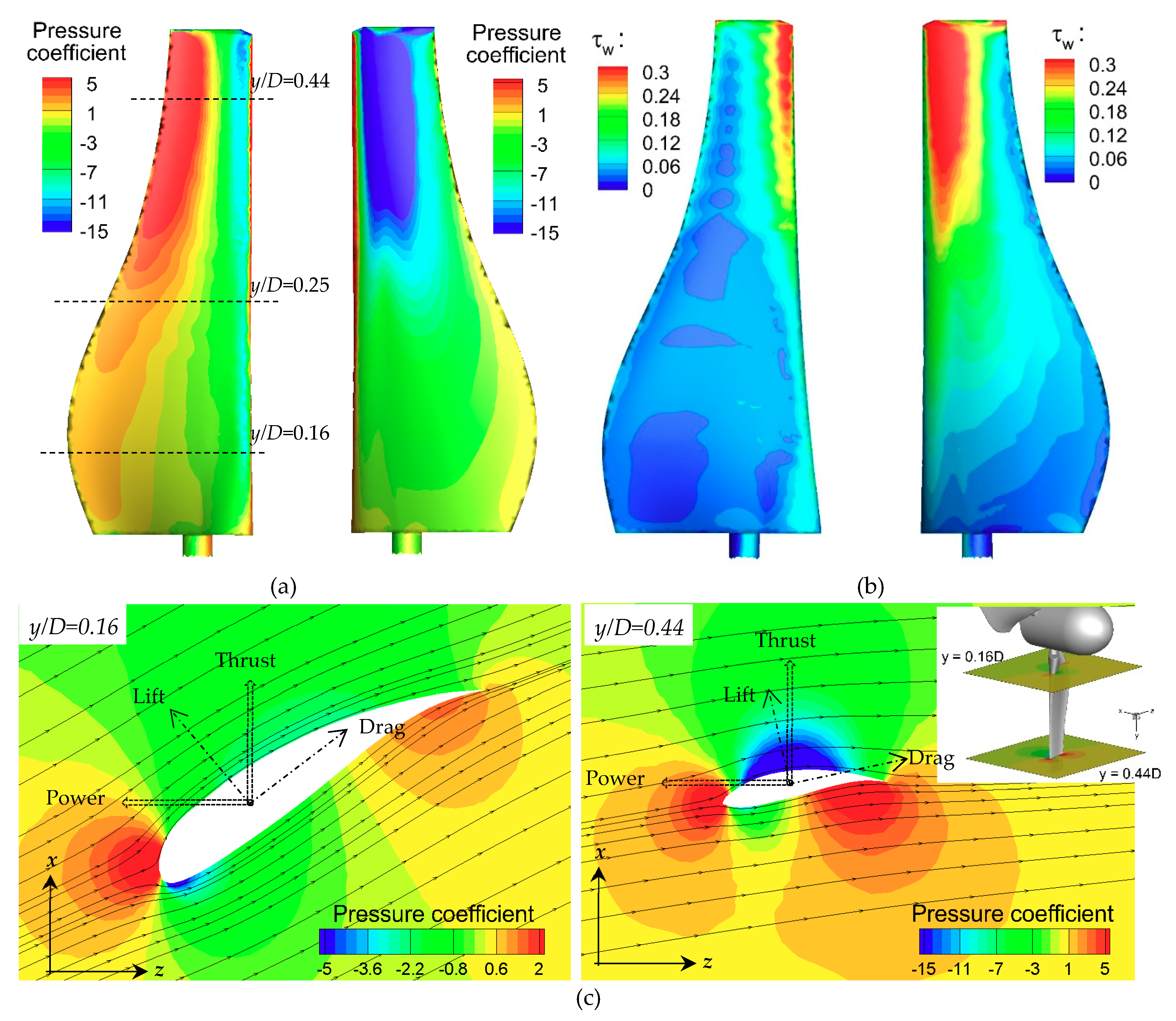
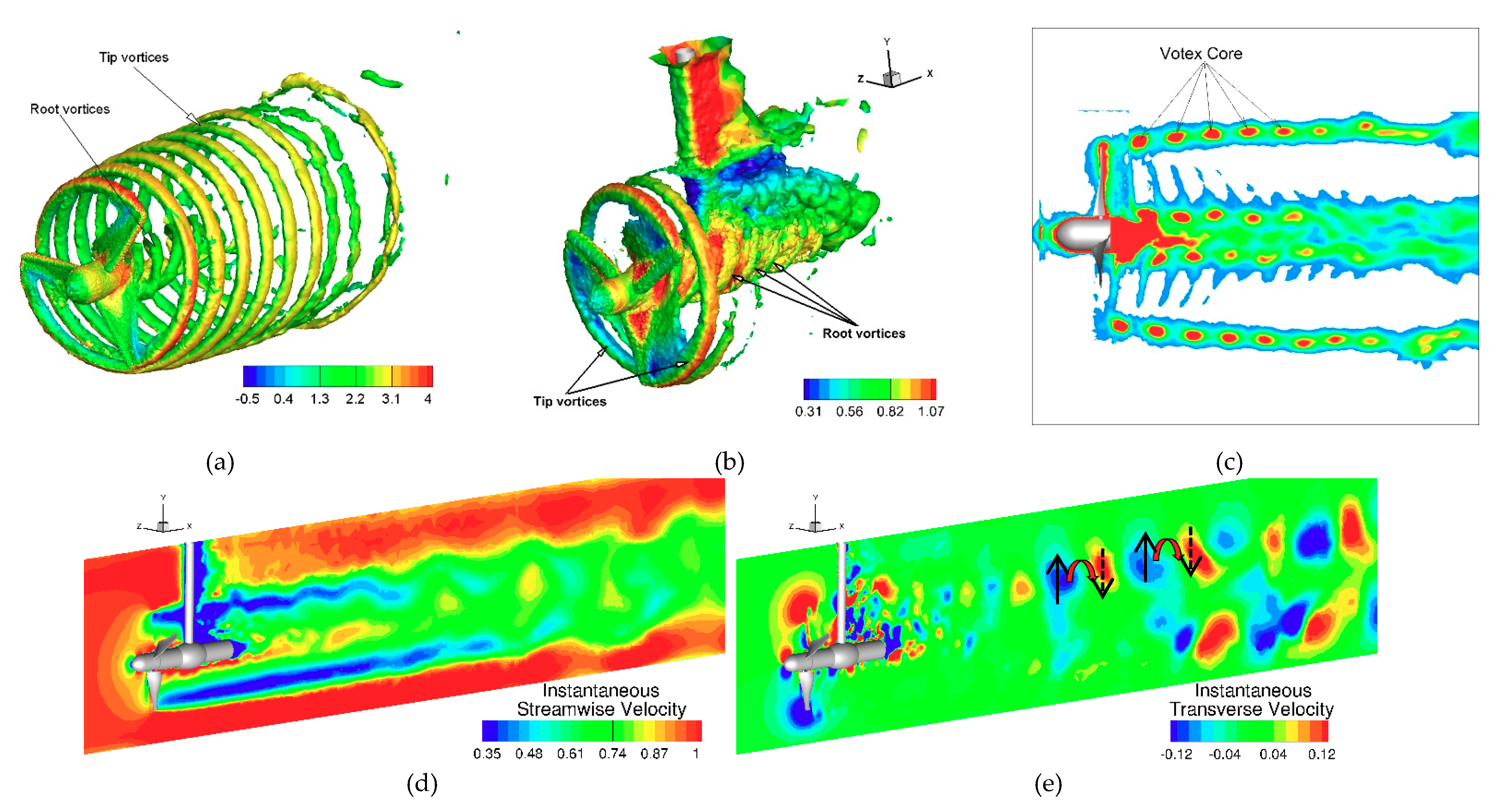
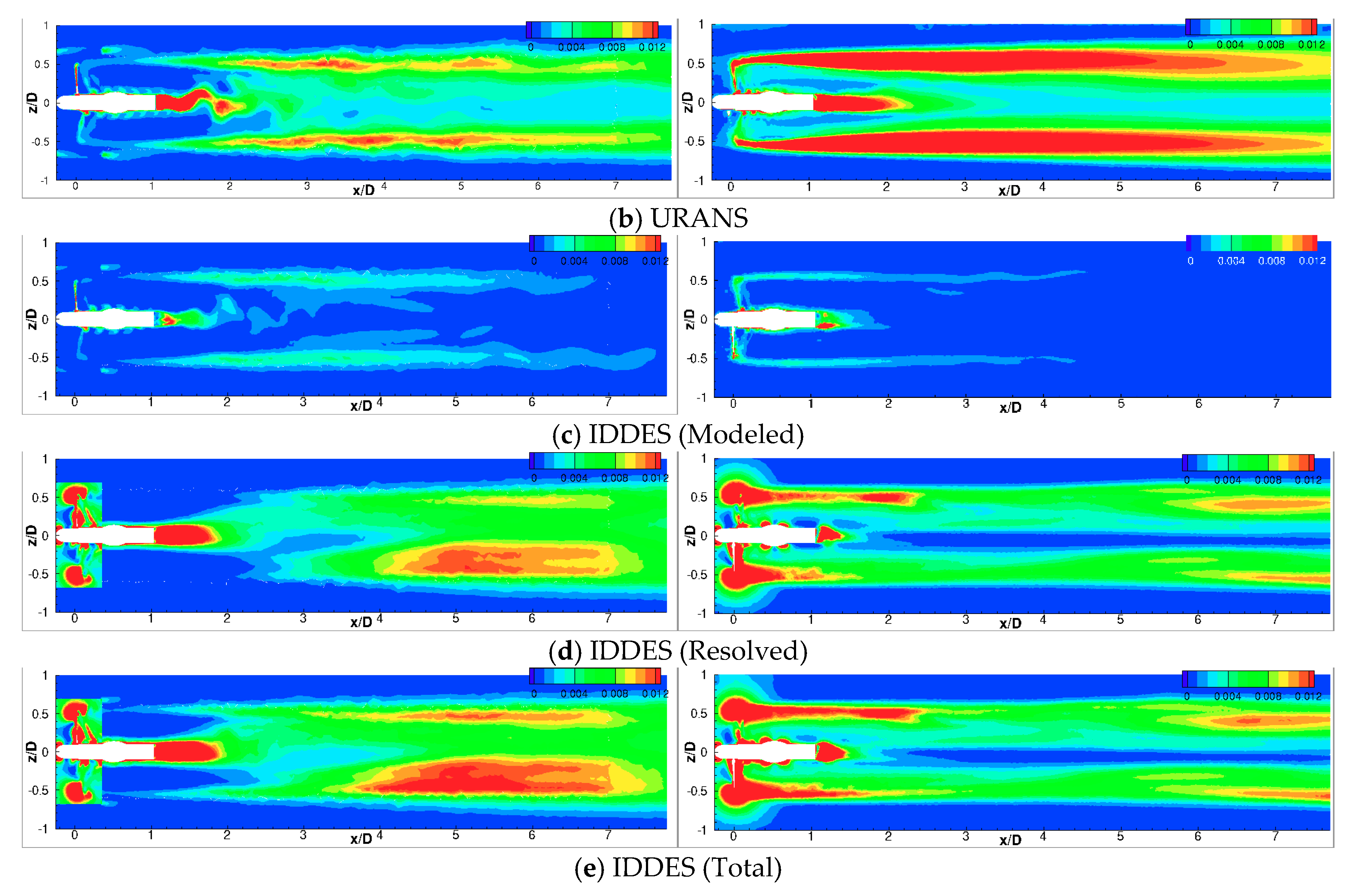
6. Discussions: Wake Recovery Mechanism
7. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. 2011: Summary for Policymakers. In IPCC Special Report on Renewable Energy Sources and Climate Change Mitigation; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Seyboth, K., Matschoss, P., Kadner, S., Zwickel, T., Eickemeier, P., Hansen, G., Schlömer, S., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2011. [Google Scholar]
- Tedds, S.C.; Owen, I.; Poole, R.J. Near wake characteristics of a model horizontal axis tidal stream turbine. Renew. Energy 2014, 63, 222–235. [Google Scholar] [CrossRef]
- Egarr, D.A.; O’Doherty, T.; Morris, T.; Ayre, R.G. Feasibility study using computational fluid dynamics for the use of a turbine for extracting energy from the tide. In Proceedings of the 15th Australasian Fluid Mechanics Conference, The University of Sydney, Sydney, Australia, 13–17 December 2004. [Google Scholar]
- Churchfield, M.J.; Li, Y.; Moriarty, P.J. A large-eddy simulation study of wake propagation and power production in an array of tidal-current turbines. Philos. Trans. R. Soc. A 2013, 371, 20120421. [Google Scholar] [CrossRef] [PubMed]
- Myers, L.W.; Bahaj, A.S. Experimental analysis of the flow field around horizontal axis tidal turbines by use of scale mesh disk rotor simulators. Ocean Eng. 2010, 37, 218–227. [Google Scholar] [CrossRef]
- Maganga, F.; Germain, G.; King, J.; Pinon, G.; Rivoalen, E. Experimental characterization of flow effects on marine current turbine behaviour and on its wake properties. Renew. Power Gener. IET 2010, 4, 498–509. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Shen, W. Numerical modeling of wind turbine wakes. J. Fluids Eng. 2002, 124, 393–402. [Google Scholar] [CrossRef]
- Mason-Jones, A.; O’Doherty, D.M.; Morris, C.E.; O’Doherty, T.; Byrne, C.B.; Prickett, P.W.; Grosvenor, R.I.; Owen, I.; Tedds, S.; Poole, R.J. Non-dimensional scaling of tidal stream turbines. Energy 2012, 44, 820–829. [Google Scholar] [CrossRef]
- Vermeer, L.J.; Sørensen, J.N.; Crespo, A. Wind turbine wake aerodynamics. Prog. Aerosp. Sci. 2003, 39, 467–510. [Google Scholar] [CrossRef]
- Shen, W.; Mikkelsen, R.; Sørensen, J.N.; Bak, C. Tip loss corrections for wind turbine computations. Wind Energy 2005, 8, 457–475. [Google Scholar] [CrossRef]
- Contreras, L.T.; Lopez, O.D.; Lain, S. Computational Fluid Dynamics Modelling and Simulation of an Inclined Horizontal Axis Hydrokinetic Turbine. Energies 2018, 11, 3151. [Google Scholar] [CrossRef]
- Brand, A.J.; Peinke, J.; Mann, J. Turbulence and wind turbines. J. Phys. Conf. Ser. 2011, 318, 072005. [Google Scholar] [CrossRef]
- Ainslie, J.F. Calculating the field in the wake of wind turbines. J. Wind Eng. Ind. Aerodyn. 1988, 27, 213–224. [Google Scholar] [CrossRef]
- Crespo, A.; Hernandez, J.; Frega, E.; Andreu, C. Experimental validation of the UPM computer code to calculate wind turbine wakes and comparison with other models. J. Wind Eng. Ind. Aerodyn. 1988, 27, 77–88. [Google Scholar] [CrossRef]
- Magnusson, M.; Smedman, A.S. Air flow behind wind turbines. J. Wind Eng. Ind. Aerodyn. 1999, 80, 169–189. [Google Scholar] [CrossRef]
- Larsen, G.; Madsen, H.; Thomsen, K.; Larsen, T. Wake meandering: A pragmatic approach. Wind Energy 2010, 11, 377–395. [Google Scholar] [CrossRef]
- Elvira, R.G.; Crespo, A.; Migoya, E.; Manuel, F.; Hernandez, J. Anisotropy of Turbulence in Wind Turbine Wakes. J. Wind Eng. Ind. Aerod. 2005, 93, 797–814. [Google Scholar] [CrossRef]
- Afgan, I.; McNaughton, J.; Rolfo, S.; Apsley, D.; Stallard, T.; Stansby, P. Turbulent flow and loading on a tidal stream turbine by LES and RANS. Int. J. Heat Fluid Flow 2013, 43, 96–108. [Google Scholar] [CrossRef]
- Ahmed, U.; Apsley, D.D.; Afgan, I.; Stallard, T.; Stansby, P.K. Fluctuating loads on a tidal turbine due to velocity shear and turbulence: Comparison of CFD with field data. Renew. Energy 2017, 112, 235–246. [Google Scholar] [CrossRef]
- Shen, W.Z.; Zhang, J.; Sørensen, J.N. The actuator surface model: A new Navier—Stokes based model for rotor computations. J. Sol. Energy Eng. 2009, 131, 011002. [Google Scholar] [CrossRef]
- Batten, W.M.J.; Harrison, M.E.; Bahaj, A.S. Accuracy of the actuator disc-RANS approach for predicting the performance and wake of tidal turbines. Philos. Trans. R. Soc. A 2013, 371, 20120293. [Google Scholar] [CrossRef] [PubMed]
- Johansen, J.; Sørensen, N.N.; Michelsen, J.A.; Schreck, S. Detached-eddy simulation of flow around the NREL phase VI blade. Wind Energy 2002, 5, 185–197. [Google Scholar] [CrossRef]
- Blackmore, T.; Batten, W.; Bahaj, A.S. Turbulence generation and its effect in LES approximations of tidal turbines. In Proceedings of the 10th European Wave and Tidal Energy Conference, Aalborg, Denmark, 2–5 September 2013. [Google Scholar]
- Bowman, J.; Bhushan, S.; Thompson, D.; O’Doherty, D.; O’Doherty, T.; Mason-Jones, A. A Physics-Based Actuator Disk Model for Hydrokinetic Turbines. In Proceedings of the 2018 Fluid Dynamics Conference, AIAA AVIATION Forum, (AIAA 2018–3227), Atlanta, Georgia, 25–29 June 2018. [Google Scholar]
- Troldborg, N.; Sørensen, J.N.; Mikkelsen, R. Actuator line simulation of wake of wind turbine operating in turbulent inflow. J. Phys. Conf. Ser. 2007, 75, 012063. [Google Scholar] [CrossRef]
- Mason-Jones, A.; O’Doherty, D.M.; Morris, C.E.; O’Doherty, T. Influence of a velocity profile & support structure on tidal stream turbine performance. Renew. Energy 2013, 52, 23–30. [Google Scholar]
- Frost, C.; Morris, C.E.; Mason-Jones, A.; O’Doherty, D.M.; O’Doherty, T. Effects of tidal directionality on tidal turbine characteristics. J. Renew. Energy 2015, 78, 609–620. [Google Scholar] [CrossRef]
- Zahle, F.; Sørensen, N.N.; Johansen, J. Wind turbine rotor–tower interaction using an incompressible overset grid method. Wind Energy 2009, 12, 594–619. [Google Scholar] [CrossRef]
- Li, Y.; Castro, A.M.; Sinokrot, T.; Prescott, W.; Carrica, P.M. Coupled multi-body dynamics and CFD for wind turbine simulation including explicit wind turbulence. Renew. Energy 2015, 76, 338–361. [Google Scholar] [CrossRef]
- Marchevsky, I.K.; Puzikova, V.V. Numerical Simulation of Wind Turbine Rotors Autorotation by Using the Modified LS-STAG Immersed Boundary Method. Int. J. Rotating Mach. 2017, 2017, 6418108. [Google Scholar] [CrossRef]
- Ouro, P.; Stoesser, T. An immersed boundary-based large-eddy simulation approach to predict the performance of vertical axis tidal turbines. Comput. Fluids 2017, 152, 74–87. [Google Scholar] [CrossRef]
- Bhushan, S.; Carrica, P.; Yang, J.; Stern, F. Scalability and Validation Study for Large Scale Surface Combatant Computations Using CFDShip-Iowa. Int. J. High-Perform. Comput. Appl. 2011, 25, 466–487. [Google Scholar] [CrossRef]
- Kasmi, A.; Masson, C. An extended k-ε model for turbulent flow through horizontal axis wind turbines. J. Wind Eng. Ind. Aerodyn. 2008, 96, 103–122. [Google Scholar] [CrossRef]
- Cabezon, D.; Migoya, E.; Crespo, A. Comparison of turbulence models for the Computational fluid dynamics simulation of wind turbine wakes in the atmospheric boundary layer. Wind Energy 2011, 14, 909–921. [Google Scholar] [CrossRef]
- O’Brien, J.M.; Young, T.M.; Early, J.M.; Griffin, P.C. An assessment of commercial CFD turbulence models for near wake HAWT modelling. J. Wind Eng. Ind. Aerodyn. 2018, 176, 32–53. [Google Scholar] [CrossRef]
- Archera, C.L.; Vasel-Be-Hagha, A.; Yana, C.; Wua, S.; Yang Pana, Y.; Brodiea, J.F.; Maguire, A.E. Review and evaluation of wake loss models for wind energy applications. Appl. Energy 2018, 226, 1187–1207. [Google Scholar] [CrossRef]
- FLUENT 6.3; User Guide FLUENT 6.3; FLUENT Inc.: Lebanon, NH, USA, 2006.
- Jasak, H.; Jemcov, A.; Tukovic, Z. Openfoam: A C++ library for complex physics simulations. In International Workshop on Coupled Methods in Numerical Dynamics; IUC Dubrovnik: Dubrovnik, Croatia, 2007. [Google Scholar]
- Salunkhe, S. Model—and Full-Scale Predictions of Hydrokinetic Turbulent Wake, Including Model-Scale Validation. Master’s Thesis, Mississippi State University, Starkville, MS, USA, 2016. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Spalart, P.R. Detached-eddy simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Grinstein, F.F.; Fureby, C. On Monotonically Integrated Large Eddy Simulation of Turbulent Flows Based on FCT Algorithms. In Flux-Corrected Transport. Scientific Computation; Kuzmin, D., Löhner, R., Turek, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Adedoyin, A.A.; Walters, D.K.; Bhushan, S. Evaluation of turbulence model and numerical scheme combinations for practical Finite-volume Large Eddy Simulations. Eng. Appl. Comput. Fluid Mech. 2015, 9, 324–342. [Google Scholar]
- Robertson, E.; Choudhury, V.; Bhushan, S.; Walters, D.K. Validation of OpenFOAM Numerical Methods and Turbulence Models for Incompressible Bluff Body Flows. Comput. Fluids 2015, 123, 122–145. [Google Scholar] [CrossRef]
- Morris, C. Influence of Solidity on the Performance, Swirl Characteristics, Wake Recovery and Blade Deflection of a Horizontal Axis Tidal Turbine. Ph.D. Thesis, Cardiff University, Cardiff, Wales, 2014. [Google Scholar]
- Morris, C.E.; O’Doherty, D.M.; Mason-Jones, A.; O’Doherty, T. Evaluation of the swirl characteristics of a tidal stream turbine wake. Int. J. Mar. Energy 2016, 14, 198–214. [Google Scholar] [CrossRef]
- Gupta, A.K.; Lilley, D.G.; Syred, N. Swirl Flows; Energy and Engineering Science Series; Abacus Press Tunbridge Wells: Kent, UK, 1984. [Google Scholar]
- Wilson, R.E.; Lissaman, P.B.S.; Walker, S.N. Aerodynamic Performance of Wind Turbines; Oregon State University: Corvallis, OR, USA, 1976. [Google Scholar]
- Salvatore, F.; Sarichloo, Z.; Calcagni, D. Marine Turbine Hydrodynamics by a Boundary Element Method with Viscous Flow Correction. J. Mar. Sci. Eng. 2018, 6, 53. [Google Scholar] [CrossRef]
- Engström, S.; Ganander, H.; Lindström, L. Short Term Power Variations in the Output of Wind Turbines. DEWI Mag. 2001, 19, 27–30. [Google Scholar]
- Bastankhan, M.; Porte-Agel, F. A new analytical model for wind turbine wakes. Renew. Energy 2014, 70, 116–123. [Google Scholar] [CrossRef]
- Bhushan, S.; Walters, D.K. A dynamic hybrid RANS/LES modeling framework. Phys. Fluids 2012, 24, 015103. [Google Scholar] [CrossRef]
- Bhushan, S.; Yoon, H.; Stern, F.; Guilmineau, E.; Visonneau, M.; Toxopeus, S.; Simonsen, C.; Aram, S.; Kim, S.-E.; Grigoropoulos, G. Assessment of CFD for Surface Combatant 5415 at Straight Ahead and Static Drift. J. Fluids Eng. 2019, 141, 051101. [Google Scholar] [CrossRef]
- Bahaj, A.S.; Myers, L.E.; Rawlinson-Smith, R.I.; Thomson, M. The Effect of Boundary Proximity Upon the Wake Structure of Horizontal Axis Marine Current Turbines. J. Offshore Mech. Arct. Eng. 2012, 134, 021104. [Google Scholar] [CrossRef]
| 1 | The experimental profiles were interpolated from the Tecplot contours plots provided by Professor Robert Poole. Thus, the symbols do not correspond the actual measurement locations. |
| Solver | Grid Size | Turbulence Model | Thrust | Power | Power Unsteadiness | Intermediate Wake | Far Wake | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CT (%E) | CT,P (%CT) | CT,F (%CT) | CP (%E) | CP,P (%CP) | CP,F (%CP) | Frequency (Hz)♥ | Amplitude (%CP) | Recovery Length (D)♣ | Prediction (%E) | Width Growth (D) | Amplitude Decay (U0/D) | |||
| Experiment, Morris et al. [42] | 1.04 | 0.226 | ||||||||||||
| Fluent (F) | 8.8 M | URANS | 1.042 (0.2%) | 1.034 (99.2%) | 0.013 (1.2%) | 0.248 (9.7%) | 0.342 (137.9%) | ‒0.094 (‒37.9%) | 10.15 | 1.07% | 13.33 | 24.1 | 0.031 | ‒0.0163 |
| IDDES | 1.036 (‒0.4%) | 1.022 (98.6%) | 0.014 (1.3%) | 0.255 (12.8%) | 0.357 (140.0%) | ‒0.102 (‒40%) | 10.19 | 1.15% | 13.21 | 23.8 | 0.026 | ‒0.0176 | ||
| MILES | 1.052 (1.2%) | 1.046 (99.4%) | 0.008 (0.6%) | 0.234 (3.5%) | 0.296 (126.4%) | ‒0.063 (‒26.9%) | 10.21 | 2.4% | 13.10 | 25.8 | 0.028 | ‒0.0183 | ||
| OpenFOAM (OF) | 11 M | URANS | 0.967 (‒7.0%) | 0.960 (99.2%) | 0.0069 (0.7%) | 0.198 (‒12.4%) | 0.303 (153%) | ‒0.105 (‒53.0%) | 10.90 | 1.14% | 11.53 | 7.4 | 0.025 | ‒0.0210 |
| IDDES | 0.959 (‒7.8%) | 0.952 (99.2%) | 0.0068 (0.6%) | 0.190 (‒15.9%) | 0.294 (154.7%) | ‒0.104 (‒54.7%) | 10.74 | 1.53% | 12.15 | 12.9 | 0.030 | ‒0.0204 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salunkhe, S.; El Fajri, O.; Bhushan, S.; Thompson, D.; O’Doherty, D.; O’Doherty, T.; Mason-Jones, A. Validation of Tidal Stream Turbine Wake Predictions and Analysis of Wake Recovery Mechanism. J. Mar. Sci. Eng. 2019, 7, 362. https://doi.org/10.3390/jmse7100362
Salunkhe S, El Fajri O, Bhushan S, Thompson D, O’Doherty D, O’Doherty T, Mason-Jones A. Validation of Tidal Stream Turbine Wake Predictions and Analysis of Wake Recovery Mechanism. Journal of Marine Science and Engineering. 2019; 7(10):362. https://doi.org/10.3390/jmse7100362
Chicago/Turabian StyleSalunkhe, Sanchit, Oumnia El Fajri, Shanti Bhushan, David Thompson, Daphne O’Doherty, Tim O’Doherty, and Allan Mason-Jones. 2019. "Validation of Tidal Stream Turbine Wake Predictions and Analysis of Wake Recovery Mechanism" Journal of Marine Science and Engineering 7, no. 10: 362. https://doi.org/10.3390/jmse7100362
APA StyleSalunkhe, S., El Fajri, O., Bhushan, S., Thompson, D., O’Doherty, D., O’Doherty, T., & Mason-Jones, A. (2019). Validation of Tidal Stream Turbine Wake Predictions and Analysis of Wake Recovery Mechanism. Journal of Marine Science and Engineering, 7(10), 362. https://doi.org/10.3390/jmse7100362








