Storm Surge Propagation and Flooding in Small Tidal Rivers during Events of Mixed Coastal and Fluvial Influence
Abstract
1. Introduction
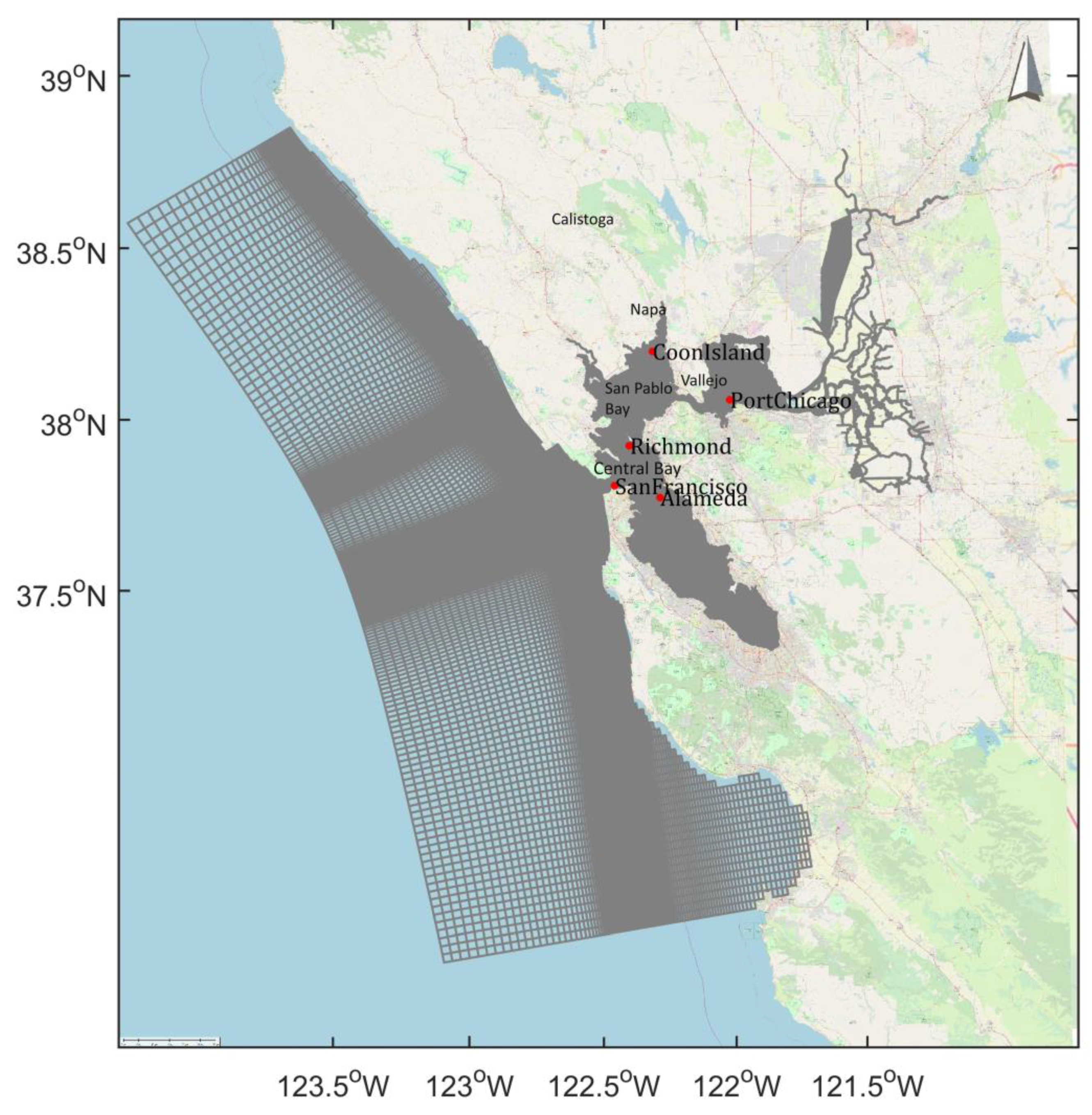
1.1. Study Area: Hydrodynamic Characteristics
1.2. Study Area: Hydrologic Characteristics
1.3. Study Area: Geology
1.4. Study Area: Human and Natural Pressures
2. Materials and Methods
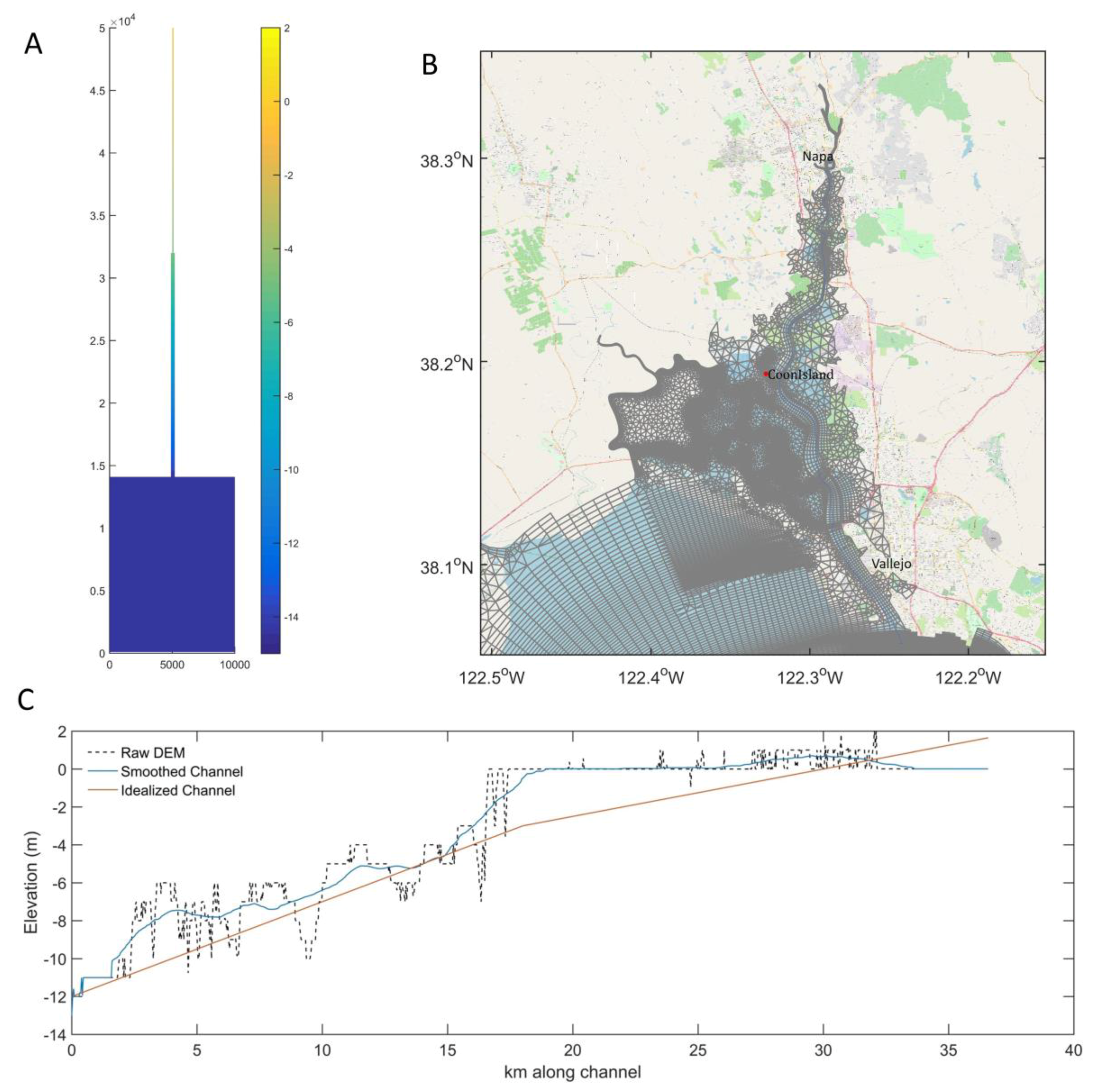
2.1. Realistic Field-Scale Model
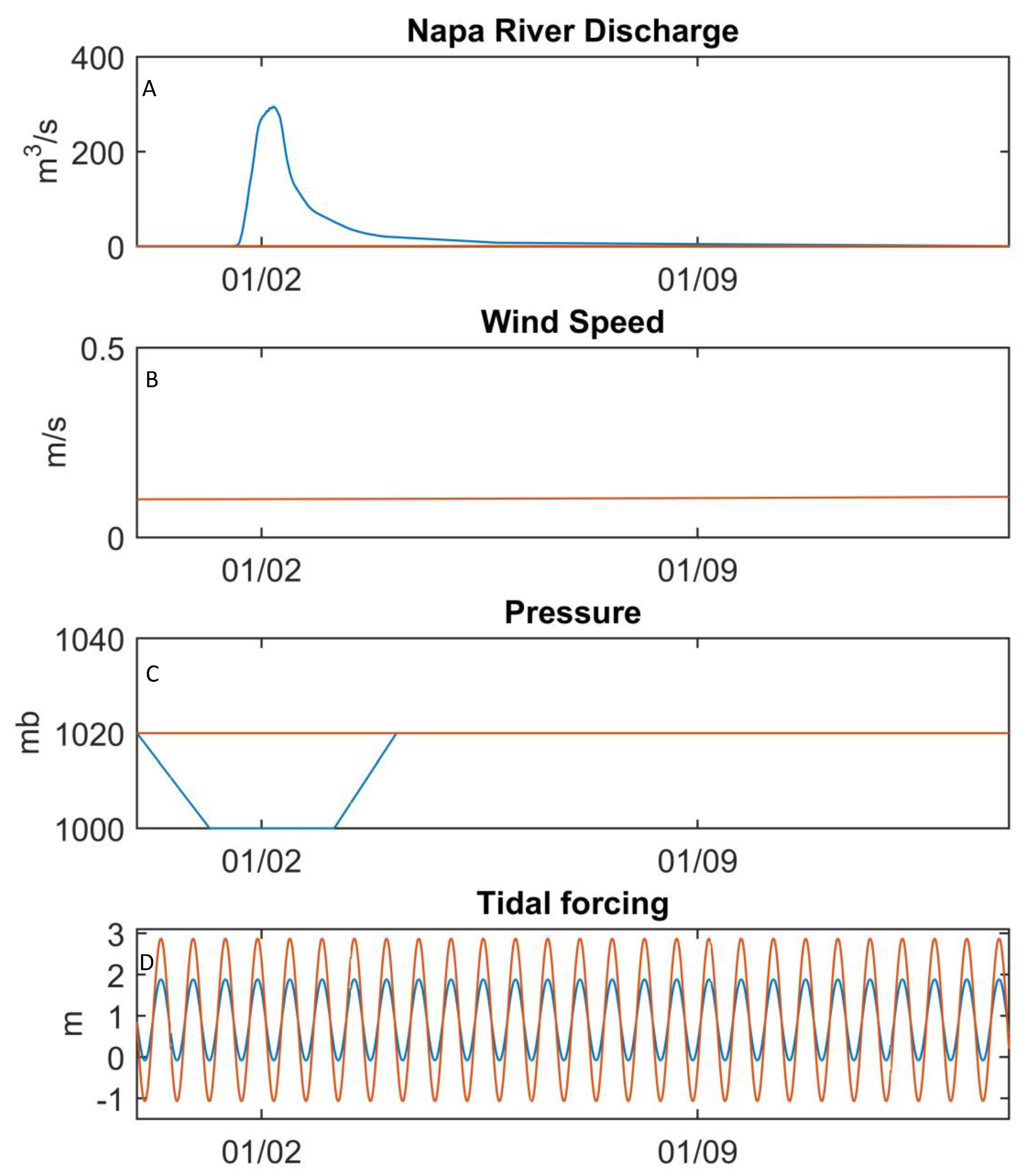
2.2. Idealized Model
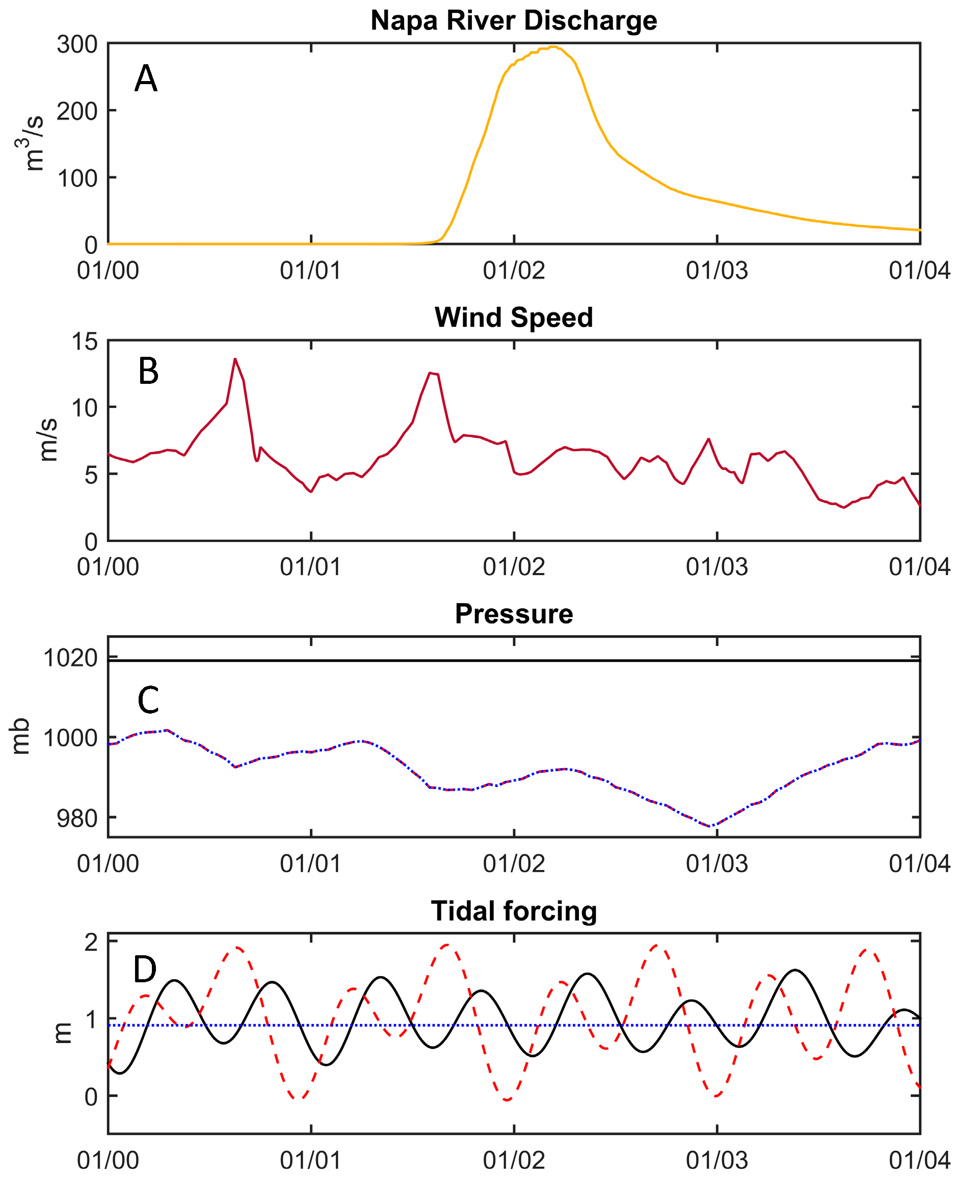
2.3. Scenarios
3. Results
3.1. Model Validation
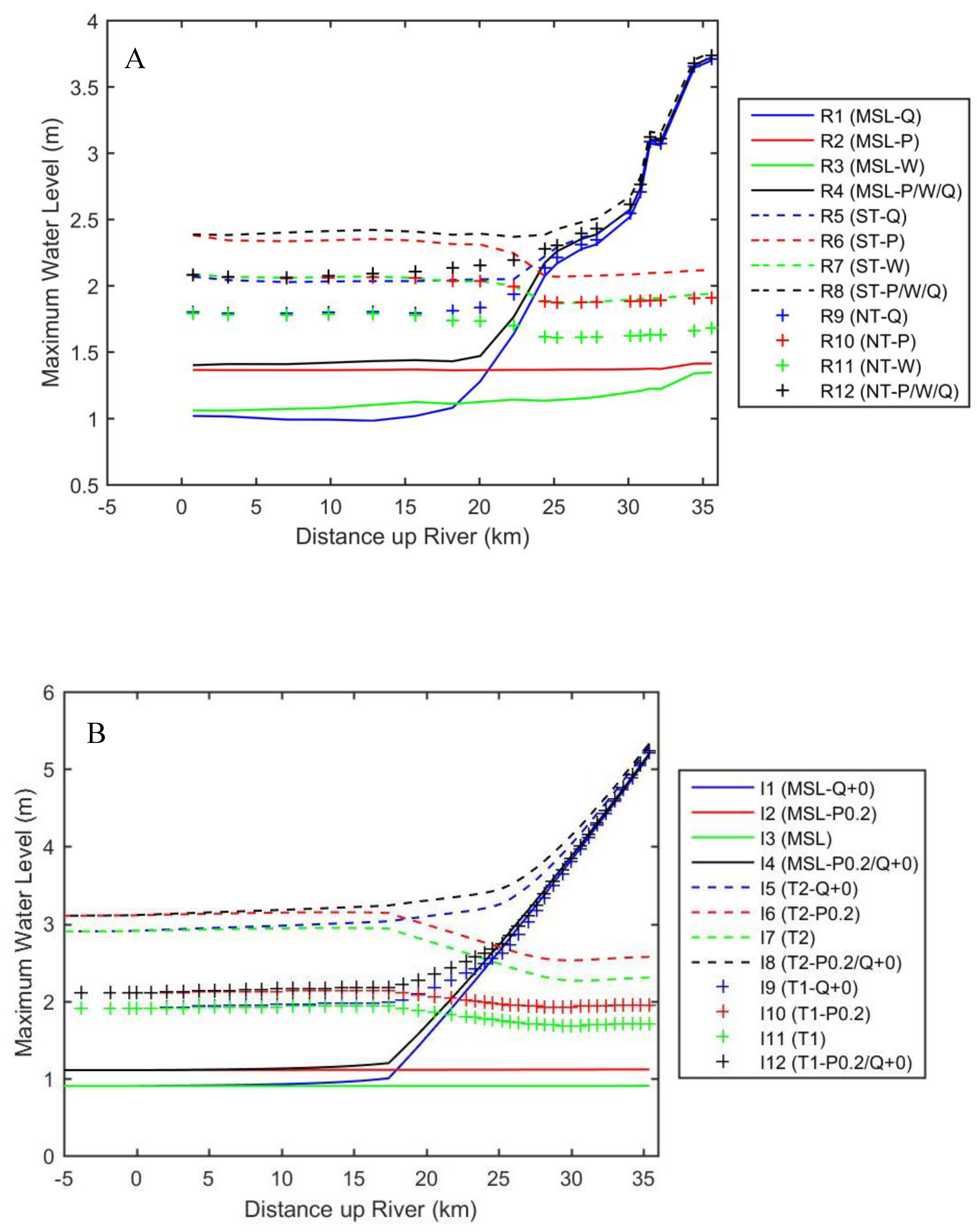
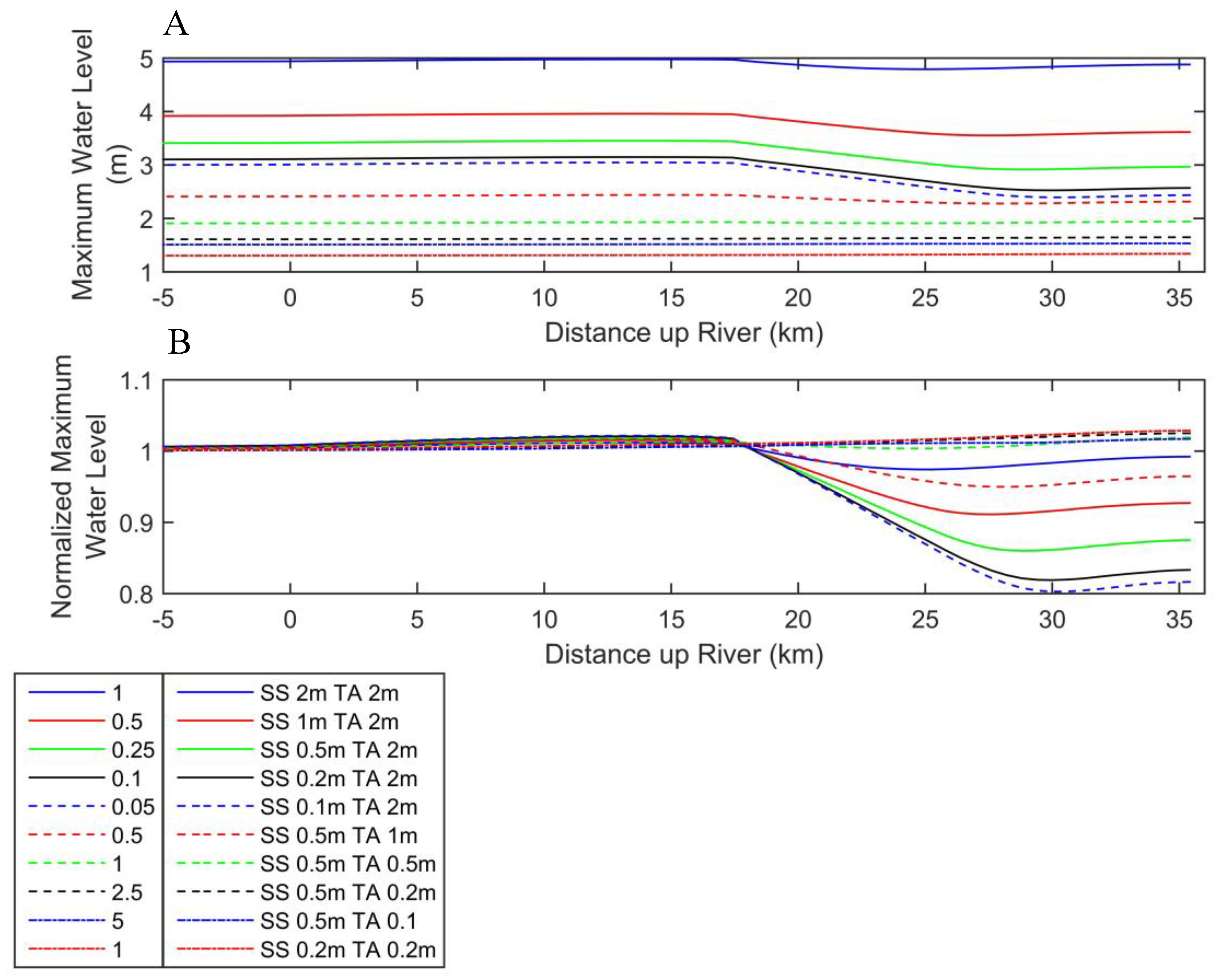
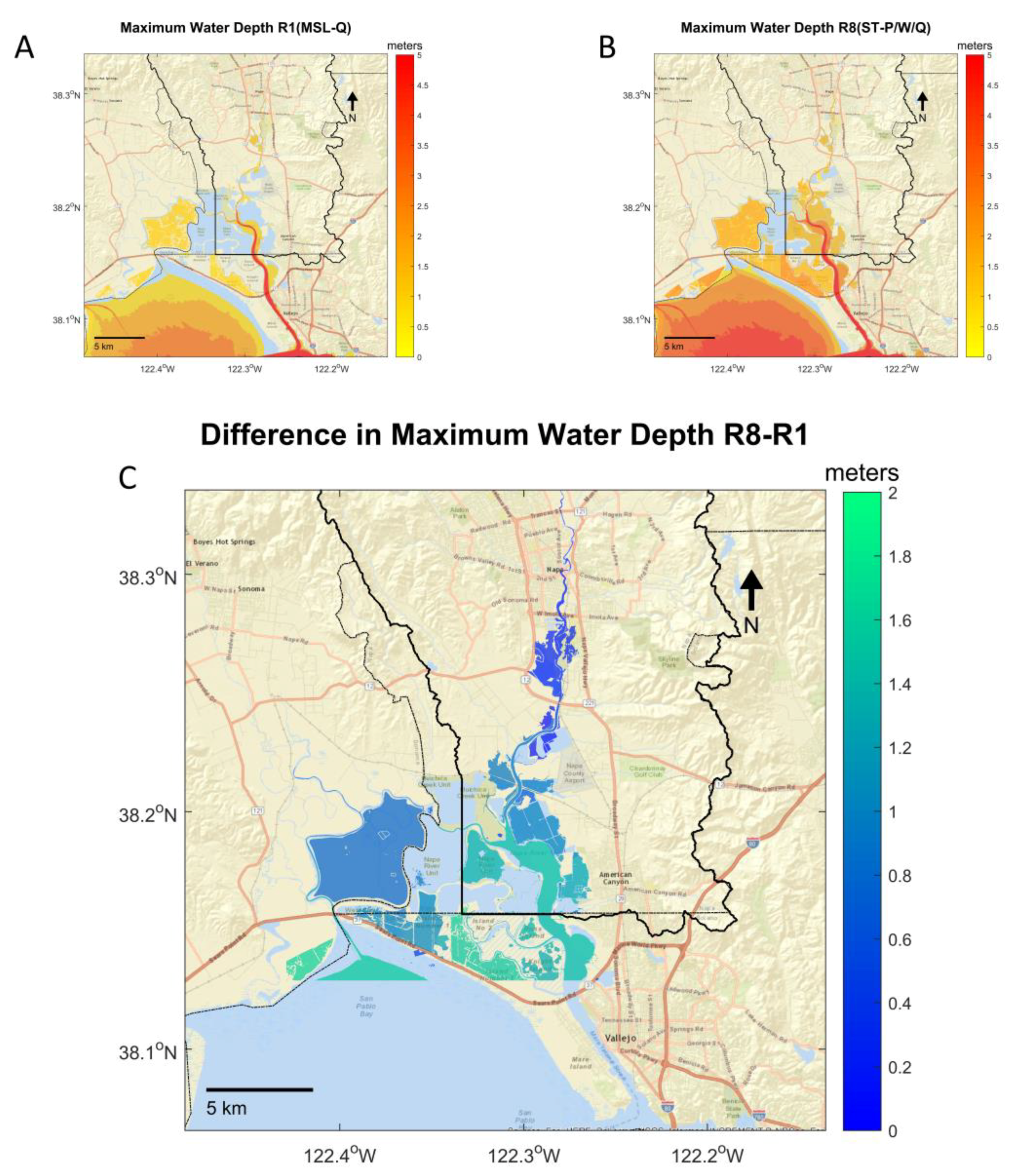
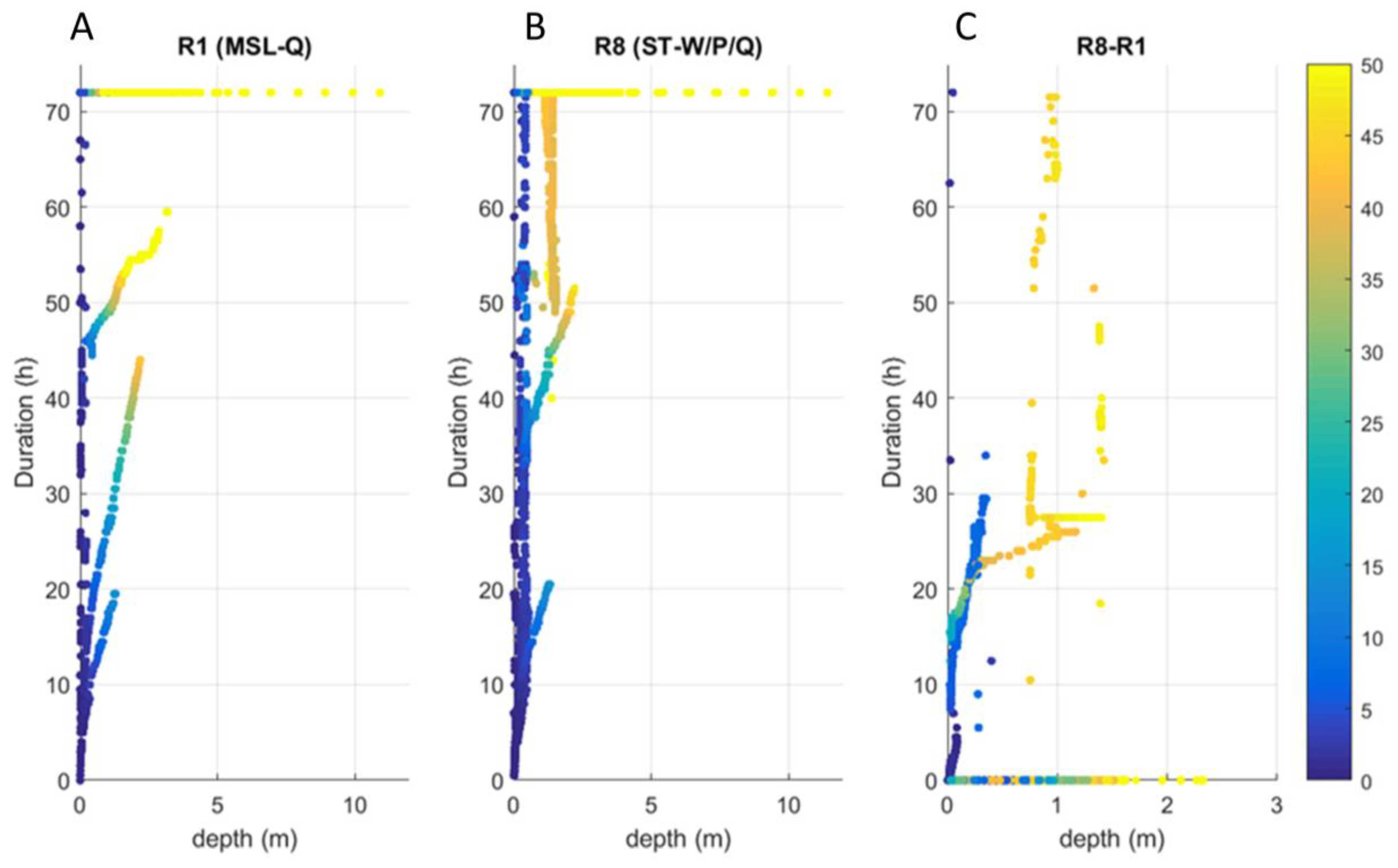
3.2. Maximum Water Levels
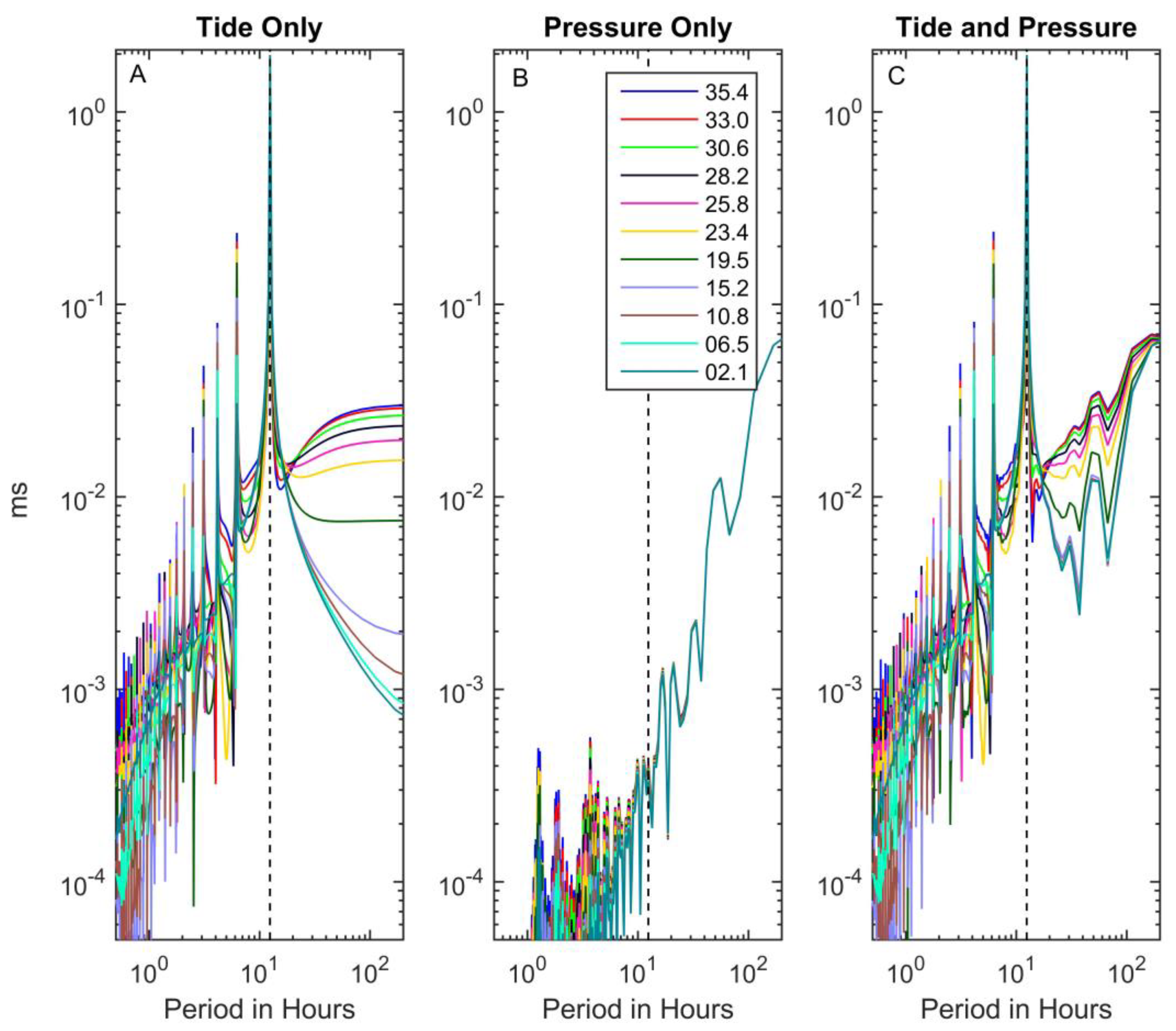
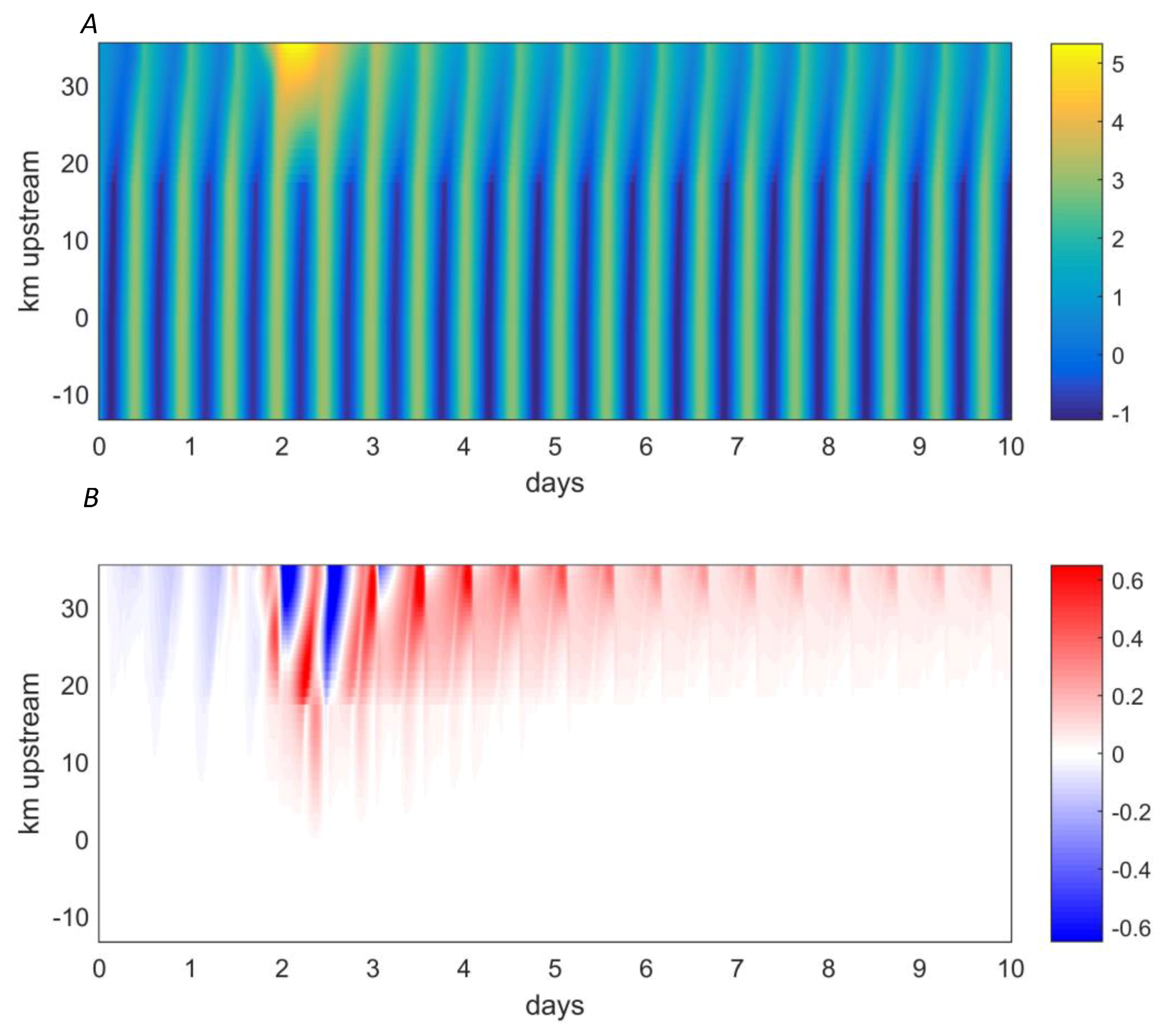
3.3. Storm Surge Only
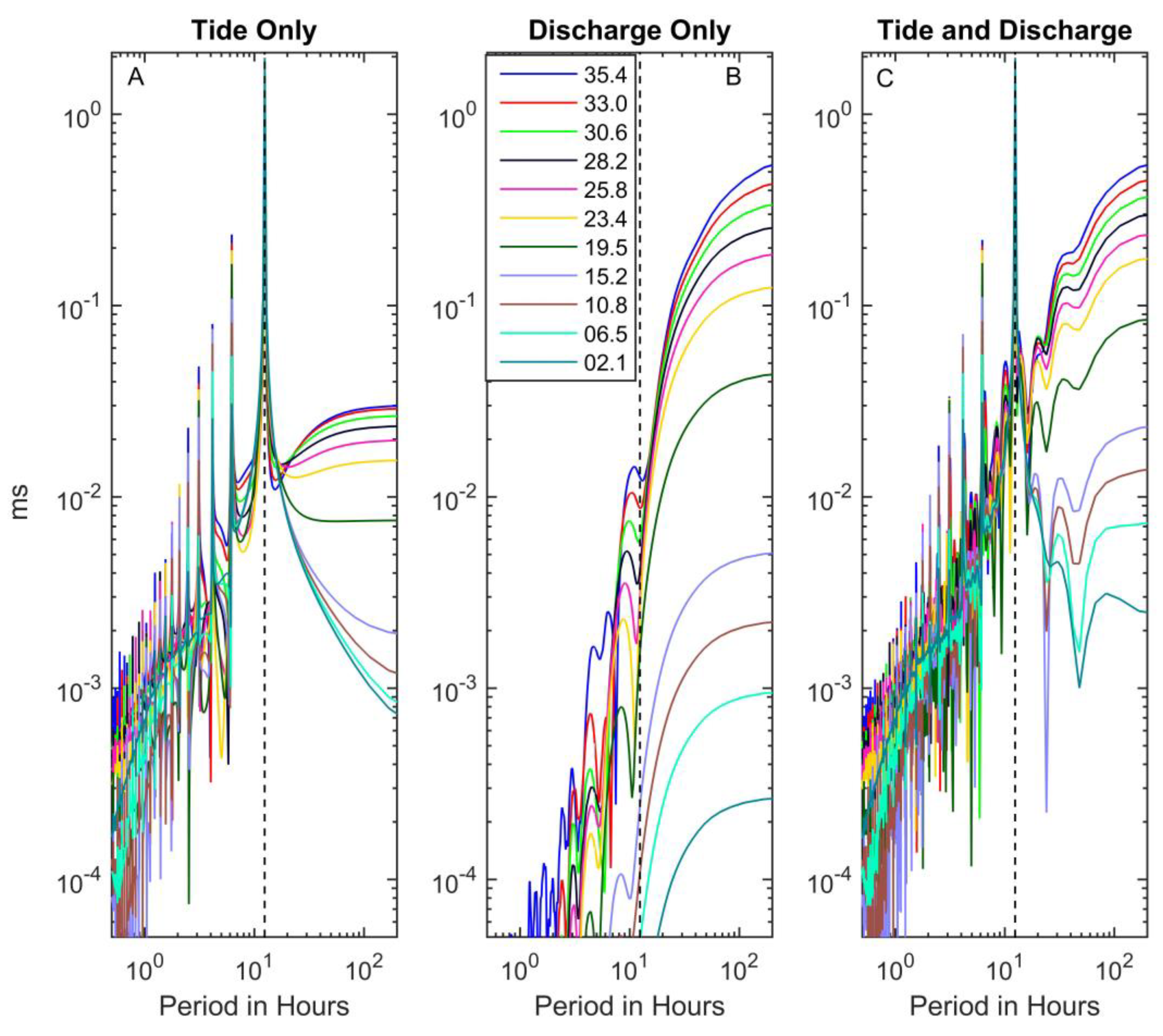
3.4. Discharge Only
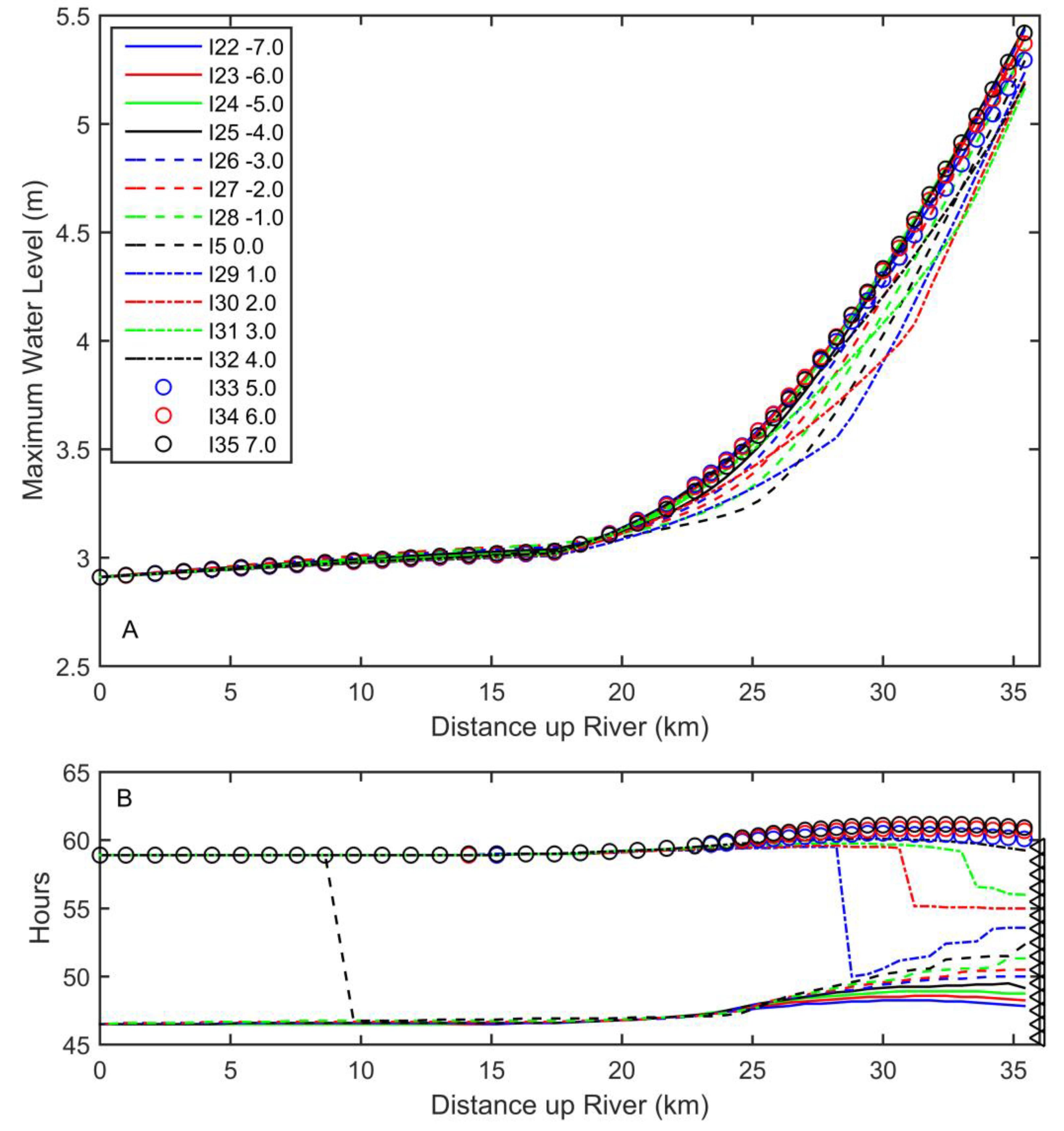
3.5. A Complete Storm
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- United States Flood Loss Report—Water Year 2014; National Oceanographic and Atmospheric Administration: Silver Spring, MD, USA, 2014; p. 6. Available online: http://www.nws.noaa.gov/os/water/Flood%20Loss%20Reports/WY14%20Flood%20Loss%20Summary.pdf (accessed on 15 January 2018).
- Easterling, D.R.; Meehl, G.A.; Parmesan, C.; Changnon, S.A.; Karl, T.R.; Mearns, L.O. Climate Extremes: Observations, Modeling, and Impacts. Science 2000, 289, 2068–2074. [Google Scholar] [CrossRef] [PubMed]
- Moftakhari, H.R.; AghaKouchak, A.; Sanders, B.F.; Feldman, D.L.; Sweet, W.; Matthew, R.A.; Luke, A. Increased nuisance flooding along the coasts of the United States due to sea level rise: Past and future. Geophys. Res. Lett. 2015, 42, 9846–9852. [Google Scholar] [CrossRef]
- Vitousek, S.; Barnard, P.L.; Fletcher, C.H.; Frazer, N.; Erikson, L.; Storlazzi, C.D. Doubling of coastal flooding frequency within decades due to sea-level rise. Sci. Rep. 2017, 7, 1399. [Google Scholar] [CrossRef] [PubMed]
- Changnon, S.A. Impacts of 1997–98 EI Niño–Generated Weather in the United States. Bull. Am. Meteorol. Soc. 1999, 80, 1819–1828. [Google Scholar] [CrossRef]
- Dusterhoff, S.D.; Beagle, J.; Collins, J.N.; Doehring, C. Initial Protocol to Identify and Delineate the Head of Tide Zone in San Francisco Bay Tributaries; No. 719; San Francisco Estuary Institute: Richmond, CA, USA, 2014; pp. 1–76. [Google Scholar]
- Barnard, P.L.; van Ormondt, M.; Erikson, L.H.; Eshleman, J.; Hapke, C.; Ruggiero, P.; Adams, P.N.; Foxgrover, A.C. Development of the Coastal Storm Modeling System (CoSMoS) for predicting the impact of storms on high-energy, active-margin coasts. Nat. Hazards 2014, 74, 1095–1125. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, H. Modeling of waves overtopping and flooding in the coastal reach by a non-hydrostatic model. Procedia IUTAM 2017, 25, 126–130. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- LeBlond, P.H. On tidal propagation in shallow rivers. J. Geophys. Res. 1978, 83. [Google Scholar] [CrossRef]
- LeBlond, P.H. Forced fortnightly tides in shallow rivers. Atmosphere-Ocean 1979, 17, 253–264. [Google Scholar] [CrossRef]
- Kosuth, P.; Callède, J.; Laraque, A.; Filizola, N., Jr.; Guyot, J.-L.; Seyler, P.; Marie Fritsch, J.; Guimaraes, V. Sea-Tide Effects on Flows in the Lower Reaches of the Amazon River. Hydrol. Process. 2009, 23, 3141–3150. [Google Scholar] [CrossRef]
- Guo, L.; van der Wegen, M.; Jay, D.A.; Matte, P.; Wang, Z.B.; Roelvink, D.; He, Q. River-tide dynamics: Exploration of nonstationary and nonlinear tidal behavior in the Yangtze River estuary. J. Geophys. Res. Oceans 2015, 120, 3499–3521. [Google Scholar] [CrossRef]
- Pu, X.; Shi, J.Z.; Hu, G.-D.; Xiong, L.-B. Circulation and mixing along the North Passage in the Changjiang River estuary, China. J. Mar. Syst. 2015, 148, 213–235. [Google Scholar] [CrossRef]
- Zhang, E.F.; Savenije, H.H.G.; Chen, S.L.; Mao, X.H. An analytical solution for tidal propagation in the Yangtze Estuary, China. Hydrol. Earth Syst. Sci. 2012, 16, 3327–3339. [Google Scholar] [CrossRef]
- Jay, D.A.; Leffler, K.; Diefenderfer, H.L.; Borde, A.B. Tidal-Fluvial and Estuarine Processes in the Lower Columbia River: I. Along-Channel Water Level Variations, Pacific Ocean to Bonneville Dam. Estuaries Coasts 2015, 38, 415–433. [Google Scholar] [CrossRef]
- Jay David, A.; Leffler, K.; Degens, S. Long-Term Evolution of Columbia River Tides. J. Waterw. Port Coast. Ocean Eng. 2011, 137, 182–191. [Google Scholar] [CrossRef]
- Sassi, M.G.; Hoitink, A.J.F. River flow controls on tides and tide-mean water level profiles in a tidal freshwater river. J. Geophys. Res. Oceans 2013, 118, 4139–4151. [Google Scholar] [CrossRef]
- van der Grinten, R.M.; de Vries, J.W.; de Swart, H.E. Impact of wind gusts on sea surface height in storm surge modelling, application to the North Sea. Nat. Hazards 2012, 66, 1313–1326. [Google Scholar] [CrossRef]
- Rego, J.L.; Li, C. On the importance of the forward speed of hurricanes in storm surge forecasting: A numerical study. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Sabatino, A.D.; O’Hara Murray, R.B.; Hills, A.; Speirs, D.C.; Heath, M.R. Modelling sea level surges in the Firth of Clyde, a fjordic embayment in south-west Scotland. Nat. Hazards 2016, 84, 1601–1623. [Google Scholar] [CrossRef]
- Bilskie, M.V.; Hagen, S.C.; Medeiros, S.C.; Passeri, D.L. Dynamics of sea level rise and coastal flooding on a changing landscape. Geophys. Res. Lett. 2014, 41, 927–934. [Google Scholar] [CrossRef]
- Smolders, S.; Plancke, Y.; Ides, S.; Meire, P.; Temmerman, S. Role of intertidal wetlands for tidal and storm tide attenuation along a confined estuary: A model study. Nat. Hazards Earth Syst. Sci. 2015, 15, 1659–1675. [Google Scholar] [CrossRef]
- Condon, A.J.; Peter Sheng, Y. Evaluation of coastal inundation hazard for present and future climates. Nat. Hazards 2011, 62, 345–373. [Google Scholar] [CrossRef]
- Wang, R.-Q.; Herdman, L.M.; Erikson, L.; Barnard, P.; Hummel, M.; Stacey, M.T. Interactions of Estuarine Shoreline Infrastructure With Multiscale Sea Level Variability. J. Geophys. Res. Oceans 2017, 122, 9962–9979. [Google Scholar] [CrossRef]
- Zheng, F.; Leonard, M.; Westra, S. Application of the design variable method to estimate coastal flood risk. J. Flood Risk Manag. 2017, 10, 522–534. [Google Scholar] [CrossRef]
- Zheng, F.; Westra, S.; Leonard, M.; Sisson, S.A. Modeling dependence between extreme rainfall and storm surge to estimate coastal flooding risk. Water Resour. Res. 2014, 50, 2050–2071. [Google Scholar] [CrossRef]
- Scripps Institute of Oceanography. U.S.D. Coastal Data Information Program; UC San Diego: La Jolla, CA, USA, 2017; Available online: http://cdip.ucsd.edu/?nav=historic&sub=data&units=metric&tz=UTC&pub=public&map_stati=1,2,3&stn=142&stream=p1 (accessed on 30 June 2017).
- Bureau, U.S.C. 2010 Census. 2011. Available online: http://www.census.gov/2010census/data/ (accessed on 7 January 2018).
- Barnard, P.L.; Erikson, L.H.; Elias, E.P.L.; Dartnell, P. Sediment transport patterns in the San Francisco Bay Coastal System from cross-validation of bedform asymmetry and modeled residual flux. Mar. Geol. 2013, 345, 72–95. [Google Scholar] [CrossRef]
- Barnard, P.L.; Schoellhamer, D.H.; Jaffe, B.E.; McKee, L.J. Sediment transport in the San Francisco Bay Coastal System: An overview. Mar. Geol. 2013, 345, 3–17. [Google Scholar] [CrossRef]
- Neary, V.S.; Wright, S.A.; Bereciartua, P. Case Study: Sediment Transport In Proposed Geomorphic Channel For Napa River. J. Hydraul. Eng. ASCE 2001, 127, 901–910. [Google Scholar] [CrossRef]
- Goetting, J. Recalling 86 While Cleaning up from 05. In Napa Valley Register; Lee Enterprises: Napa, CA, USA, 2005; Available online: https://napavalleyregister.com/news/local/article_08baa217-9e06-5e01-8154-486c84403846.html (accessed on 8 June 2018).
- Caltrans. 2016 Traffic Volumes on California State Highways; US Department of Transportation: Sacramento, CA, USA, 2016. Available online: http://www.dot.ca.gov/trafficops/census/docs/2016_aadt_volumes.pdf (accessed on 10 June 2017).
- Moore, D. Highway 37 Closure still causing headaches for motorists. In The Press Democrat; Press Democrat Media Company: Santa Rosa, CA, USA, 2017; Available online: http://www.pressdemocrat.com/news/6666970-181/highway-37-closure-still-causing?sba=AAS (accessed on 30 June 2017).
- Vandever, J.; Sudhalkar, A.; May, K.; Villafranca, J.; Lightner, M.; Shilling, F. State Route 37 Integrated Traffic, Infrastructure and Sea Level Rise Analysis; Road Ecology Center, UC Davis: Davis, CA, USA, 2015; p. 87. Available online: http://hwy37.ucdavis.edu/files/upload/resource/Phase_II_SR_37_Stewardship_FinalReport_Task%202_Risk_Assessment.pdf (accessed on 11 November 2017).
- Council, O.P. State of California Sea Level Rise Guidance, 2018 Update; Ocean Protection Council: Sacramento, CA, USA, 2018; p. 84. [Google Scholar]
- Foxgrover, A.C.; Barnard, P.L. A seamless, high-resolution digital elevation model (DEM) of the north-central California coast. In Data Series; US Geological Survey: Reston, VA, USA, 2012. Available online: http://pubs.er.usgs.gov/publication/ds684 (accessed on 25 January 2017). [CrossRef]
- Foxgrover, A.C.; Dartnell, P.; Jaffe, B.E.; Takekawa, J.Y.; Athearn, N.D. High-resolution bathymetry and topography of south San Francisco Bay, California. In Scientific Investigations Map; US Geological Survey: Reston, VA, USA, 2007. Available online: http://pubs.er.usgs.gov/publication/sim2987 (accessed on 20 July 2018). [CrossRef]
- Foxgrover, A.C.; Finlayson, D.P.; Jaffe, B.E.; Fregoso, T.A. Bathymetry and digital elevation models of Coyote Creek and Alviso Slough, South San Francisco Bay, California. In Open-File Report; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2018; p. 28. Available online: http://pubs.er.usgs.gov/publication/ofr20111315 (accessed on 20 July 2018). [CrossRef]
- Foxgrover, A.C.; Finlayson, D.P.; Jaffe, B.E.; Takekawa, J.Y.; Thorne, K.M.; Spragens, K.A. 2010 bathymetric survey and digital elevation model of Corte Madera Bay, California. In Open-File Report; USGS: Reston, VA, USA, 2011; p. i-20. Available online: http://pubs.er.usgs.gov/publication/ofr20111217 (accessed on 20 July 2018). [CrossRef]
- Institute, S.F.E. San Francisco Bay Shore Inventory: Mapping for Sea Level Rise Planning GIS Data. 2016. Available online: http://www.sfei.org/projects/SFBayShoreInventory (accessed on 30 April 2017).
- Dushaw, B.D.; Egbert, G.; Worcester, P.F.; Cornuelle, B.D.; Howe, B.; Metzger, K. A TOPEX/POSEIDON Global Tidal Model (TPXO.2) and Barotropic Tidal Currents Determined from Long-Range Acoustic Transmissions. Prog. Oceanogr. 1997, 40, 337–367. [Google Scholar] [CrossRef]
- Center for Operational Oceanographic Products and Services Tides and Currents. National Oceanic and Atmospheric Administration (NOAA). Silver Srping, Maryland. Available online: https://tidesandcurrents.noaa.gov (accessed on 8 August 2018).
- Willmott, C.J. On The Validation of Models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Thorne, K.M.; Dugger, B.D.; Buffington, K.J.; Freeman, C.M.; Janousek, C.N.; Powelson, K.W.; Gutenspergen, G.R.; Takekawa, J.Y. Marshes to Mudflats—Effects of Sea-Level Rise on Tidal Marshes Along a Latitudinal Gradient in the Pacific Northwest; U.S. Geological Survey Open-File Report: Sacramento, CA, USA, 2015. [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Bilskie, M.V.; Hagen, S.C. Defining Flood Zone Transitions in Low-Gradient Coastal Regions. Geophys. Res. Lett. 2018, 45, 2761–2770. [Google Scholar] [CrossRef]
- O’Neill, A.; Erikson, L.; Barnard, P. Downscaling wind and wavefields for 21st century coastal flood hazard projections in a region of complex terrain. Earth Space Sci. 2017, 4, 314–334. [Google Scholar] [CrossRef]
- Ganju, N.K.; Suttles, S.E.; Beudin, A.; Nowacki, D.J.; Miselis, J.L.; Andrews, B.D. Quantification of Storm-Induced Bathymetric Change in a Back-Barrier Estuary. Estuaries Coasts 2017, 40, 22–36. [Google Scholar] [CrossRef]
- Granato, G.E. Estimating Basin Lagtime and Hydrograph-Timing Indexes Used to Characterize Stormflows for Runoff-Quality Analysis; US Geological Survey: Reston, VA, USA, 2012; p. i-47. Available online: http://pubs.er.usgs.gov/publication/sir20125110 (accessed on 20 November 2018 ). [CrossRef]
- Nichols, M.M.; Boon, J.D. Chapter 7 Sediment Transport Processes in Coastal Lagoons. In Elsevier Oceanography Series; Kjerfve, B., Ed.; Elsevier: New York, NY, USA, 1994; Volume 60, pp. 157–219. [Google Scholar]
- Fritz, H.M.; Blount, C.; Sokoloski, R.; Singleton, J.; Fuggle, A.; McAdoo, B.G.; Moore, A.; Grass, C.; Tate, B. Hurricane Katrina storm surge distribution and field observations on the Mississippi Barrier Islands. Estuar. Coast. Shelf Sci. 2007, 74, 12–20. [Google Scholar] [CrossRef]
- Silva-Araya, W.; Santiago-Collazo, F.; Gonzalez-Lopez, J.; Maldonado-Maldonado, J. Dynamic Modeling of Surface Runoff and Storm Surge during Hurricane and Tropical Storm Events. Hydrology 2018, 5, 13. [Google Scholar] [CrossRef]
- Bacopoulos, P.; Tang, Y.; Wang, D.; Hagen, S.C. Integrated Hydrologic-Hydrodynamic Modeling of Estuarine-Riverine Flooding: 2008 Tropical Storm Fay. J. Hydrol. Eng. 2017, 22. [Google Scholar] [CrossRef]
| Freshwater Source | Non-Storm Discharges (m3 s−1) |
|---|---|
| Sacramento River | 500 |
| American River | 45 |
| Arcade Creek | 0.02 |
| Napa River | 5 |
| Petaluma River | 5 |
| Corte Madera Creek | 2 |
| San Joaquin River | 60 |
| San Francisquito Creek | 0.5 |
| Matadero Creek | 0.05 |
| Coyote Creek | 3 |
| Guadalupe River | 2 |
| Scenario Name | Water Level | Pressure | Discharge |
|---|---|---|---|
| R1 (MSL-Q) | MSL (Mean Sea Level) Flat | Constant | Storm |
| R2 (MSL-P) | MSL Flat | Storm | Low Normal |
| R3 (MSL-W) | MSL Flat | Constant | Low Normal |
| R4 (MSL-P/W/Q) | MSL Flat | Storm | Storm |
| R5 (ST-Q) | Spring Tide | Constant | Storm |
| R6 (ST-P) | Spring Tide | Storm | Low Normal |
| R7 (ST-W) | Spring Tide | Constant | Low Normal |
| R8 (ST-P//W/Q) | Spring Tide | Storm | Storm |
| R9 (NT-Q) | Neap Tide | Constant | Storm |
| R10 (NT-P) | Neap Tide | Storm | Low Normal |
| R11 (NT, W) | Neap Tide | Constant | Low Normal |
| R12 (NT-P/W/Q) | Neap Tide | Storm | Storm |
| Scenario Name | Water Level | Pressure | Discharge |
|---|---|---|---|
| I1 (MSL-Q + 0) | MSL Flat | Constant | Storm |
| I2 (MSL-P0.2) | MSL Flat | 0.2 m Storm | Low Normal |
| I3 (MSL) | MSL Flat | Constant | Low Normal |
| I4 (MSL-P0.2/Q + 0) | MSL Flat | 0.2 m Storm | Storm |
| I5 (T2-Q + 0) | 2 m M2 | Constant | Storm |
| I6 (T2-P0.2) | 2 m M2 | 0.2 m Storm | Low Normal |
| I7 (T2) | 2 m M2 | Constant | Low Normal |
| I8 (T2-P0.2/Q + 0) | 2 m M2 | 0.2 m Storm | Storm |
| I9 (T1-Q + 0) | 1 m M2 | Constant | Storm |
| I10 (T1-P0.2) | 1 m M2 | 0.2 m Storm | Low Normal |
| I11 (T1) | 1 m M2 | Constant | Low Normal |
| I12 (T1-P0.2/Q + 0) | 1 m M2 | 0.2 m Storm | Storm |
| I13 (T2-P2) | 2 m M2 | 2 m Storm | Low Normal |
| I14 (T2-P1) | 2 m M2 | 1 m Storm | Low Normal |
| I15 (T2-P0.5) | 2 m M2 | 0.5 m Storm | Low Normal |
| I16 (T2-P0.1) | 2 m M2 | 0.1 m Storm | Low Normal |
| I17 (T0.2-P0.2) | 0.2 m M2 | 0.2 m Storm | Low Normal |
| I18 (T1-P0.5) | 1 m M2 | 0.5 m Storm | Low Normal |
| I19 (T0.5-P0.5) | 0.5 m M2 | 0.5 m Storm | Low Normal |
| I20 (T0.2-P0.5) | 0.2 m M2 | 0.5 m Storm | Low Normal |
| I21 (T0.1-P0.5) | 0.1 m M2 | 0.5 m Storm | Low Normal |
| I22 (T2-Q − 7) | 2 m M2 | Constant | Storm − 7 h |
| I23 (T2-Q − 6) | 2 m M2 | Constant | Storm − 6 h |
| I24 (T2-Q − 5) | 2 m M2 | Constant | Storm − 5 h |
| I25 (T2-Q − 4) | 2 m M2 | Constant | Storm − 4 h |
| I26 (T2-Q − 3) | 2 m M2 | Constant | Storm − 3 h |
| I27 (T2-Q − 2) | 2 m M2 | Constant | Storm – 2 h |
| I28 (T2-Q − 1) | 2 m M2 | Constant | Storm − 1 h |
| I29 (T2-Q + 1) | 2 m M2 | Constant | Storm + 1 h |
| I30 (T2-Q + 2) | 2 m M2 | Constant | Storm + 2 h |
| I31 (T2-Q + 3) | 2 m M2 | Constant | Storm + 3 h |
| I32 (T2-Q + 4) | 2 m M2 | Constant | Storm + 4 h |
| I33 (T2-Q + 5) | 2 m M2 | Constant | Storm + 5 h |
| I34 (T2-Q + 6) | 2 m M2 | Constant | Storm + 6 h |
| I35 (T2-Q + 7) | 2 m M2 | Constant | Storm + 7 h |
| Station | Observed Diurnal Range (m) | Mean Error (m) | Wilmott Skill Score (D) | Coeff. of Efficiency (E) | |||
|---|---|---|---|---|---|---|---|
| January 2010 | March 2011 | January 2010 | March 2011 | January 2010 | March 2011 | ||
| San Francisco | 1.78 | −0.04 | −0.01 | 0.99 | 0.99 | 0.74 | 0.44 |
| Richmond | 1.85 | −0.01 | −0.05 | 0.99 | 0.98 | 0.73 | 0.43 |
| Port Chicago | 1.50 | −0.05 | −0.11 | 0.97 | 0.96 | 0.51 | 0.38 |
| Coon Island | NA | NA | −0.15 | NA | 0.87 | NA | 0.72 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herdman, L.; Erikson, L.; Barnard, P. Storm Surge Propagation and Flooding in Small Tidal Rivers during Events of Mixed Coastal and Fluvial Influence. J. Mar. Sci. Eng. 2018, 6, 158. https://doi.org/10.3390/jmse6040158
Herdman L, Erikson L, Barnard P. Storm Surge Propagation and Flooding in Small Tidal Rivers during Events of Mixed Coastal and Fluvial Influence. Journal of Marine Science and Engineering. 2018; 6(4):158. https://doi.org/10.3390/jmse6040158
Chicago/Turabian StyleHerdman, Liv, Li Erikson, and Patrick Barnard. 2018. "Storm Surge Propagation and Flooding in Small Tidal Rivers during Events of Mixed Coastal and Fluvial Influence" Journal of Marine Science and Engineering 6, no. 4: 158. https://doi.org/10.3390/jmse6040158
APA StyleHerdman, L., Erikson, L., & Barnard, P. (2018). Storm Surge Propagation and Flooding in Small Tidal Rivers during Events of Mixed Coastal and Fluvial Influence. Journal of Marine Science and Engineering, 6(4), 158. https://doi.org/10.3390/jmse6040158







