1. Introduction
Breakwaters are used to protect harbors and shorelines from waves and to limit coastal erosion. In harbors, breakwaters provide tranquility behind them to ease both navigation and berthing for vessels. Breakwaters influence coastal wave climate by breaking, reflecting, and diffracting wave energy. In a large harbor, the fetch may be sufficient for the local generation of waves to be important. Studying these influences in situ poses a challenge. In recent years, spectral wave models have become more widely used and are important in describing coastal wave behavior. However, the performance and precision of the spectral models in real harbors in the presence of the breakwaters has not been well examined.
SWAN, MIKE21SW, and Wavewatch III are three commonly used spectral wave models in coastal and ocean communities. Wavewatch III is mostly used for deep ocean and open sea applications and is not able to include breakwater structures. On the other hand, the recent versions of SWAN and MIKE21SW are equipped to handle breakwaters.
Although parabolic and elliptic mild slope models as well as Boussinesq models may be more appropriate for the simulation of waves in small harbors, where diffraction is the most important phenomenon, in large embayments and harbors wind-wave generation can be important and spectral models are useful. However, some circumstances should meet to use spectral for wave simulation in harbors [
1,
2].
In recent years, unstructured grid models have become more popular for modeling complex geometries and are an effective alternative to the grid nesting approach, [
3,
4]. In this study, we employ unstructured SWAN (v41.20) and MIKE21SW (v2017) to simulate the effects of three coastal breakwaters on the wave field in New Haven Harbor, Connecticut, and then assessed their accuracy and efficiency.
There have been previous comparisons of these models. Strauss et al. [
5] compared simulations of waves on a narrow continental shelf in Gold Coast, Australia using SWAN and MIKE21SW. SWAN was executed in the fully spectral mode with a structured grid, while MIKE21SW was executed on a directional decoupled parametric mode with an unstructured grid. The results indicated that both models overestimated significant wave height. Moeini and Etemad-Shahidi [
6] applied SWAN and MIKE21SW for hindcasting waves in Lake Erie. The study suggested SWAN simulated significant wave height better, while MIKE21SW simulated wave period and direction better. Conversely, Fonseca et al. [
7] suggested that MIKE21SW, SWAN, and STWAVE models have similar behavior and precision when examining performance on the Portuguese coast. Hoque et al. [
8] evaluated SWAN and MIKE21SW in the Mackenzie Delta in Beaufort Sea, Canada. They concluded that the results of the models were almost identical, but in water shallower than 7 m for wave height between 2 and 3 m, SWAN simulated the significant wave height better, though the peak period from MIKE21SW was more accurate.
In all previous studies, SWAN was executed on a structured grid and MIKE21SW on an unstructured grid. In this study, both SWAN and MIKE21SW were run on their optimum unstructured grids and evaluated inside New Haven Harbor which is separated from Long Island Sound by substantial breakwaters (
Figure 1). The model results are compared to data from two bottom mounted Acoustic Doppler Current Profilers (ADCP) in the harbor for all storm events, and to one outside the harbor for storms with northerly winds. The sensitivity of the model results to characteristics of the wind forcing, and the representation of diffraction, reflection, and the breakwaters are discussed. The simulation skill and the efficiency of the models are summarized and possible explanations for their differences were discussed.
2. Model Descriptions
MIKE21SW is a proprietary model developed by DHI Company. It is one of the most widely used wave models in coastal and marine engineering projects around the world. It has a graphical user interface (GUI) that makes it simple to set up the model and visualize the results. SWAN is an open source model developed by the Delft University of Technology. It is often used in academic coastal research and has been integrated to community circulation models. For simplification and clarification, we introduce the models by summarizing their similarities and differences.
SWAN [
9] and MIKE21SW [
10] are both third generation fully spectral wave models. The models solve the wave action balance equation, described by Mei [
11], Komen et al. [
12], and Young [
13]. In Cartesian coordinates, the wave action balance equation can be written as
where
is the wave action density,
is the wave group velocity,
is ambient current,
is relative frequency,
is wave direction,
is time, and
is the total source and sink terms which represent generation, dissipation, and redistribution of wave energy. ∇ is the four-dimensional differential operator with respect to
.
The source terms in both models are almost the same. Wave dissipation terms such as bed friction, wave breaking, whitecapping, nonlinear quadruplet interactions, nonlinear triad wave interactions, and diffraction are essentially the same. However, in some cases such as wind input, whitecapping and quadruplet wave interaction, SWAN provides a wider range of parameterizations and coefficients.
SWAN can be run on both structured and unstructured grids, while MIKE21SW only uses unstructured grids. The spatial discretization method differs between the models. SWAN’s spatial discretization is based on a vertex-centered method while MIKE21SW uses a cell-centered method. This implies that wave action N is stored at the grid cell vertices in SWAN and at the cell center in MIKE21SW. Thus, the control volume in SWAN is a polygon, while in MIKE21SW it is triangular.
The numerical methods used in structured and unstructured SWAN are different. In the structured mode of SWAN, a first order upwind-space backward-time (BSBT) scheme, or a second order SORDUP scheme (default for stationary mode), and second order Stelling and Leendertse scheme (default for nonstationary mode) may be selected. In unstructured SWAN the only option is the BSBT scheme which is fast but diffusive [
14]. MIKE21SW uses a first order upwind difference and second order accurate scheme in space. The first order scheme is usually sufficient for small-scale domains dominated by local wind. In the case of swell propagation, the second order scheme should be applied [
10].
The major difference between the numerical methods is that SWAN uses a fully implicit method time integration whereas MIKE21SW is an explicit approach. Consequently, MIKE21SW avoids solving a large system of equations with the drawback that the temporal step is limited by the Courant number. SWAN’s fully implicit scheme eliminates the stability constraint on the temporal step but requires a large system of equations must be solved to achieve a solution. To improve efficiency SWAN uses a point-by-point multi-directional Gauss-Seidel iteration technique that circumvents the need to construct and solve a large system of simultaneous equations as is typical in implicit methods [
14]. This technique highly improves the computational efficiency of the SWAN model.
3. Methods
In this study, the model domain is New Haven Harbor, Connecticut, USA. New Haven Harbor is located in Long Island Sound, a large estuary on the northeast coast of the United States. There are three detached breakwaters in front of the harbor to reduce the effects of waves during extreme storms. The area is frequently affected by strong winds during winter, from January to March, and occasionally by hurricanes in the summer and early fall. The significant wave height in central Long Island Sound, where New Haven Harbor is located can exceed two meters. Also, the maximum distance from New Haven breakwaters to end of estuary is 7 km, sufficient fetch for local wave generation to be important. This is the main reason that the spectral wave models, rather than mild slope or Boussinesq wave models, were employed in this study.
To observe the effect of breakwaters on waves in extreme storms, we deployed two ADCPs, one outside the harbor (NH1) and one inside (NH2), during the winter of 2015 from 21 January to 5 April. The wind data were gathered during the same period by the Central Long Island Sound Buoy (CLIS) which is located 25 km from New Haven. CLIS wind data are a good representative of New Haven wind, particularly when the winds are southerly. Northerly winds may be more influenced by the roughness of the land surrounding the harbor. However, the topography of the New Haven area does not contain features that could cause substantial influence on wind direction. Depths and locations of the observations can be found in
Table 1, and
Figure 1 illustrates the field site.
Instead of applying a nesting approach, which uses results from a large-scale model to force the boundaries of the local wave model, we used the observed wave spectrum at NH1 to force the open boundary of the models. In this way, we reduce the uncertainty that arises from simulation of the large-scale wave field. The possible variation of the wave field along the boundary was neglected since Long Island Sound is fetch limited and the bathymetric variations near the study site were small. The models were also forced by a uniform wind stress over the domain at half-hour intervals using observation from the CLIS buoy. Mean sea level variations were prescribed in the simulation using observed water level data at the NH2 station.
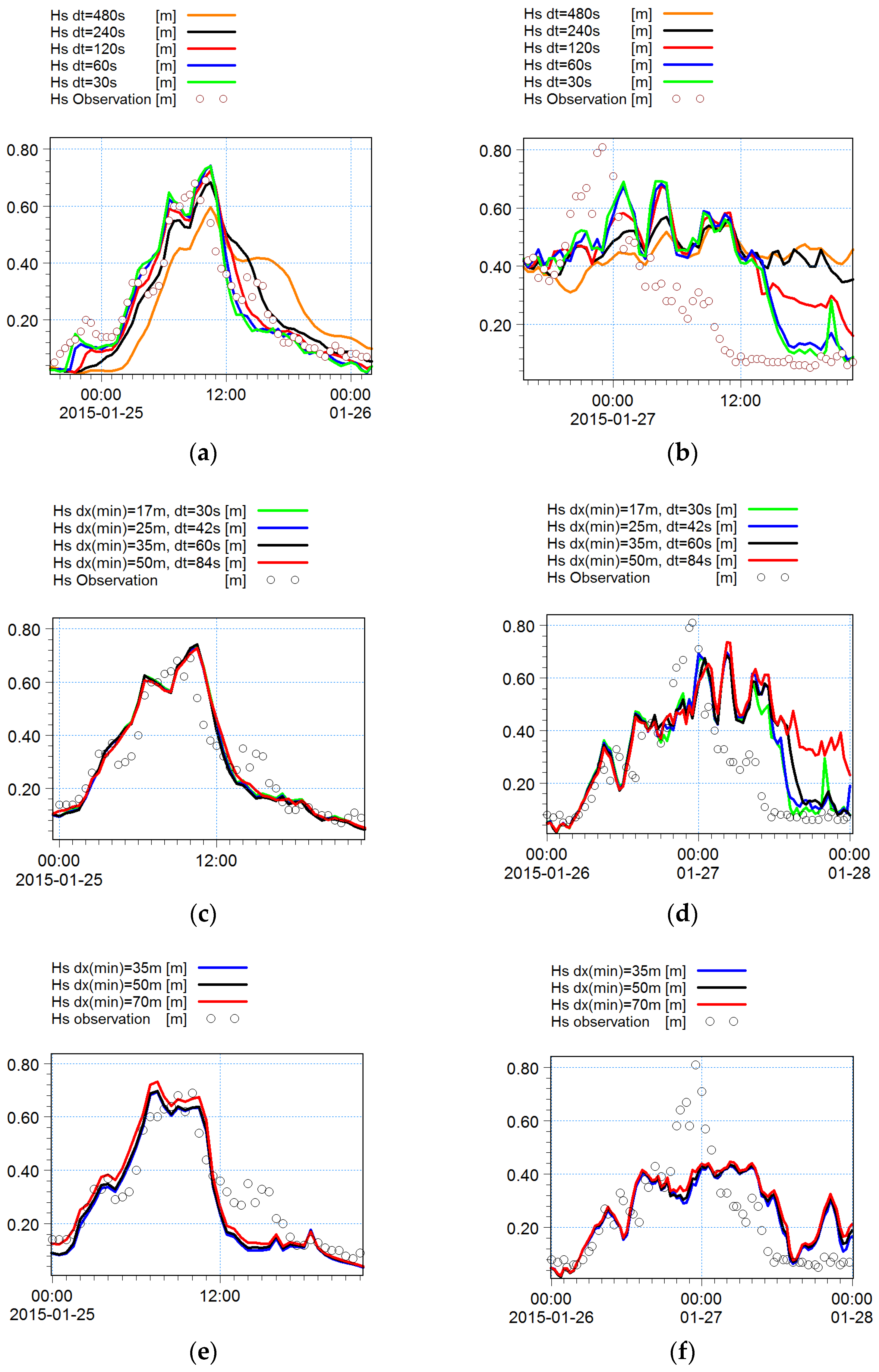
For the results from the models to be comparable, both models were set up with the same forcing and the optimum time step and grid size for each model were determined by comparison to observations. In MIKE21SW, the user selects a range for time steps (the minimum and maximum) and the model automatically determines the optimum time step based on the grid size, wave propagation speed, and Courant number. The minimum time step must meet the Courant number restriction. In SWAN, the numerical scheme is unconditionally stable but it is critical to ensure that the solution has converged. Using a grid with the resolution range
and
, we found that a time step
provided the same solution as a range of smaller time steps,
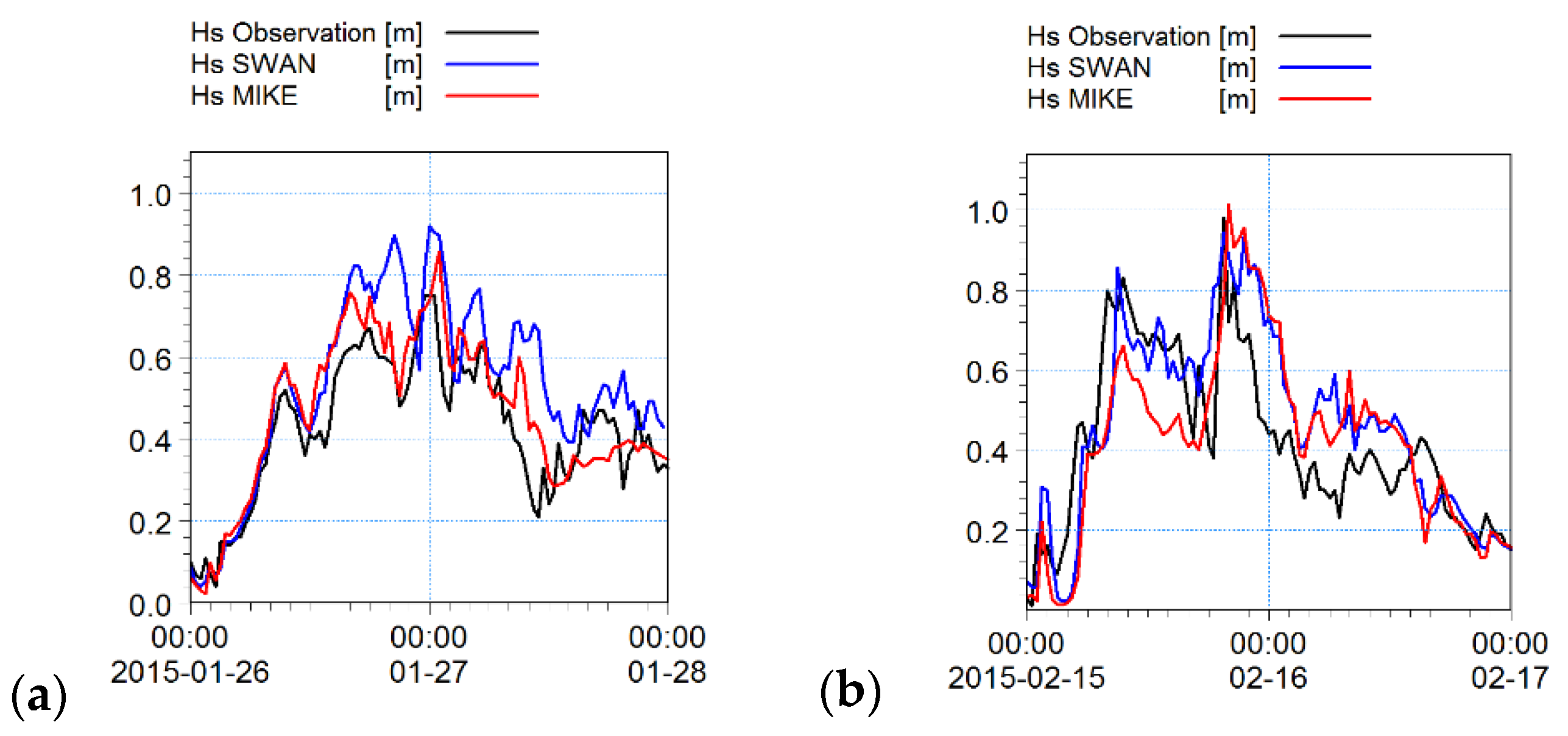
Figure 2a,b compare the solutions at the location of NH2 for two 24 h intervals together with the observations.
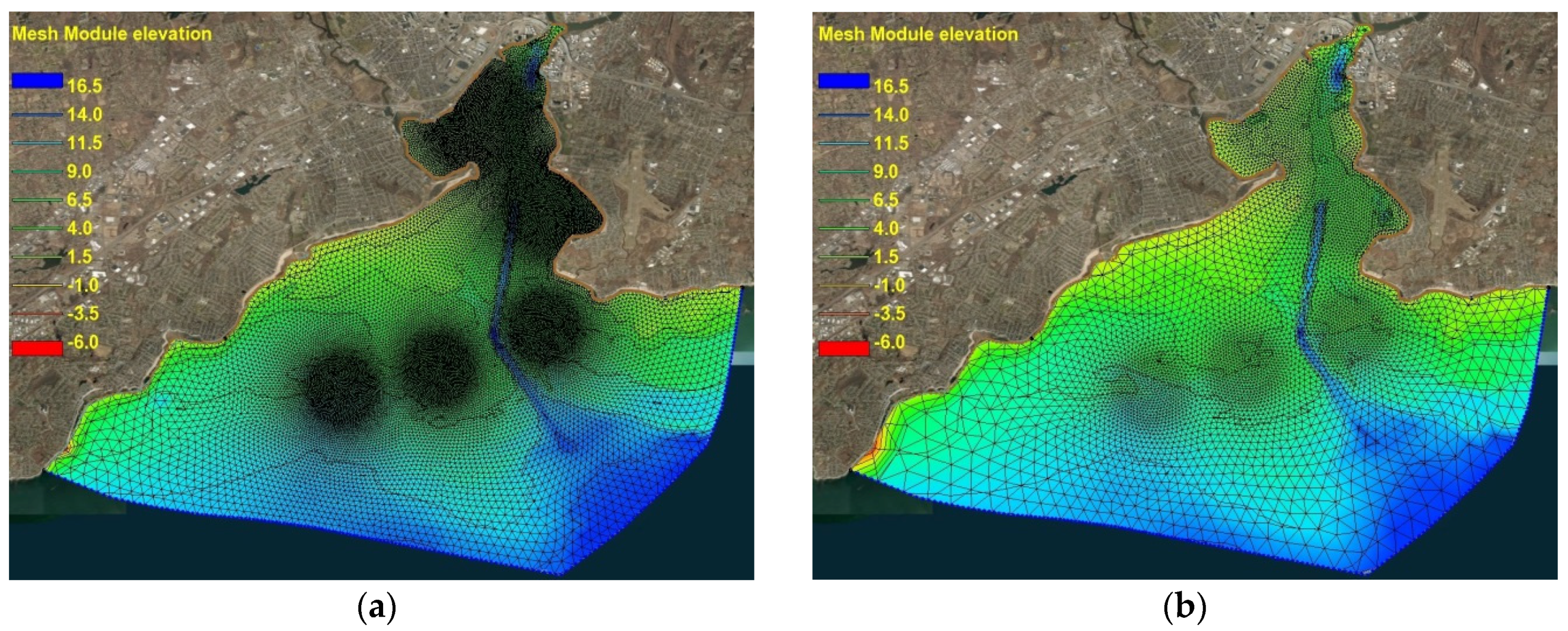
We also examined the effect of the grid generation choices. Using a grid converter, available in the MIKE21 package, and the grid generation software in the surface-water modeling system package (SMS v12) we created grids for the models using the same spatial smoothing ratio.
Figure 2c,d shows the sensitivity of SWAN solutions for different grid sizes and time steps. As the grid size is decreased, the time step also must be decreased by the same factor to avoid accumulation of numerical computation errors. For the majority of storms, the grid size
and
was adequate (
Figure 2c), but some storms required finer grid, (
Figure 2d). Refining the grid size and time step by the factor of
increases the computational time at least by the factor of
; therefore, it is vital that the optimum grid size be selected very carefully. The grid size
and
with time step
was found to provide the optimum condition for SWAN.
Figure 2e,f illustrates the sensitivity of the MIKE21SW solutions to grid size. Since MIKE21SW selects the optimum time step based on the grid size automatically, it is easier and faster to get to optimum condition by MIKE21SW. MIKE21SW also showed less sensitivity to grid size than SWAN, (
Figure 2e,f). The result was converged for grid size with
and
. The optimum unstructured triangular grid for each model is presented in
Figure 3. The grids were smoothly refined around the breakwaters and inside the harbor.
The models were calibrated using data from the period of 23 to 28 January. For each model, we tested settings and coefficients, and applied the set that achieved the best agreement with the observations. Both models were executed in third generation fully spectral and non-stationary mode. The same spectral discretization (25 frequencies and 16 directional discretizations) were applied to SWAN and MIKE21SW with a minimum frequency of 0.06 Hz and a maximum of 0.59 Hz.
The results of MIKE21SW were tested for both first and second order numerical scheme, and no significant difference was observed between the first order and second order schemes. Consequently, in order to save computational time, MIKE21SW was run on first order. As mentioned in
Section 2, the only available numerical scheme in unstructured SWAN is first order BSBT.
Options for representing the wind input source and whitecapping dissipation functions are different in the models. SWAN is configured to use the wind input source function of Janssen [
15,
16], as implemented in WAM cycle 4 [
17]; the method of Komen [
18], as implemented in WAM cycle 3 [
19]; and method of Yan [
20]. MIKE21SW only supports Janssen’s method. Dissipation through whitecapping is based on the development of Hasselmann [
21] in both Janssen’s and Komen’s methods, however, the coefficients are different (see Komen [
12,
18]). Yan’s wind input method is combined with saturation-based whitecapping as described in Van der Westhuysen [
22,
23]. Moeini and Etemad-Shahidi [
6] suggested that Komen’s method led to more accurate significant wave height than Janssen’s method for Lake Erie. Hoque [
8] indicated Westhuysen’s formulation tends to have better significant wave height in the Mackenzie Delta. We tested all three methods with SWAN. We found that Janssen’s method provides the best wave height simulations in the harbor. Therefore, Janssen’s wind input method was used for both models with the tunable coefficients set as
and
.
Wave dissipation due to bottom friction was represented in both models by the empirical JONSWAP [
24] approach. The friction coefficients introduced by Zijlema et al. [
25] were used:
for SWAN and
for MIKE21SW.
Waves breaking in shallow water was taken into account in the models using the Battjes and Janssen [
26] formulation with
and
. Also, triad wave–wave interactions were enabled in both models. Triad interactions in MIKE21SW are calculated based on Eldeberky and Battjes [
27] and in SWAN based on Eldeberky [
28], a slightly modified version of the former. Quadruplet wave–wave interactions were also enabled in the models. In both models, the quadruplet wave–wave interactions are computed with the Discrete Interaction Approximation (DIA) as proposed by Hasselmann et al. [
29].
When breakwaters are present in the model domain, diffraction computations become important. Diffraction is taken into account in the models using a phase-decoupled refraction-diffraction approximation proposed by Holthuijsen et al. [
1]. Diffraction computation in the models is almost the same, but a wave field smoothing technique for the computation of the diffraction parameter that is not available in SWAN with an unstructured grid.
The reflection coefficients for breakwaters were calculated using the method proposed in the Coastal Protection Manual: Part VI, [
30], and originally developed by Seeling [
31], for non-overtopped slopping structures with the parameter values of Davidson [
32]. The reflection coefficient for the type of structure and wave climate in the study area varied from 0.47 to 0.52. Therefore, the average reflection coefficient of 0.493 was selected.
Spectral wave models adequately simulate the effects of diffraction when breakwaters are far from the coastline and have a low reflection coefficient [
1]. In addition, the breakwaters should not cover the down-wave view substantially, [
1]. In New Haven harbor, the distance between the breakwaters and coastline varies 4 to 5.2 km, and the separation of the breakwaters is 700 m to 1000 m, which much larger than the threshold distance [
2] of twice the dominant wavelength (here 2
L ≅ 100 m, where
L is wave length). Also, the rubble mound breakwaters with low reflection coefficient, 0.493, create incoherent wave reflection.
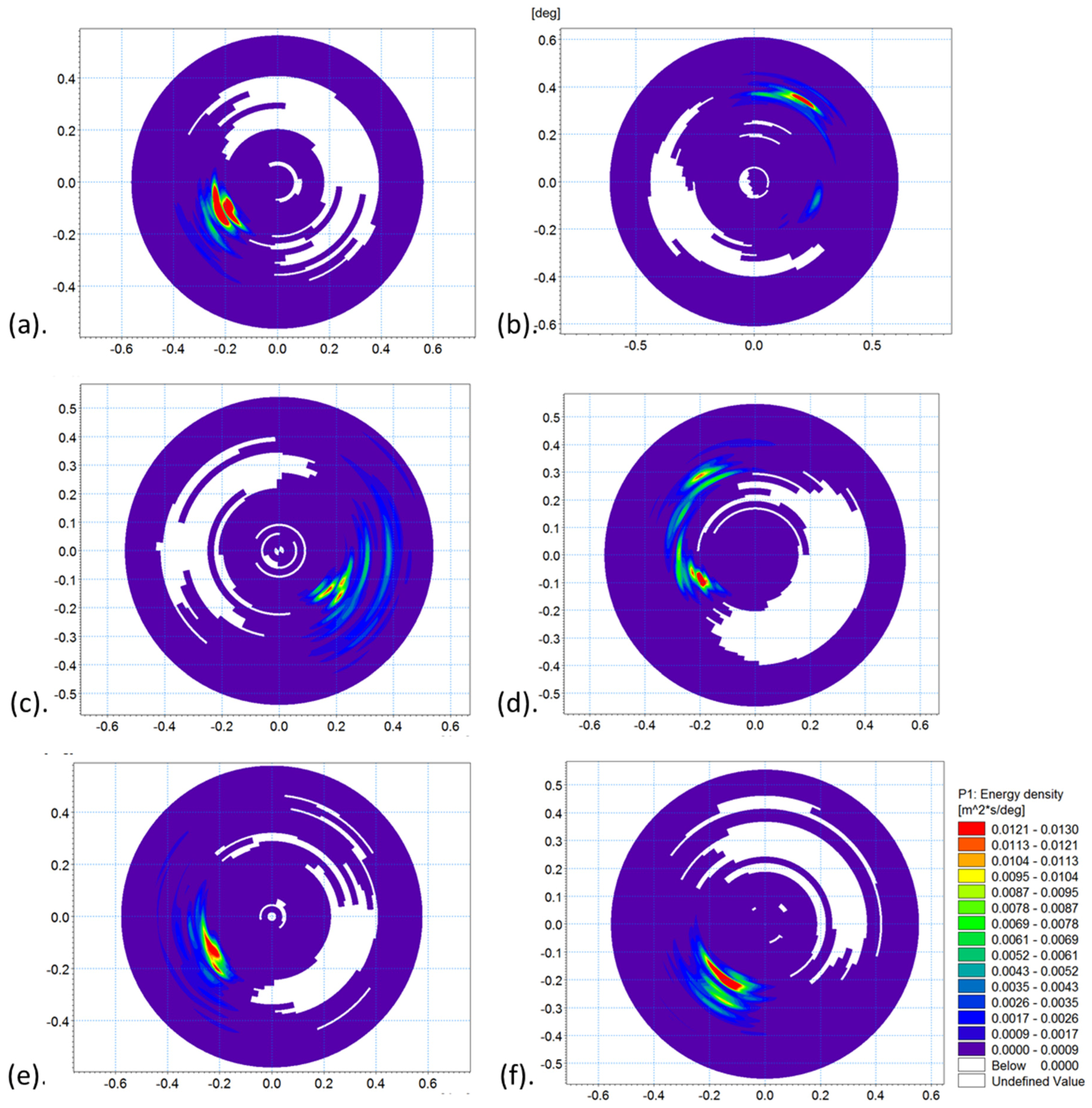
The spectral wave models such as SWAN simulate wave diffraction better for the wider directional spectrum of wind-waves than for swell [
2]. The wave spectra for the important storms are shown in
Figure 4. The wave spectra in the harbor are directionally broad, similar to those obtained in Long Island Sound. Therefore, New Haven harbor is considered a suitable case for simulating waves using the spectral models.
4. Results
The results of SWAN and MIKE21SW models were compared and assessed inside the harbor at NH2 during all storms and at NH1 for northerly storms. We divided the observations into five storm periods, detailed in
Table 2. Each of these periods is discussed separately, and then the results are summarized. The statistical parameters used for data validation are
where
, with mean
, are the observed values,
are the simulated values, and
is the number of data points.
is the root mean square error,
is the fraction of the variance in the data explained by the model,
is the estimated value by regression, and
is the mean of the observed values.
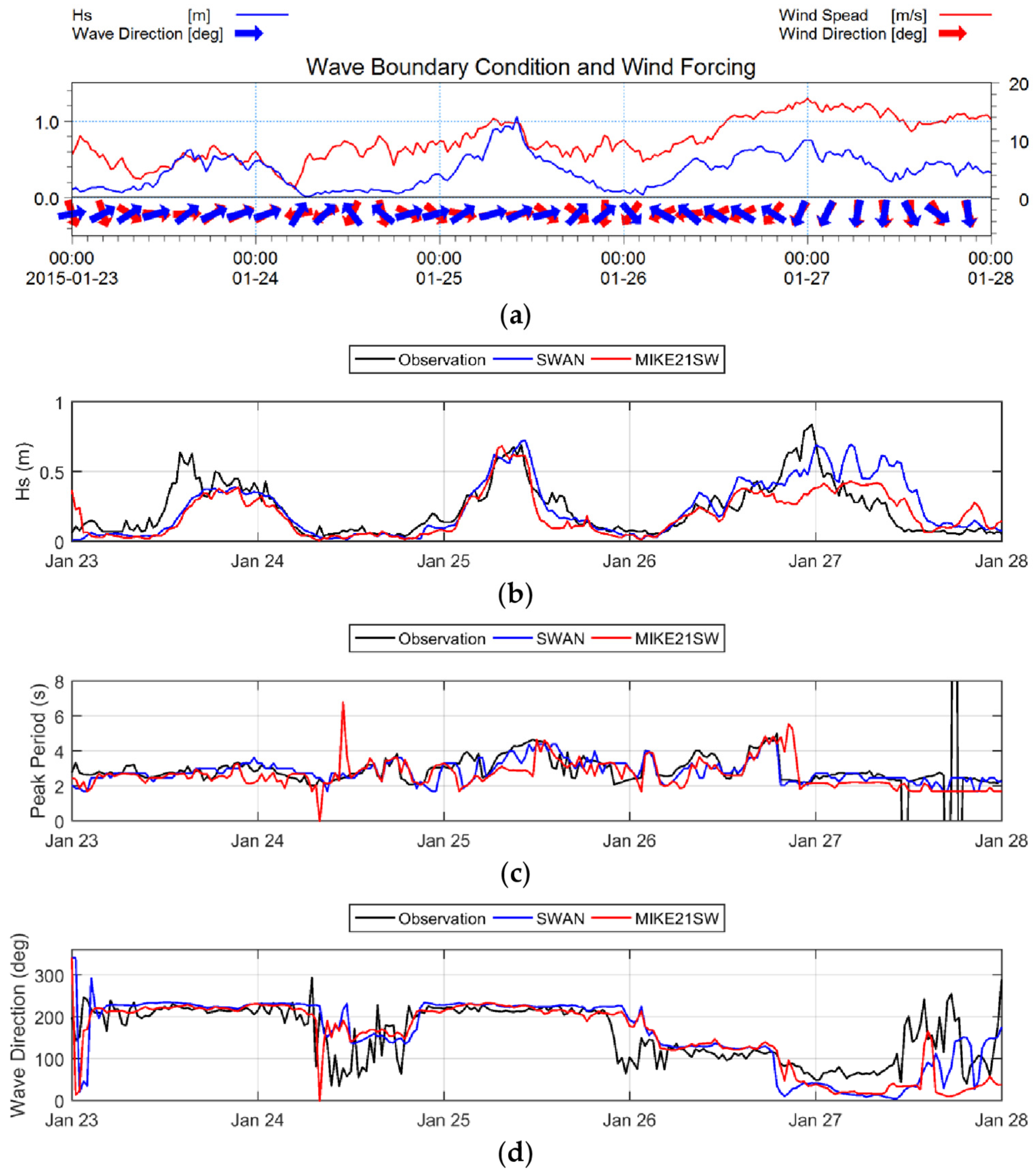
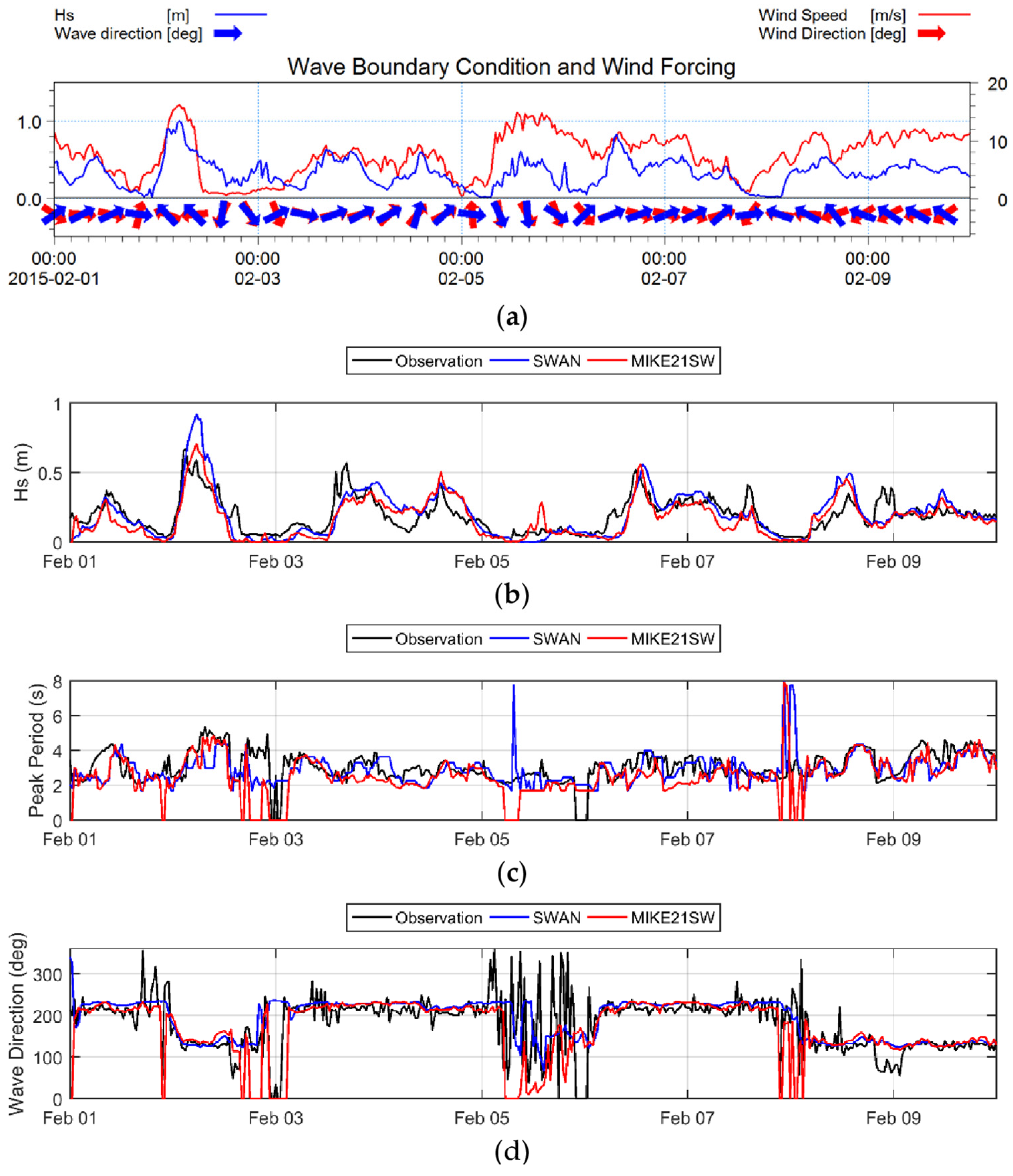
Three consecutive high wind intervals occurred during the first storm period, 23 to 28 January. Wave boundary condition and wind input data, as well as comparisons between observations and the model predictions of the significant wave height, peak wave period and wave direction for Storm Period 1 are presented in
Figure 5. The noise in observed wave periods and directions in low significant wave heights events were not included in the assessments. In this storm period, the first two storms had winds from the west and southwest. In the first storm, the predicted significant wave height (
) series were very similar to each other. Both missed the first part of the storm peak and under-predicted the second part by
(
Figure 5b). Both models were able to simulate wave period and direction correctly (
Figure 5c,d). In the second storm, both models reproduced the storm’s entire wave height peak very well. Simulated wave period and direction for the second storm also agreed well with the observations. For the third storm, the models did not perform well. On 26 January, the storm caused easterly winds, then on 27 January, wind stress vectors suddenly turned by 90 degrees and a very strong wind (in excess of 15 m/s) blew from the north. This strong wind was adequate to generate wave in a very fetch limited area as New Haven estuary. The models showed different behavior during this storm. Simulated peak wave periods were in consistent with observations. Modeled wave directions for the first part of the storm completely agreed with observation, but after the wind vector rotated on 26 January 10 p.m., there was a 25 to 40 degrees difference between observed and simulated wave direction. The observation showed a wave direction from northeast (50 degrees), while simulated wave directions were from north. The statistical parameters show that SWAN results were slightly better than MIKE21SW for this period, (
Table 3). The
in significant wave heights obtained from SWAN was 0.03 m less than that in MIKE21SW.
for SWAN was 0.60 versus 0.57 for MIKE21SW. The
values were the same (0.13) and the slope of best fitted line was better for MIKE21SW (0.89) than SWAN (0.72).
Comparison of the results of the models and observations from Storm Period 2, 1 to 10 February, are shown in
Figure 6. Both models showed similar behavior during this period though SWAN overestimated the strongest storm significant wave height on 2 February by
(
Figure 6b). There was a high wind event from the north on 5 and 6 February (
Figure 6a), and the models simulated the significant wave height very well (
Figure 6b). In other storms, the models had very similar behavior, both missed some small oscillations and overestimated others. The models correctly simulated the peak wave period and mean wave direction, (
Figure 6c,d). Statistical parameters for this period did not present any substantial preference of the models,
and
were better for SWAN and
and
were better for MIKE21SW (
Table 3).
Three storms occurred in the third period, from 14 to 21 February. As shown in
Figure 7, the models accurately simulated the first storm. The second storm started with a wind from north to south and it then rotated to the east. MIKE21SW accurately simulated significant wave height in the first part of the storm but later produced overestimates. In contrast, SWAN overestimated significant wave height over the whole storm duration. Both models provide poor estimates of the wave period for the second part of the storm. For the third storm, both models successfully simulated the wave height, period, and direction, however, MIKE21SW slightly under-predicted the first part. Overall,
error was 0.03 lower, the slope of the best-fitted line was 0.11 higher, and
was 0.01 higher for MIKE21SW. The magnitude of
values were the same (0.02) but with opposite signs, (
Table 3). Therefore, MIKE21SW results were slightly more accurate than SWAN for this time period, mostly due to better simulation of the second storm.
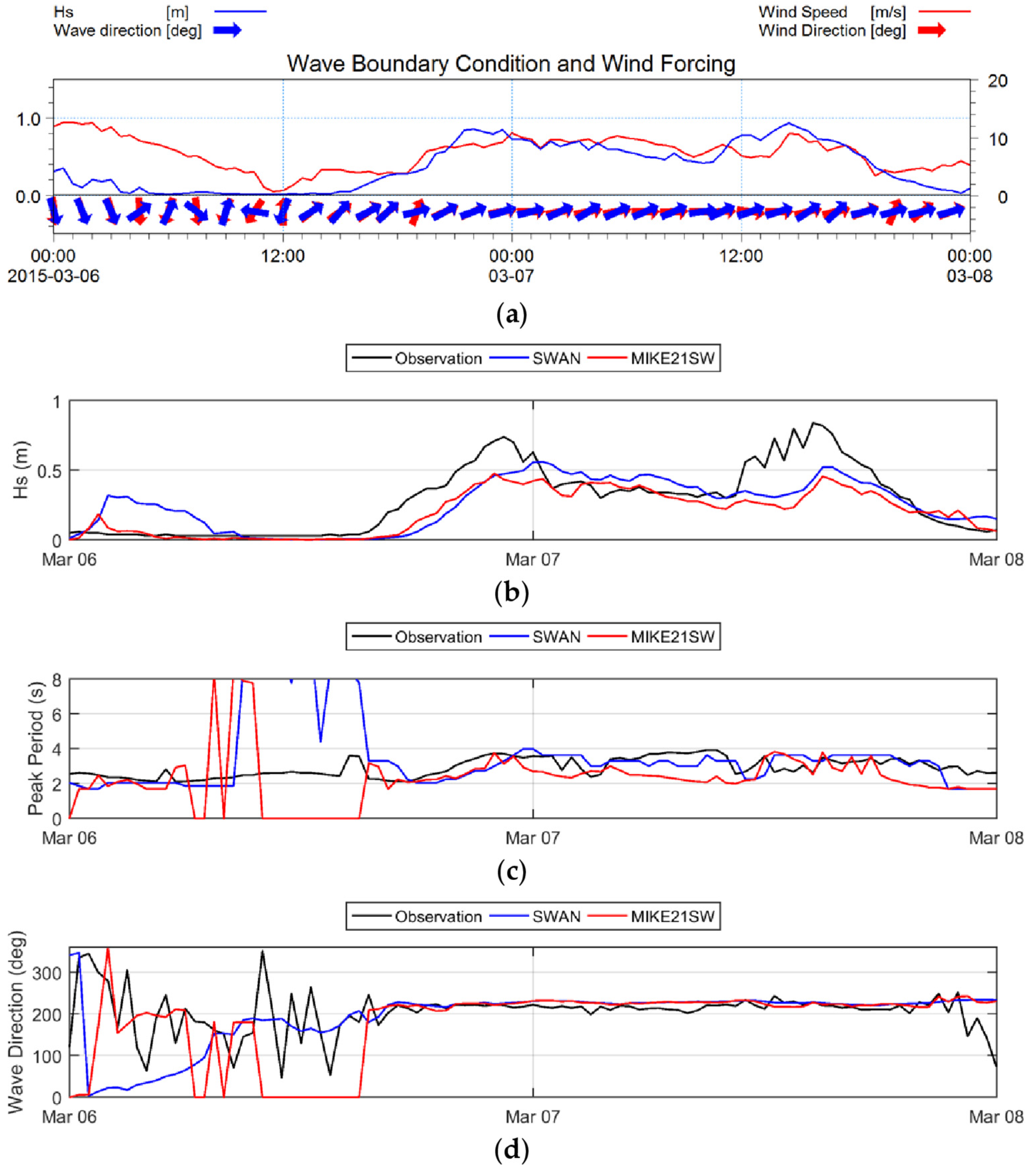
In the fourth storm period, both models failed to correctly simulate significant wave height variations between 6 and 8 March, as shown in
Figure 8. The storm includes two peaks in significant wave height, but the models underestimated both (
Figure 8b). However, they correctly estimated wave periods and directions (
Figure 8c) and the statistical parameters show similar model performance. There was two hours delay in storm growth in both models. The storm started at 3 March 03:00 p.m., according to observations, but 05:00 p.m. in the models. Also, there was no difference between wind speed at 03:00 and 05:00 p.m. (both around 5 m/s,
Figure 8a). Some statistical parameters, such as
, were better for MIKE21SW and others, such as
, for SWAN (
Table 3).
Results from Storm Period 5 are illustrated in
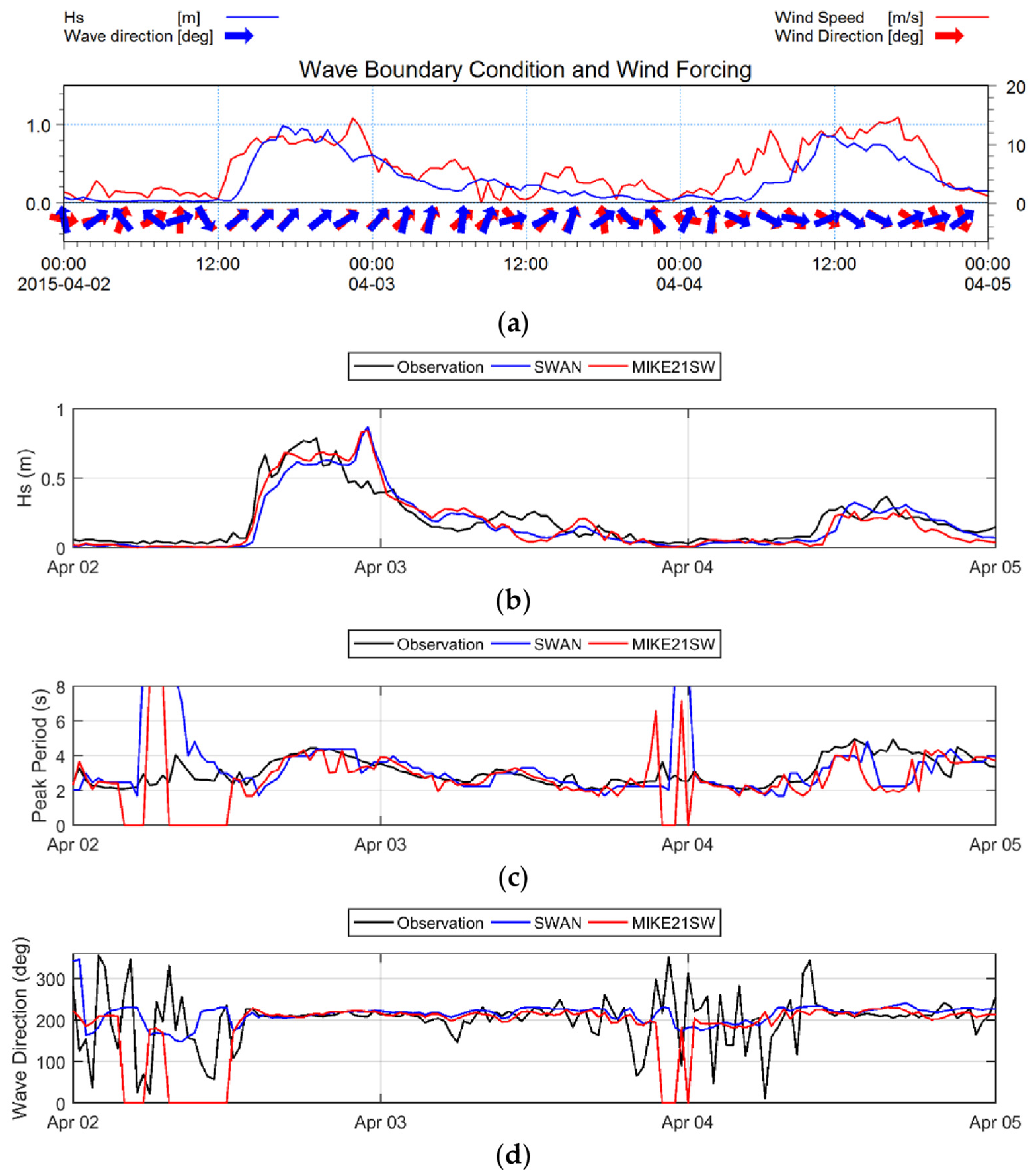
Figure 9, showing the assessment of the models results during the storm took place on 2 and 3 April. MIKE21SW was able to catch the storms highest wave height and correctly computed wave period and direction during the storm. SWAN slightly underestimated the first part of the storm and there was a short delay in storm growth (
Figure 9b). Statistical parameters were slightly better for MIKE21SW with
R2 = 0.81 versus SWAN results with
R2 = 0.77.
was better for MIKE21SW and the slope of best-fitted line was better for SWAN (
Table 3).
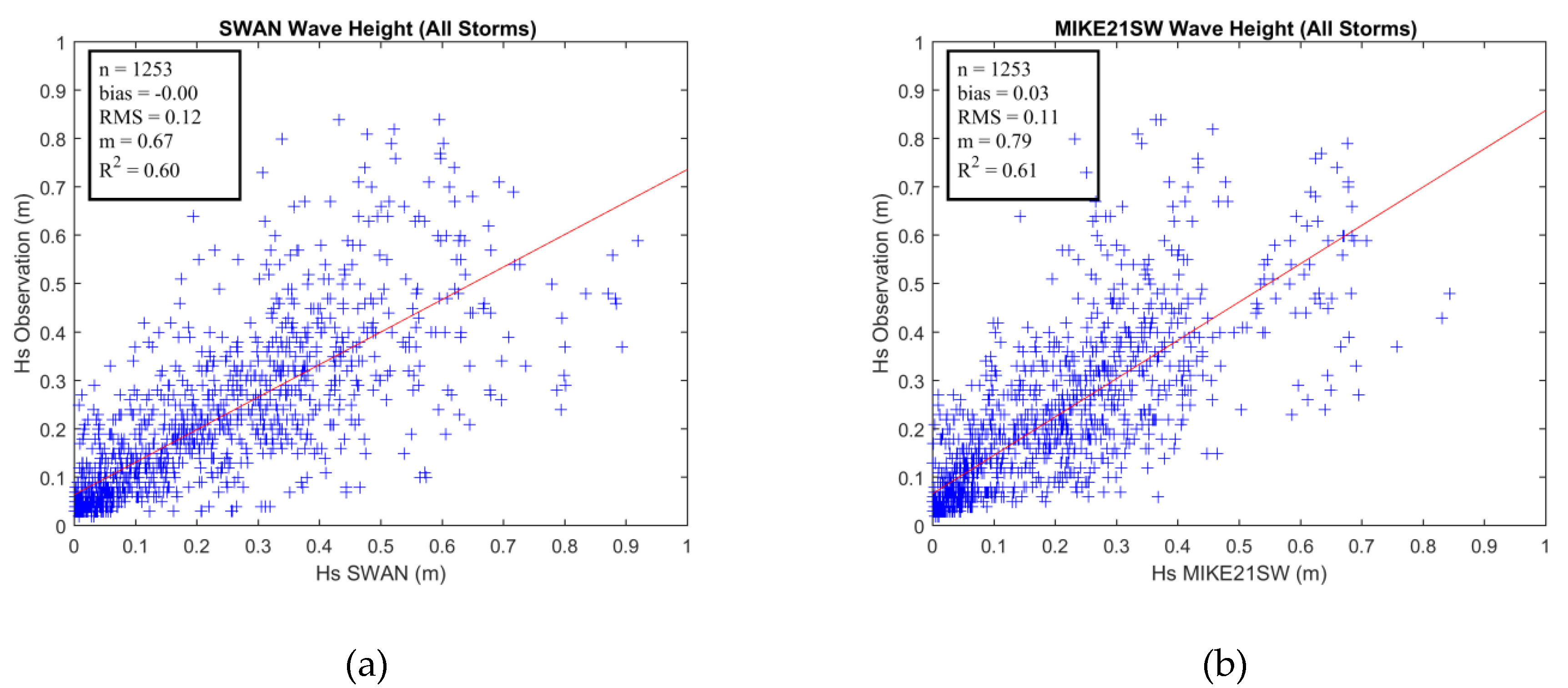
We compare all storm simulations to data in
Figure 10.
was better for SWAN.
of MIKE21SW was 0.01 lower than
obtained from SWAN results. The slope of best-fitted line for MIKE21SW was closer to one.
of the models’ results were almost the same, 0.61 for MIKE21SW versus 0.60 for SWAN. Therefore, the statistical parameters suggest the performance of both models were good and the models’ results had a lot of similarity.
The model predictions did not agree with observation at NH2, inside the harbor, for two northerly storms, 27 January and 15 February. To assess whether the errors were due to the wind speed magnitude being too high, we compared the results of the models to data obtained at NH1, at the boundary of the model domain, (
Figure 11). Note that since wave energy was propagating out of the domain during northerly wind the boundary observations were not influencing in the predictions. Both model results were biased high relative the observation at NH1 with the SWAN results having a larger bias (
Figure 11a). However, both models were more correlated with observations at NH1 than at NH2. Both models did a better job for the second northerly event on 15 February. SWAN showed lower errors early in the simulation but both models overestimated the significant wave height later in the storm just as they did in the interior of the Harbor at NH2. This may be a consequence of overestimation of the wind stress, however, the reduced correlation in the model and data time series cannot be explained by the magnitude bias alone.
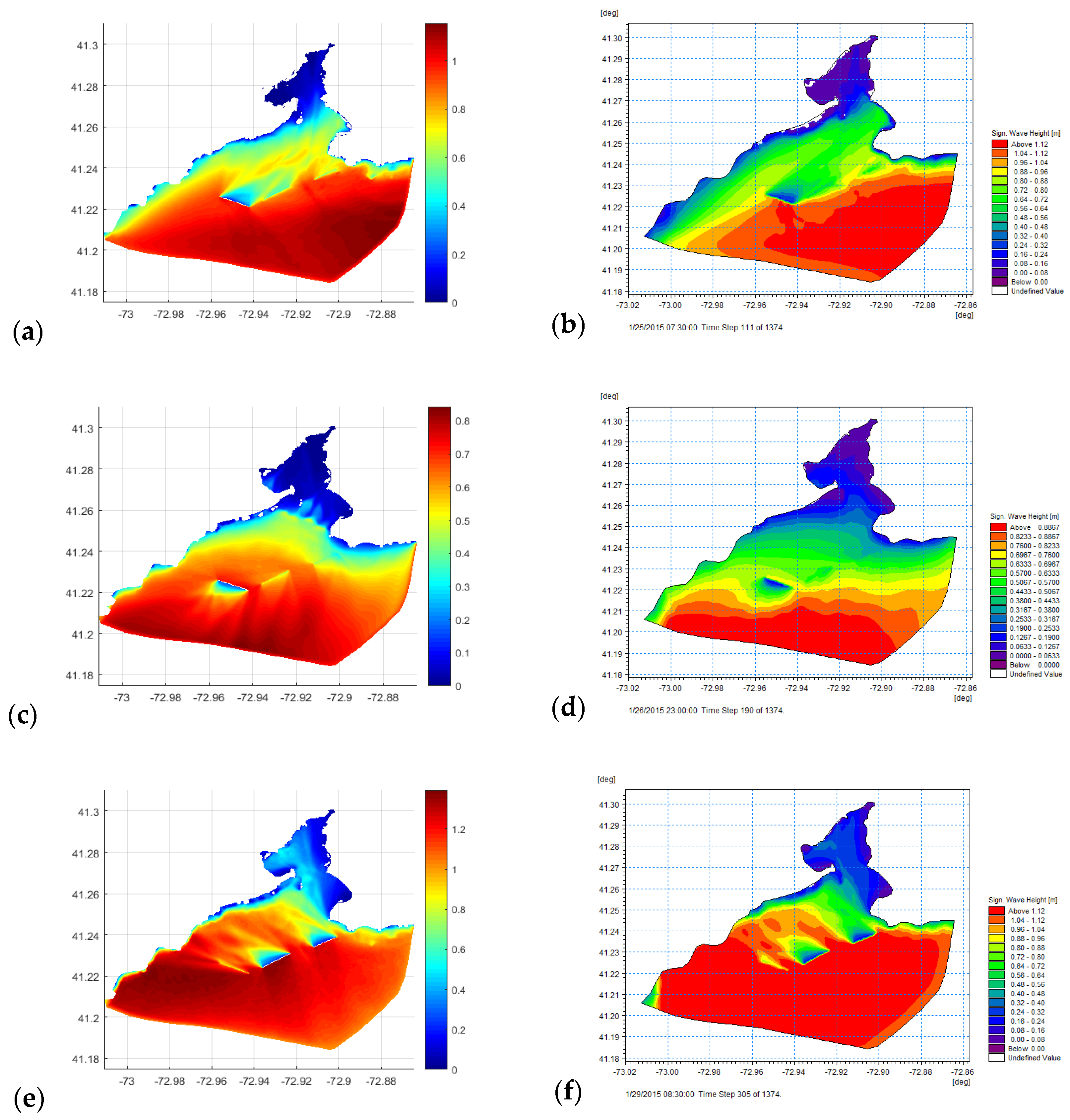
Figure 12 displays the variation of significant wave height over the model domain for three storms on 25 January (wind from the southwest), 27 January (wind from the north), and 2 February (wind from the southeast). Unfortunately, as the output format of the models were different, we were not able to plot them with the same tools, therefore, the color bars scales are slightly different. The models had similar behavior over the domain on the southern storms (
Figure 12a,b), but different on the northern storm (
Figure 12c,d). Also, it can be implied that MIKE21SW dissipates wave energy around the breakwaters more than SWAN, it may be the reason or the SWAN overestimation on 2 February.
5. Discussion
In total, 14 storms occurred in New Haven harbor during the observation period in the winter of 2015 and the models simulated similar wave fields in most of them. Both models had very good statistical performance when storm winds blew from the south, when the breakwaters are most influential. SWAN predicted the peak significant wave height for one storm (on 18 February) better than MIKE21SW, while MIKE21SW simulated three storms (on 2 February, 15 February, and 3 April) better than SWAN. The worst performance during southerly wind storms was the SWAN results for 2 February when the model overestimated the peak significant wave height by 50%.
Figure 12e suggest that the wave sensor was close to a region of high spatial gradient in the significant wave height during this storm and, therefore, slight differences in diffraction and propagation led to large differences in model solution values. The worst performance of MIKE21SW was on 18 February when the peak significant wave height was underestimated by 25%. In other storms the models had similar behavior. Notably, both models underestimated the storm peak on 7 March by 60%.
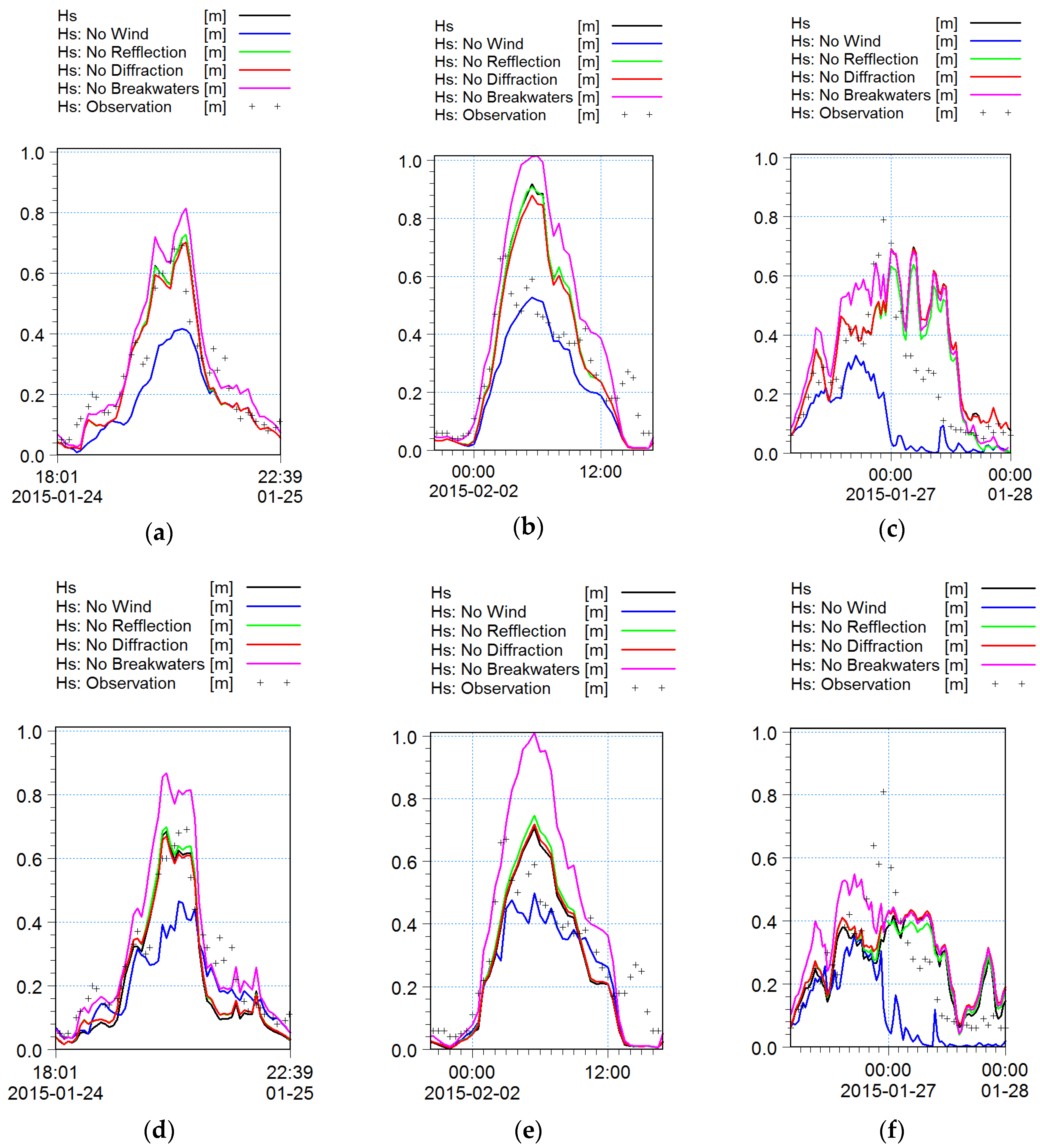
To further understand the sensitivity of the models results to different physical processes we ran the simulations with the wind forcing eliminated; zero reflection from the breakwaters; with diffraction disabled; and with the breakwaters entirely removed.
Figure 13 shows the results of these simulations at NH2.
Figure 13a,d show the observations (+symbols) and solutions at NH2 for the 25 January storm with SWAN and MIKE21SW when the wind blew from the south. The agreement between the black lines and the +symbols shows that both models performed well. The differences between the black and blue lines shows that the influence of the wind over the harbor is significant and increases the peak significant wave height during the storm by 50%. Comparison of the black line to the magenta, green, and red lines show that the next most important process is the presence of the breakwaters. Eliminating them increases the peak significant wave height by approximately 15% in SWAN and 30% in MIKE21SW.
Figure 13b,e shows the same properties for the 2 February storm period when the wind was from the south east. Since the performance of both models were not as good, due to high spatial gradients near the location of the wave sensor, the comparison of the result with (black line) and without local wind forcing (blue line) shows again that the local wind can increase the peak significant wave height by approximately 50%. Similarly, removing the breakwaters increases the peak wave heights as in
Figure 13a,d, by comparable amounts. We note that the presence of breakwaters appears to be more significant in MIKE21SW than SWAN. The spatial distributions of wave height in
Figure 12 also indicate this difference in model performance.
Comparison of the green and red lines with the black lines in
Figure 13a,b,d,e illustrates that the effects of diffraction and reflection influenced the significant wave height at NH2 by less than 5 percent in both models. NH2 is approximately 2 km (or 40
L, where
L is the dominant wave length) away from the breakwaters. This is consistent with [
2] which concluded that reflection and diffraction effects are insignificant far away the breakwaters.
Figure 13c,f show the data and solutions for the 27 January storm when the wind was from the north. As expected, comparison of the black and blue lines shows that in the absence of wind forcing the significant wave height drops to zero. The other effects do not play a large role in the model predictions though reflection, also, has a maximum effect of 7%. These results highlight the importance of wind in this case study, which is a large harbor with fetch length varies from 5 km to 7 km.
In some events, such as 6 April and 6 March, a delay in the growth of the waves was observed in the models results, however, the delay in SWAN results was about one hour more than MIKE21SW results. There were three events (27 January, 5 February, and 15 February) with high winds from the north and the models did not deliver good simulations in two, 27 January and 15 February. These events were accompanied with 90-degree rotation of wind vectors during the storm. This inconsistency may be a consequence of the uncertainty in the difference between the wind observed at the buoy and that over the harbor. The wind observation station is located about 20 km away from the coastline. When wind blow from the coast (from the north), the wind boundary layer near the coastline become very complex. This complicity may not be observed at the wind station located 20 km away from the coastline. In addition, the significant wave height evaluation outside the harbor for northerly storms,
Figure 11, demonstrates that the models overestimate the significant wave height when winds were from the north. It implies that, for northern storms, winds at CLIS are more intensive than New Haven. Also, New Haven estuary has a complex geometry. Consequently, a small change in wind direction can change the fetch length drastically. For example, for NH2 station, a wind blowing from 10 degrees has more than double fetch length of the wind from the north, (
Figure 1). The inconsistency of the models with observation for a very small fetch length with strong wind condition needs more investigation. This requires a local high frequency wind and wave observation to record precisely oscillation in wind speed and direction.
Another possible source of error is that a spectral wave model cannot simulate wave resonance due to reflected waves from the harbor edges and breakwaters.
Figure 4b,d show spectra for 27 January and 15 February, when the models failed to accurately simulate the wave field, there were two waves, a low frequency wave from the south and high frequency waves propagating from the north. In this situation, reflection could have significant role. To observe these effects more accurately, multiple high frequency wave observation stations in the harbor would be required. The wave spectra shown in
Figure 4 are not confined to a narrow range of directions and, in some events such as 2 February, the spectrum has multiple peaks. For this storm SWAN overestimated the wave height by 50%. Both models under-predicted significant wave heights during the storm on 7 March. In this event, the wave spectrum, also, have two peaks (
Figure 4e). The models had good performance for the two-peak storm on 25 January, however, this storm had two peaks from the same direction but different frequency. The models may have lower accuracy in the events that the wave spectrum have multiple peaks at different directions, but that is not always the case as MIKE21SW well predicted the storm on 2 February with multiple spectrum peaks. Further investigation is required.
The influence of currents on waves was not considered in this study. Current can be considered in the modeling using a coupled hydrodynamic-wave models such as FVCOM-SWAVE, ADCIRC-SWAN, XBEACH [
33,
34], and MIKE21 Coupled Model. This effect should be considered in modeling in forthcoming studies. Another uncertainty in the results can be due to uncertainty in the model wave boundary condition. Though we used the observed wave spectra, instead of a model or parametrization, to prescribe the open boundary condition, it is possible that there are periods when there is variation in wave conditions along the boundary. Multiple wave sensor would be needed to assess that possibility and we hope to evaluate it in the future.
Besides the accuracy of the model, the efficiency and simplicity of the models are important in assessment of the model utility. SWAN is much more efficient computationally than MIKE21SW. SWAN executes the same model grid and configuration using the same computational engine much faster than MIKE21SW. Although SWAN is equipped with a fast-computational algorithm, the total computational time of the models in the optimum conditions was almost the same. SWAN requires much finer mesh to reach the optimum condition. In this study, the grid size of the mesh used for SWAN ( and ) was half of the grid size of the mesh used for MIKE21SW ( and ). Getting to the optimum condition with MIKE21SW was faster than SWAN. MIKE21SW automatically selects the optimum time step based on the grid size. User just needs to assign the minimum and maximum time steps. In addition, MIKE21SW showed less sensitivity to grid size than SWAN. Therefore, finding the optimum condition in MIKE21SW needs fewer number of sensitivity simulations than SWAN.
The time integration and spatial discretization method employed in SWAN and MIKE21SW play the main role in determining the differences in the results and efficiency. MIKE21SW uses an explicit Euler scheme for time integration with cell-centered finite volume when computing wave propagation while SWAN uses a fully implicit method for time integration with finite difference first order BSBT scheme. This study suggests that the method used in SWAN is computationally much faster but it is more sensitive to spatial resolution and requires much finer mesh.
The application of the spectral models for simulation of waves inside the harbor in the presence breakwater is questioned by some authors [
1,
2,
35]. This implies that the spectral models are not suitable for small ports with narrow connections to the ocean. However, in situations in which breakwaters have low reflection coefficients, are far enough the shoreline and do not shade a significant portion of the basin [
1] spectral models may be useful as we have demonstrated in this work. In situ observations and sensitivity analyses are extremely valuable in assessing model effectiveness at all sites.