Towards Age Determination of Southern King Crab (Lithodes santolla) Off Southern Chile Using Flexible Mixture Modeling
Abstract
1. Introduction
2. Methods
2.1. Finite Mixtures of Flexible Distributions
- (a)
- when in (3), , we obtain the skew-t distribution (ST) [24] denoted by and with the pdf given bywhere , and denote the pdf and cumulative density function (cdf) of the standard t distribution with degrees of freedom, respectively. ST distribution was introduced to achieve a higher degree of excess kurtosis produced by extreme observations. ST distribution converges to SN distribution as and is the t distribution when ;
- (b)
- The stochastic representation (2) of SMSN allows to determine the exact density of conditional distributions necessary for the ECME algorithm. That is, using Lemma 2 of Basso et al. [23], variable Y in (2) is represented conveniently by a hierarchical representation and, in this form, makes it possible to obtain the conditional maximization (CM) steps.
2.2. Growth Modeling
2.3. Implementation
- Modal decomposition. The FMST model was carried out for southern king crab LFD with degrees of freedom and m components by zone, year, and sex. For example, degrees of freedom indicate a high presence of heavy-tails in LFD [15,16]. The order of m depends on the reported BIC for each combination, where the ’best’ model for each m is selected through the smallest BIC.
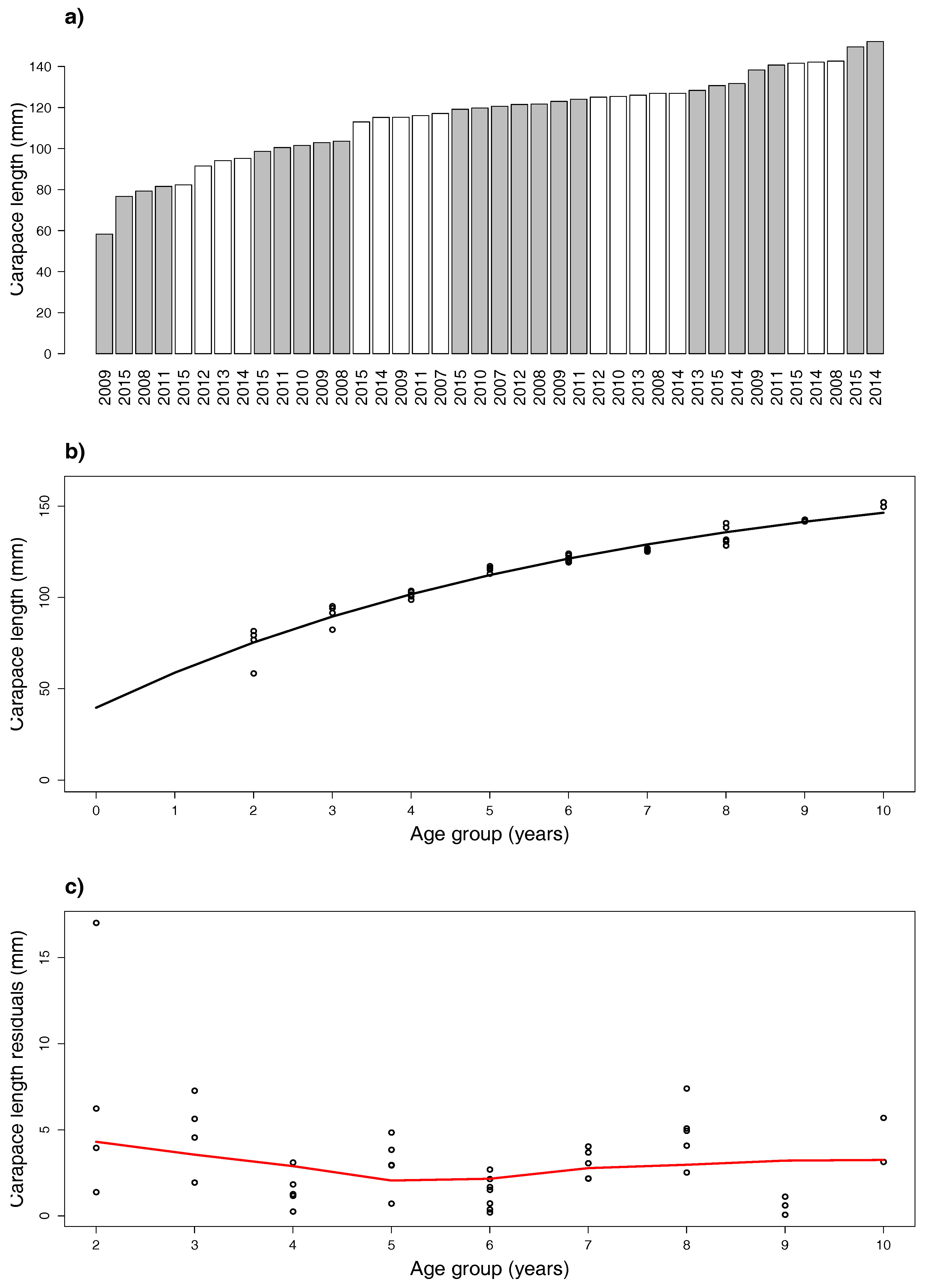
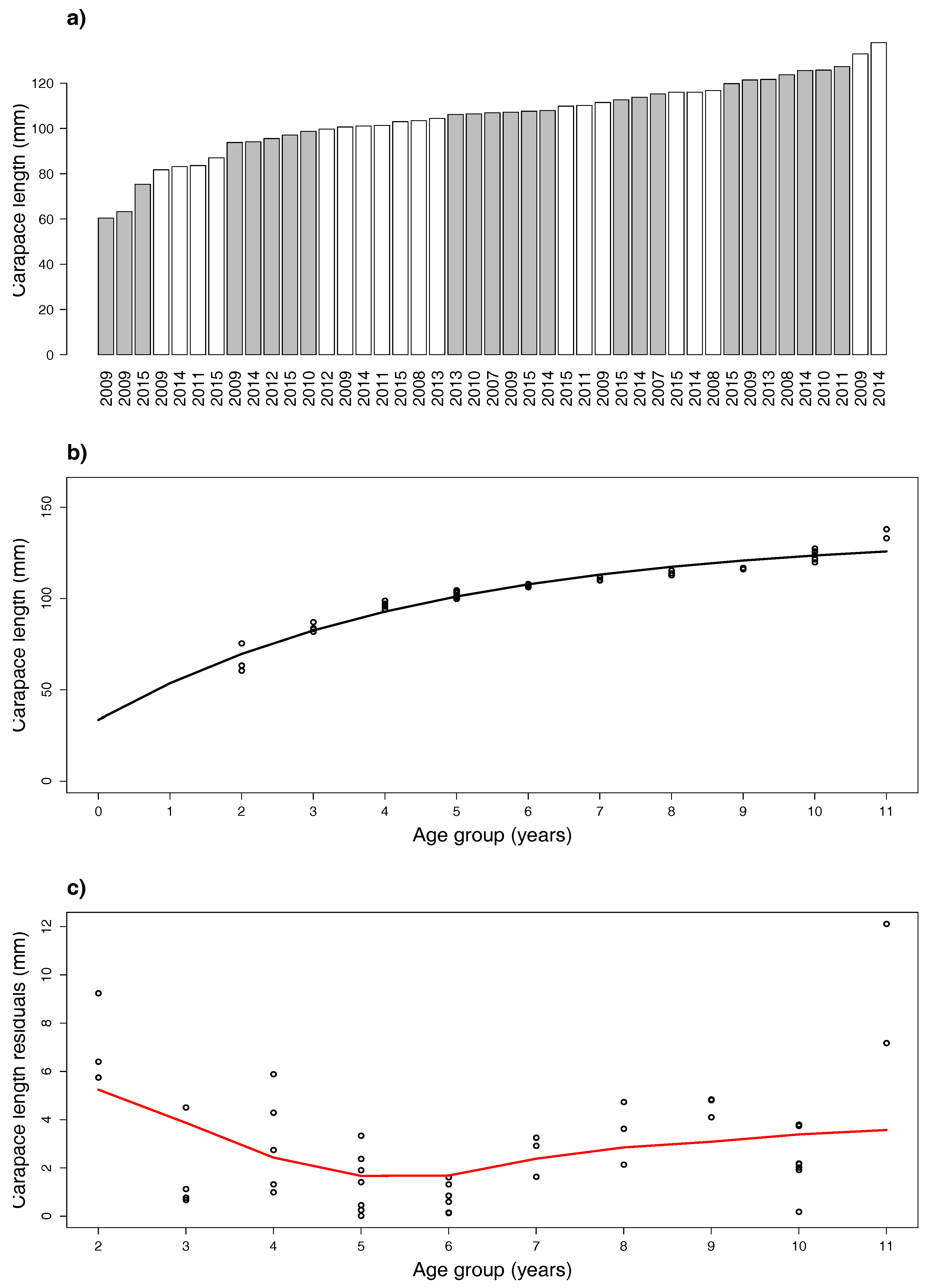
- Age-class assignment. From Step 1, take into account that m modes provide m modes used for age-class determination, which is at least m. Considering the classified carapace lengths, a bar chart of means is built where gray and white colors alternate and represent classified age classes. The cluster means are ordered and grouped into cohorts, so that no year is repeated within each group. “Premise II” of Reference [11] is considered as a criterion to determine the cohort point between age classes; textually, this is: strong assumption that each year no more than one cohort (means that it is not possible that two mean carapace lengths with the same year index fall into the same age class) and no less than one cohort (means that it is not possible that two consecutive mean carapace lengths with the same year index fall into two nonconsecutive age classes) enters the population. Given that age classes 0 and 1 include individuals with molt frequency decreasing with age (six to seven molts in the first and four to five in the second year), we opted to label the first group with Year ’2’ and then estimate the vBGF parameters.
- vBGF model. Given the estimated year in Step 2, the formed age-length data serve to evaluate the vBGF (5) growth function.
3. Computational Implementation
3.1. Data
3.2. Computational Aspects
4. Results
4.1. Males
4.2. Females
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AIC | Akaike’s information criterion |
| BIC | Bayesian information criterion |
| CM | Conditional maximization |
| ECME | Expectation/conditional maximization either |
| FMN | Finite mixture of normal |
| FMST | Finite mixture of skew-t |
| FM-SMSN | Finite mixture of scale mixtures of skew-normal |
| LFD | Length-frequency data |
| LQ | Lower quantile |
| SMSN | Scale mixtures of skew-normal |
| SE | Standard error |
| SN | Skew-normal |
| ST | Skew-t |
| UQ | Upper quantile |
| vBGF | von Bertalanffy growth function |
References
- Geaghan, J. Resultados de las Investigaciones Sobre Centolla Lithodes Antarctica Jaquinot; Publicaciones IFOP 52; Instituto de Fomento Pesquero: Provincia de Magallanes, Chile, 1973; 70p. [Google Scholar]
- Yáñez, A.; Ibarra, M. Estatus y Posibilidades de Explotación Biológicamente Sustentables de los Principales Recursos Pesqueros Nacionales 2018. Jaiba y Centolla; Informe 3 Consolidado, Convenio de Desempeño; Instituto de Fomento Pesquero: Valparaíso, Chile, 2018. [Google Scholar]
- Yáñez, A.; Ibarra, M.; Canales, C. Estatus y Posibilidades de Explotación Biológicamente Sustentables de los Principales Recursos Pesqueros Nacionales 2016. Centolla y Jaiba XIV-XII; Informe de Estatus, Convenio de Desempeño; Instituto de Fomento Pesquero: Valparaíso, Chile, 2015. [Google Scholar]
- Vinuesa, J.H.; Lovrich, G.A.; Comoglio, L.I. Maduración sexual y crecimiento de las hembras de centolla Lithodes santolla (Molina, 1782) en el Canal Beagle. Biota 1991, 7, 7–13. [Google Scholar]
- Von Bertalanffy, L. A quantitative theory of organic growth (Inquiries on growth laws. II). Hum. Biol. 1938, 10, 181–213. [Google Scholar]
- Parraga, D.; Wiff, R.; Quiroz, J.C.; Zilleruelo, M.; Bernal, C.; Azocar, J. Characterization of fishing tactics in the demersal crustacean multispecies fishery off Chile. Lat. Am. J. Aquat. Res. 2012, 40, 30–41. [Google Scholar] [CrossRef]
- Roa, R.; Tapia, F. Spatial differences in growth and sexual maturity between branches of a large population of the squat lobster Pleuroncodes monodon. Mar. Ecol. Progr. Ser. 1998, 167, 185–196. [Google Scholar] [CrossRef]
- Macdonald, P.D.M.; Pitcher, T.J. Age groups from size-frequency data: A versatile and efficient method of analyzing distribution mixtures. J. Fish. Res. Board Can. 1979, 36, 987–1001. [Google Scholar] [CrossRef]
- Richards, F.J. A Flexible Growth Function for Empirical Use. J. Exp. Bot. 1959, 10, 290–301. [Google Scholar] [CrossRef]
- Arkhipkin, A.I.; Roa-Ureta, R. Identification of ontogenetic growth models for squid. Mar. Fresh. Res. 2005, 56, 371–386. [Google Scholar] [CrossRef]
- Roa-Ureta, R.H. A likelihood-based model of fish growth with multiple length frequency data. J. Agric. Biol. Environ. Stat. 2010, 15, 416–429. [Google Scholar] [CrossRef]
- Fournier, D.A.; Sibert, J.R.; Majkowski, J.; Hampton, J. MULTIFAN a likelihood-based method for estimating growth parameters and age composition from multiple length frequency data sets illustrated using data for bluefin tuna (Thunus maccoyii). Can. J. Fish. Aquat. Sci. 1990, 47, 301–317. [Google Scholar] [CrossRef]
- Laslett, G.M.; Eveson, J.P.; Polacheck, T. Fitting growth models to length frequency data. ICES J. Mar. Sci. 2004, 61, 218–230. [Google Scholar] [CrossRef]
- Canales, C.; Arana, P.M. Growth, mortality, and stock assessment of the golden crab (Chaceon chilensis) population exploited in the Juan Fernández archipelago, Chile. Lat. Am. J. Aquat. Res. 2009, 37, 313–326. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E.; Arellano-Valle, R.B.; Canales, T.M. Comparing growth curves with asymmetric heavy-tailed errors: Application to the southern blue whiting (Micromesistius australis). Fish. Res. 2014, 159, 88–94. [Google Scholar] [CrossRef]
- López Quintero, F.O.; Contreras-Reyes, J.E.; Wiff, R. Incorporating uncertainty into a length-based natural mortality estimator in fish populations. Fish. Bull. 2017, 115, 355–364. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E.; López Quintero, F.O.; Wiff, R. Bayesian modeling of individual growth variability using back-calculation: Application to pink cusk-eel (Genypterus blacodes) off Chile. Ecol. Model. 2018, 385, 145–153. [Google Scholar] [CrossRef]
- Ouellet, P.; Chabot, D.; Calosi, P.; Orr, D.; Galbraith, P.S. Regional variations in early life stages response to a temperature gradient in the northern shrimp Pandalus borealis and vulnerability of the populations to ocean warming. J. Exp. Mar. Biol. Ecol. 2017, 497, 50–60. [Google Scholar] [CrossRef]
- Azzalini, A. A Class of Distributions which includes the Normal Ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Frühwirth-Schnatter, S.; Pyne, S. Bayesian inference for finite mixtures of univariate and multivariate skew-normal and skew-t distributions. Biostatistics 2010, 11, 317–336. [Google Scholar] [CrossRef] [PubMed]
- Cosgrove, R.; Sheridan, M.; Minto, C.; Officer, R. Application of finite mixture models to catch rate standardization better represents data distribution and fleet behavior. Fish. Res. 2014, 153, 83–88. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E.; Cortés, D.D. Bounds on Rényi and Shannon Entropies for Finite Mixtures of Multivariate Skew-normal Distributions: Application to Swordfish (Xiphias gladius Linnaeus). Entropy 2016, 18, 382. [Google Scholar] [CrossRef]
- Basso, R.M.; Lachos, V.H.; Cabral, C.R.B.; Ghosh, P. Robust Mixture Modeling Based on Scale Mixtures of Skew-normal Distributions. Comput. Stat. Data Anal. 2010, 54, 2926–2941. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t-distribution. J. R. Stat. Soc. Ser. B 2003, 65, 367–389. [Google Scholar] [CrossRef]
- Shertzer, K.W.; Fieberg, J.; Potts, J.C.; Burton, M.L. Identifying growth morphs from mixtures of size-at-age data. Fish. Res. 2017, 185, 83–89. [Google Scholar] [CrossRef]
- Kimura, D.K. Testing nonlinear regression parameters under heteroscedastic, normally distributed errors. Biometrics 1990, 46, 697–708. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017; ISBN 3-900051-07-0. Available online: http://www.R-project.org (accessed on 12 December 2018).
- Prates, M.O.; Lachos, V.H.; Cabral, C. mixsmsn: Fitting finite mixture of scale mixture of skew-normal distributions. J. Stat. Soft. 2013, 54, 1–20. [Google Scholar] [CrossRef]
- López-Serrano, A.; Villalobos, H.; Nevárez-Martínez, M.O. A probabilistic procedure for estimating an optimal echo-integration threshold using the Expectation-Maximisation algorithm. Aquat. Liv. Res. 2018, 31, 12. [Google Scholar] [CrossRef]
- Ogle, D.H. Introductory Fisheries Analyses with R; CRC Press: Boca Raton, FL, USA, 2016; Volume 32. [Google Scholar]
- Ohnishi, S.; Yamakawa, T.; Okamura, H.; Akamine, T. A note on the von Bertalanffy growth function concerning the allocation of surplus energy to reproduction. Fish. Bull. 2012, 110, 223–229. [Google Scholar]
- Kilada, R.; Acuña, E. Direct Age Determination by Growth Band Counts of Three Commercially Important Crustacean Species in Chile. Fish. Res. 2015, 170, 134–143. [Google Scholar] [CrossRef]
- Froese, R.; Binohlan, C. Simple methods to obtain preliminary growth estimates for fishes. J. Appl. Ichthyol. 2003, 19, 376–379. [Google Scholar] [CrossRef]
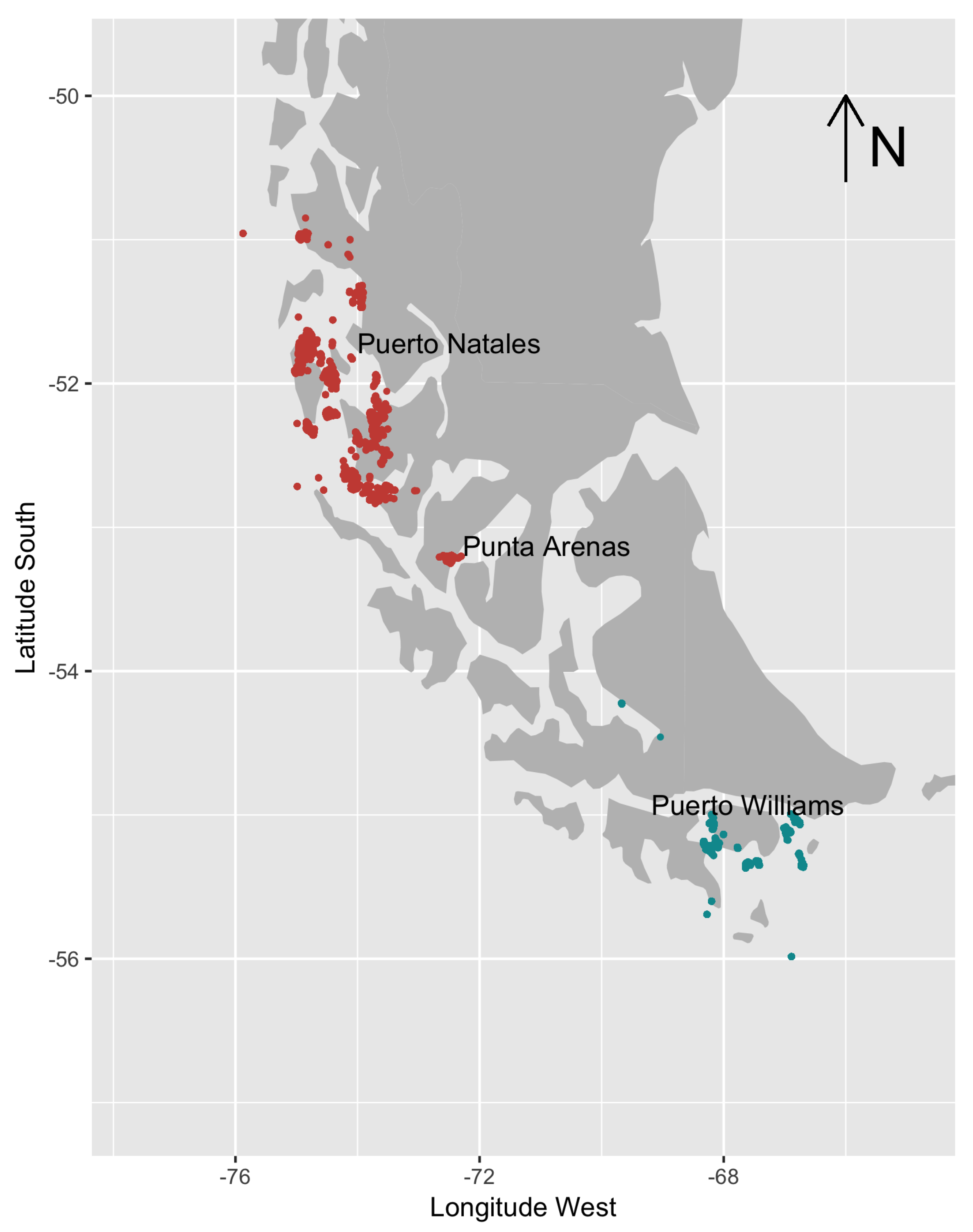
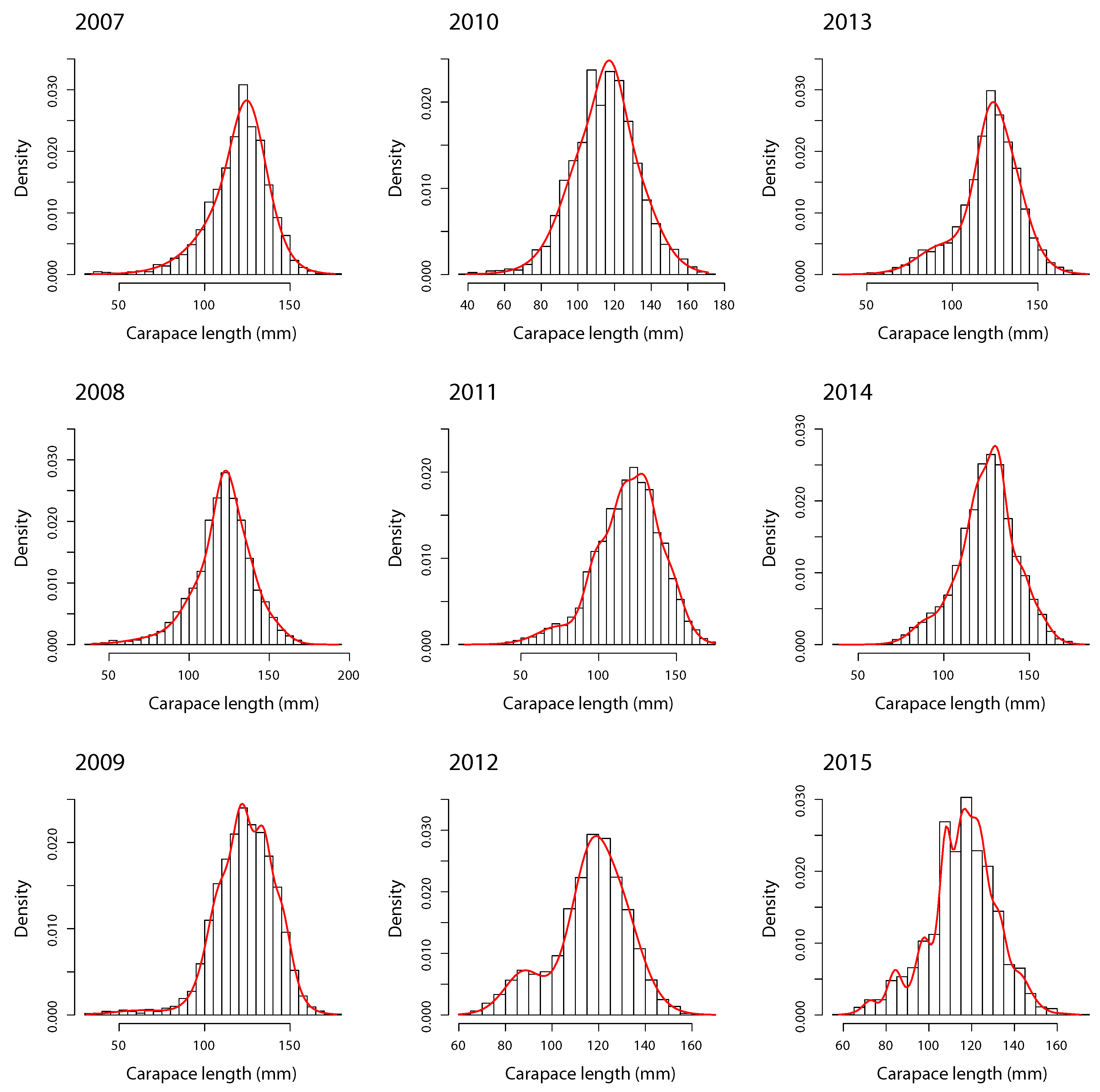
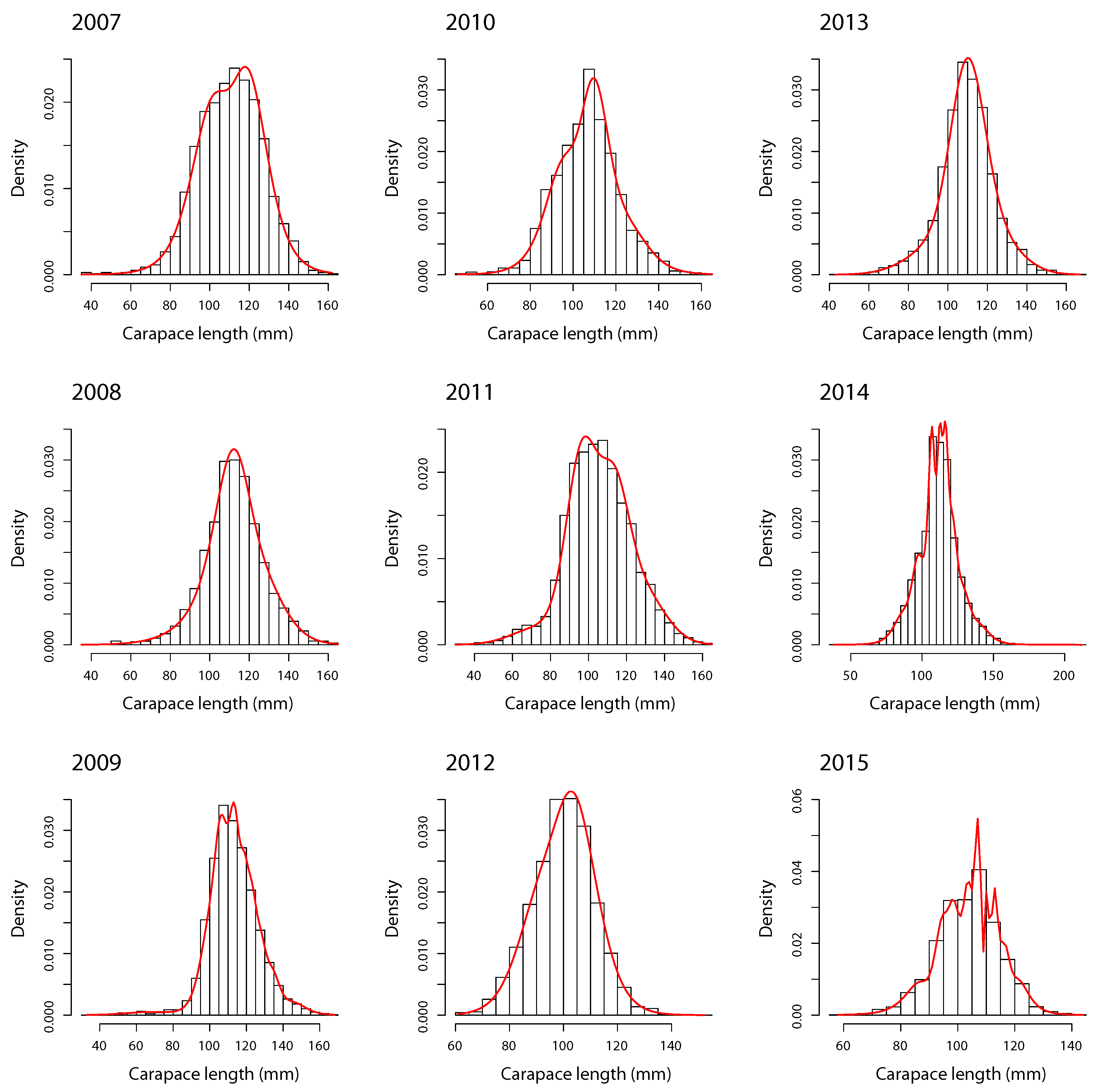
| Sex | Year | Min. | LQ | Median | Mean | UQ | Max. | SD | n |
|---|---|---|---|---|---|---|---|---|---|
| Males | 2007 | 34 | 111 | 122 | 120.1 | 132 | 176 | 17.86 | 1734 |
| 2008 | 39 | 112 | 122 | 121.340 | 132 | 193 | 18.567 | 4983 | |
| 2009 | 31 | 113 | 125 | 123.604 | 136 | 177 | 18.158 | 5759 | |
| 2010 | 39 | 104 | 116 | 115.230 | 127 | 171 | 18.261 | 3424 | |
| 2011 | 14 | 106 | 121 | 118.791 | 134 | 175 | 21.725 | 6282 | |
| 2012 | 60 | 108 | 119 | 116.589 | 128 | 170 | 16.636 | 5453 | |
| 2013 | 34 | 113 | 124 | 121.719 | 134 | 179 | 18.437 | 4256 | |
| 2014 | 39 | 115 | 126 | 125.210 | 136 | 182 | 17.499 | 80,612 | |
| 2015 | 58 | 107 | 116 | 115.510 | 126 | 171 | 16.132 | 13,683 | |
| Females | 2007 | 35 | 100 | 112 | 110.730 | 122 | 162 | 16.426 | 1586 |
| 2008 | 35 | 104 | 113 | 112.751 | 122 | 165 | 15.365 | 5883 | |
| 2009 | 33 | 105 | 113 | 113.319 | 121 | 168 | 14.105 | 7717 | |
| 2010 | 46 | 98 | 108 | 107.192 | 116 | 165 | 15.137 | 3273 | |
| 2011 | 30 | 94 | 105 | 105.844 | 117 | 165 | 17.602 | 7366 | |
| 2012 | 61 | 93 | 101 | 100.306 | 108 | 152 | 11.554 | 5530 | |
| 2013 | 43 | 102 | 110 | 109.949 | 118 | 167 | 14.113 | 3508 | |
| 2014 | 38 | 104 | 112 | 111.552 | 120 | 212 | 14.364 | 59,090 | |
| 2015 | 58 | 97 | 104 | 103.903 | 112 | 144 | 11.156 | 22,852 |
| Number of Modes (m) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sex | Model | Year | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Males | FMN | 2007 | 21,660.32 | 25,110.58 | 28,584.18 | 32,027.82 | 35,511.00 | 38,942.26 | 42,404.44 | 45,867.89 |
| 2008 | 62,812.42 | 72,732.02 | 82,687.67 | 92,642.98 | 102,607.25 | 112,582.18 | 122,534.11 | 132,498.96 | ||
| 2009 | 72,131.15 | 83,620.96 | 95,128.46 | 106,629.39 | 118,143.52 | 129,656.02 | 141,144.20 | 152,665.18 | ||
| 2010 | 43,261.16 | 50,089.41 | 56,927.93 | 63,774.23 | 70,585.84 | 77,434.39 | 84,261.89 | 91,108.33 | ||
| 2011 | 81,316.49 | 93,847.13 | 106,403.04 | 118,966.49 | 131,524.34 | 144,081.13 | 156,638.06 | 169,188.31 | ||
| 2012 | 67,406.53 | 78,299.57 | 89,191.86 | 100,106.07 | 111,008.67 | 121,889.19 | 132,817.15 | 143,720.88 | ||
| 2013 | 53,475.91 | 61,958.09 | 70,463.77 | 78,974.94 | 87,477.20 | 95,984.53 | 104,494.43 | 113,008.14 | ||
| 2014 | 1,010,474.45 | 1,171,030.24 | 1,331,999.31 | 1,493,074.55 | 1,654,157.23 | 1,815,515.11 | 1,976,135.29 | 2,137,650.73 | ||
| 2015 | 169,223.51 | 196,429.18 | 223,791.31 | 251,162.38 | 278,521.06 | 305,856.42 | 332,855.51 | 360,116.56 | ||
| FMST | 2007 | 13,364.51 | 13,371.75 | 13,375.64 | 14,843.43 | 14,878.02 | 14,892.64 | 14,910.46 | 14,932.68 | |
| 2008 | 48,624.99 | 48,585.88 | 48,595.47 | 42,986.84 | 43,009.54 | 43,059.00 | 43,061.88 | 43,096.80 | ||
| 2009 | 62,001.87 | 61,869.83 | 61,871.81 | 49,233.68 | 49,267.38 | 49,274.14 | 49,321.24 | 49,333.27 | ||
| 2010 | 27,032.18 | 27,020.63 | 27,026.80 | 29,699.00 | 29,729.53 | 29,749.19 | 29,785.83 | 29,779.53 | ||
| 2011 | 63,056.19 | 63,046.12 | 62,964.81 | 56,325.63 | 56,358.11 | 56,391.05 | 56,417.41 | 56,439.62 | ||
| 2012 | 42,731.45 | 42,730.32 | 42,738.57 | 45,750.64 | 45,783.98 | 45,817.96 | 45,845.73 | 45,874.98 | ||
| 2013 | 28,366.28 | 28,334.04 | 28,340.50 | 36,570.12 | 36,607.13 | 36,640.77 | 36,676.77 | 36,698.06 | ||
| 2014 | 687,830.5 | 687,524.6 | 687,307.9 | 687,305.38 | 687,289.56 | 687,347.91 | 687,457.90 | 687,328.14 | ||
| 2015 | 114,496.6 | 114,461.6 | 114,494.8 | 114,453.80 | 114,554.55 | 114,353.79 | 114,252.30 | 11,4437.46 | ||
| Females | FMN | 2007 | 19,713.96 | 22,852.88 | 26,023.90 | 29,192.11 | 32,359.81 | 35,532.03 | 38,696.17 | 41,875.65 |
| 2008 | 72,139.24 | 83,843.33 | 95,605.08 | 107,358.69 | 119,124.74 | 130,859.57 | 142,656.47 | 154,376.82 | ||
| 2009 | 92,895.77 | 108,137.59 | 123,550.34 | 138,974.63 | 154,408.95 | 169,848.59 | 185,267.58 | 200,701.04 | ||
| 2010 | 40,113.74 | 46,619.98 | 53,153.97 | 59,699.58 | 66,235.46 | 72,768.60 | 79,308.71 | 85,864.49 | ||
| 2011 | 92,517.32 | 107,138.55 | 121,826.14 | 136,551.47 | 151,272.19 | 166,021.39 | 180,718.50 | 195,463.84 | ||
| 2012 | 64,868.23 | 75,887.82 | 86,941.12 | 97,998.73 | 109,057.37 | 120,093.74 | 131,144.66 | 142,200.95 | ||
| 2013 | 42,350.73 | 49,353.13 | 56,369.57 | 63,378.44 | 70,397.06 | 77,409.93 | 844,25.82 | 91,438.30 | ||
| 2014 | 716,320.29 | 834,395.94 | 951,934.44 | 1,070,071.78 | 1,188,213.60 | 1,306,378.32 | 1,424,541.82 | 1,542,624.05 | ||
| 2015 | 266,204.82 | 311,746.05 | 357,317.35 | 403,020.59 | 448,584.81 | 494,297.28 | 539,896.96 | 585,635.92 | ||
| FMST | 2007 | 13,402.09 | 13,430.81 | 13,456.18 | 13,478.17 | 13,504.66 | 13,532.48 | 13,553.48 | 13,570.40 | |
| 2008 | 48,671.75 | 48,659.36 | 48,695.67 | 48,725.50 | 48,763.35 | 48,781.16 | 48,803.79 | 48,834.31 | ||
| 2009 | 62,050.53 | 61,946.29 | 61,976.07 | 62,004.46 | 62,041.64 | 62,066.87 | 62,104.48 | 61,535.19 | ||
| 2010 | 27,074.84 | 27,087.65 | 27,118.21 | 27,143.20 | 27,167.77 | 27,189.12 | 27,213.60 | 27,237.89 | ||
| 2011 | 63,104.52 | 63,122.07 | 63,068.38 | 63,074.54 | 63,102.86 | 63,149.36 | 63,181.02 | 63,210.95 | ||
| 2012 | 42,777.77 | 42,803.12 | 42,837.84 | 42,876.89 | 42,906.37 | 42,925.71 | 42,971.24 | 42,985.32 | ||
| 2013 | 28,409.42 | 28,401.83 | 28,432.94 | 28,465.27 | 28,492.60 | 28,527.44 | 28,556.07 | 28,583.88 | ||
| 2014 | 480,353.4 | 480,016.9 | 480,040.3 | 479,967.99 | 479,778.60 | 479,668.53 | 479,583.39 | 479,593.39 | ||
| 2015 | 174,927.2 | 174,939.8 | 174,752.3 | 174,863.17 | 174,746.23 | 174,709.63 | 174,691.60 | 174,687.12 | ||
| Sex | Year | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Males | 2007 | 117.098 | 120.580 | - | - | - | - | - | - | - |
| 2008 | 79.255 | 103.574 | 121.668 | 126.899 | 142.613 | - | - | - | - | |
| 2009 | 58.301 | 102.911 | 115.216 | 122.973 | 138.269 | - | - | - | - | |
| 2010 | 101.505 | 119.793 | 125.396 | - | - | - | - | - | - | |
| 2011 | 81.542 | 100.494 | 116.096 | 123.987 | 140.691 | - | - | - | - | |
| 2012 | 91.457 | 121.495 | 125.046 | - | - | - | - | - | - | |
| 2013 | 94.073 | 126.019 | 128.364 | - | - | - | - | - | - | |
| 2014 | 95.159 | 115.189 | 126.915 | 131.681 | 142.104 | 152.129 | - | - | - | |
| 2015 | 76.686 | 82.263 | 98.657 | 112.971 | 119.165 | 130.680 | 141.562 | 149.571 | - | |
| Females | 2007 | 106.905 | 115.245 | - | - | - | - | - | - | - |
| 2008 | 103.470 | 116.723 | 123.758 | - | - | - | - | - | - | |
| 2009 | 60.367 | 63.205 | 81.713 | 93.794 | 100.643 | 107.161 | 111.463 | 121.416 | 132.965 | |
| 2010 | 98.687 | 106.437 | 125.761 | - | - | - | - | - | - | |
| 2011 | 83.598 | 101.347 | 110.181 | 127.319 | - | - | - | - | - | |
| 2012 | 95.546 | 99.692 | - | - | - | - | - | - | - | |
| 2013 | 104.431 | 106.143 | 121.669 | - | - | - | - | - | - | |
| 2014 | 83.145 | 94.126 | 101.085 | 107.903 | 113.760 | 116.014 | 125.594 | 137.902 | - | |
| 2015 | 75.346 | 86.977 | 97.093 | 103.001 | 107.625 | 109.844 | 112.652 | 115.984 | 119.786 |
| Sex | Parameter | Estimate | SE | t | Pr() | K | ||
|---|---|---|---|---|---|---|---|---|
| Males | 176.756 | 12.865 | 13.739 | <0.001 | 1.000 | - | - | |
| K | 0.151 | 0.032 | 4.773 | <0.001 | −0.985 | 1.000 | - | |
| −1.678 | 0.519 | −3.231 | 0.002 | −0.897 | 0.956 | 1.000 | ||
| Females | 134.799 | 4.065 | 33.162 | <0.001 | 1.000 | - | - | |
| K | 0.220 | 0.031 | 7.029 | <0.001 | −0.950 | 1.000 | - | |
| −1.302 | 0.442 | −2.946 | 0.005 | −0.830 | 0.952 | 1.000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Contreras-Reyes, J.E.; López Quintero, F.O.; Yáñez, A.A. Towards Age Determination of Southern King Crab (Lithodes santolla) Off Southern Chile Using Flexible Mixture Modeling. J. Mar. Sci. Eng. 2018, 6, 157. https://doi.org/10.3390/jmse6040157
Contreras-Reyes JE, López Quintero FO, Yáñez AA. Towards Age Determination of Southern King Crab (Lithodes santolla) Off Southern Chile Using Flexible Mixture Modeling. Journal of Marine Science and Engineering. 2018; 6(4):157. https://doi.org/10.3390/jmse6040157
Chicago/Turabian StyleContreras-Reyes, Javier E., Freddy O. López Quintero, and Alejandro A. Yáñez. 2018. "Towards Age Determination of Southern King Crab (Lithodes santolla) Off Southern Chile Using Flexible Mixture Modeling" Journal of Marine Science and Engineering 6, no. 4: 157. https://doi.org/10.3390/jmse6040157
APA StyleContreras-Reyes, J. E., López Quintero, F. O., & Yáñez, A. A. (2018). Towards Age Determination of Southern King Crab (Lithodes santolla) Off Southern Chile Using Flexible Mixture Modeling. Journal of Marine Science and Engineering, 6(4), 157. https://doi.org/10.3390/jmse6040157






